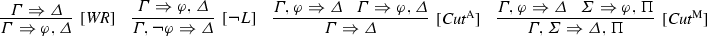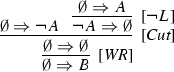Abstract
Paraconsistent logics are logical systems that reject the classical principle, usually dubbed Explosion, that a contradiction implies everything. However, the received view about paraconsistency focuses only the inferential version of Explosion, which is concerned with formulae, thereby overlooking other possible accounts. In this paper, we propose to focus, additionally, on a meta-inferential version of Explosion, i.e. which is concerned with inferences or sequents. In doing so, we will offer a new characterization of paraconsistency by means of which a logic is paraconsistent if it invalidates either the inferential or the meta-inferential notion of Explosion. We show the non-triviality of this criterion by discussing a number of logics. On the one hand, logics which validate and invalidate both versions of Explosion, such as classical logic and Asenjo–Priest’s 3-valued logic \(\mathbf {LP}\). On the other hand, logics which validate one version of Explosion but not the other, such as the substructural logics \(\mathbf {TS}\) and \(\mathbf {ST}\), introduced by Malinowski and Cobreros, Egré, Ripley and van Rooij, which are obtained via Malinowski’s and Frankowski’s q- and p-matrices, respectively.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
In this paper we will be focusing on the inferential and the meta-inferential level, but when making our closing remarks in Sect. 5 we will point towards a plausible (although not developed here) more general conception of paraconsistency, which will require looking at many more levels.
- 2.
We shall notice that in [2] Avron takes this definition to, additionally, require that Cut is taken as a primitive rule. Something that—for the sake of generality—we do not demand here.
- 3.
Let us notice, additionally, that Humberstone calls Ex Falso Quodlibet what we call Explosion, but this is just a terminological and non-substantial issue.
- 4.
q-consequence relations and q-matrices were introduced by Grzegorz Malinowski in [19].
- 5.
p-consequence relations and p-matrices were introduced by Szymon Frankowski in [12].
- 6.
Here we will adopt this terminology—i.e. talk of \(\mathscr {D}^{+}\) and \(\mathscr {D}^{-}\)—introduced by [32], emphasizing that we will take q- and p-logics to be induced by different type of structures, i.e. respectively q- and p-matrices. In this vein, what will be distinctive of these type of structures will be the properties of the sets \(\mathscr {D}^{+}\) and \(\mathscr {D}^{-}\), as detailed in Definitions 15 and 16, respectively.
- 7.
Notice that this definition takes a p-logic to be induced by a p-matrix \(\langle \mathscr {V}, \mathscr {D}^{+}, \mathscr {D}^{-}, \mathscr {O} \rangle \) where it is assumed that \(\mathscr {D}^{+} \subseteq \mathscr {D}^{-}\), whence this last clause reads: “if \(v[\varGamma ] \subseteq \mathscr {D}^{+}\), then \(v(A) \in \mathscr {D}^{-}\)”. Now, as remarked by an anonymous referee, if the same p-logic is taken to be induced by a q-matrix \(\langle \mathscr {V}, \mathscr {D}^{+}, \mathscr {D}^{-}, \mathscr {O} \rangle \) where it is assumed that \(\mathscr {D}^{+} \cap \mathscr {D}^{-} = \emptyset \)—as is done e.g. in [32, p. 210]—then this last clause should read: “if \(v[\varGamma ] \subseteq \mathscr {D}^{+}\), then \(v(A) \notin \mathscr {D}^{-}\)”.
These considerations highlight that if the sets \(\mathscr {D}^{+}\) and \(\mathscr {D}^{-}\) of a q-matrix are taken to, respectively, represent a generalized notion of truth and a generalized notion of falsity—as in [32]—then with regard to valuations on the 3-element Kleene algebra, \(\mathbf {TS}\) and \(\mathbf {ST}\) can be interpreted as follows. \(\mathbf {TS}\) consequence can be understood as requiring that for all valuations, if the premises are non-false, then the conclusion is true; whereas \(\mathbf {ST}\) consequence can be understood as requiring that for all valuations, if the premises are true, then the conclusion is non-false.
- 8.
By these rules we refer to the following, respectively.
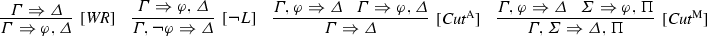
- 9.
Whence, the aforementioned equivalence is witnessed e.g. by the following derivation, where the application of \([\textit{Cut}]\) is a rightful instance of both \([\textit{Cut}^{\mathrm {A}}]\) and \([\textit{Cut}^{\mathrm {M}}]\).
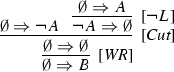
- 10.
That is, the matrix logic induced by the structure \(\mathscr {M}_{\mathbf {{K}_{3}}} = \langle \{ {\mathbf {t}}, {\mathbf {i}}, {\mathbf {f}}\}, \{ {\mathbf {t}}\}, \{ f^{\lnot }_{\mathbf {K}}, f^{\wedge }_{\mathbf {K}}, f^{\vee }_{\mathbf {K}} \} \rangle \), such that \(\langle \{ {\mathbf {t}}, {\mathbf {i}}, {\mathbf {f}}\}, \{ f^{\lnot }_{\mathbf {K}}, f^{\wedge }_{\mathbf {K}}, f^{\vee }_{\mathbf {K}} \} \rangle \) is the 3-element Kleene algebra.
- 11.
Along these lines, \(\mathbf {CL}\) can be proof-theoretically understood as Gentzen’s sequent calculi \(\mathbf {LK}\), \(\mathbf {TS}\) as \(\mathbf {LK}\) minus the structural rule of Reflexivity, and \(\mathbf {ST}\) as \(\mathbf {LK}\) minus the structural rule of Cut.
References
Asenjo, Florencio. 1966. A calculus of antinomies. Notre Dame Journal of Formal Logic 7 (1): 103–105.
Avron, Arnon. 1988. The semantics and proof theory of linear logic. Theoretical Computer Science 57 (2–3): 161–184.
Avron, Arnon. 1991. Simple consequence relations. Information and Computation 92 (1): 105–139.
Barrio, Eduardo, Lucas Rosenblatt, and Diego Tajer. 2015. The logics of strict-tolerant logic. Journal of Philosophical Logic 44 (5): 551–571.
Blok, Willem, and Bjarni Jónsson. 2006. Equivalence of consequence operations. Studia Logica 83 (1): 91–110.
Carnielli, Walter, and Marcelo Coniglio. 2016. Paraconsistent Logic: Consistency, Contradiction and Negation. Dordrecht: Springer.
Chemla, Emmanuel, Paul Egré, and Benjamin Spector. 2017. Characterizing logical consequence in many-valued logics. Journal of Logic and Computation 27 (7): 2193–2226.
Cobreros, Pablo, Paul Egré, David Ripley, and Robert van Rooij. 2012. Tolerant, classical, strict. Journal of Philosophical Logic 41 (2): 347–385.
Cobreros, Pablo, Paul Egré, David Ripley, and Robert van Rooij. 2014. Reaching transparent truth. Mind 122 (488): 841–866.
Dicher, Bogdan. 2016. A proof-theoretic defence of meaning-invariant logical pluralism. Mind 125 (499): 727–757.
Dicher, Bogdan, and Francesco Paoli. 2017. ST, LP, and Tolerant Metainferences. (Unpublished Manuscript).
Frankowski, Szymon. 2004. Formalization of a plausible inference. Bulletin of the Section of Logic 33 (1): 41–52.
Frankowski, Szymon. 2004. p-consequence versus q-consequence operations. Bulletin of the Section of Logic 33 (4): 197–207.
French, Rohan. 2016. Structural reflexivity and the paradoxes of self-reference. Ergo 3 (5): 113–131.
Gabbay, Dov. 1996. Labelled Deductive Systems. Oxford: Oxford University Press.
Girard, Jean-Yves. 1987. Proof Theory and Logical Complexity. Napoli: Bibliopolis.
Hansson, Sven Ove. 2016. Logic of belief revision. In The Stanford Encyclopedia of Philosophy, winter 2016 ed, ed. Edward N Zalta. Stanford University. http://plato.stanford.edu/archives/win2016/entries/logic-belief-revision/.
Humberstone, Lloyd. 2011. The Connectives. Cambridge: MIT Press.
Malinowski, Grzegorz. 1990. Q-consequence operation. Reports on Mathematical Logic 24 (1): 49–59.
Malinowski, Grzegorz. 2007. THAT p \(+\) q \(=\) c(onsequence). Bulletin of the Section of Logic 36 (1/2): 7–19.
Malinowski, Grzegorz. 2014. Kleene logic and inference. Bulletin of the Section of Logic 43 (1/2): 43–52.
Mares, Edwin, and Francesco Paoli. 2014. Logical consequence and the paradoxes. Journal of Philosophical Logic 43 (2–3): 439–469.
Priest, Graham. 1979. The logic of paradox. Journal of Philosophical logic 8 (1): 219–241.
Priest, Graham, Koji Tanaka, and Zach Weber. 2016. Paraconsistent logic. In The Stanford Encyclopedia of Philosophy, Winter 2016 ed, ed. Edward Zalta. Stanford University. http://plato.stanford.edu/archives/win2016/entries/logic-paraconsistent/.
Pynko, Alexej. 2010. Gentzens cut-free calculus versus the logic of paradox. Bulletin of the Section of Logic 39 (1/2): 35–42.
Ripley, David. 2012. Conservatively extending classical logic with transparent truth. The Review of Symbolic Logic 5 (02): 354–378.
Ripley, David. 2013. Paradoxes and failures of cut. Australasian Journal of Philosophy 91 (1): 139–164.
Ripley, David. 2015. Paraconsistent logic. Journal of Philosophical Logic 44 (6): 771–780.
Scott, Dana. 1971. On engendering an illusion of understanding. The Journal of Philosophy 68 (21): 787–807.
Shoesmith, David, and Timothy Smiley. 1978. Multiple-Conclusion Logic. Cambridge: Cambridge University Press.
Shramko, Yaroslav, and Heinrich Wansing. 2010. Truth values. In The Stanford Encyclopedia of Philosophy, Summer 2010 ed, ed. Edward Zalta. Stanford Uniersity. http://plato.stanford.edu/archives/sum2010/entries/truth-values/.
Shramko, Yaroslav, and Heinrich Wansing. 2011. Truth and Falsehood: An Inquiry into Generalized Logical Values. Dordrecht: Springer.
Stärk, Robert. 1991. A complete axiomatization of the three valued completion of logic programs. Journal of Logic and Computation 1 (6): 811–834.
Urbas, Igor. 1990. Paraconsistency. Studies in Soviet Thought 39 (3/4): 343–354.
Zardini, Elia. 2013. Naive modus ponens. Journal of Philosophical Logic 42 (4): 575–593.
Acknowledgements
The ideas contained in this paper were presented at the Work In Progress seminar of the Buenos Aires Logic Group, the XVI Trends in Logic conference, and the Kyoto Philosophical Logic Workshop II at Kyoto University. We are thankful to the members of those audiences for the discussion provided. We would also like to thank Rohan French, Andreas Fjellstad, Hitoshi Omori, Francesco Paoli, Graham Priest, Dave Ripley, Zach Weber and two anonymous reviewers for their helpful suggestions and comments on previous versions of this article. Finally, we are thankful to the editors of this volume, Walter Carnielli, and Jacek Malinowski, for their assistance through the editorial process.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Barrio, E., Pailos, F., Szmuc, D. (2018). What is a Paraconsistent Logic?. In: Carnielli, W., Malinowski, J. (eds) Contradictions, from Consistency to Inconsistency. Trends in Logic, vol 47. Springer, Cham. https://doi.org/10.1007/978-3-319-98797-2_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-98797-2_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-98796-5
Online ISBN: 978-3-319-98797-2
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)