A Dynamic Distributed Data Structure for Top-k and k-Select Queries

Abstract

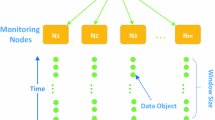
We consider a scenario where n sensor nodes observe streams of data. The nodes are connected to a central server whose task it is to compute some function over all data items observed by the nodes. Extending the capabilities of the distributed monitoring model from [8], we allow, in addition to sending messages from the sensor nodes to the server, also broadcasts from the server to the sensor nodes (see for example [9]).

In this paper, we address the problem of answering Top-k queries (report the k largest data items currently observed) and approximate k-Select queries (report an element with rank close to k). We present a communication-efficient dynamic data structure that supports these queries under updates of the data items arriving at the sensor nodes.

This work was partially supported by the German Research Foundation (DFG) within the Priority Program “Algorithms for Big Data” (SPP 1736).

1 Introduction

Consider a sensor network which is a system comprising of a huge amount of nodes. Each node continuously observes its environment and measures information (e.g., temperature, pollution or similar parameters). We are interested in aggregations describing the current observations at a central server. To keep the server’s information up to date, the server and the nodes can communicate with each other. In sensor networks, however, the amount of such communication is particularly crucial, as communication has the largest impact to energy consumption, which is limited due to battery capacities [11]. Therefore, algorithms aim at minimizing the (total) communication required for computing the respective aggregation function at the server.

We consider the following idea to potentially lower the communication used. Computations of the same aggregate should reuse parts of previous computations. We realize this by introducing a data structure which, at every point in time, keeps track of an approximation of a data item with rank k. These approximations can be exploited by the protocols for a Top-k or k-Select computation to significantly decrease the communication and interestingly also the time bounds, making this approach a very powerful tool.

1.1 The Distributed Monitoring Model with Broadcast Channel (DMBC-Model)

We consider the distributed monitoring model introduced by Cormode, Muthukrishnan, and Yi in [8], in which there are n distributed nodes, each uniquely identified by an ID from the set $\{1,\dots ,n \}$, connected to a single server. Each node observes a stream of data items over time, i.e., at any discrete time step t node i observes a data item $d_i^t$. We assume that the data items have a total order and denote by rank(d) the position of data item d in the sorted ordering. The server is asked to, given a query at time t, compute an output f(t) which depends on the data items $d_i^{t}$ with $i = 1, \ldots , n$ observed across all distributed streams.

To be able to compute the output, the nodes and the server have to communicate with each other. The distributed monitoring model introduced by Cormode, Muthukrishnan, and Yi in [8] allows exchanging single cast messages. The extension we use is the Distributed Monitoring Model with a Broadcast Channel (DMBC-Model) (proposed in [7] and exploited in [3, 4, 9, 10]) which allows, in addition, to broadcast messages from the server to all nodes. Both types of communication are instantaneous and have unit cost per message. That is, sending a single message to one specific node incurs cost of one and so does one broadcast message. Each message has a size of $\mathcal {O}\left( \mathcal {B} + \log n \right)$ bits, where $\mathcal {B}$ denotes the number of bits needed to encode a data item. A message will usually, besides a constant number of control bits, consist of a data item, and a node ID.

Between any two time steps we allow a communication protocol to take place, which may use a polylogarithmic number of rounds. The optimization goal is the minimization of the communication complexity, given by the total number of exchanged messages, required to answer the posed requests or setup/update the data structure.

1.2 Related Work

Cormode, Muthukrishnan, and Yi introduce the Continuous Monitoring Model [8] with an emphasis on systems consisting of n nodes generating or observing distributed data streams and a designated coordinator. In this model the coordinator is asked to continuously compute a function, i.e., to compute a new output with respect to all observations made up to that point. The objective is to aim at minimizing the total communication between the nodes and the coordinator. We enhance the continuous monitoring model (as proposed by Cormode, Muthukrishnan, and Yi in [7]) by a broadcast channel. Note that we are not strictly continuous in the sense that we introduce a dynamic data structure which only computes a function if there is a query for it. However, there is still a continuous aspect: In every time step, our data structure maintains elements close to all possible ranks in order to quickly answer queries (cf. [5, 6, 15, 16]).

An interesting area of problems within this model are threshold functions: The coordinator has to decide whether the function value (based on all observations) has reached a given threshold $\tau$. For well-structured functions (e.g., count-distinct or the sum-problem) asymptotically optimal bounds are known [7, 8, 13]. Functions which do not provide such structures (e.g., the entropy [1]), turn out to require much more communication volume.

A related problem is a variant of the distributed Top-k monitoring problem considered by Babcock and Olston [2]: There is a set of objects $\{O_1, \ldots , O_n\}$ given, in which each object has a numeric value. The stream of data items updates these numeric values (of the given objects). Babcock and Olston have shown by an empirical evaluation that the amount of communication is by an order of magnitude lower than that of a naive approach.

Furthermore, the Top-k computation is also considered in [9]. The proposed protocol needs a number of $\mathcal {O}(k \cdot \log N)$ messages and $\mathcal {O}(k \cdot \log N)$ rounds, where $N > n$ denotes an upper bound on the number of nodes. In this paper we improve both the number of messages and communication rounds to $k + \log n + 2$ and $\mathcal {O}(k + \log N)$ respectively. The techniques used in this paper are fundamentally based on [4] applying the idea of an inorder treewalk in a distributed searchtree and analyzing using a mixed distribution.

A model related to our (sub-)problem of finding the k-th largest values, and exploiting a broadcast channel, is investigated by the shout-echo model in [12, 14]. A communication round is defined as a broadcast by a single node, which is replied by all remaining nodes. The objective is to minimize the number of communication rounds, which differs from ours.

1.3 Contribution of the Paper

We present a distributed data structure for the DMBC-Model with the following properties: In each step t, each client i receives a data item $d_i^t$ as above. For ease of description let $s^t_1, \ldots , s^t_n$ be the sorted version of the data items $d^t_1, \ldots , d^t_n$ received at time step t. Our data structure supports the following operations:

$$\begin{aligned} \begin{array}{rl} {\textsf {TOP}}\text {-}k{:} &{}\; \text {Output } \{s^t_1, \ldots , s^t_k\}\\ {\textsf {STRONG SELECT}}{:} &{}\; \text {Output } d \in \{s^t_{(1-\varepsilon ) k}, \ldots , s^t_{(1+\varepsilon ) k} \} \\ {\textsf {WEAK SELECT}}{:} &{}\; \text {Output } d \text { with } s^t_{k \cdot \log ^{c_1} n} \le d \le s^t_{k \cdot \log ^{c_2} n}, \text {with } c_1, c_2 > 1\\ \end{array} \end{aligned}$$

Our data structure gives the following performance guarantees:

• The expected amortized total communication cost for an update (amortized over all updates of the data items received by clients) is $\mathcal {O}(1/polylog \, n)$, the number of rounds is $\mathcal {O}(\log n)$.

• WEAK SELECT does not need any communication. The output is correct with probability at least $1- 1/polylog \, n$.

• The expected total communication cost for a STRONG SELECT operation is bounded by $\mathcal {O}(1/\varepsilon ^2 \log 1/\delta \,+\,\log ^2\log n)$, the expected number of rounds is $\mathcal {O}(\log \log \frac{n}{k})$. The output is correct with probability at least $1- \delta$.

• The expected total communication cost for TOP-$k$ is $\mathcal {O}(k + \log \log n)$, the expected number of rounds is $\mathcal {O}(\log \log n)$. The output is always correct.

2 Outline of the Data Structure

Our data structure maintains an information Sketch $(t)$ about the data items received at time t in the server, at every time t.

As above, let $s_1^t, \ldots , s_n^t$ be the sorted version of the data items $d_1^t, \ldots , d_n^t$ received at time step t. Fix sufficiently large constants $c_1, c_2, c > 1$. We call Sketch $(t)$ correct if it consists of a set of data items $\{d_1, \ldots , d_{\log n}\}$ such that, for each $k = 1, \ldots , n$, there exists a $d_j$ such that $s^t_{k \cdot \log ^{c_1} n} \le d_j \le s_{k \cdot \log ^{c_2} n}^t$ holds. INIT denotes the process of computing Sketch(t), where the input $d_1^t, \ldots , d_n^t$ of step t is given to the n sensor nodes.

Observation 1

Consider a time step t at which the Init operation is called. A correct Sketch $(t)$ is also a correct Sketch $(t')$, for a $t' > t$, if at most $\log ^c(n)$ values of the clients are updated during the time interval $(t,t']$.

This observation holds, because in the worst case the rank of a fixed data item, facing $\log ^c n$ updates, can change by at most $\log ^c n$. Since we allow the data item to be upper bounded by $s^t_{k \cdot \log ^{c_2} n}$ simply observe that this still holds after $\log ^c n$ updates, for sufficiently large choices of constants. On the other hand, to prevent that the data item $d_j$ gets not smaller than $s_k^t$, the data structure computes a data item $d_j > s_{k \cdot \log ^{c_1} n}^t$. Note that the constants $c_1$ and $c_2$ depend on c. However, if the constants are (beforehand) chosen large enough, this ensures that after $\log ^c n$ updates Sketch $(t)$ is also a Sketch $(t')$.

Lemma 1

INIT is executed correctly with probability at least $1 - 1/polylog \, n$.It needs expected total communication of $\mathcal {O}(\log n)$ and $\mathcal {O}(\log n)$ rounds.

We present the INIT algorithm and the necessary technical basis to prove this lemma in Sect. 3. We prove that the algorithm computes a Sketch $(t)$ correctly in Theorem 1 and present the performance guarantees in Theorem 2.

The next operation UPD denotes the process of updating Sketch(t), in response to the updates of data items received in step t.

Lemma 2

UPD can be done using expected amortized (w.r.t. number of updates of data items in the nodes) total communication of $\mathcal {O}(1/polylog \, n)$, the amortized number of rounds is constant (assuming each update is processed at a different time step). For every step t, the computed Sketch(t) is correct with probability at least $1- 1/polylog \, n$.

The UPD algorithm is presented in Sect. 4. In this section, we shortly argue its correctness in Lemma 7 and show communication bounds in Lemma 8.

By definition of a correct Sketch(t), the following observation holds.

Observation 2

Given a correct Sketch(t), WEAK SELECT can be executed without any communication. It is correct with probability $1- 1/polylog \, n$.

We present this observation shortly in Sect. 5.

Lemma 3

Given a correct Sketch(t), STRONG SELECT can be correctly computed with probability $1-\delta$. It needs $\mathcal {O}(1/\varepsilon ^2 \log 1/\delta \,+\,\log ^2\log n)$ communication and $\mathcal {O}(\log \log n)$ communication rounds.

This result is considered in Sect. 6. The algorithm is based on three phases which are analyzed independently. The main result of this section is presented in Theorem 3.

Lemma 4

Given a correct Sketch(t), TOP-$k$ can be computed using expected total communication of $\mathcal {O}(k + \log \log n)$ and $\mathcal {O}(k + \log \log n)$ communication rounds. The output is always correct.

The TOP-$k$ algorithm is presented in Sect. 7. On the total communication is argued in Lemma 13 and the number of rounds in Lemma 14.

The lemmata above imply the performance guarantees formulated in the previous section.

3 Initialization of the Data Structure

We start the presentation of our results with the goal to prove the first lemma. We propose the algorithm INIT which computes the Sketch $(t)$ at a time step t. Since (a variation of) this algorithm is reused in later sections, we describe a procedure CFS (ConstantFactorSelect) with different parameters (see Algorithm 1).

CFS. The high-level idea of CFS is as follows: Initially each node is defined to be active. The protocol samples a node uniformly at random and broadcasts its value. All nodes with a larger data item deactivate themselves. This process is repeated until the remaining nodes are sampled with probability 1.

However, since the server does not know which nodes remain active, a sample cannot be chosen directly. Instead, we let the nodes proceed a random process such that the server can probe each node with a certain outcome based on the random process. We consider this random process in more detail: Each node i chooses a height $h_i$ from a geometric distribution, i.e., the number of coin flips with success probability p until one coin flip was successful. (Observe that based on the definition of p the expected maximal height $max _i h_i$ varies. This fact can be used to trade-off between the expected number of messages and the number of rounds the algorithm uses.)

Intuitively speaking, we build a distributed (not binary) searchtree where the heights are chosen randomly and the algorithm follows the path to the sensor node observing the minimum value. The $\log n$ nodes on this path yield an approximation of the data items with respect to their ranks. We will exploit this fact and show that a data item at a specific level can be used to approximate a given rank successfully.

Initialize. We only need a simple variant of the CFS protocol as follows: The INIT operation defines $p := 1/2$, the success probability of each coin flip. That is, each sensor node has a height of 2 in expectation. Thus, observe that the expected maximum of n nodes is $h_{max } = \log n$. For each height h the server keeps the smallest response of the sensor nodes in the data structure.

3.1 Initialize Computes Sketch $(t)$

Recall that the data structure is asked to answer each request for a data item of rank k by a data item d. We group a set of requests with different ranks which we answer with the same data item d. To this end, we divide the ranks $1, \ldots , n$ into classes $C_1, \ldots , C_m$, where m is chosen sufficiently large such that each data item belongs to a class. The exact number of classes is based on a constant which is defined by the analysis, however, note that $m = \mathcal {O}(\log n)$ holds.

We define a representative for each class which is the response for a request of any rank in the next-smaller class. Furthermore, the height of a class represents the expected maximum height found within this class, such that our representative will have a height value within the noted bounds. In the following we use the constant $\kappa > 1$ chosen sufficiently large which represents the constants in the bounds on the precision and the success probability. Furthermore, let $\mathscr {H}:= \log \log n$ to ease the notation. The idea of classes is captured in the following definition:

Definition 1

(Classes). A Class $\mathcal {C}_\ell ^t$ consists of all data items $d_j^t$ fulfilling $rank(d_j^t) \in [\log ^{6 \ell \kappa } (n), \log ^{6 (\ell +1) \kappa }(n))$. We define $h_{min }(C_\ell ) := (6 \ell \kappa + 1 \kappa ) \mathscr {H}$ and $h_{max }(C_\ell ) := (6 \ell \kappa + 7 \kappa ) \mathscr {H}$. The height of the class $C_{\ell }^t$ is given by $h(C_{\ell }^t) := (h_{min }(C_\ell ^t), h_{max }(C_\ell ^t) ]$.

By abuse of notation we introduce $d_i^t \in C_\ell ^t$ which shortens $rank(d_i^t) \in C_\ell ^t$. Furthermore let class(d) be the class where the data item d belongs to, i.e., for a given d, class(d) gives the class $C_\ell ^t$ such that $d \in C_\ell ^t$ holds.

Definition 2

(Inner Classes). We denote by an inner class $I_{\ell , \tau }^t$ (where $\tau \in \{0, 1, 2\}$ holds) the set of data items $d_i^t$ with a rank between $\log ^{6 \ell \kappa + 2 \kappa }(n)$ and $\log ^{6 \ell \kappa + 4 \kappa } (n)$. The height of $I_{\ell , \tau }^t$ is $h(I_{\ell , \tau }^t) = ((6 \ell \kappa + (2 \tau +1) \kappa ) \mathscr {H}, (6 \ell \kappa + (2\tau + 3) \kappa ) \mathscr {H}]$.

We omit the time step t in our notation whenever it is clear from the context.

Definition 3

(Well-Shaped). The data items in an inner class $I_{\ell , \tau }$ are well-shaped if for each data item $d_i \in I_{\ell , \tau }$ it holds $h_i \le (6 \ell \kappa + (2\tau + 3) \kappa ) \mathscr {H}$.

We start by analyzing the outcome of the INIT operation. That is, we show that a class is well-shaped with sufficiently large probability in Lemma 5 and argue that the data structure has one representative in Theorem 1, afterwards.

Lemma 5

After an execution of INIT, the inner class $I_{\ell , \tau }$ is well-shaped with probability at least $1- \log ^{-\kappa } (n)$.

Proof

Recall that for a fixed data item $d_i$ and sensor node i the probability for $h_i > h$ is $\phi ^h$. Fix an inner class $I_{\ell , \tau }$ and consider the data items $d_i \in I_{\ell , \tau }$. We upper bound the probability that there is a data item with a height of at least h with $h := (6 \ell \kappa + (2 \tau + 3) \kappa )\mathscr {H}$ by applying the union bound as follows:

$$\begin{aligned} \Pr [\exists d_i \in C_{\ell , \tau } \mid h_i > h]&\le \left( \log ^{6 \ell \kappa + (2 \tau + 2) \kappa } (n) - \log ^{\ell 8\kappa + 2 \tau \kappa } (n) \right) \cdot \phi ^{h}\\&\le \log ^{6 \ell \kappa + (2 \tau + 2) \kappa } (n) \cdot \log ^{- (6 \ell \kappa + (2 \tau + 3) \kappa )} (n) \\&\le \log ^{- \kappa } (n) \end{aligned}$$

   $\square$

Lemma 6

Consider the inner class $I_{\ell , 1}$. There is a data item $d_{i} \in I_{\ell , 1}$ with $h_{i} > (6 \ell \kappa + 3 \kappa ) \mathscr {H}$ with high probability.

Proof

Here we simply upper bound the probability that each data item in the inner class has a height of at most h as follows:

$$\begin{aligned} \Pr [\forall d_i&\in I_{\ell , 1} \mid h_i \le (6 \ell \kappa + 3 \kappa ) \mathscr {H}] \le \left( 1 - 2^{-(6 \ell \kappa + 3 \kappa ) \mathscr {H}} \right) ^{|I_{\ell , 1}|}\\&\le \left( 1 - {\log ^{-(6 \ell \kappa + 3 \kappa )} n} \right) ^{\log ^{6 \ell \kappa + 4 \kappa } n \, - \, \log ^{6 \ell \kappa + 2 \kappa } n}\\&\le \left( \frac{1}{e} \right) ^{\frac{1}{2} \log ^{\kappa } n } \le n^{-\frac{1}{2} \log (e) \log ^{\kappa - 1}(n)} \le n^{-c}, \end{aligned}$$

for some constant c.    $\square$

We can now prove the first part of Lemma 1, i.e., that INIT computes a correct Sketch(t). Technically, we show a result which is more restricted than the stated precision of Lemma 1, as follows:

Theorem 1

After execution of INIT there exists, for each rank k, a data item in Sketch $(t)$ with rank between $k \cdot \log ^{ 2 \kappa } (n)$ and $k \cdot \log ^{10 \kappa } (n)$ with probability at least $1-\log ^{-\kappa + 2} (n)$.

Proof

First consider a fixed inner class $I_{\ell , \tau }$ for a fixed $\ell \in \mathbb {N}$ and $\tau \in \{0, 1, 2\}$. Based on Lemma 5 we can show that the distribution of the random heights is well-shaped with probability at least $1-\log ^{-\kappa }(n)$. Now, with high probability there is a data item with such a height for sufficiently large $\kappa$ and n due to Lemma 6. These observations together show that there is a data item d identified and stored in DS with probability at least $1- \log ^{-\kappa + 1} (n)$.

Furthermore, note that the number of inner classes is upper bounded by $\log n$. The argument stated above applied to each class leads to the result that for each inner class there exists a data item in the data structure, and each inner class is well-shaped with probability at least $1 - \log ^{\kappa - 2} (n)$ (by simply applying the union bound).    $\square$

3.2 Communication Bounds

In the following we show the second part of Lemma 1, i.e., that the number of messages used by INIT is upper bounded by $\mathcal {O}(\log n)$ and the same bound holds for the number of rounds. We start by analyzing the bound on the total communication.

We show an upper bound on the communication used by the CFS protocol analyzing the expected value of a mixed distribution: Intuitively speaking, consider the path from the root to the maximum in a non-binary searchtree. For each node i on the path consider the number of siblings j with a smaller data item, i.e., $d_j < d_i$. To bound the expected number of such siblings j, we first consider on a fixed height h the number of tries $G_h$ until the first node $j'$ has drawn a height $h_{j'} > h$ (for each height h this results in the geometric sequence, Definition 4). Based on $G_h$, we consider the number of nodes that have drawn precisely the height $h_{j'} = h$ (for each height h, the geocoin-experiment Definition 5).

Note that this analysis turns out to be very simple since independence can be exploited in a restricted way and leads to a proper analysis with respect to small constants.

Definition 4

We call a sequence $G = (G_1, \ldots , G_m)$ of m random experiments a geometric sequence if each $G_h$ is chosen from a geometric distribution with $p_{h}^{geo} := \phi ^h$. We denote its $size(G) := \sum _h G_h$ and say it covers all nodes if $size(G) \ge n$.

For the analysis, we choose a fixed length of $m := \log _{\nicefrac {1}{\phi }} (n)$ and modify G to $G' = (G_1, \ldots , G_{m-1}, n)$ such that $G'$ covers all nodes with probability 1.

Based on a given geometric sequence, we define a sequence describing the number of messages sent by the nodes on a given height. We take the number of nodes $G_j$ as a basis for a Bernoulli experiment where the success probability is the probability that a node sends a message on height $h_j$. This is $\Pr [h = h_j \mid h \le h_j] = \frac{\phi ^{h-1}(1-\phi )}{1-\phi ^h}$.

Definition 5

We denote a geocoin-experiment by a sequence $C = (C_1, \ldots , C_m)$ of random variables $C_h$ which are drawn from the binomial distribution $Binom \big (n=G_h, p_h^{bin} = \frac{\phi ^{h-1}(1-\phi )}{1-\phi ^h} \big )$, i.e., $C_h$ out of $G_h$ successful coin tosses and each coin toss is successful with probability $p_h^{bin}$.

We are now prepared to prove the second part of Lemma 1, i.e., a bound on the total communication for CFS and thus for INIT.

Theorem 2

Let $h_{max } \ge \log _{\nicefrac {1}{\phi }} (n)$ hold. The CFS protocol uses an expected number of $\frac{1-\phi }{\phi } \log _{\nicefrac {1}{\phi }} (n) + \frac{1}{\phi }$ messages in total.

Proof

The number of messages sent is upper bounded by a geocoin-experiment C. Let $\mathscr {H} := \log _{\nicefrac {1}{\phi }} (n)$. For $h < \mathscr {H}$ we use that the geometric distribution is memory-less and hence

$$\begin{aligned} \mathbb {E}[C_h]&= (1-p_h^{geo}) \cdot (p_h^{bin} + \mathbb {E}[C_h]) = (1- \phi ^h) \cdot \left( \frac{\phi ^{h-1}(1-\phi )}{1-\phi ^h} + \mathbb {E}[C_i]\right) . \end{aligned}$$

This can simply be rewritten as $\mathbb {E}[C_h] = \frac{1-\phi }{\phi }$.

For $h \ge \mathscr {H} = \log _{\nicefrac {1}{\phi }} (n)$ we bound the number of messages by the total number of nodes with height at least $\mathscr {H}$. These can be described as the expectation of a Bernoulli experiment with n nodes and success probability $\phi ^{\mathscr {H}-1}$ and hence we can bound $\mathbb {E}[C_{\ge \mathscr {H}}]\le \phi ^{\mathscr {H}-1}\cdot n = \frac{1}{\phi }$.

In total, we get

$$\begin{aligned} \sum _h \mathbb {E}[C_h]&= \left( \sum _{h=1}^{\mathscr {H}-1}\mathbb {E}[C_i] \right) +\mathbb {E}[C_{\ge \mathscr {H}}] \le \frac{1-\phi }{\phi } \log _{\nicefrac {1}{\phi }} (n) + \frac{1}{\phi }, \end{aligned}$$

concluding the proof.    $\square$

We conclude the proof for the first lemma by this simple observation on the number of rounds. By the definition of the protocol it is easy to see that the server simply sends a broadcast message for each height h and receives a message by those nodes which fulfill a specific rule. Since the server can process each received message in the same round, $h_{max }$ is obviously a strict upper bound for the number of rounds.

Observation 3

The INIT operation uses at most $h_{max } = \log n$ rounds.

4 Update

To keep the data structure up to date we apply the following simple straightforward strategy: As long as there are fewer than $\log ^c n$ updates processed since the last call of INIT, the precision of the approximated ranks can also only differ by an additional $\mathcal {O}(\log ^c n)$ (for a predefined constant $c > 1$). We apply a simple standard counting technique to verify that the current number of processed UPD operations is $\mathcal {O}(\log ^c n)$ in expectation. If more UPD operations are identified, the current data items in the data structure are discarded and the Sketch $(t)$ is built from scratch.

Consider the protocol for the UPD operation as presented in Algorithm 2. It applies a randomized counting technique to identify that there are more than $\varTheta (\log ^{\kappa } n)$ updates since the last INIT operation. It is easy to verify by applying standard Chernoff bounds that the protocol identifies $cnt \le 2 \, c \, \log n$ with high probability. Thus, and applying a Chernoff bound again, it follows that the number of UPD operations that took place since the last INIT operation is upper bounded by $2 \, \log ^{2c} n$ with high probability. With this, we can show the first part of Lemma 2.

Lemma 7

After the last call of INIT, there are at most $\varTheta (\log ^\kappa n)$ UPD operations processed with high probability.

The UPD operation sends a message with probability $p_{cnt}$, so it is easy to verify that the expected number of messages sent is upper bounded by $p_{cnt}$.

Now consider a sufficiently large instance (i.e., sufficiently many UPD operations). Assume that for a time step t at which INIT is called, $t'$ denotes the next time step at which INIT is called to rebuild the data structure. Observe that $\mathcal {O}(\log n)$ messages where sent during $[t, t']$ by UPD and INIT operations in total. Since $\varOmega (\log ^{c/2} n)$ UPD operations where called with high probability, the amortized bound for one single UPD operation follows.

For the number of communication rounds, consider the same interval $[t, t']$ as described above. Since one execution of UPD uses a constant number of rounds (excluding the call of INIT) and the INIT operation is called a constant number of times, each UPD operation only uses an amortized constant number of rounds. These observations conclude the argumentation for the second part of Lemma 2:

Lemma 8

The UPD operation uses $\mathcal {O}(1/polylog \, n)$ messages in expectation and amortized $\mathcal {O}(1)$ number of rounds.

5 Weak Select

For the sake of a complete presentation we shortly describe how the Sketch $(t)$ is used to answer a weak approximate k-Select request.

The WEAK SELECT operation simply identifies the class $\ell$ in which the data item d with rank k is expected (see Algorithm 3). Then, the representative r in the class on level $\ell + 1$ is chosen.

Note that by the correctness of INIT and its analysis on the precision the correctness of the protocol follows. It is also easy to see that the protocol is executed by the server and thus does not need any further communication to the sensor nodes. Since no further argumentation is needed, we restate the following observation for completeness:

Observation 4

Given a correct Sketch(t), WEAK SELECT can be executed without any communication. It is correct with probability $1- 1/polylog \, n$.

6 Strong Approximate k-Select

In this section we present an algorithm which gives an $(\varepsilon , \delta )$-approximation for the k-Select problem, i.e., a data item d is identified with a rank between $(1-\varepsilon )k$ and $(1+\varepsilon )k$ with probability at least $1-\delta$. In other words, we propose an algorithm and analyze its performance guarantee as claimed in Lemma 3.

Algorithm Description. We apply a standard sampling technique to select a data item as required. However, the data item given by the WEAK SELECT operation is too weak to directly be followed by a sampling technique (cf. Phase 3 in Algorithm 4). Thus, we add the following two phases:

• (1) A data item $d'$ is identified, such that a polylogarithmic error bound holds with high probability. It might be that a large number of sensor nodes (i.e., $\omega (k \cdot polylog \, n)$) ‘survive’ till the last phase and apply the costly sampling technique. With this step the event only occurs with probability at most 1 / n.

• (2) The second phase applies $c \log \frac{1}{\delta '}$ calls of CFS to identify data items that have a rank between k and $42 \, k$ with constant probability each. This number of calls is to amplify the (success) probability that the final data item $d^*$ has a rank between k and $42 \, k$ to at least $1-\delta '$.

Note that the internal probability $\delta '$ will be defined as $1 / polylog \, n$ which is a result of the analysis. Important is that the calls of CFS do not change the information of Sketch $(t)$ stored in the data structure. Here, they are only used ‘read-only’ and are not overwritten.

Analysis Outline. We split our analysis and consider each phase separately. First, we show that Phase 1 determines a data item $d'$ with a rank which is by a polylogarithmic factor larger than k with high probability. This needs $\mathcal {O}(\log \log n)$ messages and $\mathcal {O}(\log \log n)$ rounds in expectation.

Afterwards, we consider Phase 2 which determines a data item $d''$ with a rank only a constant factor larger than k with probability at least $1-\delta '$, where $\delta '$ can be chosen arbitrarily small.

Finally, Phase 3 applies a sampling technique to determine the final data item d which yields the property as required by Lemma 3.

We use the notation as given in the protocol and use $d'$ to denote the data item given by the WEAK SELECT operation, $d''$ the data item determined by Phase 1, and $d^*$ the data item given by Phase 2. We do not need any further analysis for the property of data item $d'$ since we analyzed its precision (and the given success probability bounds) in the past sections.

Analysis of Phase 1. We consider Phase 1 of the STRONG SELECT operation and analyze the precision of the rank of item $d''$, the expected number of messages and the number of communication rounds.

Lemma 9

For a given constant c, there exist constants $c_1,c_2$, such that Phase 1 as given in Algorithm 4 outputs a data item $d''$ with a rank between $7k \cdot \log ^{c_1}(n)$ and $7k \cdot \log ^{c_2}(n)$ with probability at least $1-n^{-c}$.

Proof

We use a simple argument to argue on the probability to obtain a data item within a multiplicative polylogarithmic precision bound:

Consider the event that the rank is strictly smaller than $7k \cdot \log ^{c_1} n$. Thus, one node i of the $7k \log ^{c_1} n - 1$ nodes has drawn a height $h_i \ge \log (7k \log ^c n)$. We show (by applying Chernoff bounds) that this probability is upper bounded by $n^{- c'}$, where $c'$ depends on c and $c_1$. For the remaining case (i.e., the rank is strictly larger than $7k \cdot \log ^{c_2} n$) the same argument is applied.

Let X denote the rank of the data item $d''$ which is identified by STRONG SELECT. Now let $X_1$ be drawn from $Binom (n = 7k \log ^{c_1} n, p = (1/2)^{\log (7k \log ^{c}n )})$, and let $X_2 \sim Binom (n = 7k \log ^{c_2} n, p = (1/2) ^{\log (7k \log ^c n)})$. Observe that it holds $\gamma _1 = \mathbb {E}[X_1] = \log ^{c_1-c} n$ and $\gamma _2 = \mathbb {E}[X_2] = \log ^{c_2 - c}n$. Thus, $\Pr [X < 7k \log ^{c_1}n] \le \Pr [X_1 > (1+ (1/2) \log ^{c-c_1}n) \cdot \log ^{c_1 - c} n] \le \exp (-\frac{1}{12} ( \log ^{c - c_1}n )) \le n^{-\frac{c-c_1-1}{12}}$.

We obtain by the same argument similar results for the probability of the event that the rank is larger than the claimed bound.    $\square$

Lemma 10

Phase 1 uses an amount of $\mathcal {O}(\log \log n)$ messages in expectation.

Proof

We apply the law of total expectation and first consider the event that WEAK SELECT is successful. Afterwards, the number of messages for a failed call is considered.

First, consider the case that the WEAK SELECT operation is successfully within the precision bounds. Then, $\mathcal {O}(\log \log n)$ messages on expectation are used in this phase. On the other hand, consider the number of messages used if the number of nodes that take part in this phase is n. Then, the protocol needs $\mathcal {O}(\log n)$ messages. However, the probability that WEAK SELECT is not within these bounds is $1/polylog \, n$ which concludes the proof.    $\square$

To upper bound the time needed for Phase 1, simply determine the range of h and observe that this range is bounded by $\mathcal {O}(\log \log n)$. Since one data item is found with probability at least $1-1/polylog \, n$, in expectation after the second repetition a data item is found.

Observation 5

Phase 1 of Algorithm 4 uses $\mathcal {O}(\log \log n)$ number of rounds.

Analysis of Phase 2. Now consider one execution of the lines 7 to 10 as given in Algorithm 4 (and restated in Algorithm 5).

Lemma 11

One execution of lines 8 and 9 of Phase 2 in Algorithm 4 outputs a data item d with $rank(d)\in [k,42k]$, with probability at least 0.6.

Proof

The algorithm outputs the $(1/\phi )^\alpha$ smallest data item $d_j^*$ the server gets as a response on height $h = h_{min }$. To analyze its rank, simply consider the random number X of nodes i that observed smaller data items $d_i < d$. The claim follows by simple calculations: (i) $\Pr [X < k] \le \frac{1}{5}$ and (ii) $\Pr [42 k > X] \le \frac{1}{5}$.

The event that X is (strictly) smaller than k holds if there are at least $(1/\phi )^\alpha$ out of k nodes with a random height at least $h_{min }$. Let $X_1$ be drawn by a binomial distribution $Binom (n = k, p = \phi ^{h_{min }-1})$. It holds $\mathbb {E}[X_1] = k \cdot \phi ^{h_{min }-1} = \frac{1}{7} \cdot (\frac{1}{\phi })^\alpha$. Then, $\Pr [X < k] \le \Pr [ X_1 \ge (\frac{1}{\phi })^\alpha ] = \Pr [X_1 \ge (1+6) \frac{1}{7 \phi ^\alpha }] \le \exp (-\frac{1}{3} \frac{1}{7 \phi ^\alpha } 6^2) \le \frac{1}{5}$.

On the other hand, the event that X is (strictly) larger than 42k holds if there are fewer than $(1/\phi )^\alpha$ out of 42k nodes with a random height of at least $h_{min }$. Let $X_2$ be drawn by a binomial distribution $Binom (n = 42k, p = \phi ^{h_{min }-1})$. It holds $\mathbb {E}[X_2] = (42 k) \phi ^{h_{min }-1} = (42 k ) (7 k ) ^{-1} \phi ^{-\alpha } = \frac{6}{\phi ^\alpha }$. Then, $\Pr [X > 42k] \le \Pr [X_2< \frac{1}{\phi ^\alpha }] = \Pr [X_2 < (1-(1-\frac{1}{6})) \frac{6}{\phi ^\alpha }]$ $\le \exp (-\frac{1}{2} (\frac{6}{\phi ^\alpha } (1-\frac{1}{6})^2) \le \exp (-\frac{25}{12}) \le \frac{1}{5}$.    $\square$

Note that we apply a standard boosting technique, i.e., we use $\mathcal {O}(\log \frac{1}{\delta '})$ independent instances, and consider the median of the outputs of all instances to be the overall output (cf. Algorithm 5). Thus, an output in the interval $[k, 42\,k]$ is determined with probability at least $1-\delta '$.

Observation 6

Phase 2 of Algorithm 4 outputs a data item $d^*$ with $rank(d^*) \in [k, 42k]$ with probability at least $1-\delta '$.

Lemma 12

Assume $\delta ' \ge n^{-c}$ for a constant $c > 1$. The second phase of Algorithm 4 uses $\mathcal {O}( \log \frac{1}{\delta '} \cdot \log \log \frac{n}{k})$ messages in expectation.

Proof

Consider one instance of Phase 2 and applying arguments from Theorem 2, the algorithm uses $\mathcal {O}(\log \log \frac{n}{k})$ messages in expectation for each iteration of Steps 8 and 9. This number of messages is multiplied by $\mathcal {O}(\log \frac{1}{\delta '})$, since we apply this number of executions in parallel.

It remains to show that the parallel execution does not need further messages to separate each execution from the others: In more detail, each instance of Steps 8 and 9 has to be executed with an additional identifier. Since $\delta ' \le n^{-c}$ holds, the identifier has a range of integer numbers between 1 and $\mathcal {O}(\log n)$ and thus needs additional $\mathcal {O}(\log \log )$ bits. Since a machine word has a size of $\mathcal {O}(\mathscr {B} + \log n)$ the identifier can be added to the message (or sent as a separate message such that the number of messages has a constant overhead). This concludes the proof.    $\square$

Since we run the $\mathcal {O}( \log \frac{1}{\delta '})$ instances in parallel, and the server is able to process all incoming messages within the same communication round, the number of communication rounds does not increase by the parallel executions.

Observation 7

Phase 2 of Algorithm 4 uses $\mathcal {O}(\log \log n)$ rounds.

6.1 Analysis of Phase 3

We are now prepared to propose the last phase of the algorithm which fulfills the required precision as stated in Lemma 3.

We consider the final phase of the algorithm, i.e., we apply a standard sampling technique (cf. Algorithm 6): The server broadcasts the value $d^*$ which (as a result of the analysis of Phase 2) has a rank between k and $42 \, k$ with probability at least $1-1/polylog \, n$. Each node i compares its data item $d_i^t$ with $d^*$ and only takes part in the sampling process if and only if $d_i^t \le d^*$ holds. Then, with probability $p = \frac{c}{k} \frac{1}{\varepsilon ^2} \log \frac{1}{\delta }$ node i sends its data item to the server. In turn, the server sorts each data item and outputs the $p \cdot k$-th smallest item, which has a rank of k in expectation.

For the sake of readability we introduce the notation $\mathscr {S}_{\varepsilon ,\delta }:= \frac{1}{\varepsilon ^2} \log \frac{1}{\delta }$ and are now prepared to show Lemma 3:

Theorem 3

Define $\delta ' := 1 / polylog \, n$. The STRONG SELECT operation (as presented in Algorithm 4) selects a data item $d_{\tilde{k}}$ with a rank in $[(1-\varepsilon )\,k, (1+\varepsilon )\, k]$ with probability at least $1-\delta$ using $\mathcal {O}( \mathscr {S}_{\varepsilon ,\delta }+ \log ^2 \log n )$ messages in expectation and $\mathcal {O}(\log _{\nicefrac {1}{\phi }} \log n)$ communication rounds.

Proof

From Lemma 12 we get that Phase 2 of the protocol uses an amount of at most $\mathcal {O}( \log \log \frac{n}{k} \log \frac{1}{\delta '})$ messages in expectation and runs for $\mathcal {O}(\log \log n)$ communication rounds. The remaining steps of Algorithm 4 need only one additional communication round and thus the stated bound on the communication rounds follows. We omit the proof for the correctness of the algorithm, i.e., with demanded probability the k-th smallest data item is approximated, since it is based on a simple argument using Chernoff bounds.

It remains to show the upper bound on the number of messages used. Formally, we apply the law of total expectation and consider the event that Phase 2 of Algorithm 4 determined a data item $d^*$ with rank $k \le rank(d^*) \le 42k$ and the event $rank(d^*) > 42k$.

Observe that the sampling process in steps 2 and 3 yields $\mathcal {O}(\frac{rank(d^*)}{k} \mathscr {S}_{\varepsilon ,\delta })$ messages in expectation. Consider the event that Phase 2 determined a data item $d^*$ with rank $k \le rank(d) \le 42 k$. Then, Phase 3 uses $\mathcal {O}(\mathscr {S}_{\varepsilon ,\delta })$ messages in expectation. Now consider the event that Phase 2 determined a data item $d^*$ with $d > 42\, k$. It uses $\mathcal {O}\left( \frac{\log ^c n}{k} \mathscr {S}_{\varepsilon ,\delta }\right)$ messages in expectation. Since the probability for this event is upper bounded by $\delta '$, the conditional expected number of messages is $\mathcal {O}\left( \frac{\log ^c (n)}{k} \mathscr {S}_{\varepsilon ,\delta }\cdot \delta ' \right)$. Defining $\delta ' := \log ^{-c} n$ the bound follows as claimed.    $\square$

6.2 One-Shot Approximate k-Select

For the sake of self-containment we propose a bound which considers all nodes to take part in the protocol.

Corollary 1

Let c be a sufficiently large constant. Furthermore, let $N = n$, $\phi := \frac{1}{2}$, $h_{max } := \log n$, and $\delta ' := \frac{1}{\log ^c (n)}$. The protocol uses an amount of at most $\mathcal {O}(\mathscr {S}_{\varepsilon ,\delta }+ \log n)$ messages in expectation and $\mathcal {O}(\log (\frac{n}{k}))$ expected rounds.

This represents the case (with respect to the choice of $\phi$) that a small number of messages and a large number of communication rounds are used. This observation is complemented by a lower bound of $\varOmega (\log n)$ in [4].

7 Top-k

In this section we present an algorithm which identifies all k smallest data items currently observed by the sensor nodes, i.e., at a fixed time step t.

Note that by applying the MaximumProtocol (from [9]) k times and using the Sketch $(t)$ from our data structure, the problem can be solved using $\mathcal {O}(k \cdot \log \log n)$ messages in expectation and $\mathcal {O}(k \cdot \log \log n)$ rounds. By applying the STRONG SELECT operation from the previous section (denote the output by $d_K$) and selecting all of the nodes i with a data item $d_i \le d_K$, a bound of $\mathcal {O}(k + \log ^2\log n)$ expected messages and $\mathcal {O}(\log \log n)$ rounds in expectation follows. These bounds are subject to be improved to $\mathcal {O}(k + \log \log n)$ expected messages and $\mathcal {O}(k + \log \log n)$ expected rounds. Without our Sketch $(t)$ the algorithm needs $k + \log n + 2$ expected messages and $\mathcal {O}(k + \log n)$ expected rounds, which might be of independent interest. We show a more general result which allows to trade-off between number of messages and number of rounds. This translates to $k + \frac{1-\phi }{\phi } \log _{\nicefrac {1}{\phi }} n + \frac{1}{\phi }$ expected total communication and $\mathcal {O}(\phi \cdot k + \log _{\nicefrac {1}{\phi }} n)$ expected rounds for an arbitrarily chosen $1/n \le \phi \le 1/2$.

Protocol Description. Revisiting the past section, where we added additional phases to improve precision, we take this idea and add as many phases in between as possible. In detail, we apply the idea of identifying the k largest values in a distributed (non-binary) search tree: The algorithm starts by drawing a random variable $h_i$ from a geometric distribution, i.e., $\Pr [h_i = h] = \phi ^{h-1} (1-\phi )$. Observe that a smaller choice of the failure probability $\phi$ results in smaller random heights $h_i$, but a larger expected number of ‘siblings’. To perform an inorder treewalk the server identifies the siblings of a node with respect to the current path of the protocol by broadcasting values $\ell , u$ and h to identify all nodes i with values $\ell< d_i < u$ and a height of $h_i \ge h$. The protocol is shown in Algorithm 7.

Analysis. To prove that the TOP-$k$ operation uses $\mathcal {O}(k + \log \log n)$ messages in expectation simply observe that the probability to send a message for a sensor node within the Top-k is 1. Consider the remaining nodes, i.e., consider the set $V'$ of nodes that are not in the Top-k. To bound the number of messages, we simply upper bound the number of messages used to find the maximum within $V'$. Since WEAK SELECT gives a data item such that $k \cdot \log ^{c_2} n$ nodes remain, and by the arguments in Theorem 1, it holds:

Lemma 13

The TOP-$k$ operation uses $\mathcal {O}(k + \log \log n)$ messages in expectation.

We consider the number of rounds, which concludes the proof for Lemma 4.

Lemma 14

The TOP-$k$ operation uses at most $\mathcal {O}(k + \log \log n)$ exp. rounds.

Proof

We structure the proof in two steps: First, we analyze the number of rounds used to determine the minimum (i.e., the data item with rank 1), and second, the number of communication rounds used to determine the Top-$k$.

Observe that the algorithm uses a linear amount of steps (linear in h), until it reaches $h_{min } = 1$, after which the minimum is found. Afterwards, in each step the algorithm recursively probes for nodes successively smaller than the currently largest values, that are added to the output set S. Note that by the analysis in Theorem 2, the number of nodes that send a message in expectation in each round is $(1-\phi )/\phi$ (for $h < \log _{\nicefrac {1}{\phi }}(n)$). Thus, in each communication round there are $\varOmega (\frac{1}{\phi })$ nodes in expectation that send a message, such that after an expected number of $\mathcal {O}(\phi \cdot k)$ rounds the Top-$k$ protocol terminates.    $\square$

Similar to the previous section, we can state a result for a one-shot computation of Top-k. This result might be of independent interest.

Corollary 2

For $\phi := \frac{1}{2}$ and $h := \log n$, the Top-$k$ protocol uses an amount of $k+\log n + 2$ messages in expectation and $\mathcal {O}(k + \log n)$ rounds.

8 Future Research Perspectives

We see further applications of the Sketch in our data structure. Among others, one (direct) application is to output an (axis aligned) bounding box for the given data points. An interesting problem to consider is as follows: Each sensor node observes its position in the plane and our task is to output the (sensor nodes that form the) convex hull. The sensor nodes are mobile, i.e., they can move between two time steps by a bounded speed. Let $n_h$ denote the number of nodes on the convex hull and observe that $\varOmega (n_h)$ messages are needed to determine the output. With the algorithms in this paper the convex hull can be computed using $\mathcal {O}(n_h \cdot \log n)$ messages. We ask whether we may apply (some variant of) our Sketch such that $\mathcal {O}(n_h \cdot \log \log n)$ messages are sufficient to determine the points on the convex hull.

Revisiting the analysis of our data structure we observe that we reduce the communication especially if the adversary changes only a few data items at a time. Additionally, we analyze a worst-case adversary who changes data items with a small rank, i.e., with a polylogarithmic rank. It might be of interest to consider restrictions of the adversary to prove stronger bounds: The node which observes a new data item is chosen uniformly at random, or the new data item observed is ‘close’ to the old value.