Control of Condensed-Phase Explosive Behaviour by Means of Cavities and Solid Particles

Abstract

Controlling the sensitivity of condensed-phase explosives is a matter of safe handling of the materials and a necessity for efficient blasting. It is known that impurities such as air cavities or solid particles can be used to sensitise the material by reducing the time to ignition. As the ignition of the explosive is a temperature-driven event, analysing the temperature field following the interaction of a shock wave with these impurities gives a measure of the effect of the impurity on the sensitisation of the material. Air cavity collapse in explosives has been extensively studied and recently focus has shifted on the accurate recovery of the temperature field during the collapse process. The interaction of a shock wave with solid particles or with a combination of cavities and particles, has been studied to a lesser extent. In this work, we assess the effect of the different impurities in isolation, in a multi-cavity and a multi-bead configuration and as a combined particle-cavity matrix. Results indicate that the beads have a more subtle effect on the sensitisation of the material, compared to cavities. An informed combination of the two (leading order by cavities and marginal adjustment by particles) could result to a fairly accurate control of the explosive.

1 Introduction

Controlling the performance of condensed-phase explosives is of interest to the mining industry. The ability to control the ignition sensitivity of the explosive material is not only a matter of safety during handling and transportation of materials but also a necessity for efficient blasting [14]. Common techniques used to sensitise a condensed-phase explosive include the addition of air cavities, glass microbaloons and glass or other solid beads in the body of the explosive. These artificial impurities affect the sensitivity of the material to different extent, but they all result in the generation of regions where the pressure and temperature are locally higher than the rest of the material, known as hot-spots, and lead to earlier ignition than in a neat material. Moreover, the inclusion of different types of impurities will have a different effect in the performance of the explosive compared to a single type of added impurities. Understanding the effect these impurities have (in isolation, in single-impurity type matrices and in multiple-impurity type matrices) on the ignition sensitivity of the material will allow better control of the explosive performance.

To this end, experimental and numerical studies have been performed to identify the process governing the cavity collapse and determine the mechanical effects behind hot spot generation. For an extensive discussion on these see the paper by Michael and Nikiforakis [10] and references therein. However, the interaction of a shock wave with solid particles or with a matrix combining cavities and solid particles has not been studied extensively. To the authors’ knowledge, Bourne and Field [3] are the only ones who presented a study of cavity collapse in an inert liquid laden with solid (lead and nylon) particles.

Similar studies were done by numerical means, examining the shock-cavity interaction process in various configurations, mostly considering the collapse in inert gaseous or solid media, or the pressure field and pressure amplification in multi-cavity scenarios. For a detailed discussion of these the reader is refereed to [10, 11]. The two and three-dimensional isolated cavity collapse in inert and reactive nitromethane was presented by Michael and Nikiforakis in [7, 10, 11], focusing on the temperature field induced by the collapse and subsequent ignition of the explosive.

A relatively small number of numerical studies can be found on the shock interaction with deformable particles. Ling et al. [5] studied the shock interaction of an aluminium particle in nitromethane, and Zhang et al. [19] modelled the shock interaction with magnesium, tungsten, beryllium and uranium in nitromethane, in isolation and in clusters, to study the velocities attained by the particles. The acceleration and heating of aluminium particles of several sizes in detonating nitromethane was studied by Ripley et al. [15]; Sridharan et al. [18] computed the transient drag of an aluminium particle in nitromethane, after its interaction with a shock. Menikoff [6] studied the hot spot formation from glass bead shock reflections in inert nitromethane.

In conclusion, although there is some body of evidence towards understanding the generation of hot spots by cavity collapse, more insight is needed to understand the effect of shock-particle interaction on the temperature field of the material and hence on the control of the performance of the explosive. Moreover, besides [3], there are no studies on the effects of the combined effect of particles and cavities.

In this work we present and compare the effects of different types of impurities, namely PMMA particles and gas cavities, in isolation and in matrix configuration (multi-cavity, multi-bead and cavity-bead combination), assessing their effect on the ignition control of the explosive.

A multi-physics methodology is employed to perform these simulations. The hydrodynamic model presented in [8] is used to model the explosive and air cavities and a full elastoplastic model is used to describe the response of PMMA particles. The two models are of the same hyperbolic form and are thus solved with high resolution shock-capturing schemes. Communication between the two materials and the corresponding sets of equations is achieved by means of a variant of the ghost fluid method which uses mixed Riemann solvers, see [9]. This approach overcomes several challenges presented in simulating such a complex physical scenario. The hydrodynamic model used for the explosive and air cavities allows the non-trivial use of complex equations of state for describing the explosive and the cavities, retains at least 1000:1 density difference across the cavity boundary while maintaining oscillation free interfaces (in terms of pressures, velocities and temperatures) and allows the recovery of realistic temperature fields in the explosive matrix.

A major challenge worthy of special attention is the accurate and oscillation-free recovery of temperature fields in the explosive matrix. This is of critical importance as the ignition process of the energetic material is a temperature-driven effect, thus the accurate prediction of ignition relies on physically meaningful temperatures. For more information on this the reader is referred to [10, 11]. This model allows for oscillation-free temperature fields. The elastoplastic model we use to model the solid materials is rendered in hyperbolic form and thus can be solved on an Eulerian mesh, using finite volume methods. This eliminates mesh tangling issues that might occur in Lagrangian approaches and allows the immediate communication between the hyperbolic and elastoplastic materials by means of the ghost fluid method.

2 Mathematical Models

In this section, the distinct mathematical formulations used to describe the fluid and solid elastoplastic materials in the interaction of a shock wave with voids and particles in an explosive are presented.

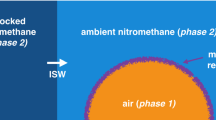
The explosives (hydrodynamic) model The air cavities immersed in nitromethane are modelled using the MiNi16 formulation [8], which is summarised below. The gas inside the cavities is described as phase 1, with density, velocity vector and pressure ($\rho _{1},\mathbf {u}_{1},p_{1}$). The nitromethane is denoted as phase 2 with density, velocity vector and pressure ($\rho _{2},\mathbf {u}_{2},p_{2}$). We denote by z a colour function, which can be considered to be the volume fraction of the air with respect to the volume of the total mixture of phases 1 and 2, with density $\rho$. For convenience, we denote z by $z_1$ and $1-z$ by $z_2$. Then, the closure condition $z_1+z_2=1$ holds. Velocity and pressure equilibrium applies between the all phases, such that $u_{\alpha }=u_{\beta }=u_1=u_2=u$ and $p_{\alpha }=p_{\beta }=p_1=p_2=p$.

Then, the MiNi16 system is described as in [8] by:

$$\begin{aligned} \frac{\partial z_1 \rho _1}{\partial t}+ \nabla \cdot (z_1 \rho _1 \mathbf {u})= & {} 0,\end{aligned}$$

(1)

$$\begin{aligned} \frac{\partial z_2 \rho _2}{\partial t}+\nabla \cdot (z_2 \rho _2 \mathbf {u})= & {} 0, \end{aligned}$$

(2)

$$\begin{aligned} \frac{\partial }{\partial t}(\rho \mathbf {u_i})+\nabla \cdot (\rho \mathbf {u_iu})+\frac{\partial p}{\partial {\mathbf {x_i}}}= & {} 0,\end{aligned}$$

(3)

$$\begin{aligned} \frac{\partial }{\partial t}(\rho E)+\nabla \cdot (\rho E+p)\mathbf {u}= & {} 0,\end{aligned}$$

(4)

$$\begin{aligned} \frac{\partial z_1 }{\partial t} + \mathbf {u} \cdot \nabla z_1= & {} 0,\end{aligned}$$

(5)

$$\begin{aligned} \frac{\partial z_2 \rho _2 \lambda }{\partial t}+\nabla \cdot (z_2 \rho _2 \mathbf {u}\lambda )= & {} z_2 \rho _2 K, \end{aligned}$$

(6)

where $\mathbf {u}=(u,v,w)$ denotes the total vector velocity, i denotes space dimension, $i=1,2,3$, $\rho$ the total density of the system and E the specific total energy given by $E=e+\frac{1}{2}\sum _{i}u_i^2$, with e the total specific internal energy of the system. We denote by $\lambda$ the mass fraction of the explosive, such that $\lambda =1$ denotes fully unburnt material and $\lambda =0$ denotes fully burnt material. As this work is restricted to the inert scenario, $\lambda =0$ everywhere and the equations reduce to those by Allaire et al. [1].

In this work, all fluid components described by the MiNi16 model are assumed to be governed by a Mie-Grüneisen equation of state, of the form:

$$\begin{aligned} p=p_{{ref}_i}+\rho _i\varGamma _i(e_i-e_{{ref}_i}), \; \text{ for } \;i=1,2. \end{aligned}$$

(7)

Material interfaces between the phases are described by a diffused interface technique. Hence, mixture rules need to be defined for the diffusion zone, relating the thermodynamic properties of the mixture with those of the individual phases. The mixture rules for the specific internal energy, density and adiabatic index ($\gamma =1+\frac{1}{\xi }$) are:

$$\begin{aligned} \rho e=z_1\rho _1e_1+z_2\rho _2e_2, \quad \rho = z_1\rho _1+z_2\rho _2, \; \text {and} \;\; \xi =z_1\xi _1+z_2\xi _2, \end{aligned}$$

(8)

where $e_1,e_2$ denote the specific internal energies of phases 1 and 2.

The sound speed also follows a mixture rule given as:

$$\begin{aligned} \xi c^2=\sum _i y_i\xi _ic_i^2, \end{aligned}$$

(9)

where $c_i$ is the individual sound speed of phase i and $y_i=\frac{\rho _i z_i}{\rho }$ its mass fraction. For more information on this as well as for the numerical evaluation of the total equation of state the reader is referred to [8]. Validation of the hydrodynamic mathematical model can be found in [10].

Equations of state for nitromethane and air To close the hydrodynamic system, the Cochran-Chan equation of state [16] is employed to describe the liquid nitromethane. This is an equation of state of Mie-Grüneisen form given by Eq. 7 with reference pressure given by

$$\begin{aligned} p_{\text {ref}}(\rho )=\mathcal {A}\Big (\frac{\rho _0}{\rho }{\Big )^{-\mathcal {E}_1}-\mathcal {B}\Big (\frac{\rho _0}{\rho }{\Big )^{-\mathcal {E}_2}}},\end{aligned}$$

(10)

reference energy given by

$$\begin{aligned} e_{\text {ref}}(\rho )=\frac{-\mathcal {A}}{\rho _0(1-\mathcal {E}_1)}\Big [\Big (\frac{\rho _0}{\rho }\Big )^{1-\mathcal {E}_1}-1\Big ] +\frac{\mathcal {B}}{\rho _0(1-\mathcal {E}_2)}\Big [\Big (\frac{\rho _0}{\rho }\Big )^{1-\mathcal {E}_2}-1\Big ] \end{aligned}$$

(11)

and Grüneisen coefficient $\varGamma (\rho )=\varGamma _0.$ The gas inside the cavity (where applicable) is modelled by the ideal gas equation of state, which is of Mie-Grüneisen form as well, with $p_{\text {ref}}=0$ and $e_{\text {ref}}=0$ . The parameters for the equations of state of the two materials are given in Table 1.

Table 1 Equation of state parameters for nitromethane and air

Recovery of temperature The multi-phase nature of the model allows for separate temperature fields to be computed for each material as

$$\begin{aligned} T_i=\frac{p-p_{\text {ref}_i}(\rho )}{\rho _i\varGamma _ic_{v_i}}, \quad \text{ for } \quad i=1,2. \end{aligned}$$

(12)

As a result, the nitromethane temperature ($T_{\text {NM}}=T_2$) is computed explicitly from the equation of state and can be used directly in the reaction rate law.

Computing the temperature of a general condensed phase explosive ($T_{\text {CF}}=T_2$) can involve completing the equation of state starting from the basic thermodynamic law $T \frac{\mathrm {d}S}{\mathrm {d}v}=c_v\frac{\mathrm {d}T}{\mathrm {d}v}+c_v\frac{\varGamma T}{v}$ and by integrating to obtain a reference temperature ($T_{{\text {ref}_\text {CF}}}$) such that:

$$\begin{aligned} T_{\text {CF}}=\frac{p-p_{{\text {ref}_\text {CF}}}(\rho )}{\rho _{\text {CF}}\varGamma _{\text {CF}}c_{v_\text {CF}}} - T_{{\text {ref}_\text {CF}}}. \end{aligned}$$

(13)

When the reference curve is an isentrope, $\mathrm {d}S/\mathrm {d}v=0$ and hence we can simply compute $T_{\text {ref}_\text {CF}}=T_0(\frac{\rho }{\rho _0})^\varGamma$. When the reference curve is a Hugoniot curve, the basic thermodynamic law cannot be integrated directly and often the Walsh Christian technique and numerical ODE-integration techniques are used to compute the reference Hugoniot temperature.

For this work, substitution of the parameters of the equation of state for nitromethane and imposing an initial temperature of ${298}\;{\text {K}}$ for $\rho =\rho _0$ gives $T_0=0$. This is in line with other work using the Cochran-Chan equation of state, where $T_0$ takes zero or very small values. The form (12) gives temperatures that match experiments as demonstrated in [10], but for other materials or other equations of state (e.g., shock Mie-Grüneisen) care should be taken as a different reference curve (as per Eq. 13) would be necessary.

The ideal gas equation of state results in the overheating of the gas inside the cavity since high pressures are reached within the cavity during the collapse process. However, the very short timescale of the process means that heat transfer does not take place and thus the cavity temperature does not affect the ambient nitromethane temperature. Since temperatures inside the cavity are not of interest for this work, they are not presented henceforth.

Note that the two-phase nature of the model allows for large (>1000:1) density gradients to be sustained across material boundaries and both the density and temperature fields are maintained oscillation-free.

The elastoplastic model In this work, we use the elastic solid model described by Schoch et al. [17] and Barton et al. [2], based on the formulation by Godunov and Romenskii [4] to describe the physical behaviour of the solid particles. Plasticity of the material is included, following the work of Miller and Colella [13].

In an Eulerian frame employed in this work, there is no mesh distortion that can be used to describe the solid material deformation. Thus the material distortion needs to be accounted for in a different way. Here, this is done by defining the elastic deformation gradient as $F^e_{ij} = \frac{\partial x_i}{\partial X_j},$ which maps the coordinate $\mathbf {X}$ in the initial configuration to the coordinate $\mathbf {x}$ in the deformed configuration.

The state of the solid is characterised by the elastic deformation gradient, velocity $u_i$ and entropy S. Following the work by Barton et al. [2], the complete three-dimensional system forms a hyperbolic system of conservation laws for momentum, strain and energy:

$$\begin{aligned} \frac{\partial {\rho u_i}}{\partial t} + \frac{\partial (\rho u_i u_m - \sigma _{im})}{\partial x_m}= & {} 0, \end{aligned}$$

(14)

$$\begin{aligned} \frac{\partial {\rho E}}{\partial t} + \frac{\partial (\rho u_m E - u_i \sigma _{im})}{\partial x_m}= & {} 0, \end{aligned}$$

(15)

$$\begin{aligned} \frac{\partial {\rho F^e_{ij}}}{\partial t} + \frac{\partial (\rho F^e_{ij}u_m-\rho F^e_{m j}u_i)}{\partial x_m}= & {} -u_i\frac{\partial \rho F^{e}_{mj}}{\partial x_m} + P_{ij}, \end{aligned}$$

(16)

$$\begin{aligned} \frac{\partial {\rho \kappa }}{\partial t} + \frac{\partial (\rho u_m \kappa )}{\partial x_m}= & {} \rho \dot{\kappa }, \end{aligned}$$

(17)

with the vector components $\cdot _i$ and tensor components $\cdot _{ij}$. The first two equations along with the density-deformation gradient relation $\rho = \rho _0 / \text {det}\mathbf {F}^e,$ where $\rho _0$ is the density of the initial unstressed medium, essentially evolve the solid material hydrodynamically. Here, $\sigma$ is the stress, E the total energy such that $E=\frac{1}{2}|u|^2+e$, with e the specific internal energy and $\kappa$ the scalar material history that tracks the work hardening of the material through plastic deformation. We denote the source terms associated with the plastic update as $P_{ij}$.

The system is closed by an analytic constitutive model relating the specific internal energy to the deformation gradient, entropy and material history parameter (if applicable) $e = e(\mathbf {F}^e,S,\kappa ).$ For more information the reader is referred to [9].

The deformation is purely elastic until the physical state is evolved beyond the yield surface ($f>0$), which in this work is taken to be:

$$\begin{aligned} f(\varvec{\sigma } )=||\text {dev}\varvec{\sigma }||-\sqrt{\frac{2}{3}}\sigma _Y = 0, \; \text {with} \;\; \text {dev} \varvec{\sigma } = \varvec{\sigma }-\frac{1}{3}(\text {tr}\varvec{\sigma })I, \end{aligned}$$

(18)

where $\sigma _Y$ is the yield stress and the matrix norm ||.|| the Shur norm ($||\varvec{\sigma }||^2=\text {tr}(\varvec{\sigma }^T\varvec{\sigma }$)).

As this identifies the maximum yield allowed to be reached by an elastic-only step, a predictor-corrector method is followed to re-map the solid state onto the yield surface. Assuming that the simulation timestep is small, this is taken to be a straight line, using the associative flow rate ($\dot{\epsilon }^p=\eta \frac{\partial F}{\partial \sigma }$), satisfying the maximum plastic dissipation principle (i.e. the steepest path). In general, this re-mapping procedure is governed by the dissipation law $\psi _{plast} =\varvec{\varSigma } :((\mathbf {F}^p)^{-1}\dot{\mathbf {F}^p}),$ where $\varvec{\varSigma }=\varvec{G}\varvec{\sigma }\varvec{F}$ and $:$ is the double contraction of tensors (e.g. $\varvec{\sigma }:\varvec{\sigma }=\text {tr}(\varvec{\sigma }^T\varvec{\sigma })$). The initial prediction is $\mathbf {F} = \mathbf {F}^e$ and $\mathbf {F}^p = \mathbf {I}$, where $\mathbf {F}$ is the specific total deformation tensor and $\mathbf {F}^p$ the plastic deformation tensor that contains the contribution from plastic deformation. This is then relaxed to the yield surface according to the procedure of Miller and Colella [13].

The explosive and solid mathematical formulations described in this section are solved numerically using high-resolution, shock-capturing, Riemann-problem based methods and structured, hierarchical adaptive mesh refinement, as described in previous work [7, 8, 12, 17].

Equation of state for PMMA To close the elastoplastic system, the PMMA is described by an energy-independent shock Mie-Grüneisen (Hugoniot) equation of state where the parameters for PMMA for $\rho _0$, the reference density for identity deformation, s the linear shock speed-particle speed ratio, $c_0$ the unshocked sound speed and $T_0$ the reference temperature are given in Table 2. Validation of the elastoplastic mathematical model can be found in [9].

Table 2 Shock Mie-Grüneisen equation of state parameters the elastoplastic (with perfect plasticity) PMMA

The multi-material approach In this work, we use level set methods to track the solid-explosive¹ interface. The behaviour of the material components at the interface is modelled by the implementation of dynamical boundary conditions with the aid of the Riemann ghost fluid method and devised mixed-material Riemann solvers to solve the interfacial Riemann problems between materials. For more details on the method the reader is referred to [9].

3 Results

In this section we study the interaction of an isolated PMMA particle, a $2\times 2$ PMMA particles matrix, an air cavity, a $2\times 2$ air cavity matrix and a $2\times 2$ matrix of 2 cavities and 2 particles with a 10.98 GPa shock wave in non-reactive liquid nitromethane. Nitromethane is modelled by the Cochran-Chan equation of state given by Eqs. (7)–(11) and PMMA using a shock Mie-Grüneisen with constant shear and perfect plasticity both described in Sect. 2. As the ignition and thermal runaway in an explosive are attributed to the complex interaction between non-linear gas dynamics and chemistry, it is intuitive to consider in the first instance the induced temperature field in the explosive in the absence of chemical reactions. This will allow the purely gas-dynamical effects to be elucidated. In effect, by controlling the induced temperature field in the explosive material (by the judiciary inclusion of voids and beads) we can control its ignition time. The simulations are performed in two dimensions, with effective grid size $\text {d}x=\text {d}y=0.625\;\upmu {\text {m}}$. The initial conditions for the simulations in this work are given in Table 3.

3.1 Single PMMA Bead

In Fig. 1 we present the temperature field generated in the nitromethane upon the interaction of the incident shock wave (S$_0$) with the PMMA bead originally centred at $(x,y)=(0.18,0.2)\,{\text {mm}}$, of radius of $0.08\,{\text {mm}}$. The temperatures in the bead are omitted as the timescales are small for heat transfer to occur between the two materials. Instead, we display a mock-schlieren plot inside the bead. As the bead is symmetric about the horizontal axis we present only the upper half of the configuration. The interaction of the incident shock wave with the bead generates two new shock waves, one travelling upstream into the nitromethane (S$_1$) and one downstream into the bead (S$_2$). The upstream travelling shock compresses again the nitromethane, which reaches temperatures of $1300\,{\text {K}}$, only ${\sim }30\,{\text {K}}$ higher than those generated by the original incident shock wave (Fig. 1a). The angle of interaction of the shock wave and the bead continuously changes, resulting to a transition from a regular shock reflection to a Mach reflection. A pair of Mach stems is generated at the top and bottom of the bead; the top one is seen in Fig. 1a. In fact, the largest temperature increase in this configuration is attributed to the Mach stem, leading to temperatures of ${\sim }400-500\,{\text {K}}$ higher than the post incident-shock temperature (Fig. 1a). The Mach stem grows and the Mach stem triple point moves away from the bead, along the incident shock wave (Fig. 1b) forming a band of high temperatures. Finally the shock wave traversing the bead exits into the nitromethane and continues travelling with the incident shock wave. The higher impedance of the bead compared to the nitromethane contributes (along with the Mach reflection) to the curvature of the wave front (S$_{0,2}$), travelling now downstream the bead. Upon exiting the beam, the shock wave (S$_2$) is weaker than the incident shock wave, leading to temperatures of only ${\sim }1000-1050\,{\text {K}}$ (Fig. 1b), which are lower than the original post-shock temperatures induced by the incident shock wave (S$_0$). Another interesting observation is that the temperature along the final downstream-travelling shock wave (S$_{0,2}$) is not uniform.

Table 3 Initial conditions for the shock-bead interaction and shock-induced cavity collapse in inert nitromethane considered in this work

Fig. 1

Temperature field in nitromethane

3.2 2 $\times$ 2 Matrix of Air Cavities

A common way of controlling the generation of higher temperatures in the explosive material is the inclusion of cavities. The authors have extensively studied single-cavity collapse in nitromethane in [10, 11] thus in this work we do not repeat these results. In multi-cavity configurations, the waves generated upon the collapse process of each cavity interact in the regions in between the voids leading to elevations of temperatures higher than in single-cavity configurations [14]. The authors have studied this scenario before for cavities collapsing in water [12] generating the same wave patterns so we will limit here the discussion to the wave interaction and its effect on the nitromethane temperature field.

The first locally high temperature ($T\sim {2960}\,{\text {K}}$) in this scenario is encountered upon the collapse of the first column of cavities, upstream of the cavities in the Back Hot Spot (BHS - as defined in [10]), at $t={0.04}\,\upmu {\text {s}}$. The next locally high temperature is found in the Mach Stem Hot Spot (MSHS) generated after the collapse of the first column of cavities at $t={0.055}\,\upmu {\text {s}}$. The superposition of the lower Mach stem of the top void and the upper Mach stem of the lower void along the centreline of the matrix generates temperatures of ${\sim }{2880}\,{\text {K}}$. The highest temperature peaks in this scenario are attributed to the supersposition of waves during the collapse of the second column of cavities. At $t={0.1}\,\upmu {\text {s}}$ the superposition of waves upstream of the second column gives temperatures of ${\sim }{5275}\,{\text {K}}$ in between the cavities’ lobes. Similarly, in between the lobes of the first column’s cavities highs of $T\sim {4660}\,{\text {K}}$ are seen at $t={0.115}\,\upmu {\text {s}}$. It is concluded that wave superposition plays the most important role in temperature increase in this multi-cavity scenario.

3.3 2 $\times$ 2 Matrix of PMMA Beads

In this section we investigate the effect of a $2\times 2$ matrix of PMMA beads on the nitromethane temperature field. In the mock schlieren plots of Fig. 2a we see the first interaction of the S$_1$ from the first two beads along the centreline of the matrix, perpendicular to the incident shock. Subsequently, S$_{1B}$, the S$_1$ wave from the bottom bead impacts onto the top bead and similarly S$_{1T}$, the S$_1$ wave from the top bead impacts onto the bottom bead. This leads to new shock waves inside and outside the beads. The shocks outside the beads interact with the Mach stems and the two Mach stems eventually intersect. After the exit of the shocks from the beads, the new lead shock (S$'_0$), along which different temperature ranges can be found, interacts with the next two beads and the shock-bead interaction as well as the wave superpositions are repeated (Fig. 2b).

Fig. 2

Mock-schlieren plots (top half) illustrating the interaction of waves and temperature field in nitromethane (bottom half) in a $2\times 2$ PMMA bead configuration

The interaction of the shock with each bead leads to the formation of a high-temperature band on each side of each bead. This can be seen, for the outer parts of the beads, in Fig. 2b. The temperature in the bands, however, is lower than in the original Mach stem. The bands on the inner sides of the beads, as seen in the same figure, are superimposed in the region in between the beads, leading to new high temperature regions. Consequently, the new lead shock (S$'_0$) has variable temperature ranges along its front and a higher temperature along its middle compared to the isolated shock-bead interaction scenario. Moreover, the part of the new lead shock that is now directly in front of the first column of beads, in the region directly in front of the beads it is actually weaker then the original incident shock wave. Thus, the subsequent beads that are in the shadow of the first column beads will feel a weaker shock, leading to lower temperatures compared to the temperatures produced by the first column.

In this configuration, the first high temperature peak is seen when the Mach stem is generated at the top and bottom of the beads of the first column ($T\sim {1770}\,{\text {K}}$) at $t={0.015}\,\upmu {\text {s}}$. The second high temperature peak is seen when the Mach stem is generated at the sides of the beads of the second column ($T\sim {1750}\,{\text {K}}$) at $t={0.065}\,\upmu {\text {s}}$.

3.4 Combination of 2 Cavities and 2 Beads

In this section, we combine two air cavities and two PMMA beads in a $2\times 2$ array, with a clockwise ordering of cavity-bead-bead-cavity. The clockwise ordering of bead-cavity-cavity-bead is the same scenario reflected about the horizontal axis and it is thus not discussed separately. In this configuration, the highest temperatures are observed during the cavity collapse and not the shock-bead interaction (Fig. 3b, d). Looking at the interaction of the incident shock wave with the first column of impurities we observe that the shock wave S$_1$ generated upon the interaction of the incident shock and the bead is superimposed with the rarefaction wave (R$_1$) generated upon the interaction of the incident shock wave and the air cavity (Fig. 3a). As a result this shock wave weakens and when it interacts with the cavity it does not lead to its asymmetric collapse (Fig. 3a). The shock waves generated upon the collapse of the top cavity, however have a significant effect on the deformation of the lower bead (Figs. 3c, 4a, c). The interaction of the shock wave emanating at the collapse of the top cavity, as well as the Mach stem generated by the interaction of the top bead with the incident shock (S$'_0$ in this case) leads, however to the asymmetric collapse of the lower cavity. The jet deviation can be seen in Fig. 4a and the earlier generation of the upper Mach stem (compared to the lower one) around the lower cavity is seen in Fig. 4c. This has as a result a higher temperature in this upper Mach stem of the lower cavity compared to the Mach stems of the upper cavity (${3295}\,{\text {K}}$ compared to ${2300}\,{\text {K}}$). The localised maxima of high temperatures in this scenario correspond to the MSHS of the top bead ($T={1645}\,{\text {K}}$) at $t={0.02}\,\upmu {\text {s}}$, the BHS of the lower void, ($T={2940}\,{\text {K}}$) at $t={0.04}\,\upmu {\text {s}}$, and lower cavity top MSHS ($T={3240}\,{\text {K}}$) at $t={0.105}\,\upmu {\text {s}}$.

Fig. 3

Mock-schlieren plots (left) illustrating the interaction of waves and the induced temperature field in nitromethane (right) in a clockwise cavity-bead-bead-cavity configuration

Fig. 4

Mock-schlieren plots (left) illustrating the interaction of waves and the induced temperature field in nitromethane (right) in a clockwise cavity-bead-bead-cavity configuration (continued from Fig. 3)

3.5 Analysis of the Temperature Field

In order to infer the effect of the impurities on the shocked material, we need to consider the maximum temperature of the explosive for any given combination of impurities. To this end we compare in Fig. 5 the maximum nitromethane temperature as a function of time, for five different impurity configurations. These include: an isolated cavity, an isolated bead, a $2\times 2$ matrix of cavities, a $2\times 2$ matrix of beads and a $2\times 2$ matrix combining 2 cavities and 2 beads. We also include as a dashed black line the post-shock temperature of neat nitromethane; i.e., the temperature that the shocked material would reach if no impurities were present.

We observe that the smallest temperature increase occurs by the single bead scenario and slightly higher temperatures in the multi-bead example, which indicates that the inclusion of beads is suitable for subtle adjustment of temperature. The inclusion of voids should be preferred when higher temperature elevations are needed, leading to a more abrupt sensitivity increase of the material. In practice, the desired temperature rise can be achieved to a leading order by means of cavities, while marginal adjustment can be done by solid particles.

These initial results have to be verified by large-scale computations, where a statistically-significant number of cavities and particles are included in a larger sample of the explosive. We also anticipate that dimensionality effects are important, as could potentially be the non-uniform distribution of the impurities and the material of the particles.

Fig. 5

Maximum temperature distribution in nitromethane over time, in the five configurations studied in this work. The dotted black line gives the reference of the post-shock temperature in neat nitromethane

4 Conclusion

In this work we employ a multi-physics computational framework to study the effect of air cavities and PMMA particles on the sensitisation of condensed-phase explosives as a means of controlling their performance. The framework simultaneously solves a multi-phase hydrodynamic model for the explosive and for the air cavities, and an elastoplastic model for the solid particles. Communication between the different states of matter (the solid and the two fluids) is achieved by means of a variant of the ghost fluid method. We study the effect of five configurations of impurities (isolated cavity, isolated bead, a multi-cavity and a multi-bead configuration and a combined cavity-bead matrix) in nitromethane and determine their relative effect on the temperature field. Initial results indicate that cavities have a more profound effect on sensitisation, compared to PMMA particles; more extended studies are necessary in order to assess the effect of dimensionality, distribution of the impurities and of the material of the particles. This knowledge can be used to accurately control the sensitivity and the performance of nonideal mining explosives.