Non-Malleable Codes for Partial Functions with Manipulation Detection

Abstract

Non-malleable codes were introduced by Dziembowski, Pietrzak and Wichs (ICS ’10) and its main application is the protection of cryptographic devices against tampering attacks on memory. In this work, we initiate a comprehensive study on non-malleable codes for the class of partial functions, that read/write on an arbitrary subset of codeword bits with specific cardinality. Our constructions are efficient in terms of information rate, while allowing the attacker to access asymptotically almost the entire codeword. In addition, they satisfy a notion which is stronger than non-malleability, that we call non-malleability with manipulation detection, guaranteeing that any modified codeword decodes to either the original message or to $\bot$. Finally, our primitive implies All-Or-Nothing Transforms (AONTs) and as a result our constructions yield efficient AONTs under standard assumptions (only one-way functions), which, to the best of our knowledge, was an open question until now. In addition to this, we present a number of additional applications of our primitive in tamper resilience.

A. Kiayias—Research partly supported by the H2020 project FENTEC (# 780108).

F.-H. Liu—Research supported by the NSF Award #CNS-1657040.

Y. Tselekounis—Research partly supported by the H2020 project PANORAMIX (# 653497).

1 Introduction

Non-malleable codes (NMC) were introduced by Dziembowski, Pietrzak and Wichs [27] as a relaxation of error correction and error detection codes, aiming to provide strong privacy but relaxed correctness. Informally, non-malleability guarantees that any modified codeword decodes either to the original message or to a completely unrelated one, with overwhelming probability. The definition of non-malleability is simulation-based, stating that for any tampering function $f$, there exists a simulator that simulates the tampering effect by only accessing $f$, i.e., without making any assumptions on the distribution of the encoded message.

The main application of non-malleable codes that motivated the seminal work by Dziembowski et al. [27] is the protection of cryptographic implementations from active physical attacks against memory, known as tampering attacks. In this setting, the adversary modifies the memory of the cryptographic device, receives the output of the computation, and tries to extract sensitive information related to the private memory. Security against such types of attacks can be achieved by encoding the private memory of the device using non-malleable codes. Besides that, various applications of non-malleable codes have been proposed in subsequent works, such as CCA secure encryption schemes [20] and non-malleable commitments [4].

Due to their important applications, constructing non-malleable codes has received a lot of attention over recent years. As non-malleability against general functions is impossible [27], various subclasses of tampering functions have been considered, such as split-state functions [1,2,3, 26, 27, 36, 37], bit-wise tampering and permutations [4, 5, 27], bounded-size function classes [32], bounded depth/fan-in circuits [6], space-bounded tampering [29], and others (cf. Sect. 1.4). One characteristic shared by those function classes is that they allow full access to the codeword, while imposing structural or computational restrictions to the way the function computes over the input. In this work we initiate a comprehensive study on non-malleability for functions that receive partial access over the codeword, which is an important yet overlooked class, as we elaborate below.

The class of partial functions. The class of partial functions contains all functions that read/write on an arbitrary subset of codeword bits with specific cardinality. Concretely, let $c$ be a codeword with length $\nu$. For $\alpha \in [0,1)$, the function class $\mathcal {F}^{\alpha \nu }$ (or $\mathcal {F}^{\alpha }$ for brevity) consists of all functions that operate over any subset of bits of $c$ with cardinality at most $\alpha \nu$, while leaving the remaining bits intact. The work of Cheraghchi and Guruswami [18] explicitly defines this class and uses a subclass (the one containing functions that always touch the first $\alpha \nu$ bits of the codeword) in a negative way, namely as the tool for deriving capacity lower bounds for information-theoretic non-malleable codes against split-state functions. Partial functions were also studied implicitly by Faust et al. [32], while aiming for non-malleability against bounded-size circuits.¹

Even though capacity lower bounds for partial functions have been derived (cf. [18]), our understanding about explicit constructions is still limited. Existential results can be derived by the probabilistic method, as shown in prior works [18, 27]², but they do not yield explicit constructions. On the other hand, the capacity bounds do not apply to the computational setting, which could potentially allow more practical solutions. We believe that this is a direction that needs to be explored, as besides the theoretical interest, partial functions is a natural model that complies with existing attacks that require partial access to the registers of the cryptographic implementation [8, 10,11,12, 44].³

Besides the importance of partial functions in the active setting, i.e., when the function is allowed to partially read/write the codeword, the passive analogue of the class, i.e., when the function is only given read access over the codeword, matches the model considered by All-Or-Nothing Transforms (AONTs), which is a notion originally introduced by Rivest [41], providing security guarantees similar to those of leakage resilience: reading an arbitrary subset (up to some bounded cardinality) of locations of the codeword does not reveal the underlying message. As non-malleable codes provide privacy, non-malleability for partial functions is the active analogue of (and in fact implies) AONTs, that find numerous applications [13, 14, 40, 41, 43].

Plausibility. At a first glance one might think that partial functions better comply with the framework of error-correction/detection codes (ECC/EDC), as they do not touch the whole codeword. However, if we allow the adversary to access asymptotically almost the entire codeword, it is conceivable it can use this generous access rate, i.e., the fraction of the codeword that can be accessed (see below), to create correlated encodings, thus we believe solving non-malleability in this setting is a natural question. Additionally, non-malleability provides simulation based security, which is not considered by ECC/EDC.

We illustrate the separation between the notions using the following example. Consider the set of partial functions that operate either on the right or on the left half of the codeword (the function chooses if it is going to be left or right), and the trivial encoding scheme that on input message $s$ outputs $(s,s)$. The decoder, on input $(s,s')$, checks if $s= s'$, in which case it outputs $s$, otherwise it outputs $\bot$. This scheme is clearly an EDC against the aforementioned function class,⁴ as the output of the decoder is in $\{s, \bot \}$, with probability 1; however, it is malleable since the tampering function can create encodings whose validity depends on the message. On the other hand, an ECC would provide a trivial solution in this setting, however it requires restriction of the adversarial access fraction to 1/2 (of the codeword); by accessing more than this fraction, the attacker can possibly create invalid encodings depending on the message, as general ECCs do not provide privacy. Thus, the ECC/EDC setting is inapt when aiming for simulation based security in the presence of attackers that access almost the entire codeword. Later in this section, we provide an extensive discussion on challenges of non-malleability for partial functions.

Besides the plausibility and the lack of a comprehensive study, partial functions can potentially allow stronger primitives, as constant functions are excluded from the class. This is similar to the path followed by Jafargholi and Wichs [34], aiming to achieve tamper detection (cf. Sect. 1.4) against a class of functions that implicitly excludes constant functions and the identity function. In this work we prove that this intuition holds, by showing that partial functions allow a stronger primitive that we define as non-malleability with manipulation detection (MD-NMC), which in addition to simulation based security, it also guarantees that any tampered codeword will either decode to the original message or to $\bot$. Again, and as in the case of ECC/EDC, we stress out that manipulation/tamper-detection codes do not imply MD-NMC, as they do not provide simulation based security (cf. Sect. 1.4).⁵

Given the above, we believe that partial functions is an interesting and well-motivated model. The goal of this work is to answer the following (informally stated) question:

Is it possible to construct efficient (high information rate) non-malleable codes for partial functions, while allowing the attacker to access almost the entire codeword?

We answer the above question in the affirmative. Before presenting our results (cf. Sect. 1.1) and the high level ideas behind our techniques (cf. Sect. 1.2), we identify the several challenges that are involved in tackling the problem.

Challenges. We first define some useful notions used throughout the paper.

• Information rate: the ratio of message to codeword length, as the message length goes to infinity.

• Access rate: the fraction of the number of bits that the attacker is allowed to access over the total codeword length, as the message length goes to infinity.

The access rate measures the effectiveness of a non-malleable code in the partial function setting and reflects the level of adversarial access to the codeword. In this work, we aim at constructing non-malleable codes for partial functions with high information rate and high access rate, i.e., both rates should approach 1 simultaneously. Before discussing the challenges posed by this requirement, we first review some known impossibility results. First, non-malleability for partial functions with concrete access rate 1 is impossible, as the function can fully decode the codeword and then re-encode a related message [27]. Second, information-theoretic non-malleable codes with constant information rate (e.g., 0.5) are not possible against partial functions with constant access rate [18]⁶, and consequently, solutions in the information-theoretic settings such as ECC and Robust Secret Sharing (RSS) do not solve our problem. Based on these facts, in order to achieve our goal, the only path is to explore the computational setting, aiming for access rate at most $1-\epsilon$, for some $\epsilon >0$.

At a first glance one might think that non-malleability for partial functions is easier to achieve, compared to other function classes, as partial functions cannot touch the whole codeword. Having that in mind, it would be tempting to conclude that existing designs/techniques with minor modifications are sufficient to achieve our goal. However, we will show that this intuition is misleading, by pointing out why prior approaches fail to provide security against partial functions with high access rate.

The current state of the art in the computational setting considers tools such as (Authenticated) Encryption [1, 22, 24, 28, 36, 37], non-interactive zero-knowledge (NIZK) proofs [22, 28, 30, 37], and $\ell$-more extractable collision resistant hashes (ECRH) [36], where others use KEM/DEM techniques [1, 24]. Those constructions share a common structure, incorporating a short secret key $sk$ (or a short encoding of it), as well as a long ciphertext, $e$, and a proof $\pi$ (or a hash value). Now, consider the partial function $f$ that gets full access to the secret key $sk$ and a constant number of bits of the ciphertext $e$, partially decrypts $e$ and modifies the codeword depending on those bits. Then, it is not hard to see that non-malleability falls apart as the security of the encryption no longer holds. The attack requires access rate only $O ((|sk|)/(|sk| + |e| + |\pi |))$, for [22, 28, 37] and $O(\mathrm {poly}(k)/|s|)$ for [1, 24, 36]. A similar attack applies to [30], which is in the continual setting.

One possible route to tackle the above challenges, is to use an encoding scheme over the ciphertext, such that partial access over it does not reveal the underlying message.⁷ The guarantees that we need from such a primitive resemble the properties of AONTs, however this primitive does not provide security against active, i.e., tampering, attacks. Another approach would be to use Reconstructable Probabilistic Encodings [6], which provide error-correcting guarantees, yet still it is unknown whether we can achieve information rate 1 for such a primitive. In addition, the techniques and tools for protecting the secret key can be used to achieve optimal information rate as they are independent of the underlying message, yet at the same time, they become the weakest point against partial functions with high access rate. Thus, the question is how to overcome the above challenges, allowing access to almost the entire codeword.

In this paper we solve the challenges presented above based on the following observation: in existing solutions the structure of the codeword is fixed and known to the attacker, and independently of the primitives that we use, the only way to resolve the above issues is by hiding the structure via randomization. This requires a structure recovering mechanism that can either be implemented by an “external” source, or otherwise the structure needs to be reflected in the codeword in some way that the attacker cannot exploit. In the present work we implement this mechanism in both ways, by first proposing a construction in the common reference string (CRS) model, and then we show how to remove the CRS using slightly bigger alphabets. Refer to Sect. 1.2 for a technical overview.

1.1 Our Results

We initiate the study of non-malleable codes with manipulation-detection (MD-NMC), and we present the first (to our knowledge) construction for this type of codes. We focus on achieving simultaneously high information rate and high access rate, in the partial functions setting, which by the results of [18], it can be achieved only in the computational setting.

Our contribution is threefold. First, we construct an information rate $1$ non-malleable code in the CRS model, with access rate $1-1/\varOmega (\log k)$, where k denotes the security parameter. Our construction combines Authenticated Encryption together with an inner code that protects the key of the encryption scheme (cf. Sect. 1.2). The result is informally summarized in the following theorem.

Theorem 1.1

(Informal). Assuming one-way functions, there exists an explicit computationally secure MD-NMC in the CRS model, with information rate $1$ and access rate $1-1/\varOmega (\log k)$, where k is the security parameter.

Our scheme, in order to achieve security with error $2^{-\varOmega (k)}$, produces codewords of length $|s|+O(k^2 \log k)$, where |s| denotes the length of the message, and uses a CRS of length $O(k^2 \log k \log (|s| +k))$. We note that our construction does not require the CRS to be fully tamper-proof and we refer the reader to Sect. 1.2 for a discussion on the topic.

In our second result we show how to remove the CRS by slightly increasing the size of the alphabet. Our result is a computationally secure MD-NMC in the standard model, achieving information and access rate $1-1/\varOmega (\log k)$. Our construction is proven secure by a reduction to the security of the scheme presented in Theorem 1.1. Below, we informally state our result.

Theorem 1.2

(Informal). Assuming one-way functions, there exists an explicit, computationally secure MD-NMC in the standard model, with alphabet length $O(\log k)$, information rate $1-1/\varOmega (\log k)$ and access rate $1-1/\varOmega (\log k)$, where k is the security parameter.

Our scheme produces codewords of length $|s|(1+1/O(\log k))+O(k^2 \log ^2 k)$.

In Sect. 1.2, we consider security against continuous attacks. We show how to achieve a weaker notion of continuous security, while avoiding the use of a self-destruct mechanism, which was originally achieved by [28]. Our notion is weaker than full continuous security [30], since the codewords need to be updated. Nevertheless, our update operation is deterministic and avoids the full re-encoding process [27, 37]; it uses only shuffling and refreshing operations, i.e., we avoid cryptographic computations such as group operations and NIZKs. We call such an update mechanism a “light update.” Informally, we prove the following result.

Theorem 1.3

(Informal). One-way functions imply continuous non-malleable codes with deterministic light updates and without self-destruct, in the standard model, with alphabet length $O(\log k)$, information rate $1-1/\varOmega (\log k)$ and access rate $1-1/\varOmega (\log k)$, where k is the security parameter.

As we have already stated, non-malleable codes against partial functions imply AONTs [41]. The first AONT was presented by Boyko [13] in the random oracle model, and then Canetti et al. [14] consider AONTs with public/private parts as well as a secret-only part, which is the full notion. Canetti et al. [14] provide efficient constructions for both settings, yet the fully secure AONT (called “secret-only” in that paper) is based on non-standard assumptions.⁸

Assuming one-way functions, our results yield efficient, fully secure AONTs, in the standard model. This resolves, the open question left in [14], where the problem of constructing AONT under standard assumptions was posed. Our result is presented in the following theorem.

Theorem 1.4

(Informal). Assuming one-way functions, there exists an explicit secret-only AONT in the standard model, with information rate $1$ and access rate $1-1/\varOmega (\log k)$, where k is the security parameter.

The above theorem is derived by the Informal Theorem 1.1 yielding an AONT whose output consists of both the CRS and the codeword produced by the NMC scheme in the CRS model. A similar theorem can be derived with respect to the Informal Theorem 1.2. Finally, and in connection to AONTs that provide leakage resilience, our results imply leakage-resilient codes [37] for partial functions.

In the full version of the paper we provide concrete instantiations of our constructions, using textbook instantiations [35] for the underlying authenticated encryption scheme. For completeness, we also provide information theoretic variants of our constructions that maintain high access rate and thus necessarily sacrifice information rate.

1.2 Technical Overview

On the manipulation detection property. In the present work we exploit the fact that the class of partial functions does not include constant functions and we achieve a notion that is stronger than non-malleability, which we call non-malleability with manipulation detection. We formalize this notion as a strengthening of non-malleability and we show that our constructions achieve this stronger notion. Informally, manipulation detection ensures that any tampered codeword will either decode to the original message or to $\bot$.

A MD-NMC in the CRS model. For the exposition of our ideas, we start with a naive scheme (which does not work), and then show how we resolve all the challenges. Let $(\mathsf {KGen},\mathsf {E},\mathsf {D})$ be a (symmetric) authenticated encryption scheme and consider the following encoding scheme: to encode a message $s$, the encoder computes $(sk||e)$, where $e\leftarrow \mathsf {E}_{sk}(s)$ is the ciphertext and $sk\leftarrow \mathsf {KGen}(1^k)$, is the secret key. We observe that the scheme is secure if the tampering function can only read/write on the ciphertext, $e$, assuming the authenticity property of the encryption scheme, however, restricting access to $sk$, which is short, is unnatural and makes the problem trivial. On the other hand, even partial access to $sk$, compromises the authenticity property of the scheme, and even if there is no explicit attack against the non-malleability property, there is no hope for proving security based on the properties of $(\mathsf {KGen},\mathsf {E},\mathsf {D})$, in black-box way.

A solution to the above problems would be to protect the secret key using an inner encoding, yet the amount of tampering is now restricted by the capabilities of the inner scheme, as the attacker knows the exact locations of the “sensitive” codeword bits, i.e., the non-ciphertext bits. In our construction, we manage to protect the secret key while avoiding the bottleneck on the access rate by designing an inner encoding scheme that provides limited security guarantees when used standalone, still when it is used in conjunction with a shuffling technique that permutes the inner encoding and ciphertext bit locations, it guarantees that any attack against the secret key will create an invalid encoding with overwhelming probability, even when allowing access to almost the entire codeword.

Our scheme is depicted in Fig. 1 and works as follows: on input message $s$, the encoder (i) encrypts the message by computing $sk\leftarrow \mathsf {KGen}(1^k)$ and $e\leftarrow \mathsf {E}_{sk}(s)$, (ii) computes an m-out-of-m secret sharing $z$ of $(sk|| sk^3)$ (interpreting both $sk$ and $sk^{3}$ as elements in some finite field),⁹ and outputs a random shuffling of $(z|| e)$, denoted as $P_{\varSigma }(z||e)$, according to the common reference string $\varSigma$. Decoding proceeds as follows: on input $c$, the decoder (i) inverts the shuffling operation by computing $(z|| e) \leftarrow P^{-1}_{\varSigma }(c)$, (ii) reconstructs $(sk|| sk')$, and (iii) if $sk^3 = sk'$, outputs $\mathsf {D}_{sk}(e)$, otherwise, it outputs $\bot$.

In Sect. 3 we present the intuition behind our construction and a formal security analysis. Our instantiation yields a rate $1$ computationally secure MD-NMC in the CRS model, with access rate $1-1/\varOmega (\log k)$ and codewords of length $|s|+O(k^2 \log k)$, under mild assumptions (e.g., one way functions).

Fig. 1.

Description of the scheme in the CRS model.

On the CRS. In our work, the tampering function, and consequently the codeword locations that the function is given access to, are fixed before sampling the CRS and this is critical for achieving security. However, proving security in this setting is non-trivial. In addition, the tampering function receives full access to the CRS when tampering with the codeword. This is in contrast to the work by Faust et al. [32] in the information-theoretic setting, where the (internal) tampering function receives partial information over the CRS.

In addition, our results tolerate adaptive selection of the codeword locations, with respect to the CRS, in the following way: each time the attacker requests access to a location, he also learns if it corresponds to a bit of $z$ or $e$, together with the index of that bit in the original string. In this way, the CRS is gradually disclosed to the adversary while picking codeword locations.

Finally, our CRS sustains a substantial amount of tampering that depends on the codeword locations chosen by the attacker: an attacker that gets access to a sensitive codeword bit is allowed to modify the part of the CRS that defines the location of that bit in the codeword. The attacker is allowed to modify all but $O(k \log (|s| + k))$ bits of the CRS, that is of length $O(k^2 \log k \log (|s|+k))$. To our knowledge, this is the first construction that tolerates, even partial modification of the CRS. In contrast, existing constructions in the CRS model are either using NIZKs [22, 28, 30, 37], or they are based on the knowledge of exponent assumption [36], thus tampering access to the CRS might compromise security.

Removing the CRS. A first approach would be to store the CRS inside the codeword together with $P_{\varSigma }(z||e)$, and give to the attacker read/write access to it. However, the tampering function, besides getting direct (partial) access to the encoding of $sk$, it also gets indirect access to it by (partially) controlling the CRS. Then, it can modify the CRS in way such that, during decoding, ciphertext locations of its choice will be treated as bits of the inner encoding, $z$, increasing the tampering rate against $z$ significantly. This makes the task of protecting $sk$ hard, if not impossible (unless we restrict the access rate significantly).

To handle this challenge, we embed the structure recovering mechanism inside the codeword and we emulate the CRS effect by increasing the size of the alphabet, giving rise to a block-wise structure.¹⁰ Notice that, non-malleable codes with large alphabet size (i.e., $\mathrm {poly}(k)+|s|$ bits) might be easy to construct, as we can embed in each codeword block the verification key of a signature scheme together with a secret share of the message, as well as a signature over the share. In this way, partial access over the codeword does not compromise the security of the signature scheme while the message remains private, and the simulation is straightforward. This approach however, comes with a large overhead, decreasing the information rate and access rate of the scheme significantly. In general, and similar to error correcting codes, we prefer smaller alphabet sizes – the larger the size is, the more coarse access structure is required, i.e., in order to access individual bits we need to access the blocks that contain them. In this work, we aim at minimizing this restriction by using small alphabets, as we describe below.

Our approach on the problem is the following. We increase the alphabet size to $O(\log k)$ bits, and we consider two types of blocks: (i) sensitive blocks, in which we store the inner encoding, $z$, of the secret key, $sk$, and (ii) non-sensitive blocks, in which we store the ciphertext, $e$, that is fragmented into blocks of size $O(\log k)$. The first bit of each block indicates whether it is a sensitive block, i.e., we set it to 1 for sensitive blocks and to 0, otherwise. Our encoder works as follows: on input message $s$, it computes $z$, $e$, as in the previous scheme and then uses rejection sampling to sample the indices, $\rho _1,\ldots ,\rho _{|z|}$, for the sensitive blocks. Then, for every $i \in \{1,\ldots ,|z|\}$, $\rho _i$ is a sensitive block, with contents $(1||i||z[i])$, while the remaining blocks keep ciphertext pieces of size $O(\log k)$. Decoding proceeds as follows: on input codeword $C=(C_1,\ldots ,C_{\mathsf {bn}})$, for each $i \in [\mathsf {bn}]$, if $C_i$ is a non-sensitive block, its data will be part of $e$, otherwise, the last bit of $C_i$ will be part of $z$, as it is dictated by the index stored in $C_i$. If the number of sensitive blocks is not the expected, the decoder outputs $\bot$, otherwise, $z$, $e$, have been fully recovered and decoding proceeds as in the previous scheme. Our scheme is depicted in Fig. 2.

The security of our construction is based on the fact that, due to our shuffling technique, the position mapping will not be completely overwritten by the attacker, and as we prove in Sect. 4, this suffices for protecting the inner encoding over $sk$. We prove security of the current scheme (cf. Theorem 4.4) by a reduction to the security of the scheme in the CRS model. Our instantiation yields a rate $1-1/\varOmega (\log k)$ MD-NMC in the standard model, with access rate $1-1/\varOmega (\log k)$ and codewords of length $|s|(1+1/O(\log k))+O(k^2 \log ^2 k)$, assuming one-way functions.

It is worth pointing out that the idea of permuting blocks containing sensitive and non-sensitive data was also considered by [42] in the context of list-decodable codes, however the similarity is only in the fact that a permutation is being used at some point in the encoding process, and our objective, construction and proof are different.

Fig. 2.

Description of the scheme in the standard model.

Continuously non-malleable codes with light updates. We observe that the codewords of the block-wise scheme can be updated efficiently, using shuffling and refreshing operations. Based on this observation, we prove that our code is secure against continuous attacks, for a notion of security that is weaker than the original one [30], as we need to update our codeword. However, our update mechanism is using cheap operations, avoiding the full decoding and re-encoding of the message, which is the standard way to achieve continuous security [27, 37]. In addition, our solution avoids the usage of a self-destruction mechanism that produces $\bot$ in all subsequent rounds after the first round in which the attacker creates an invalid codeword, which was originally achieved by [28], and makes an important step towards practicality.

The update mechanism works as follows: in each round, it randomly shuffles the blocks and refreshes the randomness of the inner encoding of $sk$. The idea here is that, due to the continual shuffling and refreshing of the inner encoding scheme, in each round the attacker learns nothing about the secret key, and every attempt to modify the inner encoding, results to an invalid key, with overwhelming probability. Our update mechanism can be made deterministic if we further encode a seed of a PRG together with the secret key, which is similar to the technique presented in [37].

Our results are presented in Sect. 5 (cf. Theorem 5.3), and the rates for the current scheme match those of the one-time secure, block-wise code.

1.3 Applications

Security against passive attackers - AONTs. Regarding the passive setting, our model and constructions find useful application in all settings where AONTs are useful (cf. [13, 14, 40, 41]), e.g., for increasing the security of encryption without increasing the key-size, for improving the efficiency of block ciphers and constructing remotely keyed encryption [13, 41], and also for constructing computationally secure secret sharing [40]. Other uses of AONTs are related to optimal asymmetric encryption padding [13].

Security against memory tampering - (Binary alphabets, Logarithmic length CRS). As with every NMC, the most notable application of the proposed model and constructions is when aiming for protecting cryptographic devices against memory tampering. Using our $\textsc {CRS}$ based construction we can protect a large tamperable memory with a small (logarithmic in the message length) tamperproof memory, that holds the $\textsc {CRS}$.

The construction is as follows. Consider any device performing cryptographic operations, e.g., a smart card, whose memory is initialized when the card is being issued. Each card is initialized with an independent CRS, which is stored in a tamper-proof memory, while the codeword is stored in a tamperable memory. Due to the independency of the CRS values, it is plausible to assume that the adversary is not given access to the CRS prior to tampering with the card; the full CRS is given to the tampering function while it tampers with the codeword during computation. This idea is along the lines of the only computation leaks information model [38], where data can only be leaked during computation, i.e., the attacker learns the CRS when the devices performs computations that depend on it. We note that in this work we allow the tampering function to read the full CRS, in contrast to [32], in which the tampering function receives partial information over it (our CRS can also be tampered, cf. the above discussion). In subsequent rounds the CRS and the codeword are being updated by the device, which is the standard way to achieve security in multiple rounds while using a one-time NMC [27].

Security against memory tampering - (Logarithmic length alphabets, no CRS). In modern architectures data is stored and transmitted in chunks, thus our block-wise encoding scheme can provide tamper-resilience in all these settings. For instance, consider the case of arithmetic circuits, having memory consisting of consecutive blocks storing integers. Considering adversaries that access the memory of such circuits in a block-wise manner, is a plausible scenario. In terms of modeling, this is similar to tamper-resilience for arithmetic circuits [33], in which the attacker, instead of accessing individual circuit wires carrying bits, it accesses wires carrying integers. The case is similar for RAM computation where the CPU operates over 32 or 64 bit registers (securing RAM programs using NMC was also considered by [22,23,24, 31]). We note that the memory segments in which the codeword blocks are stored do not have to be physically separated, as partial functions output values that depend on the whole input in which they receive access to. This is in contrast to the split-state setting in which the tampering function tampers with each state independently, and thus the states need to be physically separated.

Security against adversarial channels. In Wiretap Channels [9, 39, 45] the goal is to communicate data privately against eavesdroppers, under the assumption that the channel between the sender and the adversary is “noisier” than the channel between the sender and the receiver. The model that we propose and our block-wise construction can be applied in this setting to provide privacy against a wiretap adversary under the assumption that due to the gap of noise there is a small (of rate o(1)) fraction of symbols that are delivered intact to the receiver and dropped from the transmission to the adversary. This enables private, key-less communication between the parties, guaranteeing that the receiver will either receive the original message, or $\bot$. In this way, the communication will be non-malleable in the sense that the receiver cannot be lead to output $\bot$ depending on any property of the plaintext. Our model allows the noise in the receiver side to depend on the transmission to the wiretap adversary, that tampers with a large (of rate $1-o(1)$) fraction of symbols, leading to an “active” variant of the wiretap model.

1.4 Related Work

Manipulation detection has been considered independently of the notion of non-malleability, in the seminal paper by Cramer et al. [21], who introduced the notion of algebraic manipulation detection (AMD) codes, providing security against additive attacks over the codeword. A similar notion was considered by Jafargholi and Wichs [34], called tamper detection, aiming to detect malicious modifications over the codeword, independently of how those affect the output of the decoder. Tamper detection ensures that the application of any (admissible) function to the codeword leads to an invalid decoding.

Non-malleable codes for other function classes have been extensively studied, such as constant split-state functions [17, 25], block-wise tampering [15, 19], while the work of [2] develops beautiful connections among various function classes. In addition, other variants of non-malleable codes have been proposed, such as continuous non-malleable codes [30], augmented non-malleable codes [1], locally decodable/updatable non-malleable codes [16, 22,23,24, 31], and non-malleable codes with split-state refresh [28]. In [7] the authors consider AC0 circuits, bounded-depth decision trees and streaming, space-bounded adversaries. Leakage resilience was also considered as an additional feature, e.g., by [16, 24, 28, 37].

2 Preliminaries

In this section we present basic definitions and notation that will be used throughout the paper.

Definition 2.1

(Notation). Let t, i, j, be non-negative integers. Then, [t] is the set $\{1,\ldots ,t\}$. For bit-strings x, y, x||y, is the concatenation of x, y, |x| denotes the length of x, for $i \in [|x|]$, x[i] is the i-th bit of x, , and for $i \le j$, $x[i:j]=x[i] || \ldots || x[j]$. For a set I, |I|, $\mathcal {P}(I)$, are the cardinality and power set of I, respectively, and for $I \subseteq [|x|]$, $x_{|_{I}}$ is the projection of the bits of x with respect to I. For a string variable c and value v, $c \leftarrow v$ denotes the assignment of v to c, and $c[I] \leftarrow v$, denotes an assignment such that $c_{|_{I}}$ equals v. For a distribution D over a set $\mathcal {X}$, $x \leftarrow D$, denotes sampling an element $x \in \mathcal {X}$, according to D, $x \leftarrow \mathcal {X}$ denotes sampling a uniform element x from $\mathcal {X}$, $U_{\mathcal {X}}$ denotes the uniform distribution over $\mathcal {X}$ and $x_1,\ldots ,x_t {\mathop {\leftarrow }\limits ^{\mathsf {rs}}}\mathcal {X}$ denotes sampling a uniform subset of $\mathcal {X}$ with t distinct elements, using rejection sampling. The statistical distance between two random variables $X,\ Y$, is denoted by $\varDelta (X,Y)$, “$\approx$” and “$\approx _c$”, denote statistical and computational indistinguishability, respectively, and $\mathsf {negl}(k)$ denotes an unspecified, negligible function, in k.

Below, we define coding schemes, based on the definitions of [27, 37].

Definition 2.2

(Coding scheme [27]). A $(\kappa ,\nu )$-coding scheme, $\kappa , \nu \in \mathbb {N}$, is a pair of algorithms $(\mathsf {Enc},\mathsf {Dec})$ such that: $\mathsf {Enc}: \{0,1\}^{\kappa } \rightarrow \{0,1\}^\nu$ is an encoding algorithm, $\mathsf {Dec}: \{0,1\}^\nu \rightarrow \{0,1\}^{\kappa } \cup \{\bot \}$ is a decoding algorithm, and for every $s \in \{0,1\}^{\kappa }$, $\Pr [\mathsf {Dec}(\mathsf {Enc}(s))=s]=1$, where the probability runs over the randomness used by $(\mathsf {Enc},\mathsf {Dec})$.

We can easily generalize the above definition for larger alphabets, i.e., by considering $\mathsf {Enc}: \{0,1\}^{\kappa } \rightarrow \varGamma ^\nu$ and $\mathsf {Dec}: \varGamma ^\nu \rightarrow \{0,1\}^{\kappa } \cup \{\bot \}$, for some alphabet $\varGamma$.

Definition 2.3

(Coding scheme in the Common Reference String (CRS) Model [37]). A $(\kappa ,\nu )$-coding scheme in the CRS model, $\kappa ,\nu \in \mathbb {N}$, is a triple of algorithms $(\mathsf {Init},\mathsf {Enc},\mathsf {Dec})$ such that: $\mathsf {Init}$ is a randomized algorithm which receives $1^{k}$, where k denotes the security parameter, and produces a common reference string $\varSigma \in \{0,1\}^{\mathrm {poly}(k)}$, and $(\mathsf {Enc}(1^{k},\varSigma ,\cdot ),\mathsf {Dec}(1^{k},\varSigma ,\cdot ))$ is a $(\kappa ,\nu )$-coding scheme, $\kappa ,\nu =\mathrm {poly}(k)$.

For brevity, $1^{k}$ will be omitted from the inputs of $\mathsf {Enc}$ and $\mathsf {Dec}$.

Below we define non-malleable codes with manipulation detection, which is a stronger notion than the one presented in [27], in the sense that the tampered codeword will always decode to the original message or to $\bot$. Our definition is with respect to alphabets, as in Sect. 4 we consider alphabets of size $O(\log k)$.

Definition 2.4

(Non-Malleability with Manipulation Detection (MD-NMC)). Let $\varGamma$ be an alphabet, let $(\mathsf {Init},\mathsf {Enc},\mathsf {Dec})$ be a $(\kappa ,\nu )$-coding scheme in the common reference string model, and $\mathcal {F}$ be a family of functions $f: \varGamma ^\nu \rightarrow \varGamma ^\nu$. For any $f \in \mathcal {F}$ and $s\in \{0,1\}^\kappa$, define the tampering experiment

$$ \mathsf {Tamper}^{f}_{s} := \left\{ \begin{array}{c} \varSigma \leftarrow \mathsf {Init}(1^k), c\leftarrow \mathsf {Enc}(\varSigma ,s), \tilde{c}\leftarrow f_{\varSigma }(c), \tilde{s}\leftarrow \mathsf {Dec}(\varSigma ,\tilde{c}) \\ \text {Output}: \tilde{s}. \end{array} \right\} $$

which is a random variable over the randomness of $\mathsf {Enc}$, $\mathsf {Dec}$ and $\mathsf {Init}$. The coding scheme $(\mathsf {Init},\mathsf {Enc},\mathsf {Dec})$ is non-malleable with manipulation detection with respect to the function family $\mathcal {F}$, if for all, sufficiently large k and for all $f \in \mathcal {F}$, there exists a distribution $D_{(\varSigma ,f)}$ over $\{0,1\}^{\kappa } \cup \{\bot , \mathsf {same}^*\}$, such that for all $s \in \{0,1\}^{\kappa }$, we have:

$$ \left\{ \mathsf {Tamper}^{f}_s \right\} _{k \in \mathbb {N}} \approx \left\{ \begin{array}{c} \tilde{s} \leftarrow D_{(\varSigma ,f)} \\ \text {Output } s\text { if } \tilde{s}=\mathsf {same}^*, \text { and } \bot \text { otherwise} \end{array} \right\} _{k \in \mathbb {N}} $$

where $\varSigma \leftarrow \mathsf {Init}(1^k)$ and $D_{(\varSigma ,f)}$ is efficiently samplable given access to f, $\varSigma$. Here, “$\approx$” may refer to statistical, or computational, indistinguishability.

In the above definition, $f$ is parameterized by $\varSigma$ to differentiate tamper-proof input, i.e., $\varSigma$, from tamperable input, i.e., $c$.

Below we define the tampering function class that will be used throughout the paper.

Definition 2.5

(The class of partial functions $\mathcal {F}_{\varGamma }^{\alpha \nu }$ (or $\mathcal {F}^{\alpha }$)). Let $\varGamma$ be an alphabet, $\alpha \in [0,1)$ and $\nu \in \mathbb {N}$. Any $f \in \mathcal {F}_{\varGamma }^{\alpha \nu }$, $f: \varGamma ^{\nu } \rightarrow \varGamma ^{\nu }$, is indexed by a set $I \subseteq [\nu ]$, $|I| \le \alpha \nu$, and a function $f': \varGamma ^{\alpha \nu } \rightarrow \varGamma ^{\alpha \nu }$, such that for any $x \in \varGamma ^\nu$, $\left( f(x) \right) _{|_{I}} = f'\left( x_{|_{I}} \right)$ and $\left( f(x) \right) _{|_{I^\mathsf {c}}} = x_{|_{I^\mathsf {c}}}$, where $I^\mathsf {c}:= [\nu ] \backslash I$.

For simplicity, in the rest of the text we will use the notation f(x) and $f(x_{|_{I}})$ (instead of $f'\left( x_{|_{I}} \right)$). Also, the length of the codeword, $\nu$, according to $\varGamma$, will be omitted from the notation and whenever $\varGamma$ is omitted we assume that $\varGamma =\{0,1\}$. In Sect. 3, we consider $\varGamma =\{0,1\}$, while in Sect. 4, $\varGamma =\{0,1\}^{O(\log k)}$, i.e., the tampering function operates over blocks of size $O(\log k)$. When considering the CRS model, the functions are parameterized by the common reference string.

The following lemma is useful for proving security throughout the paper.

Lemma 2.6

Let $(\mathsf {Enc},\mathsf {Dec})$ be a $(\kappa ,\nu )$-coding scheme and $\mathcal {F}$ be a family of functions. For every $f\in \mathcal {F}$ and $s\in \{0,1\}^{\kappa }$, define the tampering experiment

$$ \mathsf {Tamper}^f_s := \left\{ \begin{array}{c} c \leftarrow \mathsf {Enc}(s), \tilde{c} \leftarrow f(c), \tilde{s} \leftarrow \mathsf {Dec}(\tilde{c}) \\ \text {Output } \mathsf {same}^* \text { if } \tilde{s}=s, \text { and } \tilde{s} \text { otherwise}. \end{array} \right\} $$

which is a random variable over the randomness of $\mathsf {Enc}$ and $\mathsf {Dec}$. $(\mathsf {Enc},\mathsf {Dec})$ is an MD-NMC with respect to $\mathcal {F}$, if for any $f \in \mathcal {F}$ and all sufficiently large k: (i) for any pair of messages $s_0$, $s_1 \in \{0,1\}^{\kappa }$, $\left\{ \mathsf {Tamper}^f_{s_0} \right\} _{k \in \mathbb {N}} \approx \left\{ \mathsf {Tamper}^f_{s_1} \right\} _{k \in \mathbb {N}}$, and (ii) for any $s$, $\Pr \left[ \mathsf {Tamper}^f_{s} \notin \{\bot , s\} \right] \le \mathsf {negl}(k)$. Here, “$\approx$” may refer to statistical, or computational, indistinguishability.

The proof of the above lemma is provided in the full version of the paper. For coding schemes in the CRS model the above lemma is similar, and $\mathsf {Tamper}^f_{s}$ internally samples $\varSigma \leftarrow \mathsf {Init}(1^k)$.

3 An MD-NMC for Partial Functions, in the CRS Model

In this section we consider $\varGamma =\{0,1\}$ and we construct a rate 1 MD-NMC for $\mathcal {F}^{\alpha }$, with access rate $\alpha = 1-1/\varOmega (\log k)$. Our construction is defined below and depicted in Fig. 1.

Construction 3.1

Let k, $m \in \mathbb {N}$, let $(\mathsf {KGen},\mathsf {E},\mathsf {D})$ be a symmetric encryption scheme, $(\mathsf {SS}_{m},\mathsf {Rec}_{m})$ be an m-out-of-m secret sharing scheme, and let $l \leftarrow 2m|sk|$, where $sk$ follows $\mathsf {KGen}(1^k)$. We define an encoding scheme $(\mathsf {Init},\mathsf {Enc},\mathsf {Dec})$, that outputs $\nu =l+|e|$ bits, $e\leftarrow \mathsf {E}_{sk}(s)$, as follows:

• $\mathsf {Init}(1^k)$: Sample $r_1,\ldots ,r_l {\mathop {\leftarrow }\limits ^{\mathsf {rs}}}\{0,1\}^{\log (\nu )}$, and output $\varSigma =(r_1,\ldots ,r_l)$.

• $\mathsf {Enc}(\varSigma ,\cdot )$: for input message $s$, sample $sk\leftarrow \mathsf {KGen}(1^k)$, $e\leftarrow \mathsf {E}_{sk}(s)$.

  • (Secret share) Sample $z\leftarrow \mathsf {SS}_{m}(sk||sk^3)$, where , $z \in \{0,1\}^{2m|sk|}$, and for $i \in \left[ |sk| \right]$, $z_i$ (resp. $z_{|sk|+i}$) is an m-out-of-m secret sharing of $sk[i]$ (resp. $sk^3[i]$).

  • (Shuffle) Compute $c\leftarrow P_{\varSigma }(z||e)$ as follows:

    • 1. (Sensitive bits): Set $c\leftarrow 0^{\nu }$. For $i \in [l]$, $c[r_i] \leftarrow z[i]$.

    • 2. (Ciphertext bits): Set $i \leftarrow 1$. For $j \in [l + |e|]$, if $j \notin \{ r_p \ | \ p \in [l] \}$, $c[j] \leftarrow e[i]$, i$++$.

  Output $c$.

• $\mathsf {Dec}(\varSigma ,\cdot )$: on input $c$, compute $(z||e) \leftarrow P_{\varSigma }^{-1}(c)$, $(sk|| sk' )\leftarrow \mathsf {Rec}_{m}(z)$, and if $sk^3 = sk'$, output $\mathsf {D}_{sk}(e)$, otherwise output $\bot$.

The set of indices of $z_i$ in the codeword will be denoted by $Z_i$.

In the above we consider all values as elements over $\mathbf {GF}(2^{\mathrm {poly}(k)})$.

Our construction combines authenticated encryption with an inner encoding that works as follows. It interprets $sk$ as an element in the finite field $\mathbf {GF}({2^{|sk|}})$ and computes $sk^3$ as a field element. Then, for each bit of $(sk||sk^3)$, it computes an m-out-of-m secret sharing of the bit, for some parameter m (we note that elements in $\mathbf {GF}(2^{|sk|})$ can be interpreted as bit strings). Then, by combining the inner encoding with the shuffling technique, we get a encoding scheme whose security follows from the observations that we briefly present below:

• For any tampering function which does not have access to all m shares of a single bit of $(sk||sk^3)$, the tampering effect on the secret key can be expressed essentially as a linear shift, i.e., as $(( sk+ \delta ) || (sk^3 + \eta ))$ for some $(\delta , \eta ) \in \mathbf {GF}(2^{|sk|}) \times \mathbf {GF}(2^{|sk|})$, independent of $sk$.

• By permuting the locations of the inner encoding and the ciphertext bits, we have that with overwhelming probability any tampering function who reads/writes on a $(1-o(1))$ fraction of codeword bits, will not learn any single bit of $(sk||sk^3)$.

• With overwhelming probability over the randomness of $sk$ and CRS, for non-zero $\eta$ and $\delta$, $(sk+ \delta )^3 \ne sk^3 + \eta$, and this property enables us to design a consistency check mechanism whose output is simulatable, without accessing $sk$.

• The security of the final encoding scheme follows by composing the security of the inner encoding scheme with the authenticity property of the encryption scheme.

Below we present the formal security proof of the above intuitions.

Theorem 3.2

Let k, $m \in \mathbb {N}$ and $\alpha \in [0,1)$. Assuming $(\mathsf {SS}_{m},\mathsf {Rec}_{m})$ is an m-out-of-m secret sharing scheme and $(\mathsf {KGen},\mathsf {E},\mathsf {D})$ is 1-IND-CPA¹¹ secure, authenticated encryption scheme, the code of Construction 3.1 is a MD-NMC against $\mathcal {F}^{\alpha }$, for any $\alpha$, m, such that $(1-\alpha )m=\omega (\log (k))$.

Fig. 3.

The hybrid experiments for the proof of Theorem 3.2.

Proof

Let I be the set of indices chosen by the attacker and $I^\mathsf {c}= [\nu ] \backslash I$, where $\nu = 2m|sk| + |e|$. The tampered components of the codeword will be denoted using the character “~” on top of the original symbol, i.e., we have $\tilde{c}\leftarrow f(c)$, the tampered secret key $sk$ (resp. $sk^3$) that we get after executing $\mathsf {Rec}_{m}(\tilde{z})$ will be denoted by $\tilde{sk}$ (resp. $\tilde{sk}'$). Also the tampered ciphertext will be $\tilde{e}$. We prove the needed using a series of hybrid experiments that are depicted in Fig. 3. Below, we describe the hybrids.

• $\mathsf {Exp}_{0}^{\varSigma ,f,s}$: We prove security of our code using Lemma 2.6, i.e., by showing that (i) for any $s_{0}$, $s_1$, $\mathsf {Tamper}_{s_0}^{f} \approx \mathsf {Tamper}_{s_1}^{f}$, and (ii) for any $s$, $\Pr \left[ \mathsf {Tamper}^f_{s} \notin \right.$ $\left. \{\bot , s\} \right] \le \mathsf {negl}(k)$, where $\mathsf {Tamper}_{s}^{f}$ is defined in Lemma 2.6. For any $f$, $s$, $\varSigma \leftarrow \mathsf {Init}(1^k)$, the first experiment, $\mathsf {Exp}_{0}^{\varSigma ,f,s}$, matches the experiment $\mathsf {Tamper}_{s}^{f}$ in the CRS model, i.e., $\varSigma$ is sampled inside $\mathsf {Tamper}_{s}^{f}$.

• $\mathsf {Exp}_{1}^{\varSigma ,f,s}$: In the second experiment we define $Z_i$, $i \in [2|sk|]$, to be the set of codeword indices in which the secret sharing $z_i$ is stored, $|Z_i|=m$. The main difference from the previous experiment is that the current one outputs $\bot$, if there exists a bit of $sk$ or $sk^3$ for which the tampering function reads all the shares of it, while accessing at most $\alpha \nu$ bits of the codeword. Intuitively, and as we prove in Claim 3.3, by permuting the location indices of $z||e$, this event happens with probability negligible in k, and the attacker does not learn any bit of $sk$ and $sk^3$, even if he is given access to $(1-o(1)) \nu$ bits of the codeword.

• $\mathsf {Exp}_{2}^{\varSigma ,f,s}$: By the previous hybrid we have that for all $i \in [2|sk|]$, the tampering function will not access all bits of $z_i$, with overwhelming probability. In the third experiment we unfold the encoding procedure, and in addition, we substitute the secret sharing procedure $\mathsf {SS}_{m}$ with $\bar{\mathsf {SS}}_{m}^{f}$ that computes shares $z_i^*$ that reveal no information about $sk||sk^3$; for each i, $\bar{\mathsf {SS}}_{m}^{f}$ simply “drops” the bit of $z_i$ with the largest index that is not being accessed by $f$. We formally define $\bar{\mathsf {SS}}_{m}^{f}$ below.

  $\bar{\mathsf {SS}}_{m}^{f}(\varSigma ,sk)$:

  • 1. Sample $\left( z_1,\ldots ,z_{2|sk|} \right) \leftarrow \mathsf {SS}_{m}\left( sk||sk^3 \right)$ and set $z_i^* \leftarrow z_i$, $i \in [2|sk|]$.

  • 2. For $i \in [2|sk|]$, let $l_i:= \max _{d} \left\{ d \in [m] \wedge \mathsf {Ind}\left( z_i[d] \right) \notin I) \right\}$, where $\mathsf {Ind}$ returns the index of $z_i[d]$ in $c$, i.e., $l_i$ is the largest index in [m] such that $z_i[l_i]$ is not accessed by $f$.

  • 3. (Output): For all i set $z_i^*[l_i]=*$, and output $z^* := \parallel _{i=1}^{2|sk|} z^*_i$.

  In $\mathsf {Exp}_{1}^{\varSigma ,f,s}$, , and each $z_i$ is an m-out-of-m secret sharing for a bit of $sk$ or $sk^3$. From Claim 3.3, we have that for all i, $|I \cap Z_i|<m$ with overwhelming probability, and we can observe that the current experiment is identical to the previous one up to the point of computing $f(c_{|_{I}})$, as $c_{|_{I}}$ and $f(c_{|_{I}})$ depend only on $z^*$, that carries no information about $sk$ and $sk^3$.

  Another difference between the two experiments is in the external “Else” branch: $\mathsf {Exp}_{1}^{\varSigma ,f,s}$ makes a call on the decoder while $\mathsf {Exp}_{2}^{\varSigma ,f,s}$, before calling $\mathsf {D}_{sk}(\tilde{e})$, checks if the tampering function has modified the shares in a way such that the reconstruction procedure $((\tilde{sk},\tilde{sk}')\leftarrow \mathsf {Rec}_{m}(\tilde{z}))$ will give $\tilde{sk}\ne sk$ or $\tilde{sk}' \ne sk'$. This check is done by the statement “If $\exists i: \bigoplus _{j \in (I \cap Z_i)} c[j] \ne \bigoplus _{j \in (I \cap Z_i)} \tilde{c}[j]$”, without touching $sk$ or $sk^3$.¹² In case modification is detected the current experiments outputs $\bot$. The intuition is that an attacker that partially modifies the shares of $sk$ and $sk^3$, creates shares of $\tilde{sk}$ and $\tilde{sk}'$, such that $\tilde{sk}^3=\tilde{sk}'$, with negligible probability in k. We prove this by a reduction to the 1-IND-CPA security of the encryption scheme: any valid modification over the inner encoding of the secret key gives us method to compute the original secret key $sk$, with non-negligible probability. The ideas are presented formally in Claim 3.4.

• $\mathsf {Exp}_{3}^{\varSigma ,f,s}$: The difference between the current experiment and the previous one is that instead of calling the decryption $\mathsf {D}_{sk}(\tilde{e})$, we first check if the attacker has modified the ciphertext, in which case the current experiment outputs $\bot$, otherwise it outputs $\mathsf {same}^*$. By the previous hybrid, we reach this newly introduced “Else” branch of $\mathsf {Exp}_{3}^{\varSigma ,f,s}$, only if the tampering function didn’t modify the secret key. Thus, the indistinguishability between the two experiments follows from the authenticity property of the encryption scheme in the presence of $z^*$: given that $\tilde{sk}= sk$ and $\tilde{sk}' = sk'$, we have that if the attacker modifies the ciphertext, then with overwhelming probability $\mathsf {D}_{sk}(\tilde{e})=\bot$, otherwise, $\mathsf {D}_{sk}(\tilde{e})=s$, and the current experiment correctly outputs $\mathsf {same}^*$ or $\bot$ (cf. Claim 3.5).

• Finally, we prove that for any $f\in \mathcal {F}^{\alpha }$, and message $s$, $\mathsf {Exp}_3^{\varSigma ,f,s}$ is indistinguishable from $\mathsf {Exp}_3^{\varSigma ,f,\mathsf {0}}$, where $\mathsf {0}$ denotes the zero-message. This follows by the semantic security of the encryption scheme, and gives us the indistinguishability property of Lemma 2.6. The manipulation detection property is derived by the indistinguishability between the hybrids and the fact that the output of $\mathsf {Exp}_{3}^{\varSigma ,f,s}$ is in the set $\{\mathsf {same}^*, \bot \}$.

In what follows, we prove indistinguishability between the hybrids using a series of claims.

Claim 3.3

For k, $m \in \mathbb {N}$, assume $(1-\alpha )m = \omega (\log (k))$. Then, for any $f\in \mathcal {F}^{\alpha }$ and any message $s$, we have $\mathsf {Exp}_{0}^{\varSigma ,f,s} \approx \mathsf {Exp}_{1}^{\varSigma ,f,s}$, where the probability runs over the randomness used by $\mathsf {Init}$, $\mathsf {Enc}$.

Proof

The difference between the two experiments is that $\mathsf {Exp}_{1}^{\varSigma ,f,s}$ outputs $\bot$ when the attacker learns all shares of some bit of $sk$ or $sk^3$, otherwise it produces output as $\mathsf {Exp}_{0}^{\varSigma ,f,s}$ does. Let E the event “$\exists i: |(I \cap Z_i)| = m$”. Clearly, $\mathsf {Exp}_{0}^{\varSigma ,f,s} = \mathsf {Exp}_{1}^{\varSigma ,f,s}$ conditioned on $\lnot E$, thus the statistical distance between the two experiments is bounded by $\Pr [E]$. In the following we show that $\Pr [E] \le \mathsf {negl}(k)$. We define by $E_i$ the event in which $f$ learns the entire $z_i$. Assuming the attacker reads n bits of the codeword, we have that for all $i \in [2|sk|]$,

We have $n=\alpha \nu$ and assuming $\alpha = 1-\epsilon$ for $\epsilon \in (0,1]$, we have $\Pr [E_i] \le (1-\epsilon )^m \le 1/e^{m\epsilon }$ and $\Pr [E]=\Pr _{\varSigma } \left[ \bigcup _{i=1}^{2|sk|} E_i \right] \le \frac{2|sk|}{e^{m\epsilon }}$, which is negligible when $(1-\alpha )m = \omega (\log (k))$, and the proof of the claim is complete.    $\blacksquare$

Claim 3.4

Assuming $(\mathsf {KGen},\mathsf {E},\mathsf {D})$ is 1-IND-CPA secure, for any $f\in \mathcal {F}^{\alpha }$ and any message $s$, $\mathsf {Exp}_{1}^{\varSigma ,f,s} \approx \mathsf {Exp}_{2}^{\varSigma ,f,s}$, where the probability runs over the randomness used by $\mathsf {Init}$, $\mathsf {Enc}$.

Proof

In $\mathsf {Exp}_{2}^{\varSigma ,f,s}$ we unfold the encoding procedure, however instead of calling $\mathsf {SS}_{m}$, we make a call to $\bar{\mathsf {SS}}_{m}^{f}$. As we have already stated above, this modification does not induce any difference between the output of $\mathsf {Exp}_{2}^{\varSigma ,f,s}$ and $\mathsf {Exp}_{1}^{\varSigma ,f,s}$, with overwhelming probability, as $z^*$ is indistinguishable from $z$ in the eyes of $f$. Another difference between the two experiments is in the external “Else” branch: $\mathsf {Exp}_{1}^{\varSigma ,f,s}$ makes a call on the decoder while $\mathsf {Exp}_{2}^{\varSigma ,f,s}$, before calling $\mathsf {D}_{sk}(\tilde{e})$, checks if the tampering function has modified the shares in a way such that the reconstruction procedure will give $\tilde{sk}\ne sk$ or $\tilde{sk}' \ne sk'$. This check is done by the statement “If $\exists i: \bigoplus _{j \in (I \cap Z_i)} c[j] \ne \bigoplus _{j \in (I \cap Z_i)} \tilde{c}[j]$”, without touching $sk$ or $sk^3$ (cf. Claim 3.3).¹³ We define the events E, $E'$ as follows

Clearly, conditioned on $\lnot E'$ the two experiments are identical, since we have $\tilde{sk}=sk$ and $\tilde{sk}'=sk'$, and the decoding process will output $\mathsf {D}_{sk}(\tilde{e})$ in both experiments. Thus, the statistical distance is bounded by $\Pr [E']$. Now, conditioned on $E' \wedge \lnot E$, both experiments output $\bot$. Thus, we need to bound $\Pr [E \wedge E']$. Assuming $\Pr [E \wedge E']>p$, for $p=1/\mathrm {poly}(k)$, we define an attacker $\mathcal {A}$ that simulates $\mathsf {Exp}_{2}^{\varSigma ,f,s}$, and uses $f$, $s$ to break the 1-IND-CPA security of $(\mathsf {KGen},\mathsf {E},\mathsf {D})$ in the presence of $z^*$, with probability at least $1/2+p''/2$, for $p''=1/\mathrm {poly}(k)$.

First we prove that any 1-IND-CPA secure encryption scheme, remains secure even if the attacker receives $z^* \leftarrow \bar{\mathsf {SS}}_{m}^{f}(\varSigma ,sk)$, as $z^*$ consists of $m-1$ shares of each bit of $sk$ and $sk^3$, i.e., for the entropy of $sk$ we have $\mathbf{H}(sk|z^*)=\mathbf{H}(sk)$. Towards contradiction, assume there exists $\mathcal {A}$ that breaks the 1-IND-CPA security of $(\mathsf {KGen},\mathsf {E},\mathsf {D})$ in the presence of $z^*$, i.e., there exist $s$, $s_0$, $s_1$ such that $\mathcal {A}$ distinguishes between $(z^*,\mathsf {E}_{sk}(s),\mathsf {E}_{sk}(s_0))$ and $(z^*,\mathsf {E}_{sk}(s),\mathsf {E}_{sk}(s_1))$, with non-negligible probability p. We define an attacker $\mathcal {A}'$ that breaks the 1-IND-CPA security of $(\mathsf {KGen},\mathsf {E},\mathsf {D})$ as follows: $\mathcal {A}'$, given $(\mathsf {E}_{sk}(s),\mathsf {E}_{sk}(s_b))$, for some $b \in \{0,1\}$, samples $\hat{sk} \leftarrow \mathsf {KGen}(1^k)$, $\hat{z}^* \leftarrow \bar{\mathsf {SS}}_{m}^{f}(\varSigma ,\hat{sk})$ and outputs $b' \leftarrow \mathcal {A}(z^*,\mathsf {E}_{sk}(s),\mathsf {E}_{sk}(s_b))$. Since $(z^*,\mathsf {E}_{sk}(s),\mathsf {E}_{sk}(s_b)) \approx (\hat{z}^*,\mathsf {E}_{sk}(s),$ $\mathsf {E}_{sk}(s_b))$ the advantage of $\mathcal {A}'$ in breaking the 1-IND-CPA security of the scheme is the advantage of $\mathcal {A}$ in breaking the 1-IND-CPA security of the scheme in the presence of $z^*$, which by assumption is non-negligible, and this completes the current proof. We note that the proof idea presented in the current paragraph also applies for proving that other properties that will be used in the rest of the proof, such as semantic security and authenticity, of the encryption scheme, are retained in the presence of $z^*$.

Now we prove our claim. Assuming $\Pr [E \wedge E']>p$, for $p=1/\mathrm {poly}(k)$, we define an attacker $\mathcal {A}$ that breaks the 1-IND-CPA security of $(\mathsf {KGen},\mathsf {E},\mathsf {D})$ in the presence of $z^*$, with non-negligible probability. $\mathcal {A}$ receives the encryption of $s$, which corresponds to the oracle query right before receiving the challenge ciphertext, the challenge ciphertext $e\leftarrow \mathsf {E}_{sk}(s_b)$, for uniform $b \in \{0,1\}$ and uniform messages $s_0$, $s_1$, as well as $z^*$. $\mathcal {A}$ is defined below.

$\mathcal {A}\left( z^* \leftarrow \bar{\mathsf {SS}}_{m}^{f}(\varSigma ,sk),e' \leftarrow \mathsf {E}_{sk}(s), e\leftarrow \mathsf {E}_{sk}(s_b) \right)$:

• 1. (Define the shares that will be accessed by $f$): For $i \in [2|sk|]$, define $w_i:=(z_i^*)_{|_{[m]\backslash \{l_i\}}}$ and for $i \in [m-1]$ define , .

• 2. (Apply $f$) Set $c \leftarrow P_{\varSigma }(z^*||e)$, compute $\tilde{c}[I] \leftarrow f_{\varSigma }(c_{|_{I}})$ and let $\tilde{C}_i$, $\tilde{D}_i$, $i \in [m]$, be the tampered shares resulting after the application of $f$ to $c_{|_{I}}$.

• 3. (Guessing the secret key) Let $U=\sum _{i=1}^{m-1} C_i$, $V=\sum _{i=1}^{m-1} D_i$, i.e., U, V denote the sum of the shares that are being accessed by the attacker (maybe partially), and $\tilde{U} = \sum _{i=1}^{m-1} \tilde{C}_i$, $\tilde{V} = \sum _{i=1}^{m-1} \tilde{D}_i$, are the corresponding tampered values after applying $f$ on U, V. Define

  $$p(X):= (U-\tilde{U})X^2 + (U^2-\tilde{U}^2)X + (U^3 - \tilde{U}^3-V+\tilde{V}),$$

  and compute the set of roots of p(X), denoted as $\mathcal {X}$, which are at most two. Then set

  $$\begin{aligned} \hat{\mathcal {SK}}:= \left\{ x+U | x \in \mathcal {X} \right\} . \end{aligned}$$

  (1)

• 4. (Output) Execute the following steps,

  • (a) For $\hat{s}k\in \hat{\mathcal {SK}}$, compute $s' \leftarrow \mathsf {D}_{\hat{sk}}(e')$, and if $s' = s$, compute $s'' \leftarrow \mathsf {D}_{\hat{sk}}(e)$. Output $b'$ such that $s_{b'}=s''$.

  • (b) Otherwise, output $b' \leftarrow \{0,1\}$.

In the first step $\mathcal {A}$ removes the dummy symbol “$*$” and computes the shares that will be partially accessed by $f$, denoted as $C_i$ for $sk$ and as $D_i$ for $sk^3$. In the second step, it defines the tampered shares, $\tilde{C}_i$, $\tilde{D}_i$. Conditioned on $E'$, it is not hard to see that $\mathcal {A}$ simulates perfectly $\mathsf {Exp}_{2}^{\varSigma ,f,s}$. In particular, it simulates perfectly the input to $f$ as it receives $e\leftarrow \mathsf {E}_{sk}(s)$ and all but $2|sk|$ of the actual bit-shares of $sk$, $sk^3$. Part of those shares will be accessed by $f$. Since for all i, $|I \cap Z_i| < m$, the attacker is not accessing any single bit of $sk$, $sk^3$. Let $C_m$, $D_m$, be the shares (not provided by the encryption oracle) that completely define $sk$ and $sk^3$, respectively. By the definition of the encoding scheme and the fact that $sk$, $sk^3 \in \mathbf {GF}(2^{\mathrm {poly}(k)})$, we have $\sum _{i=1}^{m} C_i=sk$, $\sum _{i=1}^{m} D_i=sk^3$, and

$$\begin{aligned} \left( U + C_m \right) ^3 = V + D_m. \end{aligned}$$

(2)

In order for the decoder to output a non-bottom value, the shares created by the attacker must decode to $\tilde{sk}$, $\tilde{sk}'$, such that $\tilde{sk}^3 = \tilde{sk}'$, or in other words, if

$$\begin{aligned} \left( \tilde{U} + C_m \right) ^3 = \tilde{V} + D_m. \end{aligned}$$

(3)

From 2 and 3 we receive

$$\begin{aligned} (U-\tilde{U})C_m^2 + (U^2-\tilde{U}^2)C_m + (U^3 - \tilde{U}^3)=V - \tilde{V}. \end{aligned}$$

(4)

Clearly, $\Pr [E \wedge E' \wedge (U= \tilde{U})]=0$. Thus, assuming $\Pr [E \wedge E']>p$, for $p > 1/\mathrm {poly}(k)$, we receive

(5)

and $\mathcal {A}$ manages to recover $C_m$, and thus $sk$, with non-negligible probability $p' \ge p$. Let W be the event of breaking 1-IND-CPA security. Then,

(6)

and the attacker breaks the IND-CPA security of $(\mathsf {KGen},\mathsf {E},\mathsf {D})$. Thus, we have $\Pr [E \wedge E'] \le \mathsf {negl}(k)$, and both experiments output $\bot$ with overwhelming probability.    $\blacksquare$

Claim 3.5

Assuming the authenticity property of $(\mathsf {KGen},\mathsf {E},\mathsf {D})$, for any $f\in \mathcal {F}^{\alpha }$ and any message $s$, $\mathsf {Exp}_{2}^{\varSigma ,f,s} \approx \mathsf {Exp}_{3}^{\varSigma ,f,s}$, where the probability runs over the randomness used by $\mathsf {Init}$, $\mathsf {KGen}$ and $\mathsf {E}$.

Proof

Before proving the claim, recall that the authenticity property of the encryption scheme is preserved under the presence of $z^*$ (cf. Claim 3.4). Let E be the event $\tilde{sk}=sk\wedge \tilde{sk}'=sk^3$ and $E'$ be the event $\tilde{e}\ne e$. Conditioned on $\lnot E$, the two experiments are identical, as they both output $\bot$. Also, conditioned on $E \wedge \lnot E'$, both experiments output $\mathsf {same}^*$. Thus, the statistical distance between the two experiments is bounded by $\Pr [E \wedge E']$. Let B be the event $\mathsf {D}_{sk}(\tilde{e})\ne \bot$. Conditioned on $E \wedge E' \wedge \lnot B$ both experiments output $\bot$. Thus, we need to bound $\Pr [E \wedge E' \wedge B]$.

Assuming there exist $s$, $f$, for which $\Pr [E \wedge E' \wedge B] > p$, where $p = 1/\mathrm {poly}(k)$, we define an attacker $\mathcal {A}=(\mathcal {A}_1,\mathcal {A}_2)$ that simulates $\mathsf {Exp}_{3}^{\varSigma ,f,s}$ and breaks the authenticity property of the encryption scheme in the presence of $z^*$, with non-negligible probability. $\mathcal {A}$ is defined as follows: sample $(s,st) \leftarrow \mathcal {A}_1(1^k)$, and then, on input $(z^*,e,st)$, where $e\leftarrow \mathsf {E}_{sk}(s)$, $\mathcal {A}_2$, samples $\varSigma \leftarrow \mathsf {Init}(1^k)$, sets $\tilde{c}\leftarrow 0^{\nu }$, $c\leftarrow P_{\varSigma }(z^*||e)$, computes $\tilde{c}[I] \leftarrow f(c_{|_{I}})$, $\tilde{c}[I^\mathsf {c}] \leftarrow c_{|_{I^\mathsf {c}}}$, $(\tilde{z} ^*||\tilde{e}) \leftarrow P^{-1}_{\varSigma }(\tilde{c})$, and outputs $\tilde{e}$. Assuming $\Pr [E \wedge E' \wedge B] > p$, we have that $\mathsf {D}_{sk}(\tilde{e}) \ne \bot$ and $\tilde{e}\ne e$, with non-negligible probability and the authenticity property of $(\mathsf {KGen},\mathsf {E},\mathsf {D})$ breaks.    $\blacksquare$

Claim 3.6

Assuming $(\mathsf {KGen},\mathsf {E},\mathsf {D})$ is semantically secure, for any $f\in \mathcal {F}^{\alpha }$ and any message $s$, $\mathsf {Exp}_{3}^{\varSigma ,f,s} \approx \mathsf {Exp}_{3}^{\varSigma ,f,\mathsf {0}}$, where the probability runs over the randomness used by $\mathsf {Init}$, $\mathsf {KGen}$, $\mathsf {E}$. “$\approx$” may refer to statistical or computational indistinguishability, and $\mathsf {0}$ is the zero-message.

Proof

Recall that $(\mathsf {KGen},\mathsf {E},\mathsf {D})$ is semantically secure even in the presence of $z^* \leftarrow \bar{\mathsf {SS}}_{m}^{f}(\varSigma ,sk)$ (cf. Claim 3.4), and towards contradiction, assume there exist $f\in \mathcal {F}^{\alpha }$, message $s$, and $\mathrm{PPT}$ distinguisher $\mathsf {D}$ such that

$$\left| \Pr \left[ \mathsf {D}\left( \varSigma ,\mathsf {Exp}_{3}^{\varSigma ,f,s} \right) =1 \right] - \Pr \left[ \mathsf {D}\left( \varSigma ,\mathsf {Exp}_{3}^{\varSigma ,f,\mathsf {0}} \right) \right] =1 \right| > p,$$

for $p = 1/\mathrm {poly}(k)$. We are going to define an attacker $\mathcal {A}$ that breaks the semantic security of $(\mathsf {KGen},\mathsf {E},\mathsf {D})$ in the presence of $z^*$, using $s_0:=s$, $s_1:=\mathsf {0}$. $\mathcal {A}$, given $z^*$, $e$, executes $\mathsf {Program}$.

It is not hard to see that $\mathcal {A}$ simulates $\mathsf {Exp}_{3}^{\varSigma ,f,s_b}$, thus the advantage of $\mathcal {A}$ against the semantic security of $(\mathsf {KGen},\mathsf {E},\mathsf {D})$ is the same with the advantage of $\mathsf {D}$ in distinguishing between $\mathsf {Exp}_{3}^{\varSigma ,f,s_0}$, $\mathsf {Exp}_{3}^{\varSigma ,f,s_1}$, which by assumption is non-negligible. We have reached a contradiction and the proof of the claim is complete.    $\blacksquare$

From the above claims we have that for any $f\in \mathcal {F}^{\alpha }$ and any $s$, $\mathsf {Exp}_{0}^{\varSigma ,f,s} \approx \mathsf {Exp}_{3}^{\varSigma ,f,\mathsf {0}}$, thus for any $f\in \mathcal {F}^{\alpha }$ and any $s_0$, $s_1$, $\mathsf {Exp}_{0}^{\varSigma ,f,s_0} \approx \mathsf {Exp}_{0}^{\varSigma ,f,s_1}$. Also, by the indistinguishability between $\mathsf {Exp}_{0}^{\varSigma ,f,s}$ and $\mathsf {Exp}_{3}^{\varSigma ,f,\mathsf {0}}$, the second property of Lemma 2.6 has been proven as the output of $\mathsf {Exp}_{3}^{\varSigma ,f,\mathsf {0}}$ is in $\{s,\bot \}$, with overwhelming probability, and non-malleability with manipulation detection of our code follows by Lemma 2.6, since $\mathsf {Exp}_{0}^{\varSigma ,f,s}$ is identical to $\mathsf {Tamper}^{f}_{s}$ of Lemma 2.6.    $\blacksquare$

4 Removing the CRS

In this section we increase the alphabet size to $O(\log (k))$ and we provide a computationally secure, rate 1 encoding scheme in the standard model, tolerating modification of $(1-o(1))\nu$ blocks, where $\nu$ is the total number of blocks in the codeword. Our construction is defined below and the intuition behind it has already been presented in the Introduction (cf. Sect. 1, Fig. 2). In the following, the projection operation will be also used with respect to bigger alphabets, enabling the projection of blocks.

Construction 4.1

Let k, $m \in \mathbb {N}$, let $(\mathsf {KGen},\mathsf {E},\mathsf {D})$ be a symmetric encryption scheme and $(\mathsf {SS}_{m},\mathsf {Rec}_{m})$ be an m-out-of-m secret sharing scheme. We define an encoding scheme $(\mathsf {Enc}^*,\mathsf {Dec}^*)$, as follows:

• $\mathsf {Enc}^*(1^k,\cdot )$: for input message $s$, sample $sk\leftarrow \mathsf {KGen}\left( 1^k \right)$, $e\leftarrow \mathsf {E}_{sk}(s)$.

  • (Secret share) Sample $z\leftarrow \mathsf {SS}_{m}(sk||sk^3)$, where 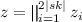, $z \in \{0,1\}^{2m|sk|}$, and for $i \in \left[ |sk| \right]$, $z_i$ (resp. $z_{|sk|+i}$) is an m-out-of-m secret sharing of $sk[i]$ (resp. $sk^3[i]$).

  • (Construct blocks & permute) Set $l \leftarrow 2m|sk|$, $\mathsf {bs}\leftarrow \log l+2$, $d \leftarrow |e|/\mathsf {bs}$, $\mathsf {bn}\leftarrow l+d$, sample $\rho :=(\rho _1,\ldots ,\rho _l) {\mathop {\leftarrow }\limits ^{\mathsf {rs}}}\{0,1\}^{\log (\mathsf {bn})}$ and compute $C\leftarrow \varPi _{\rho }(z||e)$ as follows:

    • 1. Set $t \leftarrow 1$, $C_i \leftarrow 0^{\mathsf {bs}}$, $i \in [\mathsf {bn}]$.

    • 2. (Sensitive blocks) For $i \in [l]$, set $C_{r_i} \leftarrow \left( 1||i||z[i] \right)$.

    • 3. (Ciphertext blocks) For $i \in [\mathsf {bn}]$, if $i \ne r_j$, $j \in [l]$, $C_i \leftarrow (0||e[t:t+(\mathsf {bs}-1)])$, $t \leftarrow t + (\mathsf {bs}-1)$.¹⁴

  Output $C:=(C_1||\ldots ||C_{\mathsf {bn}})$.

• $\mathsf {Dec}^*(1^k,\cdot )$: on input $C$, parse it as $(C_1||\ldots ||C_{\mathsf {bn}})$, set $t \leftarrow 1$, $l \leftarrow 2m|sk|$, $z \leftarrow 0^l$, $e\leftarrow 0$, $\mathcal {L} = \emptyset$ and compute $(z||e) \leftarrow \varPi ^{-1}(C)$ as follows:

  • For $i \in [\mathsf {bn}]$,

    • (Sensitive block) If $C_i[1] = 1$, set $j \leftarrow C_i[2:\mathsf {bs}-1]$, $z \left[ j \right] \leftarrow C_i[\mathsf {bs}]$, $\mathcal {L} \leftarrow \mathcal {L} \cup \{j \}$.

    • (Ciphertext block) Otherwise, set $e[t:t+\mathsf {bs}-1]= C_i[2:\mathsf {bs}]$, $t \leftarrow t+ \mathsf {bs}-1$.

  • If $|\mathcal {L}| \ne l$, output $\bot$, otherwise output $(z|| e)$.

  If $\varPi ^{-1}(C)= \bot$, output $\bot$, otherwise, compute $(sk|| sk' )\leftarrow \mathsf {Rec}_{m}(z)$, and if $sk^3 = sk'$, output $\mathsf {D}_{sk}(e)$, otherwise output $\bot$.

The set of indices of the blocks in which $z_i$ is stored will be denoted by $Z_i$.

We prove security for the above construction by a reduction to the security of Construction 3.1. We note that that our reduction is non-black box with respect to the coding scheme in which security is reduced to; a generic reduction, i.e., non-malleable reduction [2], from the standard model to the CRS model is an interesting open problem and thus out of the scope of this work.

In the following, we consider $\varGamma =\{0,1\}^{O(\log (k))}$. The straightforward way to prove that $(\mathsf {Enc}^*,\mathsf {Dec}^*)$ is secure against $\mathcal {F}^{\alpha }_{\varGamma }$ by a reduction to the security of the bit-wise code of Sect. 3, would be as follows: for any $\alpha \in \{0,1\}$, $f\in \mathcal {F}^{\alpha }_{\varGamma }$ and any message $s$, we have to define $\alpha '$, $g\in \mathcal {F}^{\alpha '}$, such that the output of the tampered execution with respect to $(\mathsf {Enc}^*,\mathsf {Dec}^*)$, $f$, $s$, is indistinguishable from the tampered execution with respect to $(\mathsf {Init},\mathsf {Enc},\mathsf {Dec})$, $g$, $s$, and $g$ is an admissible function for $(\mathsf {Init},\mathsf {Enc},\mathsf {Dec})$. However, this approach might be tricky as it requires the establishment of a relation between $\alpha$ and $\alpha '$ such that the sensitive blocks that $f$ will receive access to, will be simulated using the sensitive bits accessed by $g$. Our approach is cleaner: for the needs of the current proof we leverage the power of Construction 3.1, by allowing the attacker to choose adaptively the codeword locations, as long as it does not request to read all shares of the secret key. Then, for every block that is accessed by the block-wise attacker $f$, the bit-wise attacker $g$ requests access to the locations of the bit-wise code that enable him to fully simulate the input to $g$. We formally present our ideas in the following sections. In Sect. 4.1 we introduce the function class $\mathcal {F}_{\mathsf {ad}}$ that considers adaptive adversaries with respect to the CRS and we prove security of Construction 3.1 in Corollary 4.3 against a subclass of $\mathcal {F}_{\mathsf {ad}}$, and then, we reduce the security of the block-wise code $(\mathsf {Enc}^*,\mathsf {Dec}^*)$ against $\mathcal {F}^{\alpha }_{\varGamma }$ to the security of Construction 3.1 against $\mathcal {F}_{\mathsf {ad}}$ (cf. Sect. 4.2).

4.1 Security Against Adaptive Adversaries

In the current section we prove that Construction 3.1 is secure against the class of functions that request access to the codeword adaptively, i.e., depending on the CRS, as long as they access a bounded number of sensitive bits. Below, we formally define the function class $\mathcal {F}_{\mathsf {ad}}$, in which the tampering function picks up the codeword locations depending on the CRS, and we consider $\varGamma =\{0,1\}$.

Definition 4.2

(The function class $\mathcal {F}_{\mathsf {ad}}^{\nu }$). Let $(\mathsf {Init},\mathsf {Enc},\mathsf {Dec})$ be an $(\kappa ,\nu )$-coding scheme and let be the range of $\mathsf {Init}(1^k)$. For any $g=(g_1,g_2) \in \mathcal {F}_{\mathsf {ad}}^{\nu }$, we have , $g_2^{\varSigma }: \{0,1\}^{|\mathsf {range}(g_1)|} \rightarrow \{0,1\}^{|\mathsf {range}(g_1)|} \cup \{\bot \}$, and for any $c\in \{0,1\}^{\nu }$, $g^{\varSigma }\left( c\right) =g_2 \left( c_{|_{g_1(\varSigma )}} \right)$. For brevity, the function class will be denoted as $\mathcal {F}_{\mathsf {ad}}$.

Construction 3.1 remains secure against functions that receive full access to the ciphertext, as well as they request to read all but one shares for each bit of $sk$ and $sk^3$. The result is formally presented in the following corollary and its proof, which is along the lines of the proof of Theorem 3.2, is given in the full version of the paper.

Corollary 4.3

Let k, $m \in \mathbb {N}$. Assuming $(\mathsf {SS}_{m},\mathsf {Rec}_{m})$ is an m-out-of-m secret sharing scheme and $(\mathsf {KGen},\mathsf {E},\mathsf {D})$ is 1-IND-CPA secure authenticated encryption scheme, the code of Construction 4.1 is a MD-NMC against any $g=(g_1,g_2) \in \mathcal {F}_{\mathsf {ad}}$, assuming that for all $i \in [2|sk|]$, $\left( Z_i \cap g_1(\varSigma ) \right) < m$, where $sk\leftarrow \mathsf {KGen}(1^k)$ and $\varSigma \leftarrow \mathsf {Init}(1^k)$.

4.2 MD-NM Security of the Block-Wise Code

In the current section we prove security of Construction 4.1 against $\mathcal {F}^{\alpha }_{\varGamma }$, for $\varGamma =\{0,1\}^{O(\log (k))}$.

Theorem 4.4

Let k, $m \in \mathbb {N}$, $\varGamma =\{0,1\}^{O(\log (k))}$ and $\alpha \in [0,1)$. Assuming $(\mathsf {SS}_{m},\mathsf {Rec}_{m})$ is an m-out-of-m secret sharing scheme and $(\mathsf {KGen},\mathsf {E},\mathsf {D})$ is a 1-IND-CPA secure authenticated encryption scheme, the code of Construction 4.1 is a MD-NMC against $\mathcal {F}^{\alpha }_{\varGamma }$, for any $\alpha$, m, such that $(1-\alpha )m=\omega (\log (k))$.

Fig. 4.

The function $g_1$ that appears in the hybrid experiments of Fig. 7.

Fig. 5.

The function $g_2$ that appears in the hybrid experiments of Fig. 7.

Proof

Following Lemma 2.6, we prove that for any $f\in \mathcal {F}^{\alpha }_{\varGamma }$, and any pair of messages $s_0$, $s_1$, $\mathsf {Tamper}_{s_0}^{f} \approx \mathsf {Tamper}_{s_1}^{f}$, and for any $s$, $\Pr \left[ \mathsf {Tamper}^f_{s} \notin \{\bot , s\} \right] \le \mathsf {negl}(k)$, where $\mathsf {Tamper}$ denotes the experiment defined in Lemma 2.6 with respect to the encoding scheme of Construction 4.1, $(\mathsf {Enc}^*,\mathsf {Dec}^*)$. Our proof is given by a series of hybrids depicted in Fig. 7. We reduce the security $(\mathsf {Enc}^*,\mathsf {Dec}^*)$, to the security of Construction 3.1, $(\mathsf {Init},\mathsf {Enc},\mathsf {Dec})$, against $\mathcal {F}_{\mathsf {ad}}$ (cf. Corollary 4.3). The idea is to move from the tampered execution with respect to $(\mathsf {Enc}^*,\mathsf {Dec}^*)$, $f$, to a tampered execution with respect to $(\mathsf {Init},\mathsf {Enc},\mathsf {Dec})$, $g$, such that the two executions are indistinguishable and $(\mathsf {Init},\mathsf {Enc},\mathsf {Dec})$ is secure against $g$.

Let $I_{\mathsf {b}}$ be the set of indices of the blocks that $f$ chooses to tamper with, where $|I_{\mathsf {b}}| \le \alpha \nu$, and let $l \leftarrow 2m|sk|$, $\mathsf {bs}\leftarrow \log l+2$, $\mathsf {bn}\leftarrow l+|e|/\mathsf {bs}$. Below we describe the hybrids of Fig. 7.

• $\mathsf {Exp}_{0}^{f,s}$: The current experiment is the experiment $\mathsf {Tamper}_{s}^{f}$, of Lemma 2.6, with respect to $(\mathsf {Enc}^*,\mathsf {Dec}^*)$, $f$, $s$.

• $\mathsf {Exp}_{1}^{(g_1,g_2),s}$: The main difference between $\mathsf {Exp}_{0}^{f,s}$ and $\mathsf {Exp}_{1}^{(g_1,g_2),s}$, is that in the latter one, we introduce the tampering function $(g_1,g_2)$, that operates over codewords of $(\mathsf {Init},\mathsf {Enc},\mathsf {Dec})$ and we modify the encoding steps so that the experiment creates codewords of the bit-wise code $(\mathsf {Init},\mathsf {Enc},\mathsf {Dec})$. $(g_1,g_2)$ simulates partially the block-wise codeword $C$, while given partial access to the bit-wise codeword $c\leftarrow \mathsf {Enc}(s)$. As we prove in the full version, it simulates perfectly the tampering effect of $f$ against $C\leftarrow \mathsf {Enc}^*(s)$.

  $g_1$ operates as follows (cf. Fig. 4): it simulates perfectly the randomness for the permutation of the block-wise code, denoted as $\rho$, and constructs a set of indices I, such that $g_2$ will receive access to, and tamper with, $c_{|_{I}}$. The set I is constructed with respect to the set of blocks $I_{\mathsf {b}}$, that $f$ chooses to read, as well as $\varSigma$, that reveals the original bit positions, i.e., the ones before permuting $(z||e)$. $g_2$ receives $c_{|_{I}}$, reconstructs I, simulates partially the blocks of the block-wise codeword, $C$, and applies $f$ on the simulated codeword. The code of $g_2$ is given in Fig. 5. In the full version we show that $g_2$, given $c_{|_{I}}$, simulates perfectly $C_{|_{I_{\mathsf {b}}}}$, which implies that $g_2^{\varSigma }(c_{|_{I}}) = f(C_{|_{I_{\mathsf {b}}}})$, and the two executions are identical.

• $\mathsf {Exp}_{2}^{(g_1,g_3),s}$: In the current experiment, we substitute the function $g_2$ with $g_3$, and $\mathsf {Dec}^*$ with $\mathsf {Dec}$, respectively. By inspecting the code of $g_2$ and $g_3$ (cf. Figs. 5 and 6, respectively), we observe that latter function executes the code of the former, plus the “Check labels and simulate $\tilde{c}[I]$” step. Thus the two experiments are identical up to the point of computing $f(C_{|_{I_{\mathsf {b}}}})$. The main idea here is that we want the current execution to be with respect to $(\mathsf {Init},\mathsf {Enc},\mathsf {Dec})$ against $(g_1,g_3)$. Thus, we substitute $\mathsf {Dec}^*$ with $\mathsf {Dec}$, and we expand the function $g_2$ with some extra instructions/checks that are missing from $\mathsf {Dec}$. We name the resulting function as $g_3$ and we prove that the two executions are identical.

• Finally, we prove that for any $f$ and any $s$, $\mathsf {Exp}_{2}^{(g_1,g_3),s} \approx \mathsf {Exp}_{2}^{(g_1,g_3),\mathsf {0}}$ and $\Pr \left[ \mathsf {Exp}_{2}^{(g_1,g_3),s} \notin \{\bot , s\} \right] \le \mathsf {negl}(k)$. We do so by proving that $(g_1,g_3)$ is admissible for $(\mathsf {Init},\mathsf {Enc},\mathsf {Dec},)$, i.e., $(g_1,g_3) \in \mathcal {F}_{\mathsf {ad}}$, and $g_3$ will not request to access more that $m-1$ shares for each bit of $sk$, $sk^3$ (cf. Corollary 4.3). This implies security according to Lemma 2.6.

The indistinguishability between the hybrids is given in the full version of the paper.    $\blacksquare$

Fig. 6.

The function $g_3$ that appears in the hybrid experiments of Fig. 7.

Fig. 7.

The hybrid experiments for the proof of Theorem 4.4.

5 Continuous MD-NMC with Light Updates

In this section we enhance the block-wise scheme of Sect. 4 with an update mechanism, that uses only shuffling and refreshing operations. The resulting code is secure against continuous attacks, for a notion of security that is weaker than the original one [30], as we need to update our codeword. Below we define the update mechanism, which is denoted as $\mathsf {Update}^*$.

Construction 5.1

Let k, $m \in \mathbb {N}$, $(\mathsf {KGen},\mathsf {E},\mathsf {D})$, $(\mathsf {SS}_{m},\mathsf {Rec}_{m})$ be as in Construction 4.1. We define the update procedure, $\mathsf {Update}^*$, for the encoding scheme of Construction 4.1, as follows:

• $\mathsf {Update}^*(1^k,\cdot )$: on input $C$, parse it as $(C_1||\ldots ||C_{\mathsf {bn}})$, set $l \leftarrow 2m|sk|$, $\hat{\mathcal {L}}= \emptyset$, and set $\hat{C}:= (\hat{C}_1 || \ldots || \hat{C}_{\mathsf {bn}})$ to 0.

  • (Secret share $0^{2|sk|}$): Sample $z\leftarrow \mathsf {SS}_{m}\left( 0^{2|sk|} \right)$, where , $z \in \{0,1\}^{2m|sk|}$, and for $i \in \left[ 2|sk| \right]$, $z_i$ is an m-out-of-m secret sharing of the 0 bit.

  • (Shuffle & Refresh): Sample $\rho :=(\rho _1,\ldots ,\rho _l) {\mathop {\leftarrow }\limits ^{\mathsf {rs}}}\{0,1\}^{\log (\mathsf {bn})}$. For $i \in [\mathsf {bn}]$,

    • * (Sensitive block) If $C_i[1] = 1$,

      • (Shuffle): Set $j \leftarrow C_i[2:\mathsf {bs}-1]$, $\hat{C}_{\rho _j} \leftarrow C_i$.

      • (Refresh): Set $\hat{C}_{\rho _j}[\mathsf {bs}] \leftarrow \hat{C}_{\rho _j}[\mathsf {bs}] \oplus z[j]$.

    • * (Ciphertext block)

      If $C_i[1] = 0$, set $j \leftarrow \min _n \left\{ n \in [\mathsf {bn}] \big | n \notin \hat{\mathcal {L}}, n \ne \rho _i, i \in [l] \right\}$, and $\hat{C}_{j} \leftarrow C_i$, $\hat{\mathcal {L}}\leftarrow \hat{\mathcal {L}}\cup \{j \}$.

  Output $\hat{C}$.

The following definition of security is along the lines of the one given in [30], adapted to the notion of non-malleability with manipulation detection. Also, after each invocation the codewords are updated, where in our case the update mechanism is only using shuffling and refreshing operations. In addition, there is no need for self-destruct after detecting an invalid codeword [28].

Definition 5.2

(Continuously MD-NMC with light updates). Let $\mathsf {CS}=(\mathsf {Enc},\mathsf {Dec})$ be an encoding scheme, $\mathcal {F}$ be a functions class and $k,q \in \mathbb {N}$. Then, $\mathsf {CS}$ is a q-continuously non-malleable (q-CNM) code, if for every, sufficiently large $k \in \mathbb {N}$, any pair of messages $s_0$, $s_1 \in \{0,1\}^{\mathrm {poly}(k)}$, and any PPT algorithm $\mathcal {A}$, $\left\{ \mathsf {Tamper}^{\mathcal {A}}_{s_0}(k) \right\} _{k \in \mathbb {N}} \approx \left\{ \mathsf {Tamper}^{\mathcal {A}}_{s_1}(k) \right\} _{k \in \mathbb {N}}$, where,

and for each round the output of the decoder is not in $\{s, \bot \}$ with negligible probability in k, over the randomness of $\mathsf {Tamper}^{\mathcal {A}}_{s}$.

In the full version of the paper we prove the following statement.

Theorem 5.3

Let q, k, m, $\in \mathbb {N}$, $\varGamma =\{0,1\}^{O(\log (k))}$ and $\alpha \in [0,1)$. Assuming $(\mathsf {SS}_{m},\mathsf {Rec}_{m})$ is an m-out-of-m secret sharing scheme and $(\mathsf {KGen},\mathsf {E},\mathsf {D})$ is a 1-IND-CPA, authenticated encryption scheme, the scheme of Construction 5.1 is a continuously MD-NMC with light updates, against $\mathcal {F}^{\alpha }_{\varGamma }$, for any $\alpha$, m, such that $(1-\alpha )m=\omega (\log (k))$.

In the above theorem, q can be polynomial (resp. exponential) in k, assuming the underlying encryption scheme is computationally (resp. unconditionally) secure.