Abstract
The rise of machine learning as a service multiplies scenarios where one faces a privacy dilemma: either sensitive user data must be revealed to the entity that evaluates the cognitive model (e.g., in the Cloud), or the model itself must be revealed to the user so that the evaluation can take place locally. Fully Homomorphic Encryption (FHE) offers an elegant way to reconcile these conflicting interests in the Cloud-based scenario and also preserve non-interactivity. However, due to the inefficiency of existing FHE schemes, most applications prefer to use Somewhat Homomorphic Encryption (SHE), where the complexity of the computation to be performed has to be known in advance, and the efficiency of the scheme depends on this global complexity.
In this paper, we present a new framework for homomorphic evaluation of neural networks, that we call FHE–DiNN, whose complexity is strictly linear in the depth of the network and whose parameters can be set beforehand. To obtain this scale-invariance property, we rely heavily on the bootstrapping procedure. We refine the recent FHE construction by Chillotti et al. (ASIACRYPT 2016) in order to increase the message space and apply the sign function (that we use to activate the neurons in the network) during the bootstrapping. We derive some empirical results, using TFHE library as a starting point, and classify encrypted images from the MNIST dataset with more than 96% accuracy in less than 1.7 s.
Finally, as a side contribution, we analyze and introduce some variations to the bootstrapping technique of Chillotti et al. that offer an improvement in efficiency at the cost of increasing the storage requirements.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Fully Homomorphic Encryption (FHE). An FHE scheme provides a way to encrypt data while supporting computations through the encryption envelope. Given an encryption of a plaintext x, one can compute an encryption of f(x) for any computable function f. This operation does not require intermediate decryption or knowledge of the decryption key and therefore can be performed based on public information only. Applications of FHE are numerous but one particular use of interest is the privacy-preserving delegation of computations to a remote service. The first construction of FHE dates back to 2009 and is due to Gentry [Gen09]. A number of improvements have followed [vDGHV10, SS10, SV10, BV11a, BV11b, BGV12, GHS12, GSW13, BV14], leading to a biodiversity of techniques, features and complexity assumptions.
All known FHE schemes are obtained by first building a leveled Somewhat Homomorphic Encryption (SHE) scheme, which can evaluate circuits of a-priori bounded depth (usually, only the multiplicative depth is considered, because the noise growth introduced by additions is negligible compared to that introduced by multiplications). In order to obtain unbounded computation capabilities on encrypted values, an FHE scheme can be built from an SHE scheme with a technique called bootstrapping, which intuitively means using the homomorphic properties of the scheme to decrypt and then re-encrypt, refreshing the ciphertext to enable further computation. However, this process is very costly. Hence, there have been numerous works on trying to obtain more efficient bootstrappings [AP13, AP14, DM15, CGGI16b, CGGI17], and on trying to minimize the number of bootstrappings required for evaluating a circuit [LP13, PV16, BLMZ17]. Another approach is to simply avoid bootstrapping altogether and use an SHE scheme, adjusting the parameters to be able to carry out the desired computation.
In practice, there are now two main freely available libraries for fully homomorphic encryption. The first one, HElib [HS14, HS15], which implements the BGV scheme [BGV12], is the most widely used in applications. It allows for packing of ciphertexts and SIMD computations, amortizing the cost for certain tasks. It is able to perform additions and multiplications in an efficient way, but the bootstrapping operation is significantly slow. In practice, it is often used as a somewhat homomorphic scheme. The second one, TFHE [CGGI16a], features a very efficient bootstrapping operation but, as a downside, this has to be applied after every gate computation. This library is more efficient than HElib when used for realizing an FHE. However, for simple tasks requiring small computational depth, HElib used as an SHE will perform better. Moreover, TFHE is currently not capable of amortizing large SIMD computations as well as HElib does.
The quest for privacy-preserving machine learning. Machine Learning As a Service (MLAS) is becoming popular because of its versatility. These applications typically have high computation and data-storage requirements, which make them less suitable as client-side technologies. Moreover, since the process of training a cognitive model is time and resource-consuming, the trained prediction algorithm is often considered critical intellectual property by its owner, who is typically not willing to share its technology or proprietary tools, resulting in that machine learning algorithms are most conveniently cloud-based.
However, this setting raises new issues concerning the privacy of the uploaded input data. Users want to send their encrypted data to a cloud service that offers privacy-preserving predictions, and fulfills this task using its powerful yet undisclosed, state-of-the-art predictive models. In this paper, we put forward a new and versatile FHE framework that makes it efficient for the cloud to operate a neural network dedicated to some specific machine learning task. The network, previously trained on plaintext dataset, does not have access to the input data in the clear, but is only given user-provided encrypted inputs and returns encrypted predictions.
Obviously, encrypting the user’s data ensures its confidentiality, since the private key under which the data is encrypted is assumed never to leave the owner’s controlled domain. In this setting, only the legitimate owner of the secret key can decrypt the result returned by the delegated computation that has been homomorphically performed in the cloud. The cloud service only learns superficial information, but can still charge the user for using the service.
Neural networks (NNs) are often built from medical, financial or otherwise sensitive data. They are usually trained to solve a classification problem: all possible observations are categorized into classes and, given a training dataset of observation/class pairs, the network should be able to assign the correct class to new observations. Such framework can be easily applied to problems like establishing a diagnosis from medical observations.
In this work we do not consider the problem of privacy-preserving data-mining, intended as training a neural network over encrypted data, which can be addressed, e.g., with the approach of [AS00]. Instead, we assume that the neural network is trained with data in the clear and we focus on the evaluation part.
Another potential concern for the service provider is that users might be sending malicious requests in order to either learn what is considered a company secret (the neural network itself), or specific sensitive information encoded in the weights (which could be a breach into the privacy of the training dataset). In this latter case, a statistical database can be used in the training phase, as is discussed in the differential privacy literature [Dwo06].
Prior works. Cryptonets [DGBL+16] was the first initiative to address the challenge of achieving blind, non-interactive classification. The main idea consists in applying a leveled SHE scheme such as BGV [BGV12] to the network inputs and propagating the signals across the network homomorphically, thereby consuming levels of homomorphic evaluation whenever non-linearities are met. In NNs, non-linearities come from activation functions which are usually picked from a small set of non-linear functions of reference (logistic sigmoid, hyperbolic tangent, ...) chosen for their mathematical convenience. To optimally accommodate the underlying SHE scheme, Cryptonets replace their standard activation by the (depth 1) square function, which only consumes one level but does not resemble the typical sigmoidal shape. A number of subsequent works have followed the same approach and improved it, typically by adopting higher degree polynomials as activation functions for more training stability [ZYC16], or by renormalizing weighted sums prior to applying the approximate function, so that its degree can be kept as low as possible [CdWM+17]. Practical experiments have shown that training can accommodate approximated activations and generate NNs with very good accuracy.
However, this approach suffers from an inherent limitation: the homomorphic computation, local to a single neuron, depends on the total number of levels required to implement the network, which is itself roughly proportional to the number of its activated layers. Therefore, the overall performance of the homomorphic classification heavily depends on the total multiplicative depth of the circuit and rapidly becomes prohibitive as the number of layers increases. This approach does not scale well and is not adapted to deep learning, where neural networks can contain tens, hundreds or sometimes thousands of layers [HZRS15, ZK16].
Finally, we note that other approaches based on multiparty computation (MPC) have been proposed, e.g., [BPTG15, MZ17, MRSV17], but they require interactivity between the party that holds the data and the party that performs the blind classification. Even though practical performances of MPC-based solutions have been impressive compared to FHE-based solutions, they incur other issues like network latency and high bandwidth usage. Because of these downsides, FHE-based solutions seem more scalable for real-life applications. In this work, we focus on a non-interactive, blind evaluation, and we rely on FHE.
Our contributions. We adopt a scale-invariant approach to the problem. In our framework, called FHE–DiNN, each neuron’s output is refreshed through bootstrapping, resulting in that arbitrarily deep networks can be homomorphically evaluated. Of course, the entire homomorphic evaluation of the network will take time proportional to the number of its neurons or, if parallelism is involved, to the number of its layers. Evaluating one neuron is now essentially independent of the dimensions of the network: it just relies on system-wide parameters.
In FHE–DiNN, unlike in standard neural networks, the weights and biases, as well as the domain and range of the activation function cannot be real-valued and must be discretized. We call such networks Discretized Neural Networks or DiNNs. This particular form of neural networks is somehow inspired by a more restrictive one, referred to in the literature as Binarized Neural Networks (BNNs) [CB16] where signals and weights are restricted to the set \(\{-1, 1\}\) instead of \(\mathbb {Z}\) as in the case of DiNNs (so BNNs are a special case of DiNNs). Interestingly, it has been empirically observed by [CB16] that BNNs can achieve accuracies close to the ones obtained with state-of-the-art classical NNs, at the price of an overhead in the total network size, which is largely compensated by the obtained performance gains. For the sake of scale-invariance, we decided to choose as activation function the sign, so the signal which is propagated has values in \(\left\{ -1, 1\right\} \), and cannot grow out of control. So the evaluation of DiNNs boils down to repeatedly computing the sign of a weighted sum of \(\pm 1\) inputs.
In order to perform this classification on encrypted data, we adapt the recent construction by Chillotti et al., known as TFHE [CGGI16b] to support sign and weighted sum as the two basic operations of the scheme, the sign being computed during a bootstrapping procedure in order to refresh the ciphertext.
As a side contribution, we also present a few techniques to optimize the usage of TFHE in applications: how to reduce the required bandwidth, how to reduce the overall noises in the ciphertexts, and a slightly faster alternative to the bootstrapping procedure that also produces ciphertexts with less noise, at the expense of a bigger bootstrapping key.
Finally, we conducted experiments on the MNIST dataset [LBBH98]. We used the library keras [C+15] to train two simple neural networks with one hidden layer containing 30 (respectively, 100) neurons and we converted them into DiNNs by simply discretizing the weights and using the sign as activation function. Of course, this introduced a loss in accuracy, and although much better accuracies could certainly be obtained through various optimizations or by directly training a DiNN (rather than converting a canonical neural network), this was not the goal of this work. Our aim was conducting experiments to measure the accuracy of the homomorphic classification and comparing it to that in the clear. We found that, for a security level of \(80\) bits, our implementation takes about 0.49 s (respectively, 1.65 s) seconds per classification (with no underlying parallelism whatsoever) and achieves 93.71% (respectively, 96.35%) accuracy when evaluated homomorphically.
Comparison with cryptonets [DGBL+16]. In Cryptonets, propagated signals are reals properly encoded into compatible plaintexts and a single encrypted input (i.e., an image pixel) takes \(2 \,{\cdot }\, 382 \,{\cdot }\, 8192\) bits (=766 kB). Therefore, an entire image takes \(28 \cdot 28 \cdot 766\,\text {kB} \approx 586\,\text {MB}\). However, with the same storage requirements, Cryptonets can batch 8192 images together, so that the amortized size of an encrypted image is reduced to 73.3 kB. In the case of FHE–DiNN, we are able to exploit the batching technique on a single image, resulting in that each encrypted image takes \(\approx \)8.2 kB. In the case of Cryptonets, the complete homomorphic evaluation of the network takes 570 s, whereas in our case it takes 0.49 s (or 1.6 s in the case of a slightly larger network). However, it should be noted that (a) the networks that we use for our experiments are considerably smaller than that used in Cryptonets, so we also compare the time-per-neuron and, in this case, our solution is faster by roughly a factor 36; moreover (b) once again Cryptonets support image batching, so 8192 images can be classified in 570 s, resulting in only 0.07 s per image. Cryptonets’ ability to batch images together can be useful in some applications where the same user wants to classify a large number of samples together. In the simplest case where the user only wants a single image to be classified, this feature does not help.
Regarding classification accuracy, the NN used by Cryptonets achieves 98.95% of correctly classified samples, when evaluated on the MNIST dataset. In our case, a loss of accuracy occurs due to the preliminary simplification of the MNIST images, and especially because of the discretization of the network. We stress however that our prime goal was not accuracy but to achieve a qualitatively better homomorphic evaluation at the neuron level.
Finally, we also achieve scale-invariance, meaning that we can keep on computing over the encrypted outputs of our network, whereas Cryptonets are bounded by the initial choice of parameters. In Table 1 we present a detailed comparison with Cryptonets.
Outline of the paper. The paper is organized as follows: in Sect. 2 we define our notation and we introduce notions about fully homomorphic encryption and artificial neural networks; in Sect. 3 we present our Discretized Neural Networks and show a simple technique to build these models; in Sect. 4 we explain how to homomorphically evaluate a DiNN and present our main result; in Sect. 5 we present some technical refinements that allow us to improve the efficiency of the evaluation and that can be useful also for other FHE-based solutions; finally, in Sect. 6 we give experimental results on data in the clear and on encrypted inputs, draw some conclusions and identify several open problems.
2 Preliminaries
In this section we clarify our notation and recall some definitions and constructions that are going to be useful in the rest of the paper.
2.1 Notation
We denote the real numbers by \(\mathbb {R}\), the integers by \(\mathbb {Z}\) and use \(\mathbb {T}\) to indicate \(\mathbb {R}/\mathbb {Z}\), i.e., the torus of real numbers modulo 1. We use \(\mathbb {B}\) to denote the set \(\left\{ 0,1\right\} \), and we use \(\mathcal {R}\left[ X\right] \) for polynomials in the variable X with coefficients in \(\mathcal {R}\), for any ring \(\mathcal {R}\). We use \(\mathbb {R}_N\left[ X\right] \) to denote \(\mathbb {R}\left[ X\right] /\left( X^N+1\right) \) and \(\mathbb {Z}_N\left[ X\right] \) to denote \(\mathbb {Z}\left[ X\right] /\left( X^N+1\right) \) and we write their quotient as \(\mathbb {T}_N\left[ X\right] =\mathbb {R}_N\left[ X\right] /\mathbb {Z}_N\left[ X\right] \), i.e., the ring of polynomials in X quotiented by \(\left( X^N+1\right) \), with real coefficients modulo 1. Vectors are denoted by lower-case bold letters, and we use  and
and  to denote the \(L_1\) and the \(L_2\) norm of a vector, respectively. Given a vector \(\mathbf {a}\), we denote its i-th entry by \(a_i\). We use \(\langle \mathbf {a}, \mathbf {b}\rangle \) to denote the inner product between vectors \(\mathbf {a}\) and \(\mathbf {b}\).
to denote the \(L_1\) and the \(L_2\) norm of a vector, respectively. Given a vector \(\mathbf {a}\), we denote its i-th entry by \(a_i\). We use \(\langle \mathbf {a}, \mathbf {b}\rangle \) to denote the inner product between vectors \(\mathbf {a}\) and \(\mathbf {b}\).
Given a set A, we write  to indicate that a is sampled uniformly at random from A. If \(\mathcal {D}\) is a probability distribution, we will write \(d \leftarrow \mathcal {D}\) to denote that d is sampled according to \(\mathcal {D}\).
to indicate that a is sampled uniformly at random from A. If \(\mathcal {D}\) is a probability distribution, we will write \(d \leftarrow \mathcal {D}\) to denote that d is sampled according to \(\mathcal {D}\).
2.2 Fully Homomorphic Encryption over the Torus
Learning with errors. The Learning with Errors (LWE) problem was introduced by Regev in [Reg05]. Let n be a positive integer and \(\chi \) be a probability distribution over \(\mathbb {R}\) for the noise. For any vector \(\mathbf {s}\in \left\{ 0,1\right\} ^n\), we define the LWE distribution \(\mathsf {lwe}_{n, \mathbf {s}, \chi }\) as \(\left( \mathbf {a}, b\right) \), where  and \(b = \langle \mathbf {s}, \mathbf {a}\rangle + e \in \mathbb {T}\), with \(e \leftarrow \chi \).
and \(b = \langle \mathbf {s}, \mathbf {a}\rangle + e \in \mathbb {T}\), with \(e \leftarrow \chi \).
Then the LWE assumption states that, for  , it is hard to distinguish between \(\left( \mathbf {a}, b\right) \) and \(\left( \mathbf {u}, v\right) \), for \(\left( \mathbf {a}, b\right) \leftarrow \mathsf {lwe}_{n, \mathbf {s}, \chi }\) and
, it is hard to distinguish between \(\left( \mathbf {a}, b\right) \) and \(\left( \mathbf {u}, v\right) \), for \(\left( \mathbf {a}, b\right) \leftarrow \mathsf {lwe}_{n, \mathbf {s}, \chi }\) and  .
.
Sub-Gaussians. Let \(\sigma >0\) be a real Gaussian parameter. We define the Gaussian function with parameter \(\sigma \) as \(\rho _\sigma \left( x\right) = \exp \left( -\pi \left| x\right| ^2/\sigma ^2\right) \) for any \(x \in \mathbb {R}\). Then we say that a distribution \(\mathcal {D}\) is sub-Gaussian with parameter \(\sigma \) if there exists \(M > 0\) such that for all \(x\in \mathbb {R}\),
Lemma 2.1
(Pythagorean additivity of sub-Gaussians). Let \(\mathcal {D}_1\) and \(\mathcal {D}_2\) be sub-Gaussian distributions with parameters \(\sigma _1\) and \(\sigma _2\), respectively. Then \(\mathcal {D}^+\), obtained by sampling \(\mathcal {D}_1\) and \(\mathcal {D}_2\) and summing the results, is a sub-Gaussian with parameter \(\sqrt{\sigma _1^2+\sigma _2^2}\).
LWE-based private-key encryption scheme. We recall the Regev encryption scheme from [Reg05]. Let \(\mu \in \left\{ 0,1\right\} \) be a message and \(\lambda \) the security parameter; we encrypt and decrypt as follows:
-
 : for a security parameter
: for a security parameter 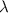 , fix
, fix 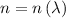 and return
and return 
-
\(\mathsf {Enc}\left( \mathbf {s}, \mu \right) \): return \(\left( \mathbf {a}, b\right) \), with
 and \(b = \langle \mathbf {s}, \mathbf {a}\rangle + e + \frac{\mu }{2}\), where \(e \leftarrow \chi \)
and \(b = \langle \mathbf {s}, \mathbf {a}\rangle + e + \frac{\mu }{2}\), where \(e \leftarrow \chi \) -
\(\mathsf {Dec}\left( \mathbf {s}, \left( \mathbf {a}, b\right) \right) \): return \(\left\lfloor 2\left( b - \langle \mathbf {s}, \mathbf {a}\rangle \right) \right\rceil \)
We usually refer to e as the noise of the ciphertext, and say that a ciphertext is a valid encryption of \(\mu \) if it decrypts to \(\mu \) with overwhelming probability.
We now give some notions on the formulation of FHE over the torus and the bootstrapping procedure. The following part is based on [CGGI16b].
TLWE. TLWE is a generalization of LWE and Ring-LWE [LPR10]. Let \(k \ge 1\) be an integer, N be a power of 2 and \(\chi \) be an error distribution over \(\mathbb {R}_N\left[ X\right] \). A TLWE secret key \(\bar{\mathbf {s}}\in \mathbb {B}_N \left[ X\right] ^k\) is a vector of k polynomials over \(\mathbb {Z}_N\left[ X\right] \) with binary coefficients. Given a message encoded as a polynomial \(\mu \in \mathbb {T}_N\left[ X\right] \), a fresh TLWE encryption of \(\mu \) under the key \(\bar{\mathbf {s}}\) is a sample \(\left( \mathbf {a}, b\right) \in \mathbb {T}_N\left[ X\right] ^k \times \mathbb {T}_N\left[ X\right] \), with  and \(b = \bar{\mathbf {s}}\cdot \mathbf {a}+ \mu + e\), where \(e \leftarrow \chi \).
and \(b = \bar{\mathbf {s}}\cdot \mathbf {a}+ \mu + e\), where \(e \leftarrow \chi \).
From a TLWE encryption \(\bar{c}\) of a polynomial \(\mu \in \mathbb {T}_N\left[ X\right] \) under a TLWE key \(\bar{\mathbf {s}}\) we can extract a LWE encryption \(c' = \mathsf {Extract}\left( \bar{c}\right) \) of the constant term of \(\mu \) under an extracted key \(\mathbf {s}' = \mathsf {ExtractKey}\left( \bar{\mathbf {s}}\right) \). For the details of the algorithms \(\mathsf {Extract}\) and \(\mathsf {ExtractKey}\), we refer the reader to [CGGI16b, Definition 4.1].
TGSW. TGSW is a generalized version of the GSW FHE scheme [GSW13]. The key concept here is that TGSW can be seen as the matrix equivalent of TLWE, just like GSW can be seen as the matrix equivalent of LWE. More details can be found in [CGGI16b].
As in previous works, our average-case noise analysis relies on the following heuristic. This assumption matches empirical results [DM15, CGGI16b]. Note that the worst-case bounds do not require this heuristic.
Assumption 1
We assume that all the error coefficients of TLWE or TGSW samples of the linear combinations we consider are independent and concentrated. In particular, we assume that they are sub-Gaussian where \(\sigma \) is the square-root of their variance.
Overview of the bootstrapping procedure. The core idea for the efficiency of the new bootstrapping procedure is the so-called external product \(\boxdot \), that performs the following mapping
Roughly speaking, the external product of a TGSW encryption of a polynomial \(\mu _1 \in \mathbb {T}_N\left[ X\right] \) and a TLWE encryption of a polynomial \(\mu _2 \in \mathbb {T}_N\left[ X\right] \) is a TLWE encryption of \(\left( \mu _1 \cdot \mu _2\right) \in \mathbb {T}_N\left[ X\right] \).
Now the bootstrapping procedure of an n-LWE sample (here, n denotes the dimension) consists of the 3 following functions:
-
BlindRotate: TGSW\(^n\) \(\times \) TLWE \(\times \) n-LWE \(\rightarrow \) TLWE
On input TGSW encryptions of \((s_i)_{i\in [n]}\), a (possibly noiseless) TLWE encryption of testVector and an n-LWE sample \((\mathbf {a},b)\), computes a TLWE encryption of \(X^\phi \cdot \) testVector, where \(\phi =b-\langle \mathbf {s}, \mathbf {a}\rangle \);
-
Extract: TLWE \(\rightarrow \) N-LWE
On input a TLWE encryption of polynomial \(\mu \in \mathbb {T}_N\left[ X\right] \), computes an N-LWE encryption of the constant term \(\mu (0)\);
-
KeySwitch: n-LWE\(^N\) \(\times \) N-LWE \(\rightarrow \) n-LWE
On input n-LWE encryptions of \((s'_i)_{i\in [N]}\), and an N-LWE sample \((\mathbf {a},b)\) computes an n-LWE encryption of \(b-\langle \mathbf {s}', \mathbf {a}\rangle \).
Then we can define a function \(\mathsf {Bootstrap}\left( \cdot , \cdot , \cdot \right) \) that takes as input a bootstrapping key \(\mathsf {bk}\), a keyswitching key \(\mathsf {ksk}\), and a ciphertext and outputs a new ciphertext. Roughly speaking,
We note that BlindRotate works on LWE samples with values in [2N] instead of \(\mathbb {T}\), thus the first step is to map \(\mathbb {T}\) to [2N] by multiplying and rounding.
When studying the noise distribution during this operation, and to measure the impact of our changes on this procedure, we note that there are actually two different relevant noises: the overhead noise which is added to the input ciphertext before its virtual decryption and the output noise, which is the one in the final output ciphertext.
2.3 Artificial Neural Networks
An artificial neural network is a computing system inspired by biological brains. Here, we consider a neural network (NN) that is composed of a population of artificial neurons arranged in layers. Each neuron of a dense layer accepts \(n_I\) real-valued inputs \(\mathbf {x}= (x_1,\dots , x_{n_I})\) and performs the following two computations:
-
1.
It computes a real value \(y = \sum _{i=1}^{n_I} w_i x_i + \beta \), which is a weighted sum of the inputs with real values called weights: \(w_i\) is the weight associated to the input \(x_i\), and \(\beta \), also real-valued, is referred to as the bias of the neuron.
-
2.
It applies a non-linear function f, the activation function, and returns f(y).
The neuron’s output can be written as \(f\left( \langle \mathbf {w}, \mathbf {x}\rangle \right) = f\left( \sum _{i=0}^{n_I} w_i x_i\right) \) if one extends the inputs and the neuron’s weights vector by setting \(\mathbf {w}= (\beta , w_1,\dots , w_{n_I})\) and \(\mathbf {x}= (1, x_1,\dots , x_{n_I})\). The neurons of a neural network are organized in successive layers, which are categorized according to their activation function. Neurons of one layer are connected to the neurons of the next layer by paths that are associated to weights. An input layer composed of the network’s inputs as well as an output layer made of the network’s output values are also added to the network. Internal layers are called hidden, since they are not directly accessible from the external world.
NNs are usually composed of layers of various types: fully connected (every neuron of the layer takes all incoming signals as inputs), convolutional (it applies a convolution to its input), pooling, and so forth. Neural networks could in principle be recurrent systems, as opposed to the purely feed-forward ones, where each neuron is only evaluated once. The universal approximation theorem (see, e.g., [Hor91, Cyb89]) states that a neural network with a single hidden layer that contains a finite amount of neurons, can approximate any continuous function. Despite this, the number of neurons in that layer can grow exponentially. Instead, a deep neural network has several layers of non-linearities, which allow to extract increasingly complex features of the input and can lead to a better ability to generalize, especially in the case of more complex tasks.
The FHE–DiNN framework presented in this work is able to evaluate NNs of arbitrary depth, comprising possibly many hidden layers.
2.4 The MNIST Dataset
The MNIST database (Modified National Institute of Standards and Technology database) is a dataset of images representing digits handwritten by more than 500 different writers, and is commonly used as a benchmark for machine learning systems [LBBH98]. The MNIST database contains 60 000 training images and 10 000 testing images. The format of the images is \(28\times 28\) and the value of each pixel represents a level of gray. Moreover, each image is labeled with the digit it depicts.
A typical neural network for the MNIST dataset has \(28\cdot 28 = 784\) input nodes (one per pixel), an arbitrary number of hidden layers with an arbitrary number of neurons per layer, and finally 10 output nodes (one per possible digit). The output values can be interpreted as “scores” given by the NN: the classification is then given by the digit that achieves the highest score.
Over the years, the MNIST dataset has been a typical benchmark for classifiers, and many approaches have been applied: linear classifiers, principal component analysis, support vector machines, neural networks, convolutional neural networks, etc. For a more complete review on these approaches, we refer the reader to, e.g., [LBBH98]. Neural networks are known to perform well on this dataset. For example, [LBBH98] proposes different architectures for neural networks and obtains more than 97% of correct classifications. More recent works even surpassed 99% of accuracy [CMS12]. For a nice overview on the results obtained on this dataset and on the techniques that were used, we refer the reader to [LCB98].
3 Discretized Neural Networks (DiNN)
In this section we formally define DiNNs and we explain how they differ from a traditional neural network and how to simply convert a NN into a DiNN.
3.1 Definition of a Discretized Neural Network
First of all, we recall that state-of-the-art fully homomorphic encryption schemes cannot support operations over real messages. Traditional neural networks have real-valued weights, and this incompatibility motivates investigating alternative architectures.
Definition 3.1
A Discretized Neural Network (DiNN) is a feed-forward artificial neural network whose inputs are integer values in \(\left\{ -I, \ldots , I\right\} \) and whose weights are integer values in \(\left\{ -W, \ldots , W\right\} \), for some \(I, W \in \mathbb {N}\). For every neuron of the network, the activation function maps the inner product between the incoming inputs vector and the corresponding weights to integer values in \(\left\{ -I, \ldots , I\right\} \).
In particular, for this paper we chose \(\left\{ -1,1\right\} \) as the input space and \(\mathsf {sign}\left( \cdot \right) \) as the activation function for the hidden layers:
These choices are inspired by the fact that we designed the model with the idea of performing homomorphic evaluations over encrypted input. As a consequence, we wanted the message space to be as small as possible, which, in turn, would allow us to increase the efficiency of the overall evaluation.
We also note that using an activation function whose output is in the same range as the network’s input allows us to maintain the same semantics across different layers. In our case, what enters a neuron is always a weighted sum of values in \(\left\{ -1,1\right\} \). In order to make the evaluation of the network compatible with FHE schemes, discretizing the input space is not sufficient: we also need to have discrete values for the weights of the networkFootnote 1.
3.2 Simple Conversion from a Traditional Neural Network to a DiNN
In this subsection we show a very simple method to convert an already-trained canonical neural network (i.e., with real weights) into a DiNN. This method is not guaranteed to be the best way to obtain such a conversion; it indeed introduces a visible loss in the classification accuracy and would probably be best used as a first step in the conversion procedure. However, we remind the reader that this work is aimed at the homomorphic evaluation of a network, thus we decided not to put too much effort in the construction of a sophisticated cleartext model. This procedure allows us to obtain a network which respects our constraints and that can be evaluated over encrypted inputs, so it is sufficient for our purposes.
It turns out that the only thing that we need to do is discretizing the weights and biases of the network. To this purpose, we define the function
where \(\tau \in \mathbb {N}\) is a parameter that controls the precision of the discretization. In the following, we implicitly take all the weights as discretized after being processed through the formula in Eq. 3.2. After fixing a value \(\tau \), the network obtained by applying \(\mathsf {processWeight}\left( \cdot , \tau \right) \) to all the weights and biases is a DiNN. The parameter \(\tau \) has to be chosen carefully, since it defines the message space that our encryption scheme must support. Thus, we want the bound on \(\langle \mathbf {w}, \mathbf {x}\rangle \) to be small for all neurons, where \(\mathbf {w}\) and \(\mathbf {x}\) are the discretized weights and the inputs associated to the neuron, respectively. In Fig. 1, we show the evaluation of a single neuron: we first compute \(\langle \mathbf {w}, \mathbf {x}\rangle \), which we refer to as a multisum, and then apply the sign function to the result.
4 Homomorphic Evaluation of a DiNN
We now give a high level description of our procedure to homomorphically evaluate a DiNN, called FHE–DiNN. We basically need two ingredients: we need to be able to compute the multisum between the encrypted inputs and the weights and we need to homomorphically extract the sign of the result. In order to maintain the scalability of our scheme across the layers of a given DiNN, we perform a bootstrapping operation for every neuron in hidden layers. This ensures that the ciphertext encrypting the sign of the result after applying one layer of the DiNN can be used for further computations without an initially fixed limit on the number of layers that the network can contain. Hence we can choose parameters that are independent of the number of layers and evaluate arbitrarily deep neural networks.
4.1 Evaluating the Multisum
In our framework, the weights of the network are available in clear, so we can evaluate the multisum just by using homomorphic additions. The only things that need our attention are the message space of our encryption scheme, which has to be large enough to accommodate for all possible values of the multisums, and the noise level that might grow too much and lead to incorrect results.
Extending the message space. In order for our FHE scheme to be able to correctly evaluate the multisum, we need all the possible values of the multisum to be inside our message space. To this end, we extend our LWE encryption scheme as follows. This idea was already used in previous works such as [PW08, KTX08, ABDP15, ALS16].
Construction 1
(Extended LWE-based private-key encryption scheme). Let B be a positive integer and let \(m \in \left[ -B,B\right] \) be a message. Then we split the torus into \(2B + 1\) slices, one for each possible message, and we encrypt and decrypt as follows:
-
 : for a security parameter
: for a security parameter 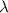 , fix
, fix 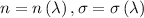 ; return
; return 
-
\(\mathsf {Enc}\left( \mathbf {s}, m\right) \): return \(\left( \mathbf {a}, b\right) \), with
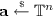 and \(b = \langle \mathbf {s}, \mathbf {a}\rangle + e + \frac{m}{2B+1}\), where \(e \leftarrow \chi _\sigma \)
and \(b = \langle \mathbf {s}, \mathbf {a}\rangle + e + \frac{m}{2B+1}\), where \(e \leftarrow \chi _\sigma \) -
\(\mathsf {Dec}\left( \mathbf {s}, \left( \mathbf {a}, b\right) \right) \): return \(\left\lfloor \left( b - \langle \mathbf {s}, \mathbf {a}\rangle \right) \cdot \left( 2B+1\right) \right\rceil \)
An input message is mapped to the center of its corresponding torus slice by scaling it by \(1/\left( 2B+1\right) \) during encryption, and decoded by scaling it by \(2B+1\) during decryption.
Correctness of homomorphically evaluating the multisum. Note that ciphertexts can be homomorphically added and scaled by a known integer constant: for any two messages \(m_1, m_2 \in \left[ -B,B\right] \), any secret key \(\mathbf {s}\), any \(c_1 = \left( \mathbf {a}_1, b_1\right) \leftarrow \mathsf {Enc}\left( \mathbf {s}, m_1\right) \), \(c_2 = \left( \mathbf {a}_2, b_2\right) \leftarrow \mathsf {Enc}\left( \mathbf {s}, m_2\right) \), and constant \(w \in \mathbb {Z}\), we have that
as long as (1) \(m_1 + w\cdot m_2 \in \left[ -B,B\right] \), and (2) the noise did not grow too much.
The first condition is easily met by choosing  for all weight vectors \(\mathbf {w}\) in the network (e.g., we can take the max).
for all weight vectors \(\mathbf {w}\) in the network (e.g., we can take the max).
Fixing the noise. Increasing the message space has an impact on the choice of parameters. Evaluating the multisum with a given weight vector \(\mathbf {w}\) means that, if the standard deviation of the initial noise is \(\sigma \), then the standard deviation of the output noise can be as high as  (see Lemma 2.1), which in turn means that our initial standard deviation must be smaller than the one in [CGGI16b] by a factor
(see Lemma 2.1), which in turn means that our initial standard deviation must be smaller than the one in [CGGI16b] by a factor  . Moreover, for correctness to hold, we need the noise to remain smaller than half a slice of the torus. As we are splitting the torus into \(2B+1\) slices rather than 2, we need to further decrease the noise by a factor B. Special attention must be paid to security: taking a smaller noise might in fact compromise the security of the scheme. In order to mitigate this problem, we can increase the dimension of the LWE problem n, but this in turn induces more noise overhead in the bootstrapping procedure due to rounding errors.
. Moreover, for correctness to hold, we need the noise to remain smaller than half a slice of the torus. As we are splitting the torus into \(2B+1\) slices rather than 2, we need to further decrease the noise by a factor B. Special attention must be paid to security: taking a smaller noise might in fact compromise the security of the scheme. In order to mitigate this problem, we can increase the dimension of the LWE problem n, but this in turn induces more noise overhead in the bootstrapping procedure due to rounding errors.
4.2 Homomorphic Computation of the Sign Function
We take advantage of the flexibility of the bootstrapping technique introduced by Chillotti et al. [CGGI16b] in order to perform the sign extraction and the bootstrapping at the same time. Concretely, in the call to BlindRotate, we change the value of testVector to
Then, if the value of the phase \(b-\langle \mathbf {s}, \mathbf {a}\rangle \) is between 1 and N (positive), the output will be an encryption of 1, otherwise if it is between \(N+1\) and 2N (negative), the output will be an encryption of \(-1\).
In order to give more intuition, we present an illustration of the bootstrapping technique in Fig. 2. The first step of the bootstrapping basically consists in mapping the torus \(\mathbb {T}\) to an object that we will refer to as the wheel. This wheel is split into 2N “ticks” that are associated to the possible values that are encrypted in the bootstrapped ciphertext. The bootstrapping procedure then consists in choosing a value for each tick, rotating the wheel by \(b-\langle {\mathbf {s}, \mathbf {a}}\rangle \) ticks counter-clockwise, and picking the value of the rightmost tick. We note that the values on the wheel are encoded in the testVector variable, which contains values for the ticks on the top part of the wheel. The bottom values are then fixed by the anticyclic property of \(\mathbb {T}_N[X]\) (the value at tick \(N+i\) is minus the value at tick i).
On the left, we show the first step of the bootstrapping, which consists in mapping the torus (the continuous circle) to the wheel (the 2N ticks on it) by rounding to the closest tick. Each slice corresponds to one of the possible results of the multisum operation. On the right we show the final result of the bootstrapping: each tick of the top part of the wheel is mapped to its \(\mathsf {sign}\) which is \(+1\) and each tick of the bottom part to \(-1\). This can roughly be seen as embedding the wheel back to the torus.
From now on, we say that a bootstrapping is correct if, given a valid encryption of a message \(\mu \), its output is a valid encryption of \(\mathsf {sign}\left( \mu \right) \) with overwhelming probability.
4.3 Scale-Invariance
If the parameters are set correctly then, by using the two operations described above, we can homomorphically evaluate neural networks of any depth. In particular, the choice of parameters is independent of the depth of the neural network. This result cannot be achieved with previous techniques relying on somewhat homomorphic evaluations of the network. In fact, they have to choose parameters that accommodate for the whole computation, whereas our method only requires the parameters to accommodate for the evaluation of a single neuron. The rest of the computation follows by induction. More precisely, our choice of parameters only depends on bounds on the norms ( and
and  ) of the input weights of a neuron. In the following, we denote these bounds by \(M_1\) and \(M_2\), respectively.
) of the input weights of a neuron. In the following, we denote these bounds by \(M_1\) and \(M_2\), respectively.
We say that the homomorphic evaluation of the neural network is correct if the decryptions of its output scores are equal to the scores given by its evaluation in the clear with overwhelming probability. Then, the scale-invariance is formally defined by the following theorem:
Theorem 4.1
(Scale-invariance of our homomorphic evaluation). For any DiNN of any depth, any correctly generated bootstrapping key \(\mathsf {bk}\) and keyswitching key \(\mathsf {ksk}\), and any ciphertext c, let \(\sigma \) be a Gaussian parameter such that the noise of \(\mathsf {Bootstrap}\left( \mathsf {bk}, \mathsf {ksk}, c\right) \) is sub-Gaussian with parameter \(\sigma \). Then, if the bootstrapping is correct on input ciphertexts with sub-Gaussian noise of parameter \(\frac{\sigma }{M_2}\) and message space larger than \(2M_1+1\), the result of the homomorphic evaluation of the DiNN is correct.
Proof
The proof is a simple induction on the structure of the neural network. First, the correctness of the evaluation of the first layer is implied by the choice of parameters for the encryptionFootnote 2.
If the evaluation is correct for all neurons of the \(\ell \)-th layer, then the correctness for all neurons of the \((\ell +1)\)-th layer follows from the two observations made in the previous subsections:
-
The result of the homomorphic evaluation of the multisum is a valid encryption of the multisum;
-
The result of the bootstrapping is a valid encryption of the sign of the multisum.
The first fact is implied by the choice of the message space, since the multisum value is contained in \(\left[ -M_1,M_1\right] \). The second one comes directly from the correctness of the bootstrapping, because the homomorphic computation of the multisum on ciphertexts with sub-Gaussian noise of parameter \(\sigma \) yields a ciphertext with sub-Gaussian noise of parameter at most \(\sigma M_2\) (cf. Lemma 2.1).
Then, the correctness of the encryption scheme ensures that the final ciphertexts are valid encryptions of the scores. \(\square \)
5 Refinements of TFHE
In this section, we present several improvements that helped us achieving better efficiency for the actual FHE–DiNN implementation. These various techniques can without any doubt be applied in other FHE-based applications.
5.1 Reducing Bandwidth Usage
One of the drawbacks of our evaluation process is that encrypting individual values for each input neuron yields a very large ciphertext, which is inconvenient from a user perspective, as a high bandwidth requirement is the direct consequence. In order to mitigate this issue, we “pack” multiple values into one ciphertext. We use the standard technique of encrypting a polynomial (using the TLWE scheme instead of LWE) whose coefficients correspond to the different values we want to encrypt:
where the \(x_i\)’s represent the values of the input neurons to be encryptedFootnote 3. This packing technique is what made Ring-LWE an attractive variant to the standard LWE problem, as was already presented in [LPR10], and is widely used in FHE applications to amortize the cost of operations [HS14, HS15].
Then, we observe that for each neuron in the first hidden layer, we can compute the multisum with coefficients \(w_i\) by scaling the input TLWE ciphertext by a factor
Indeed, it is easy to verify that the constant term of \(\left( \sum _{i} x_i X^i\right) \cdot \left( \sum _{i} w_i X^{-i}\right) \) is \(\sum _i w_i x_i\), and we can obtain an LWE encryption of this value by invoking Extract.
Remark 1
We note that this computation is actually equivalent to doing the multisum directly on LWE ciphertexts, so the resulting noise growth of this approach is exactly the same as before. We end up saving bandwidth usage (by a factor up to N, the degree of the polynomials) basically for free. Furthermore, as the weights of the neural network never change, we can precompute and store the FFT representation of the polynomials \(\sum w_i X^{-i}\), thus saving time during the online classification.
In a nutshell, we reduce the size of the ciphertexts for N elements from N LWE ciphertexts to 1 TLWE ciphertext. In terms of numbers of elements in \(\mathbb {T}\), the cost dropped from \(N(n+1)\) to \(N(k+1)\).
We remark that the resulting ciphertext is an LWE ciphertext in dimension N, and not the original n, thus requiring key-switching to become a legitimate ciphertext. However, this is not a problem thanks to the trick presented in the following subsection.
5.2 Moving KeySwitch Around
The main goal of key-switching here is to reduce the LWE dimension. The benefits in memory usage and efficiency of this reduction are extremely important, since the size of the bootstrapping key, the final noise level, and the number of external products (the most costly operation) all depend linearly on this parameter. However, we noticed that reducing this dimension in the beginning of the bootstrapping procedure instead of the end gave much better results, hence the new bootstrapping function:
The intuition is that, with this technique, the noise produced by KeySwitch will not be multiplied by  when performing the computation of the multisum, but will only be added at the end. Basically, we moved the noise of the output ciphertext produced by KeySwitch to an overhead noise.
when performing the computation of the multisum, but will only be added at the end. Basically, we moved the noise of the output ciphertext produced by KeySwitch to an overhead noise.
Doing this, we reverse the usage of the two underlying LWE schemes: everything is now done on high dimensional N-LWE, whereas the low dimensional n-LWE scheme is only used during the bootstrapping operation. Since the noise in the key-switching key is not used for any computation anymore, we can allow it to be bigger, thus reducing the dimension we need for the same security to hold and, in turn, gaining in time per bootstrapping.
The only downside is that working with higher dimensional N-LWE samples means slightly more memory usage for the server, bigger output ciphertextFootnote 4, and slightly slower addition of ciphertexts. However, as this operation is instantaneous when compared to other operations such as bootstrapping, this is not an issue.
5.3 Dynamically Changing the Message Space
In Sect. 4, we showed how to evaluate the whole neural network by induction, using a message space of \(2B+1\) slices, where B is a bound on the values of the multisums across the whole evaluation. However, in order to be able to reduce the probability of errors along the way, we are able to use different message spaces for each layer of the DiNN, and adapt the number of slots to the values given by the local computations, depending on the values of the weights \(\mathbf {w}\). In order to do so, we change the value of testVector to
where \(B_\ell \) is now indexed by the current layer \(\ell \), and is a bound on the values of the multisums for the next layer \(\ell +1\). The point of this manoeuvre is that if the number of slots is smaller, the slices are bigger, and the noise would have to be bigger in order to change the plaintext message. This trick might seem superfluous, because it decreases a probability that is already negligible. However sometimes, in practical scenarios, the correctness of the scheme is relaxed, and this trick allows us to obtain results closer to the expected values without costing any extra computation or storage.
5.4 Alternative BlindRotate Implementations
Following the technique of [ZYL+17], we try to gain efficiency in the bootstrapping by reducing the number of external products that we have to compute. In order to do so, they slightly unfold the loop computing \(X^{\langle \mathbf {s}, \mathbf {a} \rangle }\) in the BlindRotate algorithm. They group the terms of the sum two by two, using the following formula for each of the new terms:
In order to compute this new function, they change the bootstrapping key to contain encryptions of the values \(ss',s(1-s'),(1-s)s'\), and \((1-s)(1-s')\), thus expanding the size of the bootstrapping key by a factor 2. Using this idea, they cut the number of iterations of the loop by half, thus computing only half the amount of external products, which is the most costly operation of the bootstrapping. However, by doing so, they introduce the computation of 4 scalings of TGSW ciphertexts (which are matrices) by constant polynomials, and 3 TGSW additions, when TFHE’s BlindRotate only needed 1 scaling of a TLWE ciphertext, and 1 TLWE addition. Another benefit is that the homomorphic computation of \(\langle \mathbf {s}, \mathbf {a}\rangle \) induces rounding errors on only n / 2 terms instead of n. The noise of the output ciphertext is also different. On the bright side, the technique of [ZYL+17] reduces the noise induced by the precision errors during the gadget decomposition by a factor 2. On the other hand, it increases the noise coming from the bootstrapping key by a factor 2.

In this work, we suggest to use another formula in order to compute each term of the slightly unfolded sum. Observing that \(ss'+s(1-s')+(1-s)s'+(1-s)(1-s')=1\), we can save 1 element in the bootstrapping key:
The resulting BlindRotate algorithm is described in Algorithm 1. Having a 1 in the decomposition is a valuable advantage, because it means that we can move it out of the external product and instead add the previous value of the accumulator to the result. Thus, efficiency-wise, we halved the number of external products at the cost of only 3 scalings of TGSW ciphertexts by constant polynomials, 2 TGSW additions, and 1 TLWE addition. We note that while multiplying naively by a monomial might be faster than multiplying by a degree 2 polynomial, the implementation pre-computes and stores the FFT representation of the bootstrapping keys in order to speed up polynomial multiplication. Thus, multiplying by a polynomial of any degree has the same cost. The size of the bootstrapping key is now 3 / 2 times larger than the size of the one in TFHE, which is a compromise between the two previous methods. As in [ZYL+17], the noise induced by precision errors and roundings is halved compared to TFHE. On the other hand, now we increase the noise coming from the bootstrapping key by a factor 3 instead. However, we note that it is possible to reduce this noise without impacting efficiency by reducing the noise in the bootstrapping key, trading off security (depending on what the bottleneck for security of the scheme is, this could come for free), whereas in order to reduce the noise induced by the precision errors, efficiency will be impacted. We recapitulate these numbers on Table 2.
We note that this idea could be generalized to unfoldings consisting of more than two terms, yielding more possible trade-offs, but we did not explore further because of the dissuasive exponential growth in the number of operands in the general formula.
6 Experimental Results and Conclusions
We implemented the proposed approach to test its accuracy and efficiency. This section is divided into two main parts: the first one describes the training of the neural network over data in the clear and the second one details the results obtained when evaluating the network over encrypted inputs.
6.1 Pre-processing the MNIST Database
In order to respect the constraint of having inputs in \(\left\{ -1, 1\right\} \), we binarized all the images with a threshold value equal to 128: any pixel whose value is smaller than the threshold is mapped to \(-1\); the others are mapped to \(+1\). This actually reduces the amount of information available, as each 8-bit grayscale value is clamped to a single bit, and one could wonder if this could impact the accuracy of the classification. Although this is possible, a quick visual inspection of the result shows that the digits depicted in the images are still clearly recognizable.
6.2 Building a DiNN from Data in the Clear
In order to train the neural network, we first chose its topology, i.e., the number of hidden layers and neurons per hidden layer. We experimented with several values, always keeping in mind that a smaller number of neurons per layer is preferable: having more neurons means that the value of the multisum will be potentially higher, thus requiring a larger message space in the homomorphic evaluation, which in turn forces to choose bigger parameters for the scheme. After some tries, we decided to show the feasibility of our approach through the homomorphic evaluation of two neural networks. Both have 784 neurons in the input layer (one per pixel), a single hidden layer, and an output layer composed of 10 neurons (one per class). The difference between the two models is the size of the hidden layer: the first network has 30 neurons, while the second has 100.
In order to build a DiNN, we use the simple approach described in Subsect. 3.2: we (1) train a traditional neural network (i.e., with real weights and biases), and then we (2) discretize all the values by applying the function in Eq. 3.2. For step (1) we take advantage of the library keras [C+15] with Tensorflow [AAB+15], which offers a simple and highly customizable framework for defining, training and evaluating even complex models of neural networks. Through a farly simple Python script and in little time, we are able to define and train our models as desired. Given its similarity with (a scaled and shifted version of) the sign function, as an activation function we used the version of hard_sigmoid defined in Tensorflow. The reason behind this choice is that we know we will substitute this activation function with the true \(\mathsf {sign}\left( x\right) \). Thus, using a function which is already similar to it helps reducing the errors introduced by this switch.
Once we obtain the trained model, we proceed to choose a value \(\tau \in \mathbb {N}\) and discretize the weights and the biases of the network, as per Eq. 3.2, thus finally obtaining a DiNN that we can later evaluate over encrypted inputs. The choice of \(\tau \) is an important part of the process: on one hand, picking a very small value will give little resolution to the networkFootnote 5, potentially degrading the accuracy largely; on the other hand, picking a very large value will minimize the loss in accuracy but increase the message space that we will need to support for homomorphic evaluation, thus forcing us to choose larger parameters and making the overall evaluation less efficient. Also, note that it is possible to choose different values of the parameter \(\tau \) for different layers of the network. Although there might be better choices, we did not invest too much efforts in optimizing the cleartext model and simply chose the value \(\tau =10\) for both layers of each model. Finally, we switched all the activation functions from \(\mathsf {hard\_sigmoid}\left( \cdot \right) \) to \(\mathsf {sign}\left( \cdot \right) \). In order to assess the results of the training and how the accuracy varies because of these changes, in Table 3 we report the accuracies obtained on the MNIST test set. Note that these values are referred to the evaluation over cleartext inputs.
6.3 Classifying Encrypted Inputs
Implementing the homomorphic evaluation of the neural network over encrypted input was more than a mere coding exercise, but allowed us to discover several interesting properties of our DiNNs.
The starting point was the TFHE library by Chillotti et al., which is freely available on GitHub [CGGI16a] and which was used to efficiently perform the bootstrapping operation. The library takes advantage of FFT processors for fast polynomial multiplication and, although not parallelized, achieves excellent timing results. We extended the code to apply this fast bootstrapping procedure to our use case.
Parameters. We now present our setting of the parameters, following the notation of [CGGI16b], to which we refer the reader for extra details. In Table 4 we highlight the main security parameters regarding our ciphertexts, together with an estimate of the security level that this setting achieves. Other additional parameters, related to the various operations we need to perform, are the following:
-
Degree of the polynomials in the ring: \(N = 1024\);
-
Dimension of the TLWE problem: \(k = 1\);
-
Basis for the decomposition of TGSW ciphertexts: \(Bg = 1024\);
-
Length of the decomposition of TGSW ciphertexts: \(\ell =3\);
-
Basis for the decomposition during key switching: 8;
-
Length of the decomposition during key switching: \(t =5\);
With this choice of parameters, we achieve a minimum security level of 80 bits and a single bootstrapping operation takes roughly 15 ms on a single core of an Intel Core i7-4720HQ CPU @ 2.60 GHz. Also, we note that by exploiting the packing technique presented in Subsect. 5.1, we save a factor 172 in the size of the input ciphertext: instead of having \(784 \cdot \left( 450+ 1\right) \) torus elements (corresponding to a \(450\)-LWE ciphertext for each of the 784 pixels in an image), we now have only \(2 \cdot 1024\) torus elements (corresponding to the two polynomials that form a TLWE sample).
Finally, we calculated the maximum value of the norms of the weight vectors associated to each neuron, both for the first and the second layer. These values, which can be computed at setup time (since the weights are available in the clear), define the theoretical bounds on the message space that our scheme should be able to support. In practice, we evaluated the actual values of the multisums on the training set, and took a message space slightly largerFootnote 6 than what we computed. We note that with this method, it is possible that some input could make the multisum go out of bounds, but this was not observed when evaluating the network on the test set. Moreover, this allows us to take a considerably smaller message space in some cases, and thus reduce the probability of errors. In Table 5 we report the theoretical message space we would need to support and the message space we actually used for our implementation.
In order to pinpoint our noise parameters, we also calculated the maximum \(L_2\)-norms of the weight vectors in each layer: for the network with 30 hidden neurons, we have  for the first layer and \(\approx \)85 for the second layer; for the network with 100 hidden neurons, we have
for the first layer and \(\approx \)85 for the second layer; for the network with 100 hidden neurons, we have  for the first layer and \(\approx \)60 for the second layer.
for the first layer and \(\approx \)60 for the second layer.
Evaluation. Our homomorphic evaluation follows the outline presented in Fig. 3 in order to classify an encrypted image,
-
1.
Encrypt the image as a TLWE ciphertext;
-
2.
Multiply the TLWE ciphertext by the polynomial which encodes the weights associated to the hidden layer. This operation takes advantage of FFT for speeding up the calculations;
-
3.
From each of the so-computed ciphertexts, extract a 1024-LWE ciphertext, which encrypts the constant term of the result;
-
4.
Perform a key switching in order to move from a 1024-LWE ciphertext to a 450-LWE one;
-
5.
Bootstrap to decrease the noise level. By setting the testVector, this operation also applies the sign function and changes the message space of our encryption scheme for free.
-
6.
Perform the multisum of the resulting ciphertext and the weights leading to the output layer, through the technique showed in Subsect. 4.1.Footnote 7
-
7.
Return the 10 ciphertexts corresponding to the 10 scores assigned by the neural network. These ciphertext can be decrypted and the \(\text {argmax}\) can be computed to obtain the classification given by the network.
Refined homomorphic evaluation of a 784:30:10 neural network with activation function sign. The whole image (784 pixels) is packed into 1 TLWE ciphertext to minimize bandwidth usage. After evaluation, the user recovers 10 ciphertexts corresponding to the scores assigned by the network to each digit.
In Table 6 we present the complete results of our experiments, both when using the original BlindRotate algorithm from [CGGI16b] (denoted by or) and when using the modified algorithm presented in Subsect. 5.4 (denoted by un, unfolded).
The homomorphic evaluation of the network on the entire test set was compared to its classification in the clear and we observed the following facts:
Observation 1
The accuracy achieved when classifying encrypted images is close to that obtained when classifying images in the clear.
In the case of the network with 30 hidden neurons, we obtain a classification accuracy of 93.55% in the clear (cf. Table 3) and of 93.71% homomorphically. In the case of the network with 100 hidden neurons, we have 96.43% accuracy in the clear and 96.35% on encrypted inputs. These gaps are explained by the following observations.
Observation 2
During the evaluation, some signs are flipped during the bootstrapping but this does not significantly harm the accuracy of the network.
We use aggressive internal parameters (e.g., N and, in general, all the parameters that control the precision) for the homomorphic evaluation, knowing that this could sometimes lead the bootstrapping procedure to return an incorrect result when extracting the sign of a message. In fact, we conjectured that the neural network would be resilient to perturbations and experimental results proved that this is indeed the case: when running our experiment over the full test set, we noticed that the number of wrong bootstrappings is 3383 (respectively, 9088) but this did not change the outcome of the classification in more than 196 (respectively, 105) cases (cf. Table 6).
Observation 3
The classification of an encrypted image might disagree with the classification of the same image in the clear but this does not significantly worsen the overall accuracy.
This is a property that we expected during the implementation phase and our intuition to explain this fact is the following: the network is assigning 10 scores to each image, one per digit, and when two scores are close (i.e., the network is hesitating between two classes), it can happen that the classification in the clear is correct and the one over the encrypted image is wrong. But the opposite can also be true, thus leading to classifying correctly an encrypted sample that was misclassified in the clear. We experimentally verified that disagreements between the evaluations do not automatically imply that the homomorphic classification is worse than the one in the clear: out of 273 (respectively, 127) disagreements, the classification in the clear was correct 105 (respectively, 61) times, against 121 (respectively, 44) times in favor of the homomorphic oneFootnote 8 (cf. Table 6).
Observation 4
Using the modified version of the BlindRotate algorithm presented in Subsect. 5.4 decreases the number of wrong bootstrappings.
Before stating some open problems, we conclude with the following note: using a bigger neural network generally leads to a better classification accuracy, at the cost of performing more calculations and, above all, more bootstrapping operations. However, the evaluation time will always grow linearly with the number of neurons. Although it is true that evaluating a bigger network is computationally more expensive, we stress that the bootstrapping operations are independent of each other and can thus be performed in parallel. Ideally, parallelizing the execution across a number of cores equal to the number of neurons in a layer (30 or 100 in our work) would result in that the evaluation of the layer would take roughly the time of a bootstrapping (i.e., around 15 ms).
Future directions and open problems. This work opens a number of possibilities and, thus, raises several interesting open problems. The first one is about the construction of our DiNNs. In this work, we did not pay too much attention to this step and, as a consequence, we considerably worsened the accuracy when moving from a canonical neural network to a DiNN. In order to improve the classification given by these discretized networks, it would be interesting to train a DiNN, rather than simply discretizing an already-trained model. Using discrete values and the sign function for the activation makes some calculations (e.g., some derivatives) impossible. Techniques to overcome these limitations have already been proposed in the literature (e.g., [CB16]) and they can be applied to our DiNNs as well. Also, another potentially interesting approach would be mixing these two ways of constructing a DiNN, for example by first discretizing a given model and then training the resulting network to refine it. Another natural question is whether we can batch several bootstrappings together, in order to improve the overall efficiency of the evaluation. Moreover, the speed of the evaluation would benefit from taking advantage of multi-core processing units, like GPUs.
Most interestingly, our FHE–DiNN framework is flexible and can be adapted to more generic cognitive architectures: we leave this as an interesting open problem. In particular, excellent results have been obtained by using Convolutional Neural Networks (see e.g., [LBBH98]), and we believe that trying to apply FHE–DiNN to these models would be an interesting line of research. Achieving this goal would require extending the current capabilities of FHE. For example, we would need to be able to homomorphically evaluate the max function, which is required to construct the widely-used max pooling layers. To the best of our knowledge, a technique for an efficient homomorphic evaluation of the max function is currently not known. Finally, the methodology presented in this work is by no means limited to image recognition, but can be applied to other machine learning problems as well.
Notes
- 1.
As all the computations are done over the torus (i.e., modulo 1), scaling a ciphertext by any integer factor preserves the relations that make the decryption correct. However, this does not hold for non-integer factors.
- 2.
If it is not, we can bootstrap all input ciphertexts in order to ensure this holds.
- 3.
If the number of input neurons is bigger than the maximal degree of the polynomials N, we can pack the ciphertext by groups of N, compute partial multisums with our technique, and aggregate them afterwards.
- 4.
This can be circumvented by applying one last round of KeySwitch at the end of the protocol, if needed.
- 5.
This means that the number of values that the weights will be able to take will be fairly limited.
- 6.
As we do not achieve perfect correctness with our parameters, the message can be shifted. This fact has to be taken into account when choosing the number of slots.
- 7.
Note that we do not apply any activation function to the output neurons: we are only interested in being able to retrieve the scores and sorting them to recover the classification given by the network.
- 8.
In the remaining cases, the classifications were different but they were both wrong.
References
Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., Corrado, G.S., Davis, A., Dean, J., Devin, M., Ghemawat, S., Goodfellow, I., Harp, A., Irving, G., Isard, M., Jia, Y., Jozefowicz, R., Kaiser, L., Kudlur, M., Levenberg, J., Mané, D., Monga, R., Moore, S., Murray, D., Olah, C., Schuster, M., Shlens, J., Steiner, B., Sutskever, I., Talwar, K., Tucker, P., Vanhoucke, V., Vasudevan, V., Viégas, F., Vinyals, O., Warden, P., Wattenberg, M., Wicke, M., Yu, Y., Zheng, X.: TensorFlow: large-scale machine learning on heterogeneous systems (2015). Software: tensorflow.org
Abdalla, M., Bourse, F., De Caro, A., Pointcheval, D.: Simple functional encryption schemes for inner products. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 733–751. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_33
Agrawal, S., Libert, B., Stehlé, D.: Fully secure functional encryption for inner products, from standard assumptions. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part III. LNCS, vol. 9816, pp. 333–362. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_12
Alperin-Sheriff, J., Peikert, C.: Practical bootstrapping in quasilinear time. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 1–20. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_1
Alperin-Sheriff, J., Peikert, C.: Faster bootstrapping with polynomial error. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 297–314. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_17
Albrecht, M.R., Player, R., Scott, S.: On the concrete hardness of learning with errors. Cryptology ePrint Archive, Report 2015/046 (2015). http://eprint.iacr.org/2015/046
Agrawal, R., Srikant, R.: Privacy-preserving data mining. SIGMOD Rec. 29(2), 439–450 (2000)
Brakerski, Z., Gentry, C., Vaikuntanathan, V.: (Leveled) fully homomorphic encryption without bootstrapping. In: ITCS 2012, pp. 309–325. ACM, January 2012
Benhamouda, F., Lepoint, T., Mathieu, C., Zhou, H.: Optimization of bootstrapping in circuits. In: Proceedings of the Twenty-Eighth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2017, Philadelphia, PA, USA, pp. 2423–2433. Society for Industrial and Applied Mathematics (2017)
Bost, R., Popa, R.A., Tu, S., Goldwasser, S.: Machine learning classification over encrypted data. In: NDSS 2015. The Internet Society, February 2015
Brakerski, Z., Vaikuntanathan, V.: Efficient fully homomorphic encryption from (standard) LWE. In: 52nd FOCS, pp. 97–106. IEEE Computer Society Press, October 2011
Brakerski, Z., Vaikuntanathan, V.: Fully homomorphic encryption from ring-LWE and security for key dependent messages. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 505–524. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_29
Brakerski, Z., Vaikuntanathan, V.: Lattice-based FHE as secure as PKE. In: ITCS 2014, pp. 1–12. ACM, January 2014
Chollet, F., et al.: Keras (2015). https://github.com/keras-team/keras
Courbariaux, M., Bengio, Y.: Binarynet: training deep neural networks with weights and activations constrained to +1 or \(-1\). CoRR, abs/1602.02830 (2016)
Chabanne, H., de Wargny, A., Milgram, J., Morel, C., Prouff, E.: Privacy-preserving classification on deep neural network. IACR Cryptology ePrint Archive 2017:35 (2017)
Chillotti, I., Gama, N., Georgieva, M., Izabachène, M.: TFHE: Fast Fully Homomorphic Encryption Library over the Torus (2016). https://github.com/tfhe/tfhe
Chillotti, I., Gama, N., Georgieva, M., Izabachène, M.: Faster fully homomorphic encryption: bootstrapping in less than 0.1 seconds. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016, Part I. LNCS, vol. 10031, pp. 3–33. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53887-6_1
Chillotti, I., Gama, N., Georgieva, M., Izabachène, M.: Faster packed homomorphic operations and efficient circuit bootstrapping for TFHE. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017, Part I. LNCS, vol. 10624, pp. 377–408. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70694-8_14
Cireşan, D., Meier, U., Schmidhuber, J.: Multi-column deep neural networks for image classification. ArXiv e-prints, February 2012
Cybenko, G.: Approximation by superpositions of a sigmoidal function. Math. Control Sig. Syst. 2(4), 303–314 (1989)
Dowlin, N., Gilad-Bachrach, R., Laine, K., Lauter, K., Naehrig, M., Wernsing, J.: CryptoNets: applying neural networks to encrypted data with high throughput and accuracy. Technical report, February 2016
Ducas, L., Micciancio, D.: FHEW: bootstrapping homomorphic encryption in less than a second. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015, Part I. LNCS, vol. 9056, pp. 617–640. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_24
Dwork, C.: Differential privacy (invited paper). In: Bugliesi, M., Preneel, B., Sassone, V., Wegener, I. (eds.) ICALP 2006, Part II. LNCS, vol. 4052, pp. 1–12. Springer, Heidelberg (2006). https://doi.org/10.1007/11787006_1
Gentry, C.: A fully homomorphic encryption scheme. Ph.D. thesis, Stanford University (2009). crypto.stanford.edu/craig
Gentry, C., Halevi, S., Smart, N.P.: Homomorphic evaluation of the AES circuit. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 850–867. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_49
Gentry, C., Sahai, A., Waters, B.: Homomorphic encryption from learning with errors: conceptually-simpler, asymptotically-faster, attribute-based. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 75–92. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_5
Hornik, K.: Approximation capabilities of multilayer feedforward networks. Neural Netw. 4(2), 251–257 (1991)
Halevi, S., Shoup, V.: Algorithms in HElib. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 554–571. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_31
Halevi, S., Shoup, V.: Bootstrapping for HElib. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015, Part I. LNCS, vol. 9056, pp. 641–670. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_25
He, K., Zhang, X., Ren, S., Sun, J.: Deep residual learning for image recognition. CoRR, abs/1512.03385 (2015)
Kawachi, A., Tanaka, K., Xagawa, K.: Concurrently secure identification schemes based on the worst-case hardness of lattice problems. In: Pieprzyk, J. (ed.) ASIACRYPT 2008. LNCS, vol. 5350, pp. 372–389. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-89255-7_23
LeCun, Y., Bottou, L., Bengio, Y., Haffner, P.: Gradient-based learning applied to document recognition. Proc. IEEE 86(11), 2278–2324 (1998)
LeCun, Y., Cortes, C., Burges, C.: The MNIST database of handwritten digits (1998). http://yann.lecun.com/exdb/mnist/
Lepoint, T., Paillier, P.: On the minimal number of bootstrappings in homomorphic circuits. In: Adams, A.A., Brenner, M., Smith, M. (eds.) FC 2013 Workshops. LNCS, vol. 7862, pp. 189–200. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-41320-9_13
Lyubashevsky, V., Peikert, C., Regev, O.: On ideal lattices and learning with errors over rings. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 1–23. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_1
Makri, E., Rotaru, D., Smart, N.P., Vercauteren, F.: PICS: private image classification with SVM. Cryptology ePrint Archive, Report 2017/1190 (2017). https://eprint.iacr.org/2017/1190
Mohassel, P., Zhang, Y.: SecureML: a system for scalable privacy-preserving machine learning. In: 2017 IEEE Symposium on Security and Privacy, pp. 19–38. IEEE Computer Society Press, May 2017
Paindavoine, M., Vialla, B.: Minimizing the number of bootstrappings in fully homomorphic encryption. In: Dunkelman, O., Keliher, L. (eds.) SAC 2015. LNCS, vol. 9566, pp. 25–43. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-31301-6_2
Peikert, C., Waters, B.: Lossy trapdoor functions and their applications. In 40th ACM STOC, pp. 187–196. ACM Press, May 2008
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: 37th ACM STOC, pp. 84–93. ACM Press, May 2005
Stehlé, D., Steinfeld, R.: Faster fully homomorphic encryption. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 377–394. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_22
Smart, N.P., Vercauteren, F.: Fully homomorphic encryption with relatively small key and ciphertext sizes. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 420–443. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13013-7_25
van Dijk, M., Gentry, C., Halevi, S., Vaikuntanathan, V.: Fully homomorphic encryption over the integers. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 24–43. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_2
Zagoruyko, S., Komodakis, N.: Wide residual networks. CoRR, abs/1605.07146 (2016)
Zhang, Q., Yang, L.T., Chen, Z.: Privacy preserving deep computation model on cloud for big data feature learning. IEEE Trans. Comput. 65(5), 1351–1362 (2016)
Zhou, T., Yang, X., Liu, L., Zhang, W., Ding, Y.: Faster bootstrapping with multiple addends. Cryptology ePrint Archive, Report 2017/735 (2017). http://eprint.iacr.org/2017/735
Acknowledgments
Florian Bourse was supported by the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013 Grant Agreement no. 339563 – CryptoCloud), and by the French ANR Project ANR-16-CE39-0014 PERSOCLOUD. Part of this work was done while the author was employed by CNRS and visiting CryptoExperts.
Michele Minelli and Matthias Minihold were supported by European Union’s Horizon 2020 research and innovation programme under grant agreement No H2020-MSCA-ITN-2014-643161 ECRYPT-NET. This work was done while the authors were visiting CryptoExperts. The authors would like to thank CRYPTO’s anonymous reviewers for providing useful suggestions and helping improve the paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Bourse, F., Minelli, M., Minihold, M., Paillier, P. (2018). Fast Homomorphic Evaluation of Deep Discretized Neural Networks. In: Shacham, H., Boldyreva, A. (eds) Advances in Cryptology – CRYPTO 2018. CRYPTO 2018. Lecture Notes in Computer Science(), vol 10993. Springer, Cham. https://doi.org/10.1007/978-3-319-96878-0_17
Download citation
DOI: https://doi.org/10.1007/978-3-319-96878-0_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96877-3
Online ISBN: 978-3-319-96878-0
eBook Packages: Computer ScienceComputer Science (R0)


 : for a security parameter
: for a security parameter  , fix
, fix  and return
and return 
 and
and 
 : for a security parameter
: for a security parameter  , fix
, fix 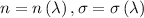 ; return
; return 
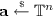 and
and 

