Abstract
We present a new approach to designing concretely efficient MPC protocols with semi-honest security in the dishonest majority setting. Motivated by the fact that within the dishonest majority setting the efficiency of most practical protocols does not depend on the number of honest parties, we investigate how to construct protocols which improve in efficiency as the number of honest parties increases. Our central idea is to take a protocol which is secure for \(n-1\) corruptions and modify it to use short symmetric keys, with the aim of basing security on the concatenation of all honest parties’ keys. This results in a more efficient protocol tolerating fewer corruptions, whilst also introducing an LPN-style syndrome decoding assumption.
We first apply this technique to a modified version of the semi-honest GMW protocol, using OT extension with short keys, to improve the efficiency of standard GMW with fewer corruptions. We also obtain more efficient constant-round MPC, using BMR-style garbled circuits with short keys, and present an implementation of the online phase of this protocol. Our techniques start to improve upon existing protocols when there are around \(n=20\) parties with \(h=6\) honest parties, and as these increase we obtain up to a 13 times reduction (for \(n=400, h=120\)) in communication complexity for our GMW variant, compared with the best-known GMW-based protocol modified to use the same threshold.
C. Hazay—Supported by the European Research Council under the ERC consolidators grant agreement No. 615172 (HIPS), and by the BIU Center for Research in Applied Cryptography and Cyber Security in conjunction with the Israel National Cyber Bureau in the Prime Minister’s Office.
E. Orsini—Supported in part by ERC Advanced Grant ERC-2015-AdG-IMPaCT.
P. Scholl—Supported by the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 731583 (SODA), and the Danish Independent Research Council under Grant-ID DFF-6108-00169 (FoCC).
E. Soria-Vazquez—Supported by the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 643161, and by ERC Advanced Grant ERC-2015-AdG-IMPaCT.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Secure multi-party computation (MPC) protocols allow a group of n parties to compute some function f on the parties’ private inputs, while preserving a number of security properties such as privacy and correctness. The former property implies data confidentiality, namely, nothing leaks from the protocol execution but the computed output. The latter requirement implies that the protocol enforces the integrity of the computations made by the parties, namely, honest parties are not lead to accept a wrong output. Security is proven either in the presence of an honest-but-curious adversary that follows the protocol specification but tries to learn more than allowed from its view of the protocol, or a malicious adversary that can arbitrarily deviate from the protocol specification in order to compromise the security of the other parties in the protocol.
The efficiency of a protocol typically also depends on how many corrupted parties can be tolerated before security breaks down, a quantity known as the threshold, t. With semi-honest security, most protocols either require \(t < n/2\) (where n is the number of parties), in which case unconditionally secure protocols [BOGW88, CCD88] based on Shamir secret-sharing can be used, or support any choice of t up to \(n-1\), as in computationally secure protocols based on oblivious transfer [GMW87, Gol04]. Interestingly, within these two ranges, the efficiency of most practical semi-honest protocols does not depend on t. For instance, the GMW [GMW87] protocol (and its many variants) is full-threshold, so supports any \(t<n\) corruptions. However, we do not know of any practical protocols with threshold, say, \(t=\frac{2}{3} n\), or even \(t=n/2+1\), that are more efficient than full-threshold GMW-style protocols. One exception to this is when the number of parties becomes very large, in which case protocols based on committees can be used. In this approach, due to an idea of Bracha [Bra85], first a random committee of size \(n' \ll n\) is chosen. Then every party secret-shares its input to the parties in the committee, who runs a secure computation protocol for \(t < n'\) to obtain the result. The committee size \(n'\) must be chosen to ensure (with high probability) that not the whole committee is corrupted, so clearly a lower threshold t allows for smaller committees, giving significant efficiency savings. However, this technique is only really useful when n is very large, at least in the hundreds or thousands.
In this paper we investigate designing MPC protocols where an arbitrary threshold for the number of corrupted parties can be chosen, which are practical both when n is very large, and also for small to medium sizes of n. Specifically, we ask the question:
Can we design concretely efficient MPC protocols where the performance improves gracefully as the number of honest parties increases?
Note that the performance of an MPC protocol can be measured both in terms of communication overhead and computational overhead. Using fully homomorphic encryption [Gen09], it is possible to achieve very low communication overhead that is independent of the circuit size [AJL+12] even in the malicious setting, but for reasonably complex functions FHE is impractical due to very high computational costs. On the other hand, practical MPC protocols typically communicate for every AND gate in the circuit, and use oblivious transfer (OT) to carry out the computation. Fast OT extension techniques allow a large number of secret-shared bit multiplicationsFootnote 1 to be performed using only symmetric primitives and an amortized communication complexity of \(O(\kappa )\) [IKNP03] or \(O(\kappa /\log {\kappa })\) [KK13, DKS+17] bits, where \(\kappa \) is a computational security parameter. This leads to an overall communication complexity which grows with \(O(n^2\kappa /\log {\kappa })\) bits per AND gate in protocols based on secret-sharing following the [GMW87] style, and \(O(n^2\kappa )\) in those based on garbled circuits in the style of [Yao86, BMR90, BLO16].
Short keys for secure computation. Our main idea towards achieving the above goal is to build a secure multi-party protocol with h honest parties, by distributing secret key material so that each party only holds a small part of the key. Instead of basing security on secret keys held by each party individually, we then base security on the concatenation of all honest parties’ keys.
As a toy example, consider the following simple distributed encryption of a message m under n keys:
where \(\mathsf {H}\) is a suitable hash function and each key \(k_i \in \{0,1\}^\ell \) belongs to party \(P_i\). In the full-threshold setting with up to \(n-1\) corruptions, to hide the message we need each party’s key to be of length \(\ell =128\) to achieve 128-bit computational security. However, if only \(t < n-1\) parties are corrupted, it seems that, intuitively, an adversary needs to guess all \(h := n-t\) honest parties’ keys to recover the message, and potentially each key \(k_i\) can be much less than 128 bits long when h is large enough. This is because the “obvious” way to try to guess m would be to brute force all h keys until decrypting “successfully”.
In fact, recovering m when there are h unknown keys corresponds to solving an instance of the regular syndrome decoding problem [AFS03], which is related to the well-known learning parity with noise (LPN) problem, and believed to be hard for suitable choices of parameters.
1.1 Our Contribution
In this work we use the above idea of short secret keys to design new MPC protocols in both the constant round and non-constant round settings, which improve in efficiency as the number of honest parties increases. We consider security against a static, honest-but-curious adversary, and leave it for future work to extend our techniques to the malicious case based on, e.g. message authentication codes. Our contribution is captured by the following:
 (Sect. 3). We present a GMW-style MPC protocol for binary circuits, where multiplications are done with OT extension using short symmetric keys. This reduces the communication complexity of OT extension-based GMW from \(O(n^2 \kappa /\log \kappa )\) [KK13] to \(O(nt\ell )\), where the key length \(\ell \) decreases as the number of honest parties, \(h=n-t\), increases. When h is large enough, we can even have \(\ell \) as small as 1.
(Sect. 3). We present a GMW-style MPC protocol for binary circuits, where multiplications are done with OT extension using short symmetric keys. This reduces the communication complexity of OT extension-based GMW from \(O(n^2 \kappa /\log \kappa )\) [KK13] to \(O(nt\ell )\), where the key length \(\ell \) decreases as the number of honest parties, \(h=n-t\), increases. When h is large enough, we can even have \(\ell \) as small as 1.
To construct this protocol, we first analyse the security of the IKNP OT extension protocol [IKNP03] when using short keys, and formalise the leakage obtained by a corrupt receiver in this case. We then show how to use this version of “leaky OT” to generate multiplication triples using a modified version of the GMW method, where pairs of parties use OT to multiply their shares of random values. We also optimize our protocol by reducing the number of communication channels using two different-sized committees, improving upon the standard approach of choosing one committee to do all the work.
 (Sect. 4). Our second contribution is the design of a constant round, BMR-style [BMR90] protocol based on garbled circuits with short keys. Our offline phase uses the multiplication protocol from the previous result in order to generate the garbled circuit, using secret-shared bit and bit/string multiplications as done in previous works [BLO16, HSS17], with the exception that the keys are shorter. In the online phase, we then use the LPN-style assumption to show that the combination of all honest parties’ \(\ell \)-bit keys suffices to obtain a secure garbling protocol. This allows us to save on the key length as a function of the number of honest parties.
(Sect. 4). Our second contribution is the design of a constant round, BMR-style [BMR90] protocol based on garbled circuits with short keys. Our offline phase uses the multiplication protocol from the previous result in order to generate the garbled circuit, using secret-shared bit and bit/string multiplications as done in previous works [BLO16, HSS17], with the exception that the keys are shorter. In the online phase, we then use the LPN-style assumption to show that the combination of all honest parties’ \(\ell \)-bit keys suffices to obtain a secure garbling protocol. This allows us to save on the key length as a function of the number of honest parties.
As well as reducing communication with a smaller garbled circuit, we also reduce computation when evaluating the circuit, since each garbled gate can be evaluated with only \(O(n^2 \ell /\kappa )\) block cipher calls (assuming the ideal cipher model), instead of \(O(n^2)\) when using \(\kappa \)-bit keys. For this protocol, \(\ell \) can be as small as 8, giving a significant saving over 128-bit keys used previously.
Concrete Efficiency Improvements. The efficiency of our protocols depends on the total number of parties, n, and the number of honest parties, h, so there is a large range of parameters to explore when comparing with other works. We discuss this in more detail in Sect. 5. Our protocols seem most significant in the dishonest majority setting, since when there is an honest majority there are unconditionally secure protocols with \(O(n\log {n})\) communication overhead and reasonable computational complexity e.g. [DN07], whilst our protocols have \(\varOmega (nt)\) communication overhead.
Our GMW-style protocol starts to improve upon previous protocols when we reach \(n=20\) parties and \(t=14\) corruptions: here, our triple generation method requires less than half the communication cost of the fastest GMW-style protocol based on OT extension [DKS+17] tolerating up to \(n-1\) corruptions. When the number of honest parties is large enough, we can use 1-bit keys, giving a 25-fold reduction in communication over previous protocols when \(n=400\) and \(t=280\). In addition, we describe a simple threshold-t variant of GMW-style protocols, which our protocol still outperforms by 1.1x and 13x, respectively, in these two scenarios.
For our constant round protocol, with \(n=20,t=10\) we can use 32-bit keys, so the size of each garbled AND gate is 1/4 the size of [BLO16]. As n increases the improvements become greater, with a 16-fold reduction in garbled AND gate size for \(n=400,t=280\). We also reduce the communication cost of creating the garbled circuit. Here, the improvement starts at around 50 parties, and goes up to a 7 times reduction in communication when \(n=400,t=280\). Note that our protocol does incur a slight additional overhead, since we need to use extra “splitter gates”, but this cost is relatively small.
To demonstrate the practicality of our approach, we also present an implementation of the online evaluation phase of our constant-round protocol for key lengths ranging between 1–4 bytes, and with an overall number of parties ranging from 15–1000; more details can be found in Sect. 5.
Applications. Our techniques seem most useful for large-scale MPC with around 70% corruptions, where we obtain the greatest concrete efficiency improvements. An important motivation for this setting is privacy-preserving statistical analysis of data collected from a large network with potentially thousands of nodes. In scenarios where the nodes are not always online and connected, our protocols can also be used with the “random committee” approach discussed earlier, so only a small subset of, say, a hundred nodes need to be online and interacting during the protocol.
An interesting example is safely measuring the Tor network [DMS04] which is among the most popular tools for digital privacy, consisting of more than 6000 relays that can opt-in for providing statistics about the use of the network. Nowadays and due to privacy risks, the statistics collected over Tor are generally poor: There is a reduced list of computed functions and only a minority of the relays provide data, which has to be obfuscated before publishing [DMS04]. Hence, the statistics provide an incomplete picture which is affected by a noise that scales with the number of relays. Running MPC in this setting would enable for more complex, accurate and private data processing, for example through anomaly detection and more sophisticated censorship detection. Moreover, our protocols are particularly well-suited to this setting since all relays in the network must be connected to one another already, by design.
Another possible application is for securely computing the interdomain routing within the Border Gateway Protocol (BGP), which is performed at a large scale of thousands of nodes. A recent solution in the dishonest majority setting [ADS+17] centralizes BGP so that two parties run this computation for all Autonomous Systems. Our techniques allow scaling to a large number of systems computing the interdomain routing themselves using MPC, hence further reducing the trust requirements.
Decisional Regular Syndrome Decoding problem. The security of our protocols relies on the Decisional Regular Syndrome Decoding (DRSD) problem, which, given a random binary matrix \({\mathbf {H}}\), is to distinguish between the syndrome obtained by multiplying \({\mathbf {H}}\) with an error vector \({\varvec{e}}= ({\varvec{e}}_1 \Vert \cdots \Vert {\varvec{e}}_h)\) where each \({\varvec{e}}_i \in \{0,1\}^{2^\ell }\) has Hamming weight one, and the uniform distribution. This can equivalently be described as distinguishing \(\bigoplus _{i=1}^h \mathsf {H}(i,k_i)\) from the uniform distribution, where \(\mathsf {H}\) is a random function and each \(k_i\) is a random \(\ell \)-bit key (as in the toy example described earlier).
We remark that when h is large enough, the problem is unconditionally hard even for \(\ell =1\), which means for certain parameter choices in our GMW-based protocol we can use 1-bit keys without introducing any additional assumptions. This introduces a significant saving in our triple generation protocol.
Additional related work. Another work which applies a similar assumption to secure computation is that of Applebaum [App16], who built garbled circuits with the free-XOR technique in the standard model under the LPN assumption. Conceptually, our work differs from Applebaum’s since our focus is to improve the efficiency of multi-party protocols with fewer corruptions, whereas in [App16], LPN is used in a more modular way in order to achieve encryption with stronger properties and under a more standard assumption.
In a recent work [NR17], Nielsen and Ranellucci designed a protocol in the dishonest majority setting with malicious, adaptive security in the presence of \(t< cn\) corruption for \(t\in [0,1)\). Their protocol is aimed to work with a large number of parties and uses committees to obtain a protocol with poly-logarithmic overhead. This protocol introduces high constants and is not useful for practical applications.
Finally, in a concurrent work [BO17], Ben-Efraim and Omri also explore how to optimize garbled circuits in the presence of non-full-threshold adversaries. By using deterministic committees they achieve AND gates of size \(4(t+1)\kappa \), where \(\kappa \) is the computational security parameter. By using the same technique we achieve a size of \(4(t+h)\ell \), where \(\ell \ll \kappa \) depends on h, a parameter for the minimum number of honest parties in the committee. The rest of their results apply only to the honest majority setting.
1.2 Technical Overview
In what follows we explain the technical side of our results in more detail.
Leaky oblivious transfer (OT). We first present a two-party secret-shared bit multiplication protocol, based on a variant of the IKNP OT extension protocol [IKNP03] with short keys. Our protocol performs a batch of r multiplications at once. Namely, the parties create r correlated OTs on \(\ell \)-bit strings using the OT extension technique of [IKNP03], by transposing a matrix of \(\ell \) OTs on r-bit strings and swapping the roles of sender and receiver. In contrast to the IKNP OT extension and followups, that use \(\kappa \) ‘base’ OTs for computational security parameter \(\kappa \), we use \(\ell = O(\log \kappa )\) base OTs.
This protocol leaks some information on the global secret \(\varDelta \leftarrow \{0,1\}^\ell \) picked by the receiver, as well as the inputs of the receiver. Roughly speaking, the leakage is of the form \(\mathsf {H}(i,\varDelta ) + x_i\), where \(x_i \in \{0,1\}\) is an input of the receiver and \(\mathsf {H}\) is a hash function with 1-bit output. Clearly, when \(\ell \) is short this is not secure to use on its own, since all of the receiver’s inputs only have \(\ell \) bits of min-entropy (based on the choice of \(\varDelta \)).
MPC from leaky OT. We then show how to apply this leaky two-party protocol to the multi-party setting, whilst preventing any leakage on the parties shares. The main observation is that, when using additive secret-sharing, we only need to ensure that the sum of all honest parties’ shares is unpredictable; if the adversary learns just a few shares, they can easily be rerandomized by adding pseudorandom shares of zero, which can be done non-interactively using a PRF. However, we still have a problem, which is that in the standard GMW approach, each party \(P_i\) uses OT to multiply their share \(x^i\) with every other party \(P_j\)’s share \(y^j\). Now, there is leakage on the same share \(x^i\) from each of the OT instances between all other parties, which seems much harder to prevent than leakage from just a single OT instance.
To work around this problem, we have the parties add shares of zero to their \(x^i\) inputs before multiplying them. So, every pair \((P_i,P_j)\) will use leaky OT to multiply \(x^i \oplus s^{i,j}\) with \(y^j\), where \(s^{i,j}\) is a random share of zero satisfying \(\bigoplus _{i=1}^n s^{i,j} = 0\). This preserves correctness of the protocol, because the parties end up computing an additive sharing of:
This also effectively removes leakage on the individual shares, so we only need to be concerned with the sum of the leakage on all honest parties’ shares, and this turns out to be of the form: \( \bigoplus _{i=1}^n (\mathsf {H}(i, \varDelta _i) + x^i) \) which is pseudorandom under the decisional regular syndrome decoding assumption.
We realize our protocol using a hash function with a polynomial-sized domain, so that is can be implemented using a CRS which simply outputs a random lookup-table. This means that, unlike when using the IKNP protocol, we do not need to rely on a random oracle or a correlation robustness assumption.
When the number of parties is large enough, we can improve our triple generation protocol using random committees. In this case the amortized communication cost is \(\le n_h n_1(\ell + \ell \kappa /r + 1)\) bits per multiplication where we need to choose two committees of sizes \(n_h\) and \(n_1\) which have at least h and 1 honest parties, respectively.
Garbled circuits with short keys. We next revisit the multi-party garbled circuits technique by Beaver, Micali and Rogaway, known as BMR, that extends the classic Yao garbling [Yao86] to an arbitrary number of parties, where essentially all the parties jointly garble using one set of keys each. This method was recently improved in a sequence of works [LPSY15, LSS16, BLO16, HSS17], where the two latter works further support the Free-XOR property.
Our garbling method uses an expansion function \(\mathsf {H}: [n] \times \{0,1\}\times \{0,1\}^{\ell } \rightarrow \{0,1\}^{n\ell +1}\), where \(\ell \) is the length of each parties’ keys used as wire labels in the garbled circuit. To garble a gate, the hash values of the input wire keys \(k^i_{u,b}\) and \(k^i_{v,b}\) are XORed over i and used to mask the output wire keys.
Specifically, for an AND gate g with input wires u, v and output wire w, the 4 garbled rows \({\tilde{g}}_{a,b}\), for each \((a,b) \in \{0,1\}^2\), are computed as:
Security then relies on the \(\mathsf {DRSD}\) assumption, which implies that the sum of h hash values on short keys is pseudorandom, which suffices to construct a secure garbling method with h honest parties.
Using this assumption instead of a PRF (as in recent works) comes with difficulties, as we can no longer garble gates with arbitrary fan-out, or use the free-XOR technique, without degrading the \(\mathsf {DRSD}\) parameters. To allow for arbitrary fan-out circuits with our protocol we use splitter gates, which take as input one wire w and provide two outputs wires u, v, representing the same wire value. Splitter gates were previously introduced as a fix for an error in the original BMR paper in [TX03]. We stress that transforming a general circuit description into a circuit with only fan-out-1 gates requires adding at most a single splitter gate per AND or XOR gate.
The restriction to fan-out-1 gates and the use of splitter gates additionally allows us to garble XOR gates for free in BMR without relying on circular security assumptions or correlation-robust hash functions, based on the FlexOR technique [KMR14] where each XOR gate uses a unique offset. Furthermore, the overhead of splitter gates is very low, since garbling a splitter gate does not use the underlying MPC protocol: shares of the garbled gate can be generated non-interactively. We note that this observation also applies to Yao’s garbled circuits, but the overhead of adding splitter gates there is more significant; this is because in most 2-party protocols, the size of the garbled circuit is the dominant cost factor, whereas in multi-party protocols the main cost is creating the garbled circuit in a distributed manner.
2 Preliminaries
We denote the security parameter by \(\kappa \). We say that a function \(\mu :\mathbb {N}\rightarrow \mathbb {N}\) is negligible if for every positive polynomial \(p(\cdot )\) and all sufficiently large \(\kappa \) it holds that \(\mu (\kappa )<\frac{1}{p(\kappa )}\). The function \(\mu \) is noticeable (or non-negligible) if there exists a positive polynomial \(p(\cdot )\) such that for all sufficiently large \(\kappa \) it holds that \(\mu (\kappa ) \ge \frac{1}{p(\kappa )}\). We use the abbreviation PPT to denote probabilistic polynomial-time. We further denote by \(a \leftarrow A\) the uniform sampling of a from a set A, and by [d] the set of elements \(\{1,\ldots ,d\}\). We often view bit-strings in \(\{0,1\}^k\) as vectors in \(\mathbb {F}_2^k\), depending on the context, and denote exclusive-or by “\(\oplus \)” or “\(+\)”. If \(a, b \in \mathbb {F}_2\) then \(a \cdot b\) denotes multiplication (or AND), and if \({\varvec{c}}\in \mathbb {F}_2^\kappa \) then \(a \cdot {\varvec{c}}\in \mathbb {F}_2^\kappa \) denotes the product of a with every component of \({\varvec{c}}\).
Security and Communication Models. We prove security of our protocols in the universal composability (UC) framework [Can01]. See We assume all parties are connected via secure, authenticated point-to-point channels, which is the default method of communication in our protocols. The adversary model we consider is a static, honest-but-curious adversary who corrupts a subset \(A \subset [n]\) of parties at the beginning of the protocol. We denote by \(\bar{A}\) the subset of honest parties, and define \(h = |\bar{A} | = n - t\).
Random Zero-Sharing. Our protocols require the parties to generate random additive sharings of zero, as in the \(\mathcal {F}_{\scriptstyle \mathrm {Zero}}\) functionality in Fig. 1. This can be done efficiently using a PRF F, with interaction only during a setup phase, as in [AFL+16].
2.1 Regular Syndrome Decoding Problem
We now describe the Regular Syndrome Decoding (RSD) problem and some of its properties.
Definition 2.1
A vector \({\varvec{e}}\in \mathbb {F}_2^m\) is (m, h)-regular if \({\varvec{e}}= ({\varvec{e}}_1 \Vert \cdots \Vert {\varvec{e}}_h)\) where each \({\varvec{e}}_i \in \{0,1\}^{m/h}\) has Hamming weight one. We denote by \(R_{m,h}\) the set of all the (m, h)-regular vectors in \(\mathbb {F}_2^m\).
Definition 2.2
(Regular Syndrome Decoding (RSD)). Let \(r, h,\ell \in \mathbb {N}\) with \(m = h \cdot 2^\ell \), \({\mathbf {H}}\leftarrow \mathbb {F}_2^{r \times m}\) and \({\varvec{e}}\leftarrow R_{m,h}\). Given \(({\mathbf {H}}, {\mathbf {H}}{\varvec{e}})\), the \(\mathsf {RSD}_{r,h,\ell }\) problem is to recover \({\varvec{e}}\) with noticeable probability.
The decisional version of the problem, given below, is to distinguish the syndrome \({\mathbf {H}}{\varvec{e}}\) from uniform.
Definition 2.3
(Decisional Regular Syndrome Decoding (DRSD)). Let \({\mathbf {H}}\leftarrow \mathbb {F}_2^{r \times m}\) and \({\varvec{e}}\leftarrow R_{m,h}\), and let \(U_r\) be the uniform distribution on r bits. The \(\mathsf {DRSD}_{r,h,\ell }\) problem is to distinguish between \(({\mathbf {H}}, {\mathbf {H}}{\varvec{e}})\) and \(({\mathbf {H}}, U_r)\) with noticeable advantage.
Hash function formulation. The \(\mathsf {DRSD}\) problem can be equivalently described as distinguishing from uniform \( \bigoplus _{i=1}^h \mathsf {H}(i,k_i) \) where \(\mathsf {H}: [h] \times \{0,1\}^\ell \rightarrow \{0,1\}^r\) is a random hash function, and each \(k_i \leftarrow \{0,1\}^\ell \). With this formulation, it is easier to see how the \(\mathsf {DRSD}\) problem arises when using our protocols with short keys, since this appears when summing up a hash function applied to h honest parties’ secret keys.
To see the equivalence, we can define a matrix \({\mathbf {H}}\in \mathbb {F}_2^{r \times h\cdot 2^\ell }\), where for each \(i \in \{0,\dots ,h-1\}\) and \(k \in [2^\ell ]\), column \(i \cdot 2^\ell + k\) of \({\mathbf {H}}\) contains \(\mathsf {H}(i,k)\). Then, multiplying \({\mathbf {H}}\) with a random (m, h)-regular vector \({\varvec{e}}\) is equivalent to taking the sum of \(\mathsf {H}\) over h random inputs, as above.
Statistical hardness of DRSD. We next observe that for certain parameters where the output size of \({\mathbf {H}}\) is sufficiently smaller than the min-entropy of the error vector \({\varvec{e}}\), the distribution in the decisional problem is statistically close to uniform. Proofs and the general case of \(\ell \)-bit keys are given in [HOSS18].
Lemma 2.1
If \(\ell = 1\) and \(h \ge r + s\) then \(\mathsf {DRSD}_{r,h,\ell }\) is statistically hard, with distinguishing probability \(2^{-s}\).
Search-to-decision reduction. For all parameter choices of \(\mathsf {DRSD}\), there is a simple reduction to the search version of the regular syndrome decoding problem with the same parameters.
Lemma 2.2
Any efficient distinguisher for the \(\mathsf {DRSD}_{r,h,\ell }\) problem can be used to efficiently solve \(\mathsf {RSD}_{r,h,\ell }\).
3 GMW-Style MPC with Short Keys
In this section we design a protocol for generating multiplication triples over \(\mathbb {F}_2\) using short secret keys, with reduced communication complexity as the number of honest parties increases. More concretely, we first design a leaky protocol for secret-shared two-party bit multiplication, based on correlated OT and OT extension techniques with short keys. This protocol is not fully secure and we precisely define the leakage obtained by the receiver. We next show how to use the leaky protocol to produce multiplication triples, removing the leakage by rerandomizing the parties’ shares with shares of zero, and using the \(\mathsf {DRSD}\) assumption. Finally, this protocol can be used with Beaver’s multiplication triple technique [Bea92] to obtain MPC for binary circuits with an amortized communication complexity of \(O(nt\ell )\) bits per triple, where t is the threshold and \(\ell \) is the secret key length. When the number of honest parties is large enough we can even use \(\ell =1\) and avoid relying on \(\mathsf {DRSD}\).
3.1 Leaky Two-Party Secret-Shared Multiplication
We first present our protocol for two-party secret-shared bit multiplication, based on a variant of the [IKNP03] OT extension protocol, modified to use short keys. With short keys we cannot hope for computational security based on standard symmetric primitives, because an adversary can search every possible key in polynomial time. Our goal, therefore, is to define the precise leakage that occurs when using short keys, in order to remove this leakage at a later stage.
OT extension and correlated OT. Recall that the main observation of the IKNP protocol for extending oblivious transfer [IKNP03] is that correlated OT is symmetric, so that \(\kappa \) correlated OTs on r-bit strings can be locally converted into r correlated OTs on \(\kappa \)-bit strings. Secondly, a \(\kappa \)-bit correlated OT can be used to obtain an OT on chosen strings with computational security. The first stage of this process is abstracted away by the functionality  in Fig. 2.
in Fig. 2.
Using IKNP to multiply an input bit \(x_k\) from the sender, \(P_A\), with an input bit \(y_k\) from \(P_B\), the receiver, \(P_B\) sends \(y_k\) as its choice bit to  and learns \({\varvec{t}}_k = {\varvec{q}}_k \oplus y_k \cdot \varDelta \). The sender \(P_A\) obtains \({\varvec{q}}_k\), and then sends
and learns \({\varvec{t}}_k = {\varvec{q}}_k \oplus y_k \cdot \varDelta \). The sender \(P_A\) obtains \({\varvec{q}}_k\), and then sends
where \(\mathsf {H}\) is a 1-bit output hash function. This allows the parties to compute an additive sharing of \(x_k \cdot y_k\) as follows: \(P_A\) defines the share \(\mathsf {H}({\varvec{q}}_k)\), and \(P_B\) computes \(\mathsf {H}({\varvec{t}}_k) \oplus y_k \cdot d_k\). This can be repeated many times with the same \(\varDelta \) to perform a large batch of \(\mathsf {poly}(\kappa )\) secret-shared multiplications, because the randomness in \(\varDelta \) serves to computationally mask each x with the hash values (under a suitable correlation robustness assumption for \(\mathsf {H}\)). The downside of this is that for \(\varDelta \in \{0,1\}^\kappa \), the communication cost is \(O(\kappa )\) bits per two-party bit multiplication, to perform the correlated OTs.
Variant with short keys. We adapt this protocol to use short keys by performing the correlated OTs on \(\ell \)-bit strings, instead of \(\kappa \)-bit, for some small key length \(\ell = O(\log \kappa )\) (we could have \(\ell \) as small as 1). This allows  to be implemented with only \(O(\ell )\) bits of communication per OT instead of \(O(\kappa )\).
to be implemented with only \(O(\ell )\) bits of communication per OT instead of \(O(\kappa )\).
Our protocol, shown in Fig. 4, performs a batch of r multiplications at once. First the parties create r correlated OTs on \(\ell \)-bit strings using  . Next, the parties hash the output strings of the correlated OTs, and \(P_A\) sends over the correction values \(d_k\), which are used by \(P_B\) to convert the random OTs into a secret-shared bit multiplication. Finally, we require the parties to add a random value (from \(\mathcal {F}_{\scriptstyle \mathrm {Zero}}\), shown in Fig. 1) to their outputs, which ensures that they have a uniform distribution.
. Next, the parties hash the output strings of the correlated OTs, and \(P_A\) sends over the correction values \(d_k\), which are used by \(P_B\) to convert the random OTs into a secret-shared bit multiplication. Finally, we require the parties to add a random value (from \(\mathcal {F}_{\scriptstyle \mathrm {Zero}}\), shown in Fig. 1) to their outputs, which ensures that they have a uniform distribution.
Note that if \(\ell \in O(\log \kappa )\) then the hash function \(\mathsf {H}_{AB}\) has a polynomial-sized domain, so can be described as a lookup table provided as a common input to the protocol by both parties. At this stage we do not make any assumptions about \(\mathsf {H}_{AB}\); this means that the leakage in the protocol will depend on the hash function, so its description is also passed to the functionality  (Fig. 3). We require \(\mathsf {H}_{AB}\) to take as additional input an index \(k \in [r]\) and a bit in \(\{0,1\}\), to provide independence between different uses, and our later protocols require the function to be different in protocol instances between different pairs of parties (we use the notation \(\mathsf {H}_{AB}\) to emphasize this).
(Fig. 3). We require \(\mathsf {H}_{AB}\) to take as additional input an index \(k \in [r]\) and a bit in \(\{0,1\}\), to provide independence between different uses, and our later protocols require the function to be different in protocol instances between different pairs of parties (we use the notation \(\mathsf {H}_{AB}\) to emphasize this).
Leakage. We now analyse the exact security of the protocol in Fig. 4 when using short keys, and explain how this is specified in the functionality  (Fig. 3). Since a random share of zero is added to the outputs, note that the output distribution is uniformly random. Also, like IKNP, the protocol is perfectly secure against a corrupt \(P_A\) (or sender), so we only need to be concerned with leakage to a corrupt \(P_B\) who also sees the intermediate values of the protocol.
(Fig. 3). Since a random share of zero is added to the outputs, note that the output distribution is uniformly random. Also, like IKNP, the protocol is perfectly secure against a corrupt \(P_A\) (or sender), so we only need to be concerned with leakage to a corrupt \(P_B\) who also sees the intermediate values of the protocol.
The leakage is different for each k, depending on whether \(y_k=0\) or \(y_k=1\), so we consider the two cases separately. Within each case, there are two potential sources of leakage: firstly, the corrupt \(P_B\)’s knowledge of \({\varvec{t}}_k\) and \(\rho _k\) may cause leakage (where \(\rho _k\) is a random share of zero), since these values are used to define \(P_A\)’s output. Secondly, the \(d_k\) values seen by \(P_B\), which equal
may leak information on \(P_A\)’s inputs \(x_k\).
Case 1 \((y_k=1)\). In this case there is only leakage from the values \({\varvec{t}}_k\) and \(\rho _k\), which are used to define \(P_A\)’s output. Since \(z_k^A = \mathsf {H}_{AB}(k,0,{\varvec{t}}_k \oplus \varDelta ) \oplus \rho _k\), all of \(P_A\)’s outputs (and hence, also inputs) where \(y_k=1\) effectively have only \(\ell \) bits of min-entropy in the view of \(P_B\), corresponding to the random choice of \(\varDelta \). In this case \(P_B\)’s output is \(z_k^B = z_k^A \oplus x_k = \mathsf {H}_{AB}(k,0,{\varvec{t}}_k \oplus \varDelta ) \oplus \rho _k \oplus x_k\). To ensure that \(P_B\)’s view is simulable the functionality needs to sample a random string \(\varDelta \leftarrow \{0,1\}^\ell \) and leak \(\mathsf {H}_{AB}(k, 0, {\varvec{t}}_k \oplus \varDelta ) \oplus x_k\) to a corrupt \(P_B\).
Concerning the \(d_k\) values, notice that when \(y_k=1\) \(P_B\) can compute \(\mathsf {H}_{AB}(k,1,{\varvec{t}}_k)\) and use (1) to recover \(\mathsf {H}_{AB}(k,0,{\varvec{q}}_k) + x_k\), which equals \(z^A_k + \rho _k + x_k\). However, this is not a problem, because in this case we have \(z^B_k = z^A_k + x_k\), so \(d_k\) can be simulated given \(P_B\)’s output.
Case 2 \((y_k=0)\). Here the \(d_k\) values seen by \(P_B\) causes leakage on \(P_A\)’s inputs, because \(\varDelta \) is short. Looking at (1), \(d_k\) leaks information on \(x_k\) because \(\varDelta \leftarrow \{0,1\}^\ell \) is the only unknown in the equation, and is fixed for every k. Similarly to the previous case, this means that all of \(P_A\)’s inputs where \(y_k=0\) have only \(\ell \) bits of min-entropy in the view of an adversary who corrupts \(P_B\). We can again handle this leakage, by defining  to leak \(\mathsf {H}_{AB}(k, 1, {\varvec{t}}_k \oplus \varDelta ) + x_k\) to a corrupt \(P_B\).
to leak \(\mathsf {H}_{AB}(k, 1, {\varvec{t}}_k \oplus \varDelta ) + x_k\) to a corrupt \(P_B\).
Note that there is no leakage from the \({\varvec{t}}_k\) values when \(y_k=0\), because then \({\varvec{t}}_k={\varvec{q}}_k\), so these messages are independent of \(\varDelta \) and the inputs of \(P_A\).
In the functionality  , we actually modify the above slightly so that the leakage is defined in terms of linear algebra, instead of the hash function \(\mathsf {H}_{AB}\), to simplify the translation to the \(\mathsf {DRSD}\) problem later on. Therefore,
, we actually modify the above slightly so that the leakage is defined in terms of linear algebra, instead of the hash function \(\mathsf {H}_{AB}\), to simplify the translation to the \(\mathsf {DRSD}\) problem later on. Therefore,  defines a matrix \({\mathbf {H}}\in \mathbb {F}_2^{r \times 2^\ell }\), which contains the \(2^\ell \) values \(\{\mathsf {H}_{AB}(k,1\oplus y_k,{\varvec{t}}_k\oplus \varDelta )\}_{\varDelta \in \{0,1\}^\ell }\) in row k, where each \({\varvec{t}}_k\) is uniformly random. Given \({\mathbf {H}}\), the leakage from the protocol can then be described by sampling a random unit vector \({\varvec{e}}\in \mathbb {F}_2^{2^\ell }\) (which corresponds to \(\varDelta \in \{0,1\}^\ell \) in the protocol) and leaking \({\varvec{u}}= {\mathbf {H}}{\varvec{e}}+ {\varvec{x}}\) to a corrupt \(P_B\).
defines a matrix \({\mathbf {H}}\in \mathbb {F}_2^{r \times 2^\ell }\), which contains the \(2^\ell \) values \(\{\mathsf {H}_{AB}(k,1\oplus y_k,{\varvec{t}}_k\oplus \varDelta )\}_{\varDelta \in \{0,1\}^\ell }\) in row k, where each \({\varvec{t}}_k\) is uniformly random. Given \({\mathbf {H}}\), the leakage from the protocol can then be described by sampling a random unit vector \({\varvec{e}}\in \mathbb {F}_2^{2^\ell }\) (which corresponds to \(\varDelta \in \{0,1\}^\ell \) in the protocol) and leaking \({\varvec{u}}= {\mathbf {H}}{\varvec{e}}+ {\varvec{x}}\) to a corrupt \(P_B\).
Communication complexity. The cost of computing r secret-shared products is that of \(\ell \) random, correlated OTs on r-bit strings, and a further r bits of communication. Using OT extension [IKNP03, ALSZ13] to implement the correlated OTs the amortized cost is \(\ell (r + \kappa )\) bits, for computational security \(\kappa \). This gives a total cost of \(\ell (r + \kappa ) + r\) bits.
In [HOSS18] we prove the following.
Theorem 3.1
Protocol  securely implements the functionality
securely implements the functionality  with perfect security in the
with perfect security in the  -hybrid model in the presence of static honest-but-curious adversaries.
-hybrid model in the presence of static honest-but-curious adversaries.
3.2 MPC for Binary Circuits From Leaky OT
We now show how to use the leaky OT protocol to compute multiplication triples over \(\mathbb {F}_2\), using a GMW-style protocol [GMW87, Gol04] optimized for the case of at least h honest parties. This can then be used to obtain a general MPC protocol for binary circuits using Beaver’s method [Bea92].
Triple generation. We implement the triple generation functionality over \(\mathbb {F}_2\), shown in Fig. 5. Recall that to create a triple using the GMW method, first each party locally samples shares \(x^i,y^i \leftarrow \mathbb {F}_2\). Next, the parties compute shares of the product based on the fact that:
where \(x^i\) denotes \(P_i\)’s share of \(x = \sum _i x^i\).
Since each party can compute \(x^iy^i\) on its own, in order to obtain additive shares of \(z = x y\) it suffices for the parties to obtain additive shares of \(x^i y^j\) for every pair \(i \ne j\). This is done using oblivious transfer between \(P_i\) and \(P_j\), since a 1-out-of-2 OT implies two-party secret-shared bit multiplication.
If we use the leaky two-party batch multiplication protocol from the previous section, this approach fails to give a secure protocol because the leakage in  allows a corrupt \(P_B\) to guess \(P_A\)’s inputs with probability \(2^{-\ell }\). When using this naively, \(P_A\) carries out a secret-shared multiplication using the same input shares with every other party, which allows every corrupt party to attempt to guess \(P_A\)’s shares, increasing the success probability further. If the number of corrupted parties is not too small then this gives the adversary a significant chance of successfully guessing the shares of every honest party, completely breaking security.
allows a corrupt \(P_B\) to guess \(P_A\)’s inputs with probability \(2^{-\ell }\). When using this naively, \(P_A\) carries out a secret-shared multiplication using the same input shares with every other party, which allows every corrupt party to attempt to guess \(P_A\)’s shares, increasing the success probability further. If the number of corrupted parties is not too small then this gives the adversary a significant chance of successfully guessing the shares of every honest party, completely breaking security.
To avoid this issue, we require \(P_A\) to randomize the shares used as input to  , in such a way that we still preserve correctness of the protocol. To do this, the parties will use \(\mathcal {F}_{\scriptstyle \mathrm {Zero}}\) to generate random zero shares \(s^{i,j}\in \mathbb {F}_2\) (held by \(P_i\)), satisfying \(\sum _i s^{i,j} = 0\) for all \(j \in [n]\), and then \(P_i\) and \(P_j\) will multiply \(x^i + s^{i,j}\) and \(y^j\). This means that all parties end up computing shares of:
, in such a way that we still preserve correctness of the protocol. To do this, the parties will use \(\mathcal {F}_{\scriptstyle \mathrm {Zero}}\) to generate random zero shares \(s^{i,j}\in \mathbb {F}_2\) (held by \(P_i\)), satisfying \(\sum _i s^{i,j} = 0\) for all \(j \in [n]\), and then \(P_i\) and \(P_j\) will multiply \(x^i + s^{i,j}\) and \(y^j\). This means that all parties end up computing shares of:
so still obtain a correct triple.
Finally, to ensure that the output shares are uniformly random, fresh shares of zero will be added to each party’s share of xy. Note that masking each \(x^i\) input to  means that it doesn’t matter if the individual shares are leaked to the adversary, as long as it is still hard to guess the sum of all shares. This means that we only need to be concerned with the sum of the leakage from
means that it doesn’t matter if the individual shares are leaked to the adversary, as long as it is still hard to guess the sum of all shares. This means that we only need to be concerned with the sum of the leakage from  . Recall that each individual instance leaks the input of an honest party \(P_i\) masked by \({\mathbf {H}}_i{\varvec{e}}_i\), where \({\mathbf {H}}_i\) is a random matrix and \({\varvec{e}}_i \in \mathbb {F}_2^{2^\ell }\) is a random unit vector. Summing up all the leakage from h honest parties, we get
. Recall that each individual instance leaks the input of an honest party \(P_i\) masked by \({\mathbf {H}}_i{\varvec{e}}_i\), where \({\mathbf {H}}_i\) is a random matrix and \({\varvec{e}}_i \in \mathbb {F}_2^{2^\ell }\) is a random unit vector. Summing up all the leakage from h honest parties, we get
This is exactly an instance of the \(\mathsf {DRSD}_{r,h,\ell }\) problem, so is pseudorandom for an appropriate choice of parameters.
We remark that the number of triples generated, r, affects the hardness of \(\mathsf {DRSD}\). However, we can create an arbitrary number of triples without changing the assumption by repeating the protocol for a fixed r.
Reducing the number of OT channels. The above approach reduces communication of GMW by a factor \(\kappa /\ell \), for \(\ell \)-bit keys, but still requires a complete network of \(n(n-1)\) OT and communication channels between the parties. We can reduce this further by again taking advantage of the fact that there are at least h honest parties. We observe that when using our two-party secret-shared multiplication protocol to generate triples, information is only leaked on the \(x^i\) shares, and not the \(y^i\) shares of each triple. This means that \(h-1\) parties can choose their shares of y to be zero, and y will still be uniformly random to an adversary who corrupts up to \(t=n-h\) parties. This reduces the number of OT channels needed from \(n(n-1)\) to \((t+1)(n-1)\).
When the number of parties is large enough, we can do even better using random committees. We randomly choose two committees, \({\mathcal P}_{(h)}\) and \({\mathcal P}_{(1)}\), such that except with negligible probability, \({\mathcal P}_{(h)}\) has at least h honest parties and \({\mathcal P}_{(1)}\) has at least one honest party. Only the parties in \({\mathcal P}_{(h)}\) choose non-zero shares of x, and parties in \({\mathcal P}_{(1)}\) choose non-zero shares of y; all other parties do not take part in any OT instances, and just output random sharings of zero. We remark that it can be useful to choose the parameter h lower than the actual number of honest parties, to enable a smaller committee size (at the cost of potentially larger keys). When the total number of parties, n, is large enough, this means the number of interacting parties can be independent of n. The complete protocol, described for two fixed committees satisfying our requirements, is shown in Fig. 6.
Communication complexity. Recall from the analysis in Sect. 3.1 that when using protocol  with \(\varPi _{\scriptstyle \mathrm {Triple}}\), the cost of computing r secret-shared triples is that of \(\ell \) random, correlated OTs on r-bit strings, and a further r bits of communication between every pair of parties. This gives a total cost of \(\ell (r + \kappa ) + r\) bits between every pair of parties who has an OT channel (ignoring \(\mathcal {F}_{\scriptstyle \mathrm {Zero}}\) and the seed OTs for OT extension, since their communication cost is independent of the number of triples). If the two committees \({\mathcal P}_{(h)},{\mathcal P}_{(1)}\) have sizes \(n_h \le n\) and \(n_1 \le t+1\) then we have the following theorem (proven in [HOSS18]).
with \(\varPi _{\scriptstyle \mathrm {Triple}}\), the cost of computing r secret-shared triples is that of \(\ell \) random, correlated OTs on r-bit strings, and a further r bits of communication between every pair of parties. This gives a total cost of \(\ell (r + \kappa ) + r\) bits between every pair of parties who has an OT channel (ignoring \(\mathcal {F}_{\scriptstyle \mathrm {Zero}}\) and the seed OTs for OT extension, since their communication cost is independent of the number of triples). If the two committees \({\mathcal P}_{(h)},{\mathcal P}_{(1)}\) have sizes \(n_h \le n\) and \(n_1 \le t+1\) then we have the following theorem (proven in [HOSS18]).
Theorem 3.2
Protocol \(\varPi _{\scriptstyle \mathrm {Triple}}\) securely realizes \(\mathcal {F}_{\scriptstyle \mathrm {Triple}}^r\) in the  -hybrid model, based on the \(\mathsf {DRSD}_{r,h,\ell }\) assumption, where h is the number of honest parties in \({\mathcal P}_{(h)}\). The amortized communication cost is \(\le n_h n_1(\ell + \ell \kappa /r + 1)\) bits per triple.
-hybrid model, based on the \(\mathsf {DRSD}_{r,h,\ell }\) assumption, where h is the number of honest parties in \({\mathcal P}_{(h)}\). The amortized communication cost is \(\le n_h n_1(\ell + \ell \kappa /r + 1)\) bits per triple.
Parameters for unconditional security. Recall from Lemma 2.1 that if \(\ell =1\) and \(h \ge r + s\) for any \(\ell \), then \(\mathsf {DRSD}_{r,h,\ell }\) is statistically hard, with statistical security \(2^{-s}\). This means when h is large enough we can use 1-bit keys, and every pair of parties who communicates only needs to send \(2 + \kappa /r\) bits over the network.Footnote 2
MPC using multiplication triples. Our protocol for multiplication triples can be used to construct a semi-honest MPC protocol for binary circuits using Beaver’s approach [Bea92]. The parties first secret-share their inputs between all other parties. Then, XOR gates can be evaluated locally on the shares, whilst an AND gate requires consuming a multiplication triple, and two openings with Beaver’s method. Each opening can be done with \(2(n-1)\) bits of communication as follows: all parties send their shares to \(P_1\), who sums the shares together and sends the result back to every other party.
In the 1-bit key case mentioned above, using two (deterministic) committees of sizes n and \(t+1\) and setting, for instance, \(r = \kappa \) implies the following corollary. Note that the number of communication channels is \((t+1)(n-1)\) and not \((t+1)n\), because in the deterministic case \({\mathcal P}_{(1)}\) is contained in \({\mathcal P}_{(h)}\), so \(t+1\) sets of the shared cross-products can be computed locally.
Corollary 3.3
Assuming OT and OWF, there is a semi-honest MPC protocol for binary circuits with an amortized communication complexity of no more than \(3(t+1)(n-1) + 4(n-1)\) bits per AND gate, if there are at least \(\kappa + s\) honest parties.
4 Multi-Party Garbled Circuits with Short Keys
In this section we present our second contribution: a constant-round MPC protocol based on garbled circuits with short keys. The protocol has two phases, a preprocessing phase independent of the parties’ actual inputs where the garbled circuit is mutually generated by all parties, and an online phase where the computation is performed. We first abstractly discuss the details of our garbling method, and then turn to the two protocols for generating and evaluating the garbled circuit.
4.1 The Multi-Party Garbling Scheme
Our garbling method is defined by the functionality \(\mathcal {F}_{\scriptstyle \mathrm {Preprocessing}}^{\ell _{\scriptscriptstyle \mathrm {BMR}}}\) (Fig. 7), which creates a garbled circuit that is given to all the parties. It can be seen as a variant of the multi-party garbling technique by Beaver, Micali and Rogaway [BMR90], known as BMR, which has been used and improved in a recent sequence of works [LPSY15, LSS16, BLO16, HSS17].
The main idea behind BMR is that every party \(P_i\) contributes a pair of keys \(k^i_{w,0}, k^i_{w,1} \in \{0,1\}^\kappa \) and a share of a wire mask \(\lambda _w^i \in \{0,1\}\) for each wire w in the circuit. To garble a gate, the corresponding output wire key from every party is encrypted under the combination of all parties’ input wire keys, using a PRF or PRG, so that no single party knows all the keys for a gate. In addition, the free-XOR property can be supported by having each party choose their keys such that \(k^i_{w,0} \oplus k^i_{w,1} = \varDelta ^i\), where \(\varDelta ^i\) is a global fixed random string known to \(P_i\).
The main difference between our work and recent related protocols is that we use short keys of length \({\ell _{\scriptscriptstyle \mathrm {BMR}}}\) instead of \(\kappa \), and then garble gates using a random, expanding function \(\mathsf {H}: [n] \times \{0,1\}\times \{0,1\}^{{\ell _{\scriptscriptstyle \mathrm {BMR}}}} \rightarrow \{0,1\}^{n{\ell _{\scriptscriptstyle \mathrm {BMR}}}+1}\). Instead of basing security on a PRF or PRG, we then reduce the security of the protocol to the pseudorandomness of the sum of \(\mathsf {H}\) when applied to each of the honest parties’ keys, which is implied by the DRSD problem from Sect. 2.1. We also use \(\mathsf {H}'\) to denote \(\mathsf {H}\) with the least significant output bit dropped, which we use for garbling splitter gates.
To garble an AND gate g with input wires u, v and output wire w, each of the 4 garbled rows \({\tilde{g}}_{a,b}\), for \((a,b) \in \{0,1\}^2\), is computed as:
where \(c= (a \oplus \lambda _u) \cdot (b \oplus \lambda _v) \oplus \lambda _w\) and \(\lambda _u, \lambda _v, \lambda _w\) are the secret-shared wire masks. Each row can be seen as an encryption of the correct n output wire keys under the corresponding input wire keys of all parties. Note that, for each wire, \(P_i\) holds the keys \(k^i_{u,0},k^i_{u,1}\) and an additive share \(\lambda _u^i\) of the wire mask. The extra bit value that \(\mathsf {H}\) takes as input is added to securely increase the stretch of \(\mathsf {H}\) when using the same input key twice, preventing a ‘mix-and-match’ attack on the rows of a garbled gate. The output of \(\mathsf {H}\) is also extended by an extra bit, to allow encryption of the output wire mask c.Footnote 3
Splitter gates. When relying on the DRSD problem, the reuse of a key in multiple gates degrades parameters and makes the problem easier (as the parameter r grows, the key length must be increased), so we cannot handle circuits with arbitrary fan-out. For this reason, we restrict our exposition of the garbling to fan-out-one circuits with so-called splitter gates. This type of gate takes as input a single wire w and provides two output wires u, v, each of them with fresh, independent keys representing the same value carried by the input wire. Converting an arbitrary circuit to use splitter gates incurs a cost of roughly a factor of two in the circuit size (see [HOSS18]).
Splitter gates were previously introduced in [TX03] as a fix for a similar issue in the original BMR paper [BMR90], where the wire “keys” were used as seeds for a PRG in order to garble the gates, so that when a wire was used as input to multiple gates, their garbled versions did not use independent pseudorandom masks. Other recent BMR-style papers avoid this issue by applying the PRF over the gate identifier as well, which produces distinct, independent PRF evaluations for each gate.
Free-XOR. The Free-XOR [KS08] optimization results in an improvement in both computation and communication for XOR gates where a global fixed random \(\varDelta _i\) is chosen by each party \(P_i\) and the input keys are locally XORed, yielding the output key of this gate. We cannot use the standard free-XOR technique [KS08, BLO16] for the same reason discussed above: reusing a single offset across multiple gates would make the DRSD problem easier and not be secure. We therefore introduce a new free-XOR technique (inspired by FleXOR [KMR14]) which, combined with our use of splitter gates, allows garbling XOR gates for free without additional assumptions. For each arbitrary fan-in XOR gate g, each party chooses a different offset \(\varDelta _g^i\), allowing for a free-XOR computation for wires using keys with that offset. For general circuits, this would normally introduce the problem that the input wires may not have the correct offset, requiring some ‘translation’ to \(\varDelta _g\). However, because we restrict to gates with fan-out-one and splitter gates, we know that each input wire to g is not an input wire to any other gate, so we can always ensure the keys use the correct offset without any further changes.
Compiling to fan-out-one circuits with splitter gates. Let \(C_f\) be an arbitrary fan-out circuit, with A AND gates and X XOR gates, both with fan-in-two. Let \(I_{C_f}\) and \(O_{C_f}\) be the number of circuit-input and circuit-output wires, respectively. We will now compute the number S of splitter gates that the compiled circuit needs. First, note that each time a wire w is used as input to another gate or as a circuit-output wire, w’s fan-out is increased by one. Each of the AND, XOR gates in the pre-compiled circuit provides a fresh output wire to be used in \(C_f\), while using for its inputs two pre-existing wires in the circuit. Output wires also use one pre-existing wire each, while input wires use no pre-existing wires. This means that, to compile \(C_f\) to be a fan-out-one circuit, we need to add up to \((2\cdot X + 2 \cdot A + O_{C_f}) - (A + X + I_{C_f})\) wires. Each of these missing wires, however, can be created by using a splitter gate in the compiled circuit, since each of these gates uses one wire to generate two fresh new wires. So, putting all the pieces together, the compiled circuit requires \(S \le X + A + O_{C_f} - I_{C_f}\) splitter gates. This gives a close upper bound, as if w is a circuit output wire and an input wire of another gate then it is being counted twice rather than once in the formula.
4.2 Protocol and Functionalities for Bit and Bit/String Multiplication
Even though we could implement both \(\mathcal {F}_{\scriptstyle \mathrm {Bit \times Bit}}\) and \(\mathcal {F}_{\scriptstyle \mathrm {BitString}}^{\ell _{\scriptscriptstyle \mathrm {BMR}}}(P_j)\) using \(\mathcal {F}_{\scriptstyle \mathrm {Triple}}\), there are more efficient ways to implement the latter: One by building directly from  , and another using [ALSZ13].
, and another using [ALSZ13].
-
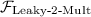 -hybrid implementation (Fig. 11): As the length-\({\ell _{\scriptscriptstyle \mathrm {BMR}}}\) string \(R_g^j\) is not secret-shared and just known to one party, we only need to perform \(n-1\) invocations of
-hybrid implementation (Fig. 11): As the length-\({\ell _{\scriptscriptstyle \mathrm {BMR}}}\) string \(R_g^j\) is not secret-shared and just known to one party, we only need to perform \(n-1\) invocations of 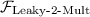 in order to multiply it with a secret-shared bit \(x = x^1 + \dots + x^n\). The protocol uses random shares of zero to mask the inputs and outputs of
in order to multiply it with a secret-shared bit \(x = x^1 + \dots + x^n\). The protocol uses random shares of zero to mask the inputs and outputs of 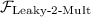 , similarly to the \(\varPi _{\scriptstyle \mathrm {Triple}}\) protocol.
, similarly to the \(\varPi _{\scriptstyle \mathrm {Triple}}\) protocol.Note that this does not directly implement the functionality shown in Fig. 9, because \(\varPi _{\scriptstyle \mathrm {Bit\times String}}^{r,{\ell _{\scriptscriptstyle \mathrm {BMR}}}}\) performs a batch of r independent multiplications in parallel. However, in the protocol \(\varPi _{\scriptstyle \mathrm {Preprocessing}}^{\ell _{\scriptscriptstyle \mathrm {BMR}}}\) all the gates can be garbled in parallel, so a batch version of the functionality (as described in Fig. 10) suffices. The amortized communication complexity obtained is \({\ell _{\scriptscriptstyle \mathrm {BMR}}}(1 + {\ell _{\scriptscriptstyle \mathrm {OT}}}+ {\ell _{\scriptscriptstyle \mathrm {OT}}}\kappa / r)\) bits.
-
[ALSZ13] implementation: The amortized communication complexity is \(\kappa +{\ell _{\scriptscriptstyle \mathrm {BMR}}}\) bits.
Communication complexity. The communication complexity of \(\varPi _{\scriptstyle \mathrm {Bit\times String}}^{r,{\ell _{\scriptscriptstyle \mathrm {BMR}}}}\) is exactly that of \((n-1){\ell _{\scriptscriptstyle \mathrm {BMR}}}\) instances of  , where \({\ell _{\scriptscriptstyle \mathrm {OT}}}\) is the leakage parameter used in the protocol
, where \({\ell _{\scriptscriptstyle \mathrm {OT}}}\) is the leakage parameter used in the protocol  . Note that \({\ell _{\scriptscriptstyle \mathrm {OT}}}\) is independent of \({\ell _{\scriptscriptstyle \mathrm {BMR}}}\) used in the bit/string protocol, but affects the security and cost of realising
. Note that \({\ell _{\scriptscriptstyle \mathrm {OT}}}\) is independent of \({\ell _{\scriptscriptstyle \mathrm {BMR}}}\) used in the bit/string protocol, but affects the security and cost of realising  . The total complexity is then \((n-1){\ell _{\scriptscriptstyle \mathrm {BMR}}}({\ell _{\scriptscriptstyle \mathrm {OT}}}(r + \kappa ) + r)\) bits, or an amortized cost of \((n-1){\ell _{\scriptscriptstyle \mathrm {BMR}}}({\ell _{\scriptscriptstyle \mathrm {OT}}}+ {\ell _{\scriptscriptstyle \mathrm {OT}}}\kappa /r + 1)\) bits per multiplication.
. The total complexity is then \((n-1){\ell _{\scriptscriptstyle \mathrm {BMR}}}({\ell _{\scriptscriptstyle \mathrm {OT}}}(r + \kappa ) + r)\) bits, or an amortized cost of \((n-1){\ell _{\scriptscriptstyle \mathrm {BMR}}}({\ell _{\scriptscriptstyle \mathrm {OT}}}+ {\ell _{\scriptscriptstyle \mathrm {OT}}}\kappa /r + 1)\) bits per multiplication.
Theorem 4.1
Protocol \(\varPi _{\scriptstyle \mathrm {Bit\times String}}^{r,{\ell _{\scriptscriptstyle \mathrm {BMR}}}}\) UC-securely realizes \(\mathcal {F}_{\scriptstyle \mathrm {BitString}}^{r,{\ell _{\scriptscriptstyle \mathrm {BMR}}}}\) in the \(\mathcal {F}_{\scriptstyle \mathrm {Zero}}^{2r}\)-hybrid in the presence of static honest-but-curious adversaries, under the \(\mathsf {DRSD}_{r,h,{\ell _{\scriptscriptstyle \mathrm {OT}}}}\) assumption.
The proof is a direct extension of the proof of Theorem 3.2.
4.3 The Preprocessing Protocol
Our protocol for generating the garbled circuit is shown in Fig. 12. We use two functionalities \(\mathcal {F}_{\scriptstyle \mathrm {Bit \times Bit}}\) (Fig. 8) and \(\mathcal {F}_{\scriptstyle \mathrm {BitString}}(P_j)\) (Fig. 9) for multiplying two additively shared bits, and multiplying an additively shared bit with a string held by \(P_j\), respectively. \(\mathcal {F}_{\scriptstyle \mathrm {Bit \times Bit}}\) can be easily implemented using a multiplication triple from \(\mathcal {F}_{\scriptstyle \mathrm {Triple}}\) in the previous section, whilst \(\mathcal {F}_{\scriptstyle \mathrm {BitString}}\) uses a variant of the \(\varPi _{\scriptstyle \mathrm {Triple}}\) protocol optimized for this task.
Most of the preprocessing protocol is similar to previous works [BLO16, HSS17], where first each party samples their sets of wire keys and shares of wire masks, and then the parties interact to obtain shares of the garbled gates. It is the second stage where our protocol differs, so we focus here on the details of the gate garbling procedures.
The Gate Garbling Protocol. We describe the details of the sub-protocol \(\varPi _{\scriptstyle \mathrm {Gate Garbling}}^{\ell _{\scriptscriptstyle \mathrm {BMR}}}\) (Fig. 13), implementing the gate garbling phase of \(\mathcal {F}_{\scriptstyle \mathrm {Preprocessing}}^{\ell _{\scriptscriptstyle \mathrm {BMR}}}\). Creating garbled AND gates is done similarly to the OT-based protocol [BLO16], with the exception that we use short wire keys of length \({\ell _{\scriptscriptstyle \mathrm {BMR}}}\) instead of \(\kappa \). We also show how to create sharings of garbled splitter gates without any interaction, so these are much cheaper than AND gates.
Suppose that for an AND gate g, each \(P_i\) holds the wire mask share \(\lambda _v^i\) and keys \(k^i_{v,0}, k^i_{v,1} \leftarrow \{0,1\}^{\ell _{\scriptscriptstyle \mathrm {BMR}}}\). \(P_i\) defines \(R^i_g=k^i_{w,0} \oplus k^i_{w,1}\). After that all parties call \(\mathcal {F}_{\scriptstyle \mathrm {Bit \times Bit}}\) once to compute additive shares of \(\lambda _{uv}= \lambda _u \cdot \lambda _v \in \{0,1\}\), which are then used to locally compute shares of \(\chi _{g,a,b} = (a \oplus \lambda _u) \cdot (b \oplus \lambda _v) \oplus \lambda _w\), for each \((a,b) \in \{0,1\}^2\). Each \(P_i\) obtains \(\chi _{g,a,b}^i\) such that \(\chi _{g,a,b} = \oplus _{i \in [n]} \chi ^i_{g,a,b}\). To compute shares of the products \(\chi _{g,a,b} \cdot R_g^i\), the parties call \(\mathcal {F}_{\scriptstyle \mathrm {BitString}}^{{\ell _{\scriptscriptstyle \mathrm {BMR}}}}(P_i)\) three times, for each \(i \in [n]\), to multiply \(R_g^i\) with each of the bits \(\lambda _u, \lambda _v, (\lambda _{uv}\oplus \lambda _w)\). These can then be used for each \(P_j\) to locally obtain the shares \((\chi _{g,a,b} \cdot R_g^i)^j\), for all \((a,b) \in \{0,1\}^2\) (just as in [BLO16]).
After computing the bit/string products, \(P_j\) then computes for each \((a,b) \in \{0,1\}^2\):
These values define shares of \(\chi _{g,a,b} \cdot R_g^i \oplus k^i_{w,0}\). Finally, each party’s share of the garbled AND gate is obtained as:
Summing up these values we obtain:
where \(c= \chi _{g,a,b}\), as required.
To garble a splitter gate, we observe that here there is no need for any secure multiplications within MPC, and the parties can produce shares of the garbled gate without any interaction. This is because the two output wire values are the same as the input wire value, so to obtain a share of the encryption of the two output keys on wires u, v with input wire w, party \(P_i\) just computes:
for \(c \in \{0,1\}\), where the right-hand vector contains \(P_i\)’s keys in positions i and \(n+i\). The parties then re-randomize this sharing with a share of zero from \(\mathcal {F}_{\scriptstyle \mathrm {Zero}}\), so that opening the shares does not leak information on the individual keys.Footnote 4
4.4 Security and Complexity
The above approach reduces size of the garbled circuit by a factor \(\kappa /{\ell _{\scriptscriptstyle \mathrm {BMR}}}\), for \({\ell _{\scriptscriptstyle \mathrm {BMR}}}\)-bit keys, but still requires n keys for every row in the garbled gates. Similarly to Sect. 3, when n is large we can reduce this by using a (random) committee \({\mathcal P}_{(h)}\) of size \(n_h\) that has at least h honest parties. \(\varPi _{\scriptstyle \mathrm {Preprocessing}}^{\ell _{\scriptscriptstyle \mathrm {BMR}}}\) and \(\varPi _{\scriptstyle \mathrm {BMR}}^{\ell _{\scriptscriptstyle \mathrm {BMR}}}\) are then run as if called only by the parties in \({\mathcal P}_{(h)}\). For circuit-input wires w where parties in \(\mathcal{P}\setminus {\mathcal P}_{(h)}\) provide input, they are sent the masks \(\lambda _w\) in \(\varPi _{\scriptstyle \mathrm {Preprocessing}}^{\ell _{\scriptscriptstyle \mathrm {BMR}}}\), so in the online phase they can then broadcast \(\varLambda _w=\rho ^i_{w} \oplus \lambda _w\) in the same way as parties in \({\mathcal P}_{(h)}\).
This reduces the size of the garbled circuit by an additional factor of \(n / n_h\). Finally, the same committee \({\mathcal P}_{(h)}\) can be combined with a (random) committee \({\mathcal P}_{(1)}\) with a single honest party in order to optimize the bit multiplications needed to compute the \(\chi _{g,a,b}\) values, as was described in Sect. 3.
In Sect. 5, we give some examples of committee sizes and key lengths that ensure security, and compare this with the naive approach of running the preprocessing phase of BMR in \({\mathcal P}_{(1)}\) only. The following theorem is proved in [HOSS18].
Theorem 4.2
Protocol \(\varPi _{\scriptstyle \mathrm {Preprocessing}}^{\ell _{\scriptscriptstyle \mathrm {BMR}}}\) UC-securely realizes the functionality \(\mathcal {F}_{\scriptstyle \mathrm {Preprocessing}}^{\ell _{\scriptscriptstyle \mathrm {BMR}}}\) with perfect security in the \((\mathcal {F}_{\scriptstyle \mathrm {Bit \times Bit}}, \mathcal {F}_{\scriptstyle \mathrm {BitString}}^{{\ell _{\scriptscriptstyle \mathrm {BMR}}}},\mathcal {F}_{\scriptstyle \mathrm {Zero}}^{2n{\ell _{\scriptscriptstyle \mathrm {BMR}}}})\)-hybrid model in the presence of static honest-but-curious adversaries.
4.5 The Online Phase
Given the previous description of the garbling phase, the online phase is quite straightforward, where upon reconstructing the garbled circuit and obtaining all input keys, the evaluation process is similar to [BMR90]. As in that work, all parties run the evaluation algorithm, which in our case involves each party computing just 2n hash evaluations per gate. During evaluation, the parties only see the randomly masked wire values, which we call “public values”, and cannot determine the actual values being computed. Upon completion, the parties obtain the actual output using the output wire masks revealed from \(\mathcal {F}_{\scriptstyle \mathrm {Preprocessing}}^{\ell _{\scriptscriptstyle \mathrm {BMR}}}\). The security of the protocol reduces to the \(\mathsf {DRSD}_{r,h,{\ell _{\scriptscriptstyle \mathrm {BMR}}}}\) problem, where \({\ell _{\scriptscriptstyle \mathrm {BMR}}}\) is the key length, h is the number of honest parties, and r is twice the output length of the function \(\mathsf {H}\) (sampled by the CRS).
We remark that in practice, we may want to implement the random function \(\mathsf {H}\) in the CRS using fixed-key AES in the ideal cipher model, as is common for garbling schemes based on free-XOR. In [HOSS18], we show that this reduces the number of AES calls from \(O(n^2)\) in previous BMR protocols to \(O(n^2 {\ell _{\scriptscriptstyle \mathrm {BMR}}}/ \kappa )\). The protocol and the complete proof can be found in [HOSS18].
5 Complexity Analysis and Implementation Results
We now compare the complexity of the most relevant aspects of our approach to the state-of-the-art prior results in semi-honest MPC protocols with dishonest majority. To demonstrate the practicality of our approach, we also present implementation results for the online evaluation phase of our BMR-based protocol. Further details can be found on [HOSS18].
5.1 Threshold Variants of Full-Threshold Protocols
Since the standard GMW and BMR-based protocols allow for up to \(n-1\) corruptions, we also show how to modify previous protocols to support some threshold t, and compare our protocols with these variants. The method is very simple (and similar to the use of committees in our protocols), but does not seem to have been explicitly mentioned in previous literature. To evaluate a circuit C, all parties first secret-share their inputs to an arbitrarily chosen committee \(\mathcal {P'}\), of size \(t+1\). Committee \(\mathcal {P'}\) runs the full-threshold protocol for a modified circuit \(C'\), which takes all the shares as input, and first XORs them together so that it computes the same function as C. The committee \(\mathcal {P'}\) then sends the output to all parties in \(\mathcal {P}\). The complexity of the threshold-t variant of a full-threshold protocol, \(\varPi \), is then essentially the same as running \(\varPi \) between \(t+1\) parties instead of n.
5.2 GMW-Style Protocol
We now compare the communication cost of our triple generation protocol with the best-known instantiation of GMW, namely a variant based on 1-out-of-4 OT to generate triples, recently optimized by [DKS+17] in the 2-party setting. This easily extends to the multi-party case with communication complexity \(O(n^2\kappa /\log {\kappa })\) bits per AND gate, so we consider both full-threshold and threshold-t (Sect. 5.1) variants. Note that our protocol from Sect. 3 has complexity \(O(nt\ell )\) when using deterministic committees.
As can be seen in Table 1 and Fig. 14, for a fixed number of honest parties h, the improvement of our protocol over GMW (threshold t) becomes greater as the total number of parties increases. Our protocol starts to beat the best-known GMW protocol for producing multiplication triples when there are just 6 honest parties. For example, with 20 parties and 14 corruptions, the communication cost of our protocol is roughly 10% lower than threshold-14 GMW, and only 2 times lower than the cost of standard, full threshold GMW. As the number of parties (and honest parties) grows, our improvements become even greater, and when the number of honest parties is more than 80, we can use 1-bit keys and improve upon the threshold variant of GMW by more than 13 times.
In [HOSS18], we also analyse the complexity of our protocol when using random committees, and compare this with the standard approach of running full-threshold GMW in a single random committee.
5.3 BMR-Style Protocol
Communication Complexity. To show the efficiency of our constant-round garbling protocol from Sect. 4.5, we provide Table 2, which has two parts. First, it compares the amortized communication complexity incurred for garbling an AND gate with [BLO16]. We recall that this is the dominating cost for BMR-style protocols using Free-XOR, and that we incur no communication for creating shares of garbled splitter gates. Note that in the first setting of \(n=20,t=10\), although our communication costs are around 3 times lower than [BLO16], we do not improve upon the threshold-t variant of that protocol, described earlier. Once we get to 50 parties, though, we start to improve upon [BLO16], with a reduction in communication going up to 7x for 400 parties and 10x for 1000 parties.
The second half of the table shows the size of the garbled circuit in terms of the total number of AND, XOR and splitter gates. Garbled circuit size only has a slight impact on communication complexity, when opening the garbled circuit, which is much lower than the communication in the rest of the garbling phase. However, if an implementation needs to store the entire garbled circuit in memory (either for evaluation, or storage for later use) then it is also important to optimize its size. Here we also compare with [BLO17], which recently showed how to construct a compact multi-party garbled circuit based on key-homomorphic PRFs. The size of their garbled circuit is constant and grows with \(O(\kappa )\) per gate, with security proven in the presence of \(n-1\) corrupted parties. On the other hand, their construction has much larger key sizes, does not support free-XOR, and has a more expensive preprocessing phase needing O(n) secret-shared finite field multiplications per gate. In Fig. 15 we show the communication complexity of garbling when \(n=100, 500\) and for different number of honest parties.
Notes
- 1.
Note that OT is equivalent to secret-shared bit multiplication, and when constructing MPC it is more convenient to use the latter definition.
- 2.
Note that we still need computational assumptions for OT and zero sharing in order to implement
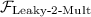 and \(\mathcal {F}_{\scriptstyle \mathrm {Zero}}\).
and \(\mathcal {F}_{\scriptstyle \mathrm {Zero}}\). - 3.
This only becomes necessary when using short keys — in BMR with full-length keys the parties can recover the wire mask by comparing the output with their own two keys, but this does not work if collisions are possible.
- 4.
For AND gates, the shares output by \(\mathcal {F}_{\scriptstyle \mathrm {BitString}}^{{\ell _{\scriptscriptstyle \mathrm {BMR}}}}\) are uniformly random, so do not need re-randomizing with sharings of zero.
References
Asharov, G., Demmler, D., Schapira, M., Schneider, T., Segev, G., Shenker, S., Zohner, M.: Privacy-preserving interdomain routing at internet scale. PoPETs 2017(3), 147 (2017)
Araki, T., Furukawa, J., Lindell, Y., Nof, A., Ohara, K.: High-throughput semi-honest secure three-party computation with an honest majority. In: Weippl, E.R., Katzenbeisser, S., Kruegel, C., Myers, A.C., Halevi, S. (eds.) ACM CCS 2016, pp. 805–817. ACM Press, October 2016
Augot, D., Finiasz, M., Sendrier, N.: A fast provably secure cryptographic hash function. IACR Cryptology ePrint Archive 2003:230 (2003)
Asharov, G., Jain, A., López-Alt, A., Tromer, E., Vaikuntanathan, V., Wichs, D.: Multiparty computation with low communication, computation and interaction via threshold FHE. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 483–501. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_29
Asharov, G., Lindell, Y., Schneider, T., Zohner, M.: More efficient oblivious transfer and extensions for faster secure computation. In: Sadeghi, A.-R., Gligor, V.D., Yung, M. (eds.) ACM CCS 2013, pp. 535–548. ACM Press, November 2013
Applebaum, B.: Garbling XOR gates “for free” in the standard model. J. Cryptol. 29(3), 552–576 (2016)
Beaver, D.: Efficient multiparty protocols using circuit randomization. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 420–432. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_34
Ben-Efraim, A., Lindell, Y., Omri, E.: Optimizing semi-honest secure multiparty computation for the internet. In: Weippl, E.R., Katzenbeisser, S., Kruegel, C., Myers, A.C., Halevi, S. (eds.) ACM CCS 2016, pp. 578–590. ACM Press, October 2016
Ben-Efraim, A., Lindell, Y., Omri, E.: Efficient scalable constant-round MPC via garbled circuits. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10625, pp. 471–498. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70697-9_17
Beaver, D., Micali, S., Rogaway, P.: The round complexity of secure protocols (extended abstract). In: 22nd ACM STOC, pp. 503–513. ACM Press, May 1990
Ben-Efraim, A., Omri, E.: Concrete efficiency improvements for multiparty garbling with an honest majority. In: Latincrypt 2017 (2017)
Ben-Or, M., Goldwasser, S., Wigderson, A.: Completeness theorems for non-cryptographic fault-tolerant distributed computation (extended abstract). In: 20th ACM STOC, pp. 1–10. ACM Press, May 1988
Bracha, G.: An \(O(\operatorname{lg} n)\) expected rounds randomized byzantine generals protocol. In: 17th ACM STOC, pp. 316–326. ACM Press, May 1985
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: 42nd FOCS, pp. 136–145. IEEE Computer Society Press, October 2001
Chaum, D., Crépeau, C., Damgård, I.: Multiparty unconditionally secure protocols (extended abstract). In: 20th ACM STOC, pp. 11–19. ACM Press, May 1988
Dessouky, G., Koushanfar, F., Sadeghi, A.-R., Schneider, T., Zeitouni, S., Zohner, M.: Pushing the communication barrier in secure computation using lookup tables. In: NDSS (2017)
Dingledine, R., Mathewson, N., Syverson, P.F.: Tor: the second-generation onion router. In: USENIX, pp. 303–320 (2004)
Damgård, I., Nielsen, J.B.: Scalable and unconditionally secure multiparty computation. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 572–590. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_32
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: Mitzenmacher, M. (ed.) 41st ACM STOC, pp. 169–178. ACM Press, May/June 2009
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game or a completeness theorem for protocols with honest majority. In: Aho, A. (ed.) 19th ACM STOC, pp. 218–229. ACM Press, May 1987
Goldreich, O.: The Foundations of Cryptography - Volume 2, Basic Applications. Cambridge University Press, Cambridge (2004)
Hazay, C., Orsini, E., Scholl, P., Soria-Vazquez, E.: Efficient MPC from syndrome decoding (or: Honey, I shrunk the keys) (2018). https://eprint.iacr.org/2018/208
Hazay, C., Scholl, P., Soria-Vazquez, E.: Low cost constant round MPC combining BMR and oblivious transfer. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10624, pp. 598–628. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70694-8_21
Ishai, Y., Kilian, J., Nissim, K., Petrank, E.: Extending oblivious transfers efficiently. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 145–161. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_9
Kolesnikov, V., Kumaresan, R.: Improved OT extension for transferring short secrets. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 54–70. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_4
Kolesnikov, V., Mohassel, P., Rosulek, M.: FleXOR: flexible garbling for XOR gates that beats free-XOR. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part II. LNCS, vol. 8617, pp. 440–457. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_25
Kolesnikov, V., Schneider, T.: Improved garbled circuit: free XOR gates and applications. In: Aceto, L., Damgård, I., Goldberg, L.A., Halldórsson, M.M., Ingólfsdóttir, A., Walukiewicz, I. (eds.) ICALP 2008, Part II. LNCS, vol. 5126, pp. 486–498. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-70583-3_40
Lindell, Y., Pinkas, B., Smart, N.P., Yanai, A.: Efficient constant round multi-party computation combining BMR and SPDZ. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part II. LNCS, vol. 9216, pp. 319–338. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_16
Lindell, Y., Smart, N.P., Soria-Vazquez, E.: More efficient constant-round multi-party computation from BMR and SHE. In: Hirt, M., Smith, A. (eds.) TCC 2016, Part I. LNCS, vol. 9985, pp. 554–581. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53641-4_21
Nielsen, J.B., Ranellucci, S.: On the computational overhead of MPC with dishonest majority. In: Fehr, S. (ed.) PKC 2017, Part II. LNCS, vol. 10175, pp. 369–395. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54388-7_13
Tate, S.R., Xu, K.: On garbled circuits and constant round secure function evaluation. CoPS Lab, University of North Texas, Technical report 2:2003 (2003)
Yao, A.C.-C.: How to generate and exchange secrets (extended abstract). In: 27th FOCS, pp. 162–167. IEEE Computer Society Press, October 1986
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Hazay, C., Orsini, E., Scholl, P., Soria-Vazquez, E. (2018). TinyKeys: A New Approach to Efficient Multi-Party Computation. In: Shacham, H., Boldyreva, A. (eds) Advances in Cryptology – CRYPTO 2018. CRYPTO 2018. Lecture Notes in Computer Science(), vol 10993. Springer, Cham. https://doi.org/10.1007/978-3-319-96878-0_1
Download citation
DOI: https://doi.org/10.1007/978-3-319-96878-0_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96877-3
Online ISBN: 978-3-319-96878-0
eBook Packages: Computer ScienceComputer Science (R0)














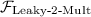 -hybrid implementation (Fig.
-hybrid implementation (Fig. 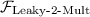 in order to multiply it with a secret-shared bit
in order to multiply it with a secret-shared bit 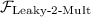 , similarly to the
, similarly to the 





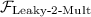 and
and 