Abstract
We present an extension of propositional dynamic logic called HOT-PDL for specifying temporal properties of higher-order functional programs. The semantics of HOT-PDL is defined over Higher-Order Traces (HOTs) that model execution traces of higher-order programs. A HOT is a sequence of events such as function calls and returns, equipped with two kinds of pointers inspired by the notion of justification pointers from game semantics: one for capturing the correspondence between call and return events, and the other for capturing higher-order control flow involving a function that is passed to or returned by a higher-order function. To allow traversal of the new kinds of pointers, HOT-PDL extends PDL with new path expressions. The extension enables HOT-PDL to specify interesting properties of higher-order programs, including stack-based access control properties and those definable using dependent refinement types. We show that HOT-PDL model checking of higher-order functional programs over bounded integers is decidable via a reduction to modal \(\mu \)-calculus model checking of higher-order recursion schemes.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Propositional Dynamic Logic (PDL)
- Higher-order Functional Programs
- Higher Order Trace (HOTs)
- Higher-order Recursion Schemes (HORS)
- Model Execution Traces
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Temporal verification of higher-order programs has been an emerging research topic [12, 14, 18, 22,23,24, 26, 27, 31, 34]. The specification languages used there are (\(\omega \)-)regular word languages (that subsume LTL) [12, 18, 26] and modal \(\mu \)-calculus (that subsumes CTL) [14, 24, 31], which are interpreted over sequences or trees consisting of events. (Extended) dependent refinement types are also used to specify temporal [23, 27] and branching properties [34]. These specification languages, however, cannot sufficiently express specifications of control flow involving (higher-order) functions. For example, let us consider the following simple higher-order program \(D_{\mathtt {tw}}\) (in OCaml syntax):

Here, \(*\) denotes a non-deterministic integer, and the higher-order function \(\mathtt {tw}:(\mathtt {int}\rightarrow \mathtt {int}) \rightarrow \mathtt {int}\rightarrow \mathtt {int}\) applies its function argument \(\mathtt {f}:\mathtt {int}\rightarrow \mathtt {int}\) to the integer argument \(\mathtt {x}\) twice. For example, for \(\mathtt {r}=0\), the program \(D_{\mathtt {tw}}\) exhibits the following call-by-value reduction sequence (with the redexes underlined).
Example properties of the program \(D_{\mathtt {tw}}\) that cannot be expressed by the previous specification languages are:
-
Prop.1.
If the function returned by a partial application of \(\mathtt {tw}\) to some function (e.g., \(\lambda x.\mathtt {inc}\ (\mathtt {inc}\ x)\) in the above sequence) is called with some integer n, the function argument passed to \(\mathtt {tw}\) (i.e., \(\mathtt {inc}\)) is eventually called with n.
-
Prop.2.
If the function returned by a partial application of \(\mathtt {tw}\) to some function is never called, then the function argument passed to \(\mathtt {tw}\) is never called.
To remedy the limitation, we introduce a notion of Higher-Order Trace (HOT) that captures the control flow of higher-order programs and propose a dynamic logic over HOTs called Higher-Order Trace Propositional Dynamic Logic (HOT-PDL) for specifying temporal properties of higher-order programs.
Intuitively, a HOT models a program execution trace which is a possibly infinite sequence of events such as function calls and returns with information about actual arguments and return values. Furthermore, HOTs are equipped with two kinds of pointers to enable precise specification of control flow: one for capturing the correspondence between call and return events, and the other for capturing higher-order control flow involving a function that is passed to or returned by a higher-order function. The two kinds of pointers are inspired by the notion of justification pointers from the game semantics of PCF [1, 2, 19, 20].
For the higher-order program \(D_{\mathtt {tw}}\), for \(\mathtt {r}=0\), we get the following HOT \(G_{\mathtt {tw}}\):Footnote 1

Here, \(\bullet \) represents some function value, \(\mathbf {call}(f,v)\) represents a call event of the function f with the argument v, and \(\mathbf {ret}(f,v)\) represents a return event of the function f with the return value v. This trace corresponds to the previous reduction sequence: the call events \(\mathbf {call}(\mathtt {tw},\bullet )\), \(\mathbf {call}(\bullet ,0)\), \(\mathbf {call}(\bullet ,0)\), and \(\mathbf {call}(\bullet ,1)\) that occur in the trace in this order correspond respectively to the redexes \(\mathtt {tw}\ \mathtt {inc}\), \((\lambda x.\mathtt {inc}\ (\mathtt {inc}\ x))\ 0\), \(\mathtt {inc}\ 0\), and \(\mathtt {inc}\ 1\). The three important points here are that (1) the call events have pointers labeled with  to the corresponding return events \(\mathbf {ret}(\mathtt {tw},\bullet )\), \(\mathbf {ret}(\bullet ,2)\), \(\mathbf {ret}(\bullet ,1)\), and \(\mathbf {ret}(\bullet ,2)\), (2) the call event \(\mathbf {call}(\mathtt {tw},\bullet )\) has two pointers labeled with
to the corresponding return events \(\mathbf {ret}(\mathtt {tw},\bullet )\), \(\mathbf {ret}(\bullet ,2)\), \(\mathbf {ret}(\bullet ,1)\), and \(\mathbf {ret}(\bullet ,2)\), (2) the call event \(\mathbf {call}(\mathtt {tw},\bullet )\) has two pointers labeled with  , where \(\bullet \) represents the function argument \(\mathtt {f}\) of \(\mathtt {tw}\) and the pointed call events \(\mathbf {call}(\bullet ,0)\) and \(\mathbf {call}(\bullet ,1)\) represent the two calls to \(\mathtt {f}\) in \(\mathtt {tw}\), and (3) the return event \(\mathbf {ret}(\mathtt {tw},\bullet )\) has a pointer labeled with
, where \(\bullet \) represents the function argument \(\mathtt {f}\) of \(\mathtt {tw}\) and the pointed call events \(\mathbf {call}(\bullet ,0)\) and \(\mathbf {call}(\bullet ,1)\) represent the two calls to \(\mathtt {f}\) in \(\mathtt {tw}\), and (3) the return event \(\mathbf {ret}(\mathtt {tw},\bullet )\) has a pointer labeled with  , where \(\bullet \) represents the partially-applied function \(\lambda x.\mathtt {inc}\ (\mathtt {inc}\ x)\) and the pointed call event \(\mathbf {call}(\bullet ,0)\) represents the call to the function.
, where \(\bullet \) represents the partially-applied function \(\lambda x.\mathtt {inc}\ (\mathtt {inc}\ x)\) and the pointed call event \(\mathbf {call}(\bullet ,0)\) represents the call to the function.
To allow traversal of the pointers, HOT-PDL extends propositional dynamic logic with new path expressions (see Sect. 3 for details). The extension enables HOT-PDL to specify interesting properties of higher-order programs, including stack-based access control properties and those definable using dependent refinement types. Here, stack-based access control is a security mechanism implemented in runtimes like JVM for ensuring secure execution of programs that have components with different levels of trust: the mechanism ensures that a security-critical function (e.g., file access) is invoked only if all the (immediate and indirect) callers in the current call stack are trusted, or one of the callers is a privileged function and its callees are all trusted. We introduce a new variant of stack-based access control properties for higher-order programs, formalized in HOT-PDL from the point of view of interactions among callers and callees.
Compared to the previous specification languages with respect to the expressiveness, HOT-PDL subsumes (\(\omega \)-)regular languages because PDL interpreted over words is already as expressive as them [15]. Temporal logics over nested words [6] such as CaRet [5] and NWTL [4] can capture the correspondence between call and return events (i.e., pointers labeled with  ) but cannot capture higher-order control flow (i.e., pointers labeled with
) but cannot capture higher-order control flow (i.e., pointers labeled with  and
and  ). Branching properties (expressible in, e.g., CTL), however, are out of the scope of the present paper, and such an extension of HOT-PDL remains an interesting future direction. Dependent refinement types are often used to specify properties of higher-order programs for partial- and total-correctness verification [29, 33, 39, 40]. For example, the following properties of the program \(D_{\mathtt {tw}}\) are expressible:
). Branching properties (expressible in, e.g., CTL), however, are out of the scope of the present paper, and such an extension of HOT-PDL remains an interesting future direction. Dependent refinement types are often used to specify properties of higher-order programs for partial- and total-correctness verification [29, 33, 39, 40]. For example, the following properties of the program \(D_{\mathtt {tw}}\) are expressible:
-
Prop.3.
The function yielded by applying \(\mathtt {tw}\) to a strictly increasing function is strictly increasing.
-
Prop.4.
The function yielded by applying \(\mathtt {tw}\) to a terminating function is terminating.
This paper shows that HOT-PDL can encode such dependent refinement types.
We also study HOT-PDL model checking: given a higher-order program D over bounded integers and a HOT-PDL formula \(\phi \), the problem is to decide whether \(\phi \) is satisfied by all the execution traces of D modeled as HOTs. We show the decidability of HOT-PDL model checking via a reduction to modal \(\mu \)-calculus model checking of higher-order recursion schemes [21, 28].
The rest of the paper is organized as follows. Section 2 formalizes HOTs and explains how to use them to model execution traces of higher-order functional programs. Section 3 defines the syntax and the semantics of HOT-PDL and Sect. 4 shows how to encode stack-based access control properties and dependent refinement types in HOT-PDL. Section 5 discusses HOT-PDL model checking. We compare HOT-PDL with related work in Sect. 6 and conclude the paper with remarks on future work in Sect. 7. Omitted proofs are given in the extended version of this paper [30].
2 Higher-Order Traces
This section defines the notion of Higher-Order Trace (HOT), which is used to model execution traces of higher-order programs. To this end, we first define \((\varSigma , \varGamma )\)-labeled directed graphs and DAGs.
Definition 1
(\((\varSigma , \varGamma )\)-labeled directed graphs). Let \(\varSigma \) be a finite set of node labels and \(\varGamma \) be a finite set of edge labels. A \((\varSigma , \varGamma )\)-labeled directed graph is defined as a triple \((V, \lambda , \nu )\), where V is a countable set of nodes, \(\lambda : V \rightarrow \varSigma \) is a node labeling function, and \(\nu : V \times V \rightarrow 2^{\varGamma }\) is an edge labeling function. We call a \((\varSigma , \varGamma )\)-labeled directed graph that has no directed cycle \((\varSigma , \varGamma )\)-labeled DAG.
Note that an edge may have multiple labels. For nodes \(u,u'\in V\), \(\nu (u,u')=\emptyset \) means that there is no edge from u to \(u'\). We use \(\sigma \) and \(\gamma \) as meta-variables ranging respectively over \(\varSigma \) and \(\varGamma \). We write \(V_{\sigma }\) for the set \(\left\{ u \in V \mid \sigma = \lambda (u)\right\} \) of all the nodes labeled with \(\sigma \). We also write \(V_{\varSigma }\) for the set \(\bigcup _{\sigma \in \varSigma } V_{\sigma }\). For \(u, u' \in V\), we write \(u \prec _{\gamma } u'\) if \(\gamma \in \nu (u, u')\). A binary relation \(\prec _{\gamma }^+\) (resp. \(\prec _{\gamma }^*\)) denotes the transitive (resp. reflexive and transitive) closure of \(\prec _{\gamma }\).
Definition 2
(HOTs). A HOT is a \((\varSigma , \varGamma )\)-DAG, \(G = (V, \lambda , \nu )\) that satisfies:
-
1.
\(V \ne \emptyset \),
 , \(\varSigma =\varSigma _{\mathbf {call}}\uplus \varSigma _{\mathbf {ret}}\), and \(\varSigma _{\mathbf {call}}= \varSigma _{\mathbf {call}}^{T}\uplus \varSigma _{\mathbf {call}}^{A}\)
, \(\varSigma =\varSigma _{\mathbf {call}}\uplus \varSigma _{\mathbf {ret}}\), and \(\varSigma _{\mathbf {call}}= \varSigma _{\mathbf {call}}^{T}\uplus \varSigma _{\mathbf {call}}^{A}\) -
2.
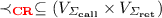 ,
, 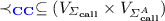 , and
, and  .
. -
3.
The elements of V are linearly ordered by \(\prec _{\mathbf {N}}\)
-
4.
If
 and
and  , then \(u'=u''\).
, then \(u'=u''\). -
5.
For all \(u'\in V_{\varSigma _{\mathbf {ret}}}\), there uniquely exists \(u\in V_{\varSigma _{\mathbf {call}}}\) such that
 holds.
holds. -
6.
For all \(u'\in V_{\varSigma _{\mathbf {call}}^{A}}\), there uniquely exists \(u\in V\) such that
 or
or  holds.
holds.
Intuitively, \(\varSigma _{\mathbf {call}}\) (resp. \(\varSigma _{\mathbf {ret}}\)) represents a set of call (resp. return) events. \(\varSigma _{\mathbf {call}}^{T}\) (resp. \(\varSigma _{\mathbf {call}}^{A}\)) represents a set of call events of top-level functions (resp. functions that are returned by or passed to (higher-order) functions). \(u \prec _{\mathbf {N}} u'\) means that \(u'\) is the next event of u in the trace.  indicates that \(u'\) is the return event corresponding to the call event u.
indicates that \(u'\) is the return event corresponding to the call event u.  represents that \(u'\) is a call event of the function argument passed at the call event u.
represents that \(u'\) is a call event of the function argument passed at the call event u.  means that \(u'\) is a call event of the partially-applied function returned at the return event u. We call the minimum node of a HOT G with respect to \(\prec _{\mathbf {N}}\) the root node, denoted by \(0_G\). For HOTs \(G_1\) and \(G_2\), we say \(G_1\) is a prefix of \(G_2\) and write \(G_1 \preceq G_2\), if \(G_1\) is a sub-graph of \(G_2\) such that \(0_{G_1} = 0_{G_2}\). Note that the HOT \(G_{\mathtt {tw}}\) in Sect. 1, where \(\mathbf {N}\)-labeled edges are omitted, satisfies the above conditions, with \(\left\{ \mathbf {call}(\mathtt {tw},\bullet ), \mathbf {call}(\mathtt {inc},0), \mathbf {call}(\mathtt {inc},1)\right\} \subseteq \varSigma _{\mathbf {call}}^{T}\), \(\left\{ \mathbf {call}(\bullet ,0), \mathbf {call}(\bullet ,1)\right\} \subseteq \varSigma _{\mathbf {call}}^{A}\), and \(\left\{ \mathbf {ret}(\mathtt {tw},\bullet ), \mathbf {ret}(\mathtt {inc},1), \mathbf {ret}(\mathtt {inc},2), \mathbf {ret}(\bullet ,1), \mathbf {ret}(\bullet ,2)\right\} \subseteq \varSigma _{\mathbf {ret}}\).
means that \(u'\) is a call event of the partially-applied function returned at the return event u. We call the minimum node of a HOT G with respect to \(\prec _{\mathbf {N}}\) the root node, denoted by \(0_G\). For HOTs \(G_1\) and \(G_2\), we say \(G_1\) is a prefix of \(G_2\) and write \(G_1 \preceq G_2\), if \(G_1\) is a sub-graph of \(G_2\) such that \(0_{G_1} = 0_{G_2}\). Note that the HOT \(G_{\mathtt {tw}}\) in Sect. 1, where \(\mathbf {N}\)-labeled edges are omitted, satisfies the above conditions, with \(\left\{ \mathbf {call}(\mathtt {tw},\bullet ), \mathbf {call}(\mathtt {inc},0), \mathbf {call}(\mathtt {inc},1)\right\} \subseteq \varSigma _{\mathbf {call}}^{T}\), \(\left\{ \mathbf {call}(\bullet ,0), \mathbf {call}(\bullet ,1)\right\} \subseteq \varSigma _{\mathbf {call}}^{A}\), and \(\left\{ \mathbf {ret}(\mathtt {tw},\bullet ), \mathbf {ret}(\mathtt {inc},1), \mathbf {ret}(\mathtt {inc},2), \mathbf {ret}(\bullet ,1), \mathbf {ret}(\bullet ,2)\right\} \subseteq \varSigma _{\mathbf {ret}}\).
2.1 Trace Semantics for Higher-Order Functional Programs
We now formalize our target language \(\mathcal {L}\), which is an ML-like typed call-by-value higher-order functional language. The syntax is defined by
Here, x and f are meta-variables ranging respectively over term variables and names of top-level functions. The meta-variable n ranges over the set of bounded integers \(\mathbb {Z}_{b}=\left\{ n_{\mathbf {min}}, \cdots , n_{\mathbf {max}}\right\} \subset \mathbb {Z}\). For simplicity of presentation, \(\mathcal {L}\) has the type \(\mathtt {int}\) of bounded integers as the only base type. \(\mathtt {op}\) represents binary operators such as \(+\), −, \(\times \), \(=\), and >. The binary relations \(=\) and > return an integer that encodes a boolean value (e.g., 1 for \(\mathtt {true}\) and 0 for \(\mathtt {false}\)). A program D maps each top-level function name \(f_i\) to its definition \(\lambda x.e_i\). We write \(\mathrm {dom}(D)\) for \(\left\{ f_1,\dots ,f_m\right\} \). We assume that D has the main function \(\mathtt {main}\) of the type \(\mathtt {int}\rightarrow \mathtt {int}\). The functions in D can be mutually recursive. Expressions e comprise variables x, function names f, lambda abstractions \(\lambda x. e\), function applications \(e_1\ e_2\), bounded integers n, binary operations \(\mathtt {op}(v_1, v_2)\), and conditional branches \(\mathtt {ifz}\ e_1\ e_2\ e_3\). We assume that expressions are simply-typed. As usual, the simple type system guarantees that an evaluation of a typed expression never causes a runtime type mismatch like \(1 + \lambda x.x\). An expression \(\mathtt {ifz}\ e_1\ e_2\ e_3\) evaluates to \(e_2\) (resp. \(e_3\)) if \(e_1\) evaluates to 0 (resp. a non-zero integer). For example, the program \(D_{\mathtt {tw}}\) in Sect. 1 is defined in \(\mathcal {L}\) as follows:
We now introduce a trace semantics of the language \(\mathcal {L}\), which will be used in Sect. 5 to define our model checking problems of higher-order programs. In the trace semantics, a program execution trace is represented by a sequence of function call and return events without an explicit representation of pointers but with enough information to construct them. We will explain how to model traces of \(\mathcal {L}\) as HOTs by presenting a translation.
The trace semantics \(\mathbin {[\![D]\!]}\) of the language \(\mathcal {L}\) is defined as \(\mathbin {[\![D]\!]}_{\mathtt {fin}} \cup \mathbin {[\![D]\!]}_{\mathtt {inf}}\) where  and
and  are respectively the sets of finite and infinite execution traces obtained by evaluating \(\mathtt {main}\ n\) for some integer n using trace-labeled multi-step reduction relations
are respectively the sets of finite and infinite execution traces obtained by evaluating \(\mathtt {main}\ n\) for some integer n using trace-labeled multi-step reduction relations  and
and  , which are presented in Fig. 1, under the program
, which are presented in Fig. 1, under the program  annotated with the number of calls to each function occurred so far (i.e., initialized to 0). There, we use \(\varpi \) (resp. \(\uppi \)) as a meta-variable ranging over finite sequences \(\alpha _1 \cdots \alpha _m\) (resp. infinite sequences \(\alpha _1 \cdot \alpha _2 \cdots \)) of events \(\alpha _i\). We write \(\epsilon \) for the empty sequence, \(\varpi _1 \cdot \varpi _2\) for the concatenation of the sequences \(\varpi _1\) and \(\varpi _2\), and \(|\varpi |\) for the length of \(\varpi \). An event \(\alpha \) is either of the form \(\mathbf {call}(h_1, i, h_2)\) or \(\mathbf {ret}(h_1, i, h_2)\), where a handle h represents a top-level function or a runtime value exchanged among functions. An event \(\mathbf {call}(h_1, i, h_2)\) represents the \((i+1)^{\mathrm {th}}\) call to the function \(h_1\) with the argument \(h_2\). On the other hand, an event \(\mathbf {ret}(h_1, i, h_2)\) represents the return of the \((i+1)^{\mathrm {th}}\) call to the function \(h_1\) with the return value \(h_2\). We thus equip call and return events of \(h_1\) with the information about (1) the number i of the calls to \(h_1\) occurred so far and (2) the runtime value \(h_2\) passed to or returned by \(h_1\), so that we can construct pointers (see Definition 3 for details). Note here that handles h are also equipped with meta-information necessary for constructing pointers. More specifically, h is any of the following: a bounded integer n, a top-level function name \(f \in \mathrm {dom}(D)\), the special identifier \(\left\lfloor h\right\rfloor _{i}\) for the function argument of the \((i+1)^{\mathrm {th}}\) call to the higher-order function h, or the special identifier \(\left\lceil h\right\rceil _{i}\) for the partially-applied function returned by the \((i+1)^{\mathrm {th}}\) call to h. We thus use handles to track for each function value where it is constructed and how many times it is called. We shall assume that the syntax of expressions e and values v is also extended with handles h. As we have seen, the finite traces \(\mathbin {[\![D]\!]}_{\mathtt {fin}}\) of a program D are collected using the terminating trace-labeled multi-step reduction relation
annotated with the number of calls to each function occurred so far (i.e., initialized to 0). There, we use \(\varpi \) (resp. \(\uppi \)) as a meta-variable ranging over finite sequences \(\alpha _1 \cdots \alpha _m\) (resp. infinite sequences \(\alpha _1 \cdot \alpha _2 \cdots \)) of events \(\alpha _i\). We write \(\epsilon \) for the empty sequence, \(\varpi _1 \cdot \varpi _2\) for the concatenation of the sequences \(\varpi _1\) and \(\varpi _2\), and \(|\varpi |\) for the length of \(\varpi \). An event \(\alpha \) is either of the form \(\mathbf {call}(h_1, i, h_2)\) or \(\mathbf {ret}(h_1, i, h_2)\), where a handle h represents a top-level function or a runtime value exchanged among functions. An event \(\mathbf {call}(h_1, i, h_2)\) represents the \((i+1)^{\mathrm {th}}\) call to the function \(h_1\) with the argument \(h_2\). On the other hand, an event \(\mathbf {ret}(h_1, i, h_2)\) represents the return of the \((i+1)^{\mathrm {th}}\) call to the function \(h_1\) with the return value \(h_2\). We thus equip call and return events of \(h_1\) with the information about (1) the number i of the calls to \(h_1\) occurred so far and (2) the runtime value \(h_2\) passed to or returned by \(h_1\), so that we can construct pointers (see Definition 3 for details). Note here that handles h are also equipped with meta-information necessary for constructing pointers. More specifically, h is any of the following: a bounded integer n, a top-level function name \(f \in \mathrm {dom}(D)\), the special identifier \(\left\lfloor h\right\rfloor _{i}\) for the function argument of the \((i+1)^{\mathrm {th}}\) call to the higher-order function h, or the special identifier \(\left\lceil h\right\rceil _{i}\) for the partially-applied function returned by the \((i+1)^{\mathrm {th}}\) call to h. We thus use handles to track for each function value where it is constructed and how many times it is called. We shall assume that the syntax of expressions e and values v is also extended with handles h. As we have seen, the finite traces \(\mathbin {[\![D]\!]}_{\mathtt {fin}}\) of a program D are collected using the terminating trace-labeled multi-step reduction relation  on configurations. A configuration (I, E[e]) is a pair of an interface I and an expression E[e] consisting of an evaluation context E and a sub-expression e under evaluation. A special evaluation context \(\mathtt {ret}(h,i,E)\) represents the calling context of the \((i+1)^{\mathrm {th}}\) call to h that waits for the return value computed by E. An interface I is defined to be
on configurations. A configuration (I, E[e]) is a pair of an interface I and an expression E[e] consisting of an evaluation context E and a sub-expression e under evaluation. A special evaluation context \(\mathtt {ret}(h,i,E)\) represents the calling context of the \((i+1)^{\mathrm {th}}\) call to h that waits for the return value computed by E. An interface I is defined to be  that maps each function handle \(h_j\) to its definition \(v_j\), where \(i_j\) records the number of calls to the function \(h_j\) occurred so far. In the derivation rules for \(\xrightarrow {\varpi }_{}\), \(\mathbin {[\![\mathtt {op}]\!]}\) represents the integer function denoted by \(\mathtt {op}\), and
that maps each function handle \(h_j\) to its definition \(v_j\), where \(i_j\) records the number of calls to the function \(h_j\) occurred so far. In the derivation rules for \(\xrightarrow {\varpi }_{}\), \(\mathbin {[\![\mathtt {op}]\!]}\) represents the integer function denoted by \(\mathtt {op}\), and  represents the interface obtained from I by adding (or replacing existing assignment to h with) the assignment
represents the interface obtained from I by adding (or replacing existing assignment to h with) the assignment  . In the rule
. In the rule  (resp.
(resp.  ) for function calls (resp. returns) with an integer n, the reduction relation is labeled with \(\mathbf {call}(h, i, n)\) (resp. \(\mathbf {ret}(h, i, n)\)). By contrast, in the rule
) for function calls (resp. returns) with an integer n, the reduction relation is labeled with \(\mathbf {call}(h, i, n)\) (resp. \(\mathbf {ret}(h, i, n)\)). By contrast, in the rule  (resp.
(resp.  ) for function calls (resp. returns) with a function value v, the special identifier \(\left\lfloor h\right\rfloor _{i}\) (resp. \(\left\lceil h\right\rceil _{i}\)) for v is used in the label \(\mathbf {call}(h, i, \left\lfloor h\right\rfloor _{i})\) (resp. \(\mathbf {ret}(h, i, \left\lceil h\right\rceil _{i})\)) of the reduction relation, and v in the expression is replaced by the identifier. For example, as shown in Fig. 2, the following finite trace \(\varpi _{\mathtt {tw}}\) is generated from the program \(D_{\mathtt {tw}}\):
) for function calls (resp. returns) with a function value v, the special identifier \(\left\lfloor h\right\rfloor _{i}\) (resp. \(\left\lceil h\right\rceil _{i}\)) for v is used in the label \(\mathbf {call}(h, i, \left\lfloor h\right\rfloor _{i})\) (resp. \(\mathbf {ret}(h, i, \left\lceil h\right\rceil _{i})\)) of the reduction relation, and v in the expression is replaced by the identifier. For example, as shown in Fig. 2, the following finite trace \(\varpi _{\mathtt {tw}}\) is generated from the program \(D_{\mathtt {tw}}\):
Similarly, the infinite traces \(\mathbin {[\![D]\!]}_{\mathtt {inf}}\) of a program D are collected using the non-terminating trace-labeled reduction relation  on configurations. Intuitively,
on configurations. Intuitively,  means that an execution from the configuration C diverges, producing an infinite event sequence \(\uppi \). In the rule
means that an execution from the configuration C diverges, producing an infinite event sequence \(\uppi \). In the rule  , the double horizontal line represents that the rule is interpreted co-inductively.
, the double horizontal line represents that the rule is interpreted co-inductively.
We now define the translation from traces \(\mathbin {[\![D]\!]}_{\mathtt {fin}}\) to HOTs with  ,
,  , and \(\varSigma _{\mathbf {ret}}=\left\{ \mathbf {ret}(f,n),\mathbf {ret}(f,\bullet ),\mathbf {ret}(\bullet ,n),\mathbf {ret}(\bullet ,\bullet ) \mid f \in \mathrm {dom}(D),n \in \mathbb {Z}_{b}\right\} \). We shall write \(\varSigma (D)\) for \(\varSigma _{\mathbf {call}}^{T}\cup \varSigma _{\mathbf {call}}^{A}\cup \varSigma _{\mathbf {ret}}\). Note that \(\varSigma (D)\) is finite because \(\mathrm {dom}(D)\) and \(\mathbb {Z}_{b}\) are finite. We write \(|\alpha |\) for the element of \(\varSigma (D)\) obtained from the event \(\alpha \) by dropping the second argument and replacing \(\left\lfloor h\right\rfloor _{i}\) and \(\left\lceil h\right\rceil _{i}\) by \(\bullet \). For example, we get \(|\mathbf {call}(\mathtt {tw}, 0, \left\lfloor \mathtt {tw}\right\rfloor _{0})| = \mathbf {call}(\mathtt {tw},\bullet )\).
, and \(\varSigma _{\mathbf {ret}}=\left\{ \mathbf {ret}(f,n),\mathbf {ret}(f,\bullet ),\mathbf {ret}(\bullet ,n),\mathbf {ret}(\bullet ,\bullet ) \mid f \in \mathrm {dom}(D),n \in \mathbb {Z}_{b}\right\} \). We shall write \(\varSigma (D)\) for \(\varSigma _{\mathbf {call}}^{T}\cup \varSigma _{\mathbf {call}}^{A}\cup \varSigma _{\mathbf {ret}}\). Note that \(\varSigma (D)\) is finite because \(\mathrm {dom}(D)\) and \(\mathbb {Z}_{b}\) are finite. We write \(|\alpha |\) for the element of \(\varSigma (D)\) obtained from the event \(\alpha \) by dropping the second argument and replacing \(\left\lfloor h\right\rfloor _{i}\) and \(\left\lceil h\right\rceil _{i}\) by \(\bullet \). For example, we get \(|\mathbf {call}(\mathtt {tw}, 0, \left\lfloor \mathtt {tw}\right\rfloor _{0})| = \mathbf {call}(\mathtt {tw},\bullet )\).
Definition 3
(Finite Traces to HOTs). Given a finite trace \(\varpi = \alpha _1 \cdots \alpha _m \in \mathbin {[\![D]\!]}_{\mathtt {fin}}\) with \(m>0\), the corresponding HOT \(G_{\varpi }=(V_{\varpi }, \lambda _{\varpi }, \nu _{\varpi })\) is defined by:
-
\(V_{\varpi } = \left\{ 1, \dots ,m\right\} \),
-
\(\lambda _{\varpi } = \left\{ j \mapsto |\alpha _j| \mid j \in V_{\varpi }\right\} \), and
-
\(\nu _{\varpi }\) is the smallest relation that satisfies: for any \(j_1,j_2 \in V_{\varpi }\),
-
\(j_1 \prec _{\mathbf {N}} j_2\) if \(j_2=j_1+1\),
-
 if \(\exists h,h',h'',i.\ \alpha _{j_1}=\mathbf {call}(h, i, h') \wedge \alpha _{j_2}=\mathbf {ret}(h, i, h'')\),
if \(\exists h,h',h'',i.\ \alpha _{j_1}=\mathbf {call}(h, i, h') \wedge \alpha _{j_2}=\mathbf {ret}(h, i, h'')\), -
 if \(\exists h,h',h'',i,i'.\ \alpha _{j_1}=\mathbf {call}(h', i, h) \wedge \alpha _{j_2}=\mathbf {call}(h, i', h'')\),
if \(\exists h,h',h'',i,i'.\ \alpha _{j_1}=\mathbf {call}(h', i, h) \wedge \alpha _{j_2}=\mathbf {call}(h, i', h'')\), -
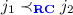 if \(\exists h,h',h'',i,i'.\ \alpha _{j_1}=\mathbf {ret}(h', i, h) \wedge \alpha _{j_2}=\mathbf {call}(h, i', h'')\).
if \(\exists h,h',h'',i,i'.\ \alpha _{j_1}=\mathbf {ret}(h', i, h) \wedge \alpha _{j_2}=\mathbf {call}(h, i', h'')\).
-
For example, the HOT \(G_{\mathtt {tw}}\) in Sect. 1 is translated from the finite trace \(\varpi _{\mathtt {tw}}\) defined above (with the call and return events of \(\mathtt {main}\) omitted).
For an infinite trace \(\uppi = \alpha _1\cdot \alpha _2\cdots \in \mathbin {[\![D]\!]}_{\mathtt {inf}}\), the HOT \(G_{\uppi } = (V_{\uppi }, \lambda _{\uppi }, \nu _{\uppi })\) is defined similarly for  and \(\lambda _{\uppi } = \left\{ j \mapsto |\alpha _j| \mid j \in V_{\uppi }\right\} \).
and \(\lambda _{\uppi } = \left\{ j \mapsto |\alpha _j| \mid j \in V_{\uppi }\right\} \).
3 Propositional Dynamic Logic over Higher-Order Traces
This section presents HOT-PDL, a propositional dynamic logic (PDL) defined over HOTs (see [16] for a general exposition of PDL). HOT-PDL extends path expressions of PDL with  and
and  for traversing edges of HOTs labeled respectively with
for traversing edges of HOTs labeled respectively with  and
and  /
/ . The syntax is defined by:
. The syntax is defined by:

Here, p is a meta-variable ranging over atomic propositions \(\mathcal {AP}\). Let \(\top \) and \(\bot \) denote tautology and contradiction, respectively. Path expressions \(\pi \) are defined using a syntax based on regular expressions: we have concatenation \(\pi _1\cdot \pi _2\), alternation \(\pi _1 + \pi _2\), and Kleene star \(\pi ^*\). We write \(\pi ^+\) for \(\pi \cdot \pi ^*\). Path expressions \(\rightarrow \),  , and
, and  are for traversing edges labeled with \(\mathbf {N}\),
are for traversing edges labeled with \(\mathbf {N}\),  , and
, and  or
or  , respectively. A path expression \(\left\{ \phi \right\} ?\) is for testing if \(\phi \) holds at the current node. A formula \(\left[ \pi \right] \phi \) means that \(\phi \) always holds if one moves along any path represented by the path expression \(\pi \). The dual formula \(\left\langle \pi \right\rangle \phi \) is defined by \(\lnot \left[ \pi \right] \lnot \phi \) and means that there is a path represented by \(\pi \) such that \(\phi \) holds if one moves along the path. \(\left\langle \pi \right\rangle \) and \(\left[ \pi \right] \) have the same priority as \(\lnot \).
, respectively. A path expression \(\left\{ \phi \right\} ?\) is for testing if \(\phi \) holds at the current node. A formula \(\left[ \pi \right] \phi \) means that \(\phi \) always holds if one moves along any path represented by the path expression \(\pi \). The dual formula \(\left\langle \pi \right\rangle \phi \) is defined by \(\lnot \left[ \pi \right] \lnot \phi \) and means that there is a path represented by \(\pi \) such that \(\phi \) holds if one moves along the path. \(\left\langle \pi \right\rangle \) and \(\left[ \pi \right] \) have the same priority as \(\lnot \).
We now define the semantics of HOT-PDL. For a given HOT \(G=(V,\lambda ,\nu )\) with \(\varSigma =\mathcal {AP}\), \(\lambda (u)\) represents the atomic proposition satisfied at the node \(u \in V\). We define the semantics \(\mathbin {[\![\phi ]\!]}_G\) of a formula \(\phi \) as the set of all nodes \(u \in V\) where \(\phi \) is satisfied, and the semantics \(\mathbin {[\![\pi ]\!]}_G\) of a path expression \(\pi \) as the set of all pairs \((u_1,u_2) \in V \times V\) such that one can move along \(\pi \) from \(u_1\) to \(u_2\).

Here, for a binary relation R, \(R^m\) denotes the m-th power of R. Note that this semantics can interpret a given HOT-PDL formula over both finite and infinite HOTs. \(\mathbin {[\![p]\!]}_G\) consists of all nodes labeled by p. \(\mathbin {[\![\left[ \pi \right] \phi ]\!]}_G\) contains all nodes from which we always reach to a node in \(\mathbin {[\![\phi ]\!]}_G\) if we take a path represented by \(\pi \). \(\mathbin {[\![\rightarrow ]\!]}_G\),  , and
, and  contain the pairs of nodes linked by an edge labeled by \(\mathbf {N}\),
contain the pairs of nodes linked by an edge labeled by \(\mathbf {N}\),  , and
, and  or
or  , respectively. We write \(G \models \phi \) if \(0_G \in \mathbin {[\![\phi ]\!]}_G\). For example, let us consider the HOT \(G_{\mathtt {tw}}\) and \(\mathcal {AP}=\varSigma (D_{\mathtt {tw}})\). Then, \(\mathbin {[\![\left\langle \rightarrow \right\rangle \mathbf {ret}(\mathtt {tw},\bullet )]\!]}_{G_{\mathtt {tw}}}\) consists of the node labeled by \(\mathbf {call}(\mathtt {tw},\bullet )\).
, respectively. We write \(G \models \phi \) if \(0_G \in \mathbin {[\![\phi ]\!]}_G\). For example, let us consider the HOT \(G_{\mathtt {tw}}\) and \(\mathcal {AP}=\varSigma (D_{\mathtt {tw}})\). Then, \(\mathbin {[\![\left\langle \rightarrow \right\rangle \mathbf {ret}(\mathtt {tw},\bullet )]\!]}_{G_{\mathtt {tw}}}\) consists of the node labeled by \(\mathbf {call}(\mathtt {tw},\bullet )\).  consists of a node labeled by \(\mathbf {call}(\bullet ,0)\) and the node labeled by \(\mathbf {call}(\bullet ,1)\).
consists of a node labeled by \(\mathbf {call}(\bullet ,0)\) and the node labeled by \(\mathbf {call}(\bullet ,1)\).  consists of the two nodes respectively labeled by \(\mathbf {call}(\mathtt {tw},\bullet )\) and \(\mathbf {ret}(\mathtt {tw},\bullet )\). The example properties of \(D_{\mathtt {tw}}\) discussed in Sect. 1 can be expressed as follows:
consists of the two nodes respectively labeled by \(\mathbf {call}(\mathtt {tw},\bullet )\) and \(\mathbf {ret}(\mathtt {tw},\bullet )\). The example properties of \(D_{\mathtt {tw}}\) discussed in Sect. 1 can be expressed as follows:
-
Prop.1.:

-
Prop.2.:

Here, \(\bigwedge _{x \in \mathbb {Z}_{b}}\phi \) abbreviates \(\left[ n_{\mathbf {min}}/x\right] \phi \wedge \dots \wedge \left[ n_{\mathbf {max}}/x\right] \phi \).
In Sect. 4, we show further examples that express interesting properties of higher-order programs, including stack based access control properties and those definable using dependent refinement types. We here prepare notations used there. First, we overload the symbols \(\varSigma _{\mathbf {call}}\), \(\varSigma _{\mathbf {ret}}\), and \(\varSigma _{\mathbf {call}}^{T}\) to denote the path expressions \(\left\{ \bigvee \varSigma _{\mathbf {call}}\right\} ?\), \(\left\{ \bigvee \varSigma _{\mathbf {ret}}\right\} ?\), and \(\left\{ \bigvee \varSigma _{\mathbf {call}}^{T}\right\} ?\), respectively. We write \(\rightarrow _F\) for the path expression  , which is used to move from a call event to the next event of the caller (by skipping to the next event of the corresponding return event). We also write \(\nearrow _F\) for the path expression \(\varSigma _{\mathbf {call}}\cdot \rightarrow \cdot \rightarrow _F^* \cdot \varSigma _{\mathbf {call}}\), which is used to move from a call event to any call event invoked by the callee. Figure 3 illustrates the pairs of nodes in \(G_{\mathtt {tw}}\) related by \(\nearrow _F\). To capture control flow of higher-order programs, where function callers and callees may exchange functions as values, we need to use
, which is used to move from a call event to the next event of the caller (by skipping to the next event of the corresponding return event). We also write \(\nearrow _F\) for the path expression \(\varSigma _{\mathbf {call}}\cdot \rightarrow \cdot \rightarrow _F^* \cdot \varSigma _{\mathbf {call}}\), which is used to move from a call event to any call event invoked by the callee. Figure 3 illustrates the pairs of nodes in \(G_{\mathtt {tw}}\) related by \(\nearrow _F\). To capture control flow of higher-order programs, where function callers and callees may exchange functions as values, we need to use  - and
- and  -labeled edges. For example, an event raised by the function argument \(f_{ arg }\) of a higher-order function f could be regarded as an event of the caller g of f, because \(f_{ arg }\) is constructed by g. Similarly, an event raised by the (partially-applied) function \(f_{ ret }\) returned by a function f could be regarded as an event of f. To formalize the idea, we introduce variants \(\rightarrow _H\) and \(\nearrow _H\) of \(\rightarrow _F\) and \(\nearrow _F\) with higher-order control flow taken into consideration: \(\rightarrow _H\) denotes
-labeled edges. For example, an event raised by the function argument \(f_{ arg }\) of a higher-order function f could be regarded as an event of the caller g of f, because \(f_{ arg }\) is constructed by g. Similarly, an event raised by the (partially-applied) function \(f_{ ret }\) returned by a function f could be regarded as an event of f. To formalize the idea, we introduce variants \(\rightarrow _H\) and \(\nearrow _H\) of \(\rightarrow _F\) and \(\nearrow _F\) with higher-order control flow taken into consideration: \(\rightarrow _H\) denotes  and \(\nearrow _F\) denotes \(\varSigma _{\mathbf {call}}^{T}\cdot \rightarrow \cdot \rightarrow _H^* \cdot \varSigma _{\mathbf {call}}^{T}\). Note that the source and the target of \(\nearrow _H\) are restricted to call events of top-level functions. Figure 4 illustrates the pairs of nodes in \(G_{\mathtt {tw}}\) related by \(\nearrow _H\), where nodes labeled with events of the same function (in the sense discussed above) are arranged in the same horizontal line.
and \(\nearrow _F\) denotes \(\varSigma _{\mathbf {call}}^{T}\cdot \rightarrow \cdot \rightarrow _H^* \cdot \varSigma _{\mathbf {call}}^{T}\). Note that the source and the target of \(\nearrow _H\) are restricted to call events of top-level functions. Figure 4 illustrates the pairs of nodes in \(G_{\mathtt {tw}}\) related by \(\nearrow _H\), where nodes labeled with events of the same function (in the sense discussed above) are arranged in the same horizontal line.
4 Applications of HOT-PDL
We show how to encode dependent refinement types and stack-based access control properties using HOT-PDL.
4.1 Dependent Refinement Types
HOT-PDL can specify pre- and post-conditions of higher-order functions, by encoding dependent refinement types \(\tau \) for partial [29, 33, 40] and total [23, 27, 34, 36, 39] correctness verification, defined as:  . Here, Q is either \(\forall \) or \(\exists \). An integer refinement type
. Here, Q is either \(\forall \) or \(\exists \). An integer refinement type  is the type of bounded integers \(\nu \) that satisfy the refinement formula \(\psi \) over bounded integers. A dependent function type \((x:\tau _1) \rightarrow \tau _2^{\forall }\) is the type of functions that, for any argument x conforming to the type \(\tau _1\), if terminating, return a value conforming to the type \(\tau _2\). By contrast, \((x:\tau _1) \rightarrow \tau _2^{\exists }\) is the type of functions that, for any argument x conforming to \(\tau _1\), always terminate and return a value conforming to \(\tau _2\). For example, Prop.3 and Prop.4 of \(D_{\mathtt {tw}}\) are expressed by the following types of \(\mathtt {tw}\):
is the type of bounded integers \(\nu \) that satisfy the refinement formula \(\psi \) over bounded integers. A dependent function type \((x:\tau _1) \rightarrow \tau _2^{\forall }\) is the type of functions that, for any argument x conforming to the type \(\tau _1\), if terminating, return a value conforming to the type \(\tau _2\). By contrast, \((x:\tau _1) \rightarrow \tau _2^{\exists }\) is the type of functions that, for any argument x conforming to \(\tau _1\), always terminate and return a value conforming to \(\tau _2\). For example, Prop.3 and Prop.4 of \(D_{\mathtt {tw}}\) are expressed by the following types of \(\mathtt {tw}\):
-
Prop.3.:

-
Prop.4.:
\( (f:(x:\mathtt {int}) \rightarrow \mathtt {int}^{\exists }) \rightarrow \left( (x : \mathtt {int}) \rightarrow \mathtt {int}^{\exists }\right) ^{\forall } \)
We here write \(\mathtt {int}\) for  . These types can be encoded in HOT-PDL as:
. These types can be encoded in HOT-PDL as:
-
Prop.3.:

-
Prop.4.:

Here,  and
and  for \(g \in \left\{ \bullet \right\} \cup \left\{ f \mid f \in \mathrm {dom}(D)\right\} \). We now define a translation F from types to HOT-PDL formulas as follows:
for \(g \in \left\{ \bullet \right\} \cup \left\{ f \mid f \in \mathrm {dom}(D)\right\} \). We now define a translation F from types to HOT-PDL formulas as follows:

4.2 Stack-Based Access Control Properties
As briefly summarized in Sect. 1, stack-based access control [13] ensures that a security-critical function (e.g., file access) is invoked only if all the (immediate and indirect) callers in the current call stack are trusted, or one of the callers is a privileged function and its callees are all trusted. We here use HOT-PDL to specify stack-based access control properties for higher-order programs. Let \(\mathbf {Critical}\), \(\mathbf {Trusted}\), and \(\mathbf {Priv}\) be HOT-PDL formulas that tell whether the current node is labeled with a call event of security-critical, trusted, and privileged functions, respectively. We assume that \(\mathbf {Critical}\), \(\mathbf {Priv}\), and \(\lnot \mathbf {Trusted}\) do not overlap each other, and a function in \(\mathbf {Priv}\) can be directly called only from a function in \(\mathbf {Trusted}\). Then, one may think we can express the specification as:
Here, the path expression \(\nearrow _F\) introduced in Sect. 3 is used to traverse the call stack bottom-up. The above formula says that an invalid call stack never occurs, where a call stack is called invalid if it contains a call to an untrusted function (represented by the part \(\nearrow _F^* \left\{ \lnot \mathbf {Trusted} \right\} ?\)), followed by a call to a critical function (represented by \(\mathbf {Critical}\)), with no intervening call to a privileged function (represented by \((\nearrow _F \cdot \left\{ \lnot \mathbf {Priv} \right\} ?)^+\)).
This definition, however, is not sufficient for our higher-order language. Let us consider the following program \(D_{ pa }\), which involves a partial application:
Here, \(\mathtt {untrusted}\not \in \mathbf {Trusted}\) and \(\mathtt {critical}\in \mathbf {Critical}\). Intuitively, \(D_{ pa }\) should be regarded as unsafe because \(\mathtt {critical}\) in the body of \(\mathtt {untrusted}\) is called. However, \(D_{ pa }\) satisfies the specification above (under the assumption that anonymous functions are in \(\mathbf {Trusted}\)), because the partial application \(\mathtt {untrusted}\ ()\) never causes a call to \(\mathtt {critical}\) but just returns the anonymous (and trusted) function \(\lambda u. \mathtt {critical}\ u\). The following higher-order program \(D_{ ho }\) is yet another unsafe example that satisfies the specification:
Here, \(\mathtt {privileged}\in \mathbf {Priv}\), \(\mathtt {trusted}\in \mathbf {Trusted}\), \(\mathtt {untrusted}\not \in \mathbf {Trusted}\), and \(\mathtt {critical}\in \mathbf {Critical}\). Note that \(\mathtt {critical}\) in the body of \(\mathtt {untrusted}\) is called as follows: the anonymous function \(\lambda x. \mathtt {crash}\ (); \mathtt {critical}\ ()\) is first passed to \(\mathtt {trusted}\) and then to \(\mathtt {privileged}\) (if \(\mathtt {test}\ ()\) returns \(\mathtt {true}\)), and is finally called by \(\mathtt {privileged}\), causing a call to \(\mathtt {critical}\).
To remedy the limitation, we introduce a new refined variant of stack-based access control properties for higher-order programs, formalized in HOT-PDL from the point of view of interactions among callers and callees as follows:
Note that this is obtained from the previous version by just replacing \(\nearrow _F\) with \(\nearrow _H\), which takes into account which function constructed each function value exchanged among functions. The refined version rejects the unsafe \(D_{ pa }\) and \(D_{ ho }\) as intended: \(D_{ pa }\) (resp. \(D_{ ho }\)) is rejected because the call event of \(\lambda u. \mathtt {critical}\ u\) (resp. \(\lambda x. \mathtt {crash}\ (); \mathtt {critical}\ ()\)) is regarded as an event of \(\mathtt {untrusted}\).
Fournet and Gordon [13] have studied variants of stack-based access control properties for a call-by-value higher-order language. We conclude this section by comparing ours with one of theirs called “stack inspection with frame capture”.Footnote 2 The ideas behind the two are similar but what follows illustrates the difference:
This program satisfies ours but violates theirs. Note that ours allows a function originally constructed by a trusted function to invoke a critical function even if the function is passed around by an untrusted function. By contrast, in their definition, a trusted function value gets “contaminated” (i.e., disabled to invoke a critical function) once it is passed to or returned by an untrusted function. In some cases, their conservative policy is useful, but we believe ours would be more semantically robust (e.g., even works well with the CPS transformation).
5 HOT-PDL Model Checking
In this section, we define HOT-PDL model checking problems for higher-order functional programs over bounded integers and sketch a proof of the decidability.
Definition 4
(HOT-PDL model checking). Given a program D and a HOT-PDL formula \(\phi \) with \(\mathcal {AP}=\varSigma (D)\), HOT-PDL model checking is the problem of deciding whether \(G_{\varpi } \models \phi \) and \(G_{\uppi } \models \phi \) for all \(\varpi \in \mathbin {[\![D]\!]}_{\mathtt {fin}}\) and \(\uppi \in \mathbin {[\![D]\!]}_{\mathtt {inf}}\).
Theorem 1
(Decidability). HOT-PDL model checking is decidable.
We show this by a reduction to modal \(\mu \)-calculus (\(\mu \)-ML) model checking of higher-order recursion schemes (HORSs), which is known decidable [21, 28]. A HORS is a grammar for generating a (possibly infinite) ranked tree, and HORSs are essentially simply-typed lambda calculus with general recursion, tree constructors, and finite data domains such as booleans and bounded integers.
In the reduction, we encode the set of HOTs that are generated from the given program D as a single tree (generated by a HORS). For example, Fig. 5 shows such a tree that encodes the HOTs of \(D_{\mathtt {tw}}\).Footnote 3 There, a node labeled with \(\mathtt {end}\) represents the termination of the program. Note that the branching at the root node is due to the input to the function \(\mathtt {main}\). The subtree with the root node labeled with \(\mathbf {call}(\mathtt {main},0)\) is obtained from the HOT \(G_{\mathtt {tw}}\) by appending a special node labeled with \(\mathtt {end}\), adding, for each edge with the label  , a new node labeled with \(\gamma \), and expanding the resulting DAG into a tree. Thus, the edge labels of \(G_{\mathtt {tw}}\) are turned into node labels of the tree.
, a new node labeled with \(\gamma \), and expanding the resulting DAG into a tree. Thus, the edge labels of \(G_{\mathtt {tw}}\) are turned into node labels of the tree.
It is also worth mentioning here that we are allowed to expand DAGs into trees because the truth value of a HOT-PDL formula is not affected by node-sharing in the given HOT. This nice property is lost if we extend the path expressions of HOT-PDL, for example, with intersections. Thus, the decidability of model checking for extensions of HOT-PDL is an open problem.
We next explain our translation from a HOT-PDL formula into a \(\mu \)-ML formula interpreted over trees that encode HOTs. Our translation is based on an existing one for ordinary PDL [11]. The syntax of \(\mu \)-ML is defined as follows:
Here, X represents a propositional variable and p represents an atomic proposition. A formula \(\square \varphi \) means that \(\varphi \) holds for any child of the current node. A formula \(\mu X.\varphi \) (resp. \(\nu X.\varphi \)) represents the least (resp. greatest) fixpoint of the function \(\lambda X.\varphi \). Here, we assume X occurs only positively in \(\varphi \). For example, the HOT-PDL formulas \(\left[ \rightarrow \right] p\),  , and
, and  are respectively translated to \(\mu \)-ML formulas: \( \square ( \nu X. (\mathbf {N}\Rightarrow \square p) \wedge (\mathbf {br}\Rightarrow \square X))\),
are respectively translated to \(\mu \)-ML formulas: \( \square ( \nu X. (\mathbf {N}\Rightarrow \square p) \wedge (\mathbf {br}\Rightarrow \square X))\),  , and
, and  , where the greatest fixpoints are used to skip the branching nodes labeled with \(\mathbf {br}\) (that may repeat infinitely).
, where the greatest fixpoints are used to skip the branching nodes labeled with \(\mathbf {br}\) (that may repeat infinitely).
Finally, we explain how to obtain a HORS for generating a tree that encodes the set of HOTs generated from the given program D. We here need to simulate pointer traversals of HOT-PDL by using purely functional features of HORSs because \(\mu \)-ML does not support pointers. Intuitively, we obtain the desired HORS from D by embedding an event monitor and an event handler. Whenever the monitor detects a function call or return event during the execution of D, the handler creates a new node labeled with the event or ignores the event until a certain event is detected by the monitor, depending on the current mode of the handler. The handler has the following three modes:
-
\(m_{\mathbf {N}}\): The handler always creates and links two new nodes \(u_{\mathbf {N}}\) and \(u_{\alpha }\) labeled respectively with \(\mathbf {N}\) and the event \(\alpha \) observed. The handler then continues as follows, depending on the form of the event \(\alpha \):
-
\(\mathbf {call}(g,n)\): Spawns a new handler with the mode
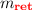 . Then, the two handlers of the modes \(m_{\mathbf {N}}\) and
. Then, the two handlers of the modes \(m_{\mathbf {N}}\) and  continue to create subtrees of \(u_{\alpha }\).
continue to create subtrees of \(u_{\alpha }\). -
\(\mathbf {call}(g,\bullet )\): Spawns two new handlers with the modes
 and
and 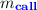 . The three handlers of \(m_{\mathbf {N}}\),
. The three handlers of \(m_{\mathbf {N}}\),  , and
, and  continue to create subtrees of \(u_{\alpha }\).
continue to create subtrees of \(u_{\alpha }\). -
\(\mathbf {ret}(g,n)\): The handler of the mode \(m_{\mathbf {N}}\) continues to create a subtree of \(u_{\alpha }\).
-
\(\mathbf {ret}(g,\bullet )\): Spawns a new handler with the mode
 . Then, the two handlers of the modes \(m_{\mathbf {N}}\) and
. Then, the two handlers of the modes \(m_{\mathbf {N}}\) and 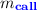 continue to create subtrees of \(u_{\alpha }\).
continue to create subtrees of \(u_{\alpha }\).
-
-
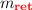 : The handler ignores all events but the return event corresponding to the call event that caused the spawn of the handler. If not ignored, the handler creates and links new nodes
: The handler ignores all events but the return event corresponding to the call event that caused the spawn of the handler. If not ignored, the handler creates and links new nodes  and \(u_{\alpha }\) labeled with
and \(u_{\alpha }\) labeled with  and the event \(\alpha \). The handler changes its mode to \(m_{\mathbf {N}}\) and continues creating a subtree of \(u_{\alpha }\).
and the event \(\alpha \). The handler changes its mode to \(m_{\mathbf {N}}\) and continues creating a subtree of \(u_{\alpha }\). -
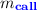 : The handler ignores all events but the call event of the function passed to or returned by the call or return event that caused the spawn of the handler. If not ignored, the handler creates and links new nodes u and \(u_{\alpha }\) labeled respectively with
: The handler ignores all events but the call event of the function passed to or returned by the call or return event that caused the spawn of the handler. If not ignored, the handler creates and links new nodes u and \(u_{\alpha }\) labeled respectively with 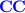 or
or  and the event \(\alpha \), duplicates itself, and changes the mode of the original to \(m_{\mathbf {N}}\). The handler of the mode \(m_{\mathbf {N}}\) (resp.
and the event \(\alpha \), duplicates itself, and changes the mode of the original to \(m_{\mathbf {N}}\). The handler of the mode \(m_{\mathbf {N}}\) (resp.  ) continues to create a subtree of \(u_{\alpha }\) (resp. the parent of u).
) continues to create a subtree of \(u_{\alpha }\) (resp. the parent of u).
For simplicity of the construction, we assume that D is in the Continuation-Passing Style (CPS). This does not lose generality because we can enforce this form by the CPS transformation. Because CPS explicates the order of function call and return events, it simplifies event monitoring, handling, and tracking of the current mode of the monitors, which often changes as monitoring proceeds.
6 Related Work
HOT-PDL can specify temporal trace properties of higher-order programs. An extension for specifying branching properties, however, remains a future work.
There have been proposed logics and formal languages on richer structures than words. Regular languages of nested words, or equivalently, Visibly Pushdown Languages (VPLs) have been introduced by Alur and Madhusudan [7]. An (\(\omega \)-)nested word is a (possibly infinite) word with additional well-nested pointers from call events to the corresponding return events. Compared to temporal logics CaRet [5] and NWTL [4] over (\(\omega \)-)nested words, HOT-PDL is defined over HOTs that have richer structures. Recall that a HOT is equipped with two kinds of pointers: one kind with the label  , which is the same as the pointers of nested words, and the other kind with the label
, which is the same as the pointers of nested words, and the other kind with the label  or
or  , which is newly introduced to capture higher-order control flow. Bollig et al. proposed nested traces as a generalization of nested words for modeling traces of concurrent (first-order) recursive programs, and presented temporal logics over nested traces [8]. Nested traces, however, cannot model traces of higher-order programs. We expect a combination of our work with theirs enables us to specify temporal trace properties of concurrent and higher-order recursive programs. Cyriac et al. have recently introduced an extension of PDL defined over traces of order-2 collapsible pushdown systems (CPDS) [3]. Interestingly, their traces are also equipped with two kinds of pointers: one kind of pointers captures the correspondence between ordinary push and pop stack operations, and the other captures the correspondence between order-2 push and pop operations for second-order stacks. Our work deals with higher-order programs that correspond to order-n CPDS for arbitrary n.
, which is newly introduced to capture higher-order control flow. Bollig et al. proposed nested traces as a generalization of nested words for modeling traces of concurrent (first-order) recursive programs, and presented temporal logics over nested traces [8]. Nested traces, however, cannot model traces of higher-order programs. We expect a combination of our work with theirs enables us to specify temporal trace properties of concurrent and higher-order recursive programs. Cyriac et al. have recently introduced an extension of PDL defined over traces of order-2 collapsible pushdown systems (CPDS) [3]. Interestingly, their traces are also equipped with two kinds of pointers: one kind of pointers captures the correspondence between ordinary push and pop stack operations, and the other captures the correspondence between order-2 push and pop operations for second-order stacks. Our work deals with higher-order programs that correspond to order-n CPDS for arbitrary n.
Finally, we compare HOT-PDL with existing logics defined over words. It is well known that LTL is less expressive than \(\omega \)-regular languages [38]. To remedy the limitation of LTL, Wolper introduced ETL [38] that allows users to define new temporal operators using right-linear grammars. Henriksen and Thiagarajan proposed DLTL [17] that generalizes the until operator of LTL using regular expressions. Leucker and Sánchez proposed RLTL [25] that combines LTL and regular expressions. Vardi and Giacomo have introduced Linear Dynamic Logic (LDL), a variant of PDL interpreted over infinite words [15, 35]. \(\mathrm {LDL}_f\), a variant of PDL interpreted over finite words, has also been studied in [15]. ETL, DLTL, RLTL, and LDL are as expressive as \(\omega \)-regular languages. Note that HOT-PDL subsumes (\(\omega \)-)regular languages because LDL and \(\mathrm {LDL}_f\) can be naturally embedded in HOT-PDL. (\(\omega \)-)VPLs strictly subsume (\(\omega \)-)regular languages. Though CaRet [5] and NWTL [4] are defined over nested words, they do not capture the full class of VPLs [10]. To remedy the limitation, VLTL [10] combines LTL and VRE [9] in the style of RLTL, where VRE is a generalization of regular expressions for VPLs. VLDL [37] extends LDL by replacing the path expressions with VPLs over finite words. VLTL and VLDL exactly characterize \(\omega \)-VPLs. Because VPLs and HOT-PDL are incomparable, it remains future work to extend HOT-PDL to subsume (\(\omega \)-)VPLs.
7 Conclusion and Future Work
We have presented HOT-PDL, an extension of PDL defined over HOTs that model execution traces of call-by-value and higher-order programs. HOT-PDL enables a precise specification of temporal trace properties of higher-order programs and consequently provides a foundation for specification in various application domains including stack-based access control and dependent refinement types. We have also studied HOT-PDL model checking and presented a reduction method to modal \(\mu \)-calculus model checking of higher-order recursion schemes.
To further widen the scope of our approach, it is worth investigating how to adapt HOTs and HOT-PDL to call-by-name and/or effectful languages. To this end, it is natural to incorporate more ideas from achievements of game semantics [1, 20, 32] and extend HOTs with new kinds of events and pointers for capturing call-by-name and/or effectful computations.
Notes
- 1.
The symbol \(\cdots \) indicates the omission of a subsequence. The two omitted subsequences are
 and
and  in this order.
in this order. - 2.
We do not compare with the other variants in [13] because they are too syntactic to be preserved by simple program transformations like inlining.
- 3.
There, for simplicity, we illustrate an unranked tree and omit the label of branching nodes. In the formalization, we express an unranked tree as a binary tree using a special node label \(\mathbf {br}\) of the arity 2 representing a binary branching.
References
Abramsky, S., Jagadeesan, R., Malacaria, P.: Full abstraction for PCF. Inf. Comput. 163, 409–470 (2000)
Abramsky, S., McCusker, G.: Call-by-value games. In: Nielsen, M., Thomas, W. (eds.) CSL 1997. LNCS, vol. 1414, pp. 1–17. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0028004
Aiswarya, C., Gastin, P., Saivasan, P.: Nested words for order-2 pushdown systems. arXiv:1609.06290 (2016)
Alur, R., Arenas, M., Barcelo, P., Etessami, K., Immerman, N., Libkin, L.: First-order and temporal logics for nested words. Log. Methods Comput. Sci. 4(4), 1–44 (2008)
Alur, R., Etessami, K., Madhusudan, P.: A temporal logic of nested calls and returns. In: Jensen, K., Podelski, A. (eds.) TACAS 2004. LNCS, vol. 2988, pp. 467–481. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24730-2_35
Alur, R., Madhusudan, P.: Visibly pushdown languages. In: STOC 2004, pp. 202–211. ACM (2004)
Alur, R., Madhusudan, P.: Adding nesting structure to words. J. ACM 56(3), 16:1–16:43 (2009)
Bollig, B., Cyriac, A., Gastin, P., Zeitoun, M.: Temporal logics for concurrent recursive programs: satisfiability and model checking. J. Appl. Log. 12(4), 395–416 (2014)
Bozzelli, L., Sánchez, C.: Visibly rational expressions. In: FSTTCS 2012. LIPIcs, vol. 18, pp. 211–223. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik (2012)
Bozzelli, L., Sánchez, C.: Visibly linear temporal logic. In: Demri, S., Kapur, D., Weidenbach, C. (eds.) IJCAR 2014. LNCS (LNAI), vol. 8562, pp. 418–433. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08587-6_33
Carreiro, F., Venema, Y.: PDL inside the \(\mu \)-calculus: a syntactic and an automata-theoretic characterization. Adv. Modal Log. 10, 74–93 (2014)
Disney, T., Flanagan, C., McCarthy, J.: Temporal higher-order contracts. In: ICFP 2011, pp. 176–188. ACM (2011)
Fournet, C., Gordon, A.D.: Stack inspection: theory and variants. In: POPL 2002, pp. 307–318. ACM (2002)
Fujima, K., Ito, S., Kobayashi, N.: Practical alternating parity tree automata model checking of higher-order recursion schemes. In: Shan, C. (ed.) APLAS 2013. LNCS, vol. 8301, pp. 17–32. Springer, Cham (2013). https://doi.org/10.1007/978-3-319-03542-0_2
Giacomo, G.D., Vardi, M.Y.: Linear temporal logic and linear dynamic logic on finite traces. In: IJCAI 2013, pp. 854–860. AAAI Press (2013)
Harel, D., Tiuryn, J., Kozen, D.: Dynamic Logic. MIT Press, Cambridge (2000)
Henriksen, J.G., Thiagarajan, P.: Dynamic linear time temporal logic. Ann. Pure Appl. Log. 96(1), 187–207 (1999)
Hofmann, M., Chen, W.: Abstract interpretation from Büchi automata. In: CSL-LICS 2014, pp. 51:1–51:10. ACM (2014)
Honda, K., Yoshida, N.: Game theoretic analysis of call-by-value computation. In: Degano, P., Gorrieri, R., Marchetti-Spaccamela, A. (eds.) ICALP 1997. LNCS, vol. 1256, pp. 225–236. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-63165-8_180
Hyland, J.M.E., Ong, C.H.L.: On full abstraction for PCF: I, II, and III. Inf. Comput. 163, 285–408 (2000)
Kobayashi, N., Ong, C.H.L.: A type system equivalent to the modal Mu-calculus model checking of higher-order recursion schemes. In: LICS 2009, pp. 179–188. IEEE (2009)
Kobayashi, N., Tsukada, T., Watanabe, K.: Higher-order program verification via HFL model checking. In: Ahmed, A. (ed.) ESOP 2018. LNCS, vol. 10801, pp. 711–738. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89884-1_25
Koskinen, E., Terauchi, T.: Local temporal reasoning. In: CSL-LICS 2014, pp. 59:1–59:10. ACM (2014)
Lester, M.M., Neatherway, R.P., Ong, C.H.L., Ramsay, S.J.: Model checking liveness properties of higher-order functional programs (2011). http://mjolnir.comlab.ox.ac.uk/papers/thors.pdf
Leucker, M., Sánchez, C.: Regular linear temporal logic. In: Jones, C.B., Liu, Z., Woodcock, J. (eds.) ICTAC 2007. LNCS, vol. 4711, pp. 291–305. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-75292-9_20
Murase, A., Terauchi, T., Kobayashi, N., Sato, R., Unno, H.: Temporal verification of higher-order functional programs. In: POPL 2016, pp. 57–68. ACM (2016)
Nanjo, Y., Unno, H., Koskinen, E., Terauchi, T.: A fixpoint logic and dependent effects for temporal property verification. In: LICS 2018. ACM (2018)
Ong, C.H.L.: On model-checking trees generated by higher-order recursion schemes. In: LICS 2006, pp. 81–90. IEEE (2006)
Rondon, P., Kawaguchi, M., Jhala, R.: Liquid types. In: PLDI 2008, pp. 159–169. ACM (2008)
Satake, Y., Unno, H.: Propositional dynamic logic for higher-order functional programs (2018). http://www.cs.tsukuba.ac.jp/~uhiro/
Suzuki, R., Fujima, K., Kobayashi, N., Tsukada, T.: Streett automata model checking of higher-order recursion schemes. In: FSCD 2017. LIPIcs, vol. 84, pp. 32:1–32:18. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik (2017)
Tzevelekos, N.: Nominal game semantics. Ph.D. thesis, University of Oxford (2008)
Unno, H., Kobayashi, N.: Dependent type inference with interpolants. In: PPDP 2009, pp. 277–288. ACM (2009)
Unno, H., Satake, Y., Terauchi, T.: Relatively complete refinement type system for verification of higher-order non-deterministic programs. Proc. ACM Program. Lang. 2(POPL), 12:1–12:29 (2017)
Vardi, M.Y.: The rise and fall of LTL. GandALF (2011)
Vazou, N., Seidel, E.L., Jhala, R., Vytiniotis, D., Peyton Jones, S.L.: Refinement types for Haskell. In: ICFP 2014, pp. 269–282. ACM (2014)
Weinert, A., Zimmermann, M.: Visibly linear dynamic logic. In: FSTTCS 2016. LIPIcs, vol. 65, pp. 28:1–28:14. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik (2016)
Wolper, P.: Temporal logic can be more expressive. Inf. Control 56(1), 72–99 (1983)
Xi, H.: Dependent types for program termination verification. In: LICS 2001, pp. 231–242. IEEE (2001)
Xi, H., Pfenning, F.: Dependent types in practical programming. In: POPL 1999, pp. 214–227. ACM (1999)
Acknowledgments
We would like to thank anonymous referees for their useful comments. This work was supported by JSPS KAKENHI Grant Numbers 15H05706, 16H05856, 17H01720, and 17H01723.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
<SimplePara><Emphasis Type="Bold">Open Access</Emphasis>This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.</SimplePara><SimplePara>The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.</SimplePara>
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Satake, Y., Unno, H. (2018). Propositional Dynamic Logic for Higher-Order Functional Programs. In: Chockler, H., Weissenbacher, G. (eds) Computer Aided Verification. CAV 2018. Lecture Notes in Computer Science(), vol 10981. Springer, Cham. https://doi.org/10.1007/978-3-319-96145-3_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-96145-3_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96144-6
Online ISBN: 978-3-319-96145-3
eBook Packages: Computer ScienceComputer Science (R0)





 ,
, 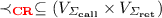 ,
, 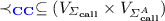 , and
, and  .
. and
and  , then
, then  holds.
holds. or
or  holds.
holds.
 and
and  for
for 
 if
if  if
if 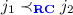 if
if 
 or
or 


 ,
,  ,
,  , or
, or 



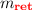 . Then, the two handlers of the modes
. Then, the two handlers of the modes  continue to create subtrees of
continue to create subtrees of  and
and 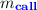 . The three handlers of
. The three handlers of  , and
, and  continue to create subtrees of
continue to create subtrees of  . Then, the two handlers of the modes
. Then, the two handlers of the modes 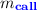 continue to create subtrees of
continue to create subtrees of 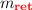 : The handler ignores all events but the return event corresponding to the call event that caused the spawn of the handler. If not ignored, the handler creates and links new nodes
: The handler ignores all events but the return event corresponding to the call event that caused the spawn of the handler. If not ignored, the handler creates and links new nodes  and
and  and the event
and the event 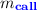 : The handler ignores all events but the call event of the function passed to or returned by the call or return event that caused the spawn of the handler. If not ignored, the handler creates and links new nodes u and
: The handler ignores all events but the call event of the function passed to or returned by the call or return event that caused the spawn of the handler. If not ignored, the handler creates and links new nodes u and 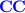 or
or  and the event
and the event  ) continues to create a subtree of
) continues to create a subtree of  and
and  in this order.
in this order.