Abstract
This paper presents a numerical algorithm to verify continuous-time Markov chains (CTMCs) against multi-clock deterministic timed automata (DTA). These DTA allow for specifying properties that cannot be expressed in CSL, the logic for CTMCs used by state-of-the-art probabilistic model checkers. The core problem is to compute the probability of timed runs by the CTMC \(\mathcal{C}\) that are accepted by the DTA \(\mathcal{A}\). These likelihoods equal reachability probabilities in an embedded piecewise deterministic Markov process (EPDP) obtained as product of \(\mathcal{C}\) and \(\mathcal{A}\)’s region automaton. This paper provides a numerical algorithm to efficiently solve the PDEs describing these reachability probabilities. The key insight is to solve an ordinary differential equation (ODE) that exploits the specific characteristics of the product EPDP. We provide the numerical precision of our algorithm and present experimental results with a prototypical implementation.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Continuous-time Markov Chain (CTMCs)
- Deterministic Timed Automata
- Reachability Probabilities
- Piecewise Deterministic Markov Processes (PDP)
- Partial Differential Equations (PDEs)
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Continuous-time Markov chains (CTMCs) [17] are ubiquitous. They are used to model safety-critical systems like communicating networks and power management systems, are key to performance and dependability analysis, and naturally describe chemical reaction networks. The algorithmic verification of CTMCs has received quite some attention. Aziz et al. [3] proved that verifying CTMCs against CSL (Continuous Stochastic Logic) is decidable. CSL is a probabilistic and timed branching-time logic that allows for expressing properties like “is the probability of a given chemical reaction within 50 time units at least \(10^{-3}\)?”. Baier et al. [5] gave efficient numerical algorithms for CSL model checking that nowadays provide the basis of CTMC model checking in PRISM [23], MRMC [22] and Storm [15], as well as GreatSPN [2]. Extensions of CSL to cascaded timed-until operators [27], conditional probabilities [19], and (simple) timed regular expressions [4] have been considered.
This paper considers the verification of CTMCs against linear-time real-time properties. These include relevant properties in the design of a gas burner [28], like “the probability that the duration of leaking is more than one twentieth over an interval with a length more than 20 s is less than \(10^{{-}6}\)”. Such real-time properties can be conveniently expressed by deterministic timed automata (DTA) [1]. The core problem in the verification of CTMC \(\mathcal {C}\) against DTA \(\mathcal {A}\) is to compute the probability of \(\mathcal {C}\)’s timed runs that are accepted by \(\mathcal {A}\), i.e.  . Chen et al. [10, 11] showed that this quantity equals the reachability probability in a piecewise deterministic Markov process (PDP) [14]. This PDP is obtained by taking the product of CTMC \(\mathcal {C}\) and the region automaton of \(\mathcal {A}\). Computing reachability probabilities in PDPs is a challenge.
. Chen et al. [10, 11] showed that this quantity equals the reachability probability in a piecewise deterministic Markov process (PDP) [14]. This PDP is obtained by taking the product of CTMC \(\mathcal {C}\) and the region automaton of \(\mathcal {A}\). Computing reachability probabilities in PDPs is a challenge.
Practical implementations of verifying CTMCs against DTA specifications are rare. Barbot et al. [7] showed that for single-clock DTA, the PDP is in fact a Markov regenerative process. (This observation is also at the heart of model-checking CSL\(^{TA}\) [16].) This implies that for single-clock DTA, off-the-shelf CSL model-checking algorithms can be employed resulting in an efficient procedure [7]. Mikeev et al. [24] generalised these ideas to infinite-state CTMCs obtained from stoichiometric equations, whereas Chen et al. [12] showed the theory to generalize verifying single-clock DTA to continuous-time Markov decision processes.
Multi-clock DTA are however much harder to handle. The characterisation of PDP reachability probabilities as the unique solution of a set of partial differential equations (PDEs) [10, 11] does not give insight into an efficient computational procedure. With the notable exception of [25], verifying PDPs has not been considered. Fu [18] provided an algorithm to approximate the probabilities using finite difference methods and gave an error bound. This method hampers scalability and therefore was never implemented. The same holds for model-checking using other linear-time real-time formalisms such as MTL and timed automata [9], linear duration invariants [8], and probabilistic duration calculus [13]. All these multi-clock approaches suffer from scalability issues due to the low efficiency of solving PDEs and/or integral equations on which they heavily depend.
This paper presents a numerical technique to approximate the reachability probability in the product PDP. The DTA \(\mathcal{A}\) is approximated by DTA \(\mathcal {A}[t_f]\) which extends \(\mathcal{A}\) with an additional clock that is never reset and that needs to be at most \(t_f\) when accepting. By increasing the time-bound \(t_f\), DTA \(\mathcal {A}[t_f]\) approximates \(\mathcal{A}\) arbitrarily closely. We show that the set of PDPs characterizing the reachability probability in the embedded PDP of \(\mathcal{C}\) and \(\mathcal {A}[t_f]\) can be reduced to solving an ordinary differential equation (ODE). The specific characteristics of the product EPDP, in particular the fact that all clocks run at the same pace, are key to obtain these ODEs. Our numerical algorithm to solve the ODEs is based on computing the approximations in a backward manner using \(t_f\) and the sum of all clocks. The complexity of the resulting procedure is linear in the EPDP size, and exponential in \(\lceil \frac{t_f}{\delta } \rceil \) where \(\delta \) is the discretization step size. We show the approximations converges to the real solution of the ODEs at a linear speed of \(\delta \). Using a prototypical tool implementation we present some results on a number of case studies such as robot navigation with varying number of clocks in their specification. The experimental results show promising results for checking CTMCs against multi-clock DTA.
Organization of the Paper. Section 2 introduces basic notions including CTMCs, DTA, and PDPs. Section 3 presents the product of a CTMC and the region graph of a DTA and shows this is an embedded PDP. Section 4 derives the PDE (fixing some flaw in [10]), the reduction to the set of ODEs and presents the numerical algorithm to solve these ODEs. Section 5 presents the experimental results and Sect. 6 concludes.
2 Preliminaries
In this section, we introduce some basic notions which will be used later.
A probability space is denoted by a triple \((\varOmega , \mathcal {F}, \textit{Pr})\), where \(\varOmega \) is a set of samples, \(\mathcal {F}\) is a \(\sigma \)-algebra over \(\varOmega \), and \(\textit{Pr}:\mathcal {F}\rightarrow [0,1]\) is a probability measure on \(\mathcal {F}\) with \(\textit{Pr}(\varOmega )=1\). Let \(\mathbb {P}_r(\varOmega )\) denote the set of all probability measures over \(\varOmega \). For a random variable X on the probability space, its expectation is denoted by \(\mathbb {E}(X)\).
2.1 Continuous-Time Markov Chain (CTMC)
Definition 1
(CTMC). A CTMC is a tuple \(\mathcal {C} = (S, \mathbf {P}, \alpha , \textit{AP}, L, E)\), where
-
S is a finite set of states;
-
\(\mathbf {P}\): \(S\times S\rightarrow [0,1]\) is the transition probability function, which is identified with the matrix \(\mathbf {P}\in [0,1]^{|S|\times |S|}\) such that \(\sum _{t\in S}\mathbf {P}(s,t)=1\), for all \(s\in S\);
-
\(\alpha \in \mathbb {P}_r(S)\) is the initial distribution;
-
\(\textit{AP}\) is a finite set of atomic propositions;
-
\(L:S\rightarrow 2^{\textit{AP}}\) is a labeling function; and
-
\(E: S\rightarrow \mathbb {R}_{>0}\) is the exit rate function.
We denote by \(s\xrightarrow {t}s'\) a transition from state s to state \(s'\) after residing in state s for t time units. The probability of the occurrence of this transition within t time units is \(\mathbf {P}(s,s') \int _0^{t}E(s)\exp ^{-E(s)x}dx\), where \(\int _0^{t}E(s)\exp ^{-E(s)x}dx\) stands for the probability to leave state s in t time units, and \(\mathbf {P}(s,s')\) for the probability to select the transition to \(s'\) from all transitions outgoing from s. A state s is called absorbing if \(\mathbf {P}(s,s)=1\). Given a CTMC \(\mathcal {C}\), removing the exit rate function E results in a discrete-time Markov chain (DMTC), which is called embedded DTMC of \(\mathcal {C}\). A CTMC \(\mathcal {C}\) is called irreducible if there exists a unique stationary distribution \(\alpha \), such that \(\alpha (s)>0\) for all \(s\in S\), and weakly irreducible if \(\alpha (s)\) may be zero for some \(s\in S\).
Definition 2
(CTMC Path). Let \(\mathcal {C}\) be a CTMC, a path \(\rho \) of \(\mathcal {C}\) starting form \(s_0\) with length n is a sequence \(\rho = s_0\xrightarrow {t_0}s_1\xrightarrow {t_1}\ldots \xrightarrow {t_{n-1}}s_n\in S\times (\mathbb {R}_{>0}\times S)^n\). The set of paths in \(\mathcal {C}\) with length n is denoted by \(\textit{Path}_{n}^{\mathcal {C}}\); the set of all finite paths of \(\mathcal {C}\) is \(\textit{Path}_{{\textit{fin}}}^{\mathcal {C}}=\cup _n \textit{Path}_{n}^{\mathcal {C}}\) and the set of infinite paths of \(\mathcal {C}\) is \(\textit{Path}_{\textit{inf}}^{\mathcal {C}}=(S\times \mathbb {R}_{>0})^{\omega }\). We use \(\textit{Path}^{\mathcal {C}}=\textit{Path}_{{\textit{fin}}}^{\mathcal {C}}\cup \textit{Path}_{\textit{inf}}^{\mathcal {C}}\) to denote all paths in \(\mathcal {C}\). As a convention, \(\varepsilon \) stands for the empty path.
Note that we assume the time to exit a state is strictly greater than 0. For an infinite path \(\rho \), we use \(\textit{Pref}(\rho )\) to denote the set of its finite prefixes. For a (finite or infinite) path \(\rho \) with prefix \(s_0\xrightarrow {t_0}s_1\xrightarrow {t_1}\ldots \), the trace of the path is the sequence of states \(\textit{trace}(\rho )=s_0s_1\ldots \). Let \(\rho (n)=s_n\) be the n-th state in the path and \(\rho [n]=t_n\) be the corresponding exit time for \(s_n\). For a finite path \(\rho = s_0\xrightarrow {t_0}s_1\xrightarrow {t_1}\ldots \xrightarrow {t_{n-1}}s_n\), we use \(T(\rho )=\sum _{i=0}^{n-1} t_i\) to denote the total time spent on this path if \(n\ge 1\), otherwise \(T(\rho )=0\). For a time \(t\le T(\rho )\), \(\rho (0\ldots t)\) denotes the prefix of \(\rho \) within t time units, i.e., \(s_0\xrightarrow {t_0}s_1\xrightarrow {t_1}\ldots \xrightarrow {t_{m-1}}s_m\) if there exists some \(m\le n\) with \(\sum _{i=0}^{m-1}\rho [m]\le t\wedge \sum _{i=0}^{m}\rho [m]>t\), otherwise \(\varepsilon \).
A basic cylinder set \(C(s_0, I_0, \cdots , I_{n-1}, s_n)\) consists of all paths \(\rho \in \textit{Path}^{\mathcal {C}}\) such that \(\rho (i)=s_i\) for \(0\le i\le n\), and \(\rho [i] \in I_i\) for \(0\le i<n\). Then the \(\sigma -\)algebra \(\mathcal {F}_{s_0}(\mathcal {C})\) associated with CTMC \(\mathcal {C}\) and initial state \(s_0\) is the smallest \(\sigma -\)algebra that contains all cylinder sets \(C(s_0, I_0, \cdots , I_{n-1}, s_n)\) with \(\alpha (s_0)>0\), and \(\mathbf {P}(s_i,s_{i+1})>0\), for \(1\le i \le n\), and \(I_0,\ldots ,I_{n-1}\) are non-empty intervals in \(\mathbb {R}_{\ge 0}\). There is a unique probability measure \(\textit{Pr}^{\mathcal {C}}\) on the \(\sigma -\)algebra \(\mathcal {F}_{s_0}(\mathcal {C})\), by which the probability for a cylinder set is given by
Example 1
An example of CTMC is shown in Fig. 1, with \(\textit{AP}=\{a,b,c\}\) and initial state \(s_0\). The exit rate \(r_i,\ i=0,1,2,3\) and transition probability are shown in the figure.
2.2 Deterministic Timed Automaton (DTA)
A timed automaton is a finite state graph equipped with a finite set of nonnegative real-valued clock variables, or clocks for short. Clocks can only be reset to zero, or proceed with rate 1 as time progresses independently. Let \(\mathcal {X}=\{x_1, \ldots , x_n\}\) be a set of clocks. \(\eta (x):\mathcal {X}\rightarrow \mathbb {R}_{\ge 0}\) is a \(\mathcal {X}\)-valuation which records the amount of time since its last reset. Let \(\textit{Val}(\mathcal {A})\) be the set of all clock valuations of \(\mathcal {A}\). For a subset \(X\subseteq \mathcal {X}\), the reset of X, denoted as \(\eta [X:=0]\), is the valuation \(\eta '\) such that \(\eta '(x)=0, \forall x\in X\), and \(\eta '(x)=\eta (x)\), otherwise. For \(d\in \mathbb {R}_{>0}\), \((\eta +d)(x)=\eta (x)+d\) for any clock \(x\in \mathcal {X}\).
A clock constraint over \(\mathcal {X}\) is a formula with the following form
where x, y are clocks, \(c\in \mathbb {N}\). Let \(\textit{Con}(\mathcal {X})\) denote the set of clock constraints over \(\mathcal {X}\). A valuation \(\eta \) satisfies a guard g, denoted as  , iff \(\eta (x)\bowtie c\) when g is \(x\bowtie c\), where \(\bowtie \,\in \{<,\le , >, \ge \}\); and
, iff \(\eta (x)\bowtie c\) when g is \(x\bowtie c\), where \(\bowtie \,\in \{<,\le , >, \ge \}\); and  and
and  iff \(g=g_1\wedge g_2\).
iff \(g=g_1\wedge g_2\).
Definition 3
(DTA). A DTA is a tuple \(\mathcal {A}=(\varSigma , \mathcal {X}, Q,\)  , where
, where
-
\(\varSigma \) is a finite set of actions;
-
\(\mathcal {X}\) is a finite set of clocks;
-
Q is a finite set of locations;
-
\(q_0\in Q\) is the initial location;
-
\(Q_F\subseteq Q\) is the set of accepting locations;
-
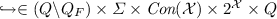 is the transition relation, satisfying if
is the transition relation, satisfying if  and
and  with \(q'\ne q''\) then \(g\cap g'=\emptyset \).
with \(q'\ne q''\) then \(g\cap g'=\emptyset \).
Each transition relation, or edge,  in \(\mathcal {A}\) is endowed with (a, g, X), where \(a\in \varSigma \) is an action, \(g \in \textit{Con}(\mathcal {X})\) is the guard of the transition, and \(X\subseteq \mathcal {X}\) is a set of clocks, which should be reset to 0 after the transition. An intuitive interpretation of the transition is that \(\mathcal {A}\) can move from q to \(q'\) by taking action a and resetting all clocks in X to be 0 only if g is satisfied. There are no outgoing transitions from any accepting location in \(Q_F\).
in \(\mathcal {A}\) is endowed with (a, g, X), where \(a\in \varSigma \) is an action, \(g \in \textit{Con}(\mathcal {X})\) is the guard of the transition, and \(X\subseteq \mathcal {X}\) is a set of clocks, which should be reset to 0 after the transition. An intuitive interpretation of the transition is that \(\mathcal {A}\) can move from q to \(q'\) by taking action a and resetting all clocks in X to be 0 only if g is satisfied. There are no outgoing transitions from any accepting location in \(Q_F\).
A finite timed path of \(\mathcal {A}\) is of the form  , where \(t_i\ge 0\), for \(i=0,\ldots ,n-1\). Moreover, there exists a sequence of transitions
, where \(t_i\ge 0\), for \(i=0,\ldots ,n-1\). Moreover, there exists a sequence of transitions  , for \(0\le j \le n-1\), such that \(\eta _0=\mathbf {{0}}\),
, for \(0\le j \le n-1\), such that \(\eta _0=\mathbf {{0}}\),  and \(\eta _{j+1}=\eta _{j}[X_j:=0]\), where \(\eta _k\) denotes the clock valuation when entering \(q_k\). \(\theta \) is said to be accepted by \(\mathcal {A}\) if there exists a state \(q_i\in Q_F\) for some \(0\le i\le n\). As normal, it is assumed all DTA are non-Zeno [6], that is any circular transition sequence takes nonzero dwelling time.
and \(\eta _{j+1}=\eta _{j}[X_j:=0]\), where \(\eta _k\) denotes the clock valuation when entering \(q_k\). \(\theta \) is said to be accepted by \(\mathcal {A}\) if there exists a state \(q_i\in Q_F\) for some \(0\le i\le n\). As normal, it is assumed all DTA are non-Zeno [6], that is any circular transition sequence takes nonzero dwelling time.
A region is a set of valuations, usually represented by a set of clock constraints. Let \(\textit{Reg}(\mathcal {X})\) be the set of regions over \(\mathcal {X}\). Given \(\varTheta ,\varTheta '\in \textit{Reg}(\mathcal {X})\), \(\varTheta '\) is called a successor of \(\varTheta \) if for all  , there exists \(t>0\) such that
, there exists \(t>0\) such that  and
and  . A region \(\varTheta \) satisfies a guard g, denoted as
. A region \(\varTheta \) satisfies a guard g, denoted as  , iff
, iff  implies
implies  . The reset operation on a region \(\varTheta \) is defined as
. The reset operation on a region \(\varTheta \) is defined as  . Then the region graph, viewed as a quotient transition system related to clock equivalence [6] can be defined as follows:
. Then the region graph, viewed as a quotient transition system related to clock equivalence [6] can be defined as follows:
Definition 4
(Region Graph). The region graph for DTA \(\mathcal {A}=(\varSigma , \mathcal {X}, Q,\)  is a tuple \(\mathcal {G}(\mathcal {A})= (\varSigma ,\mathcal {X}, \overline{Q},\overline{q_0},\overline{Q_F},\mapsto )\), where
is a tuple \(\mathcal {G}(\mathcal {A})= (\varSigma ,\mathcal {X}, \overline{Q},\overline{q_0},\overline{Q_F},\mapsto )\), where
-
\(\overline{Q}=Q\times \textit{Reg}(\mathcal {X})\) is the set of states;
-
\(\overline{q_0}=(q_0,\mathbf {0})\in \overline{Q}\) is the initial state;
-
\(\overline{Q_F} \subseteq Q_F\times \textit{Reg}(\mathcal {X})\) is the set of final states;
-
\(\mapsto \,\subseteq \overline{Q}\times ((\varSigma \times 2^{\mathcal {X}})\cup \{\lambda \})\times \overline{Q}\) is the transition relation satisfying
-
 if \(\varTheta '\) is a successor of \(\varTheta \);
if \(\varTheta '\) is a successor of \(\varTheta \); -
 if there exists \(g\in \textit{Con}(\mathcal {X})\) and transition
if there exists \(g\in \textit{Con}(\mathcal {X})\) and transition  such that
such that 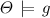 and \(\varTheta ''=\varTheta [X:=0]\).
and \(\varTheta ''=\varTheta [X:=0]\).
-
Example 2
(Adapted from [10]). Figure 2 presents an example of DTA and Fig. 3 gives its region graph, in which double circle and double rectangle stand for final states, respectively.
2.3 Piecewise-Deterministic Markov Process (PDP)
Piecewise-deterministic Markov Processes (PDPs for short) [14] cover a wide range of stochastic models in which the randomness appears as discrete events at fixed or random times, whose evolution is deterministically governed by an ODE system between these times. A PDP consists of a mixture of deterministic motion and random jumps between a finite set of locations. During staying in a location, a PDP evolves deterministically following a flow function, which is a solution to an ODE system. A PDP can jump between locations either randomly, in which case the residence time of a location is governed by an exponential distribution, or when the location invariant is violated. The successor state of the jump follows a probability measure depending on the current state. A PDP is right-continuous and has the strong Markov property [14].
Definition 5
(PDP [14]). A PDP is a tuple \(\mathcal {Q}=(Z,\mathcal {X},\textit{Inv},\phi , \varLambda ,\mu )\) with
-
Z is a finite set of locations;
-
\(\mathcal {X}\) is a finite set of variables;
-
\(\textit{Inv}:Z\rightarrow 2^{\mathbb {R}^{|\mathcal {X}|}}\) is an invariant function;
-
\(\phi :Z\times \mathbb {R}^{|\mathcal {X}|} \times \mathbb {R}_{\ge 0} \rightarrow \mathbb {R}^{|\mathcal {X}|}\), is a flow function, which is a solution of a system of ODEs with Lipschitz continuous vector fields;
-
\(\varLambda :\mathbb {S}\rightarrow \mathbb {R}_{>0}\) is an exit rate function;
-
\(\overline{\mathbb {S}}\rightarrow \mathbb {P}_r(\mathbb {S})\), is the transition probability function, where
 is the state space for \(\mathcal {Q}\), \(\overline{\mathbb {S}}\) is the closure of \(\mathbb {S}\),
is the state space for \(\mathcal {Q}\), \(\overline{\mathbb {S}}\) is the closure of \(\mathbb {S}\),  is the interior of \(\mathbb {S}\), in which \(\textit{Inv}(z)^o\) stands for the interior of \(\textit{Inv}(z)\), and \(\partial \mathbb {S}=\cup _{z\in Z} \{z\}\times \partial \textit{Inv}(z)\) is the boundary of \(\mathbb {S}\), in which \(\partial \textit{Inv}(z)=\overline{\textit{Inv}(z)}\backslash \textit{Inv}^o\) and \(\overline{\textit{Inv}(z)}\) is the closure of \(\textit{Inv}(z)\).
is the interior of \(\mathbb {S}\), in which \(\textit{Inv}(z)^o\) stands for the interior of \(\textit{Inv}(z)\), and \(\partial \mathbb {S}=\cup _{z\in Z} \{z\}\times \partial \textit{Inv}(z)\) is the boundary of \(\mathbb {S}\), in which \(\partial \textit{Inv}(z)=\overline{\textit{Inv}(z)}\backslash \textit{Inv}^o\) and \(\overline{\textit{Inv}(z)}\) is the closure of \(\textit{Inv}(z)\).
For any \(\xi =(z,\eta ) \in \mathbb {S}\), there is an \(\delta (\xi )>0\) such that \(\varLambda (z,\phi (z,\eta ,t))\) is integrable on \([0,\delta (\xi ))\). \(\mu (\xi )(A)\) is measurable for any \(A\in \mathcal {F}(\mathbb {S})\), where \(\mathcal {F}(\mathbb {S})\) is the smallest \(\sigma -\)algebra generated by \(\{\bigcup _{z\in Z}{z}\times A_z|A_z\in \mathcal {F}(\textit{Inv}(z))\}\) and \(\mu (\xi )(\{\xi \})=0\).
There are two ways to take transitions between locations in PDP \(\mathcal {Q}\). A PDP \(\mathcal {Q}\) is allowed to stay in a current location z only if \(\textit{Inv}(z)\) is satisfied. During its residence, the valuation \(\eta \) evolves time-dependently according to the flow function. Let \(\xi \oplus t=(z,\phi (z,\eta ,t))\) be the successor state of \(\xi =(z,\eta )\) after residing t time units in z. Thus, \(\mathcal {Q}\) is piecewise-deterministic since its behavior is determined by the flow function \(\phi \) in each location. In a state \(\xi =(z,\eta )\) with  , the PDP \(\mathcal {Q}\) can either evolve to a state \(\xi '=\xi \oplus t\) by delaying t time units, or take a Markovian jump to \(\xi ''=(z'',\eta '')\in \mathbb {S}\) with probability \(\mu (\xi )(\{\xi ''\})\). When
, the PDP \(\mathcal {Q}\) can either evolve to a state \(\xi '=\xi \oplus t\) by delaying t time units, or take a Markovian jump to \(\xi ''=(z'',\eta '')\in \mathbb {S}\) with probability \(\mu (\xi )(\{\xi ''\})\). When  , \(\mathcal {Q}\) is forced to take a boundary jump to \(\xi ''=(z'',\eta '')\in \mathbb {S}\) with probability \(\mu (\xi )(\{\xi ''\})\).
, \(\mathcal {Q}\) is forced to take a boundary jump to \(\xi ''=(z'',\eta '')\in \mathbb {S}\) with probability \(\mu (\xi )(\{\xi ''\})\).
3 Reduction to the Reachability Probability of EPDP
As proved in [10], model-checking of a given CTMC \(\mathcal {C}\) against a linear real-time property expressed by a DTA \(\mathcal {A}\), i.e., determining  , can be reduced to computing the reachability probability of the product of \(\mathcal {C}\) and \(\mathcal {G}(\mathcal {A})\). This can be further reduced to computing the reachability probability of the embedded PDP (EPDP) of the product. But how to efficiently compute the reachability probability of the EPDP still remains challenging, as existing approaches [7, 10, 16] can only handle DTA with one clock. We will attack this challenge in this paper. For self-containedness, we reformulate the reduction reported in [10] in this section.
, can be reduced to computing the reachability probability of the product of \(\mathcal {C}\) and \(\mathcal {G}(\mathcal {A})\). This can be further reduced to computing the reachability probability of the embedded PDP (EPDP) of the product. But how to efficiently compute the reachability probability of the EPDP still remains challenging, as existing approaches [7, 10, 16] can only handle DTA with one clock. We will attack this challenge in this paper. For self-containedness, we reformulate the reduction reported in [10] in this section.
A path \(\rho =s_0\xrightarrow {t_0}s_1\xrightarrow {t_1}\ldots \) of CTMC \(\mathcal {C}\) is accepted by DTA \(\mathcal {A}\) if  induced by some \(\rho \)’s prefix is an accepting path of \(\mathcal {A}\). Then
induced by some \(\rho \)’s prefix is an accepting path of \(\mathcal {A}\). Then  .
.
Definition 6
(Product Region Graph [7]). The product of CTMC \(\mathcal {C} = (S, \mathbf {P}, \alpha , \textit{AP}, L, E)\) and the region graph of DTA \(\mathcal {G}(\mathcal {A})= (\varSigma ,\mathcal {X}, \overline{Q},\overline{q_0},\overline{Q_F},\mapsto )\), denoted by \(\mathcal {C}\otimes \mathcal {G}(\mathcal {A})\), is a tuple \((\mathcal {X}, V, \alpha ',V_F,\rightharpoonup ,\varLambda )\), where
-
\(V=S\times \overline{Q}\) is the state space;
-
\(\alpha '(s,\overline{q_0})=\alpha (s)\) is the initial distribution;
-
\(V_F=S\times \overline{Q_F}\) is the set of accepting states;
-
\(\rightharpoonup \,\subseteq V\times (([0,1]\times 2^{\mathcal {X}})\cup \{\lambda \})\times V\) is the smallest relation satisfying
-
 (called delay transition), if
(called delay transition), if  ;
; -
 (called Markovian transition), if \(\mathbf {P}(s,s'')=p,p>0\) and
(called Markovian transition), if \(\mathbf {P}(s,s'')=p,p>0\) and 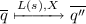 ;
;
-
-
\(\varLambda :V\rightarrow \mathbb {R}_{> 0}\) is the exit rate function, where
$$ \varLambda (s,\overline{q})=\left\{ \begin{array}{ll} E(s)&{} \text {if there exists a Markovian transition from}~ (s,\overline{q})\\ 0&{}\text {otherwise} \end{array}\right. $$
Remark 1
Note that the definition of region graph here is slightly different from the usual one in the sense that Markovian transitions starting from a boundary do not contribute to the reachability probability. Therefore we can merge the boundary into its unique delay successor.
Example 3
(Adapted from [10]). Figure 4 shows the product region graph of CTMC \(\mathcal {C}\) in Example 1 and DTA \(\mathcal {A}\) in Example 2. The graph can be split into three subgraphs in a column-wise manner, where all transitions within a subgraph are probabilistic, all transitions evolve to the next subgraph are delay transitions, and transitions with reset lead to a state in the first subgraph. For conciseness, the location \(v_9\) stands for all nodes that may be reached by a Markovian transition yet cannot reach an accepting node.
Proposition 1
([10]). For CTMC \(\mathcal {C}\) and DTA \(\mathcal {A}\),  is measurable and
is measurable and

When treated as a stochastic process, \(\mathcal {C}\otimes \mathcal {G}(\mathcal {A})\) can be interpreted as a PDP. In this way, computing the reachability probability of \(Q_F\) in \(\mathcal {C}\otimes \mathcal {G}(\mathcal {A})\) can be reduced to computing the time-unbounded reachability probability in the EPDP of \(\mathcal {C}\otimes \mathcal {G}(\mathcal {A})\).
Definition 7
(EPDP, [7]). Given \(\mathcal {C}\otimes \mathcal {G}(\mathcal {A})= (\mathcal {X}, V, \alpha ',V_F,\rightharpoonup ,\varLambda )\), the EPDP \(\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}\) is a tuple \((\mathcal {X},V,\textit{Inv},\phi ,\varLambda ,\mu )\) where for any \(v=(s,(q,\varTheta ))\in V\)
-
\(\textit{Inv}(v)=\varTheta \),
 is the state space;
is the state space; -
\(\phi (v,{\varvec{\eta }},t)={\varvec{\eta }} +t\) for
 ;
; -
\(\varLambda (v,\eta )=\varLambda (v)\) is the exit rate of \((v,\eta )\);
-
Boundary jump: for each delay transition
 in \(\mathcal {C}\otimes \mathcal {G}(\mathcal {A})\), \(\mu (\xi ,\{\xi '\})=1\) whenever \(\xi =(v,{\varvec{\eta }})\), \(\xi '=(v',{\varvec{\eta }})\) and
in \(\mathcal {C}\otimes \mathcal {G}(\mathcal {A})\), \(\mu (\xi ,\{\xi '\})=1\) whenever \(\xi =(v,{\varvec{\eta }})\), \(\xi '=(v',{\varvec{\eta }})\) and 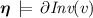 ;
; -
Markovian transition jump: for each Markovian transition
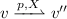 in \(\mathcal {C}\otimes \mathcal {G}(\mathcal {A})\), \(\mu (\xi ,\{\xi ''\})=p\) whenever \(\xi =(v,{\varvec{\eta }})\),
in \(\mathcal {C}\otimes \mathcal {G}(\mathcal {A})\), \(\mu (\xi ,\{\xi ''\})=p\) whenever \(\xi =(v,{\varvec{\eta }})\),  and \(\xi ''=(v'',{\varvec{\eta }}[X:=0])\).
and \(\xi ''=(v'',{\varvec{\eta }}[X:=0])\).
The flow function here describes that all clocks increase with a uniform rate (i.e., \(\dot{x_1}=1,\ldots ,\dot{x_n}=1\), or simply \(\dot{\mathcal {X}}=1\)) at all locations. The original reachability problem is then reduced to the reachability probability of the set  , given the initial state \((v_0,\mathbf {0})\) and the EPDP \(\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}\). Let \(\textit{Pr}^{\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}}_{v}({\varvec{\eta }})\) stand for the probability to reach the final states \((V_F\times *)\) from \((v,{\varvec{\eta }})\) in \(\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}\). Thus, \(\textit{Pr}^{\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}}_{v}({\varvec{\eta }})\) can be computed recursively by
, given the initial state \((v_0,\mathbf {0})\) and the EPDP \(\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}\). Let \(\textit{Pr}^{\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}}_{v}({\varvec{\eta }})\) stand for the probability to reach the final states \((V_F\times *)\) from \((v,{\varvec{\eta }})\) in \(\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}\). Thus, \(\textit{Pr}^{\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}}_{v}({\varvec{\eta }})\) can be computed recursively by

Let \(t^*_z(v,{\varvec{\eta }})\) denote the minimal time for \(\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}\) to reach \(\partial \textit{Inv}(v)\) from \((v,{\varvec{\eta }})\). More precisely,

\(\textit{Pr}^{\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}}_{v,\lambda }({\varvec{\eta }})\) is the probability from \((v,\eta )\) with a delay and then a forced jump to \((v', \eta +t^*_z(v,{\varvec{\eta }}))\), onwards evolves to an accepting state, which can be recursively computed by
\(\textit{Pr}^{\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}}_{v,v'}({\varvec{\eta }})\) is the probability that a Markovian transition  happens within \(t^*_z(v,{\varvec{\eta }})\) time units, onwards involves to an accepted state, which can be recursively computed by
happens within \(t^*_z(v,{\varvec{\eta }})\) time units, onwards involves to an accepted state, which can be recursively computed by
 is reduced to compute \(\textit{Pr}^{\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}}_{v_0}(\mathbf {0})\), equivalent to computing the least fixed point of the Eq. (1). That is,
is reduced to compute \(\textit{Pr}^{\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}}_{v_0}(\mathbf {0})\), equivalent to computing the least fixed point of the Eq. (1). That is,
Theorem 1
[10] For CTMC \(\mathcal {C}\) and DTA \(\mathcal {A}\),  is the least fixed point of (1).
is the least fixed point of (1).
Remark 2
Generally, it is difficult to solve a recursive equation like (1). As an alternative, we discuss the augmented EPDP of \(\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}\) by replacing \(\mathcal {A}\) with a bounded DTA resulting from \(\mathcal {A}\). As a consequence, using the extended generator of the augmented EPDP, we can induce a partial differential equation (PDE) whose solution is the reachability probability. We will elaborate the idea in the subsequent section.
4 Approximating the Reachability Probability of EPDP
In this section, we present a numerical method to approximate \({\textit{Pr}}^{\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}}_{v_0}(\mathbf {0})\), as we discussed previously that exactly computing is impossible, at least too expensive, in general. We will first introduce the basic idea of our approach in detail, then discuss its time complexity and convergence property. A key point is that our approach exploits the observation that the flow function of \(\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}\) is linear, only related to time t, and remains the same at all locations. This enables to reduce computing \({\textit{Pr}}^{\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}}_{v_0}(\mathbf {0})\) to solving an ODE system.
4.1 Reduction to a PDE System
In this subsection, we first show that \({\textit{Pr}}^{\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}}_{v_0}(\mathbf {0})\) can be approximated by that of the EPDP of \(\mathcal {C}\) and a bounded DTA derived from \(\mathcal {A}\), i.e., the length of all its paths is bounded. Then show that the latter can be reduced to solving a PDE system.
Given a DTA \(\mathcal {A}\), we construct a bounded DTA \(\mathcal {A}[t_f]\) by introducing a new clock y, adding a timing constraint \(y< t_f\) to the guard of each transition of \(\mathcal {A}\) ingoing to an accepting state in \(Q_F\), and never resetting y, where \(t_f\in \mathbb {N}\) is a parameter. So, the length of all accepting paths of \(\mathcal {A}[t_f]\) is time-bounded by \(t_f\). Obviously, \(\textit{Path}^{\mathcal {C}}(\mathcal {A}[t_f])\) is a subset of \(\textit{Path}^{\mathcal {C}}(\mathcal {A})\). As  is measurable and \(\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}\) is Borel right continuous, we have the following proposition.
is measurable and \(\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}\) is Borel right continuous, we have the following proposition.
Proposition 2
Given a CTMC \(\mathcal {C}\), a DTA \(\mathcal {A}\), and  ,
,

Moreover, if \(\mathcal {C}\) is weakly irreducible or satisfies some conditions (please refer to Chap. 4 of [26] for details), then there exist positive constants \(K, K_0\in \mathbb {R}_{\ge 0}\) such that

Remark 3
(2) was first observed in [7], thereof the authors pointed out the feasibility of using a bounded system to approximate the original unbounded system in order to simplify a verification obligation. (3) further indicates that such approximation is exponentially convergent w.r.t. \(-t_f\) if the CTMC is weakly irreducible.
For a path starting in a state \((v,{\varvec{\eta }})\) at time y, we use \(\textit{Path}_{(v,{\varvec{\eta }})}^{y}[t]\) to denote the set of its locations at time t, and \(\hbar _{v}(y,{\varvec{\eta }}) = \textit{Pr}(\textit{Path}_{(v,{\varvec{\eta }})}^{y}[t_f]\in V_{F})=\mathbb {E}( \mathbf {1}_{\textit{Path}_{(v,{\varvec{\eta }})}^{y}[t_f]\in V_{F}})\) as the probability of a path reaching \(V_F\) within \(t_f\) time units, where \(\mathbf {1}_{\textit{Path}_{(v,{\varvec{\eta }})}^{y}[t_f]\in V_{F}}\) is the indicator function of \(\textit{Path}_{(v,{\varvec{\eta }})}^{y}[t_f]\in V_{F}\). Then,  is the probability to reach the set of accepting states from the initial state \((0,\mathbf {0})\), which satisfies the following system of PDEs.
is the probability to reach the set of accepting states from the initial state \((0,\mathbf {0})\), which satisfies the following system of PDEs.
Theorem 2
Given a CTMC \(\mathcal {C}\), a bounded DTA \(\mathcal {A}[t_f]\), and the EPDP \(\mathcal {Q}^{\mathcal {C}\otimes \mathcal {G}(\mathcal {A}[t_f])}=(\mathcal {X},V,\textit{Inv},\phi ,\varLambda ,\mu )\), \(\hbar _{v_0}(0,\mathbf {0})\) is the unique solution of the following system of PDEs:

where  is the i-th clock variable and \(y\in [0,t_f)\). The boundary conditions are:
is the i-th clock variable and \(y\in [0,t_f)\). The boundary conditions are:
-
(i)
\(\hbar _v(y,{\varvec{\eta }})=\hbar _{v'}(y,{\varvec{\eta }})\), for every
 and transition \(v\xrightarrow []{\lambda } v'\);
and transition \(v\xrightarrow []{\lambda } v'\); -
(ii)
\(\hbar _v(y,{\varvec{\eta }})=1\), for every vertex \(v\in V_F\),
 , and \(y\in [0,t_f)\);
, and \(y\in [0,t_f)\); -
(iii)
\(\hbar _v(t_f,{\varvec{\eta }})=0\), for every vertex \(v\in V\backslash V_F\) and
 .
.
Remark 4
Note that the PDE system (4) in Theorem 2 is different from the one presented in [10] for reducing \({\textit{Pr}}^{\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}}}_{v_0}(\mathbf {0})\). In particular, the boundary condition in [10] has been corrected here.
4.2 Reduction to an ODE System
There are several classical methods to solve PDEs. Finite element method, which is a numerical technique for solving PDEs as well as integral equations, is a prominent one, of which different versions have been established to solve different PDEs with specific properties. Other numerical methods include finite difference method and finite volume method and so on, the reader is referred to [20, 21] for details. Thanks to the special form of the Eq. (4), we are able to obtain a numerical solution in a more efficient way.
The fact that the flow function (which is the solution to the ODE system\(\bigwedge _{x\in \mathcal {X}} \, \dot{x}=1 \wedge \dot{y}=1\)) is the same at all locations of the EPDP \(\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}[t_f]}\) suggests that the partial derivatives of \({{\varvec{\eta }}}\) and y in the left side of (4) evolve with the same pace. Thus, we can view all clocks as an array, and reformulate (4) as

where \(\bullet \) stands for the inner product of two vectors of the same dimension, e.g., \((a_1,\ldots , a_n) \bullet (b_1,\ldots , b_n) =\sum _{i=1}^{n} a_ib_i\), and \(\mathbf {1}\) for the vector \((\overbrace{1,\ldots ,1}^{n \, \text {times}})\).
By Theorem 2, there exist \(v_0\), \(y_0\) and \(\eta _0\) such that \(v_0\in V_F\), \(y_0=t_f\), and  . Besides, by the definition of \(\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}[t_f]}\), it follows \( \frac{\partial z}{\partial t} =1\), which implies \(d z =d t\), for any \(z\in \{y\}\cup \mathcal {X}\). Hence, we can simplify (5) as the following ODE system:
. Besides, by the definition of \(\mathcal {Q}^{\mathcal {C}\otimes \mathcal {A}[t_f]}\), it follows \( \frac{\partial z}{\partial t} =1\), which implies \(d z =d t\), for any \(z\in \{y\}\cup \mathcal {X}\). Hence, we can simplify (5) as the following ODE system:

with the initial condition \(v_0\in V_F\), \(y_0=t_f\), and  , where \(v\in V\backslash V_F\). Note that we compute the reachability probability by (6) backwards.
, where \(v\in V\backslash V_F\). Note that we compute the reachability probability by (6) backwards.
4.3 Numerical Solution
Since \(\hbar _v((y_0,{\varvec{\eta }}_0)+t)\) satisfies an ODE equation, we can apply a discretization method to (6) and obtain an approximation efficiently. To this end, the remaining obstacle is how to deal with the reset part \({\hbar _{v'}(y_0+t,({\varvec{\eta }}_0+t)[X:=0])}\). Notice that \(X\ne \emptyset \Rightarrow \text {sum}(({\varvec{\eta }}_0+t)[X:=0]) +(t_f-y_0-t))< \text {sum}({\varvec{\eta }}_{\mathbf {0}}+t)+(t_f-t_0-t)\), where \(\text {sum}({\varvec{\eta }}) = \sum _{x\in \mathcal {X}} {\varvec{\eta }}(x)\). So we just need to solve the ODE system starting from \((t_f,{\varvec{\eta }}_0)\) using the descending order over \(\text {sum}({\varvec{\eta }})\) in a backward manner. In this way, all of the reset values needed for the current iteration have been computed in the previous iterations. Therefore for each iteration, the derivation is fixed and easy to calculate.
We denote by \(\delta \) the length of discretization step, the number of total discretization steps is \(\lceil \frac{t_f}{\delta } \rceil \in \mathbb {N}\). An approximate solution to (4) can be computed efficiently by the following algorithm.
Line 4 in Algorithm 1 computes a numerical solution to (6) on \([t_f-t, t_f]\) by discretizing \(\frac{d\hbar _v((y_0,{\varvec{\eta }}_0)+t)}{d t}\) with \(\frac{1}{\delta }(\hbar _v((y_0,{\varvec{\eta }}_0)+(t+\delta ))-\hbar _v((y_0,{\varvec{\eta }}_0)+t))\). A pictorial illustration to Algorithm 1 for the two-dimensional setting is shown in Fig. 5. The blue polyhedron covers all the points we need to calculate. The algorithm starts from \((0,0,t_f)\), where \(\text {sum}({\varvec{\eta }})=x_1+x_2=0\). Then \(\text {sum}({\varvec{\eta }})\) is incremented until \(2t_f\) in a stepwise manner. For each fixed \(\text {sum}({\varvec{\eta }})\), for example \(\text {sum}({\varvec{\eta }})=t_f\), the algorithm calculates all discrete points in the gray plane following the direction \((-1,-1,-1)\), and finally reaches the two reset lines. The red line reaching the origin provides the final result.

Example 4
Consider the product \(\mathcal {C} \otimes \mathcal {G}(\mathcal {A})\) shown in Example 3 (in page 8). For state \(v_3\) in which clock x is 1 and y is arbitrary, the corresponding PDE is
Since \(\text {sum}(y,0)=y<y+1= \text {sum}(y,1)\), the value for \(\hbar _{v_0}(y,0)\), \(\hbar _{v_4}(y,0)\) and \(\hbar _{v_3}(y,0)\) have been calculated in the previous iterations, thus the value for \(\hbar _{v_3}(y,1)\) can be computed.
To optimize Algorithm 1 for multi-clock objects, we exploit the idea of “lazy computation”. In Algorithm 1, in order to determine the reset part for (6), we calculate all discretized points generated by all ODEs. The efficiency is influenced since the amount of ODEs is quite large (the same as the number of states in product automaton). However in Algorithm 2, we only compute the reset part that we need for computing \(\hbar _{v_0}(0,\mathbf {0})\). If we meet a reset part \(\hbar _{v}(y,{\varvec{\eta }}[X:=0])\) which has not been decided yet, we suspend the equation we are computing now and switch to compute the equation leading to the undecided point following the direction of \((-1,\ldots ,-1)\). The algorithm terminates since the number of points it computes is no more than that of Algorithm 1. A pseudo-code is described in Algorithm 2.

4.4 Complexity Analysis
Let |S| be the number of the states of the CTMC, and n the number of the clocks of the DTA. The worst-case time complexity of Algorithms 1 and 2 lies in \(\mathcal {O}(|V|\cdot \lceil \frac{t_f}{\delta }\rceil ^{(n+1)})\), where |V| is the number of the equations in (4), i.e., the number of the locations in the product region graph, that are not accepting. The number of states in the region graph of the DTA is bounded by \(n!\cdot 2^{n-1}\cdot \prod _{x\in \mathcal {X}}(c_x+1)\), denoted by \(C_b\), where \(c_x\) is the maximum constant occurring in the guards that constrain x. Note that \(C_{b}\) differs from the bound given in [1], since the boundaries of a region do not matter in our setting and hence can be merged into the region. Thus, the number of states in the product region graph, as well as the number of PDE equations in Theorem 2, is at most \(C_{b}\cdot |S|\). So the total complexity is \(\mathcal {O}(C_{b}\cdot |S|\cdot \lceil \frac{t_f}{\delta }\rceil ^{(n+1)})\).
Let \(\hbar _{v,n}(y_0,{\varvec{\eta }}_0)\) denote the numerical solution to ODE (6) with \(t=-n\delta \), and \(\varLambda _{max}=\max \{ \varLambda (v_i)\mid 0\le i \le |S|\}\). Let \(N=\lceil \frac{t_f}{\delta }\rceil \). By Proposition 2,  and \(\hbar _v(0,\mathbf {0})\) is monotonically increasing for \(t_f.\) In the following proposition, for simplicity of discussion, we assume \(t_f\) equal to \(N\delta \). Then, the error caused by discretization can be estimated as follows:
and \(\hbar _v(0,\mathbf {0})\) is monotonically increasing for \(t_f.\) In the following proposition, for simplicity of discussion, we assume \(t_f\) equal to \(N\delta \). Then, the error caused by discretization can be estimated as follows:
Proposition 3
For \(N\in \mathbb {N}^+\) and \(\delta =\frac{t_f}{N},\)
For function \(f(\delta )\), f is of the magnitude \(\mathcal {O}(\delta )\) if \(\varlimsup \limits _{\delta \rightarrow 0}\left| \frac{f(\delta )}{\delta }\right| =C\), where C is a constant. From Proposition 3, if we view \(\varLambda _{\max }\) and \(t_f\) as constants, then the error is \(\mathcal {O}(\delta )\) to the step length \(\delta \). By Proposition 2, the numerical solution generated by Algorithm 1 converges to the reachability probability of \(\mathcal {C}\otimes \mathcal {A}\), and the error can be as small as we expect if we decrease the size of discretization \(\delta \), and increase the time bound \(t_f\).
5 Experimental Results
We implemented a prototype including Algorithms 1 and 2 in C and a tool taking a CTMC \(\mathcal {C}\) and a DTA \(\mathcal {A}\) as input and generating a .c file to store their product in Python, which is used as an input to Algorithms 1 and 2. The first two examples (Examples 5 and 6) come from [10] to show the feasibility of our tool. The last case study is an example of robot navigation from [7]. In order to demonstrate the scalability of our approach, we revise the example with different real-time requirements, which require DTA with different number of clocks. The examples are executed in Linux 16.04 LTS with Intel(R) Core(TM) i7-4710HQ 2.50 GHz CPU and 16 G RAM. The column “time” reports the running time for Algorithm 1, and “time (lazy)” reports the running time for Algorithm 2. All time is counted in seconds.
Example 5
Consider Example 3 with \(r_i=1\), \(i=0,\ldots 3\) and \(\delta =0.01\), experimental result is shown in Table 1. The relevant error when \(t_f=30\) and \(t_f=40\) is \(5\times 10^{-7}\).
Example 6
Consider the reachability probability for the product of a CTMC and a DTA as shown in Fig. 6. A part of its region graph is shown in Fig. 7. Set \(r_0=r_1=1\), \(\delta = 0.1\), the experimental result is given in Table 1. The relevant error when \(t_f=30\) and \(t_f=40\) is \(1\times 10^{-7}\). Note that even for this simple example, none of existing tools can handle it.
The product automaton of Example 6
The reachable product region graph of Fig. 6.
Example 7
Consider a robot moves on a \(N\times N\) grid as shown in Fig. 8 (adapted from [7]). It can move up, down, left and right. For each possible direction, the robot moves with the same probability. The cells are grouped with A, B, C and D. We consider the following real-time constraints:
- \(P_1\)::
-
The robot is allowed to stay in adjacent C-cells for at most \(T_1\) time units, and D-cells for at most \(T_2\) time units;
- \(P_2\)::
-
The total time of the robot continuously resides in adjacent C-cell and D-cell is no more than \(T_3\) time units, with \(T_1\le T_3\) and \(T_2\le T_3\);
- \(P_3\)::
-
The total time of the robot continuously resides in adjacent A-cell and C-cell is no more than \(T_4\) time units, with \(T_1\le T_4\).
In this example, we are verifying whether the CTMC satisfies (i) \(P_1\); (ii) \(P_1 \wedge P_2\); (iii) \(P_1\wedge P_2\wedge P_3\). Obviously, \(P_1\) can be expressed by a DTA with one clock, see Fig. 9; to express \(P_1 \wedge P_2\), a DTA with two clocks is necessary, see Fig. 10; to express \(P_1 \wedge P_2 \wedge P_3\), A DTA with three clocks is necessary, see Fig. 11.
The experimental results are summarized in Table 2. The relevant error of \(t_f=20\) and \(t_f=21\) is smaller than \(10^{-2}\). As can be seen, the running time of our approach heavily depends on the number of clocks. Compared with the results reported in [7] for the case of one clock in this case study (when the precision is set to be \(10^{-2}\)), our result is as fast as theirs, but their tool cannot handle the cases of multiple clocks. In contrast, our approach can handle DTA with multiple clocks as indicated in the verification of \(P_2\) and \(P_3\). Algorithm 2 is much more faster than Algorithm 1 when the number of clocks grows up. To the best of our knowledge, this is the first prototypical tool verifying CTMCs against multi-clock DTA.
6 Concluding Remarks
In this paper, we present a practical approach to verify CTMCs against DTA objectives. First, the desired probability can be reduced to the reachability probability of the product region graph in the form of PDPs. Then we use the augmented PDP to approximate the reachability probability, in which the reachability probability coincides with the solution to a PDE system at the starting point. We further propose a numerical solution to the PDE system by reduction it to a ODE system. The experimental results indicate the efficiency and scalability compared with existing work, as it can handle DTA with multiple clocks.
As a future work, it deserves to investigate whether our approach also works in the verification of CTMCs against more complicated real-time properties, either expressed by timed automata and MTL as considered in [9], or by linear duration invariants as considered in [8].
References
Alur, R., Dill, D.L.: A theory of timed automata. Theoret. Comput. Sci. 126(2), 183–235 (1994)
Amparore, E.G., Beccuti, M., Donatelli, S.: (Stochastic) model checking in GreatSPN. In: Ciardo, G., Kindler, E. (eds.) PETRI NETS 2014. LNCS, vol. 8489, pp. 354–363. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-07734-5_19
Aziz, A., Sanwal, K., Singhal, V., Brayton, R.: Model-checking continous-time Markov chains. ACM Trans. Comput. Log. 1(1), 162–170 (2000)
Baier, C., Cloth, L., Haverkort, B.R., Kuntz, M., Siegle, M.: Model checking Markov chains with actions and state labels. IEEE Trans. Softw. Eng. 33(4), 209–224 (2007)
Baier, C., Haverkort, B., Hermanns, H., Katoen, J.-P.: Model-checking algorithms for continuous-time Markov chains. IEEE Trans. Softw. Eng. 29(6), 524–541 (2003)
Baier, C., Katoen, J.-P.: Principles of Model Checking. MIT Press, Cambridge (2008)
Barbot, B., Chen, T., Han, T., Katoen, J.-P., Mereacre, A.: Efficient CTMC model checking of linear real-time objectives. In: Abdulla, P.A., Leino, K.R.M. (eds.) TACAS 2011. LNCS, vol. 6605, pp. 128–142. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19835-9_12
Chen, T., Diciolla, M., Kwiatkowska, M., Mereacre, A.: Verification of linear duration properties over continuous-time Markov chains. ACM Trans. Comput. Log. 14(4), 33 (2013)
Chen, T., Diciolla, M., Kwiatkowska, M., Mereacre, A.: Time-bounded verification of CTMCs against real-time specifications. In: Fahrenberg, U., Tripakis, S. (eds.) FORMATS 2011. LNCS, vol. 6919, pp. 26–42. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-24310-3_4
Chen, T., Han, T., Katoen, J.-P., Mereacre, A.: Quantitative model checking of continuous-time Markov chains against timed automata specifications. In: LICS, pp. 309–318 (2009)
Chen, T., Han, T., Katoen, J., Mereacre, A.: Model checking of continuous-time Markov chains against timed automata specifications. Log. Methods Comput. Sci. 7(1) (2011)
Chen, T., Han, T., Katoen, J.-P., Mereacre, A.: Observing continuous-time MDPs by 1-clock timed automata. In: Delzanno, G., Potapov, I. (eds.) RP 2011. LNCS, vol. 6945, pp. 2–25. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-24288-5_2
Dang, V.H., Zhou, C.: Probabilistic duration calculus for continuous time. Formal Aspects Comput. 11(1), 21–44 (1999)
Davis, M.H.: Markov Models and Optimization, vol. 49. CRC Press, Boca Raton (1993)
Dehnert, C., Junges, S., Katoen, J.-P., Volk, M.: A Storm is coming: a modern probabilistic model checker. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017. LNCS, vol. 10427, pp. 592–600. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63390-9_31
Donatelli, S., Haddad, S., Sproston, J.: Model checking timed and stochastic properties with \({\rm CSL}^{{T\!\!A}}\). IEEE Trans. Softw. Eng. 35(2), 224–240 (2009)
Feller, W.: An Introduction to Probability Theory and Its Applications, vol. 3. Wiley, New York (1968)
Fu, H.: Approximating acceptance probabilities of CTMC-paths on multi-clock deterministic timed automata. In: HSCC, pp. 323–332. ACM (2013)
Gao, Y., Xu, M., Zhan, N., Zhang, L.: Model checking conditional CSL for continuous-time Markov chains. Inf. Process. Lett. 113(1–2), 44–50 (2013)
Grossmann, C., Roos, H.-G., Stynes, M.: Numerical Treatment of Partial Differential Equations, vol. 154. Springer, Heidelberg (2007)
Johnson, C.: Numerical Solution of Partial Differential Equations by the Finite Element Method. Courier Corporation, Chelmsford (2012)
Katoen, J.-P., Zapreev, I.S., Hahn, E.M., Hermanns, H., Jansen, D.N.: The ins and outs of the probabilistic model checker MRMC. Perform. Eval. 68(2), 90–104 (2011)
Kwiatkowska, M., Norman, G., Parker, D.: PRISM 4.0: verification of probabilistic real-time systems. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 585–591. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_47
Mikeev, L., Neuhäußer, M.R., Spieler, D., Wolf, V.: On-the-fly verification and optimization of DTA-properties for large Markov chains. Formal Methods Syst. Des. 43(2), 313–337 (2013)
Wisniewski, R., Sloth, C., Bujorianu, M.L., Piterman, N.: Safety verification of piecewise-deterministic Markov processes. In: HSCC, pp. 257–266. ACM (2016)
Yin, G.G., Zhang, Q.: Continuous-Time Markov Chains and Applications: A Two-Time-Scale Approach, vol. 37. Springer, New York (2012). https://doi.org/10.1007/978-1-4614-4346-9
Zhang, L., Jansen, D.N., Nielson, F., Hermanns, H.: Efficient CSL model checking using stratification. Log. Methods Comput. Sci. 8(2:17), 1–18 (2012)
Zhou, C., Hoare, C.A.R., Ravn, A.P.: A calculus of durations. Inf. Process. Lett. 40(5), 269–276 (1991)
Acknowledgements
This research is partly funded by the Sino-German Center for Research Promotion as part of the project CAP (GZ 1023), from Yijun Feng, Haokun Li and Bican Xia is partly funded by NSFC under grant No. 61732001 and 61532019, from Joost-Pieter Katoen is partly funded by the DFG Research Training Group 2236 UnRAVeL, from Naijun Zhan is funded partly by NSFC under grant No. 61625206 and 61732001, by “973 Program” under grant No. 2014CB340701 and by the CAS/SAFEA International Partnership Program for Creative Research Teams.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
<SimplePara><Emphasis Type="Bold">Open Access</Emphasis>This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.</SimplePara><SimplePara>The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.</SimplePara>
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Feng, Y., Katoen, JP., Li, H., Xia, B., Zhan, N. (2018). Monitoring CTMCs by Multi-clock Timed Automata. In: Chockler, H., Weissenbacher, G. (eds) Computer Aided Verification. CAV 2018. Lecture Notes in Computer Science(), vol 10981. Springer, Cham. https://doi.org/10.1007/978-3-319-96145-3_27
Download citation
DOI: https://doi.org/10.1007/978-3-319-96145-3_27
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96144-6
Online ISBN: 978-3-319-96145-3
eBook Packages: Computer ScienceComputer Science (R0)






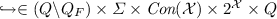 is the transition relation, satisfying if
is the transition relation, satisfying if  and
and  with
with  if
if  if there exists
if there exists  such that
such that 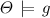 and
and 

 is the state space for
is the state space for  is the interior of
is the interior of  (called delay transition), if
(called delay transition), if  ;
; (called Markovian transition), if
(called Markovian transition), if 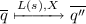 ;
;
 is the state space;
is the state space; ;
; in
in 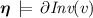 ;
;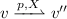 in
in  and
and  and transition
and transition  , and
, and  .
.





