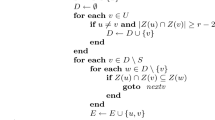A Direct Encoding for NNC Polyhedra

Abstract

We present an alternative Double Description representation for the domain of NNC (not necessarily closed) polyhedra, together with the corresponding Chernikova-like conversion procedure. The representation uses no slack variable at all and provides a solution to a few technical issues caused by the encoding of an NNC polyhedron as a closed polyhedron in a higher dimension space. A preliminary experimental evaluation shows that the new conversion algorithm is able to achieve significant efficiency improvements.

1 Introduction

The Double Description (DD) method [28] allows for the representation and manipulation of convex polyhedra by using two different geometric representations: one based on a finite collection of constraints, the other based on a finite collection of generators. Starting from any one of these representations, the other can be derived by application of a conversion procedure [10,11,12], thereby obtaining a DD pair. The procedure is incremental, capitalizing on the work already done when new constraints and/or generators need to be added to an input DD pair.

The DD method lies at the foundation of many software libraries and tools¹ which are used, either directly or indirectly, in research fields as diverse as bioinformatics [31, 32], computational geometry [1, 2], analysis of analog and hybrid systems [8, 18, 22, 23], automatic parallelization [6, 29], scheduling [16], static analysis of software [4, 13, 15, 17, 21, 24].

In the classical setting, the DD method is meant to compute geometric representations for topologically closed polyhedra in an n-dimensional vector space. However, there are applications requiring the ability to also deal with linear strict inequality constraints, leading to the definition of not necessarily closed (NNC) polyhedra. For example, this is the case for some of the analysis tools developed for the verification of hybrid systems [8, 18, 22, 23], static analysis tools such as Pagai [24], and tools for the automatic discovery of ranking functions [13].

The few DD method implementations providing support for NNC polyhedra (Apron and PPL) are all based on an indirect representation. The approach, proposed in [22, 23] and studied in more detail in [3, 5], encodes the strict inequality constraints by means of an additional space dimension, playing the role of a slack variable; the new space dimension, usually denoted as $\epsilon$, needs to be non-negative and bounded from above, i.e., the constraints $0 \le \epsilon \le 1$ are added to the topologically closed representation $\mathcal {R}$ (called $\epsilon$-representation) of the NNC polyhedron $\mathcal {P}$. The main advantage of this approach is the possibility of reusing, almost unchanged, all of the well-studied algorithms and optimizations that have been developed for the classical case of closed polyhedra. However, the addition of a slack variable carries with itself a few technical issues.

• At the implementation level, more work is needed to make the $\epsilon$ dimension transparent to the end user.

• The $\epsilon$-representation causes an intrinsic overhead: in any generator system for an $\epsilon$-polyhedron, most of the “proper” points (those having a positive $\epsilon$ coordinate) need to be paired with the corresponding “closure” point (having a zero $\epsilon$ coordinate), almost doubling the number of generators.

• The DD pair in minimal form computed for an $\epsilon$-representation $\mathcal {R}$, when reinterpreted as encoding the NNC polyhedron $\mathcal {P}$, typically includes many redundant constraints and/or generators, leading to inefficiencies. To avoid this problem, strong minimization procedures were defined in [3, 5] that are able to detect and remove those redundancies. Even though effective, these procedures are not fully integrated into the DD conversion: they can only be applied after the conversion, since they interfere with incrementality. Hence, during the iterations of the conversion the $\epsilon$-redundancies are not removed, causing the computation of bigger intermediate results.

In this paper, we pursue a different approach for the handling of NNC polyhedra in the DD method. Namely, we specify a direct representation, dispensing with the need of the slack variable. The main insight of this new approach is the separation of the (constraints or generators) geometric representation into two components, the skeleton and the non-skeleton of the representation, playing quite different roles: while keeping a geometric encoding for the skeleton component, we will adopt a combinatorial encoding for the non-skeleton one. For this new representation, we propose the corresponding variant of the Chernikova’s conversion procedure, where both components are handled by respective processing phases, so as to take advantage of their peculiarities. In particular, we develop ad hoc functions and procedures for the combinatorial non-skeleton part.

The new representation and conversion procedure, in principle, can be integrated into any of the available implementations of the DD method. Our experimental evaluation is conducted in the context of the PPL and shows that the new algorithm, while computing the correct results for all of the considered tests, achieves impressive efficiency improvements with respect to the implementation based on the slack variable.

The paper is structured as follows. Section 2 briefly introduces the required notation, terminology and background concepts. Section 3 proposes the new representation for NNC polyhedra; the proofs of the stated results are in [7]. The extension of the Chernikova’s conversion algorithm to this new representation is presented in Sect. 4. Section 5 reports the results obtained by the experimental evaluation. We conclude in Sect. 6.

2 Preliminaries

We assume some familiarity with the basic notions of lattice theory [9]. For a lattice $\langle L, \sqsubseteq , \bot , \top , \sqcap , \sqcup \rangle$, an element $a \in L$ is an atom if $\bot \sqsubset a$ and there exists no element $b \in L$ such that $\bot \sqsubset b \sqsubset a$. For $S \subseteq L$, the upward closure of S is defined as $\mathop {\uparrow }\nolimits S \mathrel {\buildrel \mathrm {def} \over {=}}\{\, x \in L \mid \exists s \in S \mathrel {.}s \sqsubseteq x \,\}$. The set $S \subseteq L$ is upward closed if $S = \mathop {\uparrow }\nolimits S$; we denote by $\mathop {\wp _{\uparrow }}\nolimits (L)$ the set of all the upward closed subsets of L. For $x \in L$, $\mathop {\uparrow }\nolimits x$ is a shorthand for $\mathop {\uparrow }\nolimits \{x \}$. The notation for downward closure is similar. Given two posets $\langle L, \sqsubseteq \rangle$ and $\langle L^\sharp , \sqsubseteq ^\sharp \rangle$ and two monotonic functions and , the pair $(\alpha , \gamma )$ is a Galois connection [14] between L and $L^\sharp$ if $\forall x \in L, x^\sharp \in L^\sharp \mathrel {:}\alpha (x) \sqsubseteq ^\sharp x^\sharp \Leftrightarrow x \sqsubseteq \gamma (x^\sharp )$.

We write $\mathbb {R}^n$ to denote the Euclidean topological space of dimension $n > 0$ and $\mathbb {R}_{\scriptscriptstyle {+}}$ for the set of non-negative reals; for $S \subseteq \mathbb {R}^n$, $\mathop {\mathrm {cl}}\nolimits (S)$ and $\mathop {\mathrm {relint}}\nolimits (S)$ denote the topological closure and the relative interior of S, respectively. A topologically closed convex polyhedron (for short, closed polyhedron) is defined as the set of solutions of a finite system $\mathcal {C}$ of linear non-strict inequality and linear equality constraints; namely, $\mathcal {P}= \mathop {\mathrm {con}}\nolimits (\mathcal {C})$ where

A vector $\varvec{r} \in \mathbb {R}^n$ such that $\varvec{r} \ne \varvec{0}$ is a ray of a non-empty polyhedron $\mathcal {P}\subseteq \mathbb {R}^n$ if, $\forall \varvec{p} \in \mathcal {P}$ and $\forall \rho \in \mathbb {R}_{\scriptscriptstyle {+}}$, it holds $\varvec{p} + \rho \varvec{r} \in \mathcal {P}$. The empty polyhedron has no rays. If both $\varvec{r}$ and $-\varvec{r}$ are rays of $\mathcal {P}$, then $\varvec{r}$ is a line of $\mathcal {P}$. The set $\mathcal {P}\subseteq \mathbb {R}^n$ is a closed polyhedron if there exist finite sets $L, R, P \subseteq \mathbb {R}^n$ such that $\varvec{0} \notin (L \mathrel {\cup }R)$ and $\mathcal {P}= \mathop {\mathrm {gen}}\nolimits \bigl (\langle L, R, P \rangle \bigr )$, where

$$\begin{aligned} \mathop {\mathrm {gen}}\nolimits \bigl ( \langle L, R, P \rangle \bigr ) \mathrel {\buildrel \mathrm {def} \over {=}}\bigl \{ L \varvec{\lambda } + R \varvec{\rho } + P \varvec{\pi } \in \mathbb {R}^n \bigm | \varvec{\lambda } \in \mathbb {R}^{\ell }, \varvec{\rho } \in \mathbb {R}_{\scriptscriptstyle {+}}^r, \varvec{\pi } \in \mathbb {R}_{\scriptscriptstyle {+}}^p, \textstyle {\sum _{i=1}^p \pi _i = 1} \bigr \}. \end{aligned}$$

When $\mathcal {P}\ne \emptyset$, we say that $\mathcal {P}$ is described by the generator system $\mathcal {G}= \langle L, R, P \rangle$. In the following, we will abuse notation by adopting the usual set operator and relation symbols to denote the corresponding component-wise extensions on systems. For instance, for $\mathcal {G}= \langle L, R, P \rangle$ and $\mathcal {G}' = \langle L', R', P' \rangle$, we will write $\mathcal {G}\subseteq \mathcal {G}'$ to mean $L \subseteq L'$, $R \subseteq R'$ and $P \subseteq P'$.

The DD method due to Motzkin et al. [28] allows combining the constraints and the generators of a polyhedron $\mathcal {P}$ into a DD pair $(\mathcal {C}, \mathcal {G})$: a conversion procedure [10,11,12] is used to obtain each description starting from the other one, also removing the redundant elements. For presentation purposes, we focus on the conversion from constraints to generators; the opposite conversion works in the same way, using duality to switch the roles of constraints and generators. We do not describe lower level details such as the homogenization process, mapping the polyhedron into a polyhedral cone, or the simplification step, needed for computing DD pairs in minimal form.

The conversion procedure starts from a DD pair $(\mathcal {C}_0, \mathcal {G}_0)$ representing the whole vector space and adds, one at a time, the elements of the input constraint system $\mathcal {C}= \{\beta _0, \dots , \beta _m \}$, producing a sequence of DD pairs $\bigl \{(\mathcal {C}_k, \mathcal {G}_k)\bigr \}_{0 \le k \le m+1}$ representing the polyhedra

$$\begin{aligned} \mathbb {R}^n = \mathcal {P}_0 \xrightarrow {\beta _0} \dots \xrightarrow {\beta _{k-1}} \mathcal {P}_k \xrightarrow {\beta _k} \mathcal {P}_{k+1} \xrightarrow {\beta _{k+1}} \dots \xrightarrow {\beta _m} \mathcal {P}_{m+1} = \mathcal {P}. \end{aligned}$$

At each iteration, when adding the constraint $\beta _k$ to polyhedron $\mathcal {P}_k = \mathop {\mathrm {gen}}\nolimits (\mathcal {G}_k)$, the generator system $\mathcal {G}_k$ is partitioned into the three components $\mathcal {G}^{+}_k$, $\mathcal {G}^{0}_k$, $\mathcal {G}^{-}_k$, according to the sign of the scalar products of the generators with $\beta _k$ (those in $\mathcal {G}^{0}_k$ are the saturators of $\beta _k$); the new generator system for polyhedron $\mathcal {P}_{k+1}$ is computed as $\mathcal {G}_{k+1} \mathrel {\buildrel \mathrm {def} \over {=}}\mathcal {G}^{+}_k \mathrel {\cup }\mathcal {G}^{0}_k \mathrel {\cup }\mathcal {G}^{\star }_k$, where $\mathcal {G}^{\star }_k = \mathop {\mathrm {comb\_adj}_{\beta _k}}\nolimits (\mathcal {G}^{+}_k, \mathcal {G}^{-}_k)$ and

$$\begin{aligned} \mathop {\mathrm {comb\_adj}_{\beta _k}}\nolimits (\mathcal {G}^{+}_k, \mathcal {G}^{-}_k) \mathrel {\buildrel \mathrm {def} \over {=}}\bigl \{\, \mathop {\mathrm {comb}_{\beta _k}}\nolimits (g^{+}, g^{-}) \bigm | g^{+} \in \mathcal {G}^{+}_k, g^{-} \in \mathcal {G}^{-}_k, \mathop {\mathrm {adj}}\nolimits _{\mathcal {P}_k}(g^{+}, g^{-}) \,\bigr \}. \end{aligned}$$

Function ‘’ computes a linear combination of its arguments, yielding a generator that saturates the constraint $\beta _k$; predicate ‘$\mathop {\mathrm {adj}}\nolimits _{\mathcal {P}_k}$’ is used to select only those pairs of generators that are adjacent in $\mathcal {P}_k$.

The set $\mathbb {CP}_n$ of all closed polyhedra on the vector space $\mathbb {R}^n$, partially ordered by set inclusion, is a lattice , where the empty set and $\mathbb {R}^n$ are the bottom and top elements, the binary meet operator is set intersection and the binary join operator ‘’ is the convex polyhedral hull. A constraint $\beta = (\varvec{a}^{\scriptscriptstyle \mathrm {T}}\varvec{x} \mathrel {\bowtie }b)$ is said to be valid for $\mathcal {P}\in \mathbb {CP}_n$ if all the points in $\mathcal {P}$ satisfy $\beta$; for each such $\beta$, the subset $F = \{\, \varvec{p} \in \mathcal {P}\mid \varvec{a}^{\scriptscriptstyle \mathrm {T}}\varvec{p} = b \,\}$ is a face of $\mathcal {P}$. We write $cFaces _{\mathcal {P}}$ (possibly omitting the subscript) to denote the finite set of faces of $\mathcal {P}\in \mathbb {CP}_n$. This is a meet sublattice of $\mathbb {CP}_n$ and $\mathcal {P}= \bigcup \bigl \{\, \mathop {\mathrm {relint}}\nolimits (F) \bigm | F \in cFaces _\mathcal {P}\,\bigr \}$.

When $\mathcal {C}$ is extended to allow for strict inequalities, $\mathcal {P}= \mathop {\mathrm {con}}\nolimits (\mathcal {C})$ is an NNC (not necessarily closed) polyhedron. The set $\mathbb {P}_n$ of all NNC polyhedra on $\mathbb {R}^n$ is a lattice and $\mathbb {CP}_n$ is a sublattice of $\mathbb {P}_n$. As shown in [3, Theorem 4.4], a description of an NNC polyhedron $\mathcal {P}\in \mathbb {P}_n$ can be obtained by extending the generator system with a finite set C of closure points. Namely, for $\mathcal {G}= \langle L, R, C, P \rangle$, we define $\mathcal {P}= \mathop {\mathrm {gen}}\nolimits (\mathcal {G})$, where

$$\begin{aligned} \mathop {\mathrm {gen}}\nolimits \bigl ( \langle L, R, C, P \rangle \bigr ) \mathrel {\buildrel \mathrm {def} \over {=}}{ \left\{ \, L \varvec{\lambda } + R \varvec{\rho } + C \varvec{\gamma } + P \varvec{\pi } \in \mathbb {R}^n \,\left| \, \begin{array}{@{}l@{}} \varvec{\lambda } \in \mathbb {R}^{\ell }, \varvec{\rho } \in \mathbb {R}_{\scriptscriptstyle {+}}^r, \\ \varvec{\gamma } \in \mathbb {R}_{\scriptscriptstyle {+}}^c, \varvec{\pi } \in \mathbb {R}_{\scriptscriptstyle {+}}^p, \varvec{\pi } \ne \varvec{0}, \\ \textstyle {\sum _{i=1}^c \gamma _i + \sum _{i=1}^p \pi _i = 1} \end{array} \right. \,\right\} }. \end{aligned}$$

For an NNC polyhedron $\mathcal {P}\in \mathbb {P}_n$, the finite set $nncFaces _\mathcal {P}$ of its faces is a meet sublattice of $\mathbb {P}_n$ and $\mathcal {P}= \bigcup \bigl \{\, \mathop {\mathrm {relint}}\nolimits (F) \bigm | F \in nncFaces _\mathcal {P}\,\bigr \}$. Letting $\mathcal {Q}= \mathop {\mathrm {cl}}\nolimits (\mathcal {P})$, the closure operator maps each NNC face of $\mathcal {P}$ into a face of $\mathcal {Q}$. The image $\mathop {\mathrm {cl}}\nolimits ( nncFaces _\mathcal {P})$ is a join sublattice of $cFaces _\mathcal {Q}$ and its nonempty elements form an upward closed subset, which can be described by recording the minimal elements only (i.e., the atoms of the $nncFaces _\mathcal {P}$ lattice).

3 Direct Representations for NNC Polyhedra

An NNC polyhedron can be described by using an extended constraint system and/or an extended generator system $\mathcal {G}= \langle L, R, C, P \rangle$. These representations are said to be geometric, meaning that they provide a precise description of the position of their elements. For a closed polyhedron $\mathcal {P}\in \mathbb {CP}_n$, the use of completely geometric representations is an adequate choice. In the case of an NNC polyhedron $\mathcal {P}\in \mathbb {P}_n$ such a choice is questionable, since the precise geometric position of some of the elements is not really needed.

Example 1

Consider the NNC polyhedron $\mathcal {P}\in \mathbb {P}_2$ in the next figure, where the (strict) inequality constraints are denoted by (dashed) lines and the (closure) points are denoted by (unfilled) circles.

$\mathcal {P}$ is described by $\mathcal {G}= \langle L, R, C, P \rangle$, where $L = R = \emptyset$, $C = \{c_0, c_1, c_2 \}$ and $P = \{p_0, p_1 \}$. However, there is no need to know the position of point $p_1$, since it can be replaced by any other point on the open segment $(c_0, c_1)$. Similarly, when considering the constraint representation, there is no need to know the exact slope of the strict inequality constraint $\beta$.

We now show that $\mathcal {P}\in \mathbb {P}_n$ can be more appropriately represented by integrating a geometric description of $\mathcal {Q}= \mathop {\mathrm {cl}}\nolimits (\mathcal {P}) \in \mathbb {CP}_n$ (the skeleton) with a combinatorial description of $nncFaces _\mathcal {P}$ (the non-skeleton). We consider here the generator system representation; the extension to constraints will be briefly outlined in a later section.

Definition 1

(Skeleton of a generator system). Let $\mathcal {G}= \langle L, R, C, P \rangle$ be a generator system in minimal form, $\mathcal {P}= \mathop {\mathrm {gen}}\nolimits (\mathcal {G})$ and $\mathcal {Q}= \mathop {\mathrm {cl}}\nolimits (\mathcal {P})$. The skeleton of $\mathcal {G}$ is $\mathcal {SK}_\mathcal {Q}= \mathop {\mathrm {skel}}\nolimits (\mathcal {G}) \mathrel {\buildrel \mathrm {def} \over {=}}\langle L, R, C \mathrel {\cup } SP , \emptyset \rangle$, where $SP \subseteq P$ holds the points that can not be obtained by combining the other generators in $\mathcal {G}$.

Note that the skeleton has no points at all, so that $\mathop {\mathrm {gen}}\nolimits (\mathcal {SK}_\mathcal {Q}) = \emptyset$. However, we can define a variant function $\mathop {\overline{\mathrm {gen}}}\nolimits \bigl ( \langle L, R, C, P \rangle \bigr ) \mathrel {\buildrel \mathrm {def} \over {=}}\mathop {\mathrm {gen}}\nolimits \bigl ( \langle L, R, \emptyset , C \mathrel {\cup }P \rangle \bigr )$, showing that the skeleton of an NNC polyhedron provides a non-redundant representation of its topological closure.

Proposition 1

If $\mathcal {P}= \mathop {\mathrm {gen}}\nolimits (\mathcal {G})$ and $\mathcal {Q}= \mathop {\mathrm {cl}}\nolimits (\mathcal {P})$, then $\mathop {\overline{\mathrm {gen}}}\nolimits (\mathcal {G}) = \mathop {\overline{\mathrm {gen}}}\nolimits (\mathcal {SK}_\mathcal {Q}) = \mathcal {Q}$. Also, there does not exist $\mathcal {G}' \subset \mathcal {SK}_\mathcal {Q}$ such that $\mathop {\overline{\mathrm {gen}}}\nolimits (\mathcal {G}') = \mathcal {Q}$.

The elements of $SP \subseteq P$ are called skeleton points; the non-skeleton points in $P \setminus SP$ are redundant when representing the topological closure; these non-skeleton points are the elements in $\mathcal {G}$ that need not be represented geometrically.

Consider a point $\varvec{p} \in \mathcal {Q}= \mathop {\mathrm {cl}}\nolimits (\mathcal {P})$ (not necessarily in P). There exists a single face $F \in cFaces _{\mathcal {Q}}$ such that $\varvec{p} \in \mathop {\mathrm {relint}}\nolimits (F)$. By definition of function ‘$\mathop {\mathrm {gen}}\nolimits$’, point $\varvec{p}$ behaves as a filler for $\mathop {\mathrm {relint}}\nolimits (F)$ meaning that, when combined with the skeleton, it generates $\mathop {\mathrm {relint}}\nolimits (F)$. Note that $\varvec{p}$ also behaves as a filler for the relative interiors of all the faces in the set $\mathop {\uparrow }\nolimits F$. The choice of $\varvec{p} \in \mathop {\mathrm {relint}}\nolimits (F)$ is actually arbitrary: any other point of $\mathop {\mathrm {relint}}\nolimits (F)$ would be equivalent as a filler. A less arbitrary representation for $\mathop {\mathrm {relint}}\nolimits (F)$ is thus provided by its own skeleton $\mathcal {SK}_F \subseteq \mathcal {SK}_{\mathcal {Q}}$; we say that $\mathcal {SK}_F$ is the support for the points in $\mathop {\mathrm {relint}}\nolimits (F)$ and that any point $\varvec{p}' \in \mathop {\mathrm {relint}}\nolimits \bigl (\mathop {\overline{\mathrm {gen}}}\nolimits (\mathcal {SK}_F)\bigr ) = \mathop {\mathrm {relint}}\nolimits (F)$ is a materialization of $\mathcal {SK}_F$.

In the following we will sometimes omit subscripts when clear from context.

Definition 2

(Support sets for a skeleton). Let $\mathcal {SK}$ be the skeleton of an NNC polyhedron and let $\mathcal {Q}= \mathop {\overline{\mathrm {gen}}}\nolimits (\mathcal {SK}) \in \mathbb {CP}_n$. The set of all supports for $\mathcal {SK}$ is defined as $\mathbb {NS}_{\mathcal {SK}} \mathrel {\buildrel \mathrm {def} \over {=}}\{\, \mathcal {SK}_F \subseteq \mathcal {SK}\mid F \in cFaces _{\mathcal {Q}} \,\}$.

We now define functions mapping a subset of the (geometric) points of an NNC polyhedron into the set of supports filled by these points, and vice versa.

Definition 3

(Filled supports). Let $\mathcal {SK}$ be the skeleton of the polyhedron $\mathcal {P}\in \mathbb {P}_n$, $\mathcal {Q}= \mathop {\mathrm {cl}}\nolimits (\mathcal {P})$ and $\mathbb {NS}$ be the corresponding set of supports. The abstraction function is defined, for each $S \subseteq \mathcal {Q}$, as

$$\begin{aligned} \alpha _{\mathcal {SK}}(S) \mathrel {\buildrel \mathrm {def} \over {=}}\bigcup \bigl \{\, \mathop {\uparrow }\nolimits \mathcal {SK}_F \bigm | \exists \varvec{p} \in S, F \in cFaces \mathrel {.}\varvec{p} \in \mathop {\mathrm {relint}}\nolimits (F) \,\bigr \}. \end{aligned}$$

The concretization function , for each $NS \in \mathop {\wp _{\uparrow }}\nolimits (\mathbb {NS})$, is defined as

$$\begin{aligned} \gamma _{\mathcal {SK}}( NS ) \mathrel {\buildrel \mathrm {def} \over {=}}\bigcup \Bigl \{\, \mathop {\mathrm {relint}}\nolimits \bigl (\mathop {\overline{\mathrm {gen}}}\nolimits ( ns )\bigr ) \Bigm | ns \in NS \,\Bigr \}. \end{aligned}$$

Proposition 2

The pair of functions $(\alpha _{\mathcal {SK}}, \gamma _{\mathcal {SK}})$ is a Galois connection. If $\mathcal {P}= \mathop {\mathrm {gen}}\nolimits \bigl ( \langle L, R, C, P \rangle \bigr ) \in \mathbb {P}_n$ and $\mathcal {SK}$ is its skeleton, then $\mathcal {P}= (\gamma _\mathcal {SK}\circ \alpha _\mathcal {SK})(P)$.

The non-skeleton component of a geometric generator system can be abstracted by ‘$\alpha _\mathcal {SK}$’ and described as a combination of skeleton generators.

Definition 4

(Non-skeleton of a generator system). Let $\mathcal {P}\in \mathbb {P}_n$ be defined by generator system $\mathcal {G}= \langle L, R, C, P \rangle$ and let $\mathcal {SK}$ be the corresponding skeleton component. The non-skeleton component of $\mathcal {G}$ is defined as $NS _\mathcal {G}\mathrel {\buildrel \mathrm {def} \over {=}}\alpha _\mathcal {SK}(P)$.

Example 2

Consider the generator system $\mathcal {G}$ of polyhedron $\mathcal {P}$ from Example 1. Its skeleton is $\mathcal {SK}= \bigl \langle \emptyset , \emptyset , \{c_0, c_1, c_2, p_0 \}, \emptyset \bigr \rangle$, so that $p_1$ is not a skeleton point. By Definition 3, $NS _{\mathcal {G}} = \alpha _\mathcal {SK}\bigl ( \{p_0, p_1 \} \bigr ) = \mathop {\uparrow }\nolimits \{p_0 \} \mathrel {\cup }\mathop {\uparrow }\nolimits \{c_0, c_1 \}$² The minimal elements in $NS _{\mathcal {G}}$ can be seen to describe the atoms of $nncFaces _\mathcal {P}$, i.e., the 0-dimension face $\{p_0 \}$ and the 1-dimension open segment $(c_0, c_1)$.

The new representation is semantically equivalent to the fully geometric one.

Corollary 1

For a polyhedron $\mathcal {P}= \mathop {\mathrm {gen}}\nolimits (\mathcal {G}) \in \mathbb {P}_n$, let $\langle \mathcal {SK}, NS \rangle$ be the skeleton and non-skeleton components for $\mathcal {G}$. Then $\mathcal {P}= \gamma _\mathcal {SK}( NS )$.

4 The New Conversion Algorithm

The conversion function in Pseudocode 1 incrementally processes each of the input constraints $\beta \in \mathcal {C}_{ in }$ keeping the generator system $\langle \mathcal {SK}, NS \rangle$ up-to-date. The distinction between the skeleton and non-skeleton allows for a corresponding separation in the conversion procedure. Moreover, a few minor adaptations to their representation, discussed below, allow for efficiency improvements.

First, observe that every support $ns \in NS$ always includes all of the lines in the L skeleton component; hence, these lines can be left implicit in the representation of the supports in $NS$. Note that, even after removing the lines, each $ns \in NS$ is still a non-empty set, since it includes at least one closure point.

When lines are implicit, those supports $ns \in NS$ that happen to be singletons³ can be seen to play a special role: they correspond to the combinatorial encoding of the skeleton points in $SP$ (see Definition 1). These points are not going to benefit from the combinatorial representation, hence we move them from the non-skeleton to the skeleton component; namely, $\mathcal {SK}= \langle L, R, C \mathrel {\cup } SP , \emptyset \rangle$ is represented as $\mathcal {SK}= \langle L, R, C, SP \rangle$. The formalization presented in Sect. 3 is still valid, replacing ‘$\gamma _{\mathcal {SK}}$’ with $\gamma '_{\mathcal {SK}}( NS ) \mathrel {\buildrel \mathrm {def} \over {=}}\mathop {\mathrm {gen}}\nolimits (\mathcal {SK}) \cup \gamma _{\mathcal {SK}}( NS )$.

At the implementation level, each support $ns \in NS$ can be encoded by using a set of indices on the data structure representing the skeleton component $\mathcal {SK}$. Since $NS$ is a finite upward closed set, the representation only needs to record its minimal elements. A support $ns \in NS$ is redundant in $\langle \mathcal {SK}, NS \rangle$ if there exists $ns ' \in NS$ such that $ns ' \subset ns$ or if $ns \mathrel {\cap } SP \ne \emptyset$, where $\mathcal {SK}= \langle L, R, C, SP \rangle$. We write $NS _1 \oplus NS _2$ to denote the non-redundant union of $NS _1, NS _2 \subseteq \mathbb {NS}_\mathcal {SK}$.

4.1 Processing the Skeleton

Line 3 of conversion partitions the skeleton $\mathcal {SK}$ into $\mathcal {SK}^+$, $\mathcal {SK}^0$ and $\mathcal {SK}^-$, according to the signs of the scalar products with constraint $\beta$. Note that the partition information is logically computed (no copies are performed) and it is stored in the $\mathcal {SK}$ component itself; therefore, any update to $\mathcal {SK}^+$, $\mathcal {SK}^0$ and $\mathcal {SK}^-$ directly propagates to $\mathcal {SK}$. In line 7 the generators in $\mathcal {SK}^+$ and $\mathcal {SK}^-$ are combined to produce $\mathcal {SK}^\star$, which is merged into $\mathcal {SK}^0$. These steps are similar to the ones for closed polyhedra, except that we now have to consider more kinds of combinations: the systematic case analysis is presented in Table 1. For instance, when processing a non-strict inequality $\beta _\ge$, if we combine a closure point in $\mathcal {SK}^+$ with a ray in $\mathcal {SK}^-$ we obtain a closure point in $\mathcal {SK}^\star$ (row 3, column 6). Since it is restricted to work on the skeleton component, this combination phase can safely apply the adjacency tests to quickly get rid of redundant elements.

Table 1. Case analysis for function ‘$\mathop {\mathrm {comb}_{\beta }}\nolimits$’ when adding an equality ($\beta _=$), a non-strict ($\beta _\ge$) or a strict ($\beta _>$) inequality constraint to a pair of generators from $\mathcal {SK}^+$ and $\mathcal {SK}^-$ (R = ray, C = closure point, SP = skeleton point).

4.2 Processing the Non-skeleton

Line 4 partitions the supports in $NS$ by exploiting the partition information for the skeleton $\mathcal {SK}$, so that no additional scalar product is computed. Namely, each support $ns \in NS$ is classified as follows:

$$\begin{aligned} ns \in NS ^+&\Longleftrightarrow ns \subseteq (\mathcal {SK}^+ \mathrel {\cup }\mathcal {SK}^0) \wedge ns \mathrel {\cap }\mathcal {SK}^+ \ne \emptyset ; \\ ns \in NS ^0&\Longleftrightarrow ns \subseteq \mathcal {SK}^0; \\ ns \in NS ^-&\Longleftrightarrow ns \subseteq (\mathcal {SK}^- \mathrel {\cup }\mathcal {SK}^0) \wedge ns \mathrel {\cap }\mathcal {SK}^- \ne \emptyset ; \\ ns \in NS ^\pm&\Longleftrightarrow ns \mathrel {\cap }\mathcal {SK}^+ \ne \emptyset \wedge ns \mathrel {\cap }\mathcal {SK}^- \ne \emptyset . \end{aligned}$$

This partitioning is consistent with the previous one. For instance, if $ns \in NS ^+$, then for every possible materialization $\varvec{p} \in \mathop {\mathrm {relint}}\nolimits (\mathop {\overline{\mathrm {gen}}}\nolimits ( ns ))$ the scalar product of $\varvec{p}$ and $\beta$ is strictly positive. The supports in $NS ^\pm$ are those whose materializations can satisfy, saturate and violate the constraint $\beta$ (i.e., the corresponding face crosses the constraint hyperplane).

In lines 8 and 9, we find the calls to the two main functions processing the non-skeleton component. A set $NS ^\star$ of new supports is built as the union of the contributes provided by functions move-ns and create-ns.

Moving Supports. The move-ns function, shown in Pseudocode 2, processes the supports in $NS ^\pm$: this function “moves” the fillers of the faces that are crossed by the new constraint, making sure they lie on the correct side.

Let $ns \in NS ^\pm$ and $F = \mathop {\mathrm {relint}}\nolimits (\mathop {\overline{\mathrm {gen}}}\nolimits ( ns ))$. Note that $ns = \mathcal {SK}_F$ before the addition of the new constraint $\beta$; at this point, the elements in $\mathcal {SK}^\star$ have been added to $\mathcal {SK}^0$, but this change still has to be propagated to the non-skeleton component $NS$. Therefore, we compute the support closure ‘$\mathop {\mathrm {supp.cl}}\nolimits _{\mathcal {SK}}( ns )$’ according to the updated skeleton $\mathcal {SK}$. Intuitively, $\mathop {\mathrm {supp.cl}}\nolimits _{\mathcal {SK}}( ns ) \subseteq \mathcal {SK}$ is the subset of all the skeleton elements that are included in face F.

At the implementation level, support closures can be efficiently computed by exploiting the same saturation information used for the adjacency tests. Namely, for constraints $\mathcal {C}$ and generators $\mathcal {G}$, we can define

$$\begin{aligned} \mathop {\mathrm {sat.inter}}\nolimits _{\mathcal {C}}(\mathcal {G})&\mathrel {\buildrel \mathrm {def} \over {=}}\{\, \beta ' \in \mathcal {C}\mid \forall g \in \mathcal {G}\mathrel {:}g\,\, \text {saturates}\,\, \beta ' \,\}, \\ \mathop {\mathrm {sat.inter}}\nolimits _\mathcal {G}(\mathcal {C})&\mathrel {\buildrel \mathrm {def} \over {=}}\{\, g \in \mathcal {G}\mid \forall \beta ' \in \mathcal {C}\mathrel {:}g\,\, \text {saturates}\,\, \beta ' \,\}. \end{aligned}$$

Then, if $\mathcal {C}$ and $\mathcal {SK}= \langle L, R, C, SP \rangle$ are the constraint system and the skeleton generator system for the polyhedron, for each $ns \in NS$ we can compute [26]:

$$\begin{aligned} \mathop {\mathrm {supp.cl}}\nolimits _\mathcal {SK}( ns )&\mathrel {\buildrel \mathrm {def} \over {=}}\mathop {\mathrm {sat.inter}}\nolimits _\mathcal {SK}\bigl (\mathop {\mathrm {sat.inter}}\nolimits _{\mathcal {C}}( ns )\bigr ) \mathrel {\setminus }L. \end{aligned}$$

Face F is split by constraint $\beta$ into $F^+$, $F^0$ and $F^-$. When $\beta$ is a strict inequality, only $F^+$ shall be kept in the polyhedron; when the new constraint is a non-strict inequality, both $F^+$ and $F^0$ shall be kept. A minimal non-skeleton representation for these subsets can be obtained by projecting the support:

$$ \mathop {\mathrm {proj}}\nolimits ^\beta _\mathcal {SK}( ns ) \mathrel {\buildrel \mathrm {def} \over {=}}{\left\{ \begin{array}{ll} ns \mathrel {\setminus }\mathcal {SK}^-, &{} \text {if}\,\, \beta \,\, \text {is a strict inequality;} \\ ns \mathrel {\cap }\mathcal {SK}^0, &{} \text {otherwise.} \end{array}\right. } $$

To summarize, by composing support closure and projection in line 3 of move-ns, each support in $NS ^\pm$ is moved to the correct side of $\beta$.

Example 3

Consider $\mathcal {P}\in \mathbb {P}_2$ in the left hand side of the next figure.

The skeleton $\mathcal {SK}= \langle \emptyset , \emptyset , C, \emptyset \rangle$ contains the closure points in $C = \{ c_0, c_1, c_2, c_3 \}$; the non-skeleton $NS = \{ ns \}$ contains a single support $ns = \{ c_0, c_3 \}$, which makes sure that the open segment $(c_0, c_3)$ is included in $\mathcal {P}$; the figure shows a single materialization for $ns$.

When processing $\beta = (y < 1)$, we obtain the polyhedron in the right hand side of the figure. In the skeleton phase of the conversion function the adjacent skeleton generators are combined: $c_4$ (from $c_0 \in \mathcal {SK}^+$ and $c_3 \in \mathcal {SK}^-$) and $c_5$ (from $c_1 \in \mathcal {SK}^+$ and $c_2 \in \mathcal {SK}^-$) are added to $\mathcal {SK}^0$. Since the non-skeleton support $ns$ belongs to $NS ^\pm$, it is processed in the move-ns function:

$$\begin{aligned} ns ^* = \mathop {\mathrm {proj}}\nolimits ^\beta _\mathcal {SK}\bigl ( \mathop {\mathrm {supp.cl}}\nolimits _\mathcal {SK}( ns ) \bigr ) = \mathop {\mathrm {proj}}\nolimits ^\beta _\mathcal {SK}\bigl ( \{ c_0, c_3, c_4 \} \bigr ) = \{ c_0, c_4 \}. \end{aligned}$$

In contrast, if we were processing the non-strict inequality $\beta ' = (y \le 1)$, we would have obtained $ns ' = \mathop {\mathrm {proj}}\nolimits ^{\beta '}_\mathcal {SK}\bigl ( \mathop {\mathrm {supp.cl}}\nolimits _\mathcal {SK}( ns ) \bigr ) = \{ c_4 \}$. Since $ns '$ is a singleton, it is upgraded to become a skeleton point by procedure promote-singletons. Hence, in this case the new skeleton is $\mathcal {SK}= \langle \emptyset , \emptyset , C, SP \rangle$, where $C = \{ c_0, c_1, c_5 \}$ and $SP = \{ c_4 \}$, while the non-skeleton component is empty.

Creating New Supports. Consider the case of a support $ns \in NS ^-$ violating a non-strict inequality constraint $\beta$: this support has to be removed from $NS$. However, the upward closed set $NS$ is represented by its minimal elements only so that, by removing $ns$, we are also implicitly removing other supports from the set $\mathop {\uparrow }\nolimits ns$, including some that do not belong to $NS ^-$ and hence should be kept. Therefore, we have to explore the set of faces and detect those that are going to lose their filler: their minimal supports will be added to $NS ^\star$. Similarly, when processing a non-strict inequality constraint, we need to consider the new faces introduced by the constraint: the corresponding supports can be found by projecting on the constraint hyperplane those faces that are possibly filled by an element in $SP ^+$ or $NS ^+$.

This is the task of the create-ns function, shown in Pseudocode 2. It uses enumerate-faces as a helper:⁴ the latter provides an enumeration of all the (higher dimensional) faces that contain the initial support $ns$. The new faces are obtained by adding to $ns$ a new generator g and then composing the support closure and projection functions, as done in move-ns. For efficiency purposes, a case analysis is performed so as to restrict the search area of the enumeration phase, by considering only the faces crossing the constraint.

Example 4

Consider $\mathcal {P}\in \mathbb {P}_2$ in the left hand side of the next figure, described by skeleton $\mathcal {SK}= \langle \emptyset , \emptyset , \{ c_0, c_1, c_2 \}, \{ p \} \rangle$ and non-skeleton $NS = \emptyset$.

The partition for $\mathcal {SK}$ induced by the non-strict inequality is as follows:

$$\begin{aligned} \mathcal {SK}^+ = \langle \emptyset , \emptyset , \emptyset , \{ p \} \rangle , \quad \mathcal {SK}^0 = \langle \emptyset , \emptyset , \{ c_0, c_2 \}, \emptyset \rangle , \quad \mathcal {SK}^- = \langle \emptyset , \emptyset , \{ c_1 \}, \emptyset \rangle . \end{aligned}$$

There are no adjacent generators in $\mathcal {SK}^+$ and $\mathcal {SK}^-$, so that $\mathcal {SK}^\star$ is empty. When processing the non-skeleton component, the skeleton point in $\mathcal {SK}^+$ will be considered in line 15 of function create-ns. The corresponding call to function enumerate-faces computes

$$\begin{aligned} ns ^\star = \mathop {\mathrm {proj}}\nolimits ^\beta _\mathcal {SK}\bigl ( \mathop {\mathrm {supp.cl}}\nolimits _\mathcal {SK}(\{ p \} \mathrel {\cup }\{ c_1 \} ) \bigr ) = \mathop {\mathrm {proj}}\nolimits ^\beta _\mathcal {SK}\bigl ( \{ c_0, c_1, c_2, p \} \bigr ) = \{ c_0, c_2 \}, \end{aligned}$$

thereby producing the filler for the open segment $(c_0, c_2)$. The resulting polyhedron, shown in the right hand side of the figure, is thus described by the skeleton $\mathcal {SK}= \langle \emptyset , \emptyset , \{ c_0, c_2 \}, \{ p \} \rangle$ and the non-skeleton $NS = \{ ns ^\star \}$.

It is worth noting that, when handling Example 4 adopting an entirely geometric representation, closure point $c_1$ needs to be combined with point p even if the two generators are not adjacent: this leads to a significant efficiency penalty. Similarly, an implementation based on the $\epsilon$-representation will have to combine closure point $c_1$ with point p (and/or with some other $\epsilon$-redundant points), because the addition of the slack variable makes them adjacent. Therefore, an implementation based on the new approach obtains a twofold benefit: first, the distinction between skeleton and non-skeleton allows for restricting the handling of non-adjacent combinations to the non-skeleton phase; second, thanks to the combinatorial representation, the non-skeleton component can be processed by using set index operations only, i.e., computing no linear combination at all.

Preparing for Next Iteration. In lines 10 to 15 of conversion the generator system is updated for the next iteration. The new supports in $NS ^\star$ are merged (using ‘$\oplus$’ to remove redundancies) into the appropriate portions of the non-skeleton component. In particular, when processing a strict inequality, in line 12 the helper function

$$ \mathop {\mathrm {points\_become\_closure\_points}}\nolimits \bigl (\langle L, R, C, SP \rangle \bigr ) \mathrel {\buildrel \mathrm {def} \over {=}}\langle L, R, C \mathrel {\cup } SP , \emptyset \rangle $$

is applied to $\mathcal {SK}^0$, making sure that all of the skeleton points saturating $\beta$ are transformed into closure points having the same position. The final processing step (line 15) calls helper procedure promote-singletons (see Pseudocode 2), making sure that all singleton supports get promoted to skeleton points.

Note that line 5 of conversion, by calling procedure violating-line (see Pseudocode 3) handles the special case of a line violating $\beta$. This is just an optimization: the helper procedure strict-on-eq-points can be seen as a tailored version of create-ns, also including the final updating of $\mathcal {SK}$ and $NS$.

4.3 Duality

The definitions given in Sect. 3 for a geometric generator system have their dual versions working on a geometric constraint system. We provide a brief overview of these correspondences, which are summarized in Table 2.

Table 2. Correspondences between generator and constraint concepts.

For a non-empty $\mathcal {P}= \mathop {\mathrm {con}}\nolimits (\mathcal {C}) \in \mathbb {P}_n$, the skeleton of $\mathcal {C}= \langle C_=, C_\ge , C_> \rangle$ includes the non-redundant constraints defining $\mathcal {Q}= \mathop {\mathrm {cl}}\nolimits (\mathcal {P})$. Denoting by $SC _>$ the skeleton strict inequalities (i.e., those whose corresponding non-strict inequality is not redundant for $\mathcal {Q}$), we have $\mathcal {SK}_\mathcal {Q}\mathrel {\buildrel \mathrm {def} \over {=}}\langle C_=, C_\ge \mathrel {\cup } SC _> , \emptyset \rangle$, so that $\mathcal {Q}= \mathop {\mathrm {con}}\nolimits (\mathcal {SK}_\mathcal {Q})$. The ghost faces of $\mathcal {P}$ are the faces of the closure $\mathcal {Q}$ that do not intersect $\mathcal {P}$: $gFaces _\mathcal {P}\mathrel {\buildrel \mathrm {def} \over {=}}\{\, F \in cFaces _\mathcal {Q}\mid F \mathrel {\cap }\mathcal {P}= \emptyset \,\}$; thus, $\mathcal {P}= \mathop {\mathrm {con}}\nolimits (\mathcal {SK}_\mathcal {Q}) \mathrel {\setminus }\bigcup gFaces _\mathcal {P}$. The set $gFaces ' \mathrel {\buildrel \mathrm {def} \over {=}} gFaces \mathrel {\cup }\{\mathcal {Q}\}$ is a meet sublattice of $cFaces$; also, $gFaces$ is downward closed and can be represented by its maximal elements.

The skeleton support $\mathcal {SK}_F$ of a face $F \in cFaces _\mathcal {Q}$ is defined as the set of all the skeleton constraints that are saturated by all the points in F. Each face $F \in gFaces$ saturates a strict inequality $\beta _> \in C_>$: we can represent such a face using its skeleton support $\mathcal {SK}_F$ of which $\beta _>$ is a possible materialization. A constraint system non-skeleton component $NS \subseteq \mathbb {NS}$ is thus a combinatorial representation of the strict inequalities of the polyhedron.

Hence, the non-skeleton components for generators and constraints have a complementary role: in the case of generators they are face fillers, marking the minimal faces that are included in $nncFaces$; in the case of constraints they are face cutters, marking the maximal faces that are excluded from $nncFaces$. Note that the non-redundant cutters in $gFaces$ are those having a minimal skeleton support, as is the case for the fillers.

As it happens with lines, all the equalities in $C_=$ are included in all the supports $ns \in NS$ so that, for efficiency, they are not represented explicitly. After removing the equalities, a singleton $ns \in NS$ stands for a skeleton strict inequality constraint, which is better represented in the skeleton component, thereby obtaining $\mathcal {SK}= \langle C_=, C_\ge , SC _> \rangle$. Hence, a support $ns \in NS$ is redundant if there exists $ns ' \in NS$ such that $ns ' \subset ns$ or if $ns \mathrel {\cap } SC _> \ne \emptyset$.

When the concepts underlying the skeleton and non-skeleton representation are reinterpreted as discussed above, it is possible to define a conversion procedure mapping a generator representation into a constraint representation which is very similar to the one from constraints to generators.

5 Experimental Evaluation

The new representation and conversion algorithms for NNC polyhedra have been implemented and tested in the context of the PPL (Parma Polyhedra Library). A full integration in the PPL domain of NNC polyhedra is not possible, since the latter assumes the presence of the slack variable $\epsilon$. The approach, summarized by the diagram in Fig. 1, is to intercept each call to the PPL’s conversion (working on $\epsilon$-representations in $\mathbb {CP}_{n+1}$) and pair it with a corresponding call to the new algorithm (working on the new representations in $\mathbb {P}_n$).

Fig. 1.

High level diagram for the experimental evaluation (non-incremental case).

On the left hand side of the diagram we see the application of the standard PPL conversion procedure: the input $\epsilon$-representation is processed by ‘old conversion’ so as to produce the output $\epsilon$-representation DD pair. The ‘$\epsilon$-less encoding’ phase produces a copy of the input without the slack variable; this is processed by ‘new conversion’ to produce the output DD pair, based on the new skeleton/non-skeleton representation. After the two conversions are completed, the outputs are checked for both semantic equivalence and non-redundancy. This final checking phase was successful on all the experiments performed, which include all of the tests in the PPL. In order to assess efficiency, additional code was added to measure the time spent inside the old and new conversion procedures, disregarding the input encoding and output checking phases. It is worth stressing that several experimental evaluations, including recent ones [2], confirm that the PPL is a state-of-the-art implementation of the DD method for a wide spectrum of application contexts.

The first experiment⁵ on efficiency is meant to evaluate the overhead incurred by the new representation and algorithm for NNC polyhedra when processing topologically closed polyhedra, so as to compare it with the corresponding overhead incurred by the $\epsilon$-representation. To this end, we considered the ppl_lcdd demo application of the PPL, which solves the vertex/facet enumeration problem. In Table 3 we report the results obtained on a selection of the test benchmarks⁶ when using: the conversion algorithm for closed polyhedra (columns 2–3); the conversion algorithm for the $\epsilon$-representation of NNC polyhedra (columns 4–5); and the new conversion algorithm for the new representation of NNC polyhedra (columns 6–7). Columns ‘time’ report the number of milliseconds spent; columns ‘sat’ report the number of saturation (i.e., bit vector) operations, in millions.

The results in Table 3 show that the use of the $\epsilon$-representation for closed polyhedra incurs a significant overhead. In contrast, the new representation and algorithm go beyond all expectations: in almost all of the tests there is no overhead at all (that is, any overhead incurred is so small to be masked by the improvements obtained in other parts of the algorithm).

Table 3. Overhead of conversion for C polyhedra. Units: time (ms), sat (M).

The second experiment is meant to evaluate the efficiency gains obtained in a more appropriate context, i.e., when processing polyhedra that are not topologically closed. To this end, we consider the same benchmark discussed in [3, Table 2],⁷ which highlights the efficiency improvement resulting from the adoption of an enhanced evaluation strategy (where a knowledgeable user of the library explicitly invokes, when appropriate, the strong minimization procedures for $\epsilon$-representations) with respect to the standard evaluation strategy (where the user simply performs the required computation, leaving the burden of optimization to the library developers). In Table 4 we report the results obtained for the most expensive test among those described in [3, Table 2], comparing the standard and enhanced evaluation strategies for the $\epsilon$-representation (rows 1 and 2) with the new algorithm (row 3). For each algorithm we show in column 2 the total number of iterations of the conversion procedures and, in the next two columns, the median and maximum sizes of the representations computed at each iteration (i.e., the size of the intermediate results); in columns from 5 to 8 we show the numbers of incremental and non-incremental calls to the conversion procedures, together with the corresponding time spent (in milliseconds); in column 9 we show the time spent in strong minimization of $\epsilon$-representations; in the final column, we show the overall time ratio, computed with respect to the time spent by the new algorithm.

Table 4. Comparing $\epsilon$-representation based (standard and enhanced) computations for NNC polyhedra with the new conversion procedures.

Even though adopting the standard computation strategy (requiring no clever guess by the end user), the new algorithm obtains impressive time improvements, outperforming not only the standard, but also the enhanced computation strategy for the $\epsilon$-representation. The reason for the latter efficiency improvement is that the enhanced computation strategy, when invoking the strong minimization procedures, interferes with incrementality: the figures in Table 4 confirm that the new algorithm performs three of the seven required conversions in an incremental way, while in the enhanced case they are all non-incremental. Moreover, a comparison of the iteration counts and the sizes of the intermediate results provides further evidence that the new algorithm is able to maintain a non-redundant description even during the iterations of a conversion.

6 Conclusion

We have presented a new approach for the representation of NNC polyhedra in the Double Description framework, avoiding the use of slack variables and distinguishing between the skeleton component, encoded geometrically, and the non-skeleton component, provided with a combinatorial encoding. We have proposed and implemented a variant of the Chernikova conversion procedure achieving significant efficiency improvements with respect to a state-of-the-art implementation of the domain of NNC polyhedra, thereby providing a solution to all the issues affecting the $\epsilon$-representation approach. As future work, we plan to develop a full implementation of the domain of NNC polyhedra based on this new representation. To this end, we will have to reconsider each semantic operator already implemented by the existing libraries (which are based on the addition of a slack variable), so as to propose, implement and experimentally evaluate a corresponding correct specification based on the new approach.