Abstract
In this paper, we propose Android Stack Machine (ASM), a formal model to capture key mechanisms of Android multi-tasking such as activities, back stacks, launch modes, as well as task affinities. The model is based on pushdown systems with multiple stacks, and focuses on the evolution of the back stack of the Android system when interacting with activities carrying specific launch modes and task affinities. For formal analysis, we study the reachability problem of ASM. While the general problem is shown to be undecidable, we identify expressive fragments for which various verification techniques for pushdown systems or their extensions are harnessed to show decidability of the problem.
This work was partially supported by UK EPSRC grant (EP/P00430X/1), ARC grants (DP160101652, DP180100691), NSFC grants (61532019, 61761136011, 61662035, 61672505, 61472474, 61572478) and the National Key Basic Research (973) Program of China (2014CB340701), the INRIA-CAS joint research project “Verification, Interaction, and Proofs”, and Key Research Program of Frontier Sciences, CAS, Grant No. QYZDJ-SSW-JSC036.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Multi-tasking plays a central role in the Android platform. Its unique design, via activities and back stacks, greatly facilitates organizing user sessions through tasks, and provides rich features such as handy application switching, background app state maintenance, smooth task history navigation (using the “back” button), etc [16]. We refer the readers to Sect. 2 for an overview.
Android task management mechanism has substantially enhanced user experiences of the Android system and promoted personalized features in app design. However, the mechanism is also notoriously difficult to understand. As a witness, it constantly baffles app developers and has become a common topic of question-and-answer websites (for instance, [2]). Surprisingly, the Android multi-tasking mechanism, despite its importance, has not been thoroughly studied before, let along a formal treatment. This has impeded further developments of computer-aided (static) analysis and verification for Android apps, which are indispensable for vulnerability analysis (for example, detection of task hijacking [16]) and app performance enhancement (for example, estimation of energy consumption [8]).
This paper provides a formal model, i.e., Android Stack Machine (ASM), aiming to capture the key features of Android multi-tasking. ASM addresses the behavior of Android back stacks, a key component of the multi-tasking machinery, and their interplay with attributes of the activity. In this paper, for these attributes we consider four basic launch modes, i.e., standard ( \(\mathsf{STD}\)), singleTop (\(\mathsf{STP}\)), singleTask (\(\mathsf{STK}\)), singleInstance (\(\mathsf{SIT}\)), and task affinities. (For simplicity more complicated activity attributes such as allowTaskReparenting will not be addressed in the present paper.) We believe that the semantics of ASM, specified as a transition system, captures faithfully the actual mechanism of Android systems. For each case of the semantics, we have created “diagnosis” apps with corresponding launch modes and task affinities, and carried out extensive experiments using these apps, ascertaining its conformance to the Android platform. (Details will be provided in Sect. 3.)
For Android, technically ASM can be viewed as the counterpart of pushdown systems with multiple stacks, which are the de facto model for (multi-threaded) concurrent programs. Being rigours, this model opens a door towards a formal account of Android’s multi-tasking mechanism, which would greatly facilitate developers’ understanding, freeing them from lengthy, ambiguous, elusive Android documentations. We remark that it is known that the evolution of Android back stacks could also be affected by the intent flags of the activities. ASM does not address intent flags explicitly. However, the effects of most intent flags (e.g., \(\mathsf FLAG\_ACTIVITY\_NEW\_TASK\), \(\mathsf FLAG\_ACTIVITY\_CLEAR\_TOP\)) can be simulated by launch modes, so this is not a real limitation of ASM.
Based on ASM, we also make the first step towards a formal analysis of Android multi-tasking apps by investigating the reachability problem which is fundamental to all such analysis. ASM is akin to pushdown systems with multiple stacks, so it is perhaps not surprising that the problem is undecidable in general; in fact, we show undecidability for most interesting fragments even with just two launch modes. In the interest of seeking more expressive, practice-relevant decidable fragments, we identify a fragment \(\mathsf{STK}\)-dominating ASM which assumes \(\mathsf{STK}\) activities have different task affinities and which further restricts the use of \(\mathsf{SIT}\) activities. This fragment covers a majority of open-source Android apps (e.g., from Github) we have found so far. One of our technical contributions is to give a decision procedure for the reachability problem of \(\mathsf{STK}\)-dominating ASM, which combines a range of techniques from simulations by pushdown systems with transductions [19] to abstraction methods for multi-stacks. The work, apart from independent interests in the study of multi-stack pushdown systems, lays a solid foundation for further (static) analysis and verification of Android apps related to multi-tasking, enabling model checking of Android apps, security analysis (such as discovering task hijacking), or typical tasks in software engineering such as automatic debugging, model-based testing, etc.
We summarize the main contributions as follows: (1) We propose—to the best of our knowledge—the first comprehensive formal model, Android stack machine, for Android back stacks, which is also validated by extensive experiments. (2) We study the reachability problem for Android stack machine. Apart from strongest possible undecidablity results in the general case, we provide a decision procedure for a practically relevant fragment.
2 Android Stack Machine: An Informal Overview
In Android, an application, usually referred to as an app, is regarded as a collection of activities. An activity is a type of app components, an instance of which provides a graphical user interface on screen and serves the entry point for interacting with the user [1]. An app typically has many activities for different user interactions (e.g., dialling phone numbers, reading contact lists, etc). A distinguished activity is the main activity, which is started when the app is launched. A task is a collection of activities that users interact with when performing a certain job. The activities in a task are arranged in a stack in the order in which each activity is opened. For example, an email app might have one activity to show a list of latest messages. When the user selects a message, a new activity opens to view that message. This new activity is pushed to the stack. If the user presses the “Back” button, an activity is finished and is popped off the stack. [In practice, the onBackPressed() method can be overloaded and triggered when the “Back” button is clicked. Here we assume—as a model abstraction—that the onBackPressed() method is not overloaded.] Furthermore, multiple tasks may run concurrently in the Android platform and the back stack stores all the tasks as a stack as well. In other words, it has a nested structure being a stack of stacks (tasks). We remark that in android, activities from different apps can stay in the same task, and activities from the same app can enter different tasks.
Typically, the evolution of the back stack is dependent mainly on two attributes of activities: launch modes and task affinities. All the activities of an app, as well as their attributes, including the launch modes and task affinities, are defined in the manifest file of the app. The launch mode of an activity decides the corresponding operation of the back stack when the activity is launched. As mentioned in Sect. 1, there are four basic launch modes in Android: “standard”, “singleTop”, “singleTask” and “singleInstance”. The task affinity of an activity indicates to which task the activity prefers to belong. By default, all the activities from the same app have the same affinity (i.e., all activities in the same app prefer to be in the same task). However, one can modify the default affinity of the activity. Activities defined in different apps can share a task affinity, or activities defined in the same app can be assigned with different task affinities. Below we will use a simple app to demonstrate the evolution of the back stack.
Example 1
In Fig. 1, an app ActivitiesLaunchDemoFootnote 1 is illustrated. The app contains four activities of the launch modes \(\mathsf{STD}\), \(\mathsf{STP}\), \(\mathsf{STK}\) and \(\mathsf{SIT}\), depicted by green, blue, yellow and red, respectively. We will use the colours to name the activities. The green, blue and red activities have the same task affinity, while the yellow activity has a distinct one. The main activity of the app is the green activity. Each activity contains four buttons, i.e., the green, blue, yellow and red button. When a button is clicked, an instance of the activity with the colour starts. Moreover, the identifiers of all the tasks of the back stack, as well as their contents, are shown in the white zones of the window. We use the following execution trace to demonstrate how the back stack evolves according to the launch modes and the task affinities of the activities: The user clicks the buttons in the order of green, blue, blue, yellow, red, and green.
-
1.
[Launch the app] When the app is launched, an instance of the main activity starts, and the back stack contains exactly one task, which contains exactly one green activity (see Fig. 1(a)). For convenience, this task is called the green task (with id: 23963).
-
2.
[Start an \(\mathsf{STD}\) activity] When the green button is clicked, since the launch mode of the green activity is \(\mathsf{STD}\), a new instance of the green activity starts and is pushed into the green task (see Fig. 1(b)).
-
3.
[Start an \(\mathsf{STP}\) activity] When the blue button is clicked, since the top activity of the green task is not the blue activity, a new instance of the blue activity is pushed into the green task (see Fig. 1(c)). On the other hand, if the blue button is clicked again, because the launch mode of the blue activity is \(\mathsf{STP}\) and the top activity of the green task is already the blue one, a new instance of the blue activity will not be pushed into the green task and its content is kept unchanged.
-
4.
[Start an \(\mathsf{STK}\) activity] Suppose now that the yellow button is clicked, since the launch mode of the yellow activity is \(\mathsf{STK}\), and the task affinity of the yellow activity is different from that of the bottom activity of the green task, a new task is created and an instance of the yellow activity is pushed into the new task (called the yellow task, with id: 23964, see Fig. 1(d), where the leftmost task is the top task of the back stack).
-
5.
[Start an \(\mathsf{SIT}\) activity] Next, suppose that the red button is clicked, because the launch mode of the red activity is \(\mathsf{SIT}\), a new task is created and an instance of the red activity is pushed into the new task (called the red task, with id: 23965, see Fig. 1(e)). Moreover, at any future moment, the red activity is the only activity of the red task. Note that here a new task is created in spite of the affinity of the red activity.
-
6.
[Start an \(\mathsf{STD}\) activity from an \(\mathsf{SIT}\) activity] Finally, suppose the green button is clicked again. Since the top task is the red task, which is supposed to contain only one activity (i.e., the red activity), the green task is then moved to the top of the back stack and a new instance of the green activity is pushed into the green task (see Fig. 1(f)).
3 Android Stack Machine
For \(k \in {\mathbb {N} }\), let \([k]=\{1,\cdots , k\}\). For a function \(f:X\rightarrow Y\), let \({\mathsf {dom} }(f)\) and \({\mathsf {rng} }(f)\) denote the domain (X) and range (Y) of f respectively.
Definition 1
(Android stack machine). An Android stack machine (ASM) is a tuple \(\mathcal {A}= (Q, \mathsf{Sig}, q_0, \varDelta )\), where
-
Q is a finite set of control states, and \(q_0 \in Q\) is the initial state,
-
\(\mathsf{Sig}= (\mathsf{Act}, \mathsf{Lmd}, \mathsf{Aft}, A_0)\) is the activity signature, where
-
\(\mathsf{Act}\) is a finite set of activities,
-
\(\mathsf{Lmd}: \mathsf{Act}\rightarrow \{\mathsf{STD}, \mathsf{STP}, \mathsf{STK}, \mathsf{SIT}\}\) is the launch-mode function,
-
\(\mathsf{Aft}: \mathsf{Act}\rightarrow [m]\) is the task-affinity function, where \(m=|\mathsf{Act}|\),
-
\(A_0 \in \mathsf{Act}\) is the main activity,
-
-
\(\varDelta \subseteq Q \times (\mathsf{Act}\cup \{\triangleright \}) \times {\mathsf {Inst} }\times Q\) is the transition relation, where \({\mathsf {Inst} }= \{\square , {\mathsf {back} }\} \cup \{{\mathsf {start} }(A) \mid A \in \mathsf{Act}\}\), such that (1) for each transition \((q, A, \alpha , q') \in \varDelta \), it holds that \(q' \ne q_0\), and (2) for each transition \((q, \triangleright , \alpha , q')\in \varDelta \), it holds that \(q=q_0\), \(\alpha ={\mathsf {start} }(A_0)\), and \(q' \ne q_0\).
For convenience, we usually write a transition \((q, A, \alpha , q') \in \varDelta \) as \(q \xrightarrow {A, \alpha } q'\), and \((q, \triangleright , \alpha , q') \in \varDelta \) as \(q \xrightarrow {\triangleright , \alpha } q'\). Intuitively, \(\triangleright \) denotes an empty back stack, \(\square \) denotes there is no change over the back stack, \({\mathsf {back} }\) denotes the pop action, and \({\mathsf {start} }(A)\) denotes the activity A being started. We assume that, if the back stack is empty, the Android stack system terminates (i.e., no further continuation is possible) unless it is in the initial state \(q_0\), We use \(\mathsf{Act}_{\star }\) to denote \(\{B \in \mathsf{Act}\mid \mathsf{Lmd}(B) = \star \}\) for \(\star \in \{\mathsf{STD}, \mathsf{STP}, \mathsf{STK}, \mathsf{SIT}\}\).
Semantics. Let \(\mathcal {A}= (Q, \mathsf{Sig}, q_0, \varDelta )\) be an ASM with \(\mathsf{Sig}=(\mathsf{Act}, \mathsf{Lmd}, \mathsf{Aft},A_0)\).
A task of \(\mathcal {A}\) is encoded as a word \(S= [A_1, \cdots , A_n] \in \mathsf{Act}^+\) which denotes the content of the stack, with \(A_1\) (resp. \(A_n\)) as the top (resp. bottom) symbol, denoted by \(\mathsf{top}(S)\) (resp. \(\mathsf{btm}(S)\)). We also call the bottom activity of a non-empty task S as the root activity of the task. (Intuitively, this is the first activity of the task.) For \(\star \in \{\mathsf{STD}, \mathsf{STP}, \mathsf{STK}, \mathsf{SIT}\}\), a task S is called a \(\star \)-task if \(\mathsf{Lmd}(\mathsf{btm}(S))=\star \). We define the affinity of a task S, denoted by \(\mathsf{Aft}(S)\), to be \(\mathsf{Aft}( \mathsf{btm}(S))\). For \(S_1 \in \mathsf{Act}^*\) and \(S_2 \in \mathsf{Act}^*\), we use \(S_1 \cdot S_2\) to denote the concatenation of \(S_1\) and \(S_2\), and \(\epsilon \) is used to denote the empty word in \(\mathsf{Act}^*\).
As mentioned in Sect. 2, the (running) tasks on Android are organized as the back stack, which is the main modelling object of ASM. Typically we write a back stack \(\rho \) as a sequence of non-empty tasks, i.e., \(\rho =(S_1,\cdots , S_n)\), where \(S_1\) and \(S_n\) are called the top and the bottom task respectively. (Intuitively, \(S_1\) is the currently active task.) \(\varepsilon \) is used to denote the empty back stack. For a non-empty back stack \(\rho =(S_1,\cdots ,S_n)\), we overload \(\mathsf{top}\) by using \(\mathsf{top}(\rho )\) to refer to the task \(S_1\), and thus \(\mathsf{top}^2(\rho )\) the top activity of \(S_1\).
Definition 2
(Configurations). A configuration of \(\mathcal {A}\) is a pair \((q, \rho )\) where \(q \in Q\) and \(\rho \) is a back stack. Assume that \(\rho =(S_1,\cdots , S_n)\) with \(S_i = [A_{i,1}, \cdots , A_{i,m_i}]\) for each \(i \in [n]\). We require \(\rho \) to satisfy the following constraints:
-
1.
For each \(A \in \mathsf{Act}_{\mathsf{STK}}\) or \(A \in \mathsf{Act}_{\mathsf{SIT}}\), A occurs in at most one task. Moreover, if A occurs in a task, then A occurs at most once in that task. [At most one instance for each \(\mathsf{STK}\)/\(\mathsf{SIT}\)-activity]
-
2.
For each \(i \in [n]\) and \(j \in [m_i-1]\) such that \(A_{i, j} \in \mathsf{Act}_{\mathsf{STP}}\), \(A_{i, j} \ne A_{i, j+1}\). [Non-stuttering for\(\mathsf{STP}\)- activities]
-
3.
For each \(i \in [n]\) and \(j \in [m_i]\) such that \(A_{i, j} \in \mathsf{Act}_{\mathsf{STK}}\), \(\mathsf{Aft}(A_{i, j}) = \mathsf{Aft}(S_i)\). [Affinities of \(\mathsf{STK}\) - activities agree to the host task]
-
4.
For each \(i \in [n]\) and \(j \in [m_i]\) such that \(A_{i, j} \in \mathsf{Act}_{\mathsf{SIT}}\), \(m_i = 1\). [\(\mathsf{SIT}\)-activities monopolize a task]
-
5.
For \(i\ne j \in [n]\) such that \( \mathsf{btm}(S_i) \not \in \mathsf{Act}_{\mathsf{SIT}}\) and \( \mathsf{btm}(S_j) \not \in \mathsf{Act}_{\mathsf{SIT}}\), \(\mathsf{Aft}(S_i) \ne \mathsf{Aft}(S_j)\). [Affinities of tasks are mutually distinct, except for those rooted at \(\mathsf{SIT}\) - activities]
By Definition 2(5), each back stack \(\rho \) contains at most \(|\mathsf{Act}_{\mathsf{SIT}}|+|{\mathsf {rng} }(\mathsf{Aft})|\) (more precisely, \(|\mathsf{Act}_{\mathsf{SIT}}|+|\{\mathsf{Aft}(A)\mid A\in \mathsf{Act}\setminus \mathsf{Act}_{\mathsf{SIT}}\}|\)) tasks. Moreover, by Definition 2(1–5), all the root activities in a configuration are pairwise distinct, which allows to refer to a task whose root activity is A as the A-task.
Let \({\mathsf {Conf} }_\mathcal {A}\) denote the set of configurations of \(\mathcal {A}\). The initial configuration of \(\mathcal {A}\) is \((q_0, \varepsilon )\). To formalize the semantics of \(\mathcal {A}\) concisely, we introduce the following shorthand stack operations and one auxiliary function. Here \(\rho =(S_1,\cdots , S_n)\) is a non-empty back stack.

Intuitively, GetNonSITTaskByAft\((\rho , k)\) returns a non-\(\mathsf{SIT}\) task whose affinity is k if it exists, otherwise returns Undef.
In the sequel, we define the transition relation \((q, \rho ) \xrightarrow {\mathcal {A}} (q', \rho ')\) on \({\mathsf {Conf} }_\mathcal {A}\) to formalize the semantics of \(\mathcal {A}\). We start with the transitions out of the initial state \(q_0\) and those with \(\square \) or \({\mathsf {back} }\) action.
-
For each transition \(q_0 \xrightarrow {\triangleright , {\mathsf {start} }(A_0)} q\), \((q_0, \varepsilon ) \xrightarrow {\mathcal {A}} (q, \) NewTask\((A_0 ))\).
-
For each transition \(q\xrightarrow {A, \square } q'\) and \((q, \rho ) \in {\mathsf {Conf} }_\mathcal {A}\) such that \(\mathsf{top}^2(\rho )=A\), \((q, \rho ) \xrightarrow {\mathcal {A}} (q', \mathsf{Noaction}(\rho ) )\).
-
For each transition \(q \xrightarrow {A, {\mathsf {back} }} q'\) and \((q, \rho ) \in {\mathsf {Conf} }_\mathcal {A}\) such that \(\mathsf{top}^2(\rho )=A\), \((q, \rho ) \xrightarrow {\mathcal {A}} (q', \mathsf{Pop}(\rho ))\).
The most interesting case is, however, the transitions of the form \(q \xrightarrow {A, {\mathsf {start} }(B)}q'\). We shall make case distinctions based on the launch mode of B. For each transition \(q \xrightarrow {A, {\mathsf {start} }(B)}q'\) and \((q, \rho ) \in {\mathsf {Conf} }_\mathcal {A}\) such that \(\mathsf{top}^2(\rho ) = A\), \((q, \rho ) \xrightarrow {\mathcal {A}} (q', \rho ')\) if one of the following cases holds. Assume \(\rho =(S_1,\cdots , S_n)\).

-
\(\mathsf{Lmd}(A) \ne \mathsf{SIT}\), then \(\rho '= \mathsf{Push}(\rho ,B)\);
-
\(\mathsf{Lmd}(A) = \mathsf{SIT}\)Footnote 2, then
-
if \(\mathsf{GetNonSITTaskByAft}(\rho , \mathsf{Aft}(B))=S_i\)Footnote 3, then \(\rho '=\) Push(Move2Top\((\rho , i),B),\)
-
if GetNonSITTaskByAft\((\rho , \mathsf{Aft}(B))=\) Undef, then \(\rho '=\) NewTask\((\rho ,B )\);

-
\(\mathsf{Lmd}(A) \ne \mathsf{SIT}\) and \(A \ne B\), then \(\rho ' = \mathsf{Push}(\rho ,B)\);
-
\(\mathsf{Lmd}(A) \ne \mathsf{SIT}\) and \(A = B\), then \(\rho ' = \mathsf{Noaction}(\rho )\);
-
\(\mathsf{Lmd}(A) = \mathsf{SIT}\) (see footnote 2),
-
if \(\mathsf{GetNonSITTaskByAft}(\rho , \mathsf{Aft}(B))=S_i\) (see footnote 3), then
-
* if \(\mathsf{top}(S_i) \ne B\), \(\rho '=\mathsf{Push}(\mathsf{Move2Top}(\rho , i),B)\),
-
* if \(\mathsf{top}(S_i) = B\), \(\rho ' = \mathsf{Move2Top}(\rho , i)\);
-
if \(\mathsf{GetNonSITTaskByAft}(\rho , \mathsf{Aft}(B))=\mathsf{Undef}\), then \(\rho '= \mathsf{NewTask}(\rho ,B )\);

-
\(A=B\) (see footnote 2), then \(\rho ' = \mathsf{Noaction}(\rho )\);
-
\(A \ne B\) and \(S_i = [B]\) for some \(i\in [n]\)Footnote 4, then \(\rho ' = \mathsf{Move2Top}(\rho , i)\);
-
\(A \ne B\) and \(S_i \ne [B]\) for each \(i \in [n]\), then \(\rho '= \mathsf{NewTask}(\rho ,B )\);

-
\(\mathsf{Lmd}(A) \ne \mathsf{SIT}\) and \(\mathsf{Aft}(B) = \mathsf{Aft}(S_1)\), then
-
if B does not occur in \(S_1\)Footnote 5, then \(\rho '= \mathsf{Push}(\rho ,B)\);
-
if B occurs in \(S_1\)Footnote 6, then \(\rho '=\mathsf{PopUntil}(\rho ,B)\);
-
\(\mathsf{Lmd}(A) \ne \mathsf{SIT}\Longrightarrow \mathsf{Aft}(B) \ne \mathsf{Aft}(S_1)\), then
-
if \(\mathsf{GetNonSITTaskByAft}(\rho , \mathsf{Aft}(B))=S_i\)Footnote 7,
-
* if B does not occur in \(S_i\) (see footnote 5), then \(\rho '=\mathsf{Push}(\mathsf{Move2Top}(\rho , i),B)\);
-
* if B occurs in \(S_i\)Footnote 8, then \(\rho '=\mathsf{PopUntil}(\mathsf{Move2Top}(\rho , i),B)\),
-
if \(\mathsf{GetNonSITTaskByAft}(\rho , \mathsf{Aft}(B))=\mathsf{Undef}\), then \(\rho '= \mathsf{NewTask}(\rho ,B )\);
This concludes the definition of the transition definition of \(\xrightarrow {\mathcal {A}}\). As usual, we use \(\mathop {\Rightarrow }\limits ^{\mathcal {A}}\) to denote the reflexive and transitive closure of \(\xrightarrow {\mathcal {A}}\).
Example 2
The ASM for the ActivitiesLaunchDemo app in Example 1 is \(\mathcal {A}= (Q, \mathsf{Sig}, q_0, \varDelta )\), where \(Q = \{q_0, q_1\}\), \(\mathsf{Sig}=(\mathsf{Act},\mathsf{Lmd}, \mathsf{Aft}, A_g)\) with
-
\(\mathsf{Act}=\{A_g, A_b, A_y, A_r\}\), corresponding to the green, blue, yellow and red activity respectively in the ActivitiesLaunchDemo app,
-
\(\mathsf{Lmd}(A_g) = \mathsf{STD}\), \(\mathsf{Lmd}(A_b) = \mathsf{STP}\), \(\mathsf{Lmd}(A_y) = \mathsf{STK}\), \(\mathsf{Lmd}(A_r) = \mathsf{SIT}\),
-
\(\mathsf{Aft}(A_g) = \mathsf{Aft}(A_b) = \mathsf{Aft}(A_r) = 1\), \(\mathsf{Aft}(A_y) = 2\),
and \(\varDelta \) comprises the transitions illustrated in Fig. 2. Below is a path in the graph \(\xrightarrow {\mathcal {A}}\) corresponding to the sequence of user actions clicking the green, blue, blue, yellow, red, blue button (cf. Example 1),

Proposition 1 reassures that \(\xrightarrow {\mathcal {A}}\) is indeed a relation on \({\mathsf {Conf} }_\mathcal {A}\) as per Definition 2.
Proposition 1
Let \(\mathcal {A}\) be an ASM. For each \((q, \rho ) \in {\mathsf {Conf} }_\mathcal {A}\) and \((q, \rho ) \xrightarrow {\mathcal {A}} (q', \rho ')\), \((q', \rho ') \in {\mathsf {Conf} }_\mathcal {A}\), namely, \((q', \rho ')\) satisfies the five constraints in Definition 2.
Remark 1
A single app can clearly be modeled by an ASM. However, ASM can also be used to model multiple apps which may share tasks/activities. (In this case, these multiple apps can be composed into a single app, where a new main activity is added.) This is especially useful when analysing, for instance, task hijacking [16]. We sometimes do not specify the main activity explicit for convenience. The translation from app source code to ASM is not trivial, but follows standard routines. In particular, in ASM, the symbols stored into the back stack are just names of activities. Android apps typically need to, similar to function calls of programs, store additional local state information. This can be dealt with by introducing an extend activity alphabet such that each symbol is of the form \(A(\mathbf {b})\), where \(A \in \mathsf{Act}\) and \(\mathbf {b}\) represents local information. When we present examples, we also adopt this general syntax.
Model validation. We validate the ASM model by designing “diagnosis” Android apps with extensive experiments. For each case in the semantics of ASM, we design an app which contains activities with the corresponding launch modes and task affinities. To simulate the transition rules of the ASM, each activity contains some buttons, which, when clicked, will launch other activities. For instance, in the case of \(\mathsf{Lmd}(B) = \mathsf{STD}\), \(\mathsf{Lmd}(A) = \mathsf{SIT}\), \(\mathsf{GetNonSITTaskByAft}(\rho , \mathsf{Aft}(B))=\mathsf{Undef}\), the app contains two activities A and B of launch modes \(\mathsf{SIT}\) and \(\mathsf{STD}\) respectively, where A is the main activity. When the app is launched, an instance of A is started. A contains a button, which, when clicked, starts an instance of B. We carry out the experiment by clicking the button, monitoring the content of the back stack, and checking whether the content of the back stack conforms to the definition of the semantics. Specifically, we check that there are exactly two tasks in the back stack, one task comprising a single instance of A and another task comprising a single instance of B, with the latter task on the top. Our experiments are done in a Redmi-4A mobile phone with Android version 6.0.1. The details of the experiments can be found at https://sites.google.com/site/assconformancetesting/.
4 Reachability of ASM
Towards formal (static) analysis and verification of Android apps, we study the fundamental reachability problem of ASM. Fix an ASM \(\mathcal {A}= (Q, \mathsf{Sig}, q_0, \varDelta )\) with \(\mathsf{Sig}= (\mathsf{Act}, \mathsf{Lmd}, \mathsf{Aft}, A_0)\) and a target state \(q \in Q\). There are usually two variants: the state reachability problem asks whether \(({q}_{0}, \varepsilon ) \xrightarrow {\mathcal {A}} (q, \rho )\) for some back stack \(\rho \), and the configuration reachability problem asks whether \(({q}_{0}, \varepsilon ) \xrightarrow {\mathcal {A}} (q, \rho )\) when \(\rho \) is also given. We show they are interchangeable as far as decidability is concerned.
Proposition 2
The configuration reachability problem and the state reachability problem of ASM are interreducible in exponential time.
Proposition 2 allows to focus on the state reachability problem in the rest of this paper. Observe that, when the activities in an ASM are of the same launch mode, the problem degenerates to that of standard pushdown systems or even finite-state systems. These systems are well-understood, and we refer to [6] for explanations. To proceed, we deal with the cases where there are exactly two launch modes, for which we have \(\left( {\begin{array}{c}4\\ 2\end{array}}\right) =6\) possibilities. The classification is given in Theorems 1 and 2. Clearly, they entail that the reachability for general ASM (with at least two launch modes) is undecidable. To show the undecidablity, we reduce from Minsky’s two-counter machines [14], which, albeit standard, reveals the expressibility of ASM. We remark that the capability of swapping the order of two distinct non-\(\mathsf{SIT}\)-tasks in the back stack—without resetting the content of any of them—is the main source of undecidability.
Theorem 1
The reachability problem of ASM is undecidable, even when the ASM contains only (1) \(\mathsf{STD}\) and \(\mathsf{STK}\) activities, or (2) \(\mathsf{STD}\) and \(\mathsf{SIT}\) activities, or (3) \(\mathsf{STK}\) and \(\mathsf{STP}\) activities, or (4) \(\mathsf{SIT}\) and \(\mathsf{STP}\) activities.
In contrast, we have some relatively straightforward positive results:
Theorem 2
The state reachability problem of ASM is decidable in polynomial time when the ASM contains \(\mathsf{STD}\) and \(\mathsf{STP}\) activities only, and in polynomial space when the ASM contains \(\mathsf{STK}\) and \(\mathsf{SIT}\) activities only.
As mentioned in Sect. 1, we aim to identify expressive fragments of ASM with decidable reachability problems. To this end, we introduce a fragment called \(\mathsf{STK}\)-dominating ASM, which accommodates all four launch modes.
Definition 3
(\(\mathsf{STK}\)-dominating ASM). An ASM is said to be \(\mathsf{STK}\)-dominating if the following two constraints are satisfied:
-
(1)
the task affinities of the \(\mathsf{STK}\) activities are mutually distinct,
-
(2)
for each transition \(q \xrightarrow {A, {\mathsf {start} }(B)} q' \in \varDelta \) such that \(A \in \mathsf{Act}_{\mathsf{SIT}}\), it holds that either \(B \in \mathsf{Act}_{\mathsf{SIT}} \cup \mathsf{Act}_{\mathsf{STK}}\), or \(B \in \mathsf{Act}_{\mathsf{STD}} \cup \mathsf{Act}_{\mathsf{STP}}\) and \(\mathsf{Aft}(B) = \mathsf{Aft}(A_0)\).
The following result explains the name “\(\mathsf{STK}\)-dominating”.
Proposition 3
Let \(\mathcal {A}=(Q, \mathsf{Sig}, q_0, \varDelta )\) be an \(\mathsf{STK}\)-dominating ASM with \(\mathsf{Sig}= (\mathsf{Act}, \mathsf{Lmd}, \mathsf{Aft}, A_0)\). Then each configuration \((q,\rho )\) that is reachable from the initial configuration \((q_0, \varepsilon )\) in \(\mathcal {A}\) satisfies the following constraints: (1) for each \(\mathsf{STK}\) activity \(A \in \mathsf{Act}\) with \(\mathsf{Aft}(A)\ne \mathsf{Aft}(A_0)\), A can only occur at the bottom of some task in \(\rho \), (2) \(\rho \) contains at most one \(\mathsf{STD}/\mathsf{STP}\)-task, which, when it exists, has the same affinity as \(A_0\).
It is not difficult to verify that the ASM given in Example 2 is \(\mathsf{STK}\)-dominating.
Theorem 3
The state reachability of \(\mathsf{STK}\)-dominating ASM is in 2-\(\mathsf{EXPTIME}\).
The proof of Theorem 3 is technically the most challenging part of this paper. We shall give a sketch in Sect. 5 with the full details in [6].
5 \(\mathsf{STK}\)-dominating ASM
For simplicity, we assume that \(\mathcal {A}\) contains \(\mathsf{STD}\) and \(\mathsf{STK}\) activities onlyFootnote 9. To tackle the (state) reachability problem for \(\mathsf{STK}\)-dominating ASM, we consider two cases, i.e., \(\mathsf{Lmd}(A_0)= \mathsf{STK}\) and \(\mathsf{Lmd}(A_0) \ne \mathsf{STK}\). The former case is simpler because, by Proposition 3, all tasks will be rooted at \(\mathsf{STK}\) activities. For the latter, more general case, the back stack may contain, apart from several tasks rooted at \(\mathsf{STK}\) activities, one single task rooted at \(A_0\). Sections 5.1 and 5.2 will handle these two cases respectively.
We will, however, first introduce some standard, but necessary, backgrounds on pushdown systems. We assume familiarity with standard finite-state automata (NFA) and finite-state transducers (FST). We emphasize that, in this paper, FST refers to a special class of finite-state transducers, namely, letter-to-letter finite-state transducers where the input and output alphabets are the same.
Preliminaries of Pushdown systems. A pushdown system (PDS) is a tuple \({\mathcal {P} }=(Q, \varGamma , \varDelta )\), where Q is a finite set of control states, \(\varGamma \) is a finite stack alphabet, and \(\varDelta \subseteq Q \times \varGamma \times \varGamma ^* \times Q\) is a finite set of transition rules. The size of \({\mathcal {P} }\), denoted by \(|{\mathcal {P} }|\), is defined as \(|\varDelta |\).
Let \({\mathcal {P} }= (Q, \varGamma , \varDelta )\) be a PDS. A configuration of \({\mathcal {P} }\) is a pair \((q, w) \in Q \times \varGamma ^*\), where w denotes the content of the stack (with the leftmost symbol being the top of the stack). Let \({\mathsf {Conf} }_{\mathcal {P} }\) denote the set of configurations of \({\mathcal {P} }\). We define a binary relation \(\xrightarrow {{\mathcal {P} }}\) over \({\mathsf {Conf} }_{\mathcal {P} }\) as follows: \((q, w) \xrightarrow {{\mathcal {P} }} (q', w')\) iff \(w = \gamma w_1\) and there exists \(w'' \in \varGamma ^*\) such that \((q, \gamma , w'', q') \in \varDelta \) and \(w' = w'' w_1\). We use \(\mathop {\Rightarrow }\limits ^{{\mathcal {P} }}\) to denote the reflexive and transitive closure of \(\xrightarrow {{\mathcal {P} }}\).
A configuration \((q', w')\) is reachable from (q, w) if \((q,w) \mathop {\Rightarrow }\limits ^{{\mathcal {P} }} (q', w')\). For \(C \subseteq {\mathsf {Conf} }_{\mathcal {P} }\), \({\mathsf {pre} }^*(C)\) (resp. \({\mathsf {post} }^*(C)\)) denotes the set of predecessor (resp. successor) reachable configurations \(\{(q', w')\mid \exists (q, w) \in C, (q', w') \mathop {\Rightarrow }\limits ^{{\mathcal {P} }} (q, w) \}\) (resp. \(\{(q', w') \mid \exists (q, w) \in C, (q, w)\mathop {\Rightarrow }\limits ^{{\mathcal {P} }} (q', w') \}\)). For \(q \in Q\), we define \(C_q = \{q\}\times \varGamma ^*\) and write \({\mathsf {pre} }^*(q)\) and \({\mathsf {post} }^*(q)\) as shorthand of \({\mathsf {pre} }^*(C_q)\) and \({\mathsf {post} }^*(C_q)\) respectively.
As a standard machinery to solve reachability for PDS, a \({\mathcal {P} }\)-multi-automaton (\({\mathcal {P} }\)-MA) is an NFA \(\mathcal {A}=(Q', \varGamma , \delta , I, F)\) such that \(I \subseteq Q \subseteq Q'\) [4]. Evidently, multi-automata are a special class of NFA. Let \(\mathcal {A}= (Q', \varGamma , \delta , I, F)\) be a \({\mathcal {P} }\)-MA and \((q, w) \in {\mathsf {Conf} }_{\mathcal {P} }\), (q, w) is accepted by \(\mathcal {A}\) if \(q \in I\) and there is an accepting run \(q_0 q_1 \cdots q_n\) of \(\mathcal {A}\) on w with \(q_0 = q\). Let \({\mathsf {Conf} }_\mathcal {A}\) denote the set of configurations accepted by \(\mathcal {A}\). Moreover, let \({\mathcal {L}}(\mathcal {A})\) denote the set of words w such that \((q, w) \in {\mathsf {Conf} }_\mathcal {A}\) for some \(q \in I\). For brevity, we usually write MA instead of \({\mathcal {P} }\)-MA when \({\mathcal {P} }\) is clear from the context. Moreover, for an MA \(\mathcal {A}= (Q', \varGamma , \delta , I, F)\) and \(q' \in Q\), we use \(\mathcal {A}(q')\) to denote the MA obtained from \(\mathcal {A}\) by replacing I with \(\{q'\}\). A set of configurations \(C\subseteq {\mathsf {Conf} }_{\mathcal {P} }\) is regular if there is an MA \(\mathcal {A}\) such that \({\mathsf {Conf} }_\mathcal {A}=C\).
Theorem 4
([4]). Given a PDS \({\mathcal {P} }\) and a set of configurations accepted by an MA \(\mathcal {A}\), we can compute, in polynomial time in \(|{\mathcal {P} }|+|\mathcal {A}|\), two MAs \(\mathcal {A}_{{\mathsf {pre} }^*}\) and \(\mathcal {A}_{{\mathsf {post} }^*}\) that recognise \({\mathsf {pre} }^*({\mathsf {Conf} }_\mathcal {A})\) and \({\mathsf {post} }^*({\mathsf {Conf} }_\mathcal {A})\) respectively.
The connection between ASM and PDS is rather obvious. In a nutshell, ASM can be considered as a PDS with multiple stacks, which is well-known to be undecidable in general. Our overall strategy to attack the state reachability problem for the fragments of ASM is to simulate them (in particular, the multiple stacks) via—in some cases, decidable extensions of—PDS.
5.1 Case \(\mathsf{Lmd}(A_0) = \mathsf{STK}\)
Our approach to tackle this case is to simulate \(\mathcal {A}\) by an extension of PDS, i.e., pushdown systems with transductions (TrPDS), proposed in [19]. In TrPDS, each transition is associated with an FST defining how the stack content is modified. Formally, a TrPDS is a tuple \({\mathcal {P} }=(Q, \varGamma , {\mathscr {T}}, \varDelta )\), where Q and \(\varGamma \) are precisely the same as those of PDS, \({\mathscr {T}}\) is a finite set of FSTs over the alphabet \(\varGamma \), and \(\varDelta \subseteq Q \times \varGamma \times \varGamma ^* \times {\mathscr {T}}\times Q\) is a finite set of transition rules. Let \({\mathcal {R} }({\mathscr {T}})\) denote the set of transductions defined by FSTs from \({\mathscr {T}}\) and \(\llbracket {\mathcal {R} }({\mathscr {T}}) \rrbracket \) denote the closure of \({\mathcal {R} }({\mathscr {T}})\) under composition and left-quotient. A TrPDS \({\mathcal {P} }\) is said to be finite if \(\llbracket {\mathcal {R} }({\mathscr {T}}) \rrbracket \) is finite.
The configurations of \({\mathcal {P} }\) are defined similarly as in PDS. We define a binary relation \(\xrightarrow {{\mathcal {P} }}\) on \({\mathsf {Conf} }_{\mathcal {P} }\) as follows: \((q,w) \xrightarrow {{\mathcal {P} }} (q', w')\) if there are \(\gamma \in \varGamma \), the words \(w_1, u, w_2\), and \({\mathcal {T} }\in {\mathscr {T}}\) such that \(w= \gamma w_1\), \((q, \gamma , u, {\mathcal {T} }, q') \in \varDelta \), \(w_1 \xrightarrow {{\mathcal {T} }} w_2\), and \(w' = u w_2\). Let \(\mathop {\Rightarrow }\limits ^{{\mathcal {P} }}\) denote the reflexive and transitive closure of \(\xrightarrow {{\mathcal {P} }}\). Similarly to PDS, we can define \({\mathsf {pre} }^*(\cdot )\) and \({\mathsf {post} }^*(\cdot )\) respectively. Regular sets of configurations of TrPDS can be represented by MA, in line with PDS. More precisely, given a finite TrPDS \({\mathcal {P} }=(Q,\varGamma , {\mathscr {T}}, \varDelta )\) and an MA \(\mathcal {A}\) for \({\mathcal {P} }\), one can compute, in time polynomial in \(|{\mathcal {P} }|+|\llbracket {\mathcal {R} }({\mathscr {T}}) \rrbracket |+|\mathcal {A}|\), two MAs \(\mathcal {A}_{{\mathsf {pre} }^*}\) and \(\mathcal {A}_{{\mathsf {post} }^*}\) that recognize the sets \({\mathsf {pre} }^*({\mathsf {Conf} }_\mathcal {A})\) and \({\mathsf {post} }^*({\mathsf {Conf} }_\mathcal {A})\) respectively [17,18,19].
To simulate \(\mathcal {A}\) via a finite TrPDS \({\mathcal {P} }\), the back stack \(\rho =(S_1,\cdots , S_n)\) of \(\mathcal {A}\) is encoded by a word \(S_1 \sharp \cdots \sharp S_n \sharp \bot \) (where \(\sharp \) is a delimiter and \(\bot \) is the bottom symbol of the stack), which is stored in the stack of \({\mathcal {P} }\). Recall that, in this case, each task \(S_i\) is rooted at an \(\mathsf{STK}\)-activity which sits on the bottom of \(S_i\). Suppose \(\mathsf{top}(S_1) = A\). When a transition \((q, A, {\mathsf {start} }(B), q')\) with \(B \in \mathsf{Act}_{\mathsf{STK}}\) is fired, according to the semantics of \(\mathcal {A}\), the B-task of \(\rho \), say \(S_i\), is switched to the top of \(\rho \) and changed into [B] (i.e., all the activities in the B-task, except B itself, are popped). To simulate this in \({\mathcal {P} }\), we replace every stack symbol in the place of \(S_i\) with a dummy symbol \(\dagger \) and keep the other symbols unchanged. On the other hand, to simulate a \({\mathsf {back} }\) action of \(\mathcal {A}\), \({\mathcal {P} }\) continues popping until the next non-dummy and non-delimiter symbol is seen.
Proposition 4
Let \(\mathcal {A}=(Q, \mathsf{Sig}, q_0, \varDelta )\) be an \(\mathsf{STK}\)-dominating ASM with \(\mathsf{Sig}=(\mathsf{Act}, \mathsf{Lmd}, \mathsf{Aft}, A_0)\) and \(\mathsf{Lmd}(A_0) = \mathsf{STK}\). Then a finite TrPDS \({\mathcal {P} }=(Q', \varGamma , {\mathscr {T}}, \varDelta ')\) with \(Q \subseteq Q'\) can be constructed in time polynomial in \(|\mathcal {A}|\) such that, for each \(q \in Q\), q is reachable from \((q_0, \varepsilon )\) in \(\mathcal {A}\) iff q is reachable from \((q_0, \bot )\) in \({\mathcal {P} }\).
For a state \(q \in Q\), \({\mathsf {pre} }^*_{\mathcal {P} }(q)\) can be effectively computed as an MA \({\mathcal {B} }_q\), and the reachability of q in \(\mathcal {A}\) is reduced to checking whether \((q_0, \bot ) \in {\mathsf {Conf} }_{{\mathcal {B} }_q}\).
5.2 Case \(\mathsf{Lmd}(A_0) \ne \mathsf{STK}\)
We then turn to the more general case \(\mathsf{Lmd}(A_0) \ne \mathsf{STK}\) which is significantly more involved. For exposition purpose, we consider an ASM \(\mathcal {A}\) where there are exactly two \(\mathsf{STK}\) activities \(A_1, A_2\), and the task affinity of \(A_2\) is the same as that of the main task \(A_0\) (and thus the task affinity of \(A_1\) is different from that of \(A_0\)). We also assume that all the activities in \(\mathcal {A}\) are “standard” except \(A_1,A_2\). Namely \(\mathsf{Act}=\mathsf{Act}_{\mathsf{STD}}\cup \{A_1, A_2\}\) and \(A_0\in \mathsf{Act}_{\mathsf{STD}}\) in particular. Neither of these two assumptions is fundamental and their generalization is given in [6].
By Proposition 3, there are at most two tasks in the back stack of \(\mathcal {A}\). The two tasks are either an \(A_0\)-task and an \(A_1\)-task, or an \(A_2\)-task and an \(A_1\)-task. An \(A_2\)-task can only surface when the original \(A_0\)-task is popped empty. If this happens, no \(A_0\)-task will be recreated again, and thus, according to the arguments in Sect. 5.1, we can simulate the ASM by TrPDS directly and we are done. The challenging case is that we have both an \(A_0\)-task and an \(A_1\)-task. To solve the state reachability problem, the main technical difficulty is that the order of the \(A_0\)-task and the \(A_1\)-task may be switched for arbitrarily many times before reaching the target state q. Readers may be wondering why they cannot simply simulate two-counter machines. The reason is that the two tasks are asymmetric in the sense that, each time when the \(A_1\)-task is switched from the bottom to the top (by starting the activity \(A_1\)), the content of the \(A_1\)-task is reset into \([A_1]\). But this is not the case for \(A_0\)-task: when the \(A_0\)-task is switched from the bottom to the top (by starting the activity \(A_2\)), if it does not contain \(A_2\), then \(A_2\) will be pushed into the \(A_0\)-task; otherwise all the activities above \(A_2\) will be popped and \(A_2\) becomes the top activity of the \(A_0\)-task. Our decision procedure below utilises the asymmetry of the two tasks.
Intuition of construction. The crux of reachability analysis is to construct a finite abstraction for the \(A_1\)-task and incorporate it into the control states of \(\mathcal {A}\), so we can reduce the state reachability of \(\mathcal {A}\) into that of a pushdown system \({\mathcal {P} }_\mathcal {A}\) (with a single stack). Observe that a run of \(\mathcal {A}\) can be seen as a sequence of task switching. In particular, an \(A_0;A_1 ;A_0\) switching denotes a path in \(\xrightarrow {\mathcal {A}}\) where the \(A_0\)-task is on the top in the first and the last configuration, while the \(A_1\)-task is on the top in all the intermediate configurations. The main idea of the reduction is to simulate the \(A_0; A_1;A_0\) switching by a “macro”-transition of \({\mathcal {P} }_\mathcal {A}\). Note that the \(A_0\)-task regains the top task in the last configuration either by starting the activity \(A_2\) or by emptying the \(A_1\)-task. Suppose that, for an \(A_0;A_1;A_0\) switching, in the first (resp. last) configuration, q (resp. \(q'\)) is the control state and \(\alpha \) (resp. \(\beta \)) is the finite abstraction of the \(A_1\)-task. Then for the “macro”-transition of \({\mathcal {P} }_\mathcal {A}\), the control state will be updated from \((q, \alpha )\) to \((q', \beta )\), and the stack content of \({\mathcal {P} }_\mathcal {A}\) is updated accordingly:
-
If the \(A_0\)-task regains the top task by starting \(A_2\), then the stack content is updated as follows: if the stack does not contain \(A_2\), then \(A_2\) will be pushed into the stack; otherwise all the symbols above \(A_2\) will be popped.
-
On the other hand, if the \(A_0\)-task regains the top task by emptying the \(A_1\)-task, then the stack content is not changed.
Roughly speaking, the abstraction of the \(A_1\)-task must carry the information that, when \(A_0\)-task and \(A_1\)-task are the top resp. bottom task of the back stack and \(A_0\)-task is emptied, whether the target state q can be reached from the configuration at that time. As a result, we define the abstraction of the \(A_1\)-task whose content is encoded by a word \(w \in \mathsf{Act}^*\), denoted by \(\alpha (w)\), as the set of all states \(q'' \in Q\) such that the target state q can be reached from \((q'', (w))\) in \(\mathcal {A}\). [Note that during the process that q is reached from \((q'', (w))\) in \(\mathcal {A}\), the \(A_0\)-task does not exist anymore, but a (new) \(A_2\)-task, may be formed.] Let \({\mathsf {Abs} }_{A_1} = 2^Q\).
To facilitate the construction of the PDS \({\mathcal {P} }_\mathcal {A}\), we also need to record how the abstraction “evolves". For each \((q', A, \alpha ) \in Q \times (\mathsf{Act}\setminus \{A_1\}) \times {\mathsf {Abs} }_{A_1}\), we compute the set \(\mathsf{Reach}(q', A, \alpha )\) consisting of pairs \((q'', \beta )\) satisfying: there is an \(A_0 ; A_1; A_0\) switching such that in the first configuration, A is the top symbol of the \(A_0\)-task, \(q'\) (resp. \(q''\)) is the control state of the first (resp. last) configuration, and \(\alpha \) (resp. \(\beta \)) is the abstraction for the \(A_1\)-task in the first (resp. last) configuration.Footnote 10
Computing \(\mathsf{Reach}(q', A, \alpha )\). Let \((q', A, \alpha ) \in Q \times (\mathsf{Act}\setminus \{A_1\}) \times {\mathsf {Abs} }_{A_1}\). We first simulate relevant parts of \(\mathcal {A}\) as follows:
-
Following Sect. 5.1, we construct a TrPDS
 to simulate the \(A_1\)-task and \(A_2\)-task of \(\mathcal {A}\) after the \(A_0\)-task is emptied, where
to simulate the \(A_1\)-task and \(A_2\)-task of \(\mathcal {A}\) after the \(A_0\)-task is emptied, where  and
and 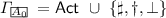 . Note that \(A_0\) may still—as a “standard” activity—occur in
. Note that \(A_0\) may still—as a “standard” activity—occur in 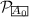 though the \(A_0\)-task disappears. In addition, we construct an MA
though the \(A_0\)-task disappears. In addition, we construct an MA  to represent
to represent 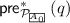 , where
, where  . Then given a stack content \(w \in \mathsf{Act}^*_\mathsf{STD}A_1\) of the \(A_1\)-task, the abstraction \(\alpha (w)\) of w, is the set of \(q'' \in I_q \cap Q\) such that \((q'', w \sharp \bot ) \in {\mathsf {Conf} }_{{\mathcal {B} }_q}\).
. Then given a stack content \(w \in \mathsf{Act}^*_\mathsf{STD}A_1\) of the \(A_1\)-task, the abstraction \(\alpha (w)\) of w, is the set of \(q'' \in I_q \cap Q\) such that \((q'', w \sharp \bot ) \in {\mathsf {Conf} }_{{\mathcal {B} }_q}\). -
We construct a PDS
 to simulate the \(A_1\)-task of \(\mathcal {A}\), where
to simulate the \(A_1\)-task of \(\mathcal {A}\), where  . In addition, to compute \(\mathsf{Reach}(q', A, \alpha )\) later, we construct an MA
. In addition, to compute \(\mathsf{Reach}(q', A, \alpha )\) later, we construct an MA  to represent
to represent 
Definition 4
\(\mathsf{Reach}(q', A, \alpha )\) comprises
-
the pairs \((q'', \beta ) \in Q \times {\mathsf {Abs} }_{A_1}\) satisfying that (1) \((q', A, {\mathsf {start} }(A_1), q_1) \in \varDelta \), (2)
 , (3) \((q_2, B, {\mathsf {start} }(A_2), q'') \in \varDelta \), and (4) \(\beta \) is the abstraction of Bw, for some \(B \in \mathsf{Act}\setminus \{A_2\}\), \(w \in (\mathsf{Act}\setminus \{A_2\})^*\) and \(q_1, q_2 \in Q\),
, (3) \((q_2, B, {\mathsf {start} }(A_2), q'') \in \varDelta \), and (4) \(\beta \) is the abstraction of Bw, for some \(B \in \mathsf{Act}\setminus \{A_2\}\), \(w \in (\mathsf{Act}\setminus \{A_2\})^*\) and \(q_1, q_2 \in Q\), -
the pairs \((q'', \bot )\) such that \((q', A, {\mathsf {start} }(A_1), q_1) \in \varDelta \) and
 for some \(q_1 \in Q\).
for some \(q_1 \in Q\).
Importantly, conditions in Definition 4 can be characterized algorithmically.
Lemma 1
For \((q', A, \alpha ) \in Q \times (\mathsf{Act}\setminus \{A_1\}) \times {\mathsf {Abs} }_{A_1}\), \(\mathsf{Reach}(q', A, \alpha )\) is the union of
-
\(\{(q'', \bot ) \mid (q'', \bot ) \in {\mathsf {Conf} }_{{\mathcal {M} }_{(q', A, \alpha )}}\}\) and
-
the set of pairs \((q'', \beta ) \in Q \times {\mathsf {Abs} }_{A_1}\) such that there exist \(q_2 \in Q\) and \(B \in \mathsf{Act}\setminus \{A_2\}\) satisfying that \((q_2, B, {\mathsf {start} }(A_2), q'')\), and \((B (\mathsf{Act}\setminus \{A_2\})^* \sharp \bot ) \cap (\mathsf{Act}_{\mathsf{STD}}^* A_1 \sharp \bot ) \cap ({\mathcal {L}}( {\mathcal {M} }_{(q', A, \alpha )}(q_2)) \langle \bot \rangle ^{-1}) \sharp \bot \cap {\mathcal {L}}_\beta \ne \emptyset ,\) where \({\mathcal {L}}( {\mathcal {M} }_{(q', A, \alpha )}(q_2)) \langle \bot \rangle ^{-1}\) is the set of words w such that \(w \bot \) belongs to \({\mathcal {L}}( {\mathcal {M} }_{(q', A, \alpha )}(q_2))\), and \({\mathcal {L}}_\beta = \bigcap \limits _{q''' \in \beta } {\mathcal {L}}({\mathcal {B} }_q(q'''))\ \cap \bigcap \limits _{q''' \in Q \setminus \beta } \overline{{\mathcal {L}}({\mathcal {B} }_q(q'''))}\), with \(\overline{{\mathcal {L}}}\) representing the complement language of \({\mathcal {L}}\).
Construction of \({\mathcal {P} }_\mathcal {A}\). We first construct a PDS \({\mathcal {P} }_{A_0}= (Q_{A_0}, \varGamma _{A_0} , \varDelta _{A_0})\), to simulate the \(A_0\)-task of \(\mathcal {A}\). Here \(Q_{A_0} = (Q \times \{0, 1\}) \cup (Q \times \{1\} \times \{\mathsf{pop}\})\), \(\varGamma _{A_0} = \mathsf{Act}_{\mathsf{STD}} \cup \{A_2,\bot \}\), and \(\varDelta _{A_0}\) comprises the transitions. Here 1 (resp. 0) marks that the activity \(A_2\) is in the stack (resp. is not in the stack) and the tag \(\mathsf{pop}\) marks that the PDS is in the process of popping until \(A_2\). The construction of \({\mathcal {P} }_{A_0}\) is relatively straightforward, the details of which can be found in [6].
We then define the PDS \({\mathcal {P} }_{\mathcal {A}}= (Q_\mathcal {A}, \varGamma _{A_0}, \varDelta _{\mathcal {A}})\), where \(Q_{\mathcal {A}} = ({\mathsf {Abs} }_{A_1} \times Q_{A_0}) \cup \{q\}\), and \(\varDelta _{\mathcal {A}}\) comprises the following transitions,
-
for each \((p, \gamma , w, p') \in \varDelta _{A_0}\) and \(\alpha \in {\mathsf {Abs} }_{A_1}\), we have \(((\alpha , p), \gamma , w, (\alpha , p')) \in \varDelta _\mathcal {A}\) (here \(p,p' \in Q_{A_0}\), that is, of the form \((q', b)\) or \((q', b, \mathsf{pop})\)), [behaviour of the \(A_0\)-task]
-
for each \((q', A, \alpha ) \in Q \times (\mathsf{Act}\setminus \{A_1\}) \times {\mathsf {Abs} }_{A_1}\) and \(b \in \{0, 1\}\) such that \({\mathcal {M} }_{(q', A, \alpha )}(q) \ne \emptyset \), we have \(((\alpha , (q',b)), A, A, q) \in \varDelta _\mathcal {A}\), [switch to the \(A_1\)-task and reach q before switching back]
-
for each \((q', A, \alpha ) \in Q \times (\mathsf{Act}\setminus \{A_1\}) \times {\mathsf {Abs} }_{A_1}\) and \((q'', \beta ) \in \mathsf{Reach}(q', A, \alpha )\) such that \(\beta \ne \bot \),
-
if \(A \ne A_2\), then we have \(((\alpha , (q', 0)), A, A_2 A, (\beta , (q'', 1))) \in \varDelta _\mathcal {A}\) and \(((\alpha , (q', 1)), A, \varepsilon , (\beta , (q'',1,\mathsf{pop}))) \in \varDelta _\mathcal {A}\),
-
if \(A=A_2\), then we have \(((\alpha , (q', 1)), A_2, A_2, (\beta , (q'',1))) \in \varDelta _\mathcal {A}\), [switch to the \(A_1\)-task and switch back to the \(A_0\)-task later by launching \(A_2\)]
-
-
for each \((q', A, \alpha ) \in Q \times (\mathsf{Act}\setminus \{A_1\}) \times {\mathsf {Abs} }_{A_1}\), \((q'', \bot ) \in \mathsf{Reach}(q', A, \alpha )\) and \(b \in \{0,1\}\), we have \(((\alpha , (q', b)), A, A, (\emptyset , (q'', b))) \in \varDelta _\mathcal {A}\), [switch to the \(A_1\)-task and switch back to the \(A_0\)-task later when the \(A_1\)-task becomes empty]
-
for each \(\alpha \in {\mathsf {Abs} }_{A_1}\), \(b \in \{0,1\}\) and \(A \in \mathsf{Act}_{\mathsf{STD}} \cup \{A_2\}\), \(((\alpha , (q, b)), A, A, q) \in \varDelta _\mathcal {A}\), [q is reached when the \(A_0\)-task is the top task]
-
for each \(q' \in Q\) and \(\alpha \in {\mathsf {Abs} }_{A_1}\) with \(q' \in \alpha \), \(((\alpha , (q', 0)), \bot , \bot , q) \in \varDelta _\mathcal {A}\). [q is reached after the \(A_0\)-task becomes empty and the \(A_1\)-task becomes the top task]
Proposition 5
Let \(\mathcal {A}\) be an \(\mathsf{STK}\)-dominating ASM where there are exactly two \(\mathsf{STK}\)-activities \(A_1, A_2\) and \(\mathsf{Aft}(A_2)=\mathsf{Aft}(A_0)\). Then q is reachable from the initial configuration \((q_0,\varepsilon )\) in \(\mathcal {A}\) iff q is reachable from the initial configuration \(((\emptyset , (q_0,0)), \bot )\) in \({\mathcal {P} }_\mathcal {A}\).
6 Related Work
We first discuss pushdown systems with multiple stacks (MPDSs) which are the most relevant to ASM. (For space reasons we will skip results on general pushdown systems though.) A multitude of classes of MPDSs have been considered, mostly as a model for concurrent recursive programs. In general, an ASM can be encoded as an MPDS. However, this view is hardly profitable as general MPDSs are obviously Turing-complete, leaving the reachability problem undecidable.
To regain decidability at least for reachability, several subclasses of MPDSs were proposed in literature: (1) bounding the number of context-switches [15], or more generally, phases [10], scopes [11], or budgets [3]; (2) imposing a linear ordering on stacks and pop operations being reserved to the first non-empty stack [5]; (3) restricting control states (e.g., weak MPDSs [7]). However, our decidable subclasses of ASM admit none of the above bounded conditions. A unified and generalized criterion [12] based on MSO over graphs of bounded tree-width was proposed to show the decidability of the emptiness problem for several restricted classes of automata with auxiliary storage, including MPDSs, automata with queues, or a mix of them. Since ASMs work in a way fairly different from multi-stack models in the literature, it is unclear—literally for us—to obtain the decidability by using bounded tree-width approach. Moreover, [12] only provides decidability proofs, but without complexity upper bounds. Our decision procedure is based on symbolic approaches for pushdown systems, which provides complexity upper bounds and which is amenable to implementation.
Higher-order pushdown systems represent another type of generalization of pushdown systems through higher-order stacks, i.e., a nested “stack of stack" structure [13], with decidable reachability problems [9]. Despite apparent resemblance, the back stack of ASM can not be simulated by an order-2 pushdown system. The reason is that the order between tasks in a back stack may be dynamically changed, which is not supported by order-2 pushdown systems.
On a different line, there are some models which have addressed, for instance, GUI activities of Android apps. Window transition graphs were proposed for representing the possible GUI activity (window) sequences and their associated events and callbacks, which can capture how the events and callbacks modify the back stack [21]. However, the key mechanisms of back stacks (launch modes and task affinities) were not covered in this model. Moreover, the reachability problem for this model was not investigated. A similar model, labeled transition graph with stack and widget (LATTE [20]) considered the effects of launch modes on the back stacks, but not task affinities. LATTE is essentially a finite-state abstraction of the back stack. However, to faithfully capture the launch modes and task affinities, one needs an infinite-state system, as we have studied here.
7 Conclusion
In this paper, we have introduced Android stack machine to formalize the back stack system of the Android platform. We have also investigated the decidability of the reachability problem of ASM. While the reachability problem of ASM is undecidable in general, we have identified a fragment, i.e., \(\mathsf{STK}\)-dominating ASM, which is expressive and admits decision procedures for reachability.
The implementation of the decision procedures is in progress. We also plan to consider other features of Android back stack systems, e.g., the “allowTaskReparenting” attribute of activities. A long-term program is to develop an efficient and scalable formal analysis and verification framework for Android apps, towards which the work reported in this paper is the first cornerstone.
Notes
- 1.
Adapted from an open-source app https://github.com/wauoen/LaunchModeDemo.
- 2.
By Definition 2(4), \(S_1=[A]\).
- 3.
If i exists, it must be unique by Definition 2(5). Moreover, \(i>1\), as \(\mathsf{Lmd}(A) = \mathsf{SIT}\).
- 4.
If i exists, it must be unique by Definition 2(1). Moreover, \(i>1\), as \(A\ne B\).
- 5.
B does not occur in \(\rho \) at all by Definition 2(3–5).
- 6.
Note that B occurs at most once in \(S_1\) by Definition 2(1).
- 7.
If i exists, it must be unique by Definition 2(5). Moreover, \(i>1\), as \(\mathsf{Lmd}(A) \ne \mathsf{SIT}\Longrightarrow \mathsf{Aft}(B) \ne \mathsf{Aft}(S_1)\).
- 8.
Note that B occurs at most once in \(S_i\) by Definition 2(1).
- 9.
The more general case that \(\mathcal {A}\) also contains \(\mathsf{STP}\) and \(\mathsf{SIT}\) activities is slightly more involved and requires more space to present, which can be found in [6].
- 10.
As we can see later, \(\mathsf{Reach}(q', A, \alpha )\) does not depend on \(\alpha \) for the two-task special case considered here. We choose to keep \(\alpha \) in view of readability.
References
Android documentation. https://developer.android.com/guide/components/activities/tasks-and-back-stack.html
Stackoverflow entry: Android singletask or singleinstance launch mode? https://stackoverflow.com/questions/3219726/
Abdulla, P.A., Atig, M.F., Rezine, O., Stenman, J.: Multi-pushdown systems with budgets. In: Formal Methods in Computer-Aided Design (FMCAD), pp. 24–33 (2012)
Bouajjani, A., Esparza, J., Maler, O.: Reachability analysis of pushdown automata: application to model-checking. In: Mazurkiewicz, A., Winkowski, J. (eds.) CONCUR 1997. LNCS, vol. 1243, pp. 135–150. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-63141-0_10
Breveglieri, L., Cherubini, A., Citrini, C., Crespi-Reghizzi, S.: Multi-push-down languages and grammars. Int. J. Found. Comput. Sci. 7(3), 253–292 (1996)
Chen, T., He, J., Song, F., Wang, G., Wu, Z., Yan, J.: Android stack machine (full version) (2018). http://www.dcs.bbk.ac.uk/~taolue/pub-papers/ASM-full.pdf
Czerwinski, W., Hofman, P., Lasota, S.: Reachability problem for weak multi-pushdown automata. In: Proceedings of the 23rd International Conference on (CONCUR), pp. 53–68 (2012)
Hao, S., Li, D., Halfond, W.G.J., Govindan, R.: Estimating mobile application energy consumption using program analysis. In: Proceedings of the 35th International Conference on Software Engineering (ICSE), pp. 92–101 (2013)
Knapik, T., Niwinski, D., Urzyczyn, P.: Higher-order pushdown trees are easy. In: Proceedings of the 5th International Conference on Foundations of Software Science and Computation Structures (FOSSACS), pp. 205–222 (2002)
La Torre, S., Madhusudan, P., Parlato, G.: A robust class of context-sensitive languages. In: Proceedings of the 22nd IEEE Symposium on Logic in Computer Science (LICS), pp. 161–170 (2007)
La Torre, S., Napoli, M.: Reachability of multistack pushdown systems with scope-bounded matching relations. In: Proceedings of the 22nd International Conference on Concurrency Theory (CONCUR), pp. 203–218 (2011)
Madhusudan, P., Parlato, G.: The tree width of auxiliary storage. In: Proceedings of the 38th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL), pp. 283–294 (2011)
Maslov, A.N.: Multilevel stack automata. Probl. Inf. Transm. 15, 1170–1174 (1976)
Minsky, M.: Computation: Finite and Infinite Machines. Prentice Hall Int., Upper Saddle River (1967)
Qadeer, S., Rehof, J.: Context-bounded model checking of concurrent software. In: Proceedings of the 11th International Conference on Tools and Algorithms for the Construction and Analysis of Systems (TACAS), pp. 93–107 (2005)
Ren, C., Zhang, Y., Xue, H., Wei, T., Liu, P.: Towards discovering and understanding task hijacking in android. In: Proceedings of the 24th USENIX Security Symposium (USENIX Security), pp. 945–959 (2015)
Song, F.: Analyzing pushdown systems with stack manipulation. Inf. Comput. 259(1), 41–71 (2018)
Song, F., Miao, W., Pu, G., Zhang, M.: On reachability analysis of pushdown systems with transductions: application to Boolean programs with call-by-reference. In: Proceedings of the 26th International Conference on Concurrency Theory (CONCUR), pp. 383–397 (2015)
Uezato, Y., Minamide, Y.: Pushdown systems with stack manipulation. In: Proceedings of the 11th International Symposium on Automated Technology for Verification and Analysis (ATVA), pp. 412–426 (2013)
Yan, J., Wu, T., Yan, J., Zhang, J.: Widget-sensitive and back-stack-aware GUI exploration for testing android apps. In: Proceedings of the 2017 IEEE International Conference on Software Quality, Reliability and Security (QRS), pp. 42–53 (2017)
Yang, S., Zhang, H., Wu, H., Wang, Y., Yan, D., Rountev, A.: Static window transition graphs for android. In: Proceedings of the 30th IEEE/ACM International Conference on Automated Software Engineering (ASE), pp. 658–668 (2015)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
<SimplePara><Emphasis Type="Bold">Open Access</Emphasis>This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.</SimplePara><SimplePara>The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.</SimplePara>
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Chen, T., He, J., Song, F., Wang, G., Wu, Z., Yan, J. (2018). Android Stack Machine. In: Chockler, H., Weissenbacher, G. (eds) Computer Aided Verification. CAV 2018. Lecture Notes in Computer Science(), vol 10982. Springer, Cham. https://doi.org/10.1007/978-3-319-96142-2_29
Download citation
DOI: https://doi.org/10.1007/978-3-319-96142-2_29
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96141-5
Online ISBN: 978-3-319-96142-2
eBook Packages: Computer ScienceComputer Science (R0)







 to simulate the
to simulate the  and
and 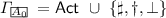 . Note that
. Note that 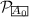 though the
though the  to represent
to represent 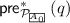 , where
, where  . Then given a stack content
. Then given a stack content  to simulate the
to simulate the  . In addition, to compute
. In addition, to compute  to represent
to represent 
 , (3)
, (3)  for some
for some