Abstract
We first introduce the Hecke ring of a \(\mathbb {Z}\)-group G and discuss it basic properties (local-global structure, compatibility with isogenies, criterion for commutativity…). An elementary description of the Hecke rings of classical groups is given. Then, we recall the notion of a square integrable automorphic form for G, and that of a discrete automorphic representation of G. When G is the symplectic group Sp2g, we explain how the theory of Siegel modular forms fits into this picture. We also show how the p-neighbor problem for even unimodular lattices in rank n may be viewed as a question about automorphic representations for the orthogonal \(\mathbb {Z}\)-group On.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The assertions h(SLn) = h(Sp2g) = 1 recalled above are also very particular cases of Kneser’s strong approximation theorem (see [123], [162, Theorem 7.12]). It asserts that we have h(G) = 1 whenever the \(\mathbb {C}\)-group \(G_{\mathbb {C}}\) is semisimple and simply connected and the topological group \(G(\mathbb {R})\) does not have a nontrivial connected, compact, normal subgroup.
- 2.
This property is not automatic if X is infinite. Consider, for example, the group
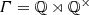 of affine transformations of \(\mathbb {Q}\) and the Γ-set X consisting of the subsets of \(\mathbb {Q}\) of the form \(a\mathbb {Z}+b\) with \(a \in \mathbb {Q}^\times \) and \(b \in \mathbb {Q}\).
of affine transformations of \(\mathbb {Q}\) and the Γ-set X consisting of the subsets of \(\mathbb {Q}\) of the form \(a\mathbb {Z}+b\) with \(a \in \mathbb {Q}^\times \) and \(b \in \mathbb {Q}\). - 3.
We refer to the article of Satake for a variant without the injectivity assumption on g. The reader will not miss much in the current discussion by assuming Γ ⊂ Γ′ and X ⊂ X′, with f and g the corresponding inclusions.
- 4.
At this point, it is useful to recall the following version of Schur’s lemma. Let U and V be Hilbert spaces endowed with unitary representations of a group Γ. We assume that U is topologically irreducible and that u: U → V is a nonzero, Γ-equivariant, continuous linear map. Then the adjoint u ∗: V → U (which is Γ-equivariant) satisfies u ∗∘ u = λIdU for some \(\lambda \in \mathbb {R}^\times \). Indeed, u ∗∘ u ∈End(U) is Hermitian and nonzero and commutes with Γ; by the spectral theorem, its spectrum is therefore reduced to a point {λ}. It follows that V is the orthogonal sum of Im(u) (which is closed) and Ker(u ∗).
- 5.
The reader should be aware that the definition we use here depends not only on \(G_{\mathbb {Q}}\) but also on G as a \(\mathbb {Z}\)-group. In the literature, our discrete automorphic representations are more commonly called “discrete automorphic representations of \(G(\mathbb {A})\) that are spherical (or unramified) with respect to \(G(\widehat {\mathbb {Z}})\).” The apparent loss of generality in our presentation is, however, at this point illusory, because every open compact subgroup of \(G(\mathbb {A}_f)\) is of the form \(G'(\widehat {\mathbb {Z}})\) for a well-chosen \(\mathbb {Z}\)-group G′ with \(G^{\prime }_{\mathbb {Q}} \simeq G_{\mathbb {Q}}\).
- 6.
In fact, a famous result of Godement shows that under this same hypothesis on G, the group \(G(\mathbb {Q})\) is cocompact in \(G(\mathbb {A})\), which implies the equality \(\mathcal {A}_{\mathrm{disc}}(G)={\mathcal {A}^2}(G)\) more directly in this specific case (see, for example, [35, Lemma 16.1]).
- 7.
A principal polarization on a lattice \(L \subset \mathbb {C}^g\) consists of a nondegenerate alternating bilinear form \(\eta \colon L \times L \rightarrow \mathbb {Z}\) whose extension of scalars \(\eta _{\mathbb {R}}\) to \(L \otimes \mathbb {R} = \mathbb {C}^g\) satisfies \(\eta _{\mathbb {R}}(ix,iy)=\eta _{\mathbb {R}}(x,y)\) for every \(x,y \in \mathbb {C}^g\) and whose associated Hermitian form \((x,y) \mapsto \eta _{\mathbb {R}}(ix,y)+i\eta _{\mathbb {R}}(x,y)\) on \(\mathbb {C}^g\) is positive definite. Riemann’s theory allows us to naturally identify \({\mathrm{Sp}}_{2g}(\mathbb {Z})\backslash \mathbb {H}_g\) with the set of \(\mathrm {GL}_g(\mathbb {C})\)-orbits of pairs (L, η), where \(L \subset \mathbb {C}^g\) is a lattice and η is a principal polarization on L.
References
A. N. Andrianov, Quadratic forms and Hecke operators, Grundlehren math. Wiss., vol. 286 (Springer-Verlag, 1987).
M. Asgari, R. Schmidt, Siegel modular forms and representations, Manuscripta Math. 104 (2001), pp. 173–200.
R. Borcherds, The Leech lattice and other lattices, Ph. D. dissertation, Univ. of Cambridge (1984).
A. Borel, Some finiteness theorems for adele groups over number fields, Publ. Math. de l’I.H.É.S. 16 (1963), pp. 101–126.
A. Borel, Linear algebraic groups, 2nd ed., Grad. Texts in Math., vol. 126 (Springer Verlag, 1991).
A. Borel, Automorphic forms on \(\mbox{SL}_2(\mathbb {R})\), Cambridge Tracts in Math., vol. 130 (Cambridge Univ. Press, 1997).
A. Borel, H. Jacquet, Automorphic forms and automorphic representation (Oregon State Univ., Corvallis, Ore.), in Automorphic forms, representations and L-functions, II, Proc. Symp. in Pure Math. XXXIII (Amer. Math. Soc., Providence, RI, 1979), pp. 189–203.
Variétés analytiques complexes et fonctions automorphes, Séminaire H. Cartan, tome 6 (Éc. Norm. Sup. Paris, 1953/54).
Fonctions automorphes, Séminaire H. Cartan, tome 10 (Éc. Norm. Sup. Paris, 1957/58).
P. Cartier, Representations of p-adic groups: a survey, in Automorphic forms, representations and L-functions, I (Oregon State Univ., Corvallis, Ore.), Proc. Symp. in Pure Math. XXXIII, (Amer. Math. Soc., Providence, RI, 1979), pp. 111–157.
G. Chenevier, D. Renard, Level one algebraic cusp form of classical groups of small rank, Mem. Amer. Math. Soc., vol. 1121 (Amer. Math. Soc., Providence, RI, 2015).
J. H. Conway, A group of order 8,315,553,613,086,720,000, Bull. London Math. Soc. 1 (1969), pp. 79–88.
J. H. Conway, N. J. A. Sloane, Sphere packings, lattices and groups, Grundlehren math. Wiss., vol. 290 (Springer-Verlag, New York, 1999).
M. Eichler, Quadratische formen und orthogonal gruppen, Grundlehren math. Wiss. (Springer Verlag, 1952).
E. Freitag, Siegelsche Modulfunktionen, Grundlehren der math. Wiss., vol. 254 (Springer Verlag, 1983).
G. van der Geer, Siegel modular forms and their applications, in The 1–2–3 of modular forms, ed. by J. H. Bruinier, G. van der Geer, G. Harder, D. Zagier, Universitext (Springer Verlag, Berlin, 2008), pp. 181–245.
I. M. Gel’fand, M. I. Graev, I. I. Pyatetskii-Shapiro, Representation theory and automorphic functions (Academic Press, 1990).
B. Gross, On the Satake isomorphism, in Galois representations in arithmetic algebraic geometry, ed. by A. Scholl, R. Taylor (Cambridge Univ. Press, 1998).
B. Gross, Algebraic modular forms, Israel J. Math. 113 (1999), pp. 61–93.
Harish-Chandra, Automorphic forms on semisimple Lie groups, Lecture Notes in Math., vol. 62 (Springer Verlag, 1968).
J. Humphreys, Linear algebraic groups, Grad. Texts in Math., vol. 21 (Springer Verlag, 1975).
A. W. Knapp, Representation theory of semisimple groups (Princeton Univ. Press, 1986).
M. Kneser, Strong approximation, algebraic groups and discontinuous subgroups, Proc. Sympos. Pure Math., vol. 9 (Amer. Math. Soc., Boulder, 1966), pp. 187–196.
H. Koch, B. Venkov, Über ganzzahlige unimodulare euklidische Gitter, J. reine angew. Math. 398 (1989), pp. 144–168.
R. Langlands, On the functional equation satisfied by Eisenstein series, Lecture Notes in Math., vol. 544 (Springer Verlag, 1976).
V. Platonov, A. Rapinchuk, Algebraic groups and number theory, Pure Appl. Math., vol 139 (1994).
W. Rudin, Real and complex analysis, 3rd edn. (McGraw-Hill Int. ed.,1987).
I. Satake, Theory of spherical functions on reductive algebraic groups over p-adic fields, Publ. Math. Inst. Hautes Études Sci. 18 (1963), pp. 5–69.
J.-P. Serre, Cours d’arithmétique (Publ. Univ. France, Paris, 1970).
G. Shimura, Introduction to the arithmetic theory of automorphic functions (Princeton Univ. Press, 1971).
O. Taïbi, Dimensions of spaces of level one automorphic forms for split classical groups using the trace formula, preprint available at http://arxiv.org/abs/1406.4247 (2014).
A. Weil, L’intégration dans les groupes topologiques et ses applications, 2nd edn. (Hermann, 1940).
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Chenevier, G., Lannes, J. (2019). Automorphic Forms and Hecke Operators. In: Automorphic Forms and Even Unimodular Lattices. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge / A Series of Modern Surveys in Mathematics, vol 69. Springer, Cham. https://doi.org/10.1007/978-3-319-95891-0_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-95891-0_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-95890-3
Online ISBN: 978-3-319-95891-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


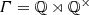 of affine transformations of
of affine transformations of