Abstract
We present a Coq formalization of Alexandre Miquel’s implicative algebras [18], which aim at providing a general algebraic framework for the study of classical realizability models. We first give a self-contained presentation of the underlying implicative structures, which roughly consist of a complete lattice equipped with a binary law representing the implication. We then explain how these structures can be turned into models by adding separators, giving rise to the so-called implicative algebras. Additionally, we show how they generalize Boolean and Heyting algebras as well as the usual algebraic structures used in the analysis of classical realizability.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Independently, very similar structures can be found in Frédéric Ruyer’s Ph.D. thesis [22] under the name of applicative lattices.
- 2.
Namely, one goal of the author’s PhD work was to define similar algebras based on the decomposition of the implication as \(\lnot A \vee B\) and \(\lnot (A \wedge \lnot B)\) (see [19]).
- 3.
In doing so, our development implicitly relies on assumptions of functional and propositional extensionnality, which we do not need nor use.
- 4.
We will not recall the definition of lattices, Heyting algebras and so on, for a more detailed introduction we refer the reader to [19, Chapter 9].
- 5.
Available at https://gitlab.com/emiquey/ImplicativeAlgebras/.
- 6.
- 7.
In partial combinatory algebras, the application is defined as a partial function.
- 8.
Observe that the application, which is written as a product, is neither commutative nor associative in general.
- 9.
This definition is related with the consttruction of a realizability tripos from an OCA \(\mathcal {A}\). Indeed, given a set X, the ordering on predicates of \(\mathcal {P}(\mathcal {A})^X\) is defined by:
$$ \varphi \vdash _X \psi \quad \triangleq \quad \exists r\in \mathcal {A}.\forall x\in X. \forall a\in \mathcal {A}.(a\in \varphi (x)\Rightarrow ra\in \psi (x)) $$where r is broadly a realizer of \(\forall x\in X.\varphi (x) \Rightarrow \psi (x)\). See [12] for further details.
- 10.
For instance, 0 contains less information than \(15-(3\times 5)\) or than \(\mathbbm {1}_{\mathbb {Q}}(\sqrt{(}2))\).
- 11.
In practice, we use Charguéraud’s locally nameless representation [2] for terms and formulas. Without giving too much details, we actually define pre-terms and pre-types which allow both for names (for free variables) and De Bruijn indices (for bounded variables). Terms and types are then defined as pre-terms and pre-types without free De Bruijn indices. As for the embedding from pre-terms (resp. pre-types) into an implicative structure, we define them by means of inductive predicates:
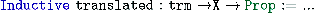 for which we proved the expected properties.
for which we proved the expected properties. - 12.
In order to avoid the certification of the corresponding compilation function, we state this well-known fact as an axiom (the only one) in our development.
- 13.
- 14.
If the implicative algebra is classical, for all \(a\in \mathcal {A}\) we saw that
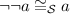 . Through the same quotient, this implies that \(\lnot \lnot [a] = [a]\) for all \(a\in \mathcal {A}\), and that the induced Heyting algebra is actually a Boolean algebra.
. Through the same quotient, this implies that \(\lnot \lnot [a] = [a]\) for all \(a\in \mathcal {A}\), and that the induced Heyting algebra is actually a Boolean algebra.
References
The POPLmark Challenge. https://www.seas.upenn.edu/~plclub/poplmark/
Charguéraud, A.: The locally nameless representation. J. Autom. Reason. 49(3), 363–408 (2012). https://doi.org/10.1007/s10817-011-9225-2
Chicli, L., Pottier, L., Simpson, C.: Mathematical quotients and quotient types in Coq. In: Geuvers, H., Wiedijk, F. (eds.) TYPES 2002. LNCS, vol. 2646, pp. 95–107. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39185-1_6
Cohen, C.: Types quotients en Coq. In: Hermann (ed.) Actes des 21éme journées francophones des langages applicatifs (JFLA 2010). INRIA, Vieux-Port La Ciotat, France (2010). http://jfla.inria.fr/2010/actes/PDF/cyrilcohen.pdf
Ferrer, W., Malherbe, O.: The category of implicative algebras and realizability. ArXiv e-prints, December 2017. https://arxiv.org/abs/1712.06043
Ferrer Santos, W., Guillermo, M., Malherbe, O.: Realizability in OCAs and AKSs. ArXiv e-prints (2015). https://arxiv.org/abs/1512.07879
Ferrer Santos, W., Frey, J., Guillermo, M., Malherbe, O., Miquel, A.: Ordered combinatory algebras and realizability. Math. Struct. Comput. Sci. 27(3), 428-458 (2017). https://doi.org/10.1017/S0960129515000432
Frey, J.: Realizability toposes from specifications. In: Altenkirch, T. (ed.) 13th International Conference on Typed Lambda Calculi and Applications (TLCA 2015). Leibniz International Proceedings in Informatics (LIPIcs), vol. 38, pp. 196–210. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, Dagstuhl, Germany (2015). https://doi.org/10.4230/LIPIcs.TLCA.2015.196
Frey, J.: Classical realizability in the CPS target language. Electron. Notes Theor. Comput. Sci. 325(Suppl. C), 111–126 (2016), The Thirty-second Conference on the Mathematical Foundations of Programming Semantics (MFPS XXXII). https://doi.org/10.1016/j.entcs.2016.09.034
Griffin, T.G.: A formulae-as-type notion of control. In: Proceedings of the 17th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 1990, pp. 47–58. ACM, New York (1990). https://doi.org/10.1145/96709.96714
Hofmann, M.: Extensional Concepts in Intensional Type Theory. Ph.D. thesis, University of Edinburgh (1995)
Hofstra, P., Van Oosten, J.: Ordered partial combinatory algebras. Math. Proc. Cambridge Philos. Soc. 134(3), 445-463 (2003). https://doi.org/10.1017/S0305004102006424
Krivine, J.L.: Realizability in classical logic. In: Interactive Models of Computation and Program Behaviour. Panoramas et synthèses 27 (2009)
Krivine, J.L.: Realizability algebras: a program to well order r. Log. Methods Comput. Sci. 7(3) (2011). https://doi.org/10.2168/LMCS-7(3:2)2011
Krivine, J.L.: Realizability algebras II : new models of ZF + DC. Log. Methods Comput. Sci. 8(1), 10, 28 p. (2012). https://doi.org/10.2168/LMCS-8(1:10)2012
Krivine, J.L.: Quelques propriétés des modèles de réalisabilité de ZF, February 2014. http://hal.archives-ouvertes.fr/hal-00940254
Miquel, A.: Existential witness extraction in classical realizability and via a negative translation. Log. Methods Comput. Sci. 7(2), 188–202 (2011). https://doi.org/10.2168/LMCS-7(2:2)2011
Miquel, A.: Implicative algebras: a new foundation for realizability and forcing. ArXiv e-prints (2018). https://arxiv.org/abs/1802.00528
Miquey, É.: Classical realizability and side-effects. Ph.D. thesis, Université Paris Diderot; Universidad de la República, Uruguay, November 2017. https://hal.inria.fr/tel-01653733
Munch-Maccagnoni, G.: Focalisation and classical realisability. In: Grädel, E., Kahle, R. (eds.) CSL 2009. LNCS, vol. 5771, pp. 409–423. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-04027-6_30
Pitts, A.M.: Tripos theory in retrospect. Math. Struct. Comput. Sci. 12(3), 265–279 (2002). https://doi.org/10.1017/S096012950200364X
Ruyer, F.: Proofs, Types and Subtypes. Ph.D. thesis, Université de Savoie, November 2006. https://tel.archives-ouvertes.fr/tel-00140046
Sozeau, M., Oury, N.: First-class type classes. In: Mohamed, O.A., Muñoz, C., Tahar, S. (eds.) TPHOLs 2008. LNCS, vol. 5170, pp. 278–293. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-71067-7_23
Streicher, T.: Krivine’s classical realisability from a categorical perspective. Math. Struct. Comput. Sci. 23(6), 1234–1256 (2013). https://doi.org/10.1017/S0960129512000989
Acknowledgments
The author wishes to thank Assia Mahboubi for pushing him to write the current paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
1 Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Miquey, É. (2018). Formalizing Implicative Algebras in Coq. In: Avigad, J., Mahboubi, A. (eds) Interactive Theorem Proving. ITP 2018. Lecture Notes in Computer Science(), vol 10895. Springer, Cham. https://doi.org/10.1007/978-3-319-94821-8_27
Download citation
DOI: https://doi.org/10.1007/978-3-319-94821-8_27
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-94820-1
Online ISBN: 978-3-319-94821-8
eBook Packages: Computer ScienceComputer Science (R0)


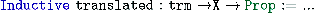 for which we proved the expected properties.
for which we proved the expected properties.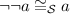 . Through the same quotient, this implies that
. Through the same quotient, this implies that