Abstract
In this work we consider (hierarchical, Lagrange) reduced basis approximation and a posteriori error estimation for elasticity problems in affinely parametrized geometries. The essential ingredients of the methodology are: a Galerkin projection onto a low-dimensional space associated with a smooth “parametric manifold”—dimension reduction; an efficient and effective greedy sampling methods for identification of optimal and numerically stable approximations—rapid convergence; an a posteriori error estimation procedures—rigorous and sharp bounds for the functional outputs related with the underlying solution or related quantities of interest, like stress intensity factor; and Offline-Online computational decomposition strategies—minimum marginal cost for high performance in the real-time and many-query (e.g., design and optimization) contexts. We present several illustrative results for linear elasticity problem in parametrized geometries representing 2D Cartesian or 3D axisymmetric configurations like an arc-cantilever beam, a center crack problem, a composite unit cell or a woven composite beam, a multi-material plate, and a closed vessel. We consider different parametrization for the systems: either physical quantities—to model the materials and loads—and geometrical parameters—to model different geometrical configurations—with isotropic and orthotropic materials working in plane stress and plane strain approximation. We would like to underline the versatility of the methodology in very different problems. As last example we provide a nonlinear setting with increased complexity.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
For the sake of simple illustration, we omit the “original” superscript o on (r, z, θ).
- 2.
- 3.
Here we note that, the Young’s modulus E in the isotropic and axisymmetric cases or E 1, E 2 and E 3 in the orthotropic case only.
- 4.
The average tangential displacement on \(\varGamma ^{\mathrm {o}}_N\) is not exactly s(μ) but rather \(s({\boldsymbol {\mu }})/l_{\varGamma ^{\mathrm {o}}_N}\), where \(l_{\varGamma ^{\mathrm {o}}_N}\) is the length of \({\varGamma ^{\mathrm {o}}_N}\). It is obviously that the two descriptions of the two outputs, “integral of” and “average of”, are pretty much equivalent to each other.
- 5.
Note that
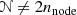 since Dirichlet boundary nodes are eliminated from the FE system.
since Dirichlet boundary nodes are eliminated from the FE system. - 6.
It is possible to show that the bifurcation point is related to the eigenvalue of the linearized model [5], so we are able to set in a proper way the range of the parameter domain.
References
Almroth, B.O., Stern, P., Brogan, F.A.: Automatic choice of global shape functions in structural analysis. AIAA J. 16, 525–528 (1978)
Benner, P., Gugercin, S., Willcox, K.: A survey of projection-based model reduction methods for parametric dynamical systems. SIAM Rev. 57(4), 483–531 (2015)
Benner, P., Cohen, A., Ohlberger, M., Willcox, K.: Model Reduction and Approximation: Theory and Algorithms. Computational Science and Engineering Series. Society for Industrial and Applied Mathematics, Philadelphia (2017)
Benner, P., Ohlberger, M., Patera, A., Rozza, G., Urban, K. (eds.): Model Reduction of Parametrized Systems. Springer, Berlin (2017)
Berger, M.: On Von Kármán equations and the buckling of a thin elastic plate, I the clamped plate. Commun. Pure Appl. Math. 20, 687–719 (1967)
Brezzi, F., Rappaz, J., Raviart, P.A.: Finite dimensional approximation of nonlinear problems. part I: branches of non singular solutions. Numer. Math. 36(1), 1–25 (1980)
Brezzi, F., Rappaz, J., Raviart, P.A.: Finite dimensional approximation of nonlinear problems. part II: limit points. Numer. Math. 37(1), 1–28 (1981)
Brezzi, F., Rappaz, J., Raviart, P.A.: Finite dimensional approximation of nonlinear problems. part III: simple bifurcation points. Numer. Math. 38(1), 1–30 (1982)
Canuto, C., Tonn, T., Urban, K.: A posteriori error analysis of the reduced basis method for nonaffine parametrized nonlinear PDEs. SIAM J. Numer. Anal. 47(3), 2001–2022 (2009)
Carroll, W.F.: A Primer for Finite Elements in Elastic Structures. Wiley, Hoboken (1998)
Chinesta, F., Ladevèze, P.: Separated Representations and PGD-Based Model Reduction: Fundamentals and Applications. CISM International Centre for Mechanical Sciences. Springer, Vienna (2014)
Chinesta, F., Huerta, A., Rozza, G., Willcox, K.: Model order reduction: a survey. In: Wiley Encyclopedia of Computational Mechanics. Wiley, Hoboken (2016)
Ciarlet, P.G.: Mathematical Elasticity, Volume I: Three-Dimensional Elasticity. Elsevier, Amsterdam (1988)
Ciarlet, P.G.: Mathematical Elasticity: Volume II: Theory of Plates. Studies in Mathematics and its Applications. Elsevier, Amsterdam (1997)
Grepl, M.A., Patera, A.T.: A posteriori error bounds for reduced-basis approximations of parametrized parabolic partial differential equations. Math. Model. Numer. Anal. 39(1), 157–181 (2005)
Grepl, M., Maday, Y., Nguyen, N., Patera, A.: Efficient reduced-basis treatment of nonaffine and nonlinear partial differential equations. Math. Model. Numer. Anal. 41(3), 575–605 (2007)
Hesthaven, J., Rozza, G., Stamm, B.: Certified Reduced Basis Methods for Parametrized Partial Differential Equations. Springer Briefs in Mathematics. Springer, Berlin (2015)
Hutchingson, J.: Nonlinear Fracture Mechanics. Monograph, Department of Solid Mechanics, Technical University, Lyngby (1979)
Huynh, D.B.P.: Reduced-basis approximation and applications in fracture mechanics. Ph.D. thesis, Singapore-MIT Alliance, National University of Singapore (2007)
Huynh, D.B.P., Patera, A.T.: Reduced basis approximation and a posteriori error estimation for stress intensity factors. Int. J. Numer. Methods Eng. 72(10), 1219–1259 (2007)
Huynh, D.B.P., Rozza, G., Sen, S., Patera, A.T.: A successive constraint linear optimization method for lower bounds of parametric coercivity and inf-sup stability constants. CR Acad. Sci. Paris Ser. I 345, 473–478 (2007)
Huynh, D.B.P., Nguyen, N.C., Rozza, G., Patera, A.T.: rbMIT software http://augustine.mit.edu/methodology/methodology_rbMIT_System.htm. Copyright MIT, Technology Licensing Office, case 12600, Cambridge, MA (2007–2009)
Huynh, D., Knezevic, D.J., Chen, Y., Hesthaven, J.S., Patera, A.T.: A natural-norm Successive Constraint Method for inf-sup lower bounds. Comput. Methods Appl. Mech. Eng. 199(29–32), 1963–1975 (2010)
Milani, R., Quarteroni, A., Rozza, G.: Reduced basis method for linear elasticity problems with many parameters. Comput. Methods Appl. Mech. Eng. 197, 4812–4829 (2008)
Murakami, Y.: Stress Intensity Factors Handbook. Elsevier, Amsterdam (2001)
Nguyen, N., Veroy, K., Patera, A.: Certified real-time solution of parametrized partial differential equations. In: Yip, S. (ed.) Handbook of Materials Modeling: Methods, pp. 1529–1564. Springer, Dordrecht (2005)
Noor, A.K.: Recent advances in reduction methods for nonlinear problems. Comput. Struct. 13, 31–44 (1981)
Noor, A.K.: On making large nonlinear problems small. Comput. Methods Appl. Mech. Eng. 34, 955–985 (1982)
Noor, A.K., Peters, J.M.: Reduced basis technique for nonlinear analysis of structures. AIAA J. 18(4), 455–462 (1980)
Parks, D.M.: A stiffness derivative finite element technique for determination of crack tip stress intensity factors. Int. J. Fract. 10(4), 487–502 (1974)
Patera, A., Rozza, G.: Reduced basis approximation and A posteriori error estimation for Parametrized Partial Differential Equation. MIT Pappalardo Monographs in Mechanical Engineering (Copyright MIT (2007–2010)). http://augustine.mit.edu
Pichi, F., Rozza, G.: Reduced basis approaches for parametrized bifurcation problems held by non-linear Von Kármán equations (2018). arXiv:1804.02014
Quateroni, A., Valli, A.: Numerical Approximation of Partial Differential Equations, 2nd edn. Springer, Berlin (1997)
Quarteroni, A., Rozza, G., Manzoni, A.: Certified reduced basis approximation for parametrized partial differential equations and applications. J. Math. Ind. 1(1), 3 (2011)
Quarteroni, A., Manzoni, A., Negri, F.: Reduced Basis Methods for Partial Differential Equations: An Introduction. UNITEXT. Springer, Berlin (2015)
Rozza, G., Huynh, D., Patera, A.: Reduced basis approximation and a posteriori error estimation for affinely parametrized elliptic coercive partial differential equations: application to transport and continuum mechanics. Arch. Comput. Meth. Eng. 15, 229–275 (2008)
Rozza, G., Nguyen, N.C., Patera, A., Deparis, S.: Reduced basis methods and a posteriori error estimators for heat transfer problems. In: Proceedings of the ASME HT 2009 Summer Conference, Heat Transfer Conference. ASME, New York (2009). Paper No. HT2009-88211, pp. 753–762
Sneddon, I., Dautray, R., Benilan, P., Lions, J., Cessenat, M., Gervat, A., Kavenoky, A., Lanchon, H.: Mathematical Analysis and Numerical Methods for Science and Technology. Volume 1: Physical Origins and Classical Methods. Mathematical Analysis and Numerical Methods for Science and Technology. Springer, Berlin (1999)
Sneddon, I., Dautray, R., Benilan, P., Lions, J., Cessenat, M., Gervat, A., Kavenoky, A., Lanchon, H.: Mathematical Analysis and Numerical Methods for Science and Technology. Volume 2: Functional and Variational Methods. Mathematical Analysis and Numerical Methods for Science and Technology. Springer, Berlin (2000)
Veroy, K.: Reduced-basis methods applied to problems in elasticity: analysis and applications. Ph.D. thesis, Massachusetts Institute of Technology (2003)
Young, W., Budynas, R.: Roark’s Formulas for Stress and Strain, 7th edn. McGraw, New York (2001)
Zanon, L.: Model order reduction for nonlinear elasticity: applications of the reduced basis method to geometrical nonlinearity and finite deformation. Ph.D. thesis, RWTH Aachen University (2017)
Zanon, L., Veroy-Grepl, K.: The reduced basis method for an elastic buckling problem. Proc. Appl. Math. Mech. 13(1), 439–440 (2013)
Zienkiewicz, O.C., Taylor, R.L., Zhu, J.Z.: The Finite Element Method: Its Basis and Fundamentals, 6th edn. Butterworth-Heinemann, Oxford (2005)
Acknowledgements
We are sincerely grateful to Prof. A.T. Patera (MIT) and Dr. C.N. Nguyen (MIT) for important suggestions, remarks, insights, and codevelopers of the rbMIT and RBniCS (http://mathlab.sissa.it/rbnics) software libraries used for the numerical tests. We acknowledge the European Research Council consolidator grant H2020 ERC CoG 2015 AROMA-CFD GA 681447 (PI Prof. G. Rozza).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
8.1.1 Stress-Strain Matrices
In this section, we denote E i, i = 1, 3 as the Young’s moduli, ν ij; i, j = 1, 2, 3 as the Poisson ratios; and G 12 as the shear modulus of the material.
8.1.1.1 Isotropic Cases
For both of the following cases, E = E 1 = E 2, and ν = ν 12 = ν 21.
Isotropic plane stress:
Isotropic plane strain:
8.1.1.2 Orthotropic Cases
Here we assume that the orthotropic material axes are aligned with the axes used for the analysis of the structure. If the structural axes are not aligned with the orthotropic material axes, orthotropic material rotation must be rotated by with respect to the structural axes. Assuming the angle between the orthogonal material axes and the structural axes is θ, the stress-strain matrix is given by \([{\mathbf {E}}] = [{{\boldsymbol {T}}}(\theta )][\hat {{\mathbf {E}}}][{{\boldsymbol {T}}}(\theta )]^T\), where
Orthotropic plane stress:
Note here that the condition
must be required in order to yield a symmetric [E].
Orthotropic plane strain:
Here Λ = (1 − ν 13 ν 31)(1 − ν 23 ν 32) − (ν 12 + ν 13 ν 32)(ν 21 + ν 23 ν 31). Furthermore, the following conditions,
must be satisfied, which leads to a symmetric [E].
An reasonable good approximation for the shear modulus G 12 in orthotropic case is given by [10] as
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Huynh, D.B.P., Pichi, F., Rozza, G. (2018). Reduced Basis Approximation and A Posteriori Error Estimation: Applications to Elasticity Problems in Several Parametric Settings. In: Di Pietro, D., Ern, A., Formaggia, L. (eds) Numerical Methods for PDEs. SEMA SIMAI Springer Series, vol 15. Springer, Cham. https://doi.org/10.1007/978-3-319-94676-4_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-94676-4_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-94675-7
Online ISBN: 978-3-319-94676-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


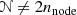 since Dirichlet boundary nodes are eliminated from the FE system.
since Dirichlet boundary nodes are eliminated from the FE system.