Ordinal Learning with Vector Space Based Binary Predicates and Its Application to Tahitian Pearls’ Luster Automatic Assessment

Abstract

Algorithms designed to solve instance ranking problems are often a trade-off between classification and regression. We propose to solve instance ranking problems where the classes have fixed boundaries by observing that such cases can be reduced to object ranking problems. Object ranking implies determining a total order, which should imply in turn a computational cost exponential with the number of items to order. However, solving this problem in the feature space allows taking advantage of linearity, so as to ensure total order properties at no particular computational cost, in particular, without having to explicitly check for acyclicity. The proposed method is tested for classifying Tahitian pearls against their luster using photographs of commercial culture pearls ranked by experts of the profession and compared with previous support vector machine (SVM) multiclass classification. While the SVM approach had more than $20\%$ of error (and more than $13\%$ after feature selection), our method allows predicting the class of a pearl with less than $10\%$ of error (and less than $8\%$ after feature selection). Ordinal learning makes better use of implicit rank information and significantly ($p < 10^{-4}$) reduces classification error.

1 Introduction

Ranking problems involve predictions of total orders out of sets of ordered pairs (i.e., out of a partial knowledge of binary relations). Fürnkranz and Hüllermeier [1] proposed a categorization of ranking problems into label ranking, instance ranking and object ranking. In a label ranking problem, we are given partial knowledge of several binary relations on a same set, each of them together with an item (typically represented as a feature vector), and solving the problem consists of finding a function that returns a total order for any given item (for an approach to label ranking, see [2, 3]). In an instance ranking problem, a set of items is given, each item together with the class of items it belongs to, the classes being ordered; solving the problem consists of finding a function which decides for any given item the class it belongs to (for an approach to instance ranking, see [3]). Object ranking consists of finding a single total order out of a partial knowledge of a single binary relation (for an approach to object ranking, see [4]). Predicting a total order out of a partial knowledge of a binary relation usually proceeds in two steps [4]: first, inferring a binary relation from the given ordered pairs; second, finding the total order which stands at the shortest distance from the inferred binary relation. The second step is nothing else than the resolution of the slater’s problem [5], which have been proved to be NP-equivalent [4, 6]; it then usually boils down to finding the best approximation of such a total order [4, 7].

1.1 Object Ranking vs. Instance Ranking

Practical Point of View. Although the operation of distributing items into ordered classes falls within the scope of the formal definition of instance ranking, it is in practice often just a compact way to describe a set of pairwise comparisons as an input of an object ranking problem. In this case, the instance ranking problem can be sought of as a hidden object ranking problem.

Tahitian black pearls quality assessment offers an excellent illustration to this. Tahitian black pearls are the second income of French Polynesia after tourism, and are the first and principal exportation of the country [8]. Pearls quality is traditionally assessed through various criteria such as size, shape, thickness of nacre, color, luster and state of the surface, and pearls are globally rated from A to D in decreasing order. Millions of Tahitian pearls are visually assessed each year by human experts, which is a difficult and weary task. The RAPA¹ project aims at bringing an automated assistance to pearls experts and at helping increase the recognition of the high quality of Tahitian black pearls. RAPA has first addressed problems such as semi-automating the measurement of the thickness of the nacre [10] and of the color of pearls [11, 12]. The present article focuses on luster, which appreciates the complex way a pearl reflects light and its surroundings.

In previous works, we reviewed the perceptual aspects of luster [13] and proposed a way to extract luster-specific features out of pictures of pearls [14]. Multiclass classification with a support vector machine (SVM) allowed predicting the class of a pearl with $77.7\%$ ($\pm 8.3$) success rate, reaching up to $87.3\%$ ($\pm 5.7$) of correct predictions by applying feature selection. However, rating quality of a pearl from A to D is not exactly a classification learning problem in the usual sense, since the classes are ordered. To be able to generalize to unseen examples, machine learning algorithms need to be biased, that is, to make (implicit or not) assumptions about the data (see [15] p. 42). The relevance of the bias of a learner with respect to the problem it has to solve determines its ability to generalize. In this respect, using a traditional classification algorithm to solve the problem of assessing Tahitian pearls’ luster represents a risk of arduous generalization.

Assessing pearls quality consists of distributing pearls into four classes, A, B, C and D ordered by decreasing quality and meets as such the definition of an instance ranking problem. However, all the consulted experts claimed they could order pearls in a finer grained fashion if needed, and even order them totally if there are not too many pearls: classes do not exist intrinsically but are set in order to alleviate the work of experts to the extent that they represent a sufficient degree of precision for pearl industry.

Theoretical Point of View. If hinges between classes are known, it implies the existence of a set H of feature vectors representing these hinges; without prejudice to the question of the relevance of additional information conveyed by classes in a ranking setting, solving the instance ranking problem on a set of feature vectors X can be done by solving the object ranking problem on $X \cup H$.

1.2 Guideline

Methods are presented in Sect. 2. An algorithm to solve such type of problem is described in Subsect. 2.1. In Subsect. 2.2 the proposed approach is tested on the problem of Tahitian pearls’ luster assessment. Section 3 presents the results, which are discussed in Sect. 4, before concluding.

2 Methods

2.1 Theory

Learning Phase. Rather than proceeding in two steps (first, finding the latent binary relation; second, finding the nearest total order) for ranking learning, we propose below to do it all at once by redefining the target function in such a way that the knowledge we want to learn consists directly of a total order.

Following the distinction between search space and search strategy in a learning process [15], there are two main methods for redefining the target function. Either the search space can be restricted such that any binary relation found in this space be a total order, or total-order related constraints can be added to the loss function such that the search strategy leads to the selection of a total order among binary relations that are not necessarily total orders. A mix of both could as well be applied, for example by choosing a search space taking care of totality and antisymmetry (or asymmetry, depending on whether a non-strict or a strict order is sought, respectively) and letting transitivity under the responsibility of the loss function.

In the present study, only the former method is explored; we propose in first approach to use vector space based binary predicates as a straightforward way to ensure total order properties. The principle is as follows:

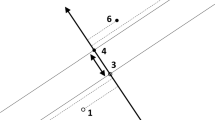
• Let an item i be represented by a point $x_i$ in the n-dimensional feature space. Let represent an ordered pair (i, j) of items by a vector $x_{i,j}=x_j-x_i$ connecting the item i to the item j. We can then draw a directed graph in the feature space out of the set of ordered pairs (i, j) given as an input.

• We learn a weight vector w minimizing the variation of the sign of $x_{i,j} \cdot w$ over the set of vectors $x_{i,j}$ derived from the input set of ordered pairs (i, j) . Let $p^+$ be the number of input ordered pairs (i, j) for which $x_{i,j} \cdot w$ is positive and $p^-$ be the number of input ordered pairs (i, j) for which $x_{i,j} \cdot w$ is negative: minimizing the variation of the sign of $x_{i,j} \cdot w$ over the set of $x_{i,j}$ is equivalent to maximizing $|p^+-p^- |$.

• Let keep track of the sign that occurs the most over all the $x_{i,j} \cdot w$ (or, in case the learner perfectly fits the training data, the only sign that occurs) by setting a value $s = {\left\{ \begin{array}{ll} \text {1 if} p^+ \ge p^-\\ \text {--1 if} p^+<p^-\\ \end{array}\right. }$.

• We can now define a binary predicate P that decides whether a given ordered pair of items belongs to the binary relation we have learned: $(i,j) \Leftrightarrow (x_{i,j} \cdot w.s>0)$.

Since the predicate is based on a strict relation, it can be shown that any binary relation belonging to this space is irreflexive, transitive and total (the property of asymmetry is implied by transitivity together with irreflexivity and need not be checked):

Irreflexivity. $P(i,i) \Leftrightarrow (x_i-x_i) \cdot w.s>0 \Rightarrow 0>0$, which is false, so $\lnot P(i,i)$.

Transitivity. P(i, j) & $P(j,k) \Leftrightarrow (x_j-x_i) \cdot w.s>0$ & $(x_k-x_j) \cdot w.s>0 \Rightarrow (x_j-x_i) \cdot w.s+(x_k-x_j) \cdot w.s>0 \Leftrightarrow (x_j-x_i+x_k-x_j) \cdot w.s>0 \Leftrightarrow (x_k-x_i) \cdot w.s>0 \Leftrightarrow P(i,k)$.

Totality. ${\left\{ \begin{array}{ll} x_{i,j} \cdot w> 0 \Leftrightarrow P(i,j).\\ x_{i,j} \cdot w < 0 \Leftrightarrow x_{j,i} \cdot w > 0 \Leftrightarrow P(j,i).\\ x_{i,j} \cdot w = 0 \Leftrightarrow i=j).\\ \end{array}\right. }$

Under the reasonable assumption of independence of the features, P allows predicting, for any given items i and j represented by feature vectors $x_i$ and $x_j$, which of the ordered pair (i, j) or (j, i) belongs to the total order that best fits the input constraints.

Pre- and Post-Learning. The problem to solve is originally in its instance ranking form and has to be translated into its object ranking form by extracting the ordinal partial knowledge about the predicate to learn. This knowledge lies in the inter-class relations of the training examples: a training set with m items equally distributed into c classes contains $\frac{(c - 1) m^2}{2c}$ ordered pairs.

Once the binary predicate has been learned, the predictions on unseen items have to be returned in their instance ranking form. Since the order is total, we do not need to compare a new element to all the elements of the training set: only the boundaries of the classes are necessary. The lower bound of the lowest class and the upper bound of the uppermost class are not needed. Among the other bounds, a dichotomous search can yield the right class (or inter-class if we allow it): for expressing an object ranking prediction in c-classes instance ranking terms, only $\lceil log_2 (c-1) \rceil$ tests are needed ($\lceil log_2 (2c-2) \rceil$ tests in case it is allowed to rank items between two adjacent classes).

Expressivity of the Search Space. Linear relations are likely to be not expressive enough to fit most of the input sets, so the original feature vectors can be extended by adding to them polynomial values. This way, higher expressivity is allowed while staying in the feature space.

Constraints on the Input Data. Depending on the situations the problem models, constraints can be added to the input set of ordered pairs [2]. For example, if the input is provided by a single expert assumed to be consistent in judgment, we can impose reflexivity, antisymmetry and transitivity to the latent binary relation, such that the set of ordered pairs can be considered as partially ordered. These constraints are nevertheless not compulsory and have to be relaxed in the case the input is provided by different experts [16].

2.2 Experiments

Data Collection. The method is tested on the same dataset as in [5]. A human expert selected 54 pearls from 3 classes of luster corresponding to the classes B, C and D of the standard 4 classes used by practitioners. Eighteen pearls have good luster (class B), 18 have medium luster (class C) and 18 have bad luster (class C). There was no pearl with very good luster (class A) available.

Feature Vectors. Feature vectors have been extracted automatically from photographs of these pearls (16 pictures per pearl) such that the 54 pearls can be represented by 54 points in the feature space (for luster features extraction, see [5]). Each feature vector is associated with the class the expert set it to.

Feature Selection. The proposed method is tested both without and with feature selection. The same feature selection as in [5] is used, as it has experimentally proved to be optimal regardless of the type of relation (linear, quadratic or Gaussian) to capture.

Feature Enrichment. In order to confer some nonlinear expressivity to the search space, we append to each vector the vector of its squared values. This way, the learner is able to capture quadratic regularities, which is enough for the problem of Tahitian pearls’ luster assessment [5].

2.3 Learner

We explore the search space with a genetic algorithm. The settings are the following: population of 100; mutation rate of 0.2.

2.4 Validation Method

The k-fold cross-validation method is employed to estimate the ability of the binary predicate to generalize. Since the dataset consists of 3 classes of 18 items, we choose $k = 9$.

The dataset is small (only 54 pearls), therefore, the p-value of the result is computed in order to test its statistical significance. Since the validation method implies 54 predictions relative to 3 balanced classes, this value follows a binomial distribution of parameters $n = 54$ and $p = 1/3$ under the null hypothesis.

Eventually, the results are compared with the results previously obtained [5] on the same dataset with an SVM and the p-value of the difference is computed.

3 Results

Table 1 summarizes the ranking results obtained both for the raw (“Linear”) and the quadratically extended (“Quadratic”) feature vectors for all features as well as for the selected features only. For each case, the ability of the predicate to fit the training data and to generalize to unseen data is mentioned. Classification results obtained in our previous work [5] with a support vector machine are reported in order to ease comparing. Table 1 reports that while the SVM classification has an accuracy of $77.7\% \pm 8.3$ ($87.3\% \pm 5.7$ with feature selection) with a linear kernel and $77.3\% \pm 8.1$ ($86.3\% \pm 6.2$ with feature selection) with a quadratic kernel, ordinal learning (OL) ranking has an accuracy of $83.3\% \pm 5.5$ ($88.9\% \pm 7.4$ with feature selection) in the linear setting and $90.7\% \pm 5.1$ ($92.6\% \pm 4.1$ with feature selection) in the quadratic setting.

Table 1. Percentage of ordinal learning (OL) ranking success estimated using 9-fold cross-validation with respect to the type of relation the predicate is capturing and the set of features. We report the corresponding previous results obtained by multiclass classification with a support vector machine (SVM). OL ranking performs better than SVM classification in both settings and both with and without feature selection. While SVM classification performs better in a linear setting than in a quadratic setting, OL ranking yields better results in a quadratic setting than in a linear setting.

The best performance of the predicate is obtained with feature selection and quadratic extension: $92.6\% \pm 4.1$ of correct prediction on unseen examples. The difference with the best result obtained from SVM classification ($87.3\% \pm 5.7$) has a p-value lower than $10^{-4}$. The confusion matrix (Table 2) is symmetric, and then the F-score of a class has the same value as its corresponding precision and recall. Classes 1 and 3 have the same precision and recall while the intermediate class has lower precision and recall. Over 54 trials, 50 have been successful; since the p-value follows the binomial distribution B(54, 1 / 3) under the null hypothesis, the probability that such a result be yielded by random is less than $10^{-19}$.

Table 2. Confusion matrix of the binary predicate with feature selection and quadratic extension of the features. The matrix is symmetric, making for each class the precision equal the recall, hence the F-score.

4 Discussion

The predicate performs better with quadratic extension of the feature vectors, no matter the set of features. It fits better with all features but generalizes better with only selected features both for linear and quadratic feature vectors.

Even though the dataset be small and thus its representativity of Tahitian pearls be questionable, the p-value indicates that OL ranking performances are statistically significant.

In both settings (linear or quadratic) and on both sets of features (with or without selection), the proposed ranking algorithm performs better than multiclass classification with an SVM on this dataset. This suggests that multiclass classification does not exploit all the available information, namely the order-related information. In this sense, OL ranking bases its predictions on a more relevant bias than that of SVM classification. The difference between the best result obtained by the SVM classification ($87.3\% \pm 5.7$) and the one obtained by the OL ranking ($92.6\% \pm 4.1$) has a p-value lower than $10^{-4}$, indicating that the improvement is statistically significant.

Regarding the nature of the underlying structure of the data, the SVM yields the best results with a linear kernel, yet it turns out that the proposed method leads to the best results with a quadratic setting. This seems contradictory since the underlying regularities lie in the data and as such, do not depend on the learner. It might be that the additional information captured by our learner has a quadratic nature. This will be studied in future research, as it seems too early to conclude at this stage.

Our learned predicate shows a weakness on class 2 (see the confusion matrix, Table 2). Indeed, the theoretical hypothesis on the knowledge about hinges between two adjacent classes does not hold in most practical cases, as there is a gap between the upper boundary of a class and the lower boundary of the subsequent class. If the predicate ranks a pearl in this gap, the way to decide to which of the two classes this pearl belongs to is at best random. Because class 1 and class 3 have only one boundary each, the probability to suffer from this boundary related issue is twice lower and could explain the slightly better performance of the predicate on these classes.

In practice, this issue could be solved easily: whenever a pearl is ranked between two classes, it is submitted to a human expert, who decides which class it belongs to, until the boundaries of two adjacent classes be so closed that one of them could indifferently be taken as hinge.

Another way to get around the search of the nearest total order could be to embed total-order related constraints in the search strategy rather than in the search space. This option would have the disadvantage to be computationally heavier but should allow in return a much more expressive search space and thus capturing more complex patterns in the data. On one hand, adding total order related constraints to the search space alleviates the computational cost of the learning phase but limits the fitting power of the learner; on the other hand, adding these constraints to the search strategy allows the learner keeping a high fitting power but is computationally more expensive. Now, total order related constraints are not monolithic and could be distributed among these two axes. It could be of great interest to investigate how to best distribute constraints among these two axes depending on the problem to solve.

5 Conclusion

We observed that under the assumption of known boundaries, we could solve an instance ranking problem by solving the corresponding object ranking problem. Solving an object ranking problem is traditionally done by, first, learning a relation that minimizes the distance to the ordered pairs given as an input and, second, removing every cycle from this relation, this latter step being NP-equivalent. Instead of ensuring a cycle-free relation a posteriori by finding the nearest total order from a learned binary relation, we proposed to ensure it a priori by restricting the search space so that only total orders can be learned. The counterpart, though, is a limited expressivity of the learner: only polynomial regularities can be captured.

Such approach has been applied to the task of classifying Tahitian black pearls against their luster. Doing so, correct predictions increased from $87.3\% \pm 5.7$ for multiclass classification by an SVM with linear kernel to $92.6\% \pm 4.1$ using the proposed quadratic setting, representing an improvement of $5.3\%$ ($p < 10^{-4}$). Incidentally, this improvement demonstrates that a total-ordering bias suits well the problem of assessing Tahitian pearls’ luster.