Abstract
Since the application of Postulate I.2 in Euclid’s Elements is not uniform, one could wonder in what way should it be applied in Euclid’s plane geometry. Besides legitimizing questions like this from the perspective of a philosophy of mathematical practice, we sketch a general perspective of conceptual analysis of mathematical texts, which involves an extended notion of mathematical theory as system of authorizations, and an audience-dependent notion of proof.
A slightly modified version of this paper, written in Spanish was published in Revista Latinoamericana de Filosofía, XLI (2), 2015. We are grateful to Oscar Esquisabel for his remarks on a preliminary version, and to Alicia Di Paolo for her valuable and indispensable linguistic help. This joint work was supported by two subsidies: CAPES/COFECUB (Number 813-14) and PDE/CNPq (Number 2200980/2015-7). The second author dedicates this paper to Roshdi, his master and friend.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
As usual, we quote definitions, postulates, common notions and propositions of the Elements in Arabic characters, preceded by the book number in Roman characters, according to Heiberg’s edition (Euclid , Elementa). We have taken into account the translation by Thomas L. Heath (Euclides EEH), but, we have also granted ourselves the freedom to make some changes in order to use, from our point of view, a more appropriate terminology. The most relevant cases of these changes are related to the adjective ‘εὺθεῖα’. After using it as a genuine adjective in Definition 1.4 and in Postulate I.1 to coin the expression ‘εὺθεῖα γραμμή’, Euclid starts using it as a nominalised adjective as well. In particular, in Postulate I.2, he uses the adjective ‘πεπερασμένη’ to coin the expression ‘πεπερασμένη εὺθεῖα’. Literally, ‘εὺθεῖα γραμμή’, as well as ‘εὺθεῖα’, when used as a nominalised adjective, should undoubtedly be translated as ‘straight line’, and ‘πεπερασμένη εὺθεῖα’ as ‘finite straight line’. Still, it seems clear that in the three cases Euclid ’s intended reference is to straight-line segments. As this is crucial, to avoid any misunderstanding, we shall directly translate the three terms as ‘straight-line segment’, or only ‘segment’ when no confusion is possible.
- 2.
As usual, we distinguish the propositions in the Elements in problems and theorems. A problem demands the construction of a geometrical object (a point, a straight, an angle, a figure, etc.) under certain conditions, and requires a solution. A theorem states that geometrical objects of a given kind have certain properties, or that they are in a certain relation, and requires a proof. However, it is important to point out that the solution of a problem always includes, at its final stage, a proof that the object constructed in the established way satisfies the conditions of the problem. This suggests understanding the solution of a problem as the proof of a (meta-)theorem which states that the problem has a solution (which can be obtained as the solution shows). In spite of the fact that, in the versions of the Elements that we have received, these two kinds of propositions are not explicitly distinguished, the distinction is made perfectly clear by the fact that Euclid adopts two different canonical forms in the two cases, both for the formulation of the proposition itself and for the subsequent arguments (solutions and proofs). The classic locus in which the distinction between problems and theorems is explicitly drawn and widely discussed is Proclus’ commentary on the first book of the Elements (Proclus CEELF, esp. pp. 77–78).
- 3.
Our exposition of Euclid ’s construction with the corresponding figure is based on Heiberg’s edition (Euclid , Elementa). The topological configuration of the diagram would be modified if the position of point A, in relation to segment BC, were different from the one that is presented here. As Proclus also observed in his commentary (Proclus CEELF, pp. 225–228), there would have to distinguish different cases (as it also happens with many other solutions or proofs of Euclid ’s propositions). In spite of the fact that the difficulty presented here would not appear in all the cases, it is not necessary to consider them (for that purpose, see Euclid EEH, pp. 245–246).
- 4.
Lassalle Casanave and Panza (2012).
- 5.
Ibid., p. 113.
- 6.
If the magnitudes which Book V are about are simply the same as the ones which Books I–IV deal with, that is to say, straight-line segments, polygons and rectilinear angles, Book V would be part of the exposition of plane geometry. It is, however, a quite complex question whether this is so, or Book V is rather intended to deal with whatever possible magnitudes (also if no mention of them is made in the foregoing Books), or, even, whether it is intended to deal with magnitudes in general, implicitly defined within the theory of proportions itself. We cannot consider this issue here.
- 7.
For a brief presentation of this idea, see Lassalle Casanave (2006).
- 8.
This does not mean denying that a formal proof is a sequence of formulae, but conceiving that sequence as the actualization of those possibilities. From this point of view, it is the coding of the space of possibilities which a mathematical theory consists of what determines what an acceptable argument in this theory is (or establishes, at least, the conditions that it has to comply with or the criteria under which it can be recognized as such). And it is also this coding which determines which of these acceptable arguments can be considered as proofs in the theory (or establishes, at least, the relevant conditions or criteria).
- 9.
The specification ‘in principle’ is used to set aside the cases in which such possibility is excluded for physical reasons, for example, if the formula is too long and complex for its structure to be identified by a subject with human cognitive limits or if it is written with ink which is too pale, etc.
- 10.
Evidently, there are also other important differences between the two cases. A very important one is related to the way in which the actualization of a possibility is associated to obtaining a piece of information by an epistemic subject who is operating within a theory.
- 11.
The notion of enthymeme is a crucial notion in Aristotle ’s rhetoric (Reth 1356b). According to Rapp (2010), for Aristotle an enthymeme is “what has the function of a proof or demonstration in the domain of public speech”. If we agree with this, our use of this notion to refer to a type of mathematical argument conveys the idea that such an argument, for example a mathematical proof, is a kind of public speech, which adapts perfectly well to what we will hold further on in section IV. However, the idea of being able to speak of enthymeme in mathematics, or, in general, of enthymemathical proofs or any other sort of conclusive arguments (as Euclid ’s solutions of problems should be taken to be), could disconcert those who see an enthymeme as a fallacy, and a proof or conclusive argument, in particular a mathematical one, as a valid argument. According to the perspective on mathematical theories developed here and the corresponding conception of arguments and proofs within such theories, both assumptions are questionable, or, at least, need qualifications. We would not like to take time and space here to argue that an enthymemathical proof or conclusive argument have to be thought of as a proof or a conclusive argument in a genuine sense, rather than as an argument which, despite being acceptable, has not succeeded in becoming valid. For a schematic presentation of the notion of enthymematical proof, see Lassalle Casanave (2008).
- 12.
This means that in order to code a theory, in the proposed sense of system of authorizations, certain conditions that a canonical proof within this theory has to respect have to be coded.
- 13.
Although the idea of viewing a mathematical proof as an enthymemathical one, at least prima facie, is not common, it is far from being totally new. An example that proves so—also in relation to the proofs in the Elements—is a quote we thank Paolo Mancosu for having pointed it out to us, taken from a lecture of John Barrow (Lesson VI, given in 1664). There, Barrow arguments in favour of the thesis that mathematical proofs are causal, thesis against which it was alleged to as counter-example the solution of I.1 of the Elements. After his argument, in which we are not interested here, Barrow asserts (Barrow 1683, p. 105; Barrow 1734, p. 95; the first reference belongs to the first edition of the original text in Latin, the second one belongs to its first translation into English, which is quoted here):
From which Observations most or all the Instances brought against Mathematical Demonstrations may be overthrown. And consequently, if the particular Syllogisms (brought either for the Construction, or Demonstration of the above said first Proposition of the Elements) be Demonstrations simply scientific, the Proposition ought to be reckoned as scientifically demonstrated. We will therefore examine them; but for brevity’s sake, we will substitute Enthymems for Syllogisms, and insinuate the Necessity of the Consequence.
- 14.
The straight line L is not represented in the diagram which Avigad, Dean and Mumma add to their reconstruction (Fig. 7.5). That depends on the fact that the only thing that matters about this line is that two different points b and c are taken on it. It is not essential either that point a is or not on L, and actually, this is not specified. As a matter of fact, this would correspond to the distinction between cases: see n.4. The diagram reproduced in Fig. 7.5 represents a configuration in which point a is not on L. A configuration in which a is on L is represented by the diagram that follows, which shows that the construction of the segment af is perfectly feasible under this configuration.
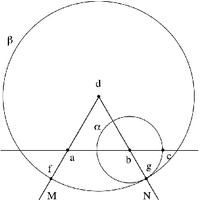
It is natural to ask oneself why Avigad, Dean and Mumma mention the straight line L in their reconstruction. The answer can be found in the following quote, which well shows the role that they assign to the straight lines in their reconstruction of Euclid ’s theory, together with their interpretation of Postulate I.2 within this reconstruction (Avigad et al. 2009, pp. 731–732; evidently, we must read “straight line” where Avigad, Dean, and Mumma write “line”):
[…] in the Elements, Euclid takes lines to be line segments, although Postulate 2 (‘to produce a finite straight line continuously in a straight line’) allows any segment to be extended indefinitely. Distinguishing between finite segments and their extensions to lines makes it clear that at any given point in a proof, the diagrammatic information is limited to a bounded portion of the plane. But, otherwise, little is lost by taking entire lines to be basic objects of the formal system. So where Euclid writes, for example, ‘let a and b be points, and extend segment ab to c,’ we would write ‘let a and b be distinct points, let L be the line through a and b, and let c be a point on L extending the segment from a to b.’ Insofar as there is a fairly straightforward translation between Euclid ’s terminology and ours, we take such differences to be relatively minor.
- 15.
When presenting their examples of proofs within the formal system E which, according to what they explain in the summary of their article (ibid., p. 700), provides “a faithful model of the proofs in Euclid ’s Elements”, Avigad, Dean and Mumma write: “We include diagrams to render the proofs intelligible, but we emphasize that they play no role in the formal system” (ibid., p. 734).
- 16.
To respect that structure, still not its heterogeneous character, is, on the contrary, Avigad, Dean, and Mumma’s aim. About the heterogeneous character (due to the joint utilization of language and diagrams) of Euclid ’s proofs, it must be mentioned here the influential “Euclid ’s Diagram (1995)” by K. Manders (published only thirteen years later: Manders 2008), of which Avigad, Dean and Mumma’s reconstruction is in debt to, although (as already observed) the authors set as a goal the logical analysis of those proofs, showing in this way the dispensability of the diagrammatic resources. Although we will not discuss it here, the reconstructions of Euclid ’s plane geometry in Mumma (2006) and Miller (2007) try to justify the use of diagrams in Euclid ’s proofs, not to dispense them. For diagrams and geometrical proofs, see also Norman (2006).
- 17.
Panza (2012), p. 89.
- 18.
But there is at least a precedent of this interpretation of Postulate I.2. In Alberto Magno’s commentary on the first book of the Elements (Lo Bello 2003, pp. 39–42) the proof of Proposition I.2 proceeds explicitly according to the mentioned rule.
- 19.
For the notion of style in mathematics, see Mancosu (2009).
- 20.
Rhetoric 1357a (translation by J. H. Freese: Aristotle Rhet).
References
Aristóteles [Rhet]. (1926). Art of Rethoric (J. H. Freese, Trans.). Cambridge, MA: Loeb Classical Library 193, Harvard Univ. Press.
Avigad, J., Dean, E., & Mumma, J. (2009). A formal system for Euclid’s elements. Review of Symbolic Logic, 2(4), 700–768.
Barrow, I. (1683). Lectiones Habita in Scholis Publicis Academiæ Cantabrigiensis An. Dom, M.DC.LXIV, Typis J. Playford, pro G. Wells in Cœmenterio D. Pauli, Londini.
Barrow, I. (1734). The usefulness of Mathematical Learning […]. Printed for S. Austin at the Angel and Bible in St. Paul’s Church-yard, London.
Euclid. (1883–1888). Elementa, vols. I–IV de Euclidi Opera Omnia. B. G. Teubneri, Lipsiæ, Edited by I. L. Heiberg and H. Menge. vols. 8 + suppl. 1. New edition by E. Stamatis.
Euclid [EEH]. (1926). The thirteen books of the elements (Translated with introduction and commentary by Sir Thomas L. Heath) (2nd ed., Vol. 3). Cambridge: Cambridge University Press.
Hilbert, D. (1899). Grundlagen der Geometrie. Leipzig: Teubner.
Lassalle Casanave, A. (2008). Entre la retórica y la dialéctica. Manuscrito, 31(1), 11–18.
Lasalle Casanave, A. (2006). Matemática elemental, cálculo y normatividad. O que nos faz pensar, 20, 67–72.
Lassalle Casanave, A., & Panza, M. (2012). Sobre el significado del Postulado 2 de los Elementos. Notae Philosophicae Scientiae Formalis, 1(2) http://gcfcf.com.br/pt/revistas/filosofia-da-pratica-matematica/.
Lo Bello, A. (2003). The commentary of Albertius Magnus on Book I of Euclid’s elements of geometry. Boston-Leyden: Brill Academic Publishers.
Mancosu, P. (Ed.). (2008). The philosophy of mathematical practice. Oxford: Oxford University Press.
Mancosu, P. (2009). ‘Style’ in mathematics. In E. N. Zalta (Ed.), The stanford encyclopedia of philosophy (First published Jul 2, 2009) http://plato.stanford.edu/entries/mathematical-style/.
Manders, K. (2008). The Euclidean diagram. In: P. Mancosu (Ed.), The philosophy of mathematical practice (pp. 80–133). Oxford: Oxford University Press.
Mumma, J. (2006). Intuition formalized: Ancient and modern methods of proof in elementary geometry. Ph.D. thesis, Carnegie Mellon University.
Miller, N. (2007). Euclid and his twentieth century rivals: Diagrams in the logic of Euclidean geometry. Stanford CSLI Publications.
Norman, J. (2006). After Euclid. Visual reasoning and the epistemology of diagrams. Stanford CSLI Publications.
Panza, M. (2012). The twofold role of diagrams in Euclid’s plane geometry. Synthese, 186(2012), 55–102.
Proclus [CEELF]. (1873). In primum Euclidis Elementorum librum commentarii. Teubner, Lipsi. Ex recognitione G. Friedlein.
Rapp, C. (2010). Aristotle’s Rhetoric. In E. N. Zalta (Ed.), The stanford encyclopedia of philosophy (First published May 2, 2002; substantive revision Feb 1, 2010).
http://plato.stanford.edu/archives/spr2010/entries/aristotle-rhetoric/.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Lassalle-Casanave, A., Panza, M. (2018). Enthymemathical Proofs and Canonical Proofs in Euclid’s Plane Geometry. In: Tahiri, H. (eds) The Philosophers and Mathematics. Logic, Epistemology, and the Unity of Science, vol 43. Springer, Cham. https://doi.org/10.1007/978-3-319-93733-5_7
Download citation
DOI: https://doi.org/10.1007/978-3-319-93733-5_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-93732-8
Online ISBN: 978-3-319-93733-5
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)


