Abstract
Dans ce chapitre, comme à la section 2.1.3, un arbre pousse de manière aléatoire, parce que chaque nœud a un nombre aléatoire de descendants, de moyenne m. Pour un arbre de Galton-Watson, à la section 5.1, nous nous demandons d’abord (section 5.1.1) si un tel arbre s’éteint ou bien grossit indéfiniment. Cela dépend de m. Puis, lorsqu’il ne s’éteint pas toujours, c’est-à-dire lorsque m > 1, nous cherchons à connaître le nombre de nœuds au niveau n. Quel est son ordre de grandeur asymptotiquement en n ? Intuitivement c’est m n et nous verrons que sous certaines hypothèses sur la loi de reproduction, c’est effectivement le cas, c’est le théorème de Kesten-Stigum de la section 5.1.3.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Cette fonction génératrice peut sans encombre être définie sur le disque de convergence de la série entière, dans le plan complexe, néanmoins c’est sur l’intervalle [0, 1] que nous allons l’étudier et utiliser ses propriétés de convexité.
- 2.
Les notions de tribu, filtration, martingale sont résumées dans la section C.8.
- 3.
ce qui signifie que pour tout n, la probabilité \(\widehat {\mathbb {P}}_{n+1}\) restreinte aux arbres de taille n est égale à \(\widehat {\mathbb {P}}_n\).
- 4.
ce qui signifie que pour tout n, la probabilité \(\widehat {\mathbb {P}}\) restreinte aux arbres de taille n est égale à \(\widehat {\mathbb {P}}_n\).
- 5.
ce qui signifie qu’il existe un événement, ici {T < ∞}, qui est de probabilité 1 pour \(\mathbb {P}\) et de probabilité 0 pour \(\widehat {\mathbb {P}}\). La notation est \(\mathbb {P}\ \bot \ \widehat {\mathbb {P}}\).
- 6.
Une mesure μ est dite absolument continue par rapport à une mesure ν lorsque pour tout événement A, μ(A) = 0⇒ν(A) = 0. La notation est μ ≪ ν.
- 7.
\(\log ^+ x\) est la partie positive du \(\log \), autrement dit : \(\log ^+ x = \max (0, \log x)\).
- 8.
Une suite (X n) de variables aléatoires est uniformément intégrable lorsque
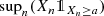 tend vers 0 quand a tend vers l’infini. Cette notion est équivalente à la convergence de la suite dans L
1.
tend vers 0 quand a tend vers l’infini. Cette notion est équivalente à la convergence de la suite dans L
1. - 9.
Le cardinal de l’ensemble \( \mathop {\mathrm {Cay}} \nolimits _n\) est n n−1, voir en section 4.5.1, mais cela n’intervient pas dans la preuve.
- 10.
Un mouvement brownien (B t)t≥0 est un processus aléatoire à temps continu, qui peut être défini comme la limite d’une marche aléatoire renormalisée (!) ou bien plus classiquement comme un processus à accroissements indépendants, de lois gaussiennes, tel que pour tous instants 0 ≤ s < t, B t − B s est de loi gaussienne centrée de variance t − s. Voir par exemple le livre de Revuz et Yor [221].
- 11.
Nous supposons ici que les déplacements sont à valeurs dans \(\mathbb {R}\), mais le modèle avec déplacements dans \(\mathbb {R}^d, d\geq 2\) est une généralisation naturelle.
References
D. Aldous, The continuum random tree. i. Ann. Probab. 19(1), 1–28 (1991)
D. Aldous, The continuum random tree. ii: an overview, in Stochastic Analysis, ed. by M. Barlow, N.H. Bingham (Cambridge University Press, Cambridge, 1991), pp. 23–70
D. Aldous, The continuum random tree. iii. Ann. Probab. 21(1), 248–289 (1993)
S. Asmussen, H. Hering, Branching Processes (Birkhäuser, Basel, 1983)
K. Athreya, P. Ney, Branching Processes (Springer, Berlin, 1972)
P. Biane, J. Pitman, M. Yor, Probability laws related to the Jacobi theta and Riemann zeta functions, and Brownian excursions. Bull. Am. Math. Soc. 38, 435–465 (2001)
J.D. Biggins, Martingale convergence in the branching random walk. Adv. Appl. Probab. 10, 62–84 (1978)
J.D. Biggins, Uniform convergence of martingales in the branching random walk. Ann. Probab. 20(1), 137–151 (1992)
P. Billingsley, Probability and Measure, 3rd edn. Wiley Series in Probability and Mathematical Statistics (Wiley, New York, 1995). A Wiley-Interscience Publication.
P. Chassaing, J.-F. Marckert, Parking functions, empirical processes and the width of rooted labeled trees. Electron. J. Comb. 8, R14 (2001)
M. Drmota, Random Trees. An Interplay between Combinatorics and Probabilities (Springer, Berlin, 2008)
M. Drmota, B. Gittenberger, On the profile of random trees. Random Struct. Algoritm. 10:4, 421–451 (1997)
M. Drmota, B. Gittenberger, The width of Galton-Watson trees conditioned by the size. Discret. Math. Theor. Comput. Sci. 6:2, 387–400 (2004)
T. Duquesne, J.-F. Le Gall, Random trees, Levy processes and spatial branching processes. Asterisque, 281 (2002). https://www.math.u-psud.fr/~jflegall/Mono-revised.pdf
P. Flajolet, A. Odlyzko, The average height of binary trees and other simple trees. J. Comput. Syst. Sci. 25, 171–213 (1982)
P. Flajolet, A. Odlyzko, Limit distributions for coefficients of iterates of polynomials with applications to combinatorial enumerations. Math. Proc. Camb. Philos. Soc. 96(2), 237–253 (1984)
P. Flajolet, R. Sedgewick, Analytic Combinatorics (Cambridge University Press, Cambridge, 2009)
P. Flajolet, Z. Gao, A. Odlyzko, B. Richmond, The distribution of heights of binary trees and other simple trees. Comb. Probab. Comput. 2, 145–156 (1993)
G. Grimmett, Random labelled trees and their branching networks. J. Aust. Math. Soc. (Ser. A) 30, 229–237 (1980)
S. Janson, Conditioned Galton–Watson trees do not grow, in Fourth Colloquium on Mathematics and Computer Science Algorithms, Trees, Combinatorics and Probabilities (2006), pp. 331–334
S. Janson, Simply generated trees, conditioned Galton-Watson trees, random allocations and condensation. Probab. Surv. 9, 103–252 (2012)
D. Kennedy, The distribution of the maximum Brownian excursion. J. Appl. Probab. 13, 371–376 (1976)
H. Kesten, Subdiffusive behavior of random walk on a random cluster. Ann. Inst. Henri Poincaré 22(4), 425–487 (1986)
V. Kolchin, Branching processes, random trees, and a generalized scheme of arrangements of particles. Math. Notes 21, 386–394 (1977)
V. Kolchin, Random Mappings (Optimization Software Inc. Publications Division, New York, 1986)
R. Lyons, A simple path to Biggins’ martingale convergence for branching random walk, in Classical and Modern Branching Processes, ed. by K.B. Athreya, P. Jagers. IMA Volumes in Mathematics and Its Applications, vol. 84 (Springer, New York, 1997)
R. Lyons, R. Pemantle, Y. Peres, Conceptual proofs of \(l\log l\) criteria for mean behavior of branching processes. Ann. Probab. 23, 1125–1138 (1995)
J.-F. Marckert, Limit of random walks and of random trees (2009). Cours. http://www.labri.fr/perso/marckert/GRAZ.pdf
Y. Peres, Probability on trees : an introductory climb. Cours Ecole d’été de Saint-Flour 1997. Lecture Notes in Mathematics, vol. 1717 (Springer, Berlin, 1999)
D. Revuz, M. Yor, Continuous Martingales and Brownian Motion, 3rd edn. (Springer, Berlin, 1999)
K. Uchiyama, Spatial growth of a branching process of particles living in R d. Ann. Probab. 10(no 4), 896–918 (1982)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Chauvin, B., Clément, J., Gardy, D. (2018). Approche probabiliste. In: Arbres pour l’Algorithmique. Mathématiques et Applications, vol 83. Springer, Cham. https://doi.org/10.1007/978-3-319-93725-0_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-93725-0_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-93724-3
Online ISBN: 978-3-319-93725-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


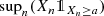 tend vers 0 quand a tend vers l’infini. Cette notion est équivalente à la convergence de la suite dans L
1.
tend vers 0 quand a tend vers l’infini. Cette notion est équivalente à la convergence de la suite dans L
1.