Keywords

1 Introduction

Poroelasticity involves fluid flow in porous media that are elastic and can deform due to fluid pressure. Poroelasticity problems exist widely in the real world, e.g., drug delivery, food processing, petroleum reservoirs, and tissue engineering [6, 7, 19] and have been attracting attention from the scientific computing community [10, 16, 17, 23] (and references therein). Some recent work can be found in [9,10,11, 20, 24].

Mathematically, poroelasticity can be modeled by coupled Darcy and elasticity equations as shown below

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle -\nabla \cdot \left( 2\mu \varepsilon (\mathbf {u}) + \lambda (\nabla \cdot \mathbf {u}) \mathbf {I} \right) + \alpha \nabla p = \mathbf {f}, \\ \displaystyle \partial _t \left( c_0 p + \alpha \nabla \cdot \mathbf {u} \right) + \nabla \cdot \left( -\mathbf {K} \nabla p \right) = s, \end{array} \right. \end{aligned}$$
(1)

where \( \mathbf {u} \) is the solid displacement, \( \varepsilon (\mathbf {u}) = \frac{1}{2} \left( \nabla \mathbf {u} + (\nabla \mathbf {u})^T \right) \) is the strain tensor, \( \lambda , \mu \) (both positive) are Lamé constants, \( \mathbf {f} \) is a body force, p is the fluid pressure, \( \mathbf {K} \) is a permeability tensor (that has absorbed fluid viscosity for notational convenience), s is a fluid source or sink (treated as negative source), \( \alpha \) (usually close to 1) is the Biot-Williams constant, \( c_0 \ge 0 \) is the constrained storage capacity. Appropriate boundary and initial conditions are posed to close the system.

An early complete theory about poroelasticity was formulated in Biot’s consolidation model [3]. A more recent rigorous mathematical analysis was presented in [18]. It is difficult to obtain analytical solutions for poroelasticity problems. Therefore, solving poroelasticity problems relies mainly on numerical methods.

According to what variables are being solved, numerical methods for poroelasticity can be categorized as

  • 2-field: Solid displacement, fluid pressure;

  • 3-field: Solid displacement, fluid pressure and velocity;

  • 4-field: Solid displacement and stress, fluid pressure and velocity.

The simplicity of the 2-field approach is always attractive and hence pursued by this paper.

Continuous Galerkin (CG), discontinuous Galerkin (DG), mixed, nonconforming, and weak Galerkin finite element methods all have been applied to poroelasticity problems. A main challenge in all these methods is the poroelasticity locking, which often appears in two modes [24]: (i) Nonphysical pressure oscillations for low permeable or low compressible media [8, 15], (ii) Poisson locking in elasticity.

Based on the displacement-pressure 2-field model, this paper presents a finite element solver for linear poroelasticity on quadrilateral meshes. The rest of this paper is organized as follows. Section 2 discusses discretization of planar linear elasticity by the 1st order Bernardi-Raugel elements on quadrilaterals. Section 3 presents discretization of 2-dim Darcy flow by the novel weak Galerkin finite element methods, in particular, WG\((Q_0,Q_0;RT_{[0]})\) on quadrilateral meshes. In Sect. 4, the above two types of finite elements are combined with the first order implicit Euler temporal discretization to establish a solver for poroelasticity on quadrilateral meshes, which couples the solid displacement and fluid pressure in a monolithic system. Section 5 presents numerical tests for this new solver to demonstrate its efficiency and robustness (locking-free property). Section 6 concludes the paper with some remarks.

2 Discretization of Elasticity by Bernardi-Raugel (BR1) Elements

In this section, we consider linear elasticity in its usual form

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle -\nabla \cdot \sigma = \mathbf {f}(\mathbf {x}), \quad \mathbf {x} \in \varOmega , \\ \displaystyle \mathbf {u}|_{\varGamma ^D} = \mathbf {u}_D, \quad \displaystyle (-\sigma \mathbf {n})|_{\varGamma ^N} = \mathbf {t}_N, \end{array} \right. \end{aligned}$$
(2)

where \( \varOmega \) is a 2-dim bounded domain occupied by a homogeneous and isotropic elastic body, \( \mathbf {f} \) is a body force, \( \mathbf {u}_D, \mathbf {t}_N \) are respectively Dirichlet and Neumann data, \( \mathbf {n} \) is the outward unit normal vector on the domain boundary \( \partial \varOmega = \varGamma ^D \cup \varGamma ^N \). As mentioned in Sect. 1, \( \mathbf {u} \) is the solid displacement,

$$\begin{aligned} \varepsilon (\mathbf {u}) = \frac{1}{2} \left( \nabla \mathbf {u} + (\nabla \mathbf {u})^T \right) \end{aligned}$$
(3)

is the strain tensor, and

$$\begin{aligned} \sigma = 2\mu \; \varepsilon (\mathbf {u}) + \lambda (\nabla \cdot \mathbf {u}) \mathbf {I}, \end{aligned}$$
(4)

is the Cauchy stress tensor, where \( \mathbf {I} \) is the order two identity matrix.

Note that the Lamé constants \( \lambda ,\mu \) are given by

$$\begin{aligned} \displaystyle \lambda = \frac{E \nu }{(1+\nu )(1-2\nu )}, \quad \quad \mu = \frac{E}{2(1+\nu )}, \end{aligned}$$
(5)

where E is the elasticity modulus and \( \nu \) is Poisson’s ratio.

In this section, we discuss discretization of linear elasticity using the first order Bernardi-Raugel elements (BR1) on quadrilateral meshes. The Bernardi-Raugel elements were originally developed for Stokes problems [2]. They can be applied to elasticity problems when combined with the “reduced integration” technique [4, 5, 24]. In this context, it means use of less quadrature points for the integrals involving the divergence term. The BR1 element on a quadrilateral can be viewed as an enrichment of the classical bilinear \( Q_1^2 \) element, which suffers Poisson locking when applied directly to elasticity.

Let E be a quadrilateral with vertices \( P_i(x_i,y_i) (i=1,2,3,4) \) starting at the lower-left corner and going counterclockwise. Let \( e_i (i=1,2,3,4) \) be the edge connecting \( P_i \) to \( P_{i+1} \) with the modulo convention \( P_5 = P_1 \). Let \( \mathbf {n}_i (i=1,2,3,4) \) be the outward unit normal vector on edge \( e_i \). A bilinear mapping from \( (\hat{x},\hat{y}) \) in the reference element \( \hat{E}=[0,1]^2 \) to (x, y) in such a generic quadrilateral is established as follows

$$\begin{aligned} \left\{ \begin{array}{l} x = x_1 + (x_2-x_1) \hat{x} + (x_4-x_1) \hat{y} + ((x_1+x_3)-(x_2+x_4)) \hat{x}\hat{y}, \\ y = y_1 + (y_2-y_1) \hat{x} + (y_4-y_1) \hat{y} + ((y_1+y_3)-(y_2+y_4)) \hat{x}\hat{y}. \end{array} \right. \end{aligned}$$
(6)

On the reference element \( \hat{E} \), we have four standard bilinear functions

$$\begin{aligned} \begin{array}{lccl} \displaystyle \hat{\phi }_4(\hat{x},\hat{y}) = (1-\hat{x}) \hat{y}, &{}&{}&{} \hat{\phi }_3(\hat{x},\hat{y}) = \hat{x} \hat{y}, \\ \hat{\phi }_1(\hat{x},\hat{y}) = (1-\hat{x}) (1-\hat{y}), &{}&{}&{} \hat{\phi }_2(\hat{x},\hat{y}) = \hat{x} (1-\hat{y}). \end{array} \end{aligned}$$
(7)

After the bilinear mapping defined by (6), we obtain four scalar basis functions on E that are usually rational functions of x, y:

$$\begin{aligned} \phi _i(x,y) = \hat{\phi }_i(\hat{x},\hat{y}), \;\; i=1,2,3,4. \end{aligned}$$
(8)

These lead to eight node-based local basis functions for \( Q_1(E)^2 \):

$$\begin{aligned} \left[ \begin{array}{c} \phi _1 \\ 0 \end{array} \right] , \left[ \begin{array}{c} 0 \\ \phi _1 \end{array} \right] , \left[ \begin{array}{c} \phi _2 \\ 0 \end{array} \right] , \left[ \begin{array}{c} 0 \\ \phi _2 \end{array} \right] , \left[ \begin{array}{c} \phi _3 \\ 0 \end{array} \right] , \left[ \begin{array}{c} 0 \\ \phi _3 \end{array} \right] , \left[ \begin{array}{c} \phi _4 \\ 0 \end{array} \right] , \left[ \begin{array}{c} 0 \\ \phi _4 \end{array} \right] . \end{aligned}$$
(9)

Furthermore, we define four edge-based scalar functions on \( \hat{E}\):

$$\begin{aligned} \begin{array}{lccl} \displaystyle \hat{\psi }_1(\hat{x},\hat{y}) = (1-\hat{x}) \hat{x} (1-\hat{y}), &{}&{}&{} \hat{\psi }_2(\hat{x},\hat{y}) = \hat{x} (1-\hat{y}) \hat{y}, \\ \displaystyle \hat{\psi }_3(\hat{x},\hat{y}) = (1-\hat{x}) \hat{x} \hat{y}, &{}&{}&{} \hat{\psi }_4(\hat{x},\hat{y}) = (1-\hat{x}) (1-\hat{y}) \hat{y}. \end{array} \end{aligned}$$
(10)

They become univariate quadratic functions on respective edges of \( \hat{E} \). For a generic convex quadrilateral E, we utilize the bilinear mapping to define

$$\begin{aligned} \psi _i(x,y) = \hat{\psi }_i(\hat{x},\hat{y}), \quad i=1,2,3,4. \end{aligned}$$
(11)

Then we have four edge-based local basis functions, see Fig. 1 (left panel):

$$\begin{aligned} \mathbf {b}_i(x,y) = \mathbf {n}_i \; \psi _i(x,y), \quad i=1,2,3,4. \end{aligned}$$
(12)

Finally the BR1 element on a quadrilateral is defined as

$$\begin{aligned} BR1(E) = Q_1(E)^2 + \text{ Span }(\mathbf {b}_1,\mathbf {b}_3,\mathbf {b}_3,\mathbf {b}_4). \end{aligned}$$
(13)
Fig. 1.
figure 1

Left panel: Four edge bubble functions needed for the 1st order Bernardi-Raugel element on a quadrilateral; Right panel: WG\((Q_0,Q_0;RT_{[0]})\) element on a quadrilateral.

Full size image

On each quadrilateral, there are totally twelve vector-valued basis functions. Their classical gradients are calculated ad hoc and so are the strains. Clearly, their classical divergences are not constants. The elementwise averages of divergence or the local projections into the space of constants are calculated accordingly.

Let \( \mathbf {V}_h \) be the space of vector-valued shape functions constructed from the BR1 elements on a shape-regular quadrilateral mesh \( \mathcal {E}_h \). Let \( \mathbf {V}_h^0 \) be the subspace of \( \mathbf {V}_h \) consisting of shape functions that vanish on \( \varGamma ^D \). Let \( \mathbf {u}_h \in \mathbf {V}_h \) and \( \mathbf {v} \in \mathbf {V}_h^0 \). Then the bilinear form in the strain-div formulation utilizing the Bernardi-Raugel elements reads as

$$\begin{aligned} \mathcal {A}_h^{SD}(\mathbf {u}_h, \mathbf {v}) = \sum _{E \in \mathcal {E}_h} 2\mu \Big ( \varepsilon (\mathbf {u}_h), \varepsilon (\mathbf {v}) \Big )_E + \lambda (\overline{\nabla \cdot \mathbf {u}_h}, \overline{\nabla \cdot \mathbf {v}})_E, \end{aligned}$$
(14)

where the overline bar indicates the elementwise averages of divergence. The linear form for discretization of the body force is simply

$$\begin{aligned} \mathcal {F}_h(\mathbf {v}) = \sum _{E \in \mathcal {E}_h} (\mathbf {f},\mathbf {v})_E, \quad \forall \mathbf {v} \in \mathbf {V}_h^0. \end{aligned}$$
(15)

Now there are two sets of basis functions: node-based and edge-based. Compatibility among these two types of functions needs to be maintained in enforcement or incorporation of boundary conditions.

  1. (i)

    For a Dirichlet edge, one can directly enforce the Dirichlet condition at the two end nodes and set the coefficient of the edge bubble function to zero;

  2. (ii)

    For a Neumann edge, integrals of the Neumann data against the three basis functions (two linear polynomials for the end nodes, one quadratic for the edge) are computed and assembled accordingly.

3 Discretization of Darcy Flow by WG\((Q_0,Q_0;RT_{[0]})\) Elements

In this section, we consider a 2-dim Darcy flow problem prototyped as

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \nabla \cdot \left( -\mathbf {K} \nabla p \right) + c \, p = f, \quad \mathbf {x} \in \varOmega , \\ \displaystyle p|_{\varGamma ^D} = p_D, \quad ((-\mathbf {K} \nabla p) \cdot \mathbf {n})|_{\varGamma ^N} = u_N, \end{array} \right. \end{aligned}$$
(16)

where \( \varOmega \) is a 2-dim bounded domain, p the unknown pressure, \( \mathbf {K} \) a conductivity matrix that is uniformly SPD, c a known function, f a source term, \( p_D\) a Dirichlet boundary condition, \( p_D\) a Neumann boundary condition, and \( \mathbf {n} \) the outward unit normal vector on \( \partial \varOmega \), which has a nonoverlapping decomposition \( \varGamma ^D \cup \varGamma ^N \).

As an elliptic boundary value problem, (16) can be solved by many types of finite element methods. However, local mass conservation and normal flux continuity are two most important properties to be respected by finite element solvers for Darcy flow computation. In this regard, continuous Galerkin methods (CG) are usable only after postprocessing. Discontinuous Galerkin methods (DG) are locally conservative by design and gain normal flux continuity after postprocessing. The enhanced Galerkin methods (EG) [21] are also good choices. The mixed finite element methods (MFEM) have both properties by design but result in indefinite discrete linear systems that need specially designed solvers. The recently developed weak Galerkin methods [12, 22], when applied to Darcy flow computation, have very attractive features in this regard: They possess the above two important properties and result in symmetric positive linear systems that are easy to solve [12,13,14].

The weak Galerkin methods [22] rely on novel concepts to develop finite elements for differential equations. Discrete weak basis functions are used separately in element interiors and on interelement boundaries (or mesh skeleton). Then discrete weak gradients of these basis functions are computed via integration by parts. These discrete weak gradients can be established in certain known spaces, e.g., the local Raviart-Thomas spaces \( RT_0 \) for triangles, the standard \( RT_{[0]} \) for rectangles, and the unmapped \( RT_{[0]} \) for quadrilaterals [14]. These discrete weak gradients are used to approximate the classical gradient in variational forms.

Recall that for a quadrilateral element E, the local unmapped Raviart-Thomas space has dimension 4 and can be generated by these four basis functions

$$\begin{aligned} RT_{[0]}(E) = \text{ Span }(\mathbf {w}_1, \mathbf {w}_2, \mathbf {w}_3, \mathbf {w}_4), \end{aligned}$$
(17)

where

$$\begin{aligned} \mathbf {w}_1 = \left[ \begin{array}{c} 1 \\ 0 \end{array} \right] , \quad \mathbf {w}_2 = \left[ \begin{array}{c} 0 \\ 1 \end{array} \right] , \quad \mathbf {w}_3 = \left[ \begin{array}{c} X \\ 0 \end{array} \right] , \quad \mathbf {w}_4 = \left[ \begin{array}{c} 0 \\ Y \end{array} \right] , \end{aligned}$$
(18)

and \( X=x-x_c \), \( Y=y-y_c \) are the normalized coordinates using the element center \( (x_c,y_c) \).

For a given quadrilateral element E, we consider 5 discrete weak functions \( \phi _i (0 \le i \le 4) \) as follows:

  • \( \phi _0 \) for element interior: It takes value 1 in the interior \( E^\circ \) but 0 on the boundary \( E^\partial \);

  • \( \phi _i (1 \le i \le 4) \) for the four sides respectively: Each takes value 1 on the i-th edge but 0 on all other three edges and in the interior.

Any such function \( \phi = \{ \phi ^\circ , \phi ^\partial \} \) has two independent parts: \( \phi ^\circ \) is defined in \( E^\circ \), whereas \( \phi ^\partial \) is defined on \( E^\partial \). Then its discrete weak gradient \( \nabla _{w,d} \phi \) is specified in \( RT_{[0]}(E) \) via integration by parts [22] (implementation wise solving a size-4 SPD linear system):

$$\begin{aligned} \displaystyle \int _{E} (\nabla _{w,d} \phi ) \cdot \mathbf {w} = \int _{E^\partial } \phi ^\partial (\mathbf {w} \cdot \mathbf {n}) - \int _{E^\circ } \phi ^\circ (\nabla \cdot \mathbf {w}), \quad \forall \mathbf {w} \in RT_{[0]}(E). \end{aligned}$$
(19)

When a quadrilateral becomes a rectangle \( E = [x_1,x_2] \times [y_1,y_2] \), we have

$$\begin{aligned} \left\{ \begin{array}{rrrrr} \displaystyle \nabla _{w,d} \phi _0 = &{} 0 \mathbf {w}_1 \;\; + &{} 0 \mathbf {w}_2 \;\; + &{} \frac{-12}{(\varDelta x)^2} \mathbf {w}_3 \;\; + &{} \frac{-12}{(\varDelta y)^2} \mathbf {w}_4, \\ \displaystyle \nabla _{w,d} \phi _1 = &{} \frac{-1}{\varDelta x} \mathbf {w}_1 \;\; + &{} 0 \mathbf {w}_2 \;\; + &{} \frac{6}{(\varDelta x)^2} \mathbf {w}_3 \;\; + &{} 0 \mathbf {w}_4, \\ \displaystyle \nabla _{w,d} \phi _2 = &{} \frac{1}{\varDelta x} \mathbf {w}_1 \;\; + &{} 0 \mathbf {w}_2 \;\; + &{} \frac{6}{(\varDelta x)^2} \mathbf {w}_3 \;\; + &{} 0 \mathbf {w}_4, \\ \displaystyle \nabla _{w,d} \phi _3 = &{} 0 \mathbf {w}_1 \;\; + &{} \frac{-1}{\varDelta y} \mathbf {w}_2 \;\; + &{} 0 \mathbf {w}_3 \;\; + &{} \frac{6}{(\varDelta y)^2} \mathbf {w}_4, \\ \displaystyle \nabla _{w,d} \phi _4 = &{} 0 \mathbf {w}_1 \;\; + &{} \frac{1}{\varDelta y} \mathbf {w}_2 \;\; + &{} 0 \mathbf {w}_3 \;\; + &{} \frac{6}{(\varDelta y)^2} \mathbf {w}_4, \end{array} \right. \end{aligned}$$
(20)

where \( \varDelta x = x_2 - x_1, \varDelta y = y_2 - y_1 \).

Let \( \mathcal {E}_h \) be a shape-regular quadrilateral mesh. Let \( \varGamma _h^D \) be the set of all edges on the Dirichlet boundary \( \varGamma ^D \) and \( \varGamma _h^N \) be the set of all edges on the Neumann boundary \( \varGamma ^N \). Let \( S_h \) be the space of discrete shape functions on \( \mathcal {E}_h \) that are degree 0 polynomials in element interiors and also degree 0 polynomials on edges. Let \( S_h^0 \) be the subspace of functions in \( S_h \) that vanish on \( \varGamma ^D_h \). For (16), we seek \( p_h = \{p_h^\circ ,p_h^\partial \} \in S_h \) such that \( p_h^\partial |_{\varGamma ^D_h} = Q_h^\partial (p_D) \) (the \( L^2 \)-projection of Dirichlet boundary data into the space of piecewise constants on \( \varGamma ^D_h \)) and

$$\begin{aligned} \mathcal {A}_h(p_h,q) = \mathcal {F}(q), \qquad \forall q=\{q^\circ ,q^\partial \} \in S_h^0, \end{aligned}$$
(21)

where

$$\begin{aligned} \displaystyle \mathcal {A}_h(p_h,q) = \sum _{E \in \mathcal {E}_h} \int _E \mathbf {K} \nabla _{w,d} p_h \cdot \nabla _{w,d} q + \sum _{E \in \mathcal {E}_h} \int _E c \, p \, q \end{aligned}$$
(22)

and

$$\begin{aligned} \displaystyle \mathcal {F}(q) = \sum _{E \in \mathcal {E}_h} \int _E f q^\circ - \sum _{\gamma \in \varGamma _h^N} \int _\gamma u_N q^\partial . \end{aligned}$$
(23)

As investigated in [14], this Darcy solver is easy to implement and results in a symmetric positive-definite system. More importantly, it is locally mass-conservative and produces continuous normal fluxes.

4 Coupling BR1 and WG\((Q_0,Q_0;RT_{[0]})\) for Linear Poroelasticity on Quadrilateral Meshes

In this section, the Bernardi-Raugel elements (BR1) and the weak Galerkin WG\((Q_0,Q_0;RT_{[0]})\) elements are combined with the implicit Euler temporal discretization to solve linear poroelasticity problems.

Assume a given domain \( \varOmega \) is equipped with a shape-regular quadrilateral mesh \( \mathcal {E}_h \). For a given time period [0, T],  let

$$ 0 = t^{(0)}< t^{(1)}< \ldots< t^{(n-1)}< t^{(n)}< \ldots < t^{(N)} = T $$

be a temporal partition. Denote \( \varDelta t_n = t^{(n)} - t^{(n-1)} \) for \( n=1,2,\ldots ,N \).

Let \( \mathbf {V}_h \) and \( \mathbf {V}_h^0 \) be the spaces of vector-valued shape functions constructed in Sect. 2 based on the first order Bernardi-Raugel elements. Let \( S_h \) and \( S_h^0 \) be the spaces of scalar-valued discrete weak functions constructed in Sect. 3 based on the WG\((Q_0,Q_0;RT_{[0]})\) elements. Let \( \mathbf {u}_h^{(n)}, \mathbf {u}_h^{(n-1)} \in \mathbf {V}_h \) be approximations to solid displacement at time moments \( t^{(n)} \) and \( t^{(n-1)} \), respectively. Similarly, let \( p_h^{(n)}, p_h^{(n-1)} \in S_h \) be approximations to fluid pressure at time moments \( t^{(n)} \) and \( t^{(n-1)} \), respectively. Note that the discrete weak trail function has two pieces:

$$\begin{aligned} p_h^{(n)} = \{ p_h^{(n),\circ }, p_h^{(n),\partial } \}, \end{aligned}$$
(24)

where \( p_h^{(n),\circ } \) lives in element interiors and \( p_h^{(n),\partial } \) lives on the mesh skeleton.

Applying the implicit Euler discretization, we establish the following time-marching scheme, for any \( \mathbf {v} \in \mathbf {V}_h^0 \) and any \( q \in S_h^0 \),

(25)

for \( n=1,2,\ldots ,N \). The above two equations are further augmented with appropriate boundary and initial conditions. This results in a large monolithic system.

This solver has two displacement degrees of freedom (DOFs) per node, one displacement DOF per edge, one pressure DOF per element, one pressure DOF per edge. Let \( N_d, N_e, N_g \) be the numbers of nodes, elements, and edges, respectively, then the total DOFs is

$$\begin{aligned} 2 * N_d + N_e + 2 * N_g, \end{aligned}$$
(26)

which is less than that for many existing solvers for poroelasticity.

5 Numerical Experiments

In this section, we test this novel 2-field solver on two widely used benchmarks. In these test cases, the permeability is \( \mathbf {K} = \kappa \mathbf {I} \), where \( \kappa \) is a piecewise constant over the test domain. Finite element meshes align with the aforementioned pieces. Rectangular meshes (as a special case of quadrilateral meshes) are used in our numerics.

Fig. 2.
figure 2

Example 1: A sandwiched low permeability layer.

Full size image
Fig. 3.
figure 3

Sandwiched low permeability layer: Numerical displacement and dilation, numerical pressure and velocity, numerical pressure contours for \( h=1/32 \) and \( \varDelta t = 0.001 \). Left column for time \( T_1 = 0.001 \); Right column for time \( T_2 = 0.01 \). Further shrinking in solid, drop of maximal fluid pressure, and pressure front moving are observed.

Full size image

Example 1

(A sandwiched low permeability layer). This problem is similar to the one tested in [8, 9], the only difference is the orientation. The domain is the unit square \( \varOmega = (0,1)^2 \), with a low permeability material (\( \kappa = 10^{-8} \)) in the middle region \( \frac{1}{4} \le x \le \frac{3}{4} \) being sandwiched by the other material (\( \kappa = 1 \)). Other parameters are \( \lambda =1 \), \( \mu =1 \), \( \alpha =1 \), \( c_0=0 \). Listed below are the boundary conditions.

  • For solid displacement:

    For the left side: Neumann (traction) \( -\sigma \mathbf {n} = \mathbf {t}_N = (1,0) \);

    For the bottom-, right-, and top-sides: homogeneous Dirichlet (rigid) \( \mathbf {u} = \mathbf {0} \);

  • For fluid pressure:

    For the left side: homogeneous Dirichlet (free to drain) \( p=0 \);

    For 3 other sides: homogeneous Neumann (impermeable) \( (-\mathbf {K} \nabla p) \cdot \mathbf {n} = 0 \).

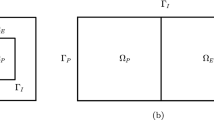
The initial displacement and pressure are assumed to be zero. See Fig. 2 for an illustration.

For this problem, we examine more details than what is shown in the literature. We use a uniform rectangular mesh with \( h = 1/32 \) for spatial discretization and \( \varDelta t = 0.001 \) for temporal discretization. This way, \( \varDelta t \approx h^2 \). Shown in Fig. 3 are the numerical displacement and dilation (div of displacement), the numerical pressure and velocity, and the numerical contours at time \( T_1=0.001 \) and \( T_2=0.01 \), respectively. As the process progresses and the fluid drains out from the left side (\( x=0 \)), it is clearly observed that

  1. (i)

    The maximal pressure is dropped from around 0.9915 to around 0.9570;

  2. (ii)

    The pressure front moves to the right and becomes more concentrated around the interface \( x=0.25 \);

  3. (iii)

    The solid is further shrunk: maximal shrinking (negative dilation) magnitude increases from around 0.2599 to around 0.3385.

Fig. 4.
figure 4

Example 2: Cantilever bracket problem.

Full size image
Fig. 5.
figure 5

Example 2: Cantilever bracket problem. Numerical pressure at time \( T = 0.005 \) is obtained by combining Bernardi-Raugel and weak Galerkin elements through the implicit Euler discretization with \( \varDelta t = 0.001 \), \( h=1/32 \).

Full size image

Example 2

(Cantilever bracket problem). This benchmark is often used to test spurious pressure oscillations [1, 17, 24]. The domain is the unit square \( \varOmega = (0,1)^2 \). A no-flux (Neumann) condition is prescribed on all four sides for the fluid pressure. The left side is clamped, that is, a homogeneous Dirichlet condition \( \mathbf {u}=\mathbf {0} \) is posed for the solid displacement for \( x=0 \). A downward traction (Neumann condition) \( -\sigma \mathbf {n} = \mathbf {t}_N = (0,-1) \) is posed on the top side, whereas the right and bottom sides are traction-free. The initial displacement and pressure are assumed to be zero. See Fig. 4.

Here we follow [1, 24] to choose the following parameter values

$$ E = 10^5, \quad \nu = 0.4, \quad \kappa = 10^{-7}, \quad \alpha = 0.93, \quad c_0 = 0. $$

We set \( \varDelta t = 0.001, h=1/32 \). Shown in Fig. 5 are the numerical pressure profile and contours at \( T = 0.005 \), obtained from using the Bernardi-Raugel elements and weak Galerkin elements. Clearly, the numerical pressure is quite smooth and there is no nonphysical oscillation.

This new finite element solver has been added to our Matlab code package DarcyLite. The implementation techniques presented in [13] are used.

It is demonstrated in [24] that nonphysicial pressure oscillations occur when the classical continuous Galerkin method is used for elasticity discretization.

6 Concluding Remarks

In this paper, we have developed a finite element solver for linear poroelasticity on quadrilateral meshes based on the two-field model (solid displacement and fluid pressure). This solver relies on the Bernardi-Raugel elements [2] for discretization of the displacement in elasticity and the novel weak Galerkin elements [14] for discretization of pressure in Darcy flow. These spatial discretizations are combined with the backward Euler temporal discretization. The solver does not involve any nonphysical penalty factor. It is efficient, since less unknowns are used, compared to other existing methods. This new solver is robust, free of poroelasticity locking, as demonstrated by experiments on two widely tested benchmarks.

This paper utilizes the unmapped local \( RT_{[0]} \) spaces for discrete weak gradients, which are used to approximate the classical gradient in the Darcy equation. Convergence can be established when quadrilateral are asymptotically parallelograms [14]. This type of new solvers are simple for practical use, since any polygonal domain can be partitioned into asymptotically parallelogram quadrilateral meshes. Efficient and robust finite element solvers for Darcy flow and poroelasticity on general convex quadrilateral meshes are currently under our investigation and will be reported in our future work.

Our discussion focuses on quadrilateral meshes, but the ideas apply to other types of meshes. For triangular meshes, one can combine the Bernardi-Raugel elements on triangles for elasticity [2] and the weak Galerkin elements on triangles for Darcy [12]. This combination provides a viable alternative to the three-field solver investigated in [24]. Similar 2-field solvers can be developed for tetrahedral and cuboidal hexahedral meshes. This is also a part of our current research efforts for developing efficient and accessible computational tools for poroelasticity.