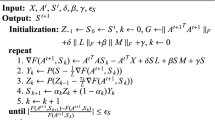Keywords

1 Introduction

In the last years, machine learning has been playing an important role in many domains, especially in image recognition and classification. It has shown the great power for effective learning. In supervised learning, a physical phenomenon is described by a mapping between predict or labeled data. In this domain, graph-based algorithms have drawn great attention [1,2,3,4,5]. A lot of efforts have been done by using graph-based learning methods to various topics, such as regression [6] and dimensionality reduction [7].

Techniques that address the latter problem were proposed to reduce the multi-dimensional data dimensionality. It aims to find relevant subsets for feature description. It yields a smaller set of representative features while preserving the optimal salient characteristics. Hence, not only the processing time can be decreased, but also a better generalization of the learning models can be achieved. The algorithms mentioned above rely on both the manifold structure and learning mechanism [8,9,10]. Therefore, in many cases, it is possible to achieve better performance than other conventional methods. However, all of these methods firstly define the characterized manifold structure and then perform a regression [5]. As a result, the constructed graphs have great effects on the performance. Indeed, the graph spectral is fixed in the following regression steps.

Taking into consideration the above remarks, we introduce in this paper a graph-based algorithm for efficient supervised image classification. It applies the models of graph-based dimensionality reduction and sparse regression simultaneously. Besides, an iterative locally linear graph weight algorithm is applied to acquire graph weights and improve the recognition accuracy. Finally, we inspect the optimization problem of the proposed approach and we demonstrate the situations to solve it.

The rest of the paper is structured as follows. In Sect. 2, the graph embedding model is introduced. Section 3 details the proposed graph-based supervised classification algorithm. Section 4 presents the experiments carried out on benchmark datasets to verify the effectiveness of the proposed algorithm by comparing with other art-of-state algorithms. The analysis of the experimental results are also given. Finally, in Sect. 5, we draw conclusions and discuss the works for the future research.

2 Related Works

2.1 Notations and Preliminaries

In order to make the paper self-contained, the notations used in the paper are introduced. \(\mathbf{{X}} = [{\mathbf{{x}}_1},{\mathbf{{x}}_2}, \cdots ,{\mathbf{{x}}_l},{\mathbf{{x}}_{l + 1}}, \cdots ,{\mathbf{{x}}_{l + u}}] \in {{\mathbb {R}}^{d \times (l + u)}}\) is defined as the sample data matrix, where \({\mathbf{{x}}_i}\left| {_{i = 1}^l} \right. \) and \({\mathbf{{x}}_j}\left| {_{j = l + 1}^{l + u}} \right. \) are the labeled and unlabeled samples, respectively. l and u are the total numbers of labeled and unlabeled samples, respectively, and d is the sample dimension. Let N be the total number of samples. The label of each sample \({\mathbf{{x}}_i}\) is denoted by \(y_i \in {1, 2,...,C}\), where C relates to the total number of classes. Let \(\mathbf{{S}} \in {{\mathbb {R}}^{(l + u) \times (l + u)}}\) be the graph similarity matrix, where \(\mathbf{{S}}_{ij}\) represents the similarity between \({\mathbf{{x}}_i}\) and \({\mathbf{{x}}_j}\) as given by the Cosine or the Gaussian Kernel (\(\mathbf {S}\) is symmetric). To make it clear, Table 1 shows all the nations and descriptions in this paper.

Table 1. Notations and descriptions.
Full size table

2.2 Graph Embedding

In graph embedding, each node of a constructed graph \(\mathbf{{G}} = \{ \mathbf{{X}},\mathbf{{S}}\} \) relates to a data point \({\mathbf{{x}}_i} \in \mathbf{{X}}\) [11]. The graph embedding is aimed at finding an optimal matrix \(\mathbf{{Y}}\) with a lower dimension that can make the best description of the similarity between the data well. The optimal \(\mathbf{{Y}}\) is given by

$$\begin{aligned}&\arg \mathop {\min }\limits _\mathbf{{Y}} ({\mathbf{{Y}}^T}{} \mathbf{{XL}}{\mathbf{{X}}^T}{} \mathbf{{Y}}) \nonumber \\&s.t.\;{\mathbf{{Y}}^T}{} \mathbf{{XD}}{\mathbf{{Y}}^T}{} \mathbf{{A}} = \mathbf{{I}} \end{aligned}$$
(1)

Where \(\mathbf{{L}} = \mathbf{{D}} - \mathbf{{S}}\) gives the Laplacian matrix, \(\mathbf {D}\) is a diagonal matrix and \(\mathbf {I}\) is an identity matrix.

In fact, different algorithms for dimensionality reduction result in various intrinsic graphs \(\mathbf{{G}} = \{ \mathbf{{X}},\mathbf{{S}}\} \). The most used algorithms to reduce the dimensionality include Principal Components Analysis (PCA), Linear Discriminant Analysis (LAD), Locally Linear Embedding (LLE) [12], Locality Preserving Projections (LPP) [2], ISOMAP [13], etc.

3 Proposed Algorithm

3.1 Similarity Matrix S

Firstly, a nearest neighbors method is used to determine k neighbors (\(k \le N\)) for each node. Asuming that i and j are two nodes linked by an edge, if i is among the k nearest neighbors of j, or if j is among the k nearest neighbors of i. It is obvious that this relation is symmetric.

Secondly, the similarity matrix \(\mathbf {S}\) is computed. It is introduced in [14, 15]. In order to acquire better performance for recognition and classification, the matrix \(\mathbf {S}\) is computed in a high-dimensional data space. The regularizer \({L_{1/2}}\) is used as an unbiased estimator in this paper. It is used to improve the sparsity of matrix \(\mathbf {S}\) for the minimization problem. Additionally, for graph embedding, the condition \(\mathbf{{S}} \ge 0\) is added. The process of minimization can be presented as:

$$\begin{aligned}&\mathop {\min }\limits _{\mathbf{{S}} \ge 0} \sum \limits _i {{{\left\| {{\mathbf{{x}}_i} - \sum \limits _j {{\mathbf{{S}}_{i,j}}{\mathbf{{x}}_j}} } \right\| }^2} + \alpha {{\left\| \mathbf{{S}} \right\| }_{\frac{1}{2}}} + \beta {{\left\| \mathbf{{S}} \right\| }^2}} \nonumber \\= & {} \mathop {\min }\limits _{\mathbf{{S}} \ge 0} {\left\| {\mathbf{{X}} - \mathbf{{XS}}} \right\| ^2} + \alpha {\left\| \mathbf{{S}} \right\| _{\frac{1}{2}}} + \beta {\left\| \mathbf{{S}} \right\| ^2} \nonumber \\\Rightarrow & {} \mathop {\min }\limits _{\mathbf{{S}} \ge 0} Tr\left( {\tilde{\kappa }- 2\tilde{\kappa }\mathbf{{S}} + {\mathbf{{S}}^T}\tilde{\kappa }\mathbf{{S}}} \right) + \alpha {\left\| \mathbf{{S}} \right\| _{\frac{1}{2}}} + \beta Tr\left( {{\mathbf{{S}}^T}{} \mathbf{{S}}} \right) \end{aligned}$$
(2)

Where \(\alpha \) and \(\beta \) are the free parameters, \(\tilde{\kappa }\) the kernel of \(\mathbf {X}\) and \({\left\| \mathbf{{S}} \right\| _{\frac{1}{2}}} = \sum \limits _i {\sum \limits _j {\mathbf{{S}}_{i,j}^{1/2}} } \).

Thus, Eq. (2) could be rewritten as:

$$\begin{aligned} \mathop {\min }\limits _{\mathbf{{S}} \ge 0} Tr\left[ {\left( {\tilde{\kappa }- 2\tilde{\kappa }\mathbf{{S}} + {\mathbf{{S}}^T}\tilde{\kappa }\mathbf{{S}}} \right) + \beta {\mathbf{{S}}^T}{} \mathbf{{S}}} \right] + \alpha {\left\| \mathbf{{S}} \right\| _{\frac{1}{2}}} \end{aligned}$$
(3)

Furthermore, Eq. (3) is equivalent to

$$\begin{aligned} \mathop {\min }\limits _{\mathbf{{S}} \ge 0} Tr\left[ {{\mathbf{{S}}^T}\left( {\beta \mathbf{{I}} + \tilde{\kappa }} \right) \mathbf{{S}} - 2\tilde{\kappa }\mathbf{{S}} + \tilde{\kappa }} \right] + \alpha {\left\| \mathbf{{S}} \right\| _{\frac{1}{2}}} \end{aligned}$$
(4)

It should be noticed that minimizing Eq.(4) is subjected to \(\mathbf{{S}} \ge 0\). Let \(\varsigma \ge 0\) be the corresponding Lagrange multipliers. The Lagrange function \(F\left( \mathbf{{S}} \right) \) can be presented as:

$$\begin{aligned} F\left( \mathbf{{S}} \right) = Tr\left[ {{\mathbf{{S}}^T}\left( {\beta \mathbf{{I}} + \tilde{\kappa }} \right) \mathbf{{S}} - 2\tilde{\kappa }\mathbf{{S}} + \tilde{\kappa }} \right] + \alpha {\left\| \mathbf{{S}} \right\| _{\frac{1}{2}}} + Tr\left( {\zeta {\mathbf{{S}}^T}} \right) \end{aligned}$$
(5)

Then, partial derivative of both sides leads to

$$\begin{aligned} \frac{{\partial F\left( \mathbf{{S}} \right) }}{{\partial {\mathbf{{S}}_{ij}}}} = {\left( { - 2\tilde{\kappa }+ 2\tilde{\kappa }\mathbf{{S}} + 2\beta \mathbf{{S}} + \frac{1}{2}\alpha {\mathbf{{S}}^{ - \frac{1}{2}}} + \zeta } \right) _{ij}} \end{aligned}$$
(6)

Where \({\mathbf{{S}}^{ - \frac{1}{2}}}\) is equivalent to the inverse matrix of principal square-rooting matrix \({\mathbf{{S}}^{\frac{1}{2}}}\).

Then, the Karush-Kuhn-Tucker(KKT) condition \(\zeta \mathbf{{S}} = 0\) for \(\mathbf{{S}}\) is

$$\begin{aligned} {\left( { - 2\mathbf{{X}} + 2\mathbf{{XS}} + 2\beta \mathbf{{S}} + \frac{1}{2}\alpha {\mathbf{{S}}^{ - \frac{1}{2}}} + \zeta } \right) _{ij}}{\mathbf{{S}}_{ij}} = 0 \end{aligned}$$
(7)

Eq. (7) can be reformulated as:

$$\begin{aligned} ( - {{\tilde{\kappa }}_{ij}} + {(\tilde{\kappa }\mathbf{{S}} + \beta \mathbf{{S}} + \frac{1}{2}\alpha {\mathbf{{S}}^{ - \frac{1}{2}}})_{ij}}){\mathbf{{S}}_{ij}} = 0 \end{aligned}$$
(8)

An iterative process to retrieve \(\mathbf {S}\) is expressed by

$$\begin{aligned} {\mathbf{{S}}_{ij}} \leftarrow \frac{\mathbf{{X}}}{{{{(\mathbf{{XS}} + \beta \mathbf{{S}} + \frac{1}{4}\alpha {\mathbf{{S}}^{ - \frac{1}{2}}})}_{ij}}}}{\mathbf{{S}}_{ij}} \end{aligned}$$
(9)

In fact, Eq. (9) only shows the computation for one iteration and it repeats many times until the result is convergence. Finally, we acquire the similarity matrix \(\mathbf {S}\) for graph projection.

3.2 Graph Embedding Learning

The work described in [16] proposed a novel graph-based embedding framework for feature selection with unsupervised learning, named Joint Embedding Learning and Sparse Regression (JELSR). This unsupervised method aims at ranking the original features by performing non-linear embedding learning and sparse regression concurrently. JELSR inspired us to develop a method with graph embedding algorithm for supervised learning in the domain of image classification.

Based on graph embedding and sparse regression optimization function, we can optimize it by making the following operation:

$$\begin{aligned} \ell (\mathbf{{W}},\mathbf{{Y}}) = \mathop {\arg \min }\limits _{\mathbf{{W}},\mathbf{{Y}}\;s.t.{\mathbf{{Y}}^T}{} \mathbf{{Y}} = \mathbf{{I}}} (trace({\mathbf{{Y}}^T}{} \mathbf{{LY}}) + \mu (\left\| {{\mathbf{{W}}^\mathbf{{T}}}{} \mathbf{{X}} - \mathbf{{Y}}} \right\| _2^2 + \gamma {\left\| \mathbf{{W}} \right\| _{2,1}})) \end{aligned}$$
(10)

Where \(\gamma \) and \(\mu \) are two regularization parameters. \(\mathbf{{W}}\) represents the linear transform matrix, m is the graph embedding dimensionality, and \(\mathbf{{Y}}\) denotes the data matrix of embedding non-linear projection of \(\mathbf{{X}}\). The \(\ell _{2,1}\) norm of \(\mathbf{{W}}\) is given by \( {\left\| \mathbf{W } \right\| _{2,1}} = \sum _{i=1}^d \Vert {\hat{\mathbf{w }}_i}\Vert _2\). \({\hat{\mathbf{w }}_i}\) is the i-th row of \(\mathbf{W }\).

Respecting to the matrix \(\mathbf {W}\), we can get the derivative of \(\ell (\mathbf{{W}},\mathbf{{Y}})\) as follows,

$$\begin{aligned} \frac{{\partial \ell (\mathbf{{W}},\mathbf{{Y}})}}{{\partial \mathbf{{W}}}} = 2\mathbf{{X}}{\mathbf{{X}}^T}{} \mathbf{{W}} - 2\mathbf{{X}}{\mathbf{{Y}}^T} + 2\gamma \mathbf{{UW}}=0 \end{aligned}$$
(11)

Where \(\mathbf{{U}} \in {{\mathbb {R}}^{d \times d}}\) is a diagonal matrix. The i-th diagonal element is \({\mathbf{{U}}_{ii}} = \frac{1}{{2{{\left\| {{{\mathbf{{\hat{w}}}}_i}} \right\| }_2}}}\).

Thus, we have the equation as follows:

$$\begin{aligned} \mathbf{{W}} = {(\mathbf{{X}}{\mathbf{{X}}^T} + \gamma \mathbf{{U}})^{ - 1}}{} \mathbf{{X}}{\mathbf{{Y}}^T} \end{aligned}$$
(12)

Equation (10) can be reformulated as:

$$\begin{aligned} \ell (\mathbf{{W}},\mathbf{{Y}})= & {} \mathop {\arg \min }\limits _{\mathbf{{W}},\mathbf{{Y}}\;s.t.{\mathbf{{Y}}^T}{} \mathbf{{Y}} = \mathbf{{I}}} (trace({\mathbf{{Y}}^T}{} \mathbf{{LY}}) + \mu (\left\| {{\mathbf{{W}}^\mathbf{{T}}}{} \mathbf{{X}} - \mathbf{{Y}}} \right\| _2^2 + \gamma {\left\| \mathbf{{W}} \right\| _{2,1}}) \nonumber \\ {}= & {} tr(\mathbf{{YL}}{\mathbf{{Y}}^T}) + \mu (tr({\mathbf{{W}}^T}{} \mathbf{{X}}{\mathbf{{X}}^T}{} \mathbf{{W}}) - 2tr({\mathbf{{W}}^T}{} \mathbf{{X}}{\mathbf{{Y}}^T}) \nonumber \\&+\, tr(\mathbf{{Y}}{\mathbf{{Y}}^T}) + \gamma tr({\mathbf{{W}}^T}{} \mathbf{{UW}})) \nonumber \\ {}= & {} tr(\mathbf{{YL}}{\mathbf{{Y}}^T}) + \mu ( - tr({\mathbf{{W}}^T}(\mathbf{{X}}{\mathbf{{X}}^T} + \gamma \mathbf{{U}})\mathbf{{W}}) + tr(\mathbf{{Y}}{\mathbf{{Y}}^T})) \nonumber \\ {}= & {} tr(\mathbf{{Y}}(\mathbf{{L}} + \mu \mathbf{{I}} - \mu {\mathbf{{X}}^T}{\mathbf{{A}}^{ - 1}}{} \mathbf{{X}}){\mathbf{{Y}}^T}) \end{aligned}$$
(13)

Where \(\mathbf{{A}} = \mathbf{{X}}{\mathbf{{X}}^T} + \gamma \mathbf{{U}}\).

Taking the objective function and the constraint \(\mathbf{{Y}}{\mathbf{{Y}}^T} = \mathbf{{I}}\) into account, the optimization problem turns to

$$\begin{aligned} \arg \mathop {\min }\limits _\mathbf{{Y}} tr(\mathbf{{Y}}(\mathbf{{L}} + \mu \mathbf{{I}} - \mu {\mathbf{{X}}^T}{\mathbf{{A}}^{ - 1}}{} \mathbf{{X}}){\mathbf{{Y}}^T})\;\;s.t.\;\mathbf{{Y}}{\mathbf{{Y}}^T} = \mathbf{{I}} \end{aligned}$$
(14)

If \(\mathbf {A}\) and \(\mathbf {L}\) are fixed, The Eigen decomposition of matrix \((\mathbf{{L}}\,+\,\mu \mathbf{{I}}\,-\,\mu {\mathbf{{X}}^T}{\mathbf{{A}}^{ -1}}{} \mathbf{{X}})\) can be used as the solution to the optimization problem in Eq. (14). We select m eigenvectors corresponding to the m smallest eigenvalues in order. These eigenvectors are suitable to build a graph-based embedding which is used for image classification.

4 Experiments

We have tested our method on four different datasets. They contains scenes (8 Sports Event Categories Dataset and Scene 15 Dataset), faces (ORL Face Dataset) and objects (COIL-20 Object Dataset). These images have been used in different groups to train and test. The details of the experiments and results are described in the following.

4.1 Dataset Configurations

The details of how the images in the four datasets are configurated are listed as follows.

8 Sports Event Categories Dataset includes 8 sports event categories (provided by Li and Fei-Fei) [17]. We have used 130 images in every category, thus a total of 1040.

Scene 15 Dataset includes 4485 gray level images of 15 different scenes including indoor and outdoor scenes [18]. We use 130 images in every category, thus a total of 1950.

ORL Face Dataset consists of 10 different images of each 40 distinct subjects [19].

COIL-20 Objects Dataset contains 1440 images of 20 objects (provided by Columbia Object Image Library) [20]. We select 70 images out of 72 for each object as a subset.

We have tested different distributions between training and testing images. For the first three datasets, we have used 50% and 70% of images for training twice, leaving 50% and 30% for testing, respectively. For the last dataset, we have used 10% and 20% of images for training, remaining 90% and 80% for testing, respectively.

4.2 Graph Performance Comparison

In this experiment, the graph calculated from the similarity matrix \(\mathbf {S}\) is firstly tested with by comparing with that of other classical similarity measure algorithms, such as KNN graph and \({\ell _1}\) graph. Table 2 displays the performance of graphs based on different similarity measure algorithms. In order to make the comparison, Laplacian Eigenmaps (LE) is chosen as the projection algorithm and the classification algorithm is 1NN classifier. From the results, it can be concluded that the kernelized sparse non-negative graph matrix \(\mathbf{{S}}\) is able to produce a graph weight matrix much better than the KNN graph and \({\ell _1}\) graph methods.

Table 2. The best average recognition rates (%) on 10 random splits of different graph algorithms.
Full size table

4.3 Effect of Proposed Algorithm

The block-based Local Binary Patterns (LBP) is used as the image descriptor, where the number of blocks is set to 10 \(\times \) 10. The LBP descriptor is the uniform one having 59 features. For ORL Face and COIL-20 Objects datasets, we use image raw brightnesses. The proposed algorithm is tested by comparing with the following five algorithms including LLE, Supervised Laplacian Eigenmaps (SLE) [21], Manifold Regularized Deep Learning Architecture (MRDL) [14], Semi-Supervised Discriminant Embedding (SDE)[22] and S-ISOMAP [23]. For MRDL method, we used two layers. Image classification is carried out in the obtained subspace using the Nearest Neighbor Classifier (NN). The experimental results are listed in Tables 3, 4, 5, and represented as graphs in Figs. 1 and 2.

Table 3. The best average recognition rates (%) of 8 Sports Event Categories Dataset on 10 random splits.
Full size table
Table 4. The best average recognition rates (%) of Scene 15 Dataset on 10 random splits.
Full size table
Table 5. The best average recognition rates (%) of COIL-20 Object Dataset on 10 random splits.
Full size table
Fig. 1.
figure 1

Recognition accuracy vs. feature dimension for 8 Sports Event Categories Dataset.

Full size image
Fig. 2.
figure 2

Recognition accuracy vs. feature dimension for Scene 15 Dataset.

Full size image

As presented by the results, we can draw the following conclusions. Generally, the proposed non-linear graph embedding method has enhanced performances compared with the other algorithms tested on different datasets in Tables 3, 4 and 5. Especially, compared with the MRDL algorithm, the best recognition rate of COIL-20 Object Dataset is increased by 15.80%. As the curves shown in Figs. 1 and 2, the recognition rates do not increase along with the dimension of features. Therefore, the proposed method can perform well without using large quantity of features. It can reduce the time and space complexity of training and classification.

5 Conclusions

By emplying a novel procedure, we proposed an image classification algorithm related to kernelized sparse non-negative graph matrix and graph-based sparse regression method. It is intended to reduce the feature dimensionality and improve the recognition accuracy in image classification. Experiments are carried out on benchmark datasets including scene, faces and object datasets to check the effectiveness of our algorithm. From the experimental results, it is obvious that the introduced algorithm outperforms the others tested. In the future, some optimization will be made to ensure the robustness of sparse regression. Some modifications are also needed to ameliorate the performance of our proposed graph-based supervised algorithm for image classification.