Abstract
This chapter uses the case of the ellipse as a new geometrical object introduced to China in the context of Aristotelian mechanics and Keplerian astronomy in order to analyse how authors in late imperial China, in particular before the introduction of differential and integral calculus, approached the rectification and quadrature of curves. It not only reveals the reliance on the classics and epistemic values when, for example, Dong Youcheng 董祐誠 (1791–1823) in 1821 proposed a solution to the problem of calculating the circumference of the ellipse by applying a problem from the Nine Chapters on Mathematical Procedures, but also argues that a shift of analysis was triggered by a change in scales of observation. It is shown in particular for the work of Xia Luanxiang 夏鸞翔 (1823–1864) that a panoptic point of view on conics, as compared to observing the ellipse as an isolated object, changes the representation, use and organization of Western concepts. The mathematical details of the calculation procedures discussed in this chapter are provided in Appendix C.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
This passage is reminiscent of Isaac Newton’s classification of curves that is related in more detail by Elias Loomis (1811–1889) in his Elements of Analytical Geometry, and of Differential and Integral Calculus in 1859 (Loomis 1851) and translated into Chinese by Li Shanlan and Alexander Wylie (chin. 偉烈亞力, 1815–1887). See Li and Wylie (1859) vol. 8, p. 6B–7B.
- 2.
I.e. the cubical parabola, the biquadratic parabola, etc.
- 3.
Cf. Loomis (1851) p. 103: “the only curves whose equations are of the second degree, are the circle, parabola, ellipse, and hyperbola.”
- 4.
The expression Zhiqi shangxiang 制器尚象 is borrowed from The Great Appendix to the Classic of Changes《周 易》易傳 繫辭下. For a translation, see Legge (1963) app. III, chap. X.59, p. 367–369.
- 5.
The common phrase yang guan fu cha 仰观 俯察 has its origins in The Great Appendix to the Classic of Changes《周 易》易傳 繫辭上: “仰以觀於天文, 俯以察於地理.” Translated in Legge (1963) app. III, chap. IV.21, p. 353:
(The sage), in accordance with (the Yî), looking up, contemplates the brilliant phenomena of the heavens, and, looking down, examines the definite arrangements of the earth.
- 6.
Translated from the Diagrammatic Explanations [of Procedures] for Curves (Zhiqu tujie 致曲圖解, 1861) in Xia (2006b) p. 438.
- 7.
See Chap. 6 p. 150 for a short explanation of the Chinese hexagrams.
- 8.
On Xia’s ideas concerning a comprehensive treatment of conics, see Liu (1990) p. 13.
- 9.
Projective transformations map lines to lines but do not necessarily preserve parallelism, whereas affine transformations respect parallel lines. The latter allow, for example, mapping a circle to an ellipse, but not an ellipse to a parabola or hyperbola.
- 10.
- 11.
See the History of the Qing Dynasty (Qingshi 清史), scroll 506 卷五百六, Biographies 292 列傳二百九十二, Mathematician-Astronomers 2 疇人二 in Qingshi (1961) vol. 7, p. 5501–5502 and the entry on Xia Luanxiang in the anonymous Qingdai xueren liezhuan 清代 學人列傳 (Biographies of Learned Men from Qing Dynasty), online http://ctext.org/wiki.pl?if=en&chapter=127281, §85:
All the principles of the ellipse and curves stem from the circle. If indeed, we unite what they have in common, then we “build tools to imitate the cosmos.” By “bowing [to the earth] and looking upwards [to the heaven], by observing [the sky] and investigating [the ground],” their applications are without limitations.
楕 圓及諸曲線其理皆出於平圓, 苟會其通, 則制器尚象, 俯仰觀察, 為用無窮。
- 12.
See the entry on Xia Luanxiang in the anonymous Biographies of learned men from Qing dynasty (Qingdai xueren liezhuan 清代 學人列傳) (Biographies of learned men from Qing dynasty), online http://ctext.org/wiki.pl?if=en&chapter=127281, §83–85.
- 13.
The term fangji used here is ambiguous, since it refers on the one hand to rectangular surfaces, but on the other to the binomial coefficients used in solving numerically polynomial equations for which Xia has developed a unique method. It is likely that the authors played on this ambiguity here in order to stress the relation between geometric objects of curved lines (here a chord of a circle) and the square (here more generally rectangular figures).
- 14.
Text quoted and translated from the History of the Qing Dynasty (Qingshi 清史), scroll 506 卷五百六, Biographies 292 列傳二百九十二, Mathematician-Astronomers 2 疇人二 in Qingshi (1961) vol. 7, p. 5501–5502.
- 15.
- 16.
- 17.
- 18.
The “arrow” (chin. shi 矢) here is not what in the history of mathematics was also called the “sagitta,” a Latin word meaning “arrow,” and which came to be used interchangeably with “versed sine.” See Newton (1999) p. 306–307. In the Chinese context, the “arrow” is rather the versed sine of half the arc under consideration. See Fig. 2.2.
- 19.
- 20.
Nowadays an outdated trigonometric function, it is defined as \( \mathop {\mathrm {versin}} \nolimits z=1-\cos z\).
- 21.
In this text, Xia uses an unusual term for expressing the square of a number: suan
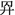 , a variant of the character suan 筭, literally meaning “to calculate”; in its nominal form it designates a “counting rod”. In the present text, for example, the expression zhengxian suan 正弦 stands for the square of the sine, the expression banjing suan 半徑 is the square of the radius.
, a variant of the character suan 筭, literally meaning “to calculate”; in its nominal form it designates a “counting rod”. In the present text, for example, the expression zhengxian suan 正弦 stands for the square of the sine, the expression banjing suan 半徑 is the square of the radius. - 22.
- 23.
For the mathematical details, see Appendix C.
- 24.
- 25.
For some examples of Xia’s procedures and a discussion of errors, see Song and Bai (2008).
- 26.
The title is probably a pun on a book written by his teacher, Xiang Mingda 項名達 (1789–1850), entitled Images and Numbers—a Single Origin (Xiang shu yi yuan 象數一原), prefaces from 1843 and 1849. Reprint in Guo et al. (1993) vol. 5, p. 473–602.
- 27.
- 28.
Style name of Xiang Mingda 項名達 (1789–1850).
- 29.
Style name of Dai Xu 戴煦 (1805–1860).
- 30.
Style name of Xu Youren 徐有壬 (1800–1860).
- 31.
Translated from Xia (1898a) Preface p. 1A.
- 32.
Idem scrolls 4–7.
- 33.
For mathematical details, see the Appendix p. 257.
- 34.
Xia (1898a) juan 3 p. 4A.
- 35.
For the derivation of this formula, see Loomis (1851) p. 225.
- 36.
See Xia (1898a) juan 4 p. 3B.
- 37.
- 38.
See for example Xu Youren’s 徐有壬 (1800–1860) Correct Procedures for the Ellipse (Tuoyuan zhengshu 橢圜 正術), posthumously published in 1872, in Xu (1985) p. 33–42, here p. 33:
The new [astronomical] methods all calculate with the ellipse for the expansion and contraction, acceleration and deceleration [of the planets], but calculation of their revolving trajectories are complicated. They all use approximations but no correct procedures.
- 39.
- 40.
- 41.
Li (1867a) p. 1a.
- 42.
The Nine Chapters give procedures for calculating a ring and segments of the circle and the sphere. See Chemla and Guo (2004) p. 141–143.
- 43.
1 mu = 240 bu [square], 1 jiao = 60 square bu [square].
- 44.
The value 10 is probably an approximation for π 2.
- 45.
Translated from Qin (1842) p. 499. The three expressions in italic represent technical terms for the coefficients of a polynomial equation in the Chinese mathematical tradition. Here, the positive root x of the quadratic equation gives the double of the surface area of the banana-leaf.
- 46.
Libbrecht (1973) p. 109 remarks that Qin’s formula was probably meant as a better approximation for the case of a circular segment where the arrow is relatively small compared to the chord sustaining the arc. For the corresponding problems, algorithm and proof in the Nine Chapters, see problems I.35 and I.36 in Chemla and Guo (2004) p. 191–193.
- 47.
For Japan, where it was commonplace to pose highly original problems about the ellipse in early nineteenth-century sangaku temple geometry riddles, foreign influence is uncertain. See for example Fukagawa and Rothman (2008) problems 19 and 21.
- 48.
Quoted from Jami (2012) p. 289.
- 49.
Deng and Wang (1830) juan 1 p. 24B. As pointed out in Zhang et al. (2008) vol. 1, p. 98, this theorem was copied from Federico Commandino’s Liber de Centro Gravitatis Solidorum. See Theorema IIII in Commandino (1565) p. 6, where also a detailed proof is given:
In circulo & ellipsi idem est figuræ & gravitatis centrum.
- 50.
- 51.
The circle with a diameter from the point 卯 to the point 辰, shown in the upper left figure in Fig. 2.7.
- 52.
- 53.
According to the catalogue (Verhaeren 1949) item 2612 the Jesuits had, for example, a 1597 edition by Adriaen van Roomen (1561–1615) of a book entitled In Archimedis circuli dimensionem Expositio & Analysis. Apologia pro Archimede ad Clariss. virum Iosephum Scaligerum … (Roomen 1597). Verhaeren (1949) item 4000 is the editio principes of the collection of Archimedean texts, Archimedes and Eutocius (1544).
- 54.
- 55.
A comparison of reference in the commentary of proposition 18 to “Yuanshu 圓書 Book I proposition 31” for example, shows clearly that De Sphaera et Cylindro is what Ricci and Li consulted when they made a statement about the fourfold surface area of the sphere with respect to a circle with the same radius. See Archimedes and Eutocius (1544) De Sphaera et Cylindro Liber Primus vol. I, p. 31–32 and Ricci and Li (1614) p. 20B.
- 56.
Contained in Archimedes and Eutocius (1544).
- 57.
In the proof of Prop. 4 it is assumed that this auxiliary circle is the one having the major axis as radius.
- 58.
- 59.
On the problem of dating Heron, see Héron d’Alexandrie (2014) p. 15–26.
- 60.
See Book I, prop. XXXIV translated in Héron d’Alexandrie (2014) p. 235. As pointed out in idem p. 235n310, this is not exactly the Archimedean formulation in De Conoidibus et Sphaeroidibus, where Archimedes gives the proportion:
Ellipse : circle = minor axis : diameter.
- 61.
Clavius (1604) Geometria Practica bk. IV, prop. V, p. 224.
- 62.
On the wider context of the book within the whole history of Jesuit astronomy in China, see Shi (2008a).
- 63.
- 64.
Translated from Qianlong 乾隆 (1773) p. 45A. According to Yang (2004) p. 49 this statement is to be found in juan 1 in the second part entitled “Finding the distance between two centers” (qiu liang xin cha 求兩心差), but it is in fact quoted from the section on “Finding the mean proportional between the major and minor axis of an ellipse” (qiu tuoyuan da xiao jing zhi zhonglü 求橢圓大小徑之中率).
- 65.
See Qianlong 乾隆 (1773) p. 41B–42A.
- 66.
- 67.
See Yunzhi 允祉 (1723) scroll 20, p. 17B–18B (Fig. 2.9). The preceding numerical example asks for the surface area of an ellipse with a major axis of 9 chi and a minor axis of 6 chi. In the solution, the argument by proportion is applied to a circle with a diameter equal to 104 and a surface area of 78 539 816, thus assuming a value of π = 4 ⋅0.785 398 16 = 3.141 592 64.
- 68.
Translated from Yunzhi 允祉 (1723) scroll 20, p. 18A.
- 69.
See Yunzhi 允祉 (1723) scroll 3, p. 53A–55A:
In general, when the diameter of a circle is equal to the major axis of the ellipse another name is “duck-egg shape,” then the ratio between the surface area of the circle and the ellipse is also equal to the ratio between the rectangles circumscribed to the two figures. The ratio between the surface area of the circle and the ellipse is also equal to the ratio between the diameter of the circle and the minor axis of the ellipse.
- 70.
Dates unknown, Jinshi in 1801. See Yan (1990) entry 0174, p. 48.
- 71.
A county in Zhejiang province, now Jiaxing 嘉興.
- 72.
Dong (1821) p. 1A.
- 73.
Chapter 9 of the Nine Chapters concerned with problems related to right triangles.
- 74.
Quoted from Ruan and Luo (1882) scroll 51 卷五十一, entry on Dong Youcheng 董祐誠.
- 75.
Equivalent, but historically unrelated, procedures were found by Colin MacLaurin (1698–1746) in his Treatise on Fluxions (1742) and by the Japanese mathematician Sakabe Kōhan 坂部 広胖 (1759–1824) in his Guide to Tenzan [Mathematical Methods] ([Sampō] Tenzan shinan roku [算法] 点竄指南錄 ) in 1815. See MacLaurin (1742) § 806, p. 658–659 and Mikami (1912).
- 76.
Lü is a technical mathematical term conceptually introduced by Liu Hui in his 263 commentary to the Nine Chapters where it designates a number that is in a ratio with another one. See Chemla and Guo (2004) p. 956–958.
- 77.
For convenience only, the expression \(\sqrt {\frac {a^2-b^2}{a^2}}\) is replaced in my transcription by e, the eccentricity of an ellipse, a concept measuring its deviation from circularity not present in Xiang Mingda’s text.
- 78.
Translated from Xiang (1888) vol. 6, p. 27B–28A.
- 79.
Translated from Xiang (1888) vol. 6, p. 28A. A different version of Xiang’s procedure is given by Dai Xu in his Diagrammatic Explanations [to the Procedure] to Find the Circumference of an Ellipse (Tuoyuan qiu zhou tujie 橢圓求周 圖解, 1857), which was published as an appendix to the posthumous publication of Xiang Mingda’s Images and Numbers—a Single Origin (Xiang shu yi yuan 象數一原). See Dai (1888) vol. 7, here p. 53A–53B.
- 80.
For a formulaic transcription of Dai Xu’s work, see Li (1955).
- 81.
See MacLaurin (1742) § 806, p. 658–659. A more detailed comparison between Xiang Mingda’s, Dai Xu’s and MacLaurin’s approach is in preparation for a future publication.
References
Anonymous (Ed.) (1931). Song ke suanjing liu zhong 宋刻算經六種 (Six Books of the [Ten Books of] Mathematical Classics Printed in the Song Dynasty). Beijing: Wenwu chubanshe 文物出版社. Reproduced from the original Song dynasty edition printed in 1213.
Archimedes and Eutocius (1544). Archimēdous tou Syrakousiou ta mechri nyn sōzomena hapanta = Archimedis Syracusani …opera, quae quidem extant, omnia : nuncque primum & Graece et Latine in lucem edita. Adiecta quoque sunt Eutocii Ascalanitae in eosdem Archimedis libros commentaria : item Graece et Latine, …/ edidit Thomas Geschauff, cognomento Venatorius. Basilea: [Hervagius].
Chemla, Karine and Shuchun Guo (2004). Les neuf chapitres sur les procédures mathématiques. Le classique mathématique de la Chine ancienne et ses commentaires. Paris: Dunod.
Chen, Jiang-Ping Jeff (2015). Trigonometric Tables: explicating their Construction Principles in China. Archive for History of Exact Sciences 69(5).
Clavius, Christophorus (1604). Geometria practica. Romae.
Clavius, Christophorus (1611). Opera mathematica V Tomis distributa. Moguntie [Mainz]: sumptibus Antonij Hierat excudebat Reinhard Eltz.
Commandino, Federico (1565). Liber de centro gravitatis solidorum. Bononiæ.
Cullen, Christopher (1996). Astronomy and Mathematics in Ancient China: The Zhou bi suan jing. New York: Cambridge University Press.
Dai, Xu 戴煦 (1888). Tuoyuan qiu zhou tujie 橢圓求周 圖解 (Diagrammatic Explanations [to the Procedure] to Find the Circumference of an Ellipse). In Dai Xu 戴煦 (Ed.), Xiang shu yi yuan 象數一原 (Images and Numbers—A Single Origin), 7 vols., 7:1A–53B. Shanghai: Jin’gui Hua shi 金匱華氏. Reprint in (Guo et al. 1993) 5:574–600.
Dechales, Claude François Milliet (1674). De sectionibus conicis. In Cursus seu Mundus mathematicus, Volume 3 (Tomus Tertius), Tractatus XXXI, 793–863. Lugduni [Lyon]: Anisson.
Deng, Yuhan 鄧玉函 (Schreck, Johannes) and Zheng Wang, 王徵 (1830). Qiqi tushuo 奇器圖說 (Diagrams and Explanations of Magnificent Machines) (Lailutang 來 鹿堂藏板 ed.). Preface by Wang Zheng from 1627.
Dong, Youcheng 董祐誠 (1819). Geyuan lianbili shu tujie 割圜 連比例術圖解 (Diagrammatic Explanations of Continued Proportions in Circle Division). In Dong Fangli yishu 董方立遺書 (The Posthumous Works of Dong Fangli), vol. 1 (1823 ed.). Reprint in (Guo et al. 1993) 5:435–460.
Dong, Youcheng 董祐誠 (1821). Tuoyuan qiu zhou shu 橢圜 求周 術 (Procedure to find the circumference of an ellipse). In Dong Fangli yishu 董方立遺書 (The Posthumous Works of Dong Fangli), vol. 1 (1823 ed.). Reprint in (Guo et al. 1993) 5:460–461.
Fu, Lanya 傅蘭雅 (Fryer, John) (1888). Quxian xuzhi 曲線須知 (Essentials of Conics), 1 vol, Volume 7 第七冊 of Gezhi xuzhi 格致須知. Shanghai: Jiangnan jiqi zhizao zongju 江南機器製造總局.
Fukagawa, Hidetoshi and Tony Rothman (2008). Sacred Mathematics: Japanese Temple Geometry. Princeton, NJ: Princeton University Press.
Gao, Hongcheng 高红成 (2009). Li Shanlan dui weijifen de lijie yu yunyong 李善兰对微积分的理解与运用 (Understanding and Application of Calculus by Li Shanlan). Zhongguo keji shi zazhi 中国科技史杂志 (The Chinese Journal for the History of Science and Technology) 30(2), 222–230.
Guo, Shuchun 郭書春 et al. (Eds.) (1993). Zhongguo kexue jishu dianji tonghui: Shuxue juan 中國科學技術典籍通彙: 數學卷 (Comprehensive Collection of Ancient Classics on Science and Technology in China: Mathematical Books), 5 vols. Zhengzhou: Henan jiaoyu chubanshe 河南教育出版社.
Han, Qi 韩琦 (2009). Li Shanlan, Ai Yuese yi Hu Weili «Zhongxue» zhi diben 李善兰 艾约瑟译胡威立《重重》之底本 (The Original Edition Underlying Li Shanlan’s and John Edkins’ Translation of William Whewell’s Elementary Treatise on Mechanics). Wakumon 或問 101(17), 101–111.
Hashimoto, Keizō 橋本敬造 (1971). Daenhō no tenkai: Rekishō kōsei kōhen no aiyō ni tsuite 橢圓法の展開 - 『 暦 象考成 後 編』の内 容 について - (The Development of Elliptical Methods. On the Contents of the Later Volumes of the Established System of Calendrical Astronomy). Tōhō Gakuho 東方學報 (Journal of Oriental Studies) 42, 245–272.
Heath, Thomas L. (1897). The Works of Archimedes: Edited in Modern Notation with Introductory Chapters. Cambridge: At the University Press.
Héron d’Alexandrie (2014). Metrica. Number 4 in Mathematica graeca antiqua. Pisa, Roma: Fabrizio Serra. Introduction, texte critique, traduction française et notes de commentaire par Fabio Acerbi et Bernard Vitrac.
Horng, Wann-Sheng (1991). Li Shanlan: The Impact of Western Mathematics in China during the Late 19th Century. Ph. D. thesis, Graduate Center, City University of New York.
Jami, Catherine (1990). Les méthodes rapides pour la trigonométrie et le rapport précis du cercle (1774). Mémoires des Hautes Études Chinoises. Paris: Collège de France.
Jami, Catherine (2012). The Emperor’s New Mathematics. Oxford: Oxford University Press.
Kepler, Johannes (1604). Ad Vitellionem Paralipomena, Quibus Astronomiae Pars Optica Traditvr Potißimum De Artificiosa Observatione Et Aestimatione Diametrorvm deliquiorumq[ue] Solis & Lunae ; Cvm Exemplis Insignivm Eclipsivm …Tractatum luculentum de modo visionis, & humorum oculi vsu, contra Opticos & Anatomicos. Francofvrti.
Legge, James (Trans.) (1899). The Yî King (2nd ed.), Volume 16 of Sacred Books of the East. Oxford: the Clarendon Press.
Legge, James (Trans.) (1963). The I Ching (2nd ed.). The Sacred Books of China. New York, NY: Dover. Unabridged and unaltered republication of (Legge 1899).
Li, Shanlan 李善蘭 (1867a). Tuoyuan sheyi 椭圜拾 遺 (Picking up on Omissions Concerning the Ellipse), 3 vols. In Zeguxizhai suanxue 則古昔齋算學 (Mathematics from the Studio Devoted to the Imitation of the Ancient Chinese Tradition) (Jinling 金陵刻本 ed.), Volume 9.
Li, Shanlan 李善蘭 (1867b). Tuoyuan xinshu 橢圜 新術 (New Procedure for the Ellipse), 1 vol. In Zeguxizhai suanxue 則古昔齋算學 (Mathematics from the Studio Devoted to the Imitation of the Ancient Chinese Tradition) (Jinling 金陵刻本 ed.), Volume 8.
Li, Shanlan 李善蘭 (1867c). Tuoyuan zhengshu jie 橢圜 正術解 (Explanations of the Right procedure for the Ellipse), 2 vols. In Zeguxizhai suanxue 則古昔齋算學 (Mathematics from the Studio Devoted to the Imitation of the Ancient Chinese Tradition) (Jinling 金陵刻本 ed.), Volume 7.
Li, Shanlan 李善蘭 and John Edkins 艾約瑟 (1898). Yuanzhui quxian shuo 圜錐曲線說 (Theory of Conic Sections). In Liu Duo 劉鐸 (Ed.), Gujin suanxue congshu 古今算學叢書 (Compendium of Mathematics, Old and New) (Weiboxie 據微波榭本等石印 ed.), Volume 3 (象數第三). Shanghai: Shanghai suanxue shuju 上海算學書局. Originally published as an Appendix to the translation of William Whewell’s Elementary Treatise on Mechanics, first published in 1859.
Li, Shanlan 李善蘭 and Alexander Wylie 偉烈亞力 (1859). Dai weiji shiji 代 微積拾級 (Elements of Analytical Geometry and of the Differential and Integral Calculus) 18 scrolls. Shanghai: Mohai shuguan 墨海書館. Original by Elias Loomis 羅密士(Loomis 1851).
Li, Yan 李儼 (1955). Zhongsuanjia de yuanzhui quxian shuo 中算家的圓錐曲線說 (Explanations of Conic sections by Chinese Mathematicians). In Li Yan 李儼 (Ed.), Zhongsuanshi luncong 中算史論叢 (Collected Writings on the History of Mathematics in China), Volume 3 第三集, 519–537. Beijing: Kexuechubanshe 科學出版社. Originally published in Kexue 科學 29-4 (1947), 115–120. Reprint in (Li and Qian 1998), 485–508.
Li, Yan 李 儼 and Baocong Qian, 錢寶琮 (1998). Li Yan Qian Baocong kexue shi quanji 李儼 錢寶琮科學史全集 (Complete Works of Li Yan and Qian Baocong), 9 vols. Shenyang: Liaoning chubanshe 遼寧出版社.
Li, Zhizao 李之藻 et al. (1965). Tianxue chuhan 天學初函 (First Collectanea of Heavenly Studies), 6 vols (Reprint ed.), scroll 23, First Series (Chubian 初編 卷二十三) of Wu Xiangxiang 吳相湘 (Ed.), Zhongguo shixue congshu 中國史學叢書. Taipei: Taiwan xuesheng shuju 臺灣學生書局.
Libbrecht, Ulrich (1973). Chinese Mathematics in the Thirteenth Century. The Shu-shu chiu-chang of Ch’in Chiu-shao. Cambridge (Mass.): MIT Press.
Liu, Dun 劉鈍 (1990). Xia Luanxiang dui yuanzhui quxian de zonghe yanjiu 夏鸾翔对圆锥曲线的综合研究 (The Comprehensive Research on Conic Sections by Xia Luanxiang). In Du Shiran 杜石然 (Ed.), Di san jie guoji Zhongguo kexueshi taolunhui lunwenji 第三届国际中国科学史讨论会论文集 (Proceedings of the Third International Conference on the History of Chinese Science), 12–18. Kexue chubanshe 科 学 出版社 .
Loomis, Elias (1851). Elements of Analytical Geometry and of the Differential and Integral Calculus. New York: Harper & Brothers.
Loomis, Elias (1877). Elements of Geometry, Conic Sections, And Plane Trigonometry (Rev. ed.). New York: Harper & Brothers.
Lu, Jing 盧靖 (1902). Wan xiang yi yuan yanshi 萬象一原演式 (Formulas for A Myriad Images—A Single Origin) 1+9 scrolls (Mianyang Lu shi 沔陽盧氏刊本 ed.). [Hubei?].
MacLaurin, Colin (1742). A Treatise of Fluxions in Two Books, Volume 2. Edinburgh: T. W. and T. Ruddimans.
Martzloff, Jean-Claude (1987). Histoire des mathématiques chinoises; préf. de J. Gernet et J. Dhombres. Paris [etc.]: Masson.
Martzloff, Jean-Claude (1997). A History of Chinese Mathematics. Berlin, Heidelberg [etc.]: Springer. Originally published in French (Martzloff 1987).
Mikami, Yoshio (1912). The rectification of the ellipse by Japanese mathematicians. Bibliotheca Mathematica 3, 225–237.
Ming, Antu 明安圖 (1774). Geyuan milü jiefa 割圜 密率捷法 (Fast Methods for the Circle Division and the Precise [circle] Ratio) (Luo Shilin 羅士琳, Guanwosheng shi huigao 觀我生室彙稿, 1839 ed.). Reprint in (Guo et al. 1993) 4:865–943.
Newton, Isaac (1999). The Principia. Mathematical Principles of Natural Philosophy. A New Translation by I. Bernard Cohen and Anne Whitman. Berkeley, Calif. et al.: University of California Press.
Qianlong 乾隆 (Ed.) (1773). Yuzhi lixiang kaocheng houbian 御製曆象考成後編 (Later Volumes of the Thorough Investigation of Calendrical Astronomy Imperially Composed), Volume 6 (子部六) of Chizao tang Sikuquanshu huiyao 摛藻堂四庫全書薈要. Originally compiled in 1738.
Qin, Jiushao 秦九韶 (1842). Shu shu jiu zhang 數書九章 (Mathematical Book in Nine Chapters) (Yijiatang congshu 宜稼堂叢書 ed.). Reprint in (Guo et al. 1993) 1:439–724.
Qingshi (1961). Qingshi 清史 (Annals of the Qing Dynasty), 8 vols. Taipei: Guofang yanjiuyuan 國防研究院.
Qiu, Desheng 求德生 (J. H. Judson) and Weishi Liu 劉維師 (Trans.) (1898). Yuanzhui quxian 圓錐曲線 (On Conic Sections). Shanghai: Meihua shuguan 美華書館. Partially translated from (Loomis 1877).
Ricci, Matteo and Zhizao Li, 李之藻 (1614). Yuanrong jiaoyi 圜 容較義 (The Meaning of Compared [figures] Inscribed in a Circle). [N.p.]. New edition Fanyu: Haishan xianguan, 1847 (Haishan xianguan congshu), reprint in (Li et al. 1965) 6:3427–3484.
Roomen, van (1561–1615), Adriaan (1597). In Archimedis circuli dimensionem Expositio & Analysis. Apologia pro Archimede, ad Clariss. virum Josephum Scaligerum. Exercitationes cyclicae contra Josephum Scaligerum, Orontium Finaeum, & Raymarum Ursum, in decem Dialogos distinctae. Authore Adriano Romano, … Wurceburgi.
Ruan, Yuan 阮元 and Luo Shilin 羅士琳 (Eds.) (光緒壬午春 1882). Chouren zhuan sishiliu juan fu Xu Chouren zhuan liu juan 疇人傳四十六卷坿續傳六卷 (Biographies of Astronomers and Mathematicians in 46 Scrolls; Continuation of Biographies of Astronomers and Mathematicians in 6 Scrolls) (Zhang 張氏重校刊 ed.). [N.p.]: Haiyan zhangjing changxing zhai 海鹽張敬常惺齋. Includes Chouren jie 疇人解 (Explanation of Astronomers and Mathematicians) by Tan Tai 談泰 (Ed.). Preface to Chouren zhuan 疇人傳 dated November 1799 (嘉慶四年十月), preface to Xu Chouren zhuan 續疇人傳 dated May 1840 (道光二十年夏四月).
Shi, Yunli (2008a). Reforming Astronomy and Compiling Imperial Science in the Post-Kangxi Era: The Social Dimension of the Yuzhi lixiang kaocheng houbian 御製曆象考成後編. EASTM 28, 36–81.
Shi, Yunli (2008b). The Yuzhi lixiang kaocheng houbian in Korea. In Luís Saraiva and Catherine Jami (Eds.), History of Mathematical Sciences: Portugal and East Asia III. The Jesuits, the Padroado and East Asian Science (1552–1773), 205–229. New Jersey [etc.]: World Scientific.
Song, Hua 宋華 and Bai Xin 白欣 (2008). Xia Luanxiang de weijifen shuiping pingxi 夏鸞翔的微積分水平評析 (Analysis of Xia Luanxiang’s Knowledge in Differential and Integral Calculus). Nei Menggu shifan daxue xuebao (Ziran kexue Hanwen ban) 內蒙古師範大學學報 (自然科學漢文版) (Journal of Inner Mongolia Normal University, Natural Science Edition) 37(4), 566–572.
Swinden, B. A. (1954). 2391. Johann Kepler: Paralipomena ad Vitellionem. The Mathematical Gazette 38(323), 44–46.
Verhaeren, Hubert (1949). Catalogue de la Bibliothèque du Pé-T’ang. Beijing: Imprimerie des Lazaristes. Reprint Paris: Les Belles Lettres, 1969.
Wang, Yusheng 王渝生 (1983). Li Shanlan: Zhongguo jindai kexue de xianquzhe 李善蘭: 中國近代 科學的先驅者 (Li Shanlan: Forerunner of Modern Science in China). Ziran bianzheng fa tongxun 自然辯證法通訊 (Dialectics of Nature) II(5), 59–72. Translated to English in (Wang 1996).
Wang, Yusheng (1996). Li Shanlan: Forerunner of Modern Science in China. In Dainian Fan (Ed.), Chinese Studies in the History and Philosophy of Science and Technology, Number 179 in Boston Studies in the Philosophy of Science, 345–368. Dordrecht: Kluwer. Originally published in Chinese as (Wang 1983).
Whewell, William 胡威立 (1859). Zhongxue 重學 (Mechanics. Translated by Li Shanlan 李善蘭 and John Edkins 艾約瑟). Shanghai: Mohai shuguan 墨海書館 (Inkstone Press).
Xia, Luanxiang 夏鸞翔 (1898a). Wan xiang yi yuan 萬象一原 (A Myriad Images—A Single Origin). In Liu Duo 劉鐸 (Ed.), Gujin suanxue congshu 古今算學叢書 (Compendium of Mathematics, Old and New), Volume 3 (象數第三). Shanghai suanxue shuju 上海算學書局. Preface dated 1862.
Xia, Luanxiang 夏鸞翔 (1898b). Zhiqu shu 致曲術 (Procedures for Curves). In Liu Duo 劉鐸 (Ed.), Gujin suanxue congshu 古今算學叢書 (Compendium of Mathematics, Old and New), Volume 3 (象數第三). Shanghai: Shanghai suanxue shuju 上海算學書局.
Xia, Luanxiang 夏鸞翔 (1898c). Zhiqu tujie 致曲圖解 (Diagrammatic Explanations [of Procedures] for Curves). In Liu Duo 劉鐸 (Ed.), Gujin suanxue congshu 古今算學叢書 (Compendium of Mathematics, Old and New), Volume 3 (象數第三). Shanghai suanxue shuju 上海算學書局.
Xia, Luanxiang 夏鸞翔 (2006a). Zhiqu shu 致曲術 (Procedures for Curves). In Xuxiu siku quanshu bianwei hui 續修四庫全書編委會 (Ed.), Xuxiu siku quanshu 續修四庫全書 (Supplement to the Complete Books in the Four Treasuries), Volume 1047, 425–437. Shanghai: Shanghai guji chubanshe 上海古籍出版社. Reprint of the manuscript ed. in the Shanghai Library 影印上海圖書館藏稿本.
Xia, Luanxiang 夏鸞翔 (2006b). Zhiqu tujie 致曲圖解 (Diagrammatic Explanations [of Procedures] for Curves). In Xuxiu siku quanshu bianwei hui 續修四庫全書編委會 (Ed.), Xuxiu siku quanshu 續修四庫全書 (Supplement to the Complete Books in the Four Treasuries), Volume 1047, 437–467. Shanghai: Shanghai guji chubanshe 上海古籍出版社. Reprint of the manuscript ed. in the Shanghai Library 影印上海圖書館藏稿本.
Xia, Luanxiang 夏鸞翔 (Guangxu 1875–1908). Zhiqu shu 致曲術 (Procedures for Curves) (蟄雲雷齋 Zhiyun leizhai ed.).
Xia, Luanxiang 夏鸞翔 (同治十二年 1873). Dongfang shu tujie er juan 洞方術圖解二卷 (Diagrammatic Explanations of Procedures for Thoroughly Understanding the Square in Two Scrolls). In Zou Zhengjun yishu (fu Xia shi suanxue si zhong, fu Xu shi suanxue san zhong) 鄒徵君遺書 (坿夏 氏算學四種 坿徐氏算學三種 ) (Posthumous Writings of Zou Zhengjun, with Four Mathematical Books by Mister Xia and Three Mathematical Books by Mister Xu Appended) (Zou Daquan shijieyuan 鄒達泉拾芥園 刊本 ed.). [Guangzhou?].
Xiang, Mingda 項名達 (1888). Tuoyuan qiu zhou shu 橢圜 求周 術 (Procedure to Find the Circumference of an Ellipse). In Dai Xu 戴煦 (Ed.), Xiang shu yi yuan 象數一原 (Images and Numbers—A Single Origin), 7 vols., 6:27B–39A. Shanghai: Jin’gui Hua shi 金匱華氏. Reprint in (Guo et al. 1993) 5:567–573.
Xu, Youren 徐有壬 (1985). Wumin yizhai suanxue 務民義齋算學 (Mathematics from the Wuminyi Studio). Congshu jicheng chubian 丛书集成初编 . Zhonghua shuju 中华书局 .
Yan, Wenyu 嚴文郁 (Ed.) (1990). Qing ruzhuan lüe 清儒傳略 (Short Biographies of Qing Scholars). Taipei: Taiwan shangwu yinshuguan 臺灣商務印書館.
Yang, Zezhong 楊澤忠 (2004). Ming mo Qing chu tuoyuan zhishi zhi donglai 明末清初橢圓知識之東來 (Knowledge on the Ellipse Coming to the East during the Late Ming and Early Qing). Shuxue jiaoxue 數學教學 3, 11, 47–49.
Yunzhi 允祉 (Ed.) (1723). Yuzhi shuli jingyun 御製數理精蘊 (Essence of Numbers and their Principles). [Beijing?]: [n.p.]. Reprint in (Guo et al. 1993) 3.
Zhang, Baichun 张柏春 , Tian Miao 田淼, Matthias Schemmel 马深梦 , Jürgen Renn 雷恩 , and Peter Damerow 戴培德 (2008). Chuanbo yu huitong: “Qiqi tushuo” yanjiu yu jiaozhu 传播与会通—《奇器图说》研究与校注 (Transmission and Integration—Qiqi tushuo (Illustrations and Descriptions of Extraordinary Devices): New Research and Annotated Edition), 2 vols. Nanjing: Jiangsu kexue jishu chubanshe 江苏科学技 术 出版社.
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Bréard, A. (2019). The Ellipse Seen from Nineteenth-Century China. In: Nine Chapters on Mathematical Modernity. Transcultural Research – Heidelberg Studies on Asia and Europe in a Global Context. Springer, Cham. https://doi.org/10.1007/978-3-319-93695-6_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-93695-6_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-93694-9
Online ISBN: 978-3-319-93695-6
eBook Packages: Social SciencesSocial Sciences (R0)


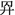 , a variant of the character suan 筭, literally meaning “to calculate”; in its nominal form it designates a “counting rod”. In the present text, for example, the expression zhengxian suan 正弦 stands for the square of the sine, the expression banjing suan 半徑 is the square of the radius.
, a variant of the character suan 筭, literally meaning “to calculate”; in its nominal form it designates a “counting rod”. In the present text, for example, the expression zhengxian suan 正弦 stands for the square of the sine, the expression banjing suan 半徑 is the square of the radius.