Abstract
While non-interactive zero-knowledge (NIZK) proofs require trusted parameters, Groth, Ostrovsky and Sahai constructed non-interactive witness-indistinguishable (NIWI) proofs without any setup; they called their scheme a non-interactive zap. More recently, Bellare, Fuchsbauer and Scafuro investigated the security of NIZK in the face of parameter subversion and observe that NI zaps provide subversion-resistant soundness and WI.
Arguments of knowledge prove that not only the statement is true, but also that the prover knows a witness for it, which is essential for anonymous identification. We present the first NIWI argument of knowledge without parameters, i.e., a NI zap of knowledge. Consequently, our scheme is also the first subversion-resistant knowledge-sound proof system, a notion recently proposed by Fuchsbauer.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The concept of zero-knowledge proof systems, first proposed by Goldwasser et al. [GMR89], is a central tool in modern cryptography. Consider an NP relation R which defines the language of all statements x for which there exists a witness w so that  . In a zero-knowledge proof for R a prover, knowing a witness, wants to convince a verifier that x is in the language. The protocol must be complete, that is, if the prover knows a witness for x then it can convince the verifier; it should be sound, in that no malicious prover can convince the verifier of a false statement, and zero-knowledge: the execution of the protocol reveals no information to the verifier (beyond the fact that x is in the language).
. In a zero-knowledge proof for R a prover, knowing a witness, wants to convince a verifier that x is in the language. The protocol must be complete, that is, if the prover knows a witness for x then it can convince the verifier; it should be sound, in that no malicious prover can convince the verifier of a false statement, and zero-knowledge: the execution of the protocol reveals no information to the verifier (beyond the fact that x is in the language).
Feige and Shamir [FS90] proposed a relaxation of zero-knowledge called witness indistinguishability, which only requires that it is indistinguishable which witness was used to compute a proof. This notion turns out to be sufficient in many contexts. Non-interactive zero-knowledge proofs (NIZK) [BFM88] allow the prover to convince the verifier by only sending a single message. However, they rely on the existence of a common-reference string (CRS) to which prover and verifier have access. The CRS is assumed to have been set up by some trusted party, which represents a serious limitation for all applications of NIZK in scenarios where parties mutually distrust each other.
Dwork and Naor [DN00] constructed a two-round witness-indistinguishable proof system for  in the plain model, that is, where no trusted CRS is assumed. In their protocol the first message (sent from the verifier to the prover) can be fixed once and for all, and the second one provides the actual proof. They called such protocols zaps. Barak et al. [BOV03] introduced the concept of non-interactive zaps, where the prover sends a single message to deliver the proof. Non-interactive zaps are thus non-interactive proof systems without a CRS. Since in this scenario it is impossible to achieve zero-knowledge [GO94], witness indistinguishability (WI) is the best one can hope for. Groth, Ostrovsky, and Sahai constructed the first non-interactive zaps from standard assumptions [GOS06a]. Subsequently [GOS06a], there have been many works extending this line of research [BW06, BW07, Gro06].
in the plain model, that is, where no trusted CRS is assumed. In their protocol the first message (sent from the verifier to the prover) can be fixed once and for all, and the second one provides the actual proof. They called such protocols zaps. Barak et al. [BOV03] introduced the concept of non-interactive zaps, where the prover sends a single message to deliver the proof. Non-interactive zaps are thus non-interactive proof systems without a CRS. Since in this scenario it is impossible to achieve zero-knowledge [GO94], witness indistinguishability (WI) is the best one can hope for. Groth, Ostrovsky, and Sahai constructed the first non-interactive zaps from standard assumptions [GOS06a]. Subsequently [GOS06a], there have been many works extending this line of research [BW06, BW07, Gro06].
All aforementioned schemes guarantee that proofs can only be computed for valid statements. Arguments of knowledge are proof systems that satisfy a stronger notion of soundness. They require the prover to know a witness for the proved statement. This is formalized via the notion of knowledge soundness that demands that for each prover there exists an efficient extractor which can extract a witness from the prover whenever the latter outputs a valid proof. (When this holds for computationally bounded provers only, we speak of arguments rather than proofs.) Since, by definition, false statements have no witnesses, knowledge soundness implies the standard notion of (computational) soundness.
Succinct non-interactive arguments of knowledge (SNARKs) are non-interactive proof systems with short (that is, independent of the size of the statement or the witness) efficiently verifiable proofs that satisfy knowledge soundness. SNARKs were initially introduced for verifiable computation and are now the most widely deployed proof systems in the real world. They are used in cryptocurrencies such as Zcash [BCG+14], which guarantees anonymity via zero-knowledge SNARKs. As for all NIZK systems, a drawback of SNARKs is that they require a CRS, that is, they require a one-time trusted setup of public parameters. Since for SNARKs every CRS has a simulation trapdoor, subversion of these parameters leads to full compromise of soundness.
Subversion Resistance. Motivated by the subversion of trusted public parameters in standardized cryptographic protocols led by mass-surveillance activities, Bellare et al. [BFS16] investigate what security properties can be maintained for NIZK when its trusted parameters are subverted. CRS’s for NIZK are especially easy to subvert, since they must be subvertible by design: zero knowledge requires that an honest CRS must be indistinguishable from a backdoored one, where the backdoor is the trapdoor used to simulate proofs.
Bellare et al. defined multiple security properties that protect against parameter subversion: subversion soundness (S-SND) means that no adversary can generate a malicious CRS together with a valid proof for a false statement; subversion zero knowledge (S-ZK) requires that even if the adversary sets up the CRS, there exists a simulator able to produce its full view; and subversion witness indistinguishability (S-WI) formalizes that even for proofs that were made under a subverted CRS, it is still infeasible to tell which of two witnesses was used.
Following Goldreich and Oren [GO94], Bellare et al. [BFS16] also showed that it is impossible to achieve subversion soundness and (standard) zero-knowledge simultaneously. For subversion-sound proof systems, subversion witness indistinguishability is thus the best one can hope for. The authors [BFS16] observe that since proof systems that do not rely on a CRS cannot succumb to CRS-subversion attacks, non-interactive zaps [GOS06a] achieve both S-SND and S-WI.
Bellare et al. did not consider the stronger notion of knowledge soundness, which is the notion achieved by SNARKs, and which in many applications is the required notion for the used proof systems. For example, for all kinds of anonymous authentication, users prove knowledge of signatures (often called certificates or credentials, depending on the context); in this case soundness is not sufficient, as signatures always exist, but in the security proof they must actually be extracted in order to rely on their unforgeability. Fuchsbauer [Fuc18] has recently defined a subversion-resistant notion of knowledge soundness but left it open to give a scheme that achieves it. Such a scheme would protect against possible parameter subversion in any context where proving knowledge of a witness is required.
Our Contribution. Our result can be summarized as follows:
-
(i)
We provide the first non-interactive zap with knowledge soundness; that is, a witness-indistinguishable proof system without parameters for which there exists an extractor that recovers a witness from every valid proof.
-
(ii)
Our zap is also the first fully subversion-resistant WI argument-of-knowledge system. In particular, it satisfies the recently defined notion of subversion knowledge soundness [Fuc18], as well as subversion witness indistinguishability [BFS16] (the strongest notion compatible with S-SND).
Bellare et al. [BFS16] introduce a new type of knowledge-of-exponent assumption, which they call DH-KE. They prove (standard) soundness and subversion zero knowledge of their main construction under DH-KE and the decision linear assumption (DLin) [BBS04]. Our construction builds on the DLin-based non-interactive zap from [GOS06a], whose soundness we upgrade to knowledge soundness, assuming DH-KE. As for this zap, the language of our proof system is circuit satisfiability and thus universal. Groth et al. [GOS06a] starting point is a “dual-mode” [GOS06b, PVW08] non-interactive proof system, for which there are two indistinguishable types of CRS: one leading to proofs that are perfectly sound and the other leading to proofs that are perfectly WI. To construct a non-interactive zap, they let the prover choose the CRS. As the prover could choose a CRS that leads to “unsound” proofs, the prover must actually choose two CRS’s that are related in a way that guarantees that at least one of them is of the “sound” type. It must then provide a proof of the statement under both of them. The authors [GOS06a] then show that this protocol still achieves computational WI.
We turn their construction into a proof of knowledge by again doubling the proof, thereby forcing the prover to prove knowledge of a trapdoor which allows to extract the witness from one of the sound proofs. We prove our non-interactive zap of knowledge secure under the same assumptions as Bellare et al.’s S-ZK+SND scheme. Our result is summarized in the following theorem.
Theorem 1
Assuming DLin and DH-KE, there exists a non-interactive zap for circuit satisfiability that satisfies knowledge soundness. The proof size is  , where
, where  is the security parameter and k is the size of the circuit.
is the security parameter and k is the size of the circuit.
Let us finally note that our system also implies a proof system which achieves (standard) knowledge soundness, (standard) zero knowledge and subversion witness indistinguishability. This is obtained by plugging our zap of knowledge into the construction by Bellare et al. [BFS16] that achieves SND, ZK and S-WI.
Their scheme uses a length-doubling pseudorandom generator (PRG) and a CRS contains a random bit string \(\sigma \) of length \(2\lambda \) (where \(\lambda \) is the security parameter). A proof for statement x is a zap for the following statement: either x is a valid statement or \(\sigma \) is in the range of the PRG. Using a zap of knowledge (ZaK), knowledge soundness follows from knowledge soundness of the ZaK since with overwhelming probability \(\sigma \) is not in the range of the PRG. (The extractor must thus extract a witness for x.) Zero knowledge follows from WI of the zap, as after replacing \(\sigma \) with an element in the range of the PRG, proofs can be simulated using a preimage of \(\sigma \). Finally, S-WI follows from S-WI of the zap.
Related Work. Since the introduction of non-interactive zaps [BOV03, GOS06a], a number of papers have studied and provided different (and more efficient) implementations of zaps. Groth and Sahai [GS08] provided a more general framework for NIWI and NIZK proofs, which leads to more efficient proofs for concrete languages (instead of circuit satisfiability). Furthermore, their proof system can also be based on other assumptions apart from DLin, such as SXDH, allowing for shorter proofs.
Bitanski and Paneth [BP15] presented a different approach to constructing zaps and WI proofs based on indistinguishability obfuscation (iO), but constructions using iO are only of theoretical interest. Ràfols [Ràf15] showed how to base non-interactive zaps on Groth-Sahai proofs, thereby achieving an improvement in efficiency (by a constant factor) over the original construction [GOS06a]. Her construction can be implemented in asymmetric (“Type-1”) pairing groups.
 is the size of an element of a group
is the size of an element of a group  .
.Her scheme can also serve as the starting point for a scheme achieving knowledge soundness and we explore this in the full version [FO18]. (See Table 1 for an overview.) Although this scheme is more efficient, we decided to concentrate on building a scheme from [GOS06a], as we can prove it secure under the assumptions that underlie Bellare et al.’s [BFS16] SND+S-ZK scheme; in contrast, a scheme built on asymmetric bilinear groups would require an analogue of the DH-KE assumption in such groups (we refer to it as ADH-KE in [FO18]). This is a qualitatively different assumption, as without a symmetric pairing it cannot be checked whether the triple returned by the adversary is of the right form (see Fig. 3); it would thus not be efficiently decidable if an adversary has won the game. Finally, our main scheme achieves tight security, whereas our proof of knowledge soundness with asymmetric pairings (which we present in the full version [FO18]) has a security loss that is linear in the circuit size.
2 Preliminaries
Notation. Let  be the security parameter. We let
be the security parameter. We let  be a length function in
be a length function in  defining the length of the randomness for a probabilistic machine \(\mathsf {M}\). When sampling the value a uniformly at random from the set S, we write
defining the length of the randomness for a probabilistic machine \(\mathsf {M}\). When sampling the value a uniformly at random from the set S, we write  . When sampling the value a from the probabilistic algorithm \(\mathsf {M}\), we write
. When sampling the value a from the probabilistic algorithm \(\mathsf {M}\), we write  . We use
. We use  to denote assignment. Elements of
to denote assignment. Elements of  are denoted in lower case, group elements are denoted with capital letters. We employ additive notation for groups. Let \(\mathsf {R}\) be a relation between statements denoted by \(\phi \) and witnesses denoted by w. By \(\mathsf {R}(\phi )\) we denote the set of possible witnesses for the statement \(\phi \) in \(\mathsf {R}\). We let
are denoted in lower case, group elements are denoted with capital letters. We employ additive notation for groups. Let \(\mathsf {R}\) be a relation between statements denoted by \(\phi \) and witnesses denoted by w. By \(\mathsf {R}(\phi )\) we denote the set of possible witnesses for the statement \(\phi \) in \(\mathsf {R}\). We let  be the language associated to \(\mathsf {R}\).
be the language associated to \(\mathsf {R}\).
We consider the language of circuit satisfiability, which is  -complete. For a binary circuit \(\texttt {C}\), the set \(\mathsf {R}(\texttt {C})\) is the set of inputs w that satisfy \(\texttt {C}(w) = 1\). Without loss of generality, we assume that circuits consist solely of NAND gates. Unless otherwise specified, all following algorithms are assumed to be randomized and to run in time
-complete. For a binary circuit \(\texttt {C}\), the set \(\mathsf {R}(\texttt {C})\) is the set of inputs w that satisfy \(\texttt {C}(w) = 1\). Without loss of generality, we assume that circuits consist solely of NAND gates. Unless otherwise specified, all following algorithms are assumed to be randomized and to run in time  . As Bellare et al. [BFS16], who follow [Gol93], we only consider uniform machines to model the adversary
. As Bellare et al. [BFS16], who follow [Gol93], we only consider uniform machines to model the adversary  and the extractor
and the extractor  . (See [BFS16, Fuc18] for discussions on how this choice affects the hardness assumptions and security guarantees.)
. (See [BFS16, Fuc18] for discussions on how this choice affects the hardness assumptions and security guarantees.)
Bilinear Groups. Throughout this work, we make use of prime-order abelian groups equipped with a (symmetric) bilinear map. Concretely, we assume the existence of groups  of odd prime order p of length
of odd prime order p of length  and an efficiently computable non-degenerate bilinear map
and an efficiently computable non-degenerate bilinear map  . That is, the map e is such that for all
. That is, the map e is such that for all  and
and  , and if U is a generator of
, and if U is a generator of  , then e(U, U) is a generator of
, then e(U, U) is a generator of  . We say that a bilinear group is verifiable if there exists an efficient verification algorithm that outputs
. We say that a bilinear group is verifiable if there exists an efficient verification algorithm that outputs  if and only if
if and only if  is the description of a bilinear group. For instance, the elliptic-curve group of [BBS04] equipped with the Weil pairing is publicly verifiable. In most practical scenarios, the group description is embedded as a part of the protocol specification and agreed upon in advance; in these cases there is no need for verification.
is the description of a bilinear group. For instance, the elliptic-curve group of [BBS04] equipped with the Weil pairing is publicly verifiable. In most practical scenarios, the group description is embedded as a part of the protocol specification and agreed upon in advance; in these cases there is no need for verification.
Throughout this paper, we assume the existence of a deterministic algorithm \(\mathsf {G}\) that, given as input the security parameter in unary  , outputs a bilinear group description \(\varGamma \). The same assumption was already employed by Bellare et al. [BFS16]. The main advantage in choosing \(\mathsf {G}\) to be deterministic is that every entity in the scheme can (re)compute the group from the security parameter, and no party must be trusted with generating the group. Moreover, real-world pairing schemes are defined for groups that are fixed for some
, outputs a bilinear group description \(\varGamma \). The same assumption was already employed by Bellare et al. [BFS16]. The main advantage in choosing \(\mathsf {G}\) to be deterministic is that every entity in the scheme can (re)compute the group from the security parameter, and no party must be trusted with generating the group. Moreover, real-world pairing schemes are defined for groups that are fixed for some  . For the sake of simplicity, we define all our schemes w.r.t. a group description \(\varGamma \) and assume that the security parameter (
. For the sake of simplicity, we define all our schemes w.r.t. a group description \(\varGamma \) and assume that the security parameter ( such that
such that  ) can be derived from \(\varGamma \).
) can be derived from \(\varGamma \).
Extractable Commitment Schemes. A commitment scheme \(\mathsf {Com}\) consists of the following three algorithms:
-
 , the key generation algorithm, outputs a CRS \(\sigma \) together with the trapdoor information \(\tau \).
, the key generation algorithm, outputs a CRS \(\sigma \) together with the trapdoor information \(\tau \). -
 , the commitment algorithm, outputs a commitment C to the given value v together with the opening information r.
, the commitment algorithm, outputs a commitment C to the given value v together with the opening information r. -
 , the opening algorithm, outputs
, the opening algorithm, outputs 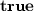 if C is a commitment to v witnessed by r, and
if C is a commitment to v witnessed by r, and  otherwise.
otherwise.
In our case, \(\mathsf {Com}.\mathsf {C}\) returns the used randomness and \(\mathsf {Com}.\mathsf {O}\) simply recomputes the commitment and checks that \(C = \mathsf {Com}.\mathsf {C}(V; r)\). Consequently, correctness of the scheme is trivial. To ease notation for commitments and openings, we will always assume that the group description \(\varGamma \) can be deduced from \(\sigma \), and omit the opening information from the returned value.
Generally, we require commitment schemes to be hiding and binding. Loosely speaking, a scheme is hiding if the commitment C reveals no information about v. A scheme is binding if a cheating committer cannot change its mind about the value it committed to. Formally, it is hard to find \(C,v,r,v'\) and \(r'\) such that \(v \ne v'\) and  .
.
We also require a perfectly binding commitment scheme to be extractable, that is, \(\mathsf {Com}\) is equipped with an efficient extraction algorithm  that, given as input the trapdoor information \(\tau \), recovers the value v to which C is bound.
that, given as input the trapdoor information \(\tau \), recovers the value v to which C is bound.
Proof Systems. A non-interactive proof system \(\mathsf {\varPi }\) for a relation \(\mathsf {R}\) consists of the following three algorithms:
-
 , the CRS generation algorithm that outputs a CRS \(\sigma \) (and possibly some trapdoor information \(\tau \)). Since we are dealing with publicly verifiable protocols, the trapdoor information \(\tau \) will be omitted in most cases and used solely in the proofs or when combining protocols.
, the CRS generation algorithm that outputs a CRS \(\sigma \) (and possibly some trapdoor information \(\tau \)). Since we are dealing with publicly verifiable protocols, the trapdoor information \(\tau \) will be omitted in most cases and used solely in the proofs or when combining protocols. -
 , a prover which takes as input some \((\phi , w) \in \mathsf {R}\) and a CRS \(\sigma \), and outputs a proof \(\pi \).
, a prover which takes as input some \((\phi , w) \in \mathsf {R}\) and a CRS \(\sigma \), and outputs a proof \(\pi \). -
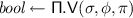 a verifier that, given as input a statement \(\phi \) together with a proof \(\pi \) outputs
a verifier that, given as input a statement \(\phi \) together with a proof \(\pi \) outputs  or
or 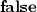 , indicating acceptance of the proof.
, indicating acceptance of the proof.
A proof is complete if every correctly generated proof verifies. If the CRS is clear from the context, we omit \(\sigma \) from the arguments of  or
or  .
.
Zaps. A zap is a two-round, witness-indistinguishable proof system where the first-round message is fixed “once and for all” [DN00] for all future instances of the protocol. The notion of witness-indistinguishability [FLS90] informally states that no  adversary can tell which of two possible witnesses has been used to construct a proof.
adversary can tell which of two possible witnesses has been used to construct a proof.
Definition 2
A proof system \(\mathsf {\varPi }\) is witness-indistinguishable (WI) for relation \(\mathsf {R}\) if  is negligible in
is negligible in  for any
for any  adversary
adversary  , where
, where  and
and  is depicted in Fig. 1.
is depicted in Fig. 1.
A zap is non-interactive if there is no first-round message from the verifier to the prover: the prover simply sends a single message. The proof system thus reduces to a pair  or can be considered as defined above, but with a CRS generation algorithm that always outputs \(\perp \). We next define the soundness notion for non-interactive arguments of knowledge.
or can be considered as defined above, but with a CRS generation algorithm that always outputs \(\perp \). We next define the soundness notion for non-interactive arguments of knowledge.
Knowledge soundness [BG93] means that for any prover able to produce a valid proof there exists an efficient algorithm, which has access to the prover’s random coins, capable of extracting a witness for the given statement.
Definition 3
A proof system \(\mathsf {\varPi }\) is knowledge-sound for \(\mathsf {R}\) if for any  adversary
adversary  there exists a
there exists a  extractor
extractor  such that
such that  is negligible in
is negligible in  , where
, where  and
and  is defined in Fig. 2. An argument of knowledge is a knowledge-sound proof system.
is defined in Fig. 2. An argument of knowledge is a knowledge-sound proof system.
Variations of this argument are often found in the literature. Most of them allow the extractor to rewind the adversary for interactive proof systems in addition to black-box access, most notably for \(\varSigma \)-protocols. In case of non-interactive provers the extractor is provided with the adversary’s random coins.
Assumptions. Our protocol is based on the DH-KE assumption and the existence of a homomorphic extractable commitment scheme. Such schemes have been widely studied and there are constructions from standard assumptions such as the subgroup decision assumption or the decisional linear (DLin) assumption [BBS04]. For this work, we rely on the latter, which is also used in [GOS06a].
The DLin assumption [BBS04] for an abelian group  of order p states that it is computationally difficult to distinguish \((uG, vG, urG,vsG,(r+s)G)\) with
of order p states that it is computationally difficult to distinguish \((uG, vG, urG,vsG,(r+s)G)\) with  from a uniformly random 5-tuple in
from a uniformly random 5-tuple in  .
.
Assumption 1
(DLin). We say that the Decisional Linear assumption holds for the group generator \(\mathsf {G}\) if for all  adversaries
adversaries  we have:
we have:

where the game  is defined in Fig. 3.
is defined in Fig. 3.
The intuition behind DH-KE [BFS16] is that it is difficult for some machine to produce a (Diffie-Hellman) DH triple (xG, yG, xyG) in  without knowing at least x or y. The assumption is in the spirit of earlier knowledge-of-exponent assumptions [Gro10, BCI+10], whose simplest form states that given
without knowing at least x or y. The assumption is in the spirit of earlier knowledge-of-exponent assumptions [Gro10, BCI+10], whose simplest form states that given  it is hard to return (yG, xyG) without knowing y.
it is hard to return (yG, xyG) without knowing y.
Assumption 2
(DH-KE). The Diffie-Hellman Knowledge of Exponent assumption holds for the bilinear group generator \(\mathsf {G}\) if for any  adversary
adversary  there exists a
there exists a  extractor
extractor  such that:
such that:

where the game  is defined in Fig. 3.
is defined in Fig. 3.
In other variants of knowledge of exponent assumptions the adversary is provided with some auxiliary information, which amounts to a stronger assumption. This is typically required as in the security proofs the reduction obtains a challenge which it needs to embed in the input to the adversary. In our specific case, all the proof material is generated by the prover itself, including the CRS. Consequently, the game DH-KE considers an adversary that simply takes as input a group description, without any auxiliary information. Compared to [BFS16], where the adversary is provided with additional information, our variant is thus weaker.
3 An Extractable Commitment Scheme from DLin
We recall the homomorphic commitment scheme based on linear encryption [BBS04] by Groth et al. [GOS06a]. It defines two types of key generation: a perfectly hiding and perfectly binding one. Given a bilinear group  , it defines two key-generation algorithms
, it defines two key-generation algorithms  and
and  producing binding and hiding keys, respectively:
producing binding and hiding keys, respectively:

In order to commit to a value  , one samples
, one samples  and returns:
and returns:
Since \( \mathsf {Com}.\mathsf {C}(m_0; r_0, s_0) + \mathsf {Com}.\mathsf {C}(m_1; r_1, s_1) = \mathsf {Com}.\mathsf {C}(m_0 + m_1; r_0 + r_1, s_0 + s_1) \), commitments are additively homomorphic. A committed value is opened by providing the randomness (r, s). Under a perfectly hiding key, a commitment to m can be opened to any value \(m'\), given trapdoor information \(\tau = (r_u, s_v)\):
Under the DLin assumption, keys output by the perfectly hiding setup are computationally indistinguishable from ones output by the perfectly binding setup. For this reason, the perfectly hiding setup leads to computationally binding commitments and vice versa.
We say that a triple of group elements is linear w.r.t. (F, H, G) if it is of the form \((rF, sH, (r+s)G)\) for some  Commitments to 0 are linear triples and every commitment under a hiding key is also a linear. Under a binding key we have:
Commitments to 0 are linear triples and every commitment under a hiding key is also a linear. Under a binding key we have:
A commitment to m is thus a linear encryption [BBS04] of  under randomness \((mr_u + r,ms_v + s)\). Given a commitment C and the trapdoor information \(\tau = (x, y, z)\), one can extract the committed message. The extraction algorithm
under randomness \((mr_u + r,ms_v + s)\). Given a commitment C and the trapdoor information \(\tau = (x, y, z)\), one can extract the committed message. The extraction algorithm  is defined as:
is defined as:

where \(\mathsf {dLog}\) can be efficiently computed if the message space is of logarithmic size; for instance, assuming  , we define
, we define  to return 0 if \((C_2 - x^{-1}C_0 - y^{-1}C_1)\) is the identity element, and 1 otherwise.
to return 0 if \((C_2 - x^{-1}C_0 - y^{-1}C_1)\) is the identity element, and 1 otherwise.
Theorem 4
([GOS06a]). Assuming DLin, \(\mathsf {Com}\), as defined above, is an extractable homomorphic commitment scheme that is:
-
perfectly binding, computationally hiding when instantiated with
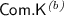 ;
; -
computationally binding, perfectly hiding when instantiated with
 .
.
The “parameter switching” technique, which defines different types of keys that are computationally indistinguishable, has proved very useful and also applies to encryption schemes. The idea has been defined (and named) several times. “Parameter switching” [GOS06a] is also called “meaningful/meaningless encryption” [KN08], “dual-mode encryption” [PVW08] and “lossy encryption” [BHY09].
Proofs of Binarity. As a building block for their zaps Groth et al. [GOS06a] first construct a witness-indistinguishable non-interactive proof system \(\mathsf {Bin}\). Given a commitment key \(\sigma = (F, H, U, V, W)\) and a commitment  , it allows to prove that C commits to a value in
, it allows to prove that C commits to a value in  under \(\sigma \). The proof is perfectly sound and perfectly witness-indistinguishable. (We recall their scheme in the full version [FO18].)
under \(\sigma \). The proof is perfectly sound and perfectly witness-indistinguishable. (We recall their scheme in the full version [FO18].)
4 Non-interactive Zaps
To construct a non-interactive zap (i.e., a WI proof system without a CRS), Groth et al. [GOS06a] first construct a proof system for circuit satisfiability with a CRS, based on the commitment scheme from Sect. 3 and their proof of binarity. Then, in order to make their scheme CRS-less, they define the prover to pick two CRS’s that are correlated in a way that makes it impossible for the adversary to cheat under both of them.
As the commitment scheme described in Sect. 3 is homomorphic, it is possible to perform linear operations on commitments, and in particular prove logical relations between them.
First, proving that either C or \(C':=C-(U,V,W)\) is linear proves that C is a commitment to a bit. In order to prove that committed values satisfy wire assignments of a NAND gate, Groth et al. [GOS06b] observe that if  then
then  iff
iff  . Reasoning with homomorphic commitments, we have that three commitments
. Reasoning with homomorphic commitments, we have that three commitments  ,
,  , and
, and  are bound respectively to the values a, b, c, such that \(c = \lnot (a ~\wedge ~ b)\), if and only if
are bound respectively to the values a, b, c, such that \(c = \lnot (a ~\wedge ~ b)\), if and only if

is a commitment to either 0 or 1. Thus, to prove that A, B, C are commitments to values in  and that C is a commitment to the NAND of the values in A and B, it is sufficient to prove that A, B, C and T are all bit commitments. With these observations, GOS construct a perfectly witness-indistinguishable proof system \(\mathsf {Circ}\) for circuit satisfiability as follows:
and that C is a commitment to the NAND of the values in A and B, it is sufficient to prove that A, B, C and T are all bit commitments. With these observations, GOS construct a perfectly witness-indistinguishable proof system \(\mathsf {Circ}\) for circuit satisfiability as follows:
The (non-interactive) \(\mathsf {ZAP}\) protocol of [GOS06a].
The key generation algorithm  simply emulates
simply emulates  , that is, it generates a hiding commitment key. The prover
, that is, it generates a hiding commitment key. The prover  takes as input a circuit \(\texttt {C}\) and a witness w satisfying \(\texttt {C}(w) = 1\), and does the following: represent the circuit evaluation \(\texttt {C}(w)\) in such a way that \(w_k\) is the value running in the k-th wire. For each \(w_k\), produce a commitment
takes as input a circuit \(\texttt {C}\) and a witness w satisfying \(\texttt {C}(w) = 1\), and does the following: represent the circuit evaluation \(\texttt {C}(w)\) in such a way that \(w_k\) is the value running in the k-th wire. For each \(w_k\), produce a commitment  to \(w_k\) and prove it is to a bit under \(\sigma \) using proof system \(\mathsf {Bin}\). For each gate, construct T from the commitments corresponding to the ingoing and outgoing wires as above and prove that it too is a commitment to 0 or 1. For the output commitment, create a commitment
to \(w_k\) and prove it is to a bit under \(\sigma \) using proof system \(\mathsf {Bin}\). For each gate, construct T from the commitments corresponding to the ingoing and outgoing wires as above and prove that it too is a commitment to 0 or 1. For the output commitment, create a commitment  to 1 that can be easily reproduced and checked by the verifier:
to 1 that can be easily reproduced and checked by the verifier:  . Let \(\varPi \) be the collection of all other commitments together with the respective proofs of binarity generated. Return \(\varPi \).
. Let \(\varPi \) be the collection of all other commitments together with the respective proofs of binarity generated. Return \(\varPi \).
The verifier  , computes
, computes  and for every gate the value T as in Eq. (3); using
and for every gate the value T as in Eq. (3); using  , it checks that all the wire commitments are to values in
, it checks that all the wire commitments are to values in  and respect the gates (by checking the values T); if all verifications succeed, return
and respect the gates (by checking the values T); if all verifications succeed, return  . Otherwise, return
. Otherwise, return  .
.
Theorem 5
([GOS06a]). Assuming DLin, \(\mathsf {Circ}\) is a non-interactive, perfectly sound computationally witness-indistinguishable proof system.
The reason why we cannot let the prover choose the CRS in \(\mathsf {Circ}\) is that it could chose it as a perfectly hiding CRS and then simulate proofs. However, if the prover must construct two proofs under two different CRS’s which are related in such a way that at least one of them is not linear (and thus binding), then the prover cannot cheat. In particular, note that given a 5-tuple  , and defining
, and defining  then at most one of \(\sigma _0, \sigma _1\) is linear. At the same time, both of them are valid CRS’s. With this last trick, it is straightforward to construct the zap scheme \(\mathsf {ZAP}\), as illustrated in Fig. 4.
then at most one of \(\sigma _0, \sigma _1\) is linear. At the same time, both of them are valid CRS’s. With this last trick, it is straightforward to construct the zap scheme \(\mathsf {ZAP}\), as illustrated in Fig. 4.
Theorem 6
([GOS06a]). Assuming DLin, \(\mathsf {ZAP}\) is a non-interactive zap with perfect soundness and computational witness indistinguishability.
Remark 7
We note that soundness of \(\mathsf {ZAP}\) relies only on the fact that \(\varGamma \) is a bilinear group. In [GOS06a] the prover is allowed to generate \(\varGamma \) and it is required that \(\varGamma \) is verifiable. We presented a zap for deterministically generated groups, as considered by Bellare et al. [BFS16], which is also required for our construction of non-interactive zaps of knowledge in the next section.
5 ZAK: A Non-interactive Zap of Knowledge
We now present our NIWI argument of knowledge for circuit satisfiability. The high-level idea of our protocol is to double the \(\mathsf {ZAP}\) proof of [GOS06a] and link the two CRS’s so the prover must know the extraction trapdoor for one of them. Whereas the protocol \(\mathsf {ZAP}\) used two \(\mathsf {Circ}\) proofs to construct a zap from a proof that requires a CRS, we will use two zap proofs to not only prove circuit satisfiability, but to prove knowledge of a satisfying assignment. More specifically, knowledge soundness is obtained by generating two independent zap proofs, and then linking the respective trapdoor information with multiple DH in a matrix of group elements \(\varDelta \). This additional matrix \(\varDelta \), that we call linking element, is constructed in such a way that (under DH-KE) it is possible to recover the trapdoor from one of the two zap proofs, and use it to extract the witness from the commitments contained in a valid zap proof. Witness indistinguishability of the single proofs follows immediately from [GOS06a], but our proofs also contain the linking element \(\varDelta \), which depend on the randomness of the CRS’s. We thus have to argue that these additional elements do not harm witness indistinguishability.
Bellare et al. [BFS16] also used an extractor to recover the trapdoor hidden in an adversarially generated CRS to construct a scheme satisfying subversion-zero knowledge. Our protocol is detailed in Fig. 5, where by \(\mathsf {DH}\) we denote the algorithm that checks that \(\delta _{i, j}\) is the CDH of \((\sigma _{0, 0})_{i}\) and \((\sigma _{1, 0})_j\) (see below).
The trapdoor information \(\tau _0 = (x_0, y_0)\) and \(\tau _1 = (x_1, y_1)\) is correlated in \(\varDelta \) to form the following products:

Correctness of \(\varDelta \) can be checked by the verification algorithm using the bilinear map. For \(i = 0, 1\), let the CRS be \( \sigma _i = (F_i, H_i, U_i, V_i, W_i), \) and let \(x_i, y_i\) be such that:

in which case \(\varDelta \) is constructed as in Eq. (4). The verifier checks that the following holds:
Let us denote by \(\mathsf {DH}\) the algorithm that, given as input \(\varSigma \) and \(\varDelta \) returns  if all equalities of Eq. (5) are satisfied, and
if all equalities of Eq. (5) are satisfied, and  otherwise. This procedure is used by the verification equation, as detailed in Fig. 5.
otherwise. This procedure is used by the verification equation, as detailed in Fig. 5.
We now proceed with the proof of our main result, Theorem 1, which we rephrase here for completeness:
Theorem 1
Assume that DLin and DH-KE hold for \(\mathsf {G}\). Then \(\mathsf {ZAK}\) as defined in Fig. 5 is a non-interactive zap that satisfies knowledge soundness and witness indistinguishability. In particular, we have

Completeness of the protocol is trivial: the prover (respectively, the verifier) simply performs 4 iterations of \(\mathsf {Circ}\) proofs (respectively, verifications), and therefore correctness is implied by Theorem 5 and the fact that \(\varDelta \) as in Eq. 4 satisfies Eq. 5. We now prove knowledge soundness and witness indistinguishability.
Proof
(of computational knowledge soundness). We show that for any adversary able to produce a valid proof we can construct a PPT extractor that can extract a witness from such a proof with overwhelming probability.
Let  be an adversarial prover in game
be an adversarial prover in game  (Fig. 2, with
(Fig. 2, with  void). On input
void). On input  ,
,  returns a proof consisting of \(\sigma _{i,0} = (F_i, H_i,U_i,V_i,W_i)\) for \(i \in \{0, 1\}\), of
returns a proof consisting of \(\sigma _{i,0} = (F_i, H_i,U_i,V_i,W_i)\) for \(i \in \{0, 1\}\), of  and
and  . From
. From  we construct four adversaries
we construct four adversaries  (for
(for  ) that execute
) that execute  and output some components of the proof produced by
and output some components of the proof produced by  , namely
, namely

where \(x_i, y_i\) are such that \(F_i = x_iG\), \(H_i = y_iG\), and these four equations hold if  returns
returns  . By the DH-KE assumption there exist extractors
. By the DH-KE assumption there exist extractors  for each of the adversaries
for each of the adversaries  that given its coins outputs:
that given its coins outputs:

if the above equations hold. The statement \((x_0 \vee x_1) \wedge (y_0 \vee x_1) \wedge (x_0 \vee y_1) \wedge (y_0 \vee y_1)\) is logically equivalent to \((x_0 \wedge y_0) \vee (x_1 \wedge y_1)\). This means that together, these four extractors allow to recover either \((x_0, y_0)\) or \((x_1, y_1)\), that is, the extraction trapdoor for one of the CRS’s. Let \(i^*\) be such that \((x_{i^*}, y_{i^*})\) is the extracted pair.
For  , let
, let  be such that \(\sigma _{i^*,j} = (F_{i^*}, H_{i^*}, U_{i^*}, V_{i^*}, W_{i^*} + jG)\). Let
be such that \(\sigma _{i^*,j} = (F_{i^*}, H_{i^*}, U_{i^*}, V_{i^*}, W_{i^*} + jG)\). Let  be the smallest integer satisfying:
be the smallest integer satisfying:
The above implies that \(\sigma _{i^*, j^*}\) is not a linear tuple, which means that it is a binding CRS. Let \(C_{(i^*, j^*), k}\) denote the commitment to the k-th wire contained in \(\pi _{i^*, j^*}\). Using the extraction algorithm described in Eq. (2) we can recover this witness:

It remains to prove that the extracted witness is indeed correct. Upon receiving a valid proof from adversary  , we know from the verification equation (the subroutine \(\mathsf {DH}\)) that each
, we know from the verification equation (the subroutine \(\mathsf {DH}\)) that each  will output a DH triple. Therefore, extractors
will output a DH triple. Therefore, extractors  together recover \(\tau _{i^*} = (x_{i^*}, y_{j^*})\) with probability at least
together recover \(\tau _{i^*} = (x_{i^*}, y_{j^*})\) with probability at least  , that is, by DH-KE, with overwhelming probability. Since the commitment scheme \(\mathsf {Com}\) is perfectly binding if the CRS is not a linear tuple (Theorem 4), a message \(w_k\) is always successfully extracted. Correctness of \(w_k\) follows from the underlying proof system: by perfect soundness of \(\mathsf {Bin}\) we are guaranteed that
, that is, by DH-KE, with overwhelming probability. Since the commitment scheme \(\mathsf {Com}\) is perfectly binding if the CRS is not a linear tuple (Theorem 4), a message \(w_k\) is always successfully extracted. Correctness of \(w_k\) follows from the underlying proof system: by perfect soundness of \(\mathsf {Bin}\) we are guaranteed that  ; by perfect soundness of \(\mathsf {Circ}\) (Theorem 5) that each gate evaluation is correct. The bound in the construction of the extractor is tight: we have
; by perfect soundness of \(\mathsf {Circ}\) (Theorem 5) that each gate evaluation is correct. The bound in the construction of the extractor is tight: we have  . \(\square \)
. \(\square \)
Overview of the simulations of the prove oracle in the first hybrid games for the proof of WI. Hybrids \(\mathsf {H_1}\) and \(\mathsf {H_4}\) are defined by ignoring all boxes (the  highlights the differences with respect to the previous hybrids), whereas
highlights the differences with respect to the previous hybrids), whereas  and
and  include the light boxes but not the gray one and
include the light boxes but not the gray one and  includes all boxes.
includes all boxes.
Proof
(of computational witness indistinguishability). Consider an adversary in the WI game (Fig. 1, where  is void) that makes
is void) that makes  queries to the \(\textsc {Prove}\) oracle, each of the form \((\texttt {C}^{(k)}, w_0^{_{(k)}}, w_1^{_{(k)}})\), for \(0 \le k < q\). Consider the following sequence of hybrid games where \(\mathsf {H_0}\) corresponds to
queries to the \(\textsc {Prove}\) oracle, each of the form \((\texttt {C}^{(k)}, w_0^{_{(k)}}, w_1^{_{(k)}})\), for \(0 \le k < q\). Consider the following sequence of hybrid games where \(\mathsf {H_0}\) corresponds to  with \(b=0\) and \(\mathsf {H_{12}}\) corresponds to
with \(b=0\) and \(\mathsf {H_{12}}\) corresponds to  with \(b=1\). The games differ in how the \(\textsc {Prove}\) oracle is implemented, which is specified in Fig. 6 for the first half of the hybrids (the second half is analogous). We give an overview of all hybrids in Table 2 below.
with \(b=1\). The games differ in how the \(\textsc {Prove}\) oracle is implemented, which is specified in Fig. 6 for the first half of the hybrids (the second half is analogous). We give an overview of all hybrids in Table 2 below.
- \(\mathsf {H_0}\) :
-
The challenger simulates an honest \(\textsc {Prove}\) oracle, using (for every \(k < q\)) the first witness \(w_0^{_{(k)}}\) supplied by the adversary. It outputs \((\varSigma ^{(k)}, \varDelta ^{(k)}, \varPi ^{(k)})\), where in particular we recall:
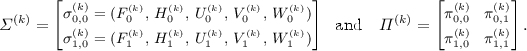
Recall that the two rows of \([\varSigma ^{(k)}|\varPi ^{(k)}]\) are independent zaps and that \(\sigma _{0,0}^{_{(k)}}\) and \(\sigma _{1,0}^{_{(k)}}\) are chosen to be hiding. The \(\textsc {Prove}\) oracle computes \(\sigma ^{_{(k)}}_{i,j}\) which is of the form \(\sigma ^{_{(k)}}_{i, j} = \big (F_i^{_{(k)}}, \,H_i^{_{(k)}}, \,U_i^{_{(k)}},\, V_i^{_{(k)}},\, \,W_i^{_{(k)}}\!+ jG\big )\), for
 . Furthermore, \(\pi _{i, j}^{_{(k)}}\) is a \(\mathsf {Circ}\) proof using \(w_0^{_{(k)}}\) under the CRS \(\sigma _{i, j}^{_{(k)}}\).
. Furthermore, \(\pi _{i, j}^{_{(k)}}\) is a \(\mathsf {Circ}\) proof using \(w_0^{_{(k)}}\) under the CRS \(\sigma _{i, j}^{_{(k)}}\). - \(\mathsf {H_1}\) :
-
For every \(\textsc {Prove}\) query, the simulator uses witness \(w_1^{_{(k)}}\) (instead of \(w_0^{_{(k)}}\)) to produce \(\pi _{0, 0}^{_{(k)}}\). As the respective CRS \(\sigma _{0, 0}^{_{(k)}}\) was generated using the perfectly hiding commitment setup
 , the two hybrids are distributed equivalently (any commitment under a hiding key is a random linear triple; cf. Eq. (1)).
, the two hybrids are distributed equivalently (any commitment under a hiding key is a random linear triple; cf. Eq. (1)). - \(\mathsf {H_2}\) :
-
For every \(\textsc {Prove}\) query, the simulator now generates CRS \(\sigma _{0, 0}^{_{(k)}}\) as a binding key via
 ; \(\sigma _{0, 1}^{_{(k)}}\) is generated as before (adding (0, 0, 0, 0, G)), and so are all proofs. Note that the linking elements \(\varDelta ^{(k)}\) can be constructed knowing only the trapdoor \( (x_1^{_{(k)}}, y_1^{_{(k)}})\) of the CRS \(\sigma _{1, 0}^{_{(k)}}\), which remained unchanged:
; \(\sigma _{0, 1}^{_{(k)}}\) is generated as before (adding (0, 0, 0, 0, G)), and so are all proofs. Note that the linking elements \(\varDelta ^{(k)}\) can be constructed knowing only the trapdoor \( (x_1^{_{(k)}}, y_1^{_{(k)}})\) of the CRS \(\sigma _{1, 0}^{_{(k)}}\), which remained unchanged: 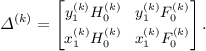 (for $\mathsf {A}_{0,0}$)
(for $\mathsf {A}_{0,0}$)\(\mathsf {H_1}\) and \(\mathsf {H_2}\) are computationally indistinguishable under the DLin assumption: given a DLin challenge (F, H, U, V, W), the reduction can exploit the random self-reducibility property of DLin to construct q instances of the DLin challenge: \(\forall k < q\) select
 and compute \(\sigma _{0, 0}^{_{(k)}}\) as \(\big ( \bar{x}^{(k)}F,\ \bar{y}^{(k)}H,\ \bar{r}^{(k)}\bar{x}^{(k)}F \!+\! \bar{z}^{(k)}\bar{x}^{(k)}U,\ \bar{s}^{(k)}\bar{y}^{(k)}H \!+\! \bar{z}^{(k)}\bar{y}^{(k)}V,\ (\bar{r}^{(k)} \!+\! \bar{s}^{(k)})G\!+\! \bar{z}^{(k)}W \big )\).
and compute \(\sigma _{0, 0}^{_{(k)}}\) as \(\big ( \bar{x}^{(k)}F,\ \bar{y}^{(k)}H,\ \bar{r}^{(k)}\bar{x}^{(k)}F \!+\! \bar{z}^{(k)}\bar{x}^{(k)}U,\ \bar{s}^{(k)}\bar{y}^{(k)}H \!+\! \bar{z}^{(k)}\bar{y}^{(k)}V,\ (\bar{r}^{(k)} \!+\! \bar{s}^{(k)})G\!+\! \bar{z}^{(k)}W \big )\).Each \(\sigma _{0, 0}^{_{(k)}}\) is a random linear tuple if and only if the DLin challenge is, and it is a uniformly random tuple if the DLin challenge is, as shown in [BFS16]. Computing \(\sigma _{1, 0}^{_{(k)}}\) as in \(\mathsf {H_1}\) (hiding) and defining \(\varDelta \) as in Eq. 6, the simulator generates the rest of the game as defined. It returns the adversary’s guess and thus breaks DLin whenever the adversary distinguishes \(\mathsf {H_1}\) and \(\mathsf {H_2}\).
- \(\mathsf {H_3}\) :
-
The simulator replaces each CRS \(\sigma _{0, 1}^{_{(k)}}\) for all \(k < q\) with a hiding commitment and defines
 , which is therefore (once again) binding. More specifically, the simulator creates a linear tuple invoking \(\mathsf {Circ}.\mathsf {K}\): $$\begin{aligned} \sigma _{0, 1}^{_{(k)}}= \big (x_0^{_{(k)}}G,\ y_0^{_{(k)}}G,\ x_0^{_{(k)}}r^{(k)}G,\ y_0^{_{(k)}}s^{(k)}G,\ (r^{(k)}+s^{(k)})G\big ) \end{aligned}$$
, which is therefore (once again) binding. More specifically, the simulator creates a linear tuple invoking \(\mathsf {Circ}.\mathsf {K}\): $$\begin{aligned} \sigma _{0, 1}^{_{(k)}}= \big (x_0^{_{(k)}}G,\ y_0^{_{(k)}}G,\ x_0^{_{(k)}}r^{(k)}G,\ y_0^{_{(k)}}s^{(k)}G,\ (r^{(k)}+s^{(k)})G\big ) \end{aligned}$$where
 .
.The two distributions are proven computationally indistinguishable under DLin by an argument analogous to the one for \(\mathsf {H_1}\) \(\rightarrow \) \(\mathsf {H_2}\). This time the challenger constructs all the instances of the DLin challenge for \(\sigma _{0, 1}^{_{(k)}}\), while \(\sigma _{0, 0}^{_{(k)}}\) is derived. From there, the proof proceeds identically.
- \(\mathsf {H_4}\) :
-
The simulator replaces each proof \(\pi _{0, 1}^{_{(k)}}\) by using \(w_1^{_{(k)}}\) instead of \(w_0^{_{(k)}}\) (\(\forall k < q\)). This hybrid is equivalently distributed as the previous one; this is proved via the same argument as for \(\mathsf {H_0}\) \(\rightarrow \) \(\mathsf {H_1}\).
- \(\mathsf {H_5}\) :
-
The simulator switches \(\sigma _{0, 1}^{_{(k)}}\) from a hiding to a binding key. This game hop is analogous to the hop \(\mathsf {H_1}\) \(\rightarrow \) \(\mathsf {H_2}\) (which switched \(\sigma _{0, 0}^{_{(k)}}\) from hiding to binding).
- \(\mathsf {H_6}\) :
-
The simulator switches \(\sigma _{0, 0}^{_{(k)}}\) from binding to hiding. Indistinguishability from the previous hybrid is shown analogously to the hop \(\mathsf {H_2}\) \(\rightarrow \) \(\mathsf {H_3}\). Note that in this hybrid the first zap \((\sigma _{0, 0}^{_{(k)}},\pi _{0,0}^{_{(k)}},\pi _{0,1}^{_{(k)}})\) is distributed according to the protocol specification, but using witness \(w_1^{_{(k)}}\).
Hybrids \(\mathsf {H_7}\) to \(\mathsf {H_{12}}\) are now defined analogously to hybrids \(\mathsf {H_1}\) to \(\mathsf {H_6}\), except for applying all changes to \(\sigma _{1}^{_{(k)}}\) and \(\pi _{1,0}^{_{(k)}}\) and \(\pi _{1,1}^{_{(k)}}\). In hybrid \(\mathsf {H_{12}}\) the adversary is then given arguments of knowledge for witness \(w_1\).
As the difference between hybrids \(\mathsf {H_1}\) and \(\mathsf {H_{12}}\) is bounded by 8 times the advantage of a DLin distinguisher, the adversary has total advantage

The bound is thus tight. \(\square \)
References
Boneh, D., Boyen, X., Shacham, H.: Short group signatures. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 41–55. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_3
Ben-Sasson, E., Chiesa, A., Garman, C., Green, M., Miers, I., Tromer, E., Virza, M.: Zerocash: decentralized anonymous payments from bitcoin. In: 2014 IEEE Symposium on Security and Privacy, pp. 459–474. IEEE Computer Society Press, May 2014
Brier, E., Coron, J.-S., Icart, T., Madore, D., Randriam, H., Tibouchi, M.: Efficient indifferentiable hashing into ordinary elliptic curves. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 237–254. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_13
Blum, M., Feldman, P., Micali, S.: Non-interactive zero-knowledge and its applications (extended abstract). In: 20th ACM STOC, pp. 103–112. ACM Press, May 1988
Bellare, M., Fuchsbauer, G., Scafuro, A.: NIZKs with an untrusted CRS: security in the face of parameter subversion. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 777–804. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_26
Bellare, M., Goldreich, O.: On defining proofs of knowledge. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 390–420. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-48071-4_28
Bellare, M., Hofheinz, D., Yilek, S.: Possibility and impossibility results for encryption and commitment secure under selective opening. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 1–35. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01001-9_1
Barak, B., Ong, S.J., Vadhan, S.: Derandomization in cryptography. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 299–315. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_18
Bitansky, N., Paneth, O.: ZAPs and non-interactive witness indistinguishability from indistinguishability obfuscation. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 401–427. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_16
Boyen, X., Waters, B.: Compact group signatures without random oracles. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 427–444. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_26
Boyen, X., Waters, B.: Full-domain subgroup hiding and constant-size group signatures. In: Okamoto, T., Wang, X. (eds.) PKC 2007. LNCS, vol. 4450, pp. 1–15. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-71677-8_1
Dwork, C., Naor, M.: Zaps and their applications. In: 41st FOCS, pp. 283–293. IEEE Computer Society Press, November 2000
Feige, U., Lapidot, D., Shamir, A.: Multiple non-interactive zero knowledge proofs based on a single random string (extended abstract). In: 31st FOCS, pp. 308–317. IEEE Computer Society Press, October 1990
Fuchsbauer, G., Orrú, M.: Non-interactive zaps of knowledge. Cryptology ePrint Archive, Report 2018/228 (2018)
Feige, U., Shamir, A.: Witness indistinguishable and witness hiding protocols. In: 22nd ACM STOC, pp. 416–426. ACM Press, May 1990
Fuchsbauer, G.: Subversion-zero-knowledge SNARKs. In: Abdalla, M., Dahab, R. (eds.) PKC 2018. LNCS, vol. 10769, pp. 315–347. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_11
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof systems. SIAM J. Comput. 18(1), 186–208 (1989)
Goldreich, O., Oren, Y.: Definitions and properties of zero-knowledge proof systems. J. Cryptol. 7(1), 1–32 (1994)
Groth, J., Ostrovsky, R., Sahai, A.: Non-interactive zaps and new techniques for NIZK. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 97–111. Springer, Heidelberg (2006). https://doi.org/10.1007/11818175_6
Groth, J., Ostrovsky, R., Sahai, A.: Perfect non-interactive zero knowledge for NP. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 339–358. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_21
Groth, J., Sahai, A.: Efficient non-interactive proof systems for bilinear groups. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 415–432. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_24
Goldreich, O.: A uniform-complexity treatment of encryption and zero-knowledge. J. Cryptol. 6(1), 21–53 (1993)
Groth, J.: Simulation-sound NIZK proofs for a practical language and constant size group signatures. In: Lai, X., Chen, K. (eds.) ASIACRYPT 2006. LNCS, vol. 4284, pp. 444–459. Springer, Heidelberg (2006). https://doi.org/10.1007/11935230_29
Groth, J.: Short pairing-based non-interactive zero-knowledge arguments. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 321–340. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_19
Kol, G., Naor, M.: Cryptography and game theory: designing protocols for exchanging information. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 320–339. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_18
Peikert, C., Vaikuntanathan, V., Waters, B.: A framework for efficient and composable oblivious transfer. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 554–571. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_31
Ràfols, C.: Stretching groth-sahai: NIZK proofs of partial satisfiability. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 247–276. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_10
Acknowledgements
The authors would like to thank the anonymous reviewers of PKC 2018 and ACNS 2018 for their helpful comments. The first author is supported by the French ANR EfTrEC project (ANR-16-CE39-0002). The second author is supported by ERC grant 639554 (project aSCEND).
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Fuchsbauer, G., Orrù, M. (2018). Non-interactive Zaps of Knowledge. In: Preneel, B., Vercauteren, F. (eds) Applied Cryptography and Network Security. ACNS 2018. Lecture Notes in Computer Science(), vol 10892. Springer, Cham. https://doi.org/10.1007/978-3-319-93387-0_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-93387-0_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-93386-3
Online ISBN: 978-3-319-93387-0
eBook Packages: Computer ScienceComputer Science (R0)





 , the key generation algorithm, outputs a CRS
, the key generation algorithm, outputs a CRS  , the commitment algorithm, outputs a commitment C to the given value v together with the opening information r.
, the commitment algorithm, outputs a commitment C to the given value v together with the opening information r. , the opening algorithm, outputs
, the opening algorithm, outputs 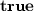 if C is a commitment to v witnessed by r, and
if C is a commitment to v witnessed by r, and  otherwise.
otherwise. , the CRS generation algorithm that outputs a CRS
, the CRS generation algorithm that outputs a CRS  , a prover which takes as input some
, a prover which takes as input some 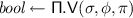 a verifier that, given as input a statement
a verifier that, given as input a statement  or
or 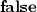 , indicating acceptance of the proof.
, indicating acceptance of the proof.


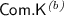 ;
; .
.


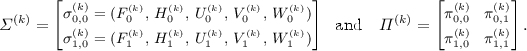
 . Furthermore,
. Furthermore,  , the two hybrids are distributed equivalently (any commitment under a hiding key is a random linear triple; cf. Eq. (
, the two hybrids are distributed equivalently (any commitment under a hiding key is a random linear triple; cf. Eq. ( ;
; 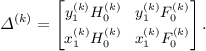
 and compute
and compute  , which is therefore (once again) binding. More specifically, the simulator creates a linear tuple invoking
, which is therefore (once again) binding. More specifically, the simulator creates a linear tuple invoking  .
.