Kinematic Constraint Maps and C-space Singularities for Planar Mechanisms with Prismatic Joints

Abstract

Singularities of the configuration space for planar parallel mechanisms involving prismatic joint are investigated using a kinematic constraint map approach. Eliminating pose parameters from the singularity conditions together with the constraint equations leads to Grashof-type conditions. We illustrate the method by the planar RRRP and 3-RPR parallel mechanisms. In the latter case, conditions for higher order singularities are also determined.

1 Introduction

A mechanism singularity physically corresponds to a configuration where an instantaneous change occurs in its degrees of freedom (dofs). Mathematically, this is determined by a drop in rank of the Jacobian matrix of some kinematic mapping. Among the various types of kinematic singularities, those of the configuration or C-space are the most basic since at such a singularity there is no regular parametrisation that can be used to define inverse or forward kinematic singularities. One goal of this paper is to extend an approach introduced in [1] which is, in principle, unified across all types of manipulators and that takes into account the impact on singularities of design parameters in a given family of mechanisms.

The approach to singularities of parallel mechanisms due to Gosselin and Angeles [7] was based on combining input and output variables in an implicit (constraint) function. Zlatanov et al. [13] observed that it may not be possible to capture the full kinematics with just these limited variables—in particular, passive joints may play a role, giving rise to a greater variety of singularity classes and providing an explanation for unexpected motion observed in some mechanisms such as the 3UPU wrist [2]. However, this approach was purely local and did not provide global singularity information for a given mechanism. Park and Kim [9, 10] developed an approach based on differential geometry that enabled the identification of configuration space singularities, as well as actuator and end-effector singularities.

In [1], the authors introduced an approach based solely on joint constraints to define the C-space. This approach was illustrated by planar parallel mechanisms whose joints are revolute kinematic pairs. The goal was to provide a robust framework for kinematic singularities that takes into account the effect of design parameters. In particular, we derived Grashof-type conditions that define those choices of design parameters for which the C-space has a singularity.

In this paper, we extend the approach to include planar mechanisms with prismatic joints. We review the notion of kinematic constraint map (KCM) as the tool for defining the C-space. We then analyse two examples, the RRRP close 4-bar and the 3-RPR planar parallel mechanism and determine the associated Grashof-type conditions for C-space singularity in terms of design parameters. We also determine the additional conditions that result in a corank 2 singularity for the KCM of the 3-RPR.

2 Kinematic Constraints

With respect to a fixed reference frame R giving ambient space coordinates and a frame M in a rigid body moving in the plane, three pose parameters $(\theta , x, y)^T \in \mathbb {R}^3$ are necessary and sufficient to express the position and orientation of the M with respect to R. They represent an element of the Euclidean group $(A,\mathbf {a})\in SE(2)$ (called the absolute displacement [11]), where A is a $2 \times 2$ matrix representing rotation by $\theta$ and $\mathbf {a}=(x,y)^T$ is the translation vector. Note that $\theta$ is unique only up to addition of multiples of $2\pi$. The absolute displacement transforms coordinates $\mathbf {q}$ in M into reference frame coordinates $\mathbf {Q}$ by:

$$\begin{aligned} \mathbf {Q} = A \mathbf {q} + \mathbf {a}. \end{aligned}$$

(1)

In a mechanism, suppose that two links $L_\pm$ are connected to each other by a joint, thereby constraining their relative motion. The two types of 1-dof joint in the plane are revolute (R) and prismatic (P). An R-joint permits rotation about a common fixed point while a P-joint permits translation along a common line. We express the corresponding constraints by equations on the pose parameters or, equivalently, the absolute displacements $(A_\pm ,\mathbf {a}_\pm )$ of the joined links $L_\pm$.

The constraints imposed by an R-joint are given in [1]. This amounts to requiring the pose parameters for the two links to return the same coordinates when mapped to the reference frame. We follow [8] to obtain the constraint equations of a P-joint. The geometric object representing the joint is a line $\ell _\pm$ in each link given parametrically in the moving frames $M_\pm$ by, respectively:

$$\begin{aligned} \ell _\pm := \mathbf p _\pm + \tau _\pm \mathbf r _\pm , \end{aligned}$$

(2)

where $\mathbf p _\pm$ is a point on the line and $\mathbf r _\pm$ is its direction.

The constraints imposed by the P-joint are that in the reference frame, the direction vectors $\mathbf {r}_\pm$ of the lines must be parallel and also parallel to the vector connecting the points $\mathbf {p}_\pm$. In the reference frame, Eq. 1 the lines transform to:

$$\begin{aligned} \varLambda _\pm := (A_\pm , \mathbf {a}_\pm ) (\mathbf {p}_\pm + \tau _\pm \mathbf {r}_\pm ) = \mathbf {P}_\pm + \tau _\pm (A_\pm \mathbf {r}_\pm ), \end{aligned}$$

(3)

where $\mathbf {P}_\pm =A_\pm \mathbf {p}_\pm +\mathbf {a}_\pm$. Hence, we require:

$$\begin{aligned} (A_+ \mathbf r _+ \times A_- \mathbf r _-)_z = 0,\qquad ([\mathbf P _+ - \mathbf P _-] \times A_- \mathbf r _-)_z = 0 \end{aligned}$$

(4)

Here, $\times$ denotes 3-dimensional cross product and we treat 2-vectors as 3-vectors by appending a third coordinate $z=0$, and the subscript z is a reminder that each equation is essentially scalar, the other components of the cross product being zero.

Fig. 1.

A prismatic joint

It will simplify the constraint equations if we assign moving frames to the links as shown in Fig. 1 (cf. Denavit–Hartenberg parameters). Given that the frame $M_-$ is already assigned, for $M_+$, choose the origin of coordinates on the line and set this to be $\mathbf {p}_+$; the $x_+$ axis lies along the line so that $\mathbf {r}_+=(1,0)^T$. Where necessary, choose the origin in $M_+$ so that the origin in a subsequent frame lies on the $y_+$ axis. The associated design parameter is the perpendicular distance $d_-$ of the line from the origin in $M_-$.

Note that for a parallel mechanism, where a link is connected to more than one other, the choice of moving frame can only be made with respect to one of the joints and there will be additional design parameters relating to the second or subsequent joints.

3 Configuration Space and Singularities

A given mechanism consists of k rigid links connected by t kinematic pairs. Its kinematic constraint map (KCM) is the function F, whose components $F_j$ are the constraint equations expressed in the form $F_j=0$:

$$\begin{aligned} F: \mathcal {M} \times \mathcal {D} \longrightarrow \mathbb {R}^c \end{aligned}$$

(5)

where $\mathcal {M} = [SE(2)]^{k-1}$ is its pose space (here we have assumed the reference frame is attached to a base link which is therefore immobile), $\mathcal {D} \subseteq \mathbb {R}^d$ its design space and $\mathbb {R}^c$ the constraint space. Here, d and c are the total number of design parameters and constraint equations, respectively, and if every joint has 1-dof, then $c=2t$. Locally, $\mathcal {M}$ can be parametrised by $p = 3(k-1)$ pose parameters. We will assume that $c<p$, though in principle this is not required and the mechanism may be over-constrained.

For a fixed choice of design parameters $\delta \in \mathcal {D}$, the KCM is:

$$\begin{aligned} F_\delta : \mathcal {M} \longrightarrow \mathbb {R}^c \end{aligned}$$

(6)

Denote by $\mathcal {C}_\delta := F_\delta ^{-1}(\mathbf {0}_c) \subset \mathcal {M}$ the configuration space (C-space) of the specific mechanism determined by $\delta$.

There is no need to include ‘loop’ constraints since these are algebraically a consequence of the joint constraint equations. From the form of the constraint equations, $\mathcal {C}_\delta$ is an analytic variety. If $\mathbf {0}_c$ is a regular value of $F_\delta$, so that at every point of $\mathcal {C}_\delta$ the derivative of $F_\delta$ has maximum rank, then $\mathcal {C}_\delta$ is a smooth manifold (no singularities).

Our aim is to determine conditions on the pose and design parameters under which the C-space is, in fact, singular. Specifically, we first determine where the $c \times p$ Jacobian matrix $JF_\delta = \left[ \partial f_j/\partial u_{i}\right]$ of first-order partial derivatives of the KCM in Eq. 6 with respect to pose parametrisations has rank $<c$. Here $i = 1,\dots ,p$ indexes the pose parameters $u_i$, and $j=1,\dots ,c$ indexes the joint constraint equations. At a regular point $\mathbf {u}_r \in \mathcal {M}$, the Jacobian has full rank—its cokernel (the quotient of the range by the image) is trivial or dimension zero. At a singular point $\mathbf {u}_s \in \mathcal {M}$, this dimension will be a positive quantity $\kappa$, the corank or rank deficiency. $\kappa$ provides a useful measure of how bad a singularity is and we can partition the singularity set:

$$\begin{aligned} \varSigma F_\delta = \{ \mathbf u _s \in \mathcal {M} \mid \text {corank} \,JF_\delta >0 \} \end{aligned}$$

(7)

into subsets $\varSigma ^\kappa F_\delta$ corresponding to corank $\kappa = 1,\dots ,\mu = p - c$, the theoretical global mobility.

We are only interested in those singular points $\mathbf {u}_s$ that lie in the C-space. The second step is to solve the singularity conditions simultaneously with the constraint equations and to eliminate pose parameters to give a condition, solely involving design parameters, under which the C-space is singular. We call these Grashof-type conditions, following the terminology of Gibson et al. [3,4,5].

4 Planar RRRP Linkage

The first example is the closed loop linkage consisting of $k=4$ rigid links connected by three R- and one P-joint, so that $t=4$ also. Assume one of the links connected by the P-joint to be fixed and label this link 0. The reference frame R and the moving frames $M_i, i = 1,2,3$ are shown in Fig. 2. The free motion of each remaining link is represented by pose parameters $(\theta _i,x_i,y_i)^T; i = 1,2,3$. Design parameters are lengths $l_1,l_2$ of the first and second links and the perpendicular distances $d_0,d_3$ in the other two.

Fig. 2.

RRRP linkage and C-space singularity configuration

Symbolically, the three R-joints give rise to (vector) constraint equations of the form:

$$\begin{aligned} A_i \mathbf p _i^i + \mathbf a _i = A_{i+1} \mathbf p _i^{i+1} + \mathbf a _{i+1} \end{aligned}$$

(8)

where $i=0,1,2$ and the joints are numbered in sequence with the links. The $\mathbf p _i^j$ denotes the coordinates of joint i with respect to frame $M_j$. The prismatic joint gives rise to two equations of the form Eq. 4.

In terms of the given choice of coordinates, the eight constraint equations give rise to the KCM $F : SE(2)^3 \times \mathcal {D} \mapsto \mathbb {R}^8$ where $\mathcal {D} \subseteq \mathbb {R}^4$ of the form:

$$\begin{aligned} (\theta _i, x_j, y_j)_{i = 1,3} \longmapsto&\left[ -x_1, d_0 - y_1, l_1 c_1 + x_1 - x_2, l_1 s_1 + y_1 - y_2,\right. \nonumber \\&\left. \quad l_2 c_2 + x_2 - x_3, l_2 s_2 + y_2 - y_3, -s_3, d_3 + s_3 x_3 - c_3 y_3 \right] ^T \end{aligned}$$

(9)

where $c_i = \cos \theta _i$ and $s_i = \sin \theta _i, i = 1,2,3$. The positive corank condition on the resulting $8 \times 9$ Jacobian matrix can be reduced, by using row operations and deleting rows and columns consisting leading 1s, to considering the following $4 \times 5$ matrix:

$$\begin{aligned} JF_\delta ^{\text {red}} = \left[ \begin{array}{ccccc} -1 &{} 0 &{} - l_1 s_1 &{} -l_2 s_2 &{} 0 \\ 0 &{} -1 &{} l_1 c_1 &{} l_2 c_2 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -c_3 \\ s_3 &{} -c_3 &{} 0 &{} 0 &{} c_3 x_3 + s_3 y_3 \\ \end{array} \right] \end{aligned}$$

(10)

The singular set $\varSigma F_\delta$ is defined by the five $4 \times 4$ minors vanishing simultaneously and the equations yield:

$$\begin{aligned} \theta _1 = \theta _2 + n_1 \pi , \theta _2 = \theta _3 + \frac{\pi }{2} + n_2 \pi , \qquad n_1,n_2 \in \mathbb {Z} \end{aligned}$$

(11)

Geometrically, the three R-joints must be collinear and perpendicular to the direction of the P-joint i.e. the first two links must be perpendicular to the translational axis of the prismatic joint.

Substituting Eq. 11 into Eq. 9 and eliminating $x_i, y_i, i=1,2,3$, we obtain the Grashof-type condition:

$$\begin{aligned} d_0 \pm l_1 \pm l_2 \pm d_3 = 0 \end{aligned}$$

(12)

The corresponding C-space singularity is illustrated in Fig. 2. This is the simplest case of the conditions found by Xue et al. [12] determining rotatability of components of closed chains with prismatic joints.

5 3-RPR Planar Parallel Manipulator

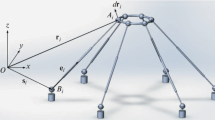
A fully general 3-RPR planar PM is shown in Fig. 3, along with a choice of moving and reference frames and design parameters. There are $k = 7$ (mobile) links hence 21 pose parameters, $t=9$ joints and 12 design parameters, namely $d_i, i = 1,\ldots ,6$, base parameters $b_1,b_2,\beta$, and the platform parameters $a_1,a_2,\alpha$. We make the non-triviality assumptions that $a_i,b_i>0$, $i=1,2$. The local coordinates of all joints in the relevant moving frames are:

$$\begin{aligned} \begin{array}{llllr} \mathbf p _1^R = (0, 0)^T, &{} \mathbf p _2^R = (b_1, 0)^T, &{} \mathbf p _3^R = (b_{2x}, b_{2y})^T, &{} \mathbf p _i^- = (0, d_{i-3})^T; &{}i = 7,8,9 \\ \mathbf p _7^7 = (0, 0)^T, &{} \mathbf p _8^7 = (a_1, 0)^T, &{} \mathbf p _9^7 = (a_{2x}, a_{2y})^T, &{} \mathbf p _i^+ = (0, 0)^T; &{}i = 1,2,3 \\ \mathbf v _i^- = (0, d_{i-3})^T, &{} \mathbf w _i^+ = (0, 0)^T, &{} \underline{\mathbf{r }}_i^- = \underline{\mathbf{r }}_i^+ = (1, 0)^T; &{}&{} i = 4,5,6 \end{array} \end{aligned}$$

(13)

Fig. 3.

A 3RPR parallel planar manipulator

Each joint imposes a pair of constraint equations giving rise to a KCM of the form of $F: SE(2)^7 \times \mathcal {D} \mapsto \mathbb {R}^{18}$ where $\mathcal {D} \subset \mathbb {R}^{12}$:

$$\begin{aligned} (\theta _i, x_i, y_i&)_{i= 1,\ldots ,7} \mapsto \left[ - x_1, - y_1, b_1 - x_2, - y_2, - x_3 + b_2 c_\beta , - y_3 + b_2 s_\beta , x_4 - x_7 - d_4 s_4,\right. \nonumber \\&\left. y_4 - y_7 + d_4 c_4, x_5 - x_7 - a_1 c_7 - d_5 s_5, y_5 - y_7 + d_5 c_5 - a_1 s_7,\right. \nonumber \\&\left. x_6 - x_7 - a_2 c_{\alpha ,7} - d_6 s_6, y_6 - y_7 + d_6 c_6 - a_2 s_{\alpha ,7}, s_{1,4}, s_{2,5}, s_{3,6},\right. \nonumber \\&\left. d_1 + y_{1,4} c_1 - x_{1,4} s_1, d_2 + y_{2,5} c_2 - x_{2,5} s_2, d_3 + y_{3,6} c_3 - x_{3,6} s_3 \right] ^T \end{aligned}$$

(14)

where $s_{i,i+3} = \sin (\theta _i - \theta _{i+3})$, $x_{i,i+3} = x_i - x_{i+3}$, $y_{i,i+3} = y_i - y_{i+3}; i = 1,2,3$, $c_{\alpha ,7} = \cos (\alpha + \theta _7)$, and $s_{\alpha ,7} = \sin (\alpha + \theta _7)$.

The associated Jacobian is a $18 \times 21$ matrix. Rather than solving first for rank deficiency, we can eliminate pose parameters from via the KCM; clearly from $s_{i,i+3}=0$, $\theta _i = \theta _i+3\mod \pi$ for $i = 1,2,3$. From this, for the purposes of rank computation the Jacobian can be reduced to the $3 \times 6$ matrix, $JF_\delta ^{\text {red}}$:

$$\begin{aligned} \left[ \begin{array}{cccccc} x_{1,4} c_1 + y_{1,4} s_1 &{} 0 &{} 0 &{} -s_1 &{} \quad c_1 &{} 0 \\ 0 &{} x_{2,5} c_2 + y_{2,5} s_2 &{} 0 &{} -s_2 &{} \quad c_2 &{} a_1 c_{2,7} \\ 0 &{} 0 &{} x_{3,6} c_3 + y_{3,6} s_3 &{} -s_3 &{} \quad c_3 &{} a_2 c_{3,7,\alpha } \end{array} \right] \end{aligned}$$

(15)

where $c_{2,7} = \cos (\theta _2 - \theta _7)$ and $c_{3,7,\alpha }=\cos (\theta _3-\theta _7-\alpha )$.

5.1 Corank 1 Singularities

The conditions for a singularity are the vanishing of 20 $3 \times 3$ minors of Eq. 15. Assuming F is well behaved, dimensional considerations (see, for example [6]) indicate that the corank 1 singular set ought to have (at least) codimension 4, so that four conditions on pose parameters are needed. There are three cases that can readily be seen to result in singularity. Clearly one of the non-trivial terms in the first three columns must vanish. When two of these terms vanish, finding two further conditions is straightforward. For example, if the first two terms vanish then the condition for singularity is realised by:

$$\begin{aligned} x_{1,4} c_1 + y_{1,4} s_1 = x_{2,5} c_2 + y_{2,5} s_2 = 0,\quad s_{1,2} = 0, \quad c_{2,7} = 0. \end{aligned}$$

(16)

Further elimination of pose parameters from Eq. 16 results in the following Grashof-type condition on design parameters:

$$\begin{aligned} d_1 \pm d_4 \pm b_1 \pm d_2 \pm d_5 \pm a_1 = 0. \end{aligned}$$

(17)

Geometrically, this relates to the lower closed 2-RPR loop comprised of the base, two legs and platform. It requires the two platform and two base anchor points to be collinear while the direction of the prismatic joints must be perpendicular to these. Similar configurations for the other two loops also correspond to singular configurations. This is illustrated in Fig. 4.

Fig. 4.

A corank 1 C-space singularity configuration for 3-RPR

5.2 Corank 2 Singularities

As for the planar 3RRR [1], there are other components of the singular set with higher codimension but we do not give an exhaustive treatment here. Rather, we examine the conditions for the KCM to have a corank 2 singularity in the C-space. At such a point, the cokernel of the Jacobian has dimension 2. This can only happen for very special geometries of the 3-RPR and is a high codimension condition. Necessary and sufficient conditions is that all $2\times 2$ minors of Eq. 15 vanish but at least one entry is non-zero. There are 45 such minors leading to 7 conditions as follows:

$$\begin{aligned}&x_{1,4} c_1 + y_{1,4} s_1 = x_{2,5} c_2 + y_{2,5} s_2 = x_{3,6} c_3 + y_{3,6} s_3 = 0; \nonumber \\&\theta _1=\theta _2=\theta _3\mod \,\pi ; \quad c_{2,7} = c_{3,7,\alpha }= 0. \end{aligned}$$

(18)

This is simply the union of the three closed-loop conditions giving corank 1 singularities. Therefore the three Grashof-type conditions Eq. 17 must hold simultaneously and these entail $\alpha =\beta =0\mod \pi$. These 5 equations correspond to four independent conditions.