Abstract
Transactional memory (TM) guarantees that a sequence of operations encapsulated into a transaction is atomic. This simple yet powerful paradigm is a promising direction for writing concurrent applications. Recent TM designs employ a time-based mechanism to leverage the performance advantage of invisible reads. With the advent of many-core architectures and non-uniform memory (NUMA) architectures, this technique is however hitting the synchronization wall of the cache coherency protocol. To address this limitation, we propose a novel and flexible approach based on a new consistency criteria named stricter serializability (\({\text {SSER}^+}\)). Workloads executed under \({\text {SSER}^+}\) are opaque when the object graph forms a tree and transactions traverse it top-down. We present a matching algorithm that supports invisible reads, lazy snapshots, and that can trade synchronization for more parallelism. Several empirical results against a well-established TM design demonstrate the benefits of our solution.
This research is partly supported by the Rainbow FS project of Agence Nationale de la Recherche, France, number ANR-16-CE25-0013-01a.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The advent of chip level multiprocessing in commodity hardware has pushed applications to be more and more parallel in order to leverage the increase of computational power. However, the art of concurrent programming is known to be a difficult task [27], and programmers always look for new paradigms to simplify it. Transactional Memory (TM) is widely considered as a promising step in this direction, in particular thanks to its simplicity and programmer’s friendliness [11].
The engine that orchestrates concurrent transactions run by the application, i.e., the concurrency manager, is one of the core aspects of a TM implementation. A large number of concurrency manager implementations exists, ranging from pessimistic lock-based implementations [1, 21] to completely optimistic ones [22], with [29] or without multi-version support [2]. For application workloads that exhibit a high degree of parallelism, these designs tend to favor optimistic concurrency control. In particular, a widely accepted approach consists in executing tentatively invisible read operations and validating them on the course of the transaction execution to enforce consistency. For performance reasons, another important property is disjoint-access parallelism (DAP) [12]. This property ensures that concurrent transactions operating on disjoint part of the application do not contend in the concurrency manager. Thus, it is key to ensures that the system scales with the numbers of cores.
From a developer’s point of view, the interleaving of transactions must satisfy some form of correctness. Strict serializability (\(\text {SSER}\)) [24] is a consistency criteria commonly encountered in database literature. This criteria ensures that committed transactions behave as if they were executed sequentially, in an order compatible with real-time. However, \(\text {SSER}\) does not specify the conditions for aborted transactions. To illustrate this point, let us consider history \(h_1\) where transaction  and
and  are executed respectively by processes p and q. In this history, \(T_1\) aborts after reading inconsistent values for x and y. Yet, \(h_1\) is compliant with \(\text {SSER}\).
are executed respectively by processes p and q. In this history, \(T_1\) aborts after reading inconsistent values for x and y. Yet, \(h_1\) is compliant with \(\text {SSER}\).

Opacity (OPA) was introduced [17] to avoid the eratic behavior of so-called doomed transactions, i.e., transactions which eventually abort (such as \(T_1\) in history \(h_1\)).Footnote 1 In addition to \(\text {SSER}\), OPA requires that aborted transactions observe a prefix of the committed transactions. This is the usual consistency criteria for TM.
Achieving OPA is known to be expensive, even for weak progress properties on the transactions [30]. In particular, ensuring that a transaction always sees a consistent snapshot when reads are invisible generally asks to re-validate the read set after each read operation, or to rely on a global clock. The former approach increases the time complexity of execution. The latter is expensive in multi-core/multi-processors architecture, due to the synchronization wall.
In this paper, we address these shortcomings with a new consistency criteria, named stricter serializability (\(\text {SSER}^+\)). This criteria extends strict serializability by avoiding specifically the inconsistency illustrated in history \(h_1\). We describe in detail a corresponding TM algorithm that ensures invisible reads, and permits transactions to commit as long as they do not contend with conflicting transactions. We further validate our design by means of a full implementation of \(\text {SSER}^+\) and several experiments. Our results show that when the workloads are embarrassingly parallel, \(\text {SSER}^+\) offers close-to-optimum performance.
Outline. This paper is organized as follows. Section 2 introduces our system model assumptions and defines precisely \(\text {SSER}^+\). The corresponding transactional memory algorithm and a formal proof of correctness are presented in Sect. 3. We present the evaluation of our prototype against several benchmarks in Sect. 4. We survey related work in Sect. 5, before concluding in Sect. 6.
2 A New Consistency Criteria
This section is organized in two parts. The first part (Sect. 2.1) present the elements of our system model as well as the notions of contention and binding (Sect. 2.2). In the second part (Sects. 2.3 and 2.4), we formulate our notion of stricter serializability and study its applicability.
2.1 System Model
Transactional memory (TM) is a recent paradigm that allows multiple processes to access concurrently a shared memory region. Each process manipulates objects in the shared memory with the help of transactions. When a process starts a new transaction, it calls operation begin. Then, the process executes a sequence of \( read \) and \( write \) operations on the shared objects according to some internal logic. Operation \( read (x)\) takes as input an object x and returns either a value in the domain of x or a flag \({\textsc {abort}}\) to indicate that the transition aborts. A write \( write (x,v)\) changes x to the value v in the domain of x. This operation does not return any value and it may also abort. At the end of the transaction execution, the process calls \( tryCommit \) to terminate the transaction. This calls returns either \({\textsc {commit}}\), to indicate that the transaction commits, or \({\textsc {abort}}\) if the transaction fails.
A history is a sequence of invocations and responses of TM operations by one or more processes. As illustrated with history \(h_2\) below, a history is commonly depicted as parallel timelines, where each timeline represents the transactions executed by a process. In history \(h_2\), process p, q and r execute respectively transactions  ,
,  then
then  , and
, and  . All the transactions but \(T_4\) complete in this history. For simplicity, a complete transaction that is not explicitly aborted in history commits immediately after its last operation. We note \( com (h)\) the set of transactions that commit during history h. In the case of history \(h_2\), we have \( com (h_2)=\{T_1,T_2,T_3\}\).
. All the transactions but \(T_4\) complete in this history. For simplicity, a complete transaction that is not explicitly aborted in history commits immediately after its last operation. We note \( com (h)\) the set of transactions that commit during history h. In the case of history \(h_2\), we have \( com (h_2)=\{T_1,T_2,T_3\}\).

A history induces a real-time order between transactions (denoted  ). The order
). The order  holds when \(T_i\) terminates in h before \(T_j\) begins. For instance in history \(h_2\), transaction \(T_1\) precedes transaction \(T_3\). When two transactions are not related with real-time, they are concurrent.
holds when \(T_i\) terminates in h before \(T_j\) begins. For instance in history \(h_2\), transaction \(T_1\) precedes transaction \(T_3\). When two transactions are not related with real-time, they are concurrent.
A version is the state of a shared object as produced by the write of a transaction. This means that when a transaction \(T_i\) writes to some object x, an operation denoted \(w_i(x_i)\), it creates the version \(x_i\) of x. Versions allow to uniquely identify the state of an object as observed by a read operation, e.g., \(r_3(x_1)\) in \(h_2\). When a transaction \(T_i\) reads version \(x_j\), we say that \(T_i\) read-from transaction \(T_j\).
Given some history h and some object x, a version order on x for h is a total order over the versions of x in h. By extension, a version order for h is the union of all the version orders for all the objects (denoted \(\ll _h\)). For instance, in history \(h_2\) above, we may consider the version order \((x_2 \ll _{h_2} x_1)\).
Consider an history h and some version order \(\ll _h\). A transaction \(T_i\) depends on some transaction \(T_j\), written  when \(T_j\) precedes \(T_i\), \(T_i\) reads-from \(T_j\), or such a relation holds transitively. Transaction \(T_i\) anti-depends from \(T_j\) on object x, when \(T_i\) reads some version \(x_k\), \(T_j\) writes version \(x_j\), and \(x_k\) precedes \(x_j\) in the version order (\(x_k \ll _{h} x_j\)). An anti-dependency between \(T_i\) and \(T_j\) on object x is a reverse-commit anti-dependency (for short, RC-anti-dependency) [20] when \(T_j\) commits before \(T_i\), and \(T_i\) writes some object \(y \ne x\).Footnote 2
when \(T_j\) precedes \(T_i\), \(T_i\) reads-from \(T_j\), or such a relation holds transitively. Transaction \(T_i\) anti-depends from \(T_j\) on object x, when \(T_i\) reads some version \(x_k\), \(T_j\) writes version \(x_j\), and \(x_k\) precedes \(x_j\) in the version order (\(x_k \ll _{h} x_j\)). An anti-dependency between \(T_i\) and \(T_j\) on object x is a reverse-commit anti-dependency (for short, RC-anti-dependency) [20] when \(T_j\) commits before \(T_i\), and \(T_i\) writes some object \(y \ne x\).Footnote 2
To illustrate the above definitions, consider again history \(h_2\). In this history, transaction \(T_3\) depends on \(T_1\) and \(T_2\). On the other hand, if \(x_2 \ll _h x_1\) holds and \(T_4\) reads \(x_2\), then this transaction exhibits an anti-dependency with \(T_1\). This anti-dependency becomes an RC-anti-dependency if \(T_4\) executes an additional step during which it writes some object \(z \ne x\).
Over the course of its execution, a transaction reads and writes versions of the shared objects. The set of versions read by the transaction forms its read set (or snapshot). The versions written define the write set.
A transaction observes a strictly consistent snapshot [5] when it never misses the effects of some transaction it depends on. In detail, the snapshot of transaction \(T_i\) in history h is strictly consistent when, for every version \(x_j\) read by \(T_i\), if \(T_k\) writes version \(x_k\), and \(T_i\) depends on \(T_{k}\), then \(x_k\) is followed by \(x_j\) in the version order.
2.2 Contention and Bindings
Internally, a transactional memory is built upon a set of base objects, such as locks or registers. When two transactions are concurrent, their steps on these base objects interleave. If the two transactions access disjoint objects and the TM is disjoint-access parallel, no contention occurs. However, in the case they access the same base object, they may slow down each other.
A transactional read is invisible when it does not change the state of the base objects implementing it. With invisible reads, read contention is basically free. From a performance point of view, this property is consequently appealing, since workloads exhibit in most case a large ratio of read operations.
When two transactions are concurrently writing to some object, it is possible to detect the contention and abort preemptively one of them. On the other hand, when a read-write conflict occurs, a race condition occurs between the reader and the writer. If the read operation takes place after the write, the reader is bound to use the version produced by the writer.
Definition 1 (Binding)
During a history h, when a transaction \(T_i\) reads some version \(x_j\) and \(T_i\) is concurrent to \(T_j\), we say that \(T_i\) is bound to \(T_j\) on x.
When a transaction \(T_i\) is bound to another transaction \(T_j\), to preserve the consistency of its snapshot, \(T_i\) must read the updates and causal dependencies of \(T_j\) that are intersecting with its read set. This is for instance the case of transaction \(T_4\) in history \(h_2\), where this transaction is bound to \(T_3\) on y. As a consequence, \(T_4\) must return \(x_1\) as the result of its read on x, or its snapshot will be inconsistent.
Tracking this causality relation is difficult for the contention manager as it requires to inspect the read set, rely on a global clock, or use large amount of metadata. We observe that this tracking is easier if each version read prior the binding is either, accessed by the writer, or one of its dependencies. In which case, we will say that the binding is fair.
Definition 2 (Fair binding)
Consider that in some history h a transaction \(T_i\) is bound to a transaction \(T_j\) on some object x. This binding is fair when, for every version \(y_k\) read by \(T_i\) before \(x_j\) in h,  holds.
holds.
Going back to history \(h_3\), the binding of \(T_4\) to \(T_3\) on y is fair. Indeed, this transaction did not read any data item before accessing the version of y written by \(T_3\). When the binding is fair, the reader can leverage the metadata left by the writer to check prior versions it has read and ensure the consistency of later read operations. In the next section, we formalize this idea with the notion of stricter serializability.
2.3 Stricter Serializability
In what follows, we introduce and describe in detail \(\text {SSER}^+\), the stricter serializability consistency criteria that we build upon in the remainder of this paper. As strict serializability, \(\text {SSER}^+\) requires that committed transactions form a sequential history which preserves the real-time order. In addition, it prohibits transactions to view inconsistencies unless one of their bindings is unfair.
Definition 3 (Strict serialization graph)
Consider some version order \(\ll _h\) for h. Below, we define a relation < to capture all the relations over \( com (h)\) induced by \(\ll _h\).

Relation can be either a partial or a total order over the committed transactions in h. The serialization graph of history h induced by \(\ll _h\), written \( SSG (h,\ll _h)\), is defined as \(( com (h),<)\).
In the above definition, (1) is a real-time order between T and \(T'\), (2) a read-write dependency, (3) a version ordering, and (4) an anti-dependency.
Definition 4 (Stricter serializability)
A history h is stricter serializable (\(h \in {\text {SSER}^+}\)) when (i) for some version order \(\ll _h\), the serialization graph \(( com (h),<)\) is acyclic, and (ii) for every transaction \(T_i\) that aborts in h, either \(T_i\) observes a strictly consistent snapshot in h, or one of its bindings is unfair.
Opacity (\({\text {OPA}}\)) and strict serializability (\({\text {SSER}}\)) coincide when aborted transactions observe strictly consistent snapshots. As a consequence of the above definition, a stricter serializable history during which all the aborted transactions exhibit fair bindings is opaque.
Proposition 1
For a history \(h \in {\text {SSER}^+}\), if every transaction T in h exhibits fair bindings then \(h \in {\text {OPA}}\) holds.
Proposition 1 offers a convenient property on histories that, when it applies, allows to reach opacity. The next section characterizes a class of applications for which this property holds. In other words, we give a robustness criteria [6] against \({\text {SSER}^+}\).
2.4 Applicability
In what follows, we give some details about the model of application we are interested with. Then, we present our robustness criteria and prove that it applies to \({\text {SSER}^+}\).
Model of Application. The state of an object commonly includes references to one or more objects in the shared memory. These references between objects form the object graph of the application.
When performing a computation, a process traverses a path in the object graph. To this end, the process knows initially an immutable root object in the graph. Starting from this root, the process executes a traversal by using the references stored in each object.
For some transaction T, a path is the sequence of versions \(\pi \) that T accesses. It should satisfy that (i) the first object in \(\pi \) corresponds to the immutable root of the object graph, and (ii) for all \(x_i \in \pi \), some \(y_j <_{\pi } x_i\) includes a reference to \(x_i\).
A Robustness Criteria. To define our criteria, we focus specifically on \({\text {SSER}^+}\) implementations that allow invisible reads. As pointed out earlier, this restriction is motivated by performance since most workloads are read-intensive. In this context, the result of Hans et al. [20] tells us that it is not possible to jointly achieve (i) \({\text {SSER}}\), (ii) read invisibility, (iii) minimal progressiveness, and (iv) accept RC-anti-dependencies. As a consequence, we remove histories that exhibit such a pattern from our analysis; hereafter, we shall note these histories \(\text {RCAD}\).
Let us consider the property \(\mathcal {P}\) below on a TM application. In what follows, we prove that if \(\mathcal {P}\) holds and the TM does not accept RC-anti-dependencies, then it is robust against \({\text {SSER}^+}\).
-
(\(\mathcal {P}\)) The object graph forms initially a tree and every transaction maintains this invariant.
Let \(\mathcal {T}\) be some set of transactions for which property \(\mathcal {P}\) holds. \(H_{\mathcal {T}}\) refers to histories built upon transactions in \(\mathcal {T}\). We wish to establish the following result:
Proposition 2
 .
.
To state this result, we note h some history in  . Since h is serializable, there exits some linearization \(\lambda \) of \( com (h)\) equivalent to h. For a transaction \(T_i\) in \(\lambda \), we let \(\pi _i\) and \(\pi _i'\) be the paths (if any) from the root to x before and after transaction \(T_i\). By property \(\mathcal {P}\), if such a path exists it is unique, because each transaction preserves that the object graph is a tree.
. Since h is serializable, there exits some linearization \(\lambda \) of \( com (h)\) equivalent to h. For a transaction \(T_i\) in \(\lambda \), we let \(\pi _i\) and \(\pi _i'\) be the paths (if any) from the root to x before and after transaction \(T_i\). By property \(\mathcal {P}\), if such a path exists it is unique, because each transaction preserves that the object graph is a tree.
Lemma 1
If transaction \(T_i\) reaches x in h, then for every \(y_j\) in  , the dependency
, the dependency  holds.
holds.
Proof
There are two cases to consider:
-
(\(y_j \in \pi _i\)) Property \(\mathcal {P}\) implies that either \(y_j\) is the root, or \(T_i\) reads the version \(z_k\) right before \(y_j\) in \(\pi _i\). Hence, by a short induction, transaction \(T_i\) reads all the versions in \(\pi _i\).
-
(\(y_j \in \pi _i'\)) Assume that \(T_i\) accesses \(y_j\) and name \(z_k\) the version right before \(y_j\) in \(\pi _i'\). Version \(z_k\) holds a reference to \(y_j\). If this reference does not exist prior to the execution of \(T_i\), object z was updated. Otherwise, T must reads \(z_k\) prior to accessing \(y_j\).
Lemma 2
If transaction \(T_i\) aborts in h then all its bindings are fair.
Proof
(By induction.). Define x and \(T_j\) such that \(T_i\) is bound to \(T_j\) on x and assume that all the prior bindings of \(T_i\) are fair.
First, consider that either (\(\pi _i = \pi _j\)) or (\(\pi _i = \pi _j'\)) is true. Choose some \(y_k\) read before \(x_j\) in \(\pi _i\). By Lemma 1, since  is true, the dependency
is true, the dependency  holds.
holds.
Otherwise, by our induction hypothesis, all the bindings of \(T_i\) prior \(x_j\) are fair. It follows that transaction \(T_i\) observes a strictly consistent snapshot in h up to \(r_i(x_j)\). Hence, there exists a committed transaction \(T_k\) such that \(\pi _i\) is the path to x after transaction \(T_k\) in \(\lambda \) (i.e., \(\pi _k'= \pi _i\)).
Depending on the relative positions of \(T_j\) and \(T_k\) in \(\lambda \), there are two cases to consider. In both cases, some transaction \(T_l\) between \(T_j\) and \(T_k\) modifies the path to x in the object graph.
-
(\(T_j <_{\lambda } T_k\)) Without lack of generality, assume that \(T_l\) is the first transaction to modify \(\pi _j'\). Transaction \(T_l\) and \(T_j\) are concurrent in h and \(T_l\) commits before \(T_j\). This comes from the fact that \(T_l\) must commit before \(T_i\) in h, \(T_j\) is concurrent to \(T_i\) in h and \(T_j\) is before \(T_l\) in \(\lambda \). Then, since \(T_l\) modifies \(\pi _j'\) and the two transactions are concurrent, \(T_l\) must update an object read by \(T_j\). It follows that h exhibits an RC-anti-dependency between \(T_j\) and \(T_l\). Contradiction.
-
(\(T_k <_{\lambda } T_j\)) Choose some \(y_{k'}\) read before \(x_j\) in \(\pi _i\). If y is still in \(\pi _j\), then \(T_j\) reads at least that version of object y. Otherwise, consider that \(T_l\) is the first transaction that removes y from the path to x in the object graph. To preserve property \(\mathcal {P}\), \(T_l\) updates some object \(y'\) read by \(T_{k'}\) that was referring to y. Because \(h \notin \text {RCAD}\), transaction \(T_{k'}\) cannot commit after \(T_l\). Hence,
 holds.
holds.
3 Algorithm
In this section, we present a transactional memory that attains \({\text {SSER}^+}\). Contrary to several existing TM implementation, our design does not require a global clock. It is weakly-progressive, aborting a transaction only if it encounters a concurrent conflicting transaction. Moreover, reads operations do not modify the base objects of the implementation (read invisibility).
We first give an overview of the algorithm, present its internals and justify some design choices. A correctness proofs follows. We close this section with a discussion on the parameters of our algorithm. In particular, we explain how to tailor it to be disjoint-access parallel.
3.1 Overview
Algorithm 1 depicts the pseudo-code of our construction of the TM interface at some process p. Our design follows the general approach of the lazy snapshot algorithm (LSA) [14], replacing the central clock with a more flexible mechanism. Algorithm 1 employs a deferred update schema that consists in two steps. A transaction first executes optimistically, buffering its updates. Then, at commit time, the transaction is certified and, if it commits, its updates are applied to the shared memory.
During the execution of a transaction, a process checks that the objects accessed so far did not change. Similarly to LSA, this check is lazily executed. Algorithm 1 executes it only if the shared object was recently updated, or when the transaction terminates.
3.2 Tracking Time
Algorithm 1 tracks time to compute how concurrent transactions interleave during an execution. To this end, the algorithm makes use of logical clocks. We model the interface of a logical clock with two operations: \( read ()\) returns a value in  , and
, and  updates the clock with value v. The sequential specification of a logical clock guarantees a single property, that the time flows forward: (Time Monotonicity) A read operation always returns at least the greatest value to which the clock advanced so far. In every sequential history h,
updates the clock with value v. The sequential specification of a logical clock guarantees a single property, that the time flows forward: (Time Monotonicity) A read operation always returns at least the greatest value to which the clock advanced so far. In every sequential history h,  .
.
Algorithm 1 associates logical clocks with both processes and transactions. To retrieve the clock associated with some object x, the algorithm uses function \( clock (x)\). Notice that in the pseudo-code, when it is clear from the context, \( clock (x)\) is a shorthand for \( clock (x){.} read ()\).
The clock associated with a transaction is always local (line 2). In the case of a process, it might be shared or not (line 3). The flexibility of our design comes from this locality choice for \( clock (p)\). When the clock is shared, it is linearizable. To implement an (obstruction-free) linearizable clock we employ the following common approach:
- (Construction 1). :
-
Let x be a shared register initialized to 0. When \( read ()\) is called, we return the value stored in x. Upon executing \( adv (v)\), we fetch the value stored in x, say u. If \(v > u\) holds, we execute a compare-and-swap to replace u with v; otherwise the operation returns. If the compare-and-swap fails, the previous steps are retried.

3.3 Internals
In Algorithm 1, each object x has a location in the shared memory, denoted \( loc (x)\). This location stores a pair (d, t), where  is a timestamp, and d is the actual content of x as seen by transactions. For simplicity, we shall name hereafter a pair (d, t) a version of object x. Since the location of object x is unique, a single version of object x may exist at a time in the memory. As usual, we assume some transaction
is a timestamp, and d is the actual content of x as seen by transactions. For simplicity, we shall name hereafter a pair (d, t) a version of object x. Since the location of object x is unique, a single version of object x may exist at a time in the memory. As usual, we assume some transaction  that initializes for every object x the location \( loc (x)\) to \((\bot ,0)\). Furthermore, we consider that each read or write operation to some location \( loc (x)\) is atomic.
that initializes for every object x the location \( loc (x)\) to \((\bot ,0)\). Furthermore, we consider that each read or write operation to some location \( loc (x)\) is atomic.
Algorithm 1 associates a lock to each object. To manipulate the lock-related functions of object x, a process p employs appropriately the functions  ,
,  and
and  .
.
For every transaction T submitted to the system, Algorithm 1 maintains three local data structures: \( clock (T)\) is the logical clock of transaction T; \( rs (T)\) is a map that contains its read set; and \( ws (T)\) is another map that stores the write set of T. Algorithm 1 updates incrementally \( rs (T)\) and \( ws (T)\) over the course of the execution. The read set serves to check that the snapshot of the shared memory as seen by the transaction is strictly consistent. The write set buffers updates. With more details, the execution of a transaction T proceeds as follows.
-
When T starts its execution, Algorithm 1 initializes \( clock (T)\) to the smallest value of \( clock (q)\) for any process q executing the TM. Then, both \( rs (T)\) and \( ws (T)\) are set to
 .
. -
When T accesses a shared object x, if x was previously written, its value is returned (line 10). Otherwise, Algorithm 1 fetches atomically the version (d, t), as seen in location \( loc (x)\). Then, the algorithm checks that (i) no lock is held on x, and (ii) in case x was previously accessed, that T observes the same version. If one of these two conditions fails, Algorithm 1 aborts transaction T (line 14). The algorithm then checks that the timestamp t associated to the content d is smaller than the clock of T. In case this does not hold (line 15), Algorithm 1 tries extending the snapshot of T by calling function \( extend ()\). This function returns
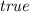 when the versions previously read by T are still valid. In which case, \( clock (T)\) is updated to the value t. If Algorithm 1 succeeds in extending (if needed) the snapshot of T, d is returned and the read set of T updated accordingly; otherwise transaction T is aborted (line 16).
when the versions previously read by T are still valid. In which case, \( clock (T)\) is updated to the value t. If Algorithm 1 succeeds in extending (if needed) the snapshot of T, d is returned and the read set of T updated accordingly; otherwise transaction T is aborted (line 16). -
Upon executing a write request on behalf of T to some object x, Algorithm 1 takes the lock associated with x (line 20), and in case of success, it buffers the update value d in \( ws (T)\) (line 25). The timestamp t of x at the time Algorithm 1 takes the lock serves two purposes. First, Algorithm 1 checks that t is lower than the current clock of T, and if not T is extended (line 23). Second, it is saved in \( ws (T)\) to ensure that at commit time the timestamp of the version of x written by T is greater than t.
-
When T requests to commit, Algorithm 1 certifies the read set by calling function \( extend ()\) with the clock of T (line 27). If this test succeeds, transaction T commits (lines 43 to 48). In such a case, \( clock (T)\) ticks to reach its final value (line 43). By construction, this value is greater than the timestamps of all the versions read or written by T (lines 14 and 23). Algorithm 1 updates the clock of p with the final value of \( clock (T)\) (line 44), then it updates the items written by T with their novel versions (line 46).
3.4 Guarantees
In this section, we assess the core properties of Algorithm 1. First, we show that our TM design is weakly progressive, i.e., that the algorithm aborts a transaction only if it encounters a concurrent conflicting transaction. Then, we prove that Algorithm 1 is stricter serializable.
(Weak-progress). A transaction executes under weak progressiveness [19], or equivalently it is weakly progressive, when it aborts only if it encounters a conflicting transaction. By extension, a TM is weakly progressive when it only produces histories during which transactions are weakly-progressive. We prove that this property holds for Algorithm 1.
In Algorithm 1, a transaction T aborts either at line 14, 16, 21, 24, or 28. We observe that in such a case either T observes an item x locked, or that the timestamp associated with x has changed. It follows that if T aborts then it observes a conflict with a concurrent transaction. From which we deduce that it is executing under weak progressiveness.
(Stricter serializability). Consider some run  of Algorithm 1, and let h be the history produced in
of Algorithm 1, and let h be the history produced in  . At the light of its pseudo-code, every function defined in Algorithm 1 is wait-free. As a consequence, we may consider without lack of generality that h is complete, i.e., every transaction executed in h terminates with either a commit or an abort event. In what follows, we let \(\ll _h\) be the order in which writes to the object locations are linearized in \(\rho \). We first prove that < is acyclic for this definition of \(\ll _h\). Then, we show that, if a transaction does not exhibit any unfair binding, then it observes a strictly consistent snapshot. For some transaction, we shall note \( clock (T_i)_f\) the final value of \( clock (T)\).
. At the light of its pseudo-code, every function defined in Algorithm 1 is wait-free. As a consequence, we may consider without lack of generality that h is complete, i.e., every transaction executed in h terminates with either a commit or an abort event. In what follows, we let \(\ll _h\) be the order in which writes to the object locations are linearized in \(\rho \). We first prove that < is acyclic for this definition of \(\ll _h\). Then, we show that, if a transaction does not exhibit any unfair binding, then it observes a strictly consistent snapshot. For some transaction, we shall note \( clock (T_i)_f\) the final value of \( clock (T)\).
Proposition 3
Consider two transactions \(T_i\) and \(T_{j \ne i}\) in h. If either  or \(x_j \ll _h x_i\) holds, then \( clock (T_i)_f \ge clock (T_j)_f\) is true. In addition, if transaction \(T_i\) is an update that commits then the ordering is strict, i.e., \( clock (T_i)_f > clock (T_j)_f\).
or \(x_j \ll _h x_i\) holds, then \( clock (T_i)_f \ge clock (T_j)_f\) is true. In addition, if transaction \(T_i\) is an update that commits then the ordering is strict, i.e., \( clock (T_i)_f > clock (T_j)_f\).
Proof
In each of the two cases, we prove that \( clock (T_i)_f \ge clock (T_i)_f\) holds before transaction \(T_i\) commits.
-
 :
: -
Let x be an object such that \(r_i(x_j)\) occurs in h. Since transaction \(T_i\) reads version \(x_j\), transaction \(T_j\) commits. We observe that \(T_j\) writes version \(x_j\) together with \( clock (T_j)_f\) at \( loc (x)\) when it commits (line 46). As a consequence, when transaction \(T_i\) returns version \(x_i\) at line 18, it assigns \( clock (T_j)_f\) to t before at line 11. The condition at line 15 implies that either \( clock (T_i) \ge t\) holds, or a call to \( extend (T_i,t)\) occurs. In the latter case, transaction \(T_i\) executes line 35, advancing its clock up to the value of t.
- (\(x_j \ll _h x_i\)).:
-
By definition, relation \(\ll _h\) forms a total order over all versions of x. Thus, we may reason by induction, considering that \(x_i\) is immediately after \(x_j\) in the order \(\ll _h\). When \(T_j\) returns from \(w_j(x_j)\) at line 25, it holds a lock on x. This lock is released at line 47 after writing to \( loc (x)\). As \(\ll _h\) follows the linearization order, \(T_i\) executes line 20 after \(T_j\) wrote \((x_j, clock (T_j)_f)\) to \( loc (x)\). Location \( loc (x)\) is not updated between \(x_j\) and \(x_i\). Hence, after\(T_i\) executes line 23, \( clock (T_i) \ge clock (T_j)\) holds.
Since a clock is monotonic, the relation holds forever. Then, if transaction \(T_i\) is an update that commits, it must executes line 43, leading to \( clock (T_i)_f > clock (T_i)_f\).
Proposition 4
History h does not exhibit any RC-anti-dependencies (\(h \notin \text {RCAD}\))
Proof
Consider \(T_i\), \(T_j\) and \(T_k\) such that \(r_i(x_k), w_j(x_j) \in h\), \(x_k \ll _h x_j\) and \(T_j\) commits before \(T_i\). When \(T_j\) invokes \( commit \), it holds a lock on x. This lock is released at line 47 after version \(x_j\) is written at location \( loc (x)\). Then, consider the time at which \(T_i\) invokes \( tryCommit \,\). The call at line 27 leads to fetching \( loc (x)\) at line 32. Since \(T_i\) reads version \(x_k\) in h, a pair \((x_k, clock (T_k)_f)\) is in \( rs (T_i)\). From the definition of \(\ll _h\) the write of \((x_k, clock (T_k)_f)\) takes place before the write of version \((x_j, clock (T_j)_f)\) in \(\rho \). Hence, \( loc (x)\) does not contain anymore \((x_k, clock (T_k)_f)\) Applying Proposition 3, \(T_i\) executes line 34 and aborts at line 29.
Proposition 5
Consider two transactions \(T_i\) and \(T_{j \ne i}\) in \( com (h)\). If \(T_i < T_j\) holds, transaction \(T_i\) invokes \( commit \) before transaction \(T_j\) in h.
Proof
Assume that \(T_i\) and \(T_j\) conflict of some object x. We examine in order each of the four cases defining relation <.
-
(
 )
)This case is immediate.
-
(\(\exists x : r_j(x_i) \in h\))
Before committing, \(T_j\) invokes \( extend \) at line 27. Since \(T_j\) commits in h, it should retrieve \((x_{i},{}_{-})\) from \( loc (x)\) when executing line 32. Hence, transaction \(T_i\) has already executed line 46 on object x. It follows that \(T_i\) invokes \( commit \) before transaction \(T_j\) in history h.
-
(\(\exists x : x_i \ll _h x_j\))
By definition of \(\ll _h\), the write of version \(x_i\) is linearized before the write of version \(x_j\) in \(\rho \). After \(T_i\) returns from \(w_i(x_i)\), it owns a lock on object x (line 46). The object is then unlocked by transaction \(T_i\) at line 47. As a consequence, transaction \(T_i\) takes a lock on object x after \(T_i\) invokes operation \( commit \). From which it follows that the claim holds.
-
(\(\exists x, T_k : x_k \ll _x x_j \wedge r_i(x_k)\))
Follows from Proposition 4.
Theorem 1
History h belongs to \({\text {SSER}^+}\).
Proof
Proposition 5 tells us that if \(T_i < T_j\) holds then \(T_i\) commits before \(T_j\). It follows that the \( SSG (h,\ll _h)\) is acyclic.
Let us now turn our attention to the second property of \({\text {SSER}^+}\). Assume that a transaction \(T_i\) aborts in h. For the sake of contradiction, consider that \(T_i\) exhibits fair bindings and yet that it observes a non-strictly consistent snapshot.
Applying the definition given in Sect. 2.1, there exist transactions \(T_j\) and \(T_k\) such that  , \(r_i(x_k)\) occurs in h and \(x_k \ll _h x_j\). Applying Proposition 5, if
, \(r_i(x_k)\) occurs in h and \(x_k \ll _h x_j\). Applying Proposition 5, if  holds, transaction \(T_i\) cannot observe version \(x_k\). Thus, transaction \(T_j\) is concurrent to \(T_i\). Moreover, by definition of
holds, transaction \(T_i\) cannot observe version \(x_k\). Thus, transaction \(T_j\) is concurrent to \(T_i\). Moreover, by definition of  , there exist a transaction \(T_l\) (possibly, \(T_j\)) and some object y such that \(T_i\) performs \(r_i(y_l)\) and
, there exist a transaction \(T_l\) (possibly, \(T_j\)) and some object y such that \(T_i\) performs \(r_i(y_l)\) and  . In what follows, we prove that \(T_i\) aborts before returning \(y_l\).
. In what follows, we prove that \(T_i\) aborts before returning \(y_l\).
For starter, relation < is acyclic, thus \(x_k \ne y_l\) holds. It then remains to investigate the following two cases:
-
(
 )
)From Proposition 5 and
 , transaction \(T_j\) is committed at the time \(T_i\) reads object x. Contradiction.
, transaction \(T_j\) is committed at the time \(T_i\) reads object x. Contradiction. -
(
 )
)We first argue that, at the time \(T_i\) executes line 11, the timestamp fetches from \( loc (y)\) is greater than \( clock (T_i)\).
Proof
First of all, observe that \(T_j\) is not committed at the time \(T_i\) reads object x (since \(x_{k} \ll _h x_{j}\) holds). Hence, denoting q the process that executes \(T_j\), \( clock (q) < clock (T_j)_f\) is true when \(T_i\) begins its execution at line 5. From the pseudo-code at line 5, \( clock (T_i) < clock (T_j)_f\) holds at the start of \(T_i\). Because \(T_j\) is concurrent to \(T_i\), \(T_l\) is also concurrent to \(T_i\) by Proposition 5. Thus, as \(r_i(y_l)\) occurs, \(T_i\) is bound to \(T_l\) on y. Now, consider some object z read by \(T_i\) before y, and name \(z_r\) the version read by \(T_i\). Since the binding of \(T_i\) to \(T_l\) is fair,  is true. Hence, applying Proposition 3, we have \( clock (T_r)_f < clock (T_l)_f\). It follows that the relation \( clock (T_i) < clock (T_l)_f\) is true.
is true. Hence, applying Proposition 3, we have \( clock (T_r)_f < clock (T_l)_f\). It follows that the relation \( clock (T_i) < clock (T_l)_f\) is true.
From what precedes, transaction \(T_i\) invokes \( extend \) at line 15. We know that transaction \(T_j\) is committed at that time (since \(T_l\) is committed and  holds). Thus, the test at line 33 fails and \(T_i\) aborts before returning \(y_l\).
holds). Thus, the test at line 33 fails and \(T_i\) aborts before returning \(y_l\).
3.5 Discussion
Algorithm 1 replaces the global clock usually employed in TM architectures with a more flexible mechanism. For some process p, \( clock (p)\) can be local to p, shared across a subset of the processes, or even all of them.
If processes need to synchronize too often, maintaining consistency among the various clocks is expensive. In this situation, it might be of interest to find a compromise between the cost of cache coherency and the need for synchronization. For instance, in a NUMA architecture, Algorithm 1 may assign a clock per hardware socket. Upon a call to \( clock (p)\), the algorithm returns the clock defined for the socket in which the processor executing process p resides.
On the other hand, when the processes use a global clock, Algorithm 1 boils down to the original TinySTM implementation [14]. In this case, a read-only transaction always sees a strictly consistent snapshot. As a consequence, it can commit right after a call to \( tryCommit \,\), i.e., without checking its snapshot at line 27.
A last observation is that our algorithm works even if one of the processes takes no step. This implies that the calls to process clocks (at lines 5 and 44) are strictly speaking not necessary and can be skipped without impacting the correctness of Algorithm 1. Clocks are solely used to avoid extending the snapshot at each step where a larger timestamp is encountered. If process clocks are not used, when two transactions access disjoint objects, they do not contend on any base object of the implementation. As a consequence, such a variation of Algorithm 1 is disjoint-access parallel (DAP).
4 Evaluation
This section presents a performance study of our \(\text {SSER}^+\) transactional memory described in Sect. 3. To conduct this evaluation we implemented and integrated our algorithm inside TinySTM [14], a state-of-the-art software transactional memory implementation. Our modifications account for approximately 500 SLOC. We run Algorithm 1 in disjoint-access parallel mode. As explained in Sect. 3.5, in this variation the clocks of the processes are not accessed. A detailed evaluation of the other variations of Algorithm 1 is left for future work.
The experiments are conducted on an AMD Opteron48, a 48-cores machine with 256 GB of RAM. This machine has 4 dodeca-core AMD Opteron 6172, and 8 NUMA nodes. To evaluate the performance of our implementation on this multi-core platform, we use the test suite included with TinySTM. This test suite is composed of several TM applications with different transaction patterns. The reminder of this section briefly describes the benchmarks and discuss our results. As a matter of a comparison, we also present the results achieved with the default TinySTM distribution, (v1.0.5).
4.1 A Bank Application
The bank benchmark consists in simulating transfers between bank accounts. A transaction updates two accounts, transferring some random amount of money from one account to another. A thread executing this benchmark performs transfers in closed-loop. Each thread is bound to some branch of the bank, and accounts are spread evenly across the branches. A locality parameter allows to tune the accounts accessed by a thread to do a transfer. This parameter serves to adjust the probability that a thread executes consecutive operations on the same data. More specifically, when locality is set to the value \(\rho \), a thread executes a transfer in its branch with probability \(\rho \) and between two random accounts with probability \((1-\rho )\). When \(\rho =1\), this workload is fully parallel.
Figure 1 presents the experimental results for the bank benchmark. In Fig. 1(a), we execute a base scenario with 10 k bank accounts, and a locality of 0.8. We measure the number of transfers performed by varying the number of threads in the application. In this figure, we observe that the performance obtained with TinySTM merely improves as the number of thread increases: 48 threads achieve 2.8 million transactions per second (MTPS), scaling-up from 2.2 MTPS with a single thread. Our implementation performs better: with 48 threads Algorithm 1 executes around 68 MTPS, executing \(\times 31\) more operations than with one thread.
To understand the impact of data locality on performance, we vary this parameter for a fixed number of threads. Figure 1(b) presents the speedup obtained when varying locality from 0, i.e., all the accounts are chosen at random, up to 1, where they are all chosen in the local branch. In this experiment, we fix the number of threads to 48, i.e. the maximum number of cores available on our test machine. As shown in Fig. 1(b), our TM implementation leverages the presence of data locality in the bank application. This is expected, since we use the disjoint-access parallel (DAP) variation of Algorithm 1. When locality increases, the contention in the application decreases. As a consequence of DAP, each thread works on independent data, thus improving performance.
4.2 Linked-List
The linked-list benchmark consists in concurrently modifying a sorted linked-list of integers. Each thread randomly adds or removes an integer from the list. We run this benchmark for a range of 512 values, i.e. a thread randomly selects a value between \(-255\) and \(+256\) before doing an insertion/removal. The linked list is initialized to contain 256 integers. We report our results in Fig. 2 (left).
We observe that TinySTM outperforms our implementation in the linked-list benchmark. This is due to the fact that, without proper clock synchronization, transactions tend to re-validate their reads frequently over their execution paths. In this scenario of high contention, it is (as expected) preferable to rely on a frequent synchronization mechanism such as the global clock used in TinySTM. To alleviate this issue, one could adjust dynamically the clocks used in Algorithm 1 accordingly to contention. Such a strategy could rely on a global lock, similarly to the mechanism used to avoid that long transactions abort. We left the implementation of this optimization for future work
4.3 Red-Black Tree
The red-black tree benchmark is similar to the linked-list benchmark except that the values are stored in a self-balancing binary search tree. We run this benchmark with a range of \(10^7\) values, and a binary tree initialized with \(10^5\) values. Figure 2 (right) reports our results.
When using the original TinySTM design, the performance of the application improves linearly up to 12 threads. It then stalls to approximately 50 MTPS due to contention on the global clock. In this benchmark, the likelihood of having two concurrent conflicting transactions is very low. Leveraging this workload property, our implementation of Algorithm 1, scales the application linearly with the number of threads. Algorithm 1 achieves 176 MTPS with 48 threads, improving performance by a \(\times 36\) factor over a single threaded execution.
5 Related Work
Transactional memory (TM) allows to design applications with the help of sequences of instructions that run in isolation one from another. This paradigm greatly simplifies the programming of modern highly-parallel computer architectures.
Ennals [13] suggests to build deadlock-free lock-based TMs rather than non-blocking ones. Empirical evidences [9] and theoretical results [18, 26] support this claim.
At first glance, it might be of interest that a TM design accepts all correct histories; a property named permissiveness [16]. Such TM algorithms need to track large dependencies [25] and/or acquire locks for read operations [2]. However, both techniques are known to have a significant impact on performance.
Early TM implementations (such as DSTM [23]) validate all the prior reads when accessing a new object. The complexity of this approach is quadratic in the number of objects read along the execution path. A time-based TM avoids this effort by relying on the use a global clock to timestamp object versions. Zhang et al. [33] compare several such approaches, namely TL2 [8], LSA [31] and GCC [32]. They provide guidelines to reduce unnecessary validations and shorten the commit sequence.
Multi-versioning [10, 15] brings a major benefit: allowing read-only transactions to complete despite contention. This clearly boosts certain workloads but managing multiple versions has a non-negligible performance cost on the TM internals. Similarly, invisible reads ensure that read operations do not contend in most cases. However, such a technique limits progress or the consistency criteria satisfied by the TM [3]. In the case of Algorithm 1, both read-only and updates transaction are certain to make progress only in the absence of contention.
New challenges arise when considering multicore architectures and cache coherency strategies for NUMA architectures. Clock contention [7] is one of them. To avoid this problem, workloads as well as TM designs should take into account parallelism [28]. Chan et al. [7] propose to group threads into zones, and that each zone shares a clock and a clock table. To timestamp a new version, the TL2C algorithm [4] tags it with a local counter together with the thread id. Each thread stores a vector of the latest timestamp it encountered. The algorithm preserves opacity by requiring that a transaction restarts if one of the vector entries is not up to date.
6 Conclusion
Transactional memory systems must handle a tradeoff between consistency and performance. It is impractical to take into account all possible combinations of read and write conflicts, as it would lead to largely inefficient solutions. For instance, accepting \(\text {RCAD}\) histories brings only a small performance benefits in the general case [20].
This paper introduces a new consistency criteria, named stricter serializability (\({\text {SSER}^+}\)). Workloads executed under \({\text {SSER}^+}\) are opaque when the object graph forms a tree and transactions traverse it top-down. We present an algorithm to attain this criteria together with a proof of its correctness. Our evaluation based on a fully implemented prototype demonstrates that such an approach is very efficient in weakly-contended workloads.
Notes
- 1.
Allowing \(T_1\) to return both \(x_0\) and \(y_2\) may have serious consequences in a non-managed environment. As pointed out in [17], transaction \(T_1\) may compute a division by 0, leading the program to crash.
- 2.
In this paper, we consider a slight generalization of an RC-anti-dependency as defined in [20], where \(T_j\) does not read x prior to its update.
References
Afek, Y., Matveev, A., Shavit, N.: Pessimistic software lock-elision. In: Aguilera, M.K. (ed.) DISC 2012. LNCS, vol. 7611, pp. 297–311. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33651-5_21
Attiya, H., Hillel, E.: A single-version STM that is multi-versioned permissive. Theory Comput. Syst. 51(4), 425–446 (2012). https://doi.org/10.1007/s00224-012-9406-3
Attiya, H., Hillel, E., Milani, A.: Inherent limitations on disjoint-access parallel implementations of transactional memory. In: Proceedings of the Twenty-First Annual Symposium on Parallelism in Algorithms and Architectures, SPAA 2009, pp. 69–78. ACM, New York (2009). https://doi.org/10.1145/1583991.1584015
Avni, H., Shavit, N.: Maintaining consistent transactional states without a global clock. In: Shvartsman, A.A., Felber, P. (eds.) SIROCCO 2008. LNCS, vol. 5058, pp. 131–140. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-69355-0_12
Bernstein, P.A., Goodman, N.: Timestamp-based algorithms for concurrency control in distributed database systems. In: Proceedings of the 6th International Conference on Very Large Data Bases, pp. 285–300, October 1980. http://dl.acm.org/citation.cfm?id=1286887.1286918
Cerone, A., Gotsman, A.: Analysing snapshot isolation. In: Proceedings of the 2016 ACM Symposium on Principles of Distributed Computing, PODC 2016, Chicago, IL, USA, 25–28 July 2016, pp. 55–64 (2016). https://doi.org/10.1145/2933057.2933096
Chan, K., Wang, C.L.: TrC-MC: decentralized software transactional memory for multi-multicore computers. In: 2011 IEEE 17th International Conference on Parallel and Distributed Systems (ICPADS), pp. 292–299 (2011). https://doi.org/10.1109/ICPADS.2011.144
Dice, D., Shalev, O., Shavit, N.: Transactional locking II. In: Dolev, S. (ed.) DISC 2006. LNCS, vol. 4167, pp. 194–208. Springer, Heidelberg (2006). https://doi.org/10.1007/11864219_14
Dice, D., Shavit, N.: What really makes transactions faster. In: Proceedings of the 1st TRANSACT 2006 Workshop, vol. 8, p. 3 (2006)
Diegues, N., Romano, P.: Time-warp: lightweight abort minimization in transactional memory. In: Proceedings of the 19th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, PPoPP 2014, pp. 167–178. ACM, New York (2014). https://doi.org/10.1145/2555243.2555259
Dragojević, A., Felber, P., Gramoli, V., Guerraoui, R.: Why STM can be more than a research toy. Commun. ACM 54(4), 70–77 (2011). https://doi.org/10.1145/1924421.1924440
Ellen, F., Fatourou, P., Kosmas, E., Milani, A., Travers, C.: Universal constructions that ensure disjoint-access parallelism and wait-freedom. Distrib. Comput. 29(4), 251–277 (2016). https://doi.org/10.1007/s00446-015-0261-8
Ennals, R.: Software transactional memory should not be obstruction-free. Technical report, Technical Report IRC-TR-06-052, Intel Research Cambridge Tech Report (2006)
Felber, P., Fetzer, C., Marlier, P., Riegel, T.: Time-based software transactional memory. IEEE Trans. Parallel Distrib. Syst. 21(12), 1793–1807 (2010). https://doi.org/10.1109/TPDS.2010.49
Fernandes, S.M., Cachopo, J.a.: Lock-free and scalable multi-version software transactional memory. In: Proceedings of the 16th ACM Symposium on Principles and Practice of Parallel Programming, PPoPP 2011, pp. 179–188. ACM, New York (2011). https://doi.org/10.1145/1941553.1941579
Guerraoui, R., Henzinger, T.A., Singh, V.: Permissiveness in transactional memories. In: Taubenfeld, G. (ed.) DISC 2008. LNCS, vol. 5218, pp. 305–319. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-87779-0_21
Guerraoui, R., Kapalka, M.: On the correctness of transactional memory. In: Proceedings of the 13th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, PPoPP 2008, pp. 175–184. ACM, New York (2008). https://doi.org/10.1145/1345206.1345233
Guerraoui, R., Kapalka, M.: On the correctness of transactional memory. In: Proceedings of the 13th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, PPoPP 2008, pp. 175–184. ACM, New York (2008)
Guerraoui, R., Kapalka, M.: The semantics of progress in lock-based transactional memory. In: Proceedings of the 36th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2009, pp. 404–415. ACM, New York (2009). https://doi.org/10.1145/1480881.1480931
Hans, S., Hassan, A., Palmieri, R., Peluso, S., Ravindran, B.: Opacity vs TMS2: expectations and reality. In: Gavoille, C., Ilcinkas, D. (eds.) DISC 2016. LNCS, vol. 9888, pp. 269–283. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53426-7_20
Harris, T., Fraser, K.: Revocable locks for non-blocking programming. In: Proceedings of the Tenth ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, PPoPP 2005, pp. 72–82. ACM, New York (2005). https://doi.org/10.1145/1065944.1065954
Hassan, A., Palmieri, R., Ravindran, B.: Optimistic transactional boosting. SIGPLAN Not. 49(8), 387–388 (2014). https://doi.org/10.1145/2692916.2555283
Herlihy, M., Luchangco, V., Moir, M., Scherer, III, W.N.: Software transactional memory for dynamic-sized data structures. In: Proceedings of the Twenty-Second Annual Symposium on Principles of Distributed Computing, PODC 2003, pp. 92–101. ACM, New York (2003). https://doi.org/10.1145/872035.872048
Herlihy, M.P., Wing, J.M.: Linearizability: a correctness condition for concurrent objects. ACM Trans. Program. Lang. Syst. 12(3), 463–492 (1990). https://doi.org/10.1145/78969.78972
Keidar, I., Perelman, D.: On avoiding spare aborts in transactional memory. In: Proceedings of the Twenty-First Annual Symposium on Parallelism in Algorithms and Architectures, SPAA 2009, pp. 59–68. ACM, New York (2009). https://doi.org/10.1145/1583991.1584013
Kuznetsov, P., Ravi, S.: Why transactional memory should not be obstruction-free. CoRR abs/1502.02725 (2015)
Lee, E.A.: The problem with threads. Computer 39(5), 33–42 (2006). https://doi.org/10.1109/MC.2006.180
Nguyen, D., Pingali, K.: What scalable programs need from transactional memory. In: Proceedings of the Twenty-Second International Conference on Architectural Support for Programming Languages and Operating Systems, ASPLOS 2017, pp. 105–118. ACM, New York (2017). https://doi.org/10.1145/3037697.3037750
Perelman, D., Byshevsky, A., Litmanovich, O., Keidar, I.: SMV: selective multi-versioning STM. In: Peleg, D. (ed.) DISC 2011. LNCS, vol. 6950, pp. 125–140. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-24100-0_9
Ravi, S.: Lower bounds for transactional memory. Bull. EATCS 121 (2017)
Riegel, T., Felber, P., Fetzer, C.: A lazy snapshot algorithm with eager validation. In: Dolev, S. (ed.) DISC 2006. LNCS, vol. 4167, pp. 284–298. Springer, Heidelberg (2006). https://doi.org/10.1007/11864219_20
Spear, M.F., Marathe, V.J., Scherer, W.N., Scott, M.L.: Conflict detection and validation strategies for software transactional memory. In: Dolev, S. (ed.) DISC 2006. LNCS, vol. 4167, pp. 179–193. Springer, Heidelberg (2006). https://doi.org/10.1007/11864219_13
Zhang, R., Budimlić, Z., Scherer, III, W.N.: Commit phase in timestamp-based STM. In: Proceedings of the Twentieth Annual Symposium on Parallelism in Algorithms and Architectures, SPAA 2008, pp. 326–335. ACM, New York (2008). https://doi.org/10.1145/1378533.1378589
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 IFIP International Federation for Information Processing
About this paper
Cite this paper
Sutra, P., Marlier, P., Schiavoni, V., Trahay, F. (2018). Boosting Transactional Memory with Stricter Serializability. In: Di Marzo Serugendo, G., Loreti, M. (eds) Coordination Models and Languages. COORDINATION 2018. Lecture Notes in Computer Science(), vol 10852. Springer, Cham. https://doi.org/10.1007/978-3-319-92408-3_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-92408-3_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-92407-6
Online ISBN: 978-3-319-92408-3
eBook Packages: Computer ScienceComputer Science (R0)




 holds.
holds. .
.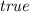 when the versions previously read by T are still valid. In which case,
when the versions previously read by T are still valid. In which case,  :
: )
) )
) , transaction
, transaction  )
)

