Abstract
We illustrate the ingredients of the state-of-the-art of model-based approach for the formal design and verification of cyber-physical systems. To capture the interaction between a discrete controller and its continuously evolving environment, we use the formal models of timed and hybrid automata. We explain the steps of modeling and verification in the tools Uppaal and SpaceEx using a case study based on a dual-chamber implantable pacemaker monitoring a human heart. We show how to design a model as a composition of components, how to construct models at varying levels of detail, how to establish that one model is an abstraction of another, how to specify correctness requirements using temporal logic, and how to verify that a model satisfies a logical requirement.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
1 Introduction
A cyber-physical system consists of computing devices communicating with one another and interacting with the physical world via sensors and actuators. Increasingly, such systems are everywhere, from smart buildings to medical devices to autonomous cars. Model-based design offers a promising approach for assisting developers to build cyber-physical systems in a systematic manner [2, 18, 26]. In this methodology, a designer first constructs a model, with mathematically precise semantics, of the system under design, and performs extensive analysis with respect to correctness requirements before generating the implementation from the model.
Models of cyber-physical systems need to capture both the controller—the system under design, and the plant—the environment with continuously evolving physical activities in which the system operates. This typically means a combination of block diagrams, state machines, and differential equations. Furthermore, we need to define models formally, that is, in a mathematically precise manner. The formal semantics allows us to answer questions such as, “what are the possible behaviors of a component” and “what does it mean to compose two components” rigorously, and forms the basis for analysis tools. In this article we do not attempt a survey of the rich literature on formal models and analysis tools for cyber-physical systems, but aim to give an introduction to the subject using a case study (see [13] for some recent surveys).
Medical devices offer an ideal test-bed for exploring the applications of formal methods in system design due to their safety-critical nature, which demands higher levels of reliability and rapidly growing complexity due to increased autonomous operation [27]. We use a dual chamber implantable pacemaker to illustrate the process of model construction and verification [10, 22, 28, 30]. The first step in modeling is to choose a modeling formalism depending on what aspects of the system a designer wants to focus on. The control algorithm of the pacemaker is best modeled as a composition of timed automata [5], while the relevant features of the heart can be described as a network of hybrid automata [4]. We introduce these two formal models using the modeling tools Uppaal [8, 25] and SpaceEx [17], respectively.
To check that the design works correctly as intended, the designer first needs to express the requirements capturing correctness in a mathematically precise manner. We explain two common ways of formalizing requirements using the pacemaker case study. The automata-based approach corresponds to designing a monitor that observes the input/output behavior of the system and enters an error state if an undesirable pattern is detected [29]. The temporal-logic-based approach corresponds to writing down a formula in a specialized formal logic—TCTL (Timed Computation Tree Logic) in our case [3], which captures the desired correctness requirement. A model checker is then tasked with the job of automatically checking that the system model satisfies the requirement, and produce feedback in the form of a counterexample if this is not the case [12]. Model checkers for continuous-time systems need to symbolically explore the infinitely many reachable states of the model. While symbolic algorithms have been developed for both timed and hybrid automata, the existing technology is more scalable for timed automata [7]. Hence, we construct a timed-automaton-based model of the heart by suppressing many details of the hybrid model, and show how the model checker Uppaal can then be used to verify requirements of the pacemaker.
Since we created a simplified heart model for the purpose of verifying requirements of the pacemaker, we are faced with a new analysis problem, namely, establishing a rigorous relationship between the two versions of the heart models. Showing that one model is a refinement or abstraction of another model is another key step in model-based design, and is essential if we want to infer properties of the more complex model based on the analysis of the simpler one [6, 11].
Related Work. In this paper, we use a dual chamber implantable pacemaker to illustrate the modeling of control software and the physical world it interacts with. Analyzing the behavior of the heart using formal methods was first proposed in [30], and our modeling of a heart cell is based on the HH model with linear differential equations from that paper. The modeling and model checking of the control algorithm within a pacemaker first appears in [22], and we use the pacemaker model as well as abstracted heart model from that paper for our case study. Note that there has been considerable research on formal modeling and verification of the pacemaker. For instance, [10] develops a more precise Simulink model of the heart cell from [30] with non-linear differential equations, and [28] describes a translator from Uppaal to Simulink/StateFlow for this purpose.
Organization of the Paper. We begin with an overview of the heart and pacemaker models in Sect. 2. Then, in Sect. 3, we use SpaceEx to construct an abstraction of the heart, and, in Sect. 4, we use Uppaal to verify the whole heart-pacemaker system. We conclude with future challenges in Sect. 5.
2 The Pacemaker Case Study
The human heart is an excellent example of a naturally occurring timed system. It spontaneously generates electrical impulses that organize the sequence of muscle contractions during each heart beat. The underlying timing pattern of these impulses is key to the proper functioning of the heart. The implantable cardiac pacemaker is a rhythm management device that monitors these patterns and corrects them via external means when needed.
Controlled by the nervous system, a specialized tissue, called the sinoatrial node, at the top of the right atrium periodically generates electrical pulses. These pulses cause both atria to contract, forcing blood into the ventricles. The electrical conduction gets delayed at the atrioventricular node, allowing the ventricles to fill fully, but then spreads rapidly across the ventricular muscles, resulting in their coordinated contraction, which pumps the blood out of the heart.
A common heart disease, called bradycardia, is due to failures in either impulse generation or impulse propagation and results in slow heart rate, leading to insufficient pumping of blood. Bradycardia can be treated by an implantable pacemaker that monitors the heart rate and delivers timely external electrical pulses to maintain an appropriate heart rate as well as atrio-ventricular coordination. Such a pacemaker usually has two leads fixed on the wall of the right atrium and the right ventricle. Activation of local tissue is sensed by these leads, and these sensing events act as inputs to the pacemaker. If these sensed events do not occur in a timely manner, then the pacemaker responds by producing pacing events that trigger electrical stimuli to the heart.
Figure 1 shows the pacemaker controller connected to a heart by two leads (black lines) attached to the walls of the right atrium and the right ventricle (blue area) from the inside. The sinoatrial pulses are propagated through the neural cells (blue lines), which can both be measured and stimulated by the pacemaker.
A modern pacemaker responds to a variety of heart conditions and can operate in different modes. We focus on two modes DDD and VDI and switching between them. In the mode DDD, the pacemaker is pacing both the atrium and the ventricle, both chambers are being sensed, and the pacemaker software responds to sensing by both activating and inhibiting further pacing, while in the mode VDI, the pacemaker paces only the ventricle, senses both chambers, and sensing causes inhibition of pacing.
2.1 Hybrid Automata: Modeling the Heart
To analyze the functionality of the pacemaker at design time, we need a model that captures how a human heart generates the sensory events. We can view the heart tissue as a network of cardiac cells, where the electric wave propagates along neighbouring cells assuring coordinated contraction. At the cellular level, the electrical signal is a change in the potential across the cell membrane, and is caused by the flow of ions, such as sodium and potassium, between the inside and outside of the cell. Mathematical modeling of the ionic processes corresponding to cell excitation has been studied extensively in computational systems biology. Typically, such a model is described using nonlinear differential equations, and consists of multiple continuous state variables corresponding to quantities such as voltage and ion concentrations and a large number of parameters.
A first step in modeling is to decide what level of detail is appropriate for the analysis task. For the purpose of this case study, we use the model proposed by [30], which is derived from the well-accepted Hodgkin-Huxley (HH) model of cell excitation. It is based on the observation that change in voltage with time that describes the cell excitation upon stimulation can be clearly separated in distinct phases, namely, upstroke, repolarization and resting, such that in each phase the dynamics can be captured by linear differential equations. This behavior can then be described using hybrid automata.
Hybrid automata offer a formal model for systems that exhibit both discrete and continuous behavior, such as the combination of heart cells (continuous behavior) and a pacemaker (discrete behavior). Continuous state change can be described by guarded differential equations, while discrete state change can be specified by guarded difference equations. The guard (or “invariant”) of a differential equation is a state predicate that specifies the condition under which the differential equation is active; the guard of a difference equation is a state predicate that specifies the condition under which the difference equation is enabled. Formally, a hybrid automaton is a graph whose vertices (or “modes”) are annotated with sets of guarded differential equations, and whose edges (or “mode transitions”) are annotated with sets of guarded difference equations [19]. A behavior of a hybrid automaton is a sequence of trajectory segments, where each trajectory segment satisfies one of the mode equations and its invariant for the duration of the segment, the last state of a segment satisfies one of the guards of a transition equation, and together with the first state of the subsequent segment, it satisfies the transition equation. Since from any initial state, there may be several mode equations and transition equations to choose from, a hybrid automaton can have many different behaviors (“nondeterminism”). Two or more hybrid automata can be composed by using, in addition, synchronization labels on the transitions.
Figure 2 shows the hybrid automaton describing the behavior of a heart cell. It has two variables \(v_x\) and \(v_y\) for voltages over cell membrane, four modes resting, stimulus, upstroke, and repolarization, and five synchronization labels in0, in1, out0, out1, and get. The difference \(v_x - v_y\) models the transmembrane voltage potential of the cell, the labels in1 and in0 model rising and falling edges of an input stimulus, and out1 and out0 of an output stimulus, respectively. The label get indicates a spike peak of the cell voltage. The parameters \(a_x\), \(a_y\), \(i_{st}\), \(b_y\), \(c_x\), \(c_y\), \(d_x\), \(d_y\), \(V_R\), \(V_T\), and \(V_O\) are constants and are defined according to the specific cell instance. Initially, the cell is in resting mode and \(v_x\) and \(v_y\) have any values that satisfy the invariant of resting, which is \(0 \le v_x - v_y \le V_R\). Afterwards, the values of \(v_x\) and \(v_y\) continuously evolve according to the differential equation of resting which is given by \(\dot{v}_x = a_x v_x\) and \(\dot{v}_y = a_y v_y\). The parameters \(a_x\) and \(a_y\) are such that \(a_x< a_y < 0\) therefore the voltage drops when in resting, and the continuous evolution progresses as long as the variables satisfy the invariant \(0 \le v_x - v_y \le V_R\). At any time, the automaton can either take a transition labelled by in0 and stay in resting or a transition labelled by in1 and switch to stimulus. In stimulus, the dynamics is governed by the flow \(\dot{v}_x = i_{st}\) and \(\dot{v}_y = b_y v_y\) for the parameters \(b_y< 0 < i_{st}\) and satisfies the invariant \(0 \le v_x - v_y \le V_T\), thus making the voltage rise up to \(V_T\). As long as the values satisfy the invariant \(0 \le v_x - v_y \le V_T\) the automaton can either execute the transition labelled with in1 and stay in stimulus or take in0 and switch back to resting, while as soon as the variable values satisfy the guard \(v_x - v_y \ge V_T\) it can take out1 and switch to upstroke. The trajectory of the potential continues to progress in this manner, namely it evolves continuously in modes and discontinuously on transitions. In the remaining modes upstroke and repolarization the parameters are such that \(c_x> c_y> 0> d_y > d_x\). As a result, we show in Fig. 3 a sample trajectory demonstrating how invariants and guards relate to the automaton modes.
The model of the whole heart consists of a composition of cells, which synchronize according to their output and input stimuli. Figure 4 shows such an example. The cells are organized in a linear fashion, where the labels out1 and out0 of a cell synchronize with the input labels in1 and in0 of the next cell. At the top of the network, we have the sinoatrial (SA) node, which is the cell that takes through in1 and in0 the input stimulus of the heart, which can come from its natural pacing or from the actuator of the pacemaker. The output labels out1 and out0 of the SA node then trigger the input labels of a second cell. The output of the second cell triggers the input of a third, and so on, creating a chain of stimuli. The whole chain can be seen as divided in two main groups, namely atrium and ventricle. The output of the cell at the boundary of the atrium then produces the output of the whole atrium, which is connected to the cell at the top of the ventricle, which is called atrioventricular (AV) node. The AV node may take the pacing coming from the atrium or from the second actuator of the pacemaker.
Hybrid automata synchronize transitions according to their labels, namely, transitions whose labels are shared fire synchronously, while transitions whose labels are not shared fire asynchronously. Figure 4 shows our naming scheme for the synchronization of output and input simili between cells. In particular, we obtain synchronization between the transition labeled by out1 and in1 (resp. out0 and in0) by renaming both to ch1[i] (resp. ch0[i]), where i is the index of the upstream cell. Complementarily, we prevent the synchronization between the transitions labeled by get by renaming each of them to get[i], where i is the index of the respective cell. Figure 5 shows part of the reachable configurations in the composition of two cells. Initially, both automata are in resting (Fig. 5, top left). In the initial configuration, the first automaton can execute all its available transitions (labeled by in1 and in0), while the second cannot execute any (labeled by ch1 and ch0). This is because ch1 and ch0 are shared between the two automata, and therefore can be executed only if both automata can. On the other hand, in1 and in0 appear only in the first automaton, and therefore they can be executed. As a result, in0 and in1 label asynchronous transitions, where the first makes a self loop to the initial configuration, and the second switches the first automaton to stimulus. The latter configuration (Fig. 5, top right) enables a transition labeled by ch1, which is synchronous and switches the first automaton to upstroke and the second to stimulus (Fig. 5, bottom right). In its turn, this configuration enables an asynchronous transition labeled by getA, and so on. The rest of the composition continues similarly.
Some configurations of a composition of two heart cells, where the events out1 and out0 of the left and in1 and in0 of the right cell are renamed, resp., to ch1 and ch0, and get to getA and getB. The active modes in each configuration of two cells are depicted by the black circles. The effect of an enabled transition is shown as a transition between configurations.
Hybrid automata can be classified according to the generality of their guards, differential equations, and difference equations. The more restrictive these equations are, the more feasible the analysis of the resulting behaviors. Assume that x is a state vector. A hybrid automaton has piece-wise affine dynamics if all mode invariants and transition guards have the form \(x \in U\), all mode equations have the form \(\dot{x} = Ax + v\) with \(v \in V\), and all transition equations have the form \(x' = Bx + w\) with \(w \in W\), for matrices A and B, and polyhedra U, V, and W. The hybrid automaton has piece-wise constant dynamics if \(A=0\). It is a timed automaton if \(A=0\) and \(V=1\). In a timed automaton, all state components always advance at the rate of time; they represent “clocks”.
2.2 Timed Automata: Modeling the Pacemaker
The pacemaker monitors the pattern of events emitted by the heart and corrects them via external means when needed. The pacemaker itself is composed of a number of components, each of which is essentially a simple state-machine producing output events triggered by timing constraints. This makes the formalism of timed automata ideal for the description of these components.
Figure 6 shows the architecture block diagram of the entire model. The pacemaker senses the voltage peaks of one cell from the atrium and one cell of the ventricle through the events Aget and Vget (which are renaming of the respective get labels), and controls the heart by sending stimuli to the SA node and the VA node though the labels AP and VP. In particular, upon the occurrence of AP the timed automaton AP-to-A generates a pulse by sending an event i1 to the SA node and after some fixed time sending i0 indicating the end of the stimulus pulse. Similarly, VP triggers VP-to-V which in its turn stimulates the VA node. The events AP and VP are generated by the internals of the pacemaker, which we introduce in this section.
To first informally explain the formalism of timed automata and how they are modelled in the tool Uppaal, we will use the  process shown in Fig. 7. Uppaal timed automaton consists of locations and edges modeling its discrete states and discrete transitions respectively. Locations and edges have labels. For example, process
process shown in Fig. 7. Uppaal timed automaton consists of locations and edges modeling its discrete states and discrete transitions respectively. Locations and edges have labels. For example, process  has an initial location with a circle O inscribed, which has a name label
has an initial location with a circle O inscribed, which has a name label  . The location
. The location  has an invariant label
has an invariant label  meaning that the automaton may stay in
meaning that the automaton may stay in  only while the clock
only while the clock  value is less or equal to the value of the
value is less or equal to the value of the  constant. Process
constant. Process  may stay in location
may stay in location  for arbitrary amount of time because there is no invariant forcing it to move, it also listens for synchronizations over channels
for arbitrary amount of time because there is no invariant forcing it to move, it also listens for synchronizations over channels  and
and  . The reception over channel
. The reception over channel  transitions it to
transitions it to  , while the reception over
, while the reception over  switches it directly to location
switches it directly to location  and reset the clock
and reset the clock  . The location
. The location  has C inscribed to denote that it is committed and the automaton’s progress cannot be interrupted neither by the time delay nor any other process, therefore it has to move immediately by taking an edge transition to location
has C inscribed to denote that it is committed and the automaton’s progress cannot be interrupted neither by the time delay nor any other process, therefore it has to move immediately by taking an edge transition to location  which is labeled with synchronization
which is labeled with synchronization  and update
and update  meaning that it emits a message on channel
meaning that it emits a message on channel  and resets the clock
and resets the clock  so the time is counted from zero in location
so the time is counted from zero in location  up to the bound of
up to the bound of  . Then process
. Then process  may move from location
may move from location  back to
back to  but only when the guard
but only when the guard  is satisfied, i.e. only after spending at least the amount
is satisfied, i.e. only after spending at least the amount  of time in location
of time in location  . As a result, the state of a timed automaton consists of its location and variable values, and there are two kinds of transitions between states: delay (when clock values increase while satisfying the current invariant) and edge-transitions when clock values satisfy the guards, synchronize, update the value and satisfy the target location invariant.
. As a result, the state of a timed automaton consists of its location and variable values, and there are two kinds of transitions between states: delay (when clock values increase while satisfying the current invariant) and edge-transitions when clock values satisfy the guards, synchronize, update the value and satisfy the target location invariant.
In addition to theoretical definition of timed automata Uppaal implements a number of practical extensions which make the modeling task easier and more succinct:
- Integer variables. :
-
Apart from constants, most programming and modeling languages use variable value manipulations. Likewise Uppaal allows bounded integer variables to be used and combined with clock constraints. On one hand, the value of an integer variable becomes an integral part of the state of the system. On the other hand, the integer variable value can be used as a constant in clock constraints because the integer variable value may change only upon edge-transitions between the timed automata states. An example of such integer use is demonstrated by
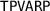 in Fig. 8d, where the bound
in Fig. 8d, where the bound 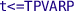 is changed by transition from
is changed by transition from 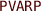 to
to 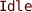 . Interestingly, the bounded integer variables do not increase the theoretical expressiveness of timed automata, therefore all theoretical results still apply. For example, we have compressed the representation of
. Interestingly, the bounded integer variables do not increase the theoretical expressiveness of timed automata, therefore all theoretical results still apply. For example, we have compressed the representation of  and
and 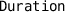 in Fig. 8g and f by encoding the
in Fig. 8g and f by encoding the  and
and  counting into local integer variables
counting into local integer variables  (originally [22] enumerated into a number of distinct locations).
(originally [22] enumerated into a number of distinct locations). - Input-output synchronization. :
-
In contrast to non-directed multi-label synchronizations in SpaceEx hybrid automata, the synchronizations between Uppaal processes are directed in the sense that one process is sending with exclamation mark (e.g.
 ) and the receiving process is listening with question mark (
) and the receiving process is listening with question mark ( respectively). By default, channel synchronizations are handshake, meaning that both sender and receiver must mutually agree for the transition to take place. Handshake synchronizations happen only in pairs of processes, i.e. only two processes may participate in the synchronization at a time, and all possible pairs are considered non-deterministically when multiple receivers are available.
respectively). By default, channel synchronizations are handshake, meaning that both sender and receiver must mutually agree for the transition to take place. Handshake synchronizations happen only in pairs of processes, i.e. only two processes may participate in the synchronization at a time, and all possible pairs are considered non-deterministically when multiple receivers are available. - Broadcast synchronization. :
-
In addition Uppaal supports broadcast synchronization where one sender may synchronize with multiple receivers. In contrast to handshake synchronization, the broadcast synchronization is non-blocking in a sense that the sender is not required to wait for any receivers and only the ready receivers participate in the synchronization. While the broadcast synchronization can be emulated by adding receiving self-loops in locations where the process does not implement the reception part, but in practice it is more succinct way of modeling, allows partial order reduction and verification is more efficient as the tool does not need to consider the extra edges. All the synchronizations in the pacemaker study use broadcast channels because non-blocking behavior is closer to how the independent processes communicate and it is easier to include additional processes without modifying the original behavior, which is useful in adding extra monitors for diagnostics and verification.
- Urgency. :
-
Sometimes the modeled process needs to execute several transitions without delaying in the locations between. We call such locations urgent and draw a letter U inside to mark that time cannot progress in them.
- Atomicity. :
-
The process in urgent location may still be interrupted by a transition in another process even though the time is not allowed to pass. Uppaal implements a committed location with C inscribed in case an uninterrupted (“atomic”) sequence of transitions is needed. Committed locations are useful in connecting multiple channel synchronizations at the same time which would be very cumbersome to model otherwise.
We have reconstructed the pacemaker model from [22] shown in Fig. 8. The overview block diagram of the processes is shown in Fig. 6 where the heart is represented by SA Node cell, two atrium and two ventricle cells. The cells can be stimulated by  and
and  channels synchronizations denoting the start and ending of the stimulus. The heart can be self-stimulating by a SA Node cell or by a pacemaker by a signal over channel
channels synchronizations denoting the start and ending of the stimulus. The heart can be self-stimulating by a SA Node cell or by a pacemaker by a signal over channel  (Atrium Pulse). Normally the atrium cells relay the signal to ventricle cells, but if the stimulus is too weak (or too short), then the ventricle is stimulated by the pacemaker over
(Atrium Pulse). Normally the atrium cells relay the signal to ventricle cells, but if the stimulus is too weak (or too short), then the ventricle is stimulated by the pacemaker over  (Ventricle Pulse) channel. The pacemaker monitors the activity of the atrium and ventricle by receiving from the signals over the corresponding channels
(Ventricle Pulse) channel. The pacemaker monitors the activity of the atrium and ventricle by receiving from the signals over the corresponding channels  and
and  . All channels used in Fig. 8 are of broadcast type, meaning that one sending event can be sensed by zero or more receivers at once and the sending process is not blocked by the absence of receivers.
. All channels used in Fig. 8 are of broadcast type, meaning that one sending event can be sensed by zero or more receivers at once and the sending process is not blocked by the absence of receivers.
Low Rate Interval ( , Fig. 8a) maintains the minimum heart rate by providing pulses to the heart (
, Fig. 8a) maintains the minimum heart rate by providing pulses to the heart ( in DDD mode and
in DDD mode and  in VDI mode) if there was no signal from atrium (
in VDI mode) if there was no signal from atrium ( ) after the last ventricle pulse for longer than
) after the last ventricle pulse for longer than  time interval. The time interval is measured by the clock
time interval. The time interval is measured by the clock  which is reset after the last ventricle pulse (by sensing either
which is reset after the last ventricle pulse (by sensing either  or
or  ). The LRI also monitors the mode switching by reacting to inputs
). The LRI also monitors the mode switching by reacting to inputs  and
and  and starts pacing the ventricle (
and starts pacing the ventricle ( ) instead of atrium (
) instead of atrium ( ).
).
Atrioventricular Interval ( , Fig. 8c) maintains the maximum interval between the atrium and ventricle activation by issuing ventricle pacing
, Fig. 8c) maintains the maximum interval between the atrium and ventricle activation by issuing ventricle pacing  if no ventricular event received
if no ventricular event received  within
within  time after the last atrial event (
time after the last atrial event ( or
or  ). The interval is measured by the clock
). The interval is measured by the clock  shared with Upper Rate Interval (
shared with Upper Rate Interval ( , Fig. 8b) which prevents pacing the ventricle too fast by resetting
, Fig. 8b) which prevents pacing the ventricle too fast by resetting  upon ventricular event (
upon ventricular event ( or
or  ).
).
Postventricular Atrial Refractory Period ( , Fig. 8d) converts atrium events
, Fig. 8d) converts atrium events  and
and  into sensed event
into sensed event  and filters the sensed noise during the blanking period (
and filters the sensed noise during the blanking period ( ) after the ventricular event followed by a refractory period (
) after the ventricular event followed by a refractory period ( ). The blocked events are converted to
). The blocked events are converted to  and
and  for advanced diagnostics.
for advanced diagnostics.
Ventricular Refractory Period ( , Fig. 7) similarly translates the ventricle peak events over
, Fig. 7) similarly translates the ventricle peak events over  into sensed events over
into sensed events over  and filters out by not re-transmitting for a time interval
and filters out by not re-transmitting for a time interval  after the last event.
after the last event.
We use the same set of constants as in the original publication [22]:  .
.
3 Relating and Combining Models
Hybrid automata can be numerically simulated, or formally analyzed. While simulation generates one behavior at a time, formal analysis can answer questions about all possible behaviors of a hybrid automaton. The most basic behavioral analysis question about a hybrid automaton is the reachability question. The bounded reachability question asks, given two state sets S and T, and a time bound t, if there is a behavior from a state in S to a state in T of total duration no more than t. The unbounded reachability question asks, given two sets S and T, if there is a behavior of any duration from a state in S to a state in T. In general, both the bounded and unbounded reachability questions are formally undecidable even for hybrid automata with piece-wise constant dynamics [21]. However, methods and tools have been developed for solving many interesting instances of these problems [17, 20]. Moreover, both questions can always be answered algorithmically for the special case of timed automata [5].
Unfortunately, the heart-pacemaker model is not a timed automaton, as heart cells fall in the class of hybrid automata with piece-wise affine dynamics, and so does their composition with the pacemaker. On the other hand, if each cell model was a timed automaton, the whole system would be a timed automaton, and therefore the verification answer solvable. Can we model each cell with timed automata, so that by verifying the resulting system we verify the original system too? To this aim, we exploit the notion of abstraction: if the timed automaton abstracts the original cell model, then any negative answer for the reachability question in the abstract composed system implies the same negative answer in the original composed system. In the following, we construct such a timed automaton, we explain its relation with the original hybrid automaton, and we demonstrate how to use SpaceEx to mechanically prove that the former abstracts the latter.
3.1 A Timed Abstraction of the Heart Cell Model
We construct a timed automaton A with the same discrete structure of the heart cell model in Fig. 2 and one clock variable. In the abstract model, the clock is reset upon entering each mode, and the transition guards out of a mode are chosen based on the duration of time spent in that mode. Figure 9 shows such construction. The clock variable is t and the times \(T_{out1}\), \(T_{out0}\), and \(T_{get}\) bound respectively the duration before the occurrence of the symbols out1, out0, and get.
Timed abstraction of the hybrid automaton in Fig. 2.
The abstraction has been constructed manually, by making the following observations about the original model in Fig. 2. Initially the cell is in resting mode, where \(v_x - v_y\) drops towards 0, therefore the invariant \(0 \le v_x - v_y \le V_T\) is always satisfied. In mode resting the events in1 and in0 can occur at any time, where in0 is ignored and in1 switches to stimulus. In stimulus the automaton is also driven by the difference \(v_x - v_y\) which may increase and force automaton to move to upstroke. The time bound \(T_{out1}\) models the largest time where \(v_x - v_y\) hits \(V_T\) and satisfies the guard for out1, i.e., \(v_x - v_y \ge V_T\). The symbol out1 may occur any time before \(T_{out1}\), as well as in1 and in0 which may happen as long as the invariant \(0 \le v_x - v_y \le V_T\) of stimulus is satisfied. Upon the occurrence of out1 the value of \(v_x - v_y\) is exactly \(V_T\), the process switches to upstroke in which it stays until the value of \(v_x - v_y\) hits exactly \(V_O\), whose time is modeled by \(V_O\). Similarly, upon get the process switches to repolarization and stays until it takes out0 when \(v_x - v_y\) hits \(V_R\), which must happen no later than \(T_{out0}\) time.
Whether the timed automaton in Fig. 9 is an abstraction of the heart cell model in Fig. 2 requires us to first rigorously define what we mean by abstraction, namely, what are the features of the original system that are to be conserved by the abstract system. Second, we need to instantiate the parameters \(T_{out0}\), \(T_{out1}\), and \(T_{get}\) and prove that the so obtained timed automaton abstracts the original hybrid automaton. We discuss these points in Sects. 3.2 and 3.3. For the time being, the construction of the timed abstraction relies on the intuition and the expertise of the designer. In this phase, the only formal requirement is that the timed automaton needs to deterministic, so that in the next phase we can construct its complement. A timed automaton is deterministic if at every mode every pair of transitions with common symbol have disjoint guards [5]. The timed abstraction of Fig. 9 is deterministic simply because at every mode each symbol has at most one switch.
3.2 The Timed Language of Hybrid Automata
A hybrid automaton A abstracts a hybrid automaton B when all observable behaviors of the latter are also observable behaviors of the former. The observable behaviors are the features of the system dynamics that we need to observe in order to decide whether a specification is satisfied. The more detailed the observable behaviors, the harder is constructing an abstraction, but the more sophisticated are the properties that we can verify. For verifying properties such as Tachycardia, Bradycardia, and so on, we want to observe sequences of labels \(\sigma = \sigma _0\sigma _1\dots \) with the exact times \(\tau = \tau _0\tau _1\dots \) at which each of these events has occurred. Each of such pairs of sequences \((\sigma , \tau )\) is called a timed word. For instance, the word that repeats the pattern \(\mathtt{in1},\mathtt{out1},\mathtt{get},\mathtt{out0}\) is a timed word when coupled with the times of staying respectively in modes resting, stimulus, upstroke, and repolarization, repeatedly. The set of all the timed words of the hybrid automaton H is called its timed language \(\mathcal {L}_H\).
Abstraction with respect to timed languages can be phrased as timed language inclusion, that is to say that the timed automaton A abstracts the hybrid automaton H if \(\mathcal {L}_H \subseteq \mathcal {L}_A\). Alternatively, one can prove that A abstracts H by saying that there does not exist a timed word of H that is not a timed word of A. This is indeed a reachability question for the composition of H with the complement of A, which can be tackled by SpaceEx. To this aim, we first construct the complement automaton for A, i.e., the timed automaton for which all timed words from language \(\mathcal {L}_A\) end up in accepting mode (corresponding to modes in the original automaton) and any other word end up hitting some auxiliary rejecting mode. Then, we use SpaceEx to search for any timed word of H that is rejected by the complement automaton of A, namely a word of their composition that hits a rejecting mode of the latter. If no such word is found, then we can conclude that A abstracts H.
Complement of the timed abstraction in Fig. 9.
The timed abstraction A is deterministic. To complement a deterministic timed automaton we need first to add dummy transitions so to make the automaton accept any timed word (on the same alphabet \(\varSigma = \{ \mathtt{in0}, \mathtt{in1}, \mathtt{out0}, \mathtt{out1}, \mathtt{get}\}\)), yet remaining deterministic. Figure 10 shows the result. From mode resting only in1 and in0 can be received, therefore we add a dummy transition, i.e., a transition to a dummy mode, which receives any other symbol, i.e., out1, out0, and get. From stimulus, in1, in0, and out1 can be received and can be received as long as \(t \le T_{out1}\), therefore we add a dummy transition with guard \(t > T_{out1}\) that receives such events, so as to ensure all guards of transitions with common symbol to be disjoint and maintain the automaton deterministic. The symbols out0 and get cannot be received at all from stimulus, therefore we add a dummy transition with unconstrained guard. Similarly, we make the same construction on modes upstroke and repolarization. Finally, one can observe that every trajectory that ends in any dummy mode corresponds to a timed word that is not in \(\mathcal {L}_A\). The dummy modes are those that recognise the complement language, thus we mark them as rejecting modes.
In summary, we formulate the question of whether the timed abstraction in Fig. 9 abstracts the heart cell model in Fig. 2 by asking SpaceEx whether the composition of the heart cell model in Fig. 2 with the complement automaton in Fig. 10 can reach any of the rejecting modes. The result is a reachability question on hybrid automata with affine dynamics.
3.3 Verifying the Abstraction Using SpaceEx
SpaceEx is a modeling framework for the composition of hybrid automata that collects several reachability analysis techniques, which are called scenarios. We can divide the currently available scenarios in three main categories: simulation based, support function based, and the polyhedra based scenarios. The simulation based scenario generates time-bounded sample trajectories, and can be used to reject an abstraction, but not to verify one. The support function and the polyhedra based scenarios perform reachability analysis by generating sequences of polyhedra that over-approximate the whole space of reachable states and both are possibly suitable for verifying an abstraction. In fact, when they answer that all rejecting modes are unreachable, then the rejecting modes are actually unreachable, and the abstraction is proven. The converse is not necessarily true and, moreover, termination is not guaranteed either. For this reason, successfully concluding an abstraction proof requires several trial and error attempts in tuning the parameters and the multiple heuristic options of SpaceEx.
We use the polyhedral based scenario which is also know as the PHAVer scenario. The PHAVer scenario over-approximates the continuous flow of every mode by piece-wise constant differential inclusions [16]. In other words, it turns affine dynamics of the form \(\dot{x} = Ax + v\) with \(v \in V\) into differential inclusions of the form \(\dot{x} \in U\), where U is a set the contains all values that the derivative \(\dot{x}\) can possibly take. Both such transformation and the symbolic reachability analysis on the so obtained hybrid automaton are then done by quantifier elimination, e.g., by the Fourier Motzkin algorithm [4].
The main challenge is then to choose the time bounds \(T_{out1}\), \(T_{out0}\), and \(T_{get}\). Indeed, if we let \(v_x\) and \(v_y\) take arbitrary negative values it is impossible to find finite bounds, therefore we add the extra invariant \(v_x, v_y \ge 0\) to all modes of the heart cell. Then, we proceed as follows. First, we set all constants using a set of values the original article [30], which we show in Table 1 (except for \(i_{st}\), which is not specified there). Second, we decide a value for \(i_{st}\) and third, we search for tight enough values for \(T_{out1}\), \(T_{out0}\), and \(T_{get}\) until SpaceEx concludes that all rejecting modes are unreachable. Table 2 shows a few attempts to prove reachability of any of the rejecting modes \(r_0\), \(r_1\), \(r_2\), or \(r_4\). The parameters were chosen manually, and SpaceEx converged on each of these proofs in less than a second. The parameters for which none of the rejecting modes are reachable are parameters for which the abstraction is verified.
3.4 Abstraction Refinement
An abstraction captures specific aspects of the original model while it may ignore others, and in some cases, an abstraction may be too coarse for proving a property. For instance, the timed automaton of Fig. 9 captures the upper bounds of the transition times for the labels out1, out0, and get, while it ignores the lower bounds. Without a lower bound for the duration of an output stimulus, properties such as the efficient propagation of a signal through cells (see Sect. 4.3) cannot be proven. In fact, often an abstraction requires to be adapted to the property of interest. This is usually done incrementally, by adding a few important details at a time, through a process of abstraction refinement. In the following, we show how to refine our abstraction by exploiting the compositionality of hybrid and timed automata.
The timed automaton of Fig. 11 captures the requirement that output stimulus of a heart cell should last at least time \(T_{stim}\). As previously, we compute its complement, and we use SpaceEx to prove that for certain parameters of the heart cell model, certain lower bounds are satisfied (see Table 3), in this way obtaining a second abstraction for the original heart cell. We use the new abstraction B to refine the previous abstraction A by composing them, obtaining the timed automaton in Fig. 12, which is again an abstraction of the original system. Table 3 shows the proven parameters. In particular, for the original model (parameters from Table 1, first line in Table 3) we cannot prove any lower bound unless we reduce \(V_R\) and additionally specify the global invariant that x and y do not exceed a maximum voltage \(V_{max}\). For instance, with \(V_{max} = 100\) and \(V_R = 5\), we have a lower bound of 0.86. The lower bound for the stimulus length depends on \(V_{max}\), \(V_R\), and the coefficient \(d_x\), e.g., with \(d_x = -0.83\), we have \(T_{stim} = 1.001\).
In summary, we construct a sequence of time abstractions for a heart cell and formally proved that they indeed abstract its timed language. The abstraction question turns out to be a reachability question on a heart cell composed with the complement of its timed abstraction, which is a rather small system. We employ SpaceEx on this problem, and then we modify the heart-pacemaker model by replacing each cell with the abstraction. The whole model is now a timed automaton, which can be verified by Uppaal.
4 Verifying Temporal Requirements
Several behavioural properties of (composite) timed and hybrid automata models may be expressed as simple reachability properties. This is already illustrated previously in Sect. 3.2, where we saw that language inclusion between the “exact” hybrid automaton model H of a heart cell and a proposed timed automaton abstraction A could be stated as a simple reachability property of rejecting locations in a product between H and the complement of A. However, it may often be more convenient to express desired properties of a timed or hybrid automaton directly as formulas of temporal logic, thus permitting properties to be combined using boolean connectives. In fact the whole spectrum of temporal-logic has been extended to the setting of timed labelled transition systems, with model checking suitably extended to timed automata, see e.g. [9]. In this section we demonstrate how timed automata verification using Uppaal may be used in establishing key properties of the pace-maker.
4.1 Timed Automaton of a Heart Cell in Uppaal
Figure 12 shows the Uppaal version of the heart cell timed automaton abstract model of Fig. 9. The locations in the timed automaton match their corresponding modes in the hybrid automaton and the timings are taken from Table 3 and converted into microseconds as shown in Fig. 12b. Note that  was determined as a minimum delay between
was determined as a minimum delay between  and
and  events, therefore we use an extra clock
events, therefore we use an extra clock  to enforce this constraint. This lower bound on the repolarization time turned out to be important to ensure a successful signal handover as verified in Sect. 4.3.
to enforce this constraint. This lower bound on the repolarization time turned out to be important to ensure a successful signal handover as verified in Sect. 4.3.
4.2 Requirement Specifications
The model checker Uppaal supports verification of requirements expressed within a fragment of Timed Computation Tree Logic (TCTL). Among TCTL properties we consider here the following:
-
\(\mathbf {A}\Box \varphi \), which is satisfied if any reachable state satisfies \(\varphi \) (Invariance),
-
\(\mathbf {A}\Box _{\le T}\varphi \), which is satisfied if any state reachable within T time-units satisfies \(\phi \) (Time-bounded Invariance),
-
\(\mathbf {A}\Diamond \varphi \), which is satisfied if on any path the properties \(\varphi \) is (eventually) satisfied at some point (Eventual),
-
\(\mathbf {A}\Diamond _{\le T}\varphi \) which is satisfied if on any path the property \(\varphi \) is satisfied within T time-units \(\varphi \) (Time-Bounded Eventual),
-
\(\varphi \leadsto _{\le T}\psi \), which requires than whenever a state is reached satisfying \(\varphi \), then any path from this state must eventually satisfy \(\psi \) – and within a total of T time-units. Logically, the (time-bounded) leads-to property is equivalent to \(\mathbf {A}(\varphi \Rightarrow \mathbf {A}\Diamond _{\le T}\psi )\) (Time-Bounded Leads-to).
For deterministic timed labelled transition systems, it may easily be shown that all of the above properties – as they all quantify universally over execution sequences out of a state – are preserved by language inclusion. Thus, if \(\mathcal{L}_H\subseteq \mathcal{L}_A\) and A has been verified to satisfy a TCTL property \(\varphi \) of the above type, then it may readily be concluded that the “exact” model H also satisfies \(\varphi \).
Moreover, as demonstrated in [1] all of the above properties may be expressed directly as a reachability property—i.e. invariance properties—of the given timed automaton composed with a monitor corresponding to the property.
4.3 Healthy Heart Requirements
Figure 13 shows the state evolution of 10 heart cell timed automata connected in series. In the beginning all cells are in  (red bar), then the first cell is stimulated and moves to
(red bar), then the first cell is stimulated and moves to  (yellow bar). After a short while the first cell stimulates the second one and moves to
(yellow bar). After a short while the first cell stimulates the second one and moves to  (green bar), then it moves to
(green bar), then it moves to  (blue bar) and back to
(blue bar) and back to  (red bar). The second cell then stimulates the third and so on.
(red bar). The second cell then stimulates the third and so on.
Gantt chart of state evolution of 10 cell automaton from Fig. 12.
A healthy heart should propagate the signal all the way from SA node to atrium and then ventricle. This requirement can be formulated as the following leads-to property:

which says that for every stimuli of the first cell ( ) we should eventually observe the signal at the end of the chain (
) we should eventually observe the signal at the end of the chain ( ), where
), where  is the number of cells. Uppaal verifies that this property holds when
is the number of cells. Uppaal verifies that this property holds when  , i.e. the lower bound of being in repolarization is greater than the time spent in
, i.e. the lower bound of being in repolarization is greater than the time spent in  , and the signal propagates successfully just like in the Gantt chart in Fig. 13b. It takes 0.2 s to verify an instance of four cells, 6.8 s for five and 28 min for six, which shows signs of the state space explosion in terms of the number of processes due to non-deterministic behavior. Interestingly the property is not satisfied if the cell stays in
, and the signal propagates successfully just like in the Gantt chart in Fig. 13b. It takes 0.2 s to verify an instance of four cells, 6.8 s for five and 28 min for six, which shows signs of the state space explosion in terms of the number of processes due to non-deterministic behavior. Interestingly the property is not satisfied if the cell stays in  longer than in
longer than in  , i.e.
, i.e.  , because the signaling cell may go from
, because the signaling cell may go from  to
to  , stop the stimulus and bring the next cell back to
, stop the stimulus and bring the next cell back to  , thus disrupting the signal. One such particular scenario is visualized in Fig. 13c: the
, thus disrupting the signal. One such particular scenario is visualized in Fig. 13c: the  of
of  is interrupted by
is interrupted by  by a quick move back to
by a quick move back to  before
before  reaches
reaches  , hence
, hence  stays in
stays in  and the signal is lost. We conclude that the relation between maximum delay in
and the signal is lost. We conclude that the relation between maximum delay in  and total delay in
and total delay in  and
and  is crucial for correct signal propagation through heart cell network.
is crucial for correct signal propagation through heart cell network.
In addition to checking the signal propagation we can also estimate the minimum and maximum delay time between the start and end of the signal by using the duration monitor automaton and queries shown in Fig. 14. The infimum and supremum queries instruct Uppaal to record the minimum and maximum values of clock  when the automaton in the corresponding locations
when the automaton in the corresponding locations  and
and  . Note that the automaton always stays in location
. Note that the automaton always stays in location  in between the
in between the  and
and  events, therefore the supremum of
events, therefore the supremum of  corresponds to the time duration between those events. And the automaton visits
corresponds to the time duration between those events. And the automaton visits  when
when  has its maximum value, therefore the infimum of
has its maximum value, therefore the infimum of  in
in  corresponds to the shortest observed duration between events.
corresponds to the shortest observed duration between events.
In case of our chain of heart cell timed automata – using the above pattern – the duration between  and
and  is found to be bounded by the interval of [0, N]ms, where N is the number of cells in series. Due to congruence properties of abstraction, this bound is guaranteed to be valid also for the composition of hybrid heart cells in Fig. 5.
is found to be bounded by the interval of [0, N]ms, where N is the number of cells in series. Due to congruence properties of abstraction, this bound is guaranteed to be valid also for the composition of hybrid heart cells in Fig. 5.
4.4 Abstraction of Cell Composition
Once we have estimated the duration of a signal travel through the chain of cells, we can model the entire chain as one automaton re-transmitting the signal with a delay. By replacing a chain of cells with one process we reduce the verification effort significantly without losing the precision. We model the atrium and the ventricle as separate processes representing a sequence of individual heart cells. Figure 15a shows a healthy atrium which relays its activation signal to the recipient (ventricle and pacemaker) by delaying 150 ms. We model an atrium which may loose a signal by taking an extra transition without notifying the recipient in Fig. 15a to reflect abnormal behavior. The ventricle part of the heart is modeled likewise. The sinoatrial node is responsible for triggering the heart beating process and is modelled in Fig. 15b. In principle, healthy SANode may beat with interval of 500–2000 ms (30–120 bpm), but a faulty one may beat more or less frequently or stop beating altogether, thus we do not put any constraints to allow all possible (healthy and faulty) behavior to allow a pacemaker to do its job, there the verification will cover all possible scenarios (failure may occur at any time, in SANode, atrium or ventricle). The result is a sequence of signals: the SANode stimulates atrium and atrium stimulates ventricle, but atrium and ventricle may also be stimulated by a pacemaker, thus we also add a pacing process which multiplexes the pacing events ( and
and  ) with heart events (
) with heart events ( and
and  ) into atrium (
) into atrium ( ) and ventricle (
) and ventricle ( ) stimuli as shown in Fig. 15c.
) stimuli as shown in Fig. 15c.
4.5 Pacemaker Requirements
The pacemaker is required not to issue ventricle pace events ( ) for at least
) for at least  time units since the last ventricle pulse (
time units since the last ventricle pulse ( ) or the ventricle sense (
) or the ventricle sense ( ) events. This requirement can be formulated into the following TCTL property:
) events. This requirement can be formulated into the following TCTL property:

This property expresses that the action  may only occur after a time-separation of at least
may only occur after a time-separation of at least  time-units from a previous
time-units from a previous  of
of  action. Dually, the requirement that the interval between two ventricular events (either
action. Dually, the requirement that the interval between two ventricular events (either  or
or  ) should be less than
) should be less than  can be expressed as the following property:
can be expressed as the following property:

which says that the actions  and
and  must occur with at most a time-separation of
must occur with at most a time-separation of  time-units.
time-units.
Uppaal implements TCTL referring to system states rather than synchronization events, therefore the above properties are converted into the event-monitoring automata (Fig. 16a and b respectively) and the requirements are reformulated in terms of monitoring automata locations and clock values. The monitor transitions are labeled with  and
and  synchronizing with the corresponding events
synchronizing with the corresponding events  and
and  , and the local clocks
, and the local clocks  are reset accordingly, so that the value of the local clock
are reset accordingly, so that the value of the local clock  in locations
in locations  and
and  corresponds to the time duration between two successive events. The property then verifies that the duration is within bounds
corresponds to the time duration between two successive events. The property then verifies that the duration is within bounds  and
and  .
.
Automata and queries for timed properties from [22].
The model with abstracted heart cell chain had too large state space to verify due too many non-deterministic processes in the heart. Interestingly the unrestricted “random” heart model (as described in [22]) takes much less resources as it does not need to remember the complex heart state. We used a heart model with arbitrary rate \((0,\infty )\) which may beat at any time or not at all. Such heart captures all possible heart behaviors and hence verification provides a much stronger safety guarantee than with the more realistic and detailed heart model. Table 4 shows that the basic DDD pacemaker model is simple enough that it hardly takes any time to verify (0.01 s, 5.37 MB). The DDD-VDI pacemaker includes counters and thus the behavior is much more complicated leading to more verification effort (129.57 s, 248.26 MB). We found that the lower rate limit property does not hold with  bound on more complex DDD-VDI pacemaker (the result is “Not OK”), but the basic DDD satisfies the lower rate limit with twice as large
bound on more complex DDD-VDI pacemaker (the result is “Not OK”), but the basic DDD satisfies the lower rate limit with twice as large  bound, meaning that the pacemaker may delay longer before pacing, but the bound is still reasonable (one pulse per 1.5 s).
bound, meaning that the pacemaker may delay longer before pacing, but the bound is still reasonable (one pulse per 1.5 s).
5 Future Directions and Challenges
As illustrated by the case study presented in this paper, model-based design and verification is a promising approach to the development of cyber-physical systems in a principled manner, and the foundations of this methodology lie in cross-fertilization of ideas from mathematical modeling and algorithmic analysis. As systems keep getting more and more complex, and society increasingly relies upon the internet of things, advances in tools for designing such systems are crucial to ensuing the safe and reliable operation of systems. This calls for continued research in core areas of formal methods such as identification of analyzable design abstractions, analysis techniques, and scalability of tools. We conclude this paper by highlighting some directions for future research.
Scalability: Given the computational intractability of the computational problems in formal verification, developing tools that can analyze real-world systems will always remain a challenge. The experience with tools such as Uppaal demonstrates that small steps in advancing the scalability collectively contribute towards impressive results over the long haul. For the verification of hybrid systems, tools based on robustness analysis offer promising opportunities [14, 15]. Robust analysis means that results obtained should not be too sensitive with respect to the actual quantities (timing, voltages, energy, etc.) used in the underlying model. Efforts on identifying metrics that will ensure “continuity” of various behavioral properties are currently being researched for a number of quantitative modeling formalisms. As illustrated in Sect. 3, abstraction is an effective way of reducing the complexity of a system, and developing techniques for constructing abstractions automatically remains a challenge.
Quantitative Analysis: Traditionally, models and techniques used for establishing correctness and for evaluating performance have been disjoint. In our pacemaker case study, beyond functional correctness of the control algorithm, we are also interested in estimating, for instance, the average energy used by the pacemaker. A promising new direction in formal methods research these days is the development of probabilistic models, with associated tools for quantitative evaluation of system performance along with correctness (see [23]).
Applications: Given the scalability challenges, formal methods for the design and analysis of cyber-physical systems are not yet widely applicable. Thus, identifying application domains and problems where the current techniques and tools can be applied effectively is itself a challenge that requires an understanding of formal methods as well as the application domains. As our example of pacemaker suggests, medical cyber-physical systems is a promising domain, and other interesting recent case studies include an infusion pump and an artificial pancreas [27]. Another promising domain of application is ensuring the safety of controllers used in autonomous vehicles [24].
Data-Driven Models: As our case study illustrates, a key step is the construction of the heart model. Mathematical models of physical systems are hard to obtain, but increasingly, due to the rapid proliferation of sensors, lots of data is available. This leads to a new research question: given the pacemaker algorithm and the property that we want to verify, can we construct a patient-specific model of the heart derived from the sensory data obtained from a patient? Deriving models suitable for formal analysis from data is a challenging, and relatively unexplored, research area.
References
Aceto, L., Bouyer, P., Burgueño, A., Larsen, K.G.: The power of reachability testing for timed automata. In: Arvind, V., Ramanujam, S. (eds.) FSTTCS 1998. LNCS, vol. 1530, pp. 245–256. Springer, Heidelberg (1998). https://doi.org/10.1007/978-3-540-49382-2_22
Alur, R.: Principles of Cyber-Physical Systems. MIT Press, Cambridge (2015)
Alur, R., Courcoubetis, C., Dill, D.: Model-checking in dense real-time. Inf. Comput. 104(1), 2–34 (1993)
Alur, R., Courcoubetis, C., Halbwachs, N., Henzinger, T., Ho, P.-H., Nicollin, X., Olivero, A., Sifakis, J., Yovine, S.: The algorithmic analysis of hybrid systems. Theoret. Comput. Sci. 138, 3–34 (1995)
Alur, R., Dill, D.L.: A theory of timed automata. Theoret. Comput. Sci. 126(2), 183–235 (1994)
Alur, R., Henzinger, T., Lafferriere, G., Pappas, G.: Discrete abstractions of hybrid systems. Proc. IEEE 88(7), 971–984 (2000)
Behrmann, G., David, A., Larsen, K., Pettersson, P., Yi, W.: Developing uppaal over 15 years. Softw. - Pract. Exp. 41(2), 133–142 (2011)
Behrmann, G., David, A., Larsen, K.G.: A tutorial on Uppaal. In: Bernardo, M., Corradini, F. (eds.) SFM-RT 2004. LNCS, vol. 3185, pp. 200–236. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30080-9_7
Bouyer, P., Fahrenberg, U., Larsen, K.G., Markey, N., Ouaknine, J., Worrell, J.: Model checking real-time systems. In: Clarke, E., Henzinger, T., Veith, H. (eds.) Handbook of Model Checking. Springer, Heidelberg (2017)
Chen, T., Diciolla, M., Kwiatkowska, M., Mereacre, A.: Quantitative verification of implantable cardiac pacemakers over hybrid heart models. Inf. Comput. 236, 87–101 (2014). Special Issue on Hybrid Systems and Biology
Clarke, E., Grumberg, O., Long, D.: Model checking and abstraction. In: Proceedings of 19th ACM Symposium on Principles of Programming Languages, pp. 343–354 (1992)
Clarke, E., Grumberg, O., Peled, D.: Model Checking. MIT Press, Cambridge (2000)
Derler, P., Lee, E.A., Sangiovanni-Vincentelli, A.L.: Modeling cyber-physical systems. Proc. IEEE 100(1), 13–28 (2012)
Duggirala, P.S., Fan, C., Mitra, S., Viswanathan, M.: Meeting a powertrain verification challenge. In: Kroening, D., Păsăreanu, C.S. (eds.) CAV 2015. LNCS, vol. 9206, pp. 536–543. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21690-4_37
Fainekos, G.E., Sankaranarayanan, S., Ueda, K., Yazarel, H.: Verification of automotive control applications using S-TaLiRo. In: IEEE American Control Conference, pp. 3567–3572 (2012)
Frehse, G.: PHAVer: algorithmic verification of hybrid systems past HyTech. In: Morari, M., Thiele, L. (eds.) HSCC 2005. LNCS, vol. 3414, pp. 258–273. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-31954-2_17
Frehse, G., et al.: SpaceEx: scalable verification of hybrid systems. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 379–395. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22110-1_30
Henzinger, T.A., Sifakis, J.: The embedded systems design challenge. In: Misra, J., Nipkow, T., Sekerinski, E. (eds.) FM 2006. LNCS, vol. 4085, pp. 1–15. Springer, Heidelberg (2006). https://doi.org/10.1007/11813040_1
Henzinger, T.A.: The theory of hybrid automata. In: Inan, M.K., Kurshan, R.P. (eds.) Verification of Digital and Hybrid Systems, vol. 170, pp. 265–292. Springer, Heidelberg (2000). https://doi.org/10.1007/978-3-642-59615-5_13
Henzinger, T.A., Ho, P.-H., Wong-Toi, H.: HyTech: a model checker for hybrid systems. In: Grumberg, O. (ed.) CAV 1997. LNCS, vol. 1254, pp. 460–463. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-63166-6_48
Henzinger, T.A., Kopke, P.W., Puri, A., Varaiya, P.: What’s decidable about hybrid automata? J. Comput. Syst. Sci. 57(1), 94–124 (1998)
Jiang, Z., Pajic, M., Moarref, S., Alur, R., Mangharam, R.: Modeling and verification of a dual chamber implantable pacemaker. In: Flanagan, C., König, B. (eds.) TACAS 2012. LNCS, vol. 7214, pp. 188–203. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28756-5_14
Kwiatkowska, M.: Quantitative verification: models, techniques, and tools. In: Proceedings of ACM SIGSOFT Symposium on Foundations of Software Engineering, pp. 449–458 (2007)
Larsen, K.G., Mikučionis, M., Taankvist, J.H.: Safe and optimal adaptive cruise control. In: Meyer, R., Platzer, A., Wehrheim, H. (eds.) Correct System Design. LNCS, vol. 9360, pp. 260–277. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-23506-6_17
Larsen, K.G., Pettersson, P., Yi, W.: Uppaal in a nutshell. Int. J. Softw. Tools Technol. Transf. 1(1–2), 134–152 (1997)
Lee, E.A.: What’s ahead for embedded software. IEEE Comput. 33, 18–26 (2000)
Lee, I., Sokolsky, O., Chen, S., Hatcliff, J., Jee, E., Kim, B., King, A., Mullen-Fortino, M., Park, S., Roederer, A., Venkatasubramanian, K.: Challenges and research directions in medical cyber-physical systems. Proc. IEEE 100(1), 75–90 (2012)
Pajic, M., Jiang, Z., Lee, I., Sokolsky, O., Mangharam, R.: Safety-critical medical device development using the UPP2SF model translation tool. ACM Trans. Embed. Comput. Syst. 13(4), 127:1–127:26 (2014)
Vardi, M., Wolper, P.: Reasoning about infinite computations. Inf. Comput. 115(1), 1–37 (1994)
Ye, P., Entcheva, E., Grosu, R., Smolka, S.A.: Efficient modeling of excitable cells using hybrid automata. In: Proceedings of Computational Methods in System Biology, pp. 216–227 (2005)
Acknowledgements
This research was supported in part by the Austrian Science Fund (FWF) under grants S11402-N23(RiSE/SHiNE) and Z211-N23 (Wittgenstein Award). This research has received funding from the Sino-Danish Basic Research Centre, IDEA4CPS, funded by the Danish National Research Foundation and the National Science Foundation, China, the Innovation Fund Denmark centre DiCyPS, as well as the ERC Advanced Grant LASSO.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Alur, R., Giacobbe, M., Henzinger, T.A., Larsen, K.G., Mikučionis, M. (2019). Continuous-Time Models for System Design and Analysis. In: Steffen, B., Woeginger, G. (eds) Computing and Software Science. Lecture Notes in Computer Science(), vol 10000. Springer, Cham. https://doi.org/10.1007/978-3-319-91908-9_22
Download citation
DOI: https://doi.org/10.1007/978-3-319-91908-9_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-91907-2
Online ISBN: 978-3-319-91908-9
eBook Packages: Computer ScienceComputer Science (R0)












 ).
).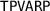 in Fig.
in Fig. 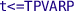 is changed by transition from
is changed by transition from 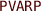 to
to 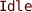 . Interestingly, the bounded integer variables do not increase the theoretical expressiveness of timed automata, therefore all theoretical results still apply. For example, we have compressed the representation of
. Interestingly, the bounded integer variables do not increase the theoretical expressiveness of timed automata, therefore all theoretical results still apply. For example, we have compressed the representation of  and
and 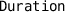 in Fig.
in Fig.  and
and  counting into local integer variables
counting into local integer variables 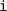 (originally [
(originally [ ) and the receiving process is listening with question mark (
) and the receiving process is listening with question mark ( respectively). By default, channel synchronizations are handshake, meaning that both sender and receiver must mutually agree for the transition to take place. Handshake synchronizations happen only in pairs of processes, i.e. only two processes may participate in the synchronization at a time, and all possible pairs are considered non-deterministically when multiple receivers are available.
respectively). By default, channel synchronizations are handshake, meaning that both sender and receiver must mutually agree for the transition to take place. Handshake synchronizations happen only in pairs of processes, i.e. only two processes may participate in the synchronization at a time, and all possible pairs are considered non-deterministically when multiple receivers are available.






 and
and  events.
events.
