Surface Prediction for Spatial Augmented Reality

Abstract

Image projection in spatial augmented reality requires tracking of non-rigid surfaces to be effective. When a surface is moving quickly, simply using the measured deformation of the surface may not be adequate as projectors often suffer from lag and timing delays. This paper uses a novel approach for predicting the motion of a non-rigid surface so images can be projected ahead of time to compensate for any delays. The extended Kalman filter based algorithm is evaluated using an experimental setup where an image is project onto a deformable surface being perturbed by “random” forces. The results are quite positive, showing a visible improvement over using standard projection techniques. Additionally, the error results show that the algorithm can be used in most surface tracking applications.

1 Introduction

In spatial augmented reality (SAR) applications, the projection of images onto non-rigid surfaces can pose many issues. As the surface geometry is not necessarily stationary, standard projection techniques can fail to create a realistic experience for the user due to improper image mapping. For applications where realism is of great importance, this can affect how well a user can perform their intended task. An obvious approach to solving this problem is to track the surface geometry and project warped images onto the measured surface. There have been a number of studies that have investigated tracking and projecting onto non-rigid surfaces [7, 10, 11]; however, for quickly changing surfaces, there is no mention of how well these techniques perform. When a surface being projected onto is moving quickly, the computational time of processing images, in addition to surface tracking, may cause delays that lead to distortions in the images. To combat this, a prediction scheme can be used to approximate the position of the surface at the time of projection, resulting in a smoother experience for the user. The aim of this paper is to show that a prediction based surface tracking algorithm [3] does in fact improve the realism of SAR by running the algorithm on a real-time experiment. There are many industries that could benefit from using this kind of technology namely the entertainment and fashion industries, and the field of surgical training [2]. Specifically, simulated surgery using spatial augmented reality is a growing method of surgical training that requires non-rigid surface projection, as the surface (the body) changes shape during the course of the procedure. In fashion, SAR is used to display images on clothing for artistic expression, and non-rigid surface tracking lends itself naturally to this application. It is expected that the methods introduced in this paper will be applicable to each of these fields. This paper does not cover any image warping or projection techniques as it is assumed standard techniques will be used for projection. This paper is organized as follows: Sect. 1 discusses the modelling of the non-rigid surface, Sect. 2 introduces the prediction based surface tracking algorithm, Sect. 3 provides a description of the experimental procedure for real-time application of the algorithm, Sect. 4 presents the results of the experiment and Sect. 5 lists conclusions and future work.

2 System Model

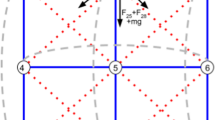
To implement a prediction scheme for surface tracking, a physically accurate deformable model that describes the motion of a surface needs to be developed. A large number of deformable models have been studied in the field of computer graphics, ranging from aesthetically pleasing models to physically accurate models. In this research, mass-spring systems are used to model the dynamics of deformable surfaces due to their simplicity, speed and ease of construction. Mass-spring systems are so popular that they are being used for simulations of deformable bodies in new applications [6]. First developed by Provot [9], the mass-spring model represents a surface by an interconnection of point masses, also called nodes, springs and dampers. As seen in Fig. 1, each point mass is connected to all adjacent nodes with structural springs (or dampers), diagonal nodes with shear springs (or dampers) and nodes that are two steps away with flexion springs (or dampers). Thus, point masses can be connected to anywhere from 3 to 12 other nodes.

Fig. 1.

Connection of point masses with structural springs (blue), shear springs (red dashed), and flexion springs (grey dashed) (Color figure online)

The dynamics of the system can be written in the state space form:

$$\begin{aligned} x[k+1]=f(x[k],u[k]), \end{aligned}$$

(1)

$$\begin{aligned} y[k]=Cx[k], \end{aligned}$$

(2)

where x[k] is the state vector containing the position and velocity information of each node at time-step k, f(x, u) contains the nonlinear dynamics of the system and u[k] is a vector of input forces. The matrix C in Eq. (2) selects only the position states from the state vector to be the output of the model.

To account for errors between the model and the real-life plant, a random process w[k], with covariance $Q_k$, is added to the state Eq. (1) and a random process v[k], with covariance $R_k$, is added to the output Eq. (2). The state and output equations now become:

$$\begin{aligned} x[k+1]=f(x[k],u[k])+w[k], \end{aligned}$$

(3)

$$\begin{aligned} y[k]=Cx[k]+v[k]. \end{aligned}$$

(4)

Although the inner dynamics of the model are linear, the geometry of the model causes nonlinearities (similar to those of a pendulum) that require linearization to be used with the estimation algorithm presented in Sect. 3. Using the standard approach of linearization, the dynamics are converted to the simpler form of

$$\begin{aligned} x[k+1]=Fx[k]+Bu[k]+w[k], \end{aligned}$$

(5)

where F is the Jacobian matrix of f(x, u) with respect to x and B is a matrix that selects the inputs related to the velocity states.

With the dynamics of the surface defined in a state space form, the model can easily be implemented into estimation filters; one of which will be used in the algorithm described in the next section.

3 Prediction Algorithm

A common technique to predict states of a nonlinear dynamic system is the extended Kalman filter (EKF) algorithm [1]. The EKF is a extension of the standard Kalman filter, which is an algorithm that uses measured outputs of a system to make estimates of the internal behaviour of the system. The Kalman filter can be used to find state estimates when measurements are corrupted with noise, but can also be used as an algorithm for state prediction. The standard Kalman filter produces the optimal estimate of a system under the condition that the dynamics of system are linear and any measurement or modelling error is Gaussian distributed. The EKF extends the Kalman filter to systems that have nonlinear dynamics. As a result, since the dynamics of the mass-spring system are nonlinear, the EKF can be used to predict the motion of a non-rigid surface. The EKF uses the linearized model, Eq. (5), to update the estimates of the system; thus, it only gives a first-order approximation of system states. As a result, the EKF only gives a “near-optimal” estimate of the system.

Figure 2 shows a simple flow chart of the EKF algorithm where the function f(x, u) describes the dynamics of mass-spring model and the plant is the real-life system on which measurements are made. At each prediction time-step, $T_m$, the most recent estimate of the non-rigid surface, $x_{k-1|k-1}$, is passed through the mass-spring model, Eq. (1), and a prediction of the surface position and velocity, $x_{k|k-1}$, is made. This prediction is used as the best “guess” of what the surface will look like one time-step into the future. The state covariance matrix $P_{k-1|k-1}$ is sent through the linearized model to produce the predicted state covariance matrix $P_{k|k-1}$. The state covariance matrix gives a description of how correlated the states of the system are to one another at each iteration of the algorithm. This entire step is known as the Kalman prediction step of the EKF. After a new measurement, y, is made from the real-world surface, it is combined with the state prediction $x_{k|k-1}$ and predicted covariance matrix $P_{k|k-1}$ to produce the “near-optimal” state estimate $x_{k|k}$. This part of the algorithm is called the Kalman update step. The state estimate will then be used to create a new prediction for the next time-step, and the algorithm repeats itself. An issue that can arise when measuring the position of a surface is the occlusion of markers. If only measurement data was used to determine the surface geometry, losing vision of a marker would make the projection nearly impossible. However, using this prediction algorithm, the lost marker’s position can be approximated using the Kalman prediction, which is a very close estimate of the true position of the marker. This allows occlusion compensation to be nearly free, provided the markers are not covered for an extended period of time.

When running the EKF algorithm for SAR applications, a projector needs to project images on the predicted surface. This can pose issues as the projector takes a certain amount of time to receive and process images from a computer and an additional amount of time to draw a frame. It is well known that projectors suffer from delays when processing images and these delays usually range from 20 ms to 100 ms depending on the type of projector [4]. This delay, $T_d$, is troublesome when using the EKF for surface prediction in real-time. Since an image needs to be sent to the projector $T_d$ seconds in advance to be projected at the correct time, the EKF needs to predict the geometry of the surface $T_d$ seconds in the future at each Kalman predict step. Now, since measurements are received every $T_m$ seconds, the EKF can only update the state estimate every $T_m$ seconds. An issue arises when the delay time $T_d$ and measurement time $T_m$ do not match (i.e. are vastly different). The time of the current state prediction and the time at which the measurement is made will never be the same. This means the traditional EKF algorithm will not work, as the prediction and measurement times need to line up. To fix this issue, a further prediction, using numerical integration, is made to align the time of the current state prediction with the current measurement. At this stage, a new estimate can be made using the regular EKF algorithm.

When compensating for the delay caused by the drawing of a frame, it is imperative to consider the speed at which the surface is moving compared to the drawing rate. Surfaces that move quickly with respect to the drawing rate of the projector may incur additional image distortion because the projector is still drawing an “old” image. To compensate for the effects of surface movement during the drawing of frames, an inter-frame prediction (IFP) method is proposed. Considering that the update rate of the EKF is $T_m$ seconds, if the cloth’s position changes significantly during inter-sample periods, there may be significant error between the prediction and the actual position of the cloth when a new measurement is made. To compensate for this, an interpolation approach is used. As the cloth is moving, the EKF solves for an estimate of the velocity states, and using a first-order approximation, the inter-sample position of every node is calculated. This estimation is based on the assumption that drawing horizontally is instantaneous.

Fig. 2.

Block diagram of the EKF algorithm with the mass-spring model

Using the state prediction ${x}_{k|k-1}$, which was solved with Eq. (1) and the corresponding time-step, $n\varDelta T$, where n is the row number and the time-step $\varDelta T$ is defined by

$$\begin{aligned} \varDelta T=\frac{1}{\text {frame rate}\times (\#\text {rows}-1)}, \end{aligned}$$

(6)

the inter-frame prediction can be computed. First the state prediction vector is split into a position prediction vector ${p}_{k|k-1}$ and a velocity prediction vector ${v}_{k|k-1}$. The position predictions are then reordered, such that the elements are ordered based on their horizontal position with respect to the projector. More specifically, the first i elements of the position vector would contain the positional information of the first horizontal row of nodes with respect to the projector, the next j elements would contain the positional information of the second horizontal row of nodes with respect to the projector, and so on (Fig. 3).

Fig. 3.

Orientation of cloth with respect to projector for inter-frame prediction

After reordering the states, the predictions are passed through the state transition function f(x, u), described by Eq. (1). This returns the derivative of the position state predictions, and as a result, the velocities to obtain the next position vector. The velocity vector is then multiplied by a matrix describing the time at which each row of the object is predicted. The result is added to the position estimates to obtain the inter-frame position predictions ${p}_{k|k-1}'$. At a time $t_0$, when the system receives a measurement from the cameras, the current prediction at $t_0$ is combined with the measurement to produce the new estimate. This is done using the aforementioned Kalman update step. Since the time between measurements, $T_m$, is quite large, the IFP algorithm is run at a time-step of $\varDelta T$ to counteract the effects of surface motion while drawing. When each new estimate is calculated, every $T_m$ seconds, the Kalman predict step of the EKF is run to create a prediction $T_d$ seconds into the future. This is done to have a prediction of the surface when the projector is ready to draw a frame. This new Kalman prediction replaces the prediction from the IFP algorithm, and the whole sequence repeats itself until termination. The entire EKF-IFP algorithm, compensating for projector delay, is shown in Fig. 4.

Fig. 4.

Timing diagram of EKF-IFP algorithm. $\varDelta T$ is the IFP time-step, $T_m$ is the measurement time, and $T_d$ is the delay time.

4 Experimental Setup

In order to validate the algorithm proposed in Sect. 3, an experimental procedure is designed in this section. The goal of the experiment is to show the effectiveness of using the EKF-IFP algorithm when compared to simply projecting with no compensation. This will be done by projecting an image onto a perturbed surface, and using subjective measures to determine whether using the EKF-IFP algorithm is superior to using no compensation. An obvious choice of material to act as the non-rigid surface for the experiment is something cloth-like, as it would be quite deformable. Thus, a towel is chosen as the surface to be projected onto since it is quite sensitive to external forces. A number of different techniques can be used for capturing positional data of the towel’s surface, such as image processing techniques or 3D scanning systems; however, for greater data accuracy, a motion capture system is used in this experiment. The NaturalPoint OptiTrack system [8] is an infra-red (IR) camera-based motion capture system that provides positional data, both translational and rotational, within millimeter precision. For this experiment, a three camera configuration is used to measure the position of 12.7 mm diameter infra-red markers. The markers are placed on the towel to match the initial positions of the mass nodes in the model. Specifically, 20 markers are placed on the towel corresponding to a $5 \times 4$ node mass-spring system used to model the system. The towel is hung vertically, just as it would be on a standard towel rack, such that all the IR markers are visible to the cameras. An Epson VS240 short-throw projector is placed directly in front of the towel, and below the cameras as to not interfere with the cameras’ view. Figure 5 shows the complete experimental setup.

Fig. 5.

Photo of experimental setup with three motion capture cameras, a projector and a towel being projected onto.

To implement the algorithm presented in Sect. 3, the mass-spring model parameters need to be chosen so that the deformable model has similar characteristics to the real-life system. Using visual inspection, mass values of 0.025 kg for each node, spring constant values of , and damper values of for each spring and damper connection are chosen. It is assumed that any error in parameter choice can be lumped into the process noise term w[k] and will be dealt with by the EKF. The initial position states of the mass-spring model are set to be equal to the position of the IR markers on the towel and the velocity states are set to 0, as the towel is at rest. Since the initial states of the mass-spring model match the initial conditions of the real-life surface, the initial state covariance matrix is set to the zero matrix, as there is no uncertainty between the initial state and the true position of the surface. The measurement noise covariance matrix $R_k$ is set so that the variance of each position state is 0.01 mm$^2$, and the covariance between any two position states is 0 mm$^2$ (considered independent). These values of variance are chosen based on the error specifications given by the Optitrack system. The model noise covariance matrix $Q_k$ is chosen to be an identity matrix, as 1 m can easily be assumed to be an extreme upper bound for the uncertainty in node position. Covariance tuning to optimize the EKF will be explored in future revisions of this work.

To begin the experiment, a still image is projected onto the towel when the towel is at rest, as seen in Fig. 5. To project the image on the towel, the system needs to be calibrated so that the computer knows where the projector is relative to the surface. To finish calibration, the timing parameters $T_m$ and $T_d$ are tuned so that the speed of motion of the model matches that of the towel. The measurement time-step is set to 10 ms and the delay time-step is set to 30 ms. After the system adequately matches the mass-spring model to the towel, a rotating fan is placed behind the towel to create a “random” motion on the surface. This is done to test the robustness of the EKF-IFP algorithm under conditions of randomness. The results of the projection method are visually inspected and predictions of the surface position states are stored to be compared to the real-world values offline.

Fig. 6.

Visual comparison of standard projection and EKF-IFP algorithm

5 Results

To evaluate the effectiveness of the EKF-IFP algorithm presented in Sect. 3 on the experimental setup described in Sect. 4, qualitative and quantitative methods are used. Qualitatively, the results of the prediction algorithm are visually compared to the results of simply projecting on the surface without any compensation. When the image is projected onto a flat surface (the towel at rest), both projection methods produce the exact same results. However, once the towel is moved, the EKF-IFP method produces more true-to-life results. The images move with the towel, matching its geometry, making it a substantial upgrade over simply just projecting images onto the surface. Projecting directly on the surface clips images and produces generally undesirable results. Figure 6 shows a comparison of a simpler scenario where the towel is put into three orientations. Both projection methods look identical when the towel is at rest. However, when the towel is placed the two other positions (pushed forwards and pulled backwards), the EKF-IFP algorithm produces far more appealing results. Specifically, the uncompensated projection method displays parts of the image past the towel, onto the wall, while the EKF-IFP algorithm “paints” the image on the towel. It should be noted that any distortion in the images when using the EKF-IFP algorithm can be attributed to the short-throw feature of the projector. Short-throw projectors display unequally magnified images so they can be placed closer to walls while keeping the image size intact. Quantitatively, the success of the EKF-IFP algorithm is evaluated using the mean error between the measured position of the markers and the predicted position of the mass nodes. At every measurement time-step, the difference between measured position of node and the predicted position of the node are squared and then averaged. The mean error is defined as

$$\begin{aligned} E[k]=\frac{1}{N}\sum _{k=1}^N\Vert y[k]-Cx_{k|k-1}\Vert \end{aligned}$$

(7)

where N is the total number of nodes (20 in this case), y[k] as defined in Eq. (2) is the output vector, and $x_{k|k-1}$ is the state prediction vector. Figure 7 shows the mean error (ME) between measured and predicted node positions over a 10 second window. It can be seen that after every large input (strong gust from the fan), the ME increases drastically. This is due to the non-anticipatory behaviour of real systems. After this peak in error, the ME exponentially decreases to a point where there is almost no difference between predictions and measurements. The mean error peaks at roughly 3.5 cm when the towel is most affected by the input force, and 0.6 cm when the towel comes back to rest. This is a very promising result as it shows how effective the EKF-IFP algorithm is at surface tracking. Furthermore, the results imply that the algorithm can in fact be used in any application where surface tracking is required, not just applications of spatial augmented reality.

Fig. 7.

Mean error graph display the average error between measured and predicted node positions over time.

6 Conclusion

This paper implements a novel technique for predicting the motion of non-rigid surfaces for image projection. The EKF based algorithm, named the EKF-IFP algorithm, predicts the position of a non-rigid surface by using the measured position of the surface while the surface is moving. The algorithm is able to handle the delays often associated with projectors and is robust enough to handle brief occlusions of the surface when measurements are taken. Using a mass-spring system to model the dynamics of a towel, the EKF-IFP algorithm was able to predict the position of the nodes with errors ranging between 3.5 cm and less than 1 cm on average. These results were observed when the non-rigid surface was being perturbed by random forces. If information was known about the input forces, the algorithm would have produced even better results. Using visual observation, the algorithm was also able to project images onto a moving surface with little image distortion. The results show that surface tracking for image projection provides significantly better results than using standard projection techniques in applications of spatial augmented reality. Projection using the EKF-IFP algorithm made interacting with objects far more realistic than using normal image projection, which will make it an indispensable tool for a number of entertainment and training applications.

6.1 Future Work

As the mass, spring and damper parameters for the model were chosen quite arbitrarily, finding parameters that match the surface material properties would allow for more robust prediction. Future work will include using machine learning techniques for parameter identification. Additional future work includes using less obstructive motion capturing systems since the marker based motion capture system is quite expensive and sensitive to environmental conditions. A more cost-effective camera based system, combined with computer vision techniques, can instead be used to capture the position of surfaces in real-time. Although this will likely cause an increase in sensor noise in the system, the prediction algorithm should be able to compensate for the additional measurement error.

A future work of most interest is applying the EKF-IFP algorithm to a scoliosis surgery simulator where a haptic-based robot is used to train surgeons [5]. Current training methods for scoliosis surgery require the use of cadavers. Training on cadavers cannot replicate the “feel” of the surgery and is a very costly approach. A haptic-based simulator is a less expensive alternative that can create a more realistic experience for the trainee. To improve the visual aspect of the simulator, images of the current procedure are projected onto the torso so that the surgeon can interact with the body as they would in the normal procedure. This entails adjusting the visuals to account for deformations of the torso, which is a natural application of the EKF-IFP surface prediction algorithm. The overall goal of this combined system is to replicate both the tactile and visual sensations of the real-life surgery so that surgeons are best equipped to handle this high-risk procedure.