Filtering Spurious Events from Event Streams of Business Processes

Abstract

Process mining aims at gaining insights into business processes by analysing event data recorded during process execution. The majority of existing process mining techniques works offline, i.e. using static, historical data stored in event logs. Recently, the notion of online process mining has emerged, whereby techniques are applied on live event streams, as process executions unfold. Analysing event streams allows us to gain instant insights into business processes. However, current techniques assume the input stream to be completely free of noise and other anomalous behaviours. Hence, applying these techniques to real data leads to results of inferior quality. In this paper, we propose an event processor that enables us to filter out spurious events from a live event stream. Our experiments show that we are able to effectively filter out spurious events from the input stream and, as such, enhance online process mining results.

R. Conforti and M. La Rosa—Part of the work was done while the authors was at the Queensland University of Technology.

1 Introduction

Nowadays, information systems can accurately record the execution of the business processes they support. Common examples include order-to-cash and procure-to-pay processes, which are tracked by ERP systems. Process mining [1] aims at turning such event data into valuable, actionable knowledge, so that process performance or compliance issues can be identified and rectified. Different process mining techniques are available. These include techniques for automated process discovery, conformance checking, performance mining and process variant analysis. For example, in process discovery we aim at reconstructing the underlying structure of the business process in the form of a process model, while in conformance checking we assess to what degree the recorded data aligns with a normative process model available in the organisation.

The vast majority of process mining techniques are defined in an offline setting, i.e. they work over historical data of completed process executions (e.g. over all orders fulfilled in the past six months). They are typically not adequate to directly work in online settings, i.e. from live streams of events rather than historical data. Hence, they cannot be used for operational support, but only for a-posteriori analysis. Online process mining provides a wealth of opportunities. For example, when applying conformance checking techniques, compliance deviations could be detected as soon as they occur, or better, their occurrence could be predicted in advance. In turn, the insights gained could be used to rectify the affected process executions on the fly, avoiding the deviations to occur altogether.

As a result, several process mining techniques have recently been designed to specifically work online. These include, for example, techniques for drift detection [16, 19, 20], automated discovery [7, 15, 25], conformance checking [8, 26] and predictive process monitoring [18]. Such techniques tap into an event stream produced by an information system. However, they typically assume the stream to be free of noise and anomalous behaviour. In reality however, several factors cause this assumption to be wrong, e.g. the supporting system may trigger the execution of an inappropriate activity that does not belong to the process, or the system may be overloaded resulting in logging errors. The existence of these anomalies in event streams easily leads to unreliable results. For example, in drift detection, sporadic stochastic oscillations caused by noise can negatively impact drift detection accuracy [16, 20].

In this paper, we propose a general-purpose event stream filter designed to detect and remove spurious events from event streams. We define a spurious event as an event emitted onto the stream, whose occurrence is extremely unlikely, given the underlying process and process context. Our approach relies on a time-evolving subset of behaviour of the total event stream, out of which we infer an incrementally-updated model that represents this behaviour. In particular, we build a collection of probabilistic automata, which are dynamically updated to filter out spurious events.

We implemented our filter as a stream processor, taking an event stream as an input and returning a filtered stream. Using the implementation, we evaluated accuracy and performance of the filter by means of multiple quantitative experiments. To illustrate the applicability of our approach w.r.t. existing online process mining techniques, we assessed the benefits of our filter when applied prior to drift detection.

The remainder of this paper is structured as follows. In Sect. 2, we discuss related work, while in Sect. 3 we present background concepts introducing (online) process mining concepts. In Sect. 4, we present our approach, which we evaluate in Sect. 5. We conclude the paper and discuss several avenues for future work in Sect. 6.

2 Related Work

Work in the areas of online process mining and noise filtering are of particular relevance to the work presented in this paper. In the area of online process mining, the majority of work concerns automated process discovery algorithms. For example, Burattin et al. [7] propose a basic algorithm that lifts an existing offline process discovery algorithm to an online setting. Additionally, in [6], Burattin et al. propose an online process discovery technique for the purpose of discovering declarative models. Hassani et al. [15] extend [7] by proposing the use of indexed prefix-trees in order to increase memory efficiency. Finally, van Zelst et al. [25] extend [7, 15] and generalize it for a large class of existing process discovery algorithms. More recently, event streams have been used for online conformance checking [8, 26] and online concept drift detection [19, 20]. In the context of online conformance checking, Burattin et al. [8] propose an approach that uses an enriched version of the original process model to detect deviant behaviour. In [26], van Zelst et al. propose to detect deviant behaviour by incrementally computing prefix-alignments. In the context of online concept drift detection, Ostovar et al. [20] detect drifts on event streams by monitoring the distribution of behavioural abstractions (i.e. $\alpha ^+$ relations) of the event stream across adjacent time sliding-windows. In follow-up work, Ostovar et al. [19] extend [20] to allow for concept drift characterization.

With respect to noise filtering in context of event logs, three approaches are described in literature [10, 13, 23]. The approach proposed by Wang et al. [23] relies on a reference process model to repair a log whose events are affected by labels that do not match the expected behaviour of the reference model. The approach proposed by Conforti et al. [10] removes events that cannot be reproduced by an automaton constructed using frequent process behaviour recorded in the log. Finally, Fani Sani et al. [13] propose an approach that uses conditional probabilities between sequences of activities to remove events that are unlikely to occur in a given sequence.

Existing noise filtering techniques have shown to improve the quality of process mining techniques [10, 13], yet they are not directly applicable in an online context. Similarly, online process mining techniques do not address the problem of noise in event streams. Our approach bridges the gap between these techniques providing, to the best of our knowledge, the first noise filter for business process event streams.

Finally, the problem of detecting spurious events from event stream of business processes shares similarities with the problem of outlier detection in temporal data, e.g. reading sensor data. In this context, we observe three types of techniques: (i) techniques detecting if entire sequences of events are anomalous; (ii) techniques detecting if a single data point within a sequence is an outlier; and (iii) techniques detecting anomalous patterns within a sequences. For a detailed discussion about techniques for outlier detection in temporal data we refer to the works by Gupta et al. [14] for events with continuous values, and by Chandola et al. [9] for events with discrete values.

3 Background

Here we introduce our notation and basic concepts such as event logs and event streams.

3.1 Mathematical Preliminaries and Notation

Let X denote an arbitrary set and let $\mathcal {P}(X)$ denote the power set of X. We let $\mathbb {N}$ denote the set of natural numbers including 0. $\mathbb {B}= \{0,1\}$ represents the boolean domain. A multiset M over X generalizes the notion of a set and allows for multiple instances of its elements, i.e. $M :X \rightarrow \mathbb {N}$. We let $\mathcal {M}(X)$ denote the set of all possible multisets over X. We write a multiset M as $[x^{i_1}_1,...,x^{i_n}_n]$ where $M(x_j) = i_j$ for $1 \le j \le n$. If for $x \in X$, $M(x) = 0$ we omit it form multiset notation, and, if $M(x) = 1$ we omit x’s superscript. A sequence $\sigma$ of length n is a function $\sigma :\{1,...,n\} \rightarrow X$. We write $\sigma = \langle x_1, ..., x_n \rangle$, where for $1 \le i \le n$ we have $\sigma (i) = x_i$. The set of all sequences over set X is denoted $X^*$. Given an n-ary Cartesian product $X_1 \times X_2 \times \cdots \times X_n$ and corresponding element $\varvec{e}=(x_1,x_2,...,x_n)$, for $1 \le i \le n$, we write $\pi _i(\varvec{e}) = x_i$. We overload notation to define projection of sequences, i.e. let $\varvec{\sigma }=\langle \varvec{e}_1, \varvec{e}_2, ..., \varvec{e}_m\rangle \in (X_1 \times X_2 \times \cdots X_n)^*$, we have $\pi _i(\varvec{\sigma }) = \langle \pi _i(\varvec{e}_1), \pi _i(\varvec{e}_2), ..., \pi _i(\varvec{e}_m)\rangle$ for $1\le i \le n$. A pair $(X,\npreceq )$ is a partial order if $\npreceq$ is a reflexive, anti-symmetric and transitive binary relation on X.

Our approach builds on the notion of a probabilistic automaton ($PA$). Such automaton is an extension of a conventional non-deterministic automaton, where each transition has an associated probability of occurrence.

Definition 1

(Probabilistic Automaton). A probabilistic automaton $(PA)$ is a 6-tuple $(Q, \varSigma , \delta , q_0, F, \gamma )$, where $Q$ is a finite set of states, $\varSigma$ is a finite set of symbols, $\delta :Q\times \varSigma \rightarrow \mathcal {P}(Q)$ is a transition relation, $q^0 \in Q$ is the initial state, $F\subseteq Q$ is the set of final states, $\gamma :Q\times \varSigma \times Q\rightarrow [0,1]$ is the transition probability function.

Additionally we require:

• 1. $\forall q, q' \in Q, a\in \varSigma (q' \in \delta (q, a) \Leftrightarrow \gamma (q, a, q') > 0)$: if an arc labelled $a$ connects $q$ to $q'$, then the corresponding probability is non-zero.

• 2. $\forall q\in Q\setminus F(\exists q' \in Q, a\in \varSigma (q' \in \delta (q, a)))$: non-final states have outgoing arc(s).

• 3. $\forall q\in Q(\exists a\in \varSigma , q' \in Q( q' \in \delta (q,a)) \Rightarrow \sum \limits _{\{ (a,q') \in \varSigma \times Q\mid q' \in \delta (q, a)\}} \gamma (q, a, q') = 1)$: the sum of probabilities of outgoing arcs of a state equals one.

For given $q, q' \in Q$ and $a\in \varSigma$ s.t. $\delta (q,a) = q'$, $\gamma (q,a,q')$ represents the probability of reaching state $q'$ from state $q$ by means of label $a$. We write such probability as $P(a\mid q\rightarrow q')$ and we define $P(a\mid q) = \sum \limits _{q' \in Q}P(a\mid q\rightarrow q')$.

3.2 Event Logs

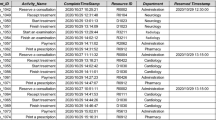
Modern information systems track, often in great detail, what specific activity is performed for a running instance of the process, i.e. a case, at a certain point in time. Traditional process mining techniques aim to analyse such data, i.e. event logs, in a static/a-posteriori setting. Consider Table 1, depicting an example of an event log. Each line refers to the execution of an activity, i.e. an event, in context of a process instance, which is identified by means of a case-id. In this example the case-id equals the id of the ticket for which a compensation request is filed. In general the case-id depends on the process under study, e.g. a customer type or product-id are often used as a case-id.

Table 1. Example event log fragment.

Consider the events related to case-id 417. The first event, i.e. with id 572, describes that Marcello executed a register request activity. Subsequently, Mohammad performed a causal examination of the request (event 574). In-between event 572 and 574, event 573 is executed that relates to a case with id 412, which reflects that several process instances run in parallel. An event $e$, i.e. the execution of an activity, is defined as a tuple $(\iota , c, a) \in \mathcal {E}$, where $\mathcal {E}= \mathcal {I}\times \mathcal {C}\times \mathcal {A}$, $\mathcal {I}$ denotes the universe of event identifiers, $\mathcal {C}$ denotes the universe of case identifiers, and $\mathcal {A}$ denotes the universe of activities. Typically, more event attributes are available, e.g. the resource(s) executing the activity and/or the time-stamp of the activity. However, here we only consider the ordering of activities in context of a process instance, i.e. the control-flow perspective.

Definition 2

(Event Log, Trace). Given a collection of events $E \subseteq \mathcal {E}$, an event log $L$ is a partially ordered set of events, i.e. $L= (E, \preceq )$ s.t. $\forall e=(\iota , c, a), e'=(\iota ',c',a') \in E(\iota = \iota ' \Rightarrow (c= c' \wedge a= a'))$.

A trace related to case $c\in \mathcal {C}$ is a sequence $\sigma \in E^*$ for which:

• 1. $\forall 1 \le i \le |\sigma |(\pi _{2}(\sigma (i)) = c)$; Events in $\sigma$ relate to case $c$.

• 2. $\forall e\in E(\pi _2(e) = c\Rightarrow \exists 1 \le i \le |\sigma |(\sigma (i) = e))$; Each event related to $c$ is in $\sigma$.

• 3. $\forall 1 \le i < j \le |\sigma |(\sigma (i) \ne \sigma (j))$; All events in $\sigma$ are unique.

• 4. $\forall 1 \le i < j \le |\sigma |(\sigma (j) \npreceq \sigma (i))$; Events in $\sigma$ respect their order.

The partial order of the events of an event log is usually imposed by means of recorded times-stamps. A log is partially ordered due to, for example, inherent parallelism of and/or mixed time-stamp granularity. A trace is a sequence of events related to the same case identifier that respect the partial order. Consider the trace related to case 417 of Table 1, which we write as $\langle (572,417,\text {register request}), (574,417,\text {examine causally}), (575,417,\text {check ticket}),$ $(576,417,\text {decide}), (577,417,\text {pay compensation}) \rangle$, or simply $\langle (572,417,a),$ $(574,417,b), (575,417,d), (576,417,e), (577,417,f) \rangle$ using short-hand activity names. Most process mining techniques ignore the event- and case-identifiers stored within events and simply distil a sequence of activities from the given trace. For example, by projecting the example trace, we obtain $\langle a,b,d,e,f \rangle$. When adopting such view on traces, a multitude of cases exist which project onto the same sequence of activities.

3.3 Event Streams

We adopt the notion of online/real-time event stream-based process mining, in which the data is assumed to be an infinite sequence of events. Since in practice, several instances of a process run in parallel, we have no guarantees w.r.t. the arrival of events related to the same case. Thus, new events related to a case are likely to be emitted onto the stream in a dispersed manner, which implies that our knowledge of the activities related to cases changes over time.

Definition 3

(Event Stream). An event stream $S$ is a (possibly infinite) sequence of unique events, i.e. $S\in \mathcal {E}^*$ s.t. $\forall 1 \le i < j \le |S|(S(i) \ne S(j))$.

Fig. 1.

Example event stream $S$.

Consider Fig. 1, in which we depict a few of the (short-hand) events that we also presented in Table 1. The first event depicted is $(572,417,\text {register request})$, the second event is $(574,417,\text {examine causally})$, and so on. We assume that one event arrives per unit of time, i.e. we do not assume the existence of a multi-channel stream. Moreover, we assume that the order of event arrival corresponds to the order of execution.

4 Approach

In this section, we present our approach. We aim to build and maintain a collection of probabilistic automata which we use to filter out spurious events. Each automaton represents a different view on the behaviour of the underlying process, as described by the event stream. The main idea of the approach is that dominant behaviour attains higher occurrence probabilities within the automata compared to spurious behaviour.

4.1 General Architecture

The proposed filter uses a subset of all behaviour emitted onto the stream and is intended to be updated incrementally when new events arrive on the stream. Since we need to maintain the possibly infinite event stream in finite memory, we need to “forget” behaviour observed in the past. Hence, we account for removal of events as well.

In Fig. 2, we depict the main architecture of the proposed filter. We assume an input event stream $S$ that contains spurious events. As indicated, events related to different cases are typically dispersed over an event stream. Hence, we need means to track, given case $c$, what behaviour was received in the past for case $c$. The exact nature of such data structure is outside the scope of this paper. We assume the existence of a finite event window $w:\mathcal {C}\times \mathbb {N}\rightarrow \mathcal {E}^*$, where $w(c, t)$ represents the sequence of events stored in the event window at time $t$. As such, the event window maintains a set of relevant recently received events, grouped by case-identifier.

Fig. 2.

Schematic overview of the proposed filtering architecture.

In order to determine what events need to be removed from the event window (i.e. we need to maintain a finite view of the stream), we are able to use a multitude of existing stream-based approaches, e.g. we are able to us techniques such as (adaptive) sliding windows [4, 5], reservoir sampling [3, 22] or (forward) decay methods [11]. The only strict assumption we pose on $w$, is that event removal respects the order of arrival w.r.t. the corresponding case. Thus, whenever we have a stream of the form $\langle ..., (\iota , c, a), (\iota ', c', a') ,(\iota '', c, a''), ... \rangle$, we assume event $(\iota , c, a)$ to be removed prior to event $(\iota '', c, a'')$. A new event e is, after storage within $w$, forwarded to event filter $f$. From an architectural point of view we do not pose any strict requirements on the dynamics of the filter. We do however aim to let filter $f$ reflect the behaviour captured within window $w$. Hence, the filter typically needs to process the event within its internal representation, prior to the actual filtering. For the newly received event, the filter $f$ either decides to emit the event onto output stream $S'$, or, to discard it.

4.2 Automaton Based Filtering

Given the general architecture, in this section, we propose an instantiation of filter $f$. We first present the conceptual idea of the use of probabilistic automata for the purpose of spurious event filtering, after which we describe the main approach.

Prefix-Based Automata. In our approach, a collection of probabilistic automata represents recent behaviour observed on the event stream. These automata are subsequently used to determine whether new events are, according to the probability distributions described by the automata, likely to be spurious or not. Each state within an automaton refers to the recent history of cases as described by recently received events on the event stream. The probabilities of the outgoing arcs of a state are based on cases that have been in that state before, and subsequently moved on to a new state by means of a new event. Upon receiving a new event, we assess the state of the corresponding case and check, based on the distribution as defined by that state’s outgoing arcs, whether the new event is likely to be spurious or not.

We construct probabilistic automata in which states represent recent behaviour for a newly related event based on its case-identifier, i.e. prefix-based automata. In prefix-based automata, a state $q$ represents a possible prefix of executed activities, whereas outgoing arcs represent those activities $a\in \mathcal {A}$ that are likely to follow the prefix represented by $q$, and their associated probability of occurrence. We define two types of parameters, that allow us to deduce states in the corresponding prefix automaton based on a prefix, i.e.:

• 1. Maximal Prefix Size; Represents the size of the prefix to take into account when constructing states in the automaton.

• 2. Abstraction; Represents an abstraction that we apply on the prefix in order to define a state. We identify the following abstractions:

  • Identity; Given $\sigma \in \mathcal {A}^*$, the identity abstraction ${\varvec{id}}$ yields the prefix as a state, i.e. ${\varvec{id}}:\mathcal {A}^* \rightarrow \mathcal {A}^*$, where ${\varvec{id}}(\sigma )=\sigma$

  • Parikh; Given $\sigma \in \mathcal {A}^*$, the Parikh abstraction ${\varvec{p}}$ yields a multiset with the number of occurrences of $a\in \mathcal {A}$ in $\sigma$, i.e. ${\varvec{p}}:\mathcal {A}^* \rightarrow \mathcal {M}(\mathcal {A})$, where:

    $$ {\varvec{p}}(\sigma ) = \left[ a^n \mid a\in \mathcal {A}\wedge n = \sum \limits _{i=1}^{|\sigma |}\left( {\left\{ \begin{array}{ll}1 &{} \text {if } \sigma (i) = a\\ 0 &{} \text {otherwise} \end{array}\right. }\right) \right] $$

  • Set; Given $\sigma \in \mathcal {A}^*$ the set abstraction ${\varvec{s}}$ indicates the presence of $a\in \mathcal {A}$ in $\sigma$, i.e. ${\varvec{s}}:\mathcal {A}^* \rightarrow \mathcal {P}(\mathcal {A})$, where ${\varvec{s}}(\sigma ) = \{a\in \mathcal {A}\mid \exists 1 \le i \le |\sigma | (\sigma (i) = a)\}$

Fig. 3.

Two examples of prefix-based automata, based on traces $\langle a,b,b,c,d \rangle$, $\langle a,b,c,b,d \rangle$ and $\langle a,c,b,b,d \rangle$.

In Fig. 3, we depict two different automata based on the traces $\langle a,b,b,c,d \rangle$, $\langle a,b,c,b,d \rangle$ and $\langle a,c,b,b,d \rangle$, which we assume to occur equally often. In Fig. 3a, we limit the prefix size to 1 and use the identity abstraction. Note that any of the possible abstractions in combination with prefix size 1 always yields the same automaton. Consider the state related to abstraction $\langle b \rangle$ which states that $P(b\mid \langle b \rangle ) = P(c \mid \langle b \rangle ) = P(d \mid \langle b \rangle ) = \frac{1}{3}$, i.e. we are equally likely to observe activity b, c or d after $\langle b \rangle$. In Fig. 3b, we limit the prefix size to 2 and use the Parikh abstraction. In this case, since we use a larger prefix size, we have more fine-grained knowledge regarding the input data. For example in Fig. 3a, the automaton describes that sequence $\langle a,b,d \rangle$ is likely, whereas in Fig. 3b we have $P(d \mid [a,b]) = 0$.

Incrementally Maintaining Collections of Automata. As new events are emitted on the stream, we aim to keep the automata up-to-date in such a way that they reflect the behaviour present in event window w. Let $k > 0$ represent the maximal prefix length we want to take into account when building automata. We maintain k prefix-automata, where for $1 \le i \le k$, automaton $PA_i = (Q_i, \varSigma _i, \delta _i, q^0_i, F_i, \gamma _i)$ uses prefix-length i to define its state set $Q_i$. As exemplified by the two automata in Fig. 3, the prefix length influences the degree of generalization of the corresponding automaton. Moreover, increasing the maximal prefix length considered is likely to generate automata of larger size, and thus it is more memory intensive.

Upon receiving a new event, we incrementally update the k maintained automata. Consider new event $e=(\iota , c, a)$ arriving at time $t$ and let $\sigma = \sigma ' \cdot \langle a \rangle = w(c, t)$. To update automaton $PA_i$ we apply the abstraction of choice on the prefix of length i of the newly received event in $\sigma '$, i.e. $\langle \sigma '(|\sigma '| - i + 1), ..., \sigma '(|\sigma '| - i + i) \rangle$ to deduce corresponding state $q_{\sigma '} \in Q_i$. The newly received event influences the probability distribution as defined by the outgoing arcs of $q_{\sigma '}$, i.e. it describes that $q_{\sigma '}$ can be followed by activity a. Therefore, instead of storing the probabilities of each $\gamma _i$, we store the weighted outdegree of each state $q_i \in Q_i$, i.e. $\deg ^+_i(q_i)$. Moreover, we store the individual contribution of each $a\in \mathcal {A}$ to the outdegree of $q_i$, i.e. $\deg ^+_i(q_i,a)$ with $\deg ^+_i(q_i, a) = 0 \Leftrightarrow \delta (q_i,a) = \emptyset$. Observe that $\deg ^+_i(q_i) = \sum \limits _{a\in \mathcal {A}}\deg ^+_i(q_i, a)$, and, that deducing the probability of activity $a$ in state $q_i$ is trivial, i.e. $P(a\mid q_i) = \frac{\deg ^+_i(q_i, a)}{\deg ^+_i(q_i)}$.

Updating the automata based on events that are removed from event window $w$ is performed as follows. Assume that we receive a new event $e$ at time $t>0$. For each $c\in \mathcal {C}$, let $\sigma _{c}' = w(c,t-1)$, $\sigma _{c} = w(c,t)$ and let $\varDelta _{c}(t) = |\sigma _{c}'| - |\sigma _{c}|$. Observe that for any case $c$ that does not relate to the newly received event, we have $\varDelta _{c}(t) \ge 0$, i.e. some events may have been dropped for that case, yet no new events are received, hence $|\sigma _{c}| \le |\sigma _{c}'|$. In a similar fashion, for the case $c$ that relates to the new event $e$, we have $\varDelta _{c}(t) \ge -1$, i.e. either $|\sigma _{c}| = |\sigma '_{c}| + 1$, or, $|\sigma _{c}| \le |\sigma _{c}'|$. Thus, to keep the automata in line with the events stored in the event window, in the former case we need to update the automata if $\varDelta _{c}(t) > 0$, i.e. at least one event is removed for the corresponding case-id, whereas in the latter case we need to update the automata if $\varDelta _{c}(t) \ge 0$. Therefore, we define $\varDelta '_{c}(t) = \varDelta _{c}(t)$ for the former case and $\varDelta '_{c}(t) = \varDelta _{c}(t) + 1$ in the latter case. Henceforth, if for any $c\in \mathcal {C}$, we have $\varDelta '_{c}(t) > 0$, we need to update the maintained automata to account for removed events. To update the collection of k maintained automata, for each $1 \le i \le \varDelta _{c}'(t)$ we generate sequences $\langle \sigma '(i) \rangle$, $\langle \sigma '(i), \sigma '(i)+1 \rangle$, ..., $\langle \sigma '(i), ..., \sigma '(i+k) \rangle$ (subject to $|\sigma '| > i + k$). For each generated sequence we apply the abstraction of choice to determine corresponding state $q$, and subsequently reduce the value of $\deg ^+(q)$ by 1. Moreover, assume the state $q$ corresponds to sequence $\langle \sigma '(i), \sigma '(i+1), ..., \sigma '(i+j) \rangle$ with $1 \le i \le \varDelta '_{c}(t)$ and $1 \le j < k$, we additionally reduce $\deg ^+(q, a)$ by 1, where $a= \sigma '(i+j+1)$. As an example, consider that we use maximal prefix length 2, i.e. $k=2$, a identity abstraction, and assume that for some $c\in \mathcal {C}$ we have $\sigma ' = \langle a,b,c,d,e \rangle$ and $\sigma = \langle b,c,d,e \rangle$, i.e. the event related to activity a is removed. We have $\varDelta '_{c}(t) = 1$, thus we generate sequences $\langle \sigma '(1) \rangle = \langle a \rangle$ and $\langle \sigma '(1), \sigma '(1+1) \rangle = \langle a,b \rangle$. Since we use identity abstraction these two sequence correspond to a state in their associated automaton, and we reduce $\deg ^+(\langle a \rangle )$, $\deg ^+(\langle a \rangle , b)$, $\deg ^+(\langle a,b \rangle )$ and $\deg ^+(\langle a,b \rangle , c)$ by one.

Filtering Events. After receiving an event and subsequently updating the collection of automata, we determine whether the new event is spurious or not. To assess whether the newly arrived event is spurious we assess to what degree the probability of occurrence of the activity described by the new event is an outlier w.r.t. the probabilities of other outgoing activities of the current state. Given the set of k automata, for automaton $PA_i = (Q_i, \varSigma _i, \delta _i, q^0_i, F_i, \gamma _i)$ with prefix-length i ($1 \le i \le k$), we characterize an automaton specific filter as $f_i :Q_i \times \varSigma _i \rightarrow \mathbb {B}$. Note that an instantiation of a filter $f_i$ often needs additional input, e.g. a threshold value or range. The exact characterization of $f_i$ is a parameter of the approach, however, we propose the following instantiations:

• Fractional; Considers whether the probability obtained is higher than a given threshold, i.e. $f^{F}_i :Q_i~\times ~\varSigma _i~\times ~[0,1] \rightarrow \mathbb {B}$, where, $f^{F}_i(q_i, a, \kappa ) = 1 \text { if } P(a\mid q_i) < \kappa$.

• Heavy Hitter; Considers whether the probability obtained is higher than a fraction of the maximum outgoing probability, i.e. $f^{H}_i :Q_i \times \varSigma _i \times [0,1] \rightarrow \mathbb {B}$, where, $f^{H}_i(q_i, a, \kappa ) = 1 \text { if } P(a\mid q_i) < \kappa \cdot \max \limits _{a'\in \mathcal {A}} P(a' \mid q_i)$.

• Smoothened Heavy Hitter; Considers whether the probability obtained is higher than a fraction of the maximum outgoing probability subtracted with the non-zero average probability. Let $NZ = \{a\in \varSigma _i \mid P(a\mid q_i)>0\}$, we define $f^{SH}_i :Q_i \times \varSigma _i \times [0,1] \rightarrow \mathbb {B}$, where, $f^{SH}_i(q_i, a, \kappa ) = 1 \text { if } P(a\mid q_i) < \kappa \cdot \left( \max \limits _{a'\in \mathcal {A}} P(a' \mid q_i) - \frac{ \sum \limits _{a' \in NZ}P(a' \mid q_i)}{|NZ|}\right)$.

For a newly received event, each automaton, combined with a filter of choice yields a boolean result indicating whether or not the new event is spurious. In context of this paper we assume that we apply the same filter on each automaton. Moreover, we assume that when any of the k maintained automata signals an event to be spurious, the event itself is spurious. Note that maintaining/filtering the automata can be parallelized, i.e. we maintain an automaton on each node within a cluster.

5 Evaluation

We implemented our filter as an open-source plugin for both ProM [21] and RapidProM [2]. The filter source code is available at https://github.com/s-j-v-zelst/prom-StreamBasedEventFilter. All raw results, including process models, associated event data, scientific workflows and charts are available at https://github.com/s-j-v-zelst/research/releases/tag/2018_caise.

Using the RapidProM plugin, we conducted a two-pronged evaluation. First, we assessed filtering accuracy and time performance on randomly generated event streams, based on synthetic process models, i.e. a collection of process models that resemble business processes often present in organizations. Second, we assessed the applicability of our filter in combination with an existing class of online process mining techniques, namely concept drift detection. In the latter experiment we used both synthetic and real-life datasets.

5.1 Filtering Accuracy and Time Performance

For this first set of experiments, we generated several event streams using 21 variations of the loan application process model presented in [12]. These variations are inspired by the change patterns of [24]. Out of 21 stable models, we generated 5 different random event logs, each containing 5000 cases, with a varying amount of events. For each generated log we randomly inserted spurious events with probabilities ranging from 0.025 to 0.15 in steps of 0.025. In these experiments we use a simple sliding window with fixed size as an implementation for $w$. Given a sliding window of size $|w|$, the first $|w|$ events are used for training and are ignored. Each event arriving after the first $|w|$ events that relates to a case that was received within the first $|w|$ events is ignored.

Table 2. Parameters of Data generation and experiments with synthetic data

Fig. 4.

Average F1-score for different prefix sizes, abstractions, filtering methods and window sizes, per threshold/noise combination.

Accuracy. We assess the impact of a wide variety of parameters on filtering accuracy. These are the prefix size, the particular abstraction used, the filtering technique and the filter threshold. The values of these parameters are presented in Table 2. Here, we mainly focus on the degree in which prefix size, abstraction, filtering method and window size influence the filtering quality. The results for each of these parameters are presented in Fig. 4. Note that, to reduce the amount of data points, we show results for noise levels 0.025, 0.05, 0.1 and 0.15, and threshold levels 0.05–0.25.

For the maximal prefix size (see Fig. 4a), we observe that a prefix-size of 1 tends to outperform prefix-sizes of 3 and 5. This is interesting as it shows that, for this collection of models and associated streams, ignoring history improves the results. Note that, for maximal prefix length k, we use k automata, and signal an event to be spurious whenever one of these signals that this is the case. Using a larger maximal prefix-length potentially identifies more spurious events, yielding higher recall values. However, a side effect is potentially lower precision values. Upon inspection, this indeed turns out to be the case, i.e. the differences in F1-score are explained by higher recall values for increased maximal prefix lengths, however, at the cost of lower precision.

As for the abstraction used (see Fig. 4b), we observe that the Identity- outperforms both the Parikh- and the Set abstraction (for these results prefix length 1 is ignored.). The results are explained by the fact that within the collection of models used, the amount of parallelism is rather limited, which does not allow us to make full use of the generalizing power of both the Parikh and Set abstraction. At the same time, loops of short length exist in which order indeed plays an important role, which is ignored by the two aforementioned abstractions. Upon inspection, the recall values of all three abstractions is relatively equal, however, precision is significantly lower for both the Parikh- and Set abstraction. This can be explained by the aforementioned generalizing power of these abstractions, and, in turn, explains the difference in F1-score.

For the filter method used (see Fig. 4c), we observe that the Smoothened Heavy Hitter and Heavy Hitter outperform the Fractional filter for increasing threshold values. This is explained by the fact that the fractional filter poses a rigorous requirement on events to be considered non-spurious, e.g. threshold $\frac{1}{4}$ requires an activity to occur at least in $25\%$ of the observed cases. The other two filters solve this by using the maximal observed value, i.e. if a lot of behaviour is possible, the maximum value is lower and hence the requirement to be labelled non-spurious is lower.

Finally, we observe that an increased sliding window size does not affect the filter results significantly (see Fig. 4d). Since the process is stable, i.e. there is no concept-drift within the generated streams, this indicates that both window sizes used are large enough to deduce automata that allow us to accurately filter the event stream.

Figure 5 shows how the average F1-score varies based on percentage of noise and threshold level. We observe that the F1-score slightly converges for the different threshold levels as noise increases (cf. Fig. 5a). Interestingly, in Fig. 5b, we observe that for relatively low threshold values, the range of F1-score values for various noise levels is very narrow, i.e. the filtering accuracy is less sensitive to changes in the noise level. This effect diminishes as the threshold increases, leading more scattered yet lower F-score values. Observe that, these observations coincide with the Kendall rank correlation coefficient values of 0, 1792 (Fig. 5a) and $-0,8492$ (Fig. 5b) respectively. We conclude that, for the dataset used, the threshold level seems to be the most dominant factor in terms of the F1-score.

Fig. 5.

Average F1-score per noise (a)/threshold level (b).

Time Performance. Window $w$ maintains a finite representation of the stream, thus, memory consumption of the proposed filter is finite as well. Hence we focus on time performance, which we measured in RapidProM, using one stream per base model with $15\%$ noise, and several different parameter values. The experiments were performed on an Intel Xeon CPU (6 cores) 3.47 GHz system with 24 GB memory. Average event handling time was $\sim$0.017 ms, leading to handling $\sim$58.8 events per ms. These results show that our filter is suitable to work in real-time settings.

5.2 Drift Detection Accuracy

In a second set of experiments, we evaluate the impact of our filter on the accuracy of process drift detection. For this, we chose a state-of-the-art technique for drift detection that works on event streams [20]. We apply our filter to the event streams generated from a variety of synthetic and real-life logs, with different levels of noise, and compare drift detection accuracy with and without the use of our filter.

Experimental Setup. For these experiments, we used the 18 event logs proposed in [20]. These event logs were generated by simulating a model featuring 28 different activities (combined with different intertwined structural patterns). Additionally, each event log contains nine drifts obtained by injecting control-flow changes into the model. Each event log features one of the twelve simple change patterns [24] or a combination of them. Simple change patterns may be combined through the insertion (“I”), resequentialization (“R”) and optionalization (“O”) of a pattern. This produces a total of six possible nested change patterns, i.e. “IOR”, “IRO”, “OIR”, “ORI”, “RIO”, and “ROI”. For a description of each change pattern we refer to [20].

Starting from these 18 event logs, we generated 36 additional event logs (two for each original event log) containing $2.5\%$ and $5\%$ of noise (generated inserting random events into traces of each log). This led to a data set of 54 event logs (12 simple patterns and 6 composite patterns with $0\%$, $2.5\%$, and $5\%$ noise), each containing 9 drifts and approximately 250, 000 events.

Results on Synthetic Data. In this experiment, we evaluated the impact that our approach has on the accuracy of the drift detection technique proposed in [20]. Figure 6 illustrates F1-score and mean delay of the drift detection before and after the application of our filter over each change pattern.

The filter successfully removed on average 95% of the injected noise, maintaining and even improving the accuracy of the drift detection (with F1-score of above 0.9 in all but two change patterns). This was achieved while delaying the detection of a drift by less than 720 events on average (approximately 28 traces).

When considering noise-free event streams (cf. Fig. 6a), our filter preserved the accuracy of the drift detection. For some change patterns (“rp”, “cd”, “IOR”, and “OIR”), our filter improved the accuracy of the detection by increasing its precision. This is due to the removal of sporadic event relations, that cause stochastic oscillations in the statistical test used for drift detection. Figure 6b and 6c show that noise negatively affects drift detection, causing the F1-score to drop, on average, to 0.61 and 0.55 for event streams with 2.5% and 5% of noise, respectively. This is not the case when our filter is applied, where an F1-score of 0.9 on average is achieved.

Finally, in terms of detection delay, the filter on average increased the delay by 370, 695, and 1087 events (15, 28, and 43 traces) for the logs with 0%, 2.5%, and 5% noise, respectively. This is the case since changes in process behaviour immediately following a drift are treated as noise.

Fig. 6.

Drift detection F1-score and mean delay per change pattern, obtained from the drift detection technique in [20] over filtered vs. unfiltered event streams.

Results on Real-Life Data. In this experiment, we checked if the positive effects of our filter on drift detection, observed on synthetic data, translate to real-life data. For this, we used an event log containing cases of Sepsis (a life-threatening complication of an infection) from the ERP system of a hospital [17]. Overall, the event log contains 1, 050 cases with a total of 15, 214 events belonging to 16 different activities.

For this experiment, we attempted the detection of drift over the last 5, 214 events, as the first 10, 000 events are used to train the filter. Figure 7 plots the P-value curves of the statistical tests used for drift detection, both without (left figure) and with (right figure) the use of our filter. When comparing these two curves, what appears evident is that drifts detected after the ${2067}^\mathrm{th}$ event and after the ${4373}^\mathrm{th}$ event are no longer there after the application of our filter. In the experiments with synthetic logs, we observed that our filter reduced the number of false positives (drift detected when it did actually not occur). To verify if this was also the case for the real-life event log, we profiled the direct-follows dependencies occurring before and after the drifts.

The profiling showed that while direct-follows dependencies “IV Antibiotics $\longrightarrow$ Admission NC” and “ER Sepsis Triage $\longrightarrow$ IV Liquid” could be observed several times across the entire event stream, the infrequent direct-follows dependencies “Admission NC $\longrightarrow$ IV Antibiotics” and “IV Liquid $\longrightarrow$ ER Sepsis Triage” appeared only in the proximity of the two drifts. These two infrequent dependencies cause a change in the $\alpha$+ relations between the activities (changing from causal to concurrent), which then results in the detection of the drifts. These infrequent dependencies are removed by our filter. In light of these insights, we can argue that the two drifts detected over the unfiltered event stream are indeed false positives, confirming what we already observed on the experiments with synthetic logs, i.e. that our filter has a positive effect on drift detection accuracy.

Fig. 7.

P-value without filtering (left) and with our filtering (right) for the Sepsis log.

5.3 Threats to Validity

The collection of models used within the synthetic experiments related to filtering accuracy, i.e. as presented in Sect. 5.1, represent a set of closely related process models. As such these results are only representative of models that exhibit similar types and relative amounts of control-flow constructs compared to the process models used. Similarly within these experiments, the events are streamed trace by trace, rather than using event-level time stamps. Note that, since the process is stable we expect the automata to be based on a sufficient amount of behaviour, similar to streaming parallel cases. Finally note that, we do observe that our filter can be applied on real-life data, yet whether the results obtained are valid is hard to determine due to the absence of a ground-truth.

6 Conclusion

We proposed an event stream filter for online process mining, based on probabilistic automata which are updated dynamically as the event stream evolves. A state in these automata represents a potentially abstract view on the recent history of cases emitted onto the stream. The probability distribution defined by the outgoing arcs of a state is used to classify new behaviour as spurious or not.

The time measurements on our implementation indicate that our filter is suitable to work in real-time settings. Moreover, our experiments on accuracy show that, on a set of stable event streams, we achieve high filtering accuracy for different instantiations of the filter. Finally, we show that our filter significantly increases the accuracy of state-of-the-art online drift detection techniques.

As a next step, we plan to use our filter in combination with other classes of online process mining techniques, such as techniques for predictive process monitoring and automated process discovery.

Currently, filtering is immediately applied when an event arrives, taking into account only the recent history for that event. To increase filtering accuracy, we plan to experiment with different buffering strategies for incoming events, to keep track both of the recent history as well as the immediate future for each event. We also plan to test different strategies for adapting the length of the sliding window used to build our automata. For example, in our experiments we often observed windows with a large number of events with low relative frequency, due to a high number of parallel cases and due to case inactivity. The hypothesis here is that in these cases a larger window leads to less false positives.