Skip to main content
SpringerLink
Log in

Spontaneous Emission of Light Quanta from the Vacuum

  • Chapter
  • First Online:
Negative Frequency at the Horizon

Part of the book series: Springer Theses ((Springer Theses))

  • 360 Accesses

Abstract

In the previous chapter of this dissertation we used the classical theory of Physics that rules the dynamics of the Universe on large scales—General Relativity—to study the behaviour of spacetime around spherical bodies. We introduced the idea of black holes, regions of spacetime bounded by their event horizon from which nothing can escape. In this section, we will try to tie General Relativity with Thermodynamics—broadly speaking, the theory that rules the organization of the Universe. For this purpose, we will follow the arguments which scientists of the early 1970s had to contend with, and see how they found that these theories can be united at the event horizon of black holes. This will eventually lead us to call upon Quantum Physics to explain how black holes can be in a state of thermal equilibrium—thus introducing the concept of spontaneous emission of light quanta from the vacuum.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 84.99
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 109.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD 109.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    The nuclear mass loss associated with fusion results in energy release that heats up the star.

  2. 2.

    In that sense, the black hole represents the state of maximal entropy, that is the equilibrium end state of gravitational collapse.

  3. 3.

    The future of a set is the collection of all spacetime points that can be reached by future-going timelike or null curves from that set.

  4. 4.

    The past of future null infinity of \(\mathcal {S}\), \(j^-(\mathcal {F}^+)\), physically represents the set of all events from which an observer could escape to the asymptotic region.

  5. 5.

    This is a closed, spacelike, 2-surface whose ingoing and outgoing null normal geodesics are both converging. For example, a sphere at constant r and v in Eddington-Finkelstein coordinates is a trapped surface if it lies inside the horizon.

  6. 6.

    A partial Cauchy surface is a hypersurface which is intersected by any causal curve at most once.

  7. 7.

    A spacetime in which certain observers can never escape to the asymptotic region, i.e., for which the past of future null infinity is not the entire spacetime, is a spacetime that has an event horizon. It is said to possess a black hole.

  8. 8.

    \(\delta A\) is the change in surface area of the event horizon of the black hole.

  9. 9.

    Note that it was Hawking who discovered that black hole horizons must grow if there is only positive energy that falls in, and Bekenstein who later established the link between this observation and entropy.

  10. 10.

    The acceleration of the particle arbitrarily close to the horizon goes to infinity, but from afar this is multiplied by the redshit factor, which also tends to infinity in this case, yielding a finite constant.

  11. 11.

    The first law of black hole mechanics states that \(S\leftrightarrow A\).

  12. 12.

    The calculation (3.38)–(3.43) was historically performed by means of \(\Gamma \)-functions [3, 26].

  13. 13.

    Particles will be present because \(\bar{\left| 0\right\rangle }\) will not be annihilated by \(a_\omega \):

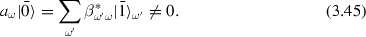
    figure a

    .

  14. 14.

    Black hole explosion refers to the fact that the emission rate goes as \(1/M^2\) so that for small holes this becomes very large, and the lifetime (which goes as \(M^3\)) becomes very small.

  15. 15.

    Although a step-like profile models an infinite slope at the horizon, which would correspond to an infinite surface gravity and temperature, the calculations show a totally different result. As we will see, the spectral densities we calculate are finite. I think this is because, ultimately, the amplitude of waves is limited by dispersion.

  16. 16.

    In the experiment only smooth profiles can be realised. Calculations with an infinitely steep profile only have a suggestive role in understanding the experiment.

  17. 17.

    The model does not account for the dispersion changes due to the finiteness of the intersites distance.

  18. 18.

    Note that in this section, the partial derivative with respect to a variable is denoted by \(\partial _t\equiv \frac{\partial }{\partial t}\). We do not use the relativistic-covariant formulation.

  19. 19.

    Note that the lowest branch is approximately a massless polariton: it can be fitted with a dispersion relation of the form \(|\omega |=c|k|\) for low wavenumbers (close to \(k=0\)).

  20. 20.

    Note that (2.78) is an approximate version of this dispersion relation where we have assumed that \(\omega <|\Omega |\) for a medium with only one resonant frequency.

  21. 21.

    Note that, by replacing the conjugate momenta of the electromagnetic and polarisation fields by their expression in terms of derivatives of the fields (Eqs. 3.53 and 3.54), one obtains the usual form of the pseudo norm—as in Eq. (1.12), with \(\phi \) a field. Because of dispersion, this expression would of course be slightly more complicated, although as readily computable.

  22. 22.

    An alternative proof follows from the observation that, given \(\partial _\tau \rho =0\) and \(\left\langle V_1,V_2\right\rangle =\alpha \left\langle V_1,V_1\right\rangle +\sum _{i=1}^3\bar{\alpha }_i\left\langle V_i,V_i^\dagger \right\rangle \), being the second term of the latter equation zero, the assessment of time conservation consists in calculating \(\partial _\tau \int \alpha \left\langle V_1,V_1\right\rangle \mathrm {d}\zeta +\partial _\tau \left\langle V_1,V_1\right\rangle =\int \partial _\tau \alpha \left\langle V_1,V_1\right\rangle \mathrm {d}\zeta \). \(\partial _\tau \alpha \left\langle V_1,V_1\right\rangle =0\), and thus \(\partial _\tau \alpha \left\langle V_1,V_2\right\rangle \)=0.

  23. 23.

    Remark that the change in the refractive index described by (3.71) is frequency-dependent.

  24. 24.

    The magnitude of the refractive index change giving rise to the various mode configurations depends on the medium properties. For the sake of the argument presented in this section it suffices to identify three categories of refractive index change: small, medium, and large—exact numbers will be provided by the numerical analysis carried in Sect. (4.3).

  25. 25.

    The commutation of the out modes on the in modes gives zero and all the mixed terms go to zero.

References

  1. B. Carter, Republication of: black hole equilibrium states: part i analytic and geometric properties of the kerr solutions. Gen. Relat. Gravit. 41(12), 2873–2938 (2009)

    Article  ADS  Google Scholar 

  2. P.C.W. Davies, Thermodynamics of black holes. Rep. Prog. Phys. 41 (1978)

    Article  ADS  Google Scholar 

  3. N.D. Birrell, P.C.W. Davies, Quantum fields in curved space, repr edn. Cambridge monographs on mathematical physics. (Cambridge Univ. Press, Cambridge, 1994)

    Google Scholar 

  4. T. Jacobson, Introductory Lectures on Black Hole Thermodynamics (1996)

    Google Scholar 

  5. D. Lynden-Bell, R. Wood, A. Royal, The gravo-thermal catastrophe in isothermal spheres and the onset of red-giant structure for stellar systems. Mon. Not. R. Astron. Soc. 138(4), 495–525 (1968)

    Article  ADS  Google Scholar 

  6. P.C.W. Davies. The Physics of Time Asymmetry. (University of California Press, Berkeley and Los Angeles, 1977). OCLC: 232966619

    Google Scholar 

  7. S.W. Hawking, G.F.R. Ellis, The Large Scale Structure of Space-time. Cambridge monographs on mathematical physics. (Cambridge Univ. Press, Cambridge, 21. printing edition, 2008). OCLC: 552219048

    Google Scholar 

  8. S.W. Hawking, Black holes in general relativity. Commun. Math. Phys. 25(2), 152–166 (1972)

    Article  ADS  MathSciNet  Google Scholar 

  9. S. Chandrasekhar, The maximum mass of ideal white dwarfs. Astrophys. J. 74, 81 (1931)

    Article  ADS  Google Scholar 

  10. R. Penrose, Gravitational collapse: the role of general relativity. Riv. Nuovo Cim. 1, 252–276 (1969)

    ADS  Google Scholar 

  11. G.W. Gibbons, Vacuum polarization and the spontaneous loss of charge by black holes. Commun. Math. Phys. 44(3), 245–264 (1975)

    Article  ADS  MathSciNet  Google Scholar 

  12. R. Penrose, G. Collapse, S.-T. Singularities, Phys. Rev. Lett. 14(3), 57–59 (1965)

    Article  ADS  MathSciNet  Google Scholar 

  13. J.M. Bardeen, B. Carter, S.W. Hawking, The four laws of black hole mechanics. Commun. Math. Phys. 31(2), 161–170 (1973)

    Article  ADS  MathSciNet  Google Scholar 

  14. H.B. Callen, Thermodynamics and an Introduction to Thermostatistics, 2nd edn. (Wiley, New York, 1985)

    MATH  Google Scholar 

  15. J.D. Bekenstein, Black holes and entropy. Phys. Rev. D 7(8), 2333–2346 (1973)

    Article  ADS  MathSciNet  Google Scholar 

  16. L. Smarr, Mass formula for kerr black holes. Phys. Rev. Lett. 30, 71–73 (1973)

    Article  ADS  Google Scholar 

  17. S.W. Hawking, Black holes and thermodynamics. Phys. Rev. D 13(2), 191–197 (1976)

    Article  ADS  Google Scholar 

  18. R. Penrose, Black holes and gravitational theory. Nature 236(5347), 377–380 (1972)

    Article  ADS  Google Scholar 

  19. Y.B. Zel’dovich, Pis’ma. Zh. Eksp. Teor. Fiz 12, 443 (1970)

    Google Scholar 

  20. C.W. Misner, Interpretation of gravitational-wave observations. Phys. Rev. Lett. 28(15), 994–997 (1972)

    Article  ADS  Google Scholar 

  21. Y.B. Zel’dovich, Amplification of cylindrical electromagnetic waves reflected from a rotating body. Sov. Phys. JETP 35(6) (1972)

    Google Scholar 

  22. A.A. Starobinski, Y.B. Zel’dovich, Pis’ma. Zh. Eksp. Teor. Fiz 26, 373 (1977)

    Google Scholar 

  23. W.G. Unruh, Origin of the particles in black-hole evaporation. Phys. Rev. D 15(2), 365–369 (1977)

    Article  ADS  Google Scholar 

  24. K.S. Thorne, Black Holes and Time Warps: Einstein’s Outrageous Legacy. (1994). OCLC: 28147932

    Google Scholar 

  25. S.W. Hawking, Black hole explosions? Nature 248(5443), 30–31 (1974)

    Article  ADS  Google Scholar 

  26. S.W. Hawking, Particle creation by black holes. Commun. Math. Phys. 43(3), 199–220 (1975)

    Article  ADS  MathSciNet  Google Scholar 

  27. C.W. Misner, K.S. Thorne, J.A. Wheeler, Gravitation. (W.H. Freeman, San Francisco, 1973)

    Google Scholar 

  28. L. Parker, Probability distribution of particles created by a black hole. Phys. Rev. D 12(6), 1519–1525 (1975)

    Article  ADS  Google Scholar 

  29. L. Parker, Cincinnati, Proceedings, Asymptotic Structure of Space-time (1976), pp. 107–226

    Chapter  Google Scholar 

  30. N.N. Bogoljubov, On a new method in the theory of superconductivity. J. Exp. Theor. Phys. 34(1) (1958)

    Google Scholar 

  31. S. Corley, T. Jacobson, Hawking spectrum and high frequency dispersion. Phys. Rev. D 54(2), 1568–1586 (1996)

    Article  ADS  Google Scholar 

  32. T. Jacobson, Black-hole evaporation and ultrashort distances. Phys. Rev. D 44(6), 1731–1739 (1991)

    Article  ADS  MathSciNet  Google Scholar 

  33. P.C.W. Davies, S.A. Fulling, W.G. Unruh, Energy-momentum tensor near an evaporating black hole. Phys. Rev. D 13(10), 2720–2723 (1976)

    Article  ADS  Google Scholar 

  34. T.G. Philbin, C. Kuklewicz, S. Robertson, S. Hill, F. König, U. Leonhardt, Fiber-optical analog of the event horizon. Science 319(5868), 1367–1370 (2008)

    Article  ADS  Google Scholar 

  35. W.G. Unruh, Experimental black-hole evaporation? Phys. Rev. Lett. 46(21), 1351–1353 (1981)

    Article  ADS  Google Scholar 

  36. A.A. Penzias, R.W. Wilson, A measurement of excess antenna temperature at 4080 Mc/s. Astrophys. J. 142, 419 (1965)

    Article  ADS  Google Scholar 

  37. F. Belgiorno, S.L. Cacciatori, M. Clerici, V. Gorini, G. Ortenzi, L. Rizzi, E. Rubino, V.G. Sala, D. Faccio, Hawking radiation from ultrashort laser pulse filaments. Phys. Rev. Lett. 105(20) (2010)

    Google Scholar 

  38. D. Bermudez, U. Leonhardt, Hawking spectrum for a fiber-optical analog of the event horizon. Phys. Rev. A 93(5) (2016)

    Google Scholar 

  39. K.E. Webb, M. Erkintalo, Y. Xu, N.G.R. Broderick, J.M. Dudley, G. Genty, S.G. Murdoch, Nonlinear optics of fibre event horizons. Nat. Commun. 5, 4969 (2014)

    Article  ADS  Google Scholar 

  40. E. Rubino, F. Belgiorno, S.L. Cacciatori, M. Clerici, V. Gorini, G. Ortenzi, L. Rizzi, V.G. Sala, M. Kolesik, D. Faccio, Experimental evidence of analogue hawking radiation from ultrashort laser pulse filaments. New J. Phys. 13(8), 085005 (2011)

    Article  ADS  Google Scholar 

  41. E. Rubino, A. Lotti, F. Belgiorno, S.L. Cacciatori, A. Couairon, U. Leonhardt, D. Faccio, Soliton-induced relativistic-scattering and amplification. Sci. Rep. 2 (2012)

    Google Scholar 

  42. M. Petev, N. Westerberg, D. Moss, E. Rubino, C. Rimoldi, S.L. Cacciatori, F. Belgiorno, D. Faccio, Blackbody emission from light interacting with an effective moving dispersive medium. Phys. Rev. Lett. 111(4) (2013)

    Google Scholar 

  43. S. Liberati, A. Prain, M. Visser, Quantum vacuum radiation in optical glass. Phys. Rev. D 85(8) (2012)

    Google Scholar 

  44. F. Belgiorno, S.L. Cacciatori, F.D. Piazza, Perturbative photon production in a dispersive medium. Eur. Phys. J. D 68(5) (2014)

    Google Scholar 

  45. S.F. Wang, A. Mussot, M. Conforti, A. Bendahmane, X.L. Zeng, A. Kudlinski, Optical event horizons from the collision of a soliton and its own dispersive wave. Phys. Rev. A 92(2) (2015)

    Google Scholar 

  46. D. Faccio, S. Cacciatori, V. Gorini, V.G. Sala, A. Averchi, A. Lotti, M. Kolesik, J.V. Moloney, Analogue gravity and ultrashort laser pulse filamentation. EPL (Europhys. Lett.) 89(3), 34004 (2010)

    Article  ADS  Google Scholar 

  47. S. Finazzi, I. Carusotto, Quantum vacuum emission in a nonlinear optical medium illuminated by a strong laser pulse. Phys. Rev. A 87(2) (2013)

    Google Scholar 

  48. F. Belgiorno, S.L. Cacciatori, F.D. Piazza, Hawking effect in dielectric media and the hopfield model. Phys. Rev. D 91(12) (2015)

    Google Scholar 

  49. M.F. Linder, R. Schützhold, W.G. Unruh, Derivation of hawking radiation in dispersive dielectric media. Phys. Rev. D 93(10) (2016)

    Google Scholar 

  50. S. Finazzi, I. Carusotto, Kinematic study of the effect of dispersion in quantum vacuum emission from strong laser pulses. Eur. Phys. J. Plus 127(7) (2012)

    Google Scholar 

  51. S. Finazzi, I. Carusotto, Spontaneous quantum emission from analog white holes in a nonlinear optical medium. Phys. Rev. A 89(5) (2014)

    Google Scholar 

  52. S. Robertson, Integral method for the calculation of Hawking radiation in dispersive media. II. Asymmetric asymptotics. Phys. Rev. E 90(5) (2014)

    Google Scholar 

  53. M. Jacquet, F. König, Quantum vacuum emission from a refractive-index front. Phys. Rev. A 92(2) (2015)

    Google Scholar 

  54. J.J. Hopfield, Theory of the contribution of excitons to the complex dielectric constant of crystals. Phys. Rev. 112(5), 1555–1567 (1958)

    Article  ADS  Google Scholar 

  55. R. Schützhold, G. Plunien, G. Soff, Dielectric black hole analogs. Phys. Rev. Lett. 88, 061101 (2002)

    Article  ADS  Google Scholar 

  56. U. Fano, Atomic theory of electromagnetic interactions in dense materials. Phys. Rev. 103(5), 1202–1218 (1956)

    Article  ADS  Google Scholar 

  57. S.I. Pekar, Theory of electromagnetic waves in a crystal with excitons. J. Phys. Chem. Solids 5(1–2), 11–22 (1958)

    Article  ADS  Google Scholar 

  58. C. Kittel, Introduction to Solid State Physics, 8th edn. (Wiley, Hoboken, NJ, 2005)

    MATH  Google Scholar 

  59. C. Cohen-Tannoudji, J. Dupont-Roc, G. Grynberg, Photons and Atoms: Introduction to Quantum Electrodynamics. Physics textbook. (Wiley, Weinheim, nachdr. edition, 2004). OCLC: 254806943

    Google Scholar 

  60. E. Noether, Invariante variationsprobleme. Nachr. von der Ges. der Wiss zu Gött. Math.-Phys. Kl. 1918, 235–257 (1918)

    Google Scholar 

  61. M. Jacquet, Quantum vacuum emission at the event horizon. M.Sc. thesis, University of St Andrews, St Andrews, 2013

    Google Scholar 

  62. S. Weinfurtner, E.W. Tedford, M.C.J. Penrice, W.G. Unruh, G.A. Lawrence, Measurement of stimulated hawking emission in an analogue system. Phys. Rev. Lett. 106(2) (2011)

    Google Scholar 

  63. G. Rousseaux, C. Mathis, P. Maïssa, T.G. Philbin, U. Leonhardt, Observation of negative-frequency waves in a water tank: a classical analogue to the hawking effect? New J. Phys. 10(5), 053015 (2008)

    Article  ADS  Google Scholar 

  64. E. Rubino, J. McLenaghan, S.C. Kehr, F. Belgiorno, D. Townsend, S. Rohr, C.E. Kuklewicz, U. Leonhardt, F. König, D. Faccio, Negative-frequency resonant radiation. Phys. Rev. Lett. 108(25) (2012)

    Google Scholar 

  65. J.S. McLenaghan, Negative frequency waves in optics: control and investigation of their generation and evolution. Ph.D. thesis, University of St Andrews, St Andrews, 2014

    Google Scholar 

  66. J. McLenaghan, F. König, Few-cycle fiber pulse compression and evolution of negative resonant radiation. New J. Phys. 16(6), 063017 (2014)

    Article  ADS  Google Scholar 

  67. S.M. Barnett, B. Huttner, R. Loudon, Spontaneous emission in absorbing dielectric media. Phys. Rev. Lett. 68(25), 3698–3701 (1992)

    Article  ADS  Google Scholar 

  68. B. Huttner, J.J. Baumberg, S.M. Barnett, Canonical quantization of light in a linear dielectric. Europhys. Lett. (EPL) 16(2), 177–182 (1991)

    Article  ADS  Google Scholar 

  69. B. Huttner, S.M. Barnett, Dispersion and loss in a hopfield dielectric. Europhys. Lett. (EPL) 18(6), 487–492 (1992)

    Article  ADS  Google Scholar 

  70. R. Matloob, R. Loudon, S.M. Barnett, J. Jeffers, Electromagnetic field quantization in absorbing dielectrics. Phys. Rev. A 52(6), 4823–4838 (1995)

    Article  ADS  Google Scholar 

  71. S.M. Barnett, R. Matloob, R. Loudon, Quantum theory of a dielectric-vacuum interface in one dimension. J. Mod Opt. 42(6), 1165–1169 (1995)

    Article  ADS  Google Scholar 

  72. D.J. Santos, R. Loudon, Electromagnetic-field quantization in inhomogeneous and dispersive one-dimensional systems. Phys. Rev. A 52(2), 1538–1549 (1995)

    Article  ADS  Google Scholar 

  73. J. Macher, R. Parentani, Black/white hole radiation from dispersive theories. Phys. Rev. D 79(12) (2009)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Physics, University of Vienna, Vienna, Austria

    Maxime J. Jacquet

Authors
  1. Maxime J. Jacquet
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Maxime J. Jacquet .

Rights and permissions

Reprints and permissions

Copyright information

© 2018 Springer International Publishing AG, part of Springer Nature

About this chapter

Check for updates. Verify currency and authenticity via CrossMark

Cite this chapter

Jacquet, M.J. (2018). Spontaneous Emission of Light Quanta from the Vacuum. In: Negative Frequency at the Horizon. Springer Theses. Springer, Cham. https://doi.org/10.1007/978-3-319-91071-0_3

Download citation

Publish with us

Policies and ethics

Search

Navigation