Abstract
State-of-the-art (semi-)decision procedures for non-linear real arithmetic address polynomial inequalities by mean of symbolic methods, such as quantifier elimination, or numerical approaches such as interval arithmetic. Although (some of) these methods offer nice completeness properties, their high complexity remains a limit, despite the impressive efficiency of modern implementations. This appears to be an obstacle to the use of SMT solvers when verifying, for instance, functional properties of control-command programs.
Using off-the-shelf convex optimization solvers is known to constitute an appealing alternative. However, these solvers only deliver approximate solutions, which means they do not readily provide the soundness expected for applications such as software verification. We thus investigate a-posteriori validation methods and their integration in the SMT framework. Although our early prototype, implemented in the Alt-Ergo SMT solver, often does not prove competitive with state of the art solvers, it already gives some interesting results, particularly on control-command programs.
This work has been partially supported by the French ANR projects ANR-12-INSE-0007 Cafein and ANR-14-CE28-0020 Soprano and the project SEFA IKKY.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords

1 Introduction
Systems of non-linear polynomial constraints over the reals are known to be solvable since Tarski proved that the first-order theory of the real numbers is decidable, by providing a quantifier elimination procedure. This procedure has then been much improved, particularly with the cylindrical algebraic decomposition. Unfortunately, its doubly exponential complexity remains a serious limit to its scalability. It is now integrated into SMT solvers [23]. Although it demonstrates very good practical results, symbolic quantifier elimination seems to remain an obstacle to scalability on some problems. In some cases, branch and bound with interval arithmetic constitutes an interesting alternative [17].
We investigate the use of numerical optimization techniques, called semi-definite programming, as an alternative. We show in this paper how solvers based on these techniques can be used to design a sound semi-decision procedure that outperforms symbolic and interval-arithmetic methods on problems of practical interest. A noticeable characteristic of the algorithms implemented in these solvers is to only compute approximate solutions.
We explain this by making a comparison with linear programming. There are two competitive methods to optimize a linear objective under linear constraints: the interior point and the simplex algorithms. The interior point algorithm starts from some initial point and performs steps towards an optimal value. These iterations converge to the optimum but not in finitely many steps and have to be stopped at some point, yielding an approximate answer. In contrast, the simplex algorithm exploits the fact that the feasible set is a polyhedra and that the optimum is achieved on one of its vertices. The number of vertices being finite, the optimum can be exactly reached after finitely many iterations. Unfortunately, this nice property does not hold for spectrahedra, the equivalent of polyhedra for semi-definite programming. Thus, all semi-definite programming solvers are based on the interior-point algorithm, or a variant thereof.
To illustrate the consequences of these approximate solutions, consider the proof of \(e \le c\) with e a complicated ground expression and c a constant. \(e \le c\) can be proved by exactly computing e, giving a constant \(c'\), and checking that \(c' \le c\). However, if e is only approximately computed: \(e \in [c'-\epsilon , c'+\epsilon ]\), this is conclusive only when \(c'+\epsilon \le c\). In particular, if e is equal to c, an exact computation is required. This inability to prove inequalities that are not satisfied with some margin is a well known property of numerical verification methods [42] which can then be seen as a trade-off between completeness and computation cost.
The main point of this paper is that, despite their incompleteness, numerical verification methods remain an interesting option when they enable to practically solve problems for which other methods offer an untractable complexity. Our contributions are:
-
(1)
a comparison of two sound semi-decision procedures for systems of non-linear constraints, which rely on off-the-shelf numerical optimization solvers,
-
(2)
an integration of these procedures in the Alt-Ergo SMT solver,
-
(3)
an experimental evaluation of our approach on a set of benchmarks coming from various application domains.
The rest of this paper is organized as follows: Sect. 2 gives a practical example of a polynomial problem, coming from control-command program verification, better handled by numerical methods. Section 3 is dedicated to preliminaries. It introduces basic concepts of sum of squares polynomials and semi-definite programming. In Sect. 4, we compare two methods to derive sound solutions to polynomial problems from approximate answers of semi-definite programming solvers. Section 5 provides some implementation details and discuss experimental results. Finally, Sect. 6 concludes with some related and future works.
2 Example: Control-Command Program Verification
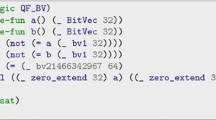
Control-command programs usually iterate linear assignments periodically over time. These assignments take into account a measure (via some sensor) of the state of the physical system to control (called plant by control theorists) to update an internal state and eventually output orders back to the physical system (through some actuator). Figure 1 gives an example of such an update, in0 being the input and s the internal state. The comments beginning by @ in the example are annotations in the ACSL language [12]. They specify that before the execution of the function (requires) s must be a valid pointer satisfying the predicate inv and \(\left| \mathtt {in0}\right| \le 1\) must hold. Under these hypotheses, s still satisfies inv after executing the function (ensures).
To prove that the internal state remains bounded over any execution of the system, a quadratic polynomialFootnote 1 can be used as invariantFootnote 2. Checking the validity of these invariants then leads to arithmetic verification conditions (VCs) involving quadratic polynomials. Such VCs can for instance be generated from the program of Fig. 1 by the Frama-C/Why3 program verification toolchain [12, 16]. Unfortunately, proving the validity of these VCs seem out of reach for current state-of-the-art SMT solvers. For instance, although Z3 [13] can solve smaller examples with just two internal state variables in a matter of seconds, it ran for a few days on the three internal state variable example of Fig. 1 without reaching a conclusionFootnote 3. In contrast, our prototype can prove it in a fraction of second, as well as other examples with up to a dozen variables.
Verification of control-command programs is a good candidate for numerical methods. These systems are designed to be robust to many small errors, which means that the verified properties are usually satisfied with some margin. Thus, the incompleteness of numerical methods is not an issue for this kind of problems.
3 Preliminaries
3.1 Emptiness of Semi-algebraic Sets
Our goal is to prove that conjunctions of polynomial inequalities are unsatisfiable, that is, given some polynomials with real coefficients \(p_1,\ldots , p_m \in \mathbb {R}[x]\), we want to prove that there does not exist any assignment for the n variables \(x_1,\ldots , x_n \in \mathbb {R}^n\) such that all inequalities \(p_1(x_1,\ldots , x_n) \ge 0,\ldots , p_m(x_1,\ldots , x_n) \ge 0\) hold simultaneously. In the rest of this paper, the notation \(p \ge 0\) (resp. \(p > 0\)) means that for all \(x \in \mathbb {R}^n\), \(p(x) \ge 0\) (resp. \(p(x) > 0\)).
Theorem 1
If there exist polynomials \(r_i \in \mathbb {R}[x]\) such that
then the conjunction \(\bigwedge _i p_i \ge 0\) is unsatisfiableFootnote 4.
Proof
Assume there exist \(x \in \mathbb {R}^n\) such that for all i, \(p_i(x) \ge 0\). Then, since \(r_i \ge 0\), we have \(r_i(x)\,p_i(x) \ge 0\) hence \(\left( \sum _i r_i\, p_i\right) (x) \ge 0\) which contradicts \(-\sum _i r_i\, p_i > 0\).
In fact, under some hypothesesFootnote 5 on the \(p_i\), the condition (1) is not only sufficient but also necessary, as stated by the Putinar’s Positivstellensatz [27, Sect. 2.5.1]. Unfortunately, no practical bound is known on the degrees of the polynomials \(r_i\). In our prototype, we restrict the degrees of each \(r_i\) toFootnote 6 \(d - \deg (p_i)\) where \(d := \max _i(\deg (p_i))\), so that \(\sum _i r_i\, p_i\) is a polynomial of degree d. This is a first source of incompleteness, although benchmarks show that it already enables to solve many interesting problems.
The sum of squares (SOS) technique [26, 36] is an efficient way to numerically solve polynomial problems such as (1). The next sections recall its main ideas.
3.2 Sum of Squares (SOS) Polynomials
A polynomial \(p \in \mathbb {R}[x]\) is said to be SOS if there exist polynomials \(h_i \in \mathbb {R}[x]\) such that for all x,
Although not all non negative polynomials are SOS, being SOS is a sufficient condition to be non negative.
Example 1
(from [36]). Considering \(p(x_1, x_2) = 2x_1^4 + 2x_1^3x_2 - x_1^2 x_2^2 + 5x_2^4\), there exist \(h_1(x_1, x_2) = \frac{1}{\sqrt{2}}\left( 2x_1^2-3x_2^2+x_1x_2\right) \) and \(h_2(x_1, x_2) = \frac{1}{\sqrt{2}}\left( x_2^2+3x_1x_2\right) \) such that \(p = h_1^2 + h_2^2\). This proves that for all \(x_1, x_2 \in \mathbb {R}\), \(p(x_1, x_2) \ge 0\).
Any polynomial p of degree 2d (a non negative polynomial is necessarily of even degree) can be written as a quadratic form in the vector of all monomials of degree less or equal to d:
where \(z = \left[ 1, x_1,\ldots , x_n, x_1 x_2,\ldots , x_n^d\right] ^T\) and Q is a constant symmetric matrix.
Example 2
For \(p(x_1, x_2) = 2x_1^4 + 2x_1^3x_2 - x_1^2x_2^2 + 5x_2^4\) , we haveFootnote 7
Thus \(q_{11} = 2\), \(2q_{13} = 2\), \(q_{33}+2q_{12} = -1\), \(2q_{23} = 0\) and \(q_{22} = 5\). Two possible examples for the matrix Q are shown below:
The polynomial p is then SOS if and only if there exists a positive semi-definite matrix Q satisfying (2). A matrix Q is called positive semi-definite, noted \(Q \succeq 0\), if, for all vector x, \(x^T Q\, x \ge 0\). Just as a scalar \(q \in \mathbb {R}\) is non negative if and only if \(q = r^2\) for some \(r \in \mathbb {R}\) (typically \(r =\sqrt{q}\)), \(Q \succeq 0\) if and only if \(Q = R^TR\) for some matrix R (then, for all x, \(x^TQx = (Rx)^T(Rx) = \Vert Rx\Vert _2^2 \ge 0\)). The vector Rz is then a vector of polynomials \(h_i\) such that \(p = \sum _i h_i^2\).
Example 3
In the previous example, the matrix Q is not positive semi-definite (for \(x = \left[ 0, 0, 1\right] ^T\), \(x^TQ\,x = -3\)). In contrast, \(Q' \succeq 0\) as \(Q' = R^T R\) with
giving the decomposition of Example 1.
3.3 Semi-Definite Programming (SDP)
Given symmetric matrices \(C, A_1,\ldots , A_m \in \mathbb {R}^{s\times s}\) and scalars \(a_1,\ldots , a_m \in \mathbb {R}\), the following optimization problem is called semi-definite programming
where the symmetric matrix \(Q \in \mathbb {R}^{s\times s}\) is the variable, \(\mathrm{tr}(M) = \sum _i M_{i,i}\) denotes the trace of the matrix M and \(Q \succeq 0\) means Q positive semi-definite.
Remark 1
Since the matrices are symmetric, \(\mathrm{tr}(A Q) = \mathrm{tr}(A^T Q) = \sum _{i, j} A_{i, j} Q_{i, j}\). The constraints \(\mathrm{tr}(A Q) = a\) are then affine constraints between the entries of Q.
As we have just seen in Sect. 3.2, existence of a SOS decomposition amounts to existence of a positive semi-definite matrix satisfying a set of affine constraints, that is a solution of a semi-definite program. Semi-definite programming is a convex optimization problem for which there exist efficient numerical solvers [7, 44], thus enabling to solve problems involving polynomial inequalities over the reals.
3.4 Parametric Problems
Up to now, we have only seen how to check whether a given polynomial p with fixed coefficients is SOS (which implies its non negativeness). However, according to Sect. 3.1, we need to solve problems in which polynomials p have coefficients that are not fixed but parameters. One of the great strengths of SOS programming is its ability to solve such problems.
An unknown polynomial \(p\in \mathbb {R}[x]\) of degree d with n variables can be written
where the \(p_\alpha \) are scalar parameters. A constraint such as \(r_i \ge 0\) in (1) can then be replaced by \(r_i\) is SOS, that is: \(\exists \, Q \succeq 0, r_i = z^TQ\,z\), which is a set of affine equalities between the coefficients of Q and the coefficients \(r_{i, \alpha }\) of \(r_i\). This can be cast as a semi-definite programming problemFootnote 8.
Thus, problems with unknown polynomials p, as the one presented in Sect. 3.1, can be numerically solved through SOS programming.
Remark 2
(Complexity). The number s of monomials in n variables of degree less than or equal to d, i.e., the size of the vector z in the decomposition \(p(x) = z^T Q\,z\), is \(s := \left( {\begin{array}{c}n+d\\ d\end{array}}\right) \). This is polynomial in n for a fixed d (and vice versa). In practice, current SDP solvers can solve problems where s is about a few hundreds. This makes the SOS relaxation tractable for small values of n and d (\(n \sim 10\) and \(d \sim 3\), for instance). Our benchmarks indicate this is already enough to solve some practical problems that remain out of reach for other methods.
4 Numerical Verification of SOS
According to Sect. 3.1, a conjunction of polynomial constraints can be proved unsatisfiable by exhibiting other polynomials satisfying some constraints. Section 3.4 shows that such polynomials can be efficiently found by some numerical optimization solvers. Unfortunately, due to the algorithms they implement, we cannot directly trust the results of these solvers. This section details this issue and reviews two a-posteriori validation methods, with their respective weaknesses.
4.1 Approximate Solutions from SDP Solvers
In practice, the matrix Q returned by SDP solvers upon solving an SDP problem (3) does not precisely satisfy the equality constraints, due both to the algorithms used and their implementation with floating-point arithmetic. Therefore, although the SDP solver returns a positive answer for a SOS program, this does not constitute a valid proof that a given polynomial is SOS.
Most SDP solvers start from some \(Q \succeq 0\) not satisfying the equality constraints (for instance the identity matrix) and iteratively modify it in order to reduce the distance between \(\mathrm{tr}(A_i Q)\) and \(a_i\) while keeping Q positive semi-definite. This process is stopped when the distance is deemed small enough. This final distance \(\epsilon \) is called the primal infeasibility, and is one of the result quality measures displayed by SDP solversFootnote 9. Therefore, we do not obtain a Q satisfying \(\mathrm{tr}(A_i Q) = a_i\) but rather \(\mathrm{tr}(A_i Q) = a_i + \epsilon _i\) for some small \(\epsilon _i\) such that \(\left| \epsilon _i\right| \le \epsilon \).
4.2 Proving Existence of a Nearby Solution
This primal infeasibility has a simple translation in terms of our original SOS problem. The polynomial equality \(p = z^TQ\,z\) is encoded as one scalar constraint \(\mathrm{tr}(A_iQ) = a_i\) for each coefficient \(a_i\) of the polynomial p (c.f., Examples 2). coefficients of the polynomials p and \(z^TQ\,z\) differ by some \(\epsilon _i\) and, since \(\left| \epsilon _i\right| \le \epsilon \), there exists a matrix \(E \in \mathbb {R}^{s\times s}\) such that, for all i, j, \(\left| E_{i,j}\right| \le \epsilon \) and
Proving that \(Q+E \succeq 0\) is now enough to prove that the polynomial p is SOS, hence non negative. A sufficient condition is to checkFootnote 10 \(Q - s\epsilon I \succeq 0\).
As seen in Sect. 3.2, checking that a matrix M is positive semi-definite amounts to exhibiting a matrix R such that \(M = R^TR\). The Cholesky decomposition algorithm [45, Sect. 1.4] computes such a matrix R. Given a matrix \(M \in \mathbb {R}^{s\times s}\), it attempts to compute R such that \(M = R^TR\) and when M is not positive semi-definite, it fails by attempting to take the square root of a negative value or perform a division by zero.
Due to rounding errors, a simple floating-point Cholesky decomposition would produce a matrix R not exactly satisfying the equality \(M = R^TR\), hence not proving \(M \succeq 0\). However, these rounding errors can be bounded by a matrix B so that, when the floating-point Cholesky decomposition of \(M-B\) succeeds, then \(M \succeq 0\) is guaranteed to hold. Moreover, B can be easily computed from the matrix M and the characteristics of the floating-point format used [41].
To sum up, the following verification procedure can prove that a given polynomial p is SOSFootnote 11.

Complexity. Note that step 1 can be achieved using floating-point interval arithmetic in \(\varTheta (s^2)\) operations while the Cholesky decomposition in step 2 requires \(\varTheta (s^3)\) floating-point operations. Thus, the whole verification method takes \(\varTheta (s^3)\) floating-point operations which, in practice, constitutes a very small overhead compared to the time required by the SDP solver to compute Q.
Soundness. It is interesting to notice that the soundness of the method does not rely on the SDP solver. Thanks to this pessimistic method, the trusted code-base remains small, and efficient off-the-shelf solvers can be used as untrusted oracles. The method was even verified [31, 38] within the Coq proof assistant.
Incompleteness. Numerical verification methods can only prove inequalities satisfied with some margin. Here, if the polynomial p to prove SOS (hence \(p \ge 0\)) reaches the value 0, this usually means that the feasible set of the SDP problem  has an empty relative interior (i.e., there is no point Q in this set such that a small ball centered on Q is included in
has an empty relative interior (i.e., there is no point Q in this set such that a small ball centered on Q is included in  ) and the method does not work, as illustrated on Fig. 2. This is a second source of incompleteness of our approach, that adds to the limitation of degrees of polynomials searched for, as presented in Sect. 3.1.
) and the method does not work, as illustrated on Fig. 2. This is a second source of incompleteness of our approach, that adds to the limitation of degrees of polynomials searched for, as presented in Sect. 3.1.
Remark 3
The floating-point Cholesky decomposition is theoretically a third source of incompleteness. However, it is negligible as the entries of the bound matrix B are, in practice, orders of magnitude smallers than the accuracy \(\epsilon \) of the SDP solvers [40].
4.3 Rounding to an Exact Rational Solution
The most common solution to verify results of SOS programming is to round the output of the SDP solver to an exact rational solution [19, 24, 33].
To sum up, the matrix Q returned by the SDP solver is first projected to the subspace  then all its entries are rounded to rationals with small denominators (first integers, then multiples of \(\frac{1}{2}, \frac{1}{3},\ldots \))Footnote 12. For each rounding, positive semi-definiteness of the resulting matrix Q is tested using a complete check, based on a LDLT decompositionFootnote 13 [19]. The rationale behind this choice is that problems involving only simple rational coefficients can reasonably be expected to admit simple rational solutionsFootnote 14.
then all its entries are rounded to rationals with small denominators (first integers, then multiples of \(\frac{1}{2}, \frac{1}{3},\ldots \))Footnote 12. For each rounding, positive semi-definiteness of the resulting matrix Q is tested using a complete check, based on a LDLT decompositionFootnote 13 [19]. The rationale behind this choice is that problems involving only simple rational coefficients can reasonably be expected to admit simple rational solutionsFootnote 14.
Using exact solutions potentially enables to verify SDP problems with empty relative interiors. This means the ability to prove inequalities without margin, to distinguish strict and non-strict inequalities and even to handle (dis)equalities. All of this nevertheless requires a different relaxation scheme than (1).
Example 4
To prove \(x_1 \ge 0 \wedge x_2 \ge 0 \wedge q_1 = 0 \wedge q_2 = 0 \wedge p > 0\) unsatisfiable, with \(q_1 := x_1^2 + x_2^2 - x_3^2 - x_4^2 - 2\), \(q_2 := x_1 x_3 + x_2 x_4\) and \(p := x_3 x_4 - x_1 x_2\), one can look for polynomials \(l_1, l_2\) and SOS polynomials \(s_1,\ldots , s_8\) such that \(l_1 q_1 + l_2 q_2 + s_1 + s_2 p + s_3 x_1 + s_4 x_1 p + s_5 x_2 + s_6 x_2 p + s_7 x_1 x_2 + s_8 x_1 x_2 p + p = 0 \).
Rounding the result of an SDP solver yields \(l_1 = -\frac{1}{2}\left( x_1 x_2 - x_3 x_4\right) \), \(l_2 = -\frac{1}{2}\left( x_2 x_3 + x_1 x_4\right) \), \(s_2 = \frac{1}{2}\left( x_3^2 + x_4^2\right) \), \(s_7 = \frac{1}{2}\left( x_1^2 + x_2^2 + x_3^2 + x_4^2\right) \) and \(s_1 = s_3 = s_4 = s_5 = s_6 = s_8 = 0\). This problem has no margin, since when replacing \(p > 0\) by \(p \ge 0\), \((x_1, x_2, x_3, x_4) = (0, \sqrt{2}, 0, 0)\) becomes a solution.
Under some hypotheses, this relaxation scheme is complete, as stated by a theorem from Stengle [27, Theorem 2.11]. However, similarly to Sect. 3.1, no practical bound is known on the degrees of the relaxation polynomials.
Complexity. The relaxation scheme involves products of all polynomials appearing in the original problem constraints. The number of such products, being exponential in the number of constraints, limits the scalability of the approach.
Moreover, to actually enjoy the benefits of exact solutions, the floating-point Cholesky decomposition introduced in Sect. 4.2 cannot be used and has to be replaced by an exact rational decompositionFootnote 15. Computing decompositions of large matrices can then become particularly costly as the size of the involved rationals can blow up exponentially during the computation.
Soundness. The exact solutions make for an easy verification. The method is thus implemented in the HOL Light [19] and Coq [4] proof assistants.
Incompleteness. Although this verification method can work for some SDP problems with an empty relative interior, the rounding heuristic is not guaranteed to provide a solution. In practice, it tends to fail on large problems or problems whose coefficients are not rationals with small numerators and denominators.
5 Experimental Results
5.1 The OSDP Library
The SOS to SDP translation described in Sect. 3, as well as the validation methods described in Sect. 4 have been implemented in our OCaml library OSDP. This library offers a common interface to the SDP solversFootnote 16 Csdp [6], Mosek [2] and SDPA [46], giving simple access to SOS programming in contexts where soundness matters, such as SMT solvers or program static analyzers. It is composed of 5 kloc of OCaml and 1 kloc of C (interfaces with SDP solvers) and is available under LGPL license at https://cavale.enseeiht.fr/osdp/.
5.2 Integration of OSDP in Alt-Ergo
Alt-Ergo [5] is a very effective SMT solver for proving formulas generated by program verification frameworks. It is used as a back-end of different tools and in various settings, in particular via the Why3 [16] platform. For instance, the Frama-C [12] suite relies on it to prove formulas generated from C code, and the SPARK [21] toolset uses it to check formulas produced from Ada programs. It is also used by EasyCrypt [3] to prove formulas issued from cryptographic protocols verification, from the Cubicle [10] model-checker, and from Atelier-B [1].
Alt-Ergo’s native input language is a polymorphic first-order logic à la ML modulo theories, a very suitable language for expressing formulas generated in the context of program verification. Its reasoning engine is built on top of a SAT solver that interacts with a combination of decision procedures to look for a model for the input formula. Universally quantified formulas, that naturally arise in program verification, are handled via E-matching techniques. Currently, Alt-Ergo implements decision procedures for the free theory of equality with uninterpreted symbols, linear arithmetic over integers and rationals, fragments of non-linear arithmetic, enumerated and records datatypes, and the theory of associative and commutative function symbols (hereafter AC).
Figure 3 shows the simplified architecture of arithmetic reasoning framework in Alt-Ergo, and the OSDP extension. The first component in the figure is a completion-like algorithm AC(LA) that reasons modulo associativity and commutativity properties of non-linear multiplication, as well as its distributivity over additionFootnote 17. AC(LA) is a modular extension of ground AC completion with a decision procedure for reasoning modulo equalities of linear integer and rational arithmetic [9]. It builds and maintains a convergent term-rewriting system modulo arithmetic equalities and the AC properties of the non-linear multiplication symbol. The rewriting system is used to update a union-find data-structure.
The second component is an Interval Calculus algorithm that computes bounds of (non-linear) terms: the initial non-linear problem is first relaxed by abstracting non-linear parts, and a Fourier-Motzkin extensionFootnote 18 is used to infer bounds on the abstracted linear problem. In a second step, axioms of non-linear arithmetic are internally applied by intervals propagation. These two steps allow to maintain a map associating the terms of the problems (that are normalized w.r.t. the union-find) to unions of intervals.
Finally, the last part is the SAT solver that dispatches equalities and inequalities to the right component and performs case-split analysis over finite domains. Of course, this presentation is very simplified and the exact architecture of Alt-Ergo is much more complicated.
The integration of OSDP in Alt-Ergo is achieved via the extension of the Interval Calculus component of the solver, as shown in Fig. 3: terms that are polynomials, and their corresponding interval bounds, form the problem (1) which is given to OSDP. OSDP attempts to verify its result with the method of Sect. 4.2. When it succeeds, the original conjunction of constraints is proved unsat. Otherwise, (dis)equalities are added and OSDP attempts a new proof by the method of Sect. 4.3. In case of success, unsat is proved, otherwise satisfiability or unsatisfiability cannot be deduced. Outlines of the first algorithm are given in Fig. 4 whereas the second one follows the original implementation [19].
Our modified version of Alt-Ergo is available under CeCILL-C license at https://cavale.enseeiht.fr/osdp/aesdp/.
Semi-decision procedure to prove \(\displaystyle \bigwedge _{i=1}^k p_i \in [a_i, b_i]\) unsat. \(\#|z|\) is the size of the vector z and \(\succ 0\) is tested with a floating-point Cholesky decomposition [41].
Incrementality. In the SMT context, our theory solver is often succesively called with the same problem with a few additional constraints each time. It would then be interesting to avoid doing the whole computation again when a constraint is added, as is usually done with the simplex algorithm for linear arithmetic.
Some SDP solvers do offer to provide an initial point. Our experiments however indicated that this significantly speeds up the computation only when the provided point is extremely close to the solution. A bad initial point could even slow down the computation or, worse, make it fail. This is due to the very different nature of the interior point algorithms, compared to the simplex, and their convergence properties [7, Part III]. Thus, speed ups could only be obtained when the previous set of constraints was already unsatisfiable, ı.e. a useless case.
Small Conflict Sets. When a set of constraints is unsatisfiable, some of them may not play any role in this unsatisfiability. Returning a small subset of unsatisfiable constraints can help the underlying SAT solver. Such useless constraints can easily be identified in (1) when the relaxation polynomial \(r_i\) is 0. A common heuristic to maximize their number is to ask the SDP solver to minimize (the sum of) the traces of the matrices \(Q_i\).
When using the exact method of Sect. 4.3, the appropriate \(r_i\) are exactly 0. Things are not so clear when using the approximate method of Sect. 4.2 since the \(r_i\) are only close to 0. A simple solution is to rank the \(r_i\) by decreasing trace of \(Q_i\) before performing a dichotomy search for the smallest prefix of this sequence proved unsatisfiable. Thus, for n constraints, \(\log (n)\) SDPs are solved.
5.3 Experimental Results
We compared our modified version of Alt-Ergo (v. 1.30) to the SMT solvers ran in both the QF_NIA and QF_NRA sections of the last SMT-COMP. We ran the solvers on two sets of benchmarks. The first set comes from the QF_NIA and QF_NRA benchmarks for the last SMT-COMP. The second set contains four subsets. The C problems are generated by Frama-C/Why3 [12, 16] from control-command C programs such as the one from Sect. 2, with up to a dozen variables [11, 39]. To distinguish difficulties coming from the handling of the memory model of C, for which Alt-Ergo was particularly designed, and from the actual non-linear arithmetic problem, the quadratic benchmarks contain simplified versions of the C problems with a purely arithmetic goal. To demonstrate that the interest of our approach is not limited to this initial target application, the flyspeck benchmarks come from the benchmark sets of dRealFootnote 19 [18] and global-opt are global optimization benchmarks [34]. All these benchmarks are available at https://cavale.enseeiht.fr/osdp/aesdp/. Since our solver only targets unsat proofs, benchmarks known sat were removed from both sets.
All experiments were conducted on an Intel Xeon 2.30 GHz processor, with individual runs limited to 2 GB of memory and 900 s. The results are presented in Tables 1, 2 and 3. For each subset of problems, the first column indicates the number of problems that each solver managed to prove unsat and the second presents the cumulative time (in seconds) for these problems. AE is the original Alt-Ergo, AESDP our new version, AESDPap the same but using only the approximate method of Sect. 4.2 and AESDPex using only the exact method of Sect. 4.3. All solvers were run with default options, except CVC4 which was run with all its –nl-ext* options.
As seen in Tables 1 and 2, despite an improvement over Alt-Ergo alone, our development is not competitive with state-of-the-art solvers on the QF_NIA and QF_NRA benchmarks. In fact, the set of problems solved by any of our Alt-Ergo versions is strictly included in the set of problems solved by at least one of the other solvers. The most commonly observed source of failure for AESDPap here comes from SDPs with empty relative interior. Although AESDPex can handle such problems, it is impaired by its much higher complexity.
However good results are obtained on the more numericalFootnote 20 second set of benchmarks. In particular, control-command programs with up to a dozen variables are verified while other solvers remain limited to two variables. Playing a key point in this result, the inequalities in these benchmarks are satisfied with some margin. For control command programs, this comes from the fact that they are designed to be robust to many small errors. This opens new perspectives for the verification of functional properties of control-command programs, particularly in the aerospace domain, our main application field at ONERAFootnote 21.
Although solvers such as dReal, based on branch and bound with interval arithmetic could be expected to perform well on these numerical benchmarks, dReal solves less benchmarks than most other solvers. Geometrically speaking, the C benchmarks require to prove that an ellipsoid is included in a slightly larger one, i.e., the borders of both ellipsoids are close from one another. This requires to subdivide the space between the two borders in many small boxes so that none of them intersects both the interior of the first ellipsoid and the exterior of the second one. Whereas this can remain tractable for small dimensional ellipsoids, the number of required boxes grows exponentially with the dimension, which explains the poor results of dReal. This issue is unfortunately shared, to a large extent, by any linear relaxation, including more elaborate ones [30].
6 Related Work and Conclusion
Related work. Monniaux and Corbineau [33] improved the rounding heuristic of Harrison [19]. This has unfortunately no impact on the complexity of the relaxation scheme. Platzer et al. [37] compared their early versions with the symbolic methods based on quantifier elimination and Gröbner basis. An intermediate solution is offered by Magron et al. [29] but only handling a restricted class of parametric problems.
Branch-and-bound and interval arithmetic constitute another numerical approach to non-linear arithmetic, as implemented in the SMT solver dReal by Gao et al. [17, 18]. These methods easily handle non-linear functions such as the trigonometric functions \(\sin \) or \(\cos \), not yet considered in our prototypeFootnote 22. In the case of polynomial inequalities Muñoz and Narkawicz [34] offer Bernstein polynomials as an improvement to simple interval arithmetic.
Finally, VSDP [20, 22] is a wrapper to SDP solvers offering a similar method to the one of Sect. 4.2. Moreover, an implementation is also offered by Löfberg [28] in the popular Matlab interface Yalmip but remains unsound, since all computations are performed with floating-point arithmetic, ignoring rounding errors.
Using convex optimization into an SMT solver was already proposed by Nuzzo et al. [35, 43]. However, they intentionally made their solver unsound in order to lean toward completeness. While this can make sense in a bounded model checking context, soundness is required for many applications, such as program verification. Moreover, this proposal was limited to convex formulas. Although this enables to provide models for satisfiable formulas, while only unsat formulas are considered in this paper, and whereas this seems a perfect choice for bounded model checking applications, non convex formulas are pervasive in applications such as program verificationFootnote 23.
The use of numerical off-the-shelf solvers in SMT tools has also been studied in the framework of linear arithmetic [15, 32]. Some comparison with state-of-the-art exact simplex procedures show mitigated results [14] but better results can be obtained by combining both approaches [25].
Conclusion. We presented a semi-decision procedure for non-linear polynomial constraints over the reals, based on numerical optimization solvers. Since these solvers only compute approximate solutions, a-posteriori soundness checks were investigated. Our first prototype implemented in the Alt-Ergo SMT solver shows that, although the new numerical method does not strictly outperform state-of-the-art symbolic methods, it enables to solve practical problems that are out of reach for other methods. In particular, this is demonstrated on the verification of functional properties of control-command programs. Such properties are of significant importance for critical cyber-physical systems.
It could thus be worth studying the combination of symbolic and numerical methods in the hope to benefit from the best of both worlds.
Notes
- 1.
For instance, the three variables polynomial in
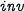 in Fig. 1.
in Fig. 1. - 2.
Control theorists call these invariants sublevel sets of a quadratic Lyapunov function. Such functions exist for linear systems if and only if they do not diverge.
- 3.
This is the case even on a simplified version with just arithmetic constructs, i.e., expurgated of all the reasoning about pointers and the C memory model.
- 4.
Or, with different words, the semi-algebraic set
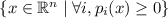 is empty.
is empty. - 5.
For instance, when one of the sets
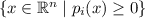 is bounded.
is bounded. - 6.
More precisely to \(2\left\lceil \frac{d-\deg (p_i)}{2}\right\rceil \) as \(deg(r_i)\) is necessarily even since \(r_i \ge 0\).
- 7.
All monomials of p are of degree 4, so z does not need to contain 1, \(x_1\) and \(x_2\).
- 8.
By encoding the \(r_{i, \alpha } \in \mathbb {R}\) as \(r_{i, \alpha }^+-r_{i, \alpha }^-\) with \(r_{i, \alpha }^+, r_{i, \alpha }^- \ge 0\) and putting the new variables in a block diagonal matrix variable \(Q' := \mathrm{diag}(Q,\ldots , r_{i, \alpha }^+, r_{i, \alpha }^-,\ldots )\).
- 9.
Typically, \(\epsilon \sim 10^{-8}\).
- 10.
In order to get good likelihood for this to hold, we ask the SDP solver for \(Q - 2s\epsilon I \succeq 0\) rather than \(Q \succeq 0\), as solvers often return matrices Q slightly not positive definite.
- 11.
It is worth noting that the value reported by the solver for \(\epsilon \), being just computed with floating-point arithmetic, cannot be formally trusted. It must then be recomputed.
- 12.
- 13.
The LDLT decomposition expresses a positive semi-definite matrix M as \(M = LDL^T\) with L a lower triangular matrix and D a diagonal matrix.
- 14.
However, there exist rational SDP problems that do not admit any rational solution.
- 15.
The Cholesky decomposition, involving square roots, cannot be computed in rational arithmetic, however its LDLT variant can.
- 16.
Csdp is used for the following benchmarks as it provides the best results.
- 17.
Addition and multiplication by a constant is directly handled by the LA module.
- 18.
We can also use a simplex-based algorithm [8] for bounds inference.
- 19.
Removing problems containing functions \(\sin \) and \(\cos \), not handled by our tool.
- 20.
Involving polynomials with a few dozen monomials or more and whose coefficients are not integers or rationals with small numerators and denominators.
- 21.
French public agency for aerospace research.
- 22.
Polynomial approximations such as Taylor expansions should be investigated.
- 23.
Typically, to prove a convex loop invariant I for a loop body f, one need to prove \(I \Rightarrow I(f)\), that is \(\lnot I \vee I(f)\) which is likely non convex (\(\lnot I\) being concave).
References
Abrial, J.-R.: The B-Book - Assigning Programs to Meanings. Cambridge University Press, Cambridge (2005)
MOSEK ApS: The MOSEK C Optimizer API Manual Version 7.1 (Rev. 40) (2015)
Barthe, G., Dupressoir, F., Grégoire, B., Kunz, C., Schmidt, B., Strub, P.-Y.: EasyCrypt: a tutorial. In: Aldini, A., Lopez, J., Martinelli, F. (eds.) FOSAD 2012-2013. LNCS, vol. 8604, pp. 146–166. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10082-1_6
Besson, F.: Fast reflexive arithmetic tactics the linear case and beyond. In: Altenkirch, T., McBride, C. (eds.) TYPES 2006. LNCS, vol. 4502, pp. 48–62. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74464-1_4
Bobot, F., Conchon, S., Contejean, E., Iguernlala, M., Lescuyer, S., Mebsout, A.: Alt-Ergo, Version 0.99.1. CNRS, Inria, Université Paris-Sud 11, and OCamlPro, December 2014. http://alt-ergo.lri.fr/
Borchers, B.: CSDP, A C Library for Semidefinite Programming. Optimization Methods and Software (1999)
Boyd, S., Vandenberghe, L.: Convex Optimization. Cambridge University Press, Cambridge (2004)
Bobot, F., Conchon, S., Contejean, E., Iguernelala, M., Mahboubi, A., Mebsout, A., Melquiond, G.: A simplex-based extension of Fourier-Motzkin for solving linear integer arithmetic. In: Gramlich, B., Miller, D., Sattler, U. (eds.) IJCAR 2012. LNCS (LNAI), vol. 7364, pp. 67–81. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31365-3_8
Conchon, S., Contejean, É., Iguernelala, M.: Canonized rewriting and ground AC completion modulo Shostak theories: design and implementation. In: Logical Methods in Computer Science, Selected Papers of TACAS (2012)
Conchon, S., Goel, A., Krstić, S., Mebsout, A., Zaïdi, F.: Cubicle: a parallel SMT-based model checker for parameterized systems. In: Madhusudan, P., Seshia, S.A. (eds.) CAV 2012. LNCS, vol. 7358, pp. 718–724. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31424-7_55
Cox, A., Sankaranarayanan, S., Chang, B.-Y.E.: A bit too precise? Bounded verification of quantized digital filters. In: Flanagan, C., König, B. (eds.) TACAS 2012. LNCS, vol. 7214, pp. 33–47. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28756-5_4
Cuoq, P., Kirchner, F., Kosmatov, N., Prevosto, V., Signoles, J., Yakobowski, B.: Frama-C - a software analysis perspective. In: Eleftherakis, G., Hinchey, M., Holcombe, M. (eds.) SEFM 2012. LNCS, vol. 7504, pp. 233–247. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33826-7_16
de Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78800-3_24
de Oliveira, D.C.B., Monniaux, D.: Experiments on the feasibility of using a floating-point simplex in an SMT solver. In: PAAR@IJCAR (2012)
Faure, G., Nieuwenhuis, R., Oliveras, A., Rodríguez-Carbonell, E.: SAT modulo the theory of linear arithmetic: exact, inexact and commercial solvers. In: Kleine Büning, H., Zhao, X. (eds.) SAT 2008. LNCS, vol. 4996, pp. 77–90. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-79719-7_8
Filliâtre, J.-C., Paskevich, A.: Why3—Where programs meet provers. In: Felleisen, M., Gardner, P. (eds.) ESOP 2013. LNCS, vol. 7792, pp. 125–128. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37036-6_8
Gao, S., Avigad, J., Clarke, E.M.: \(\delta \)-Complete decision procedures for satisfiability over the reals. In: Gramlich, B., Miller, D., Sattler, U. (eds.) IJCAR 2012. LNCS (LNAI), vol. 7364, pp. 286–300. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31365-3_23
Gao, S., Kong, S., Clarke, E.M.: dReal: an SMT solver for nonlinear theories over the reals. In: Bonacina, M.P. (ed.) CADE 2013. LNCS (LNAI), vol. 7898, pp. 208–214. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38574-2_14
Harrison, J.: Verifying nonlinear real formulas via sums of squares. In: Schneider, K., Brandt, J. (eds.) TPHOLs 2007. LNCS, vol. 4732, pp. 102–118. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74591-4_9
Härter, V., Jansson, C., Lange, M.: VSDP: verified semidefinite programming. http://www.ti3.tuhh.de/jansson/vsdp/
Hoang, D., Moy, Y., Wallenburg, A., Chapman, R.: SPARK 2014 and gnatprove - a competition report from builders of an industrial-strength verifying compiler. In: STTT (2015)
Jansson, C., Chaykin, D., Keil, C.: Rigorous error bounds for the optimal value in semidefinite programming. SIAM J. Numer. Anal. 46(1), 180–200 (2007)
Jovanović, D., de Moura, L.: Solving non-linear arithmetic. In: Gramlich, B., Miller, D., Sattler, U. (eds.) IJCAR 2012. LNCS (LNAI), vol. 7364, pp. 339–354. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31365-3_27
Kaltofen, E., Li, B., Yang, Z., Zhi, L.: Exact certification in global polynomial optimization via sums-of-squares of rational functions with rational coefficients. J. Symb. Comput. 47(1), 1–15 (2012)
King, T., Barrett, C.W., Tinelli, C.: Leveraging linear and mixed integer programming for SMT. In: FMCAD (2014)
Lasserre, J.B.: Global optimization with polynomials and the problem of moments. SIAM J. Optim. 11(3), 796–817 (2001)
Lasserre, J.B.: Moments, Positive Polynomials and Their Applications. Imperial College Press Optimization. Imperial College Press, World Scientific, Singapore (2009)
Löfberg, J.: Pre- and post-processing sum-of-squares programs in practice. IEEE Trans. Autom. Control 5, 1007–1011 (2009)
Magron, V., Allamigeon, X., Gaubert, S., Werner, B.: Formal proofs for nonlinear optimization. J. Formalized Reason. 8(1), 1–24 (2015)
Maréchal, A., Fouilhé, A., King, T., Monniaux, D., Périn, M.: Polyhedral approximation of multivariate polynomials using handelman’s theorem. In: Jobstmann, B., Leino, K.R.M. (eds.) VMCAI 2016. LNCS, vol. 9583, pp. 166–184. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49122-5_8
Martin-Dorel, É., Roux, P.: A reflexive tactic for polynomial positivity using numerical solvers and floating-point computations. In: CPP (2017)
Monniaux, D.: On using floating-point computations to help an exact linear arithmetic decision procedure. In: Bouajjani, A., Maler, O. (eds.) CAV 2009. LNCS, vol. 5643, pp. 570–583. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02658-4_42
Monniaux, D., Corbineau, P.: On the generation of positivstellensatz witnesses in degenerate cases. In: van Eekelen, M., Geuvers, H., Schmaltz, J., Wiedijk, F. (eds.) ITP 2011. LNCS, vol. 6898, pp. 249–264. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22863-6_19
Muñoz, C., Narkawicz, A.: Formalization of Bernstein polynomials and applications to global optimization. J. Autom. Reason. 51(2), 151–196 (2013)
Nuzzo, P., Puggelli, A., Seshia, S.A., Sangiovanni-Vincentelli, A.L.: CalCS: SMT solving for non-linear convex constraints. In: FMCAD (2010)
Parrilo, P.A.: Semidefinite programming relaxations for semialgebraic problems. Math. Program. 96(2), 293–320 (2003)
Platzer, A., Quesel, J.-D., Rümmer, P.: Real world verification. In: Schmidt, R.A. (ed.) CADE 2009. LNCS (LNAI), vol. 5663, pp. 485–501. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-02959-2_35
Roux, P.: Formal proofs of rounding error bounds - with application to an automatic positive definiteness check. J. Autom. Reasoning 57(2), 135–156 (2016)
Roux, P., Jobredeaux, R., Garoche, P.-L., Féron, É: A generic ellipsoid abstract domain for linear time invariant systems. In: HSCC (2012)
Roux, P., Voronin, Y.-L., Sankaranarayanan, S.: Validating numerical semidefinite programming solvers for polynomial invariants. In: Rival, X. (ed.) SAS 2016. LNCS, vol. 9837, pp. 424–446. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53413-7_21
Rump, S.M.: Verification of positive definiteness. BIT Num. Math. 46(2), 433–452 (2006)
Rump, S.M.: Verification methods: rigorous results using floating-point arithmetic. Acta Numerica 19, 287–449 (2010)
Shoukry, Y., Nuzzo, P., Sangiovanni-Vincentelli, A.L., Seshia, S.A., Pappas, G.J., Tabuada, P.: SMC: satisfiability modulo convex optimization. In: HSCC (2017)
Vandenberghe, L., Boyd, S.: Semidefinite programming. SIAM Rev. 38(1), 49–95 (1996)
Watkins, D.S.: Fundamentals of matrix computations. Wiley, New York (2004)
Yamashita, M., Fujisawa, K., Nakata, K., Nakata, M., Fukuda, M., Kobayashi, K., Goto, K.: A high-performance software package for semidefinite programs: SDPA 7. Technical report B-460, Tokyo Institute of Technology, Tokyo (2010)
Data Availability Statement and Acknowledgements
The source code, benchmarks and instructions to replicate the results of Sect. 5 are available in the figshare repository: http://doi.org/10.6084/m9.figshare.5900260.v1.
The authors thank Rémi Delmas for insightful discussions and technical help, particularly with the dReal solver.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Roux, P., Iguernlala, M., Conchon, S. (2018). A Non-linear Arithmetic Procedure for Control-Command Software Verification. In: Beyer, D., Huisman, M. (eds) Tools and Algorithms for the Construction and Analysis of Systems. TACAS 2018. Lecture Notes in Computer Science(), vol 10806. Springer, Cham. https://doi.org/10.1007/978-3-319-89963-3_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-89963-3_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89962-6
Online ISBN: 978-3-319-89963-3
eBook Packages: Computer ScienceComputer Science (R0)





 is tangent to
is tangent to  . Thus the ball
. Thus the ball  intersecting the subspace almost never lies in
intersecting the subspace almost never lies in  , making the proof fail.
, making the proof fail.

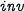 in Fig.
in Fig. 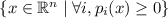 is empty.
is empty.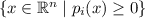 is bounded.
is bounded.