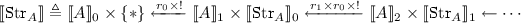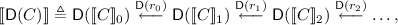Relational Reasoning for Markov Chains in a Probabilistic Guarded Lambda Calculus

  • Alejandro Aguirre
  • Gilles Barthe
  • Lars Birkedal
  • Aleš Bizjak
  • Marco Gaboardi
  • Deepak Garg
Open Access
Conference paper
First Online:
Part of the Lecture Notes in Computer Science book series (LNCS, volume 10801)

Abstract

We extend the simply-typed guarded \(\lambda \)-calculus with discrete probabilities and endow it with a program logic for reasoning about relational properties of guarded probabilistic computations. This provides a framework for programming and reasoning about infinite stochastic processes like Markov chains. We demonstrate the logic sound by interpreting its judgements in the topos of trees and by using probabilistic couplings for the semantics of relational assertions over distributions on discrete types.

The program logic is designed to support syntax-directed proofs in the style of relational refinement types, but retains the expressiveness of higher-order logic extended with discrete distributions, and the ability to reason relationally about expressions that have different types or syntactic structure. In addition, our proof system leverages a well-known theorem from the coupling literature to justify better proof rules for relational reasoning about probabilistic expressions. We illustrate these benefits with a broad range of examples that were beyond the scope of previous systems, including shift couplings and lump couplings between random walks.

Download conference paper PDF

1 Introduction

Stochastic processes are often used in mathematics, physics, biology or finance to model evolution of systems with uncertainty. In particular, Markov chains are “memoryless” stochastic processes, in the sense that the evolution of the system depends only on the current state and not on its history. Perhaps the most emblematic example of a (discrete time) Markov chain is the simple random walk over the integers, that starts at 0, and that on each step moves one position either left or right with uniform probability. Let \(p_i\) be the position at time i. Then, this Markov chain can be described as:
$$ p_0 = 0 \quad \quad p_{i+1} = {\left\{ \begin{array}{ll} p_i + 1\ \text {with probability}\ 1/2 \\ p_i - 1\ \text {with probability}\ 1/2 \end{array}\right. } $$
The goal of this paper is to develop a programming and reasoning framework for probabilistic computations over infinite objects, such as Markov chains. Although programming and reasoning frameworks for infinite objects and probabilistic computations are well-understood in isolation, their combination is challenging. In particular, one must develop a proof system that is powerful enough for proving interesting properties of probabilistic computations over infinite objects, and practical enough to support effective verification of these properties.

Modelling Probabilistic Infinite Objects. A first challenge is to model probabilistic infinite objects. We focus on the case of Markov chains, due to its importance. A (discrete-time) Markov chain is a sequence of random variables \(\{X_i\}\) over some fixed type T satisfying some independence property. Thus, the straightforward way of modelling a Markov chain is as a stream of distributions over T. Going back to the simple example outlined above, it is natural to think about this kind of discrete-time Markov chain as characterized by the sequence of positions \(\{p_i\}_{i \in \mathbb {N}}\), which in turn can be described as an infinite set indexed by the natural numbers. This suggests that a natural way to model such a Markov chain is to use streams in which each element is produced probabilistically from the previous one. However, there are some downsides to this representation. First of all, it requires explicit reasoning about probabilistic dependency, since \(X_{i+1}\) depends on \(X_i\). Also, we might be interested in global properties of the executions of the Markov chain, such as “The probability of passing through the initial state infinitely many times is 1”. These properties are naturally expressed as properties of the whole stream. For these reasons, we want to represent Markov chains as distributions over streams. Seemingly, one downside of this representation is that the set of streams is not countable, which suggests the need for introducing heavy measure-theoretic machinery in the semantics of the programming language, even when the underlying type is discrete or finite.

Fortunately, measure-theoretic machinery can be avoided (for discrete distributions) by developing a probabilistic extension of the simply-typed guarded \(\lambda \)-calculus and giving a semantic interpretation in the topos of trees [1]. Informally, the simply-typed guarded \(\lambda \)-calculus [1] extends the simply-typed lambda calculus with a later modality, denoted by Open image in new window . The type Open image in new window ascribes expressions that are available one unit of logical time in the future. The Open image in new window modality allows one to model infinite types by using “finite” approximations. For example, a stream of natural numbers is represented by the sequence of its (increasing) prefixes in the topos of trees. The prefix containing the first i elements has the type Open image in new window , representing that the first element is available now, the second element a unit time in the future, and so on. This is the key to representing probability distributions over infinite objects without measure-theoretic semantics: We model probability distributions over non-discrete sets as discrete distributions over their (the sets’) approximations. For example, a distribution over streams of natural numbers (which a priori would be non-discrete since the set of streams is uncountable) would be modelled by a sequence of distributions over the finite approximations \(S_1, S_2, \ldots \) of streams. Importantly, since each \(S_i\) is countable, each of these distributions can be discrete.

Reasoning About Probabilistic Computations. Probabilistic computations exhibit a rich set of properties. One natural class of properties is related to probabilities of events, saying, for instance, that the probability of some event E (or of an indexed family of events) increases at every iteration. However, several interesting properties of probabilistic computation, such as stochastic dominance or convergence (defined below) are relational, in the sense that they refer to two runs of two processes. In principle, both classes of properties can be proved using a higher-order logic for probabilistic expressions, e.g. the internal logic of the topos of trees, suitably extended with an axiomatization of finite distributions. However, we contend that an alternative approach inspired from refinement types is desirable and provides better support for effective verification. More specifically, reasoning in a higher-order logic, e.g. in the internal logic of the topos of trees, does not exploit the structure of programs for non-relational reasoning, nor the structural similarities between programs for relational reasoning. As a consequence, reasoning is more involved. To address this issue, we define a relational proof system that exploits the structure of the expressions and supports syntax-directed proofs, with necessary provisions for escaping the syntax-directed discipline when the expressions do not have the same structure. The proof system manipulates judgements of the form:
$$\begin{aligned} \varDelta \mid \varSigma \mid \varGamma \mid \varPsi \vdash t_1 : A_1 \sim t_2 : A_2 \mid \phi \end{aligned}$$
where \(\varDelta \) and \(\varGamma \) are two typing contexts, \(\varSigma \) and \(\varPsi \) respectively denote sets of assertions over variables in these two contexts, \(t_1\) and \(t_2\) are well-typed expressions of type \(A_1\) and \(A_2\), and \(\phi \) is an assertion that may contain the special variables \(\mathbf {r}_1\) and \(\mathbf {r}_2\) that respectively correspond to the values of \(t_1\) and \(t_2\). The context \(\varDelta \) and \(\varGamma \), the terms \(t_1\) and \(t_2\) and the types \(A_1\) and \(A_2\) provide a specification, while \(\varSigma \), \(\varPsi \), and \(\phi \) are useful for reasoning about relational properties over \(t_1,t_2\), their inputs and their outputs. This form of judgement is similar to that of Relational Higher-Order Logic [2], from which our system draws inspiration.

In more detail, our relational logic comes with typing rules that allow one to reason about relational properties by exploiting as much as possible the syntactic similarities between \(t_1\) and \(t_2\), and to fall back on pure logical reasoning when these are not available. In order to apply relational reasoning to guarded computations the logic provides relational rules for the later modality Open image in new window and for a related modality \(\square {}\), called “constant”. These rules allow the relational verification of general relational properties that go beyond the traditional notion of program equivalence and, moreover, they allow the verification of properties of guarded computations over different types. The ability to reason about computations of different types provides significant benefits over alternative formalisms for relational reasoning. For example, it enables reasoning about relations between programs working on different data structures, e.g. a relation between a program working on a stream of natural numbers, and a program working on a stream of pairs of natural numbers, or having different structures, e.g. a relation between an application and a case expression.

Importantly, our approach for reasoning formally about probabilistic computations is based on probabilistic couplings, a standard tool from the analysis of Markov chains [3, 4]. From a verification perspective, probabilistic couplings go beyond equivalence properties of probabilistic programs, which have been studied extensively in the verification literature, and yet support compositional reasoning [5, 6]. The main attractive feature of coupling-based reasoning is that it limits the need of explicitly reasoning about the probabilities—this avoids complex verification conditions. We provide sound proof rules for reasoning about probabilistic couplings. Our rules make several improvements over prior relational verification logics based on couplings. First, we support reasoning over probabilistic processes of different types. Second, we use Strassen’s theorem [7] a remarkable result about probabilistic couplings, to achieve greater expressivity. Previous systems required to prove a bijection between the sampling spaces to show the existence of a coupling [5, 6], Strassen’s theorem gives a way to show their existence which is applicable in settings where the bijection-based approach cannot be applied. And third, we support reasoning with what are called shift couplings, coupling which permits to relate the states of two Markov chains at possibly different times (more explanations below).

Case Studies. We show the flexibility of our formalism by verifying several examples of relational properties of probabilistic computations, and Markov chains in particular. These examples cannot be verified with existing approaches.

First, we verify a classic example of probabilistic non-interference which requires the reasoning about computations at different types. Second, in the context of Markov chains, we verify an example about stochastic dominance which exercises our more general rule for proving the existence of couplings modelled by expressions of different types. Finally, we verify an example involving shift relations in an infinite computation. This style of reasoning is motivated by “shift” couplings in Markov chains. In contrast to a standard coupling, which relates the states of two Markov chains at the same time t, a shift coupling relates the states of two Markov chains at possibly different times. Our specific example relates a standard random walk (described earlier) to a variant called a lazy random walk; the verification requires relating the state of standard random walk at time t to the state of the lazy random walk at time 2t. We note that this kind of reasoning is impossible with conventional relational proof rules even in a non-probabilistic setting. Therefore, we provide a novel family of proof rules for reasoning about shift relations. At a high level, the rules combine a careful treatment of the later and constant modalities with a refined treatment of fixpoint operators, allowing us to relate different iterates of function bodies.

1.1 Summary of Contributions

With the aim of providing a general framework for programming and reasoning about Markov chains, the three main contributions of this work are:
  1. 1.

    A probabilistic extension of the guarded \(\lambda \)-calculus, that enables the definition of Markov chains as discrete probability distributions over streams.

     
  2. 2.

    A relational logic based on coupling to reason in a syntax-directed manner about (relational) properties of Markov chains. This logic supports reasoning about programs that have different types and structures. Additionally, this logic uses results from the coupling literature to achieve greater expressivity than previous systems.

     
  3. 3.

    An extension of the relational logic that allows to relate the states of two streams at possibly different times. This extension supports reasoning principles, such as shift couplings, that escape conventional relational logics.

     

Omitted technical details can be found in the full version of the paper with appendix at https://arxiv.org/abs/1802.09787.

2 Mathematical Preliminaries

This section reviews the definition of discrete probability sub-distributions and introduces mathematical couplings.

Definition 1 (Discrete probability distribution)

Let C be a discrete (i.e., finite or countable) set. A (total) distribution over C is a function \(\mu : C \rightarrow [0,1]\) such that \( \sum _{x\in C} \mu (x) = 1\). The support of a distribution \(\mu \) is the set of points with non-zero probability, \( \mathsf {supp}\ \mu \triangleq \{x \in C \mid \mu (x) > 0 \}\). We denote the set of distributions over C as \(\mathsf {D}(C)\). Given a subset \(E \subseteq C\), the probability of sampling from \(\mu \) a point in E is denoted \(\Pr _{x\leftarrow \mu }[x \in E]\), and is equal to \(\sum _{x \in E} \mu (x)\).

Definition 2 (Marginals)

Let \(\mu \) be a distribution over a product space \(C_1\times C_2\). The first (second) marginal of \(\mu \) is another distribution \(\mathsf {D}(\pi _1)(\mu )\) \((\mathsf {D}(\pi _2)(\mu ))\) over \(C_1\) \((C_2)\) defined as:
$$\mathsf {D}(\pi _1)(\mu )(x) = \sum _{y \in C_2} \mu (x,y) \qquad \left( \mathsf {D}(\pi _2)(\mu )(y) = \sum _{x \in C_1} \mu (x,y) \right) $$

Probabilistic Couplings. Probabilistic couplings are a fundamental tool in the analysis of Markov chains. When analyzing a relation between two probability distributions it is sometimes useful to consider instead a distribution over the product space that somehow “couples” the randomness in a convenient manner.

Consider for instance the case of the following Markov chain, which counts the total amount of tails observed when tossing repeatedly a biased coin with probability of tails p:
$$ n_0 = 0 \quad \quad n_{i+1} = \left\{ \begin{array}{l} n_i + 1\ \text {with probability}\ p \\ n_i\ \text {with probability}\ (1-p) \end{array}\right. $$
If we have two biased coins with probabilities of tails p and q with \(p\le q\) and we respectively observe \(\{n_i\}\) and \(\{m_i\}\) we would expect that, in some sense, \(n_i \le m_i\) should hold for all i (this property is known as stochastic dominance). A formal proof of this fact using elementary tools from probability theory would require to compute the cumulative distribution functions for \(n_i\) and \(m_i\) and then to compare them. The coupling method reduces this proof to showing a way to pair the coin flips so that if the first coin shows tails, so does the second coin.

We now review the definition of couplings and state relevant properties.

Definition 3 (Couplings)

Let \(\mu _1\in \mathsf {D}(C_1)\) and \(\mu _2\in \mathsf {D}(C_2)\), and \(R\subseteq C_1\times C_2\).

  • A distribution \(\mu \in \mathsf {D}(C_1\times C_2)\) is a coupling for \(\mu _1\) and \(\mu _2\) iff its first and second marginals coincide with \(\mu _1\) and \(\mu _2\) respectively, i.e. \(\mathsf {D}(\pi _1)(\mu )=\mu _1\) and \(\mathsf {D}(\pi _2)(\mu )=\mu _2\).

  • A distribution \(\mu \in \mathsf {D}(C_1\times C_2)\) is a R-coupling for \(\mu _1\) and \(\mu _2\) if it is a coupling for \(\mu _1\) and \(\mu _2\) and, moreover, \(\Pr _{(x_1,x_2)\leftarrow \mu } [R~x_1~x_2]=1\), i.e., if the support of the distribution \(\mu \) is included in R.

Moreover, we write \(\diamond _{\mu _1, \mu _2}. R\) iff there exists a R-coupling for \(\mu _1\) and \(\mu _2\).

Couplings always exist. For instance, the product distribution of two distributions is always a coupling. Going back to the example about the two coins, it can be proven by computation that the following is a coupling that lifts the less-or-equal relation (0 indicating heads and 1 indicating tails):The following theorem in [7] gives a necessary and sufficient condition for the existence of R-couplings between two distributions. The theorem is remarkable in the sense that it proves an equivalence between an existential property (namely the existence of a particular coupling) and a universal property (checking, for each event, an inequality between probabilities).

Theorem 1 (Strassen’s theorem)

Consider \(\mu _1\in \mathsf {D}(C_1)\) and \(\mu _2\in \mathsf {D}(C_2)\), and \(R\subseteq C_1 \times C_2\). Then \(\diamond _{\mu _1, \mu _2}. R\) iff for every \(X \subseteq C_1\), \(\Pr _{x_1\leftarrow \mu _1}[x_1\in X] \le \Pr _{x_2\leftarrow \mu _2}[x_2\in R(X)]\), where R(X) is the image of X under R, i.e. \(R(X) =\{ y \in C_2 \mid \exists x \in X.~R~x~y\}\).

An important property of couplings is closure under sequential composition.

Lemma 1 (Sequential composition couplings)

Let \(\mu _1\in \mathsf {D}(C_1)\), \(\mu _2\in \mathsf {D}(C_2)\), \(M_1:C_1\rightarrow \mathsf {D}(D_1)\) and \(M_2:C_2\rightarrow \mathsf {D}(D_2)\). Moreover, let \(R\subseteq C_1\times C_2\) and \(S\subseteq D_1\times D_2\). Assume: (1) \(\diamond _{\mu _1, \mu _2}. R\); and (2) for every \(x_1\in C_1\) and \(x_2\in C_2\) such that \(R~x_1~x_2\), we have \(\diamond _{M_1(x_1), M_2(x_2)}. S\). Then \(\diamond _{(\mathsf {bind}~\mu _1~M_1), (\mathsf {bind}~\mu _2~M_2)}. S\), where \(\mathsf {bind}~\mu ~M\) is defined as
$$(\mathsf {bind}~\mu ~M)(y) =\sum _x \mu (x) \cdot M(x)(y)$$

We conclude this section with the following lemma, which follows from Strassen’s theorem:

Lemma 2 (Fundamental lemma of couplings)

Let \(R\subseteq C_1 \times C_2\), \(E_1\subseteq C_1\) and \(E_2\subseteq C_2\) such that for every \(x_1\in E_1\) and \(x_2\in C_2\), \(R~x_1~x_2\) implies \(x_2\in E_2\), i.e. \(R(E_1)\subseteq E_2\). Moreover, let \(\mu _1\in \mathsf {D}(C_1)\) and \(\mu _2\in \mathsf {D}(C_2)\) such that \(\diamond _{\mu _1, \mu _2}. R\). Then

This lemma can be used to prove probabilistic inequalities from the existence of suitable couplings:

Corollary 1

Let \(\mu _1,\mu _2\in \mathsf {D}(C)\):
  1. 1.

    If \(\diamond _{\mu _1, \mu _2}. (=)\), then for all \(x\in C\), \(\mu _1(x) = \mu _2(x)\).

     
  2. 2.

    If \(C = \mathbb {N}\) and \(\diamond _{\mu _1, \mu _2}. (\ge )\), then for all \(n\in \mathbb {N}\), \(\Pr _{x\leftarrow \mu _1}[x\ge n] \ge \Pr _{x\leftarrow \mu _2}[x\ge n]\)

     
In the example at the beginning of the section, the property we want to prove is precisely that, for every k and i, the following holds:Since we have a \(\le \)-coupling, this proof is immediate. This example is formalized in Subsect. 3.3.

3 Overview of the System

In this section we give a high-level overview of our system, with the details on Sects. 4, 5 and 6. We start by presenting the base logic, and then we show how to extend it with probabilities and how to build a relational reasoning system on top of it.

3.1 Base Logic: Guarded Higher-Order Logic

Our starting point is the Guarded Higher-Order Logic [1] (Guarded HOL) inspired by the topos of trees. In addition to the usual constructs of HOL to reason about lambda terms, this logic features the Open image in new window and Open image in new window modalities to reason about infinite terms, in particular streams. The Open image in new window modality is used to reason about objects that will be available in the future, such as tails of streams. For instance, suppose we want to define an \({\text {All}}(s,\phi )\) predicate, expressing that all elements of a stream \(s \equiv n\! \,{:}{:}\,\! xs\) satisfy a property \(\phi \). This can be axiomatized as follows:We use \(x. \phi \) to denote that the formula \(\phi \) depends on a free variable x, which will get replaced by the first argument of \({\text {All}}\). We have two antecedents. The first one states that the head n satisfies \(\phi \). The second one, Open image in new window , states that all elements of xs satisfy \(\phi \). Formally, xs is the tail of the stream and will be available in the future, so it has type Open image in new window . The delayed substitution \(\triangleright [s\leftarrow xs]\) replaces s of type Open image in new window with xs of type Open image in new window inside \({\text {All}}\) and shifts the whole formula one step into the future. In other words, Open image in new window states that \({\text {All}}(-, x.\phi )\) will be satisfied by xs in the future, once it is available.

3.2 A System for Relational Reasoning

When proving relational properties it is often convenient to build proofs guided by the syntactic structure of the two expressions to be related. This style of reasoning is particularly appealing when the two expressions have the same structure and control-flow, and is appealingly close to the traditional style of reasoning supported by refinement types. At the same time, a strict adherence to the syntax-directed discipline is detrimental to the expressiveness of the system; for instance, it makes it difficult or even impossible to reason about structurally dissimilar terms. To achieve the best of both worlds, we present a relational proof system built on top of Guarded HOL, which we call Guarded RHOL. Judgements have the shape:
$$\begin{aligned} \varDelta \mid \varSigma \mid \varGamma \mid \varPsi \vdash t_1 : A_1 \sim t_2 : A_2 \mid \phi \end{aligned}$$
where \(\phi \) is a logical formula that may contain two distinguished variables \(\mathbf {r}_1\) and \(\mathbf {r}_2\) that respectively represent the expressions \(t_1\) and \(t_2\). This judgement subsumes two typing judgements on \(t_1\) and \(t_2\) and a relation \(\phi \) on these two expressions. However, this form of judgement does not tie the logical property to the type of the expressions, and is key to achieving flexibility while supporting syntax-directed proofs whenever needed. The proof system combines rules of two different flavours: two-sided rules, which relate expressions with the same top-level constructs, and one-sided rules, which operate on a single expression.

We then extend Guarded HOL with a modality \(\diamond \) that lifts assertions over discrete types \(C_1\) and \(C_2\) to assertions over \(\mathsf {D}(C_1)\) and \(\mathsf {D}(C_2)\). Concretely, we define for every assertion \(\phi \), variables \(x_1\) and \(x_2\) of type \(C_1\) and \(C_2\) respectively, and expressions \(t_1\) and \(t_2\) of type \(\mathsf {D}(C_1)\) and \(\mathsf {D}(C_2)\) respectively, the modal assertion \(\diamond _{ [x_1\leftarrow t_1,x_2\leftarrow t_2]} \phi \) which holds iff the interpretations of \(t_1\) and \(t_2\) are related by the probabilistic lifting of the interpretation of \(\phi \). We call this new logic Probabilistic Guarded HOL.

We accordingly extend the relational proof system to support reasoning about probabilistic expressions by adding judgements of the form:
$$\varDelta \mid \varSigma \mid \varGamma \mid \varPsi \vdash t_1 : \mathsf {D}(C_1) \sim t_2 : \mathsf {D}(C_2) \mid \diamond _{[x_1\leftarrow \mathbf {r}_1, x_2\leftarrow \mathbf {r}_2]} \phi $$
expressing that \(t_1\) and \(t_2\) are distributions related by a \(\phi \)-coupling. We call this proof system Probabilistic Guarded RHOL. These judgements can be built by using the following rule, that lifts relational judgements over discrete types \(C_1\) and \(C_2\) to judgements over distribution types \(\mathsf {D}(C_1)\) and \(\mathsf {D}(C_2)\) when the premises of Strassen’s theorem are satisfied.Recall that (discrete time) Markov chains are “memoryless” probabilistic processes, whose specification is given by a (discrete) set C of states, an initial state \(s_0\) and a probabilistic transition function \(\mathsf {step}:C \rightarrow \mathsf {D}(C)\), where \(\mathsf {D}(S)\) represents the set of discrete distributions over C. As explained in the introduction, a convenient modelling of Markov chains is by means of probabilistic streams, i.e. to model a Markov chain as an element of Open image in new window , where S is its underlying state space. To model Markov chains, we introduce a Open image in new window operator with type Open image in new window that, given an initial state and a transition function, returns a Markov chain. We can reason about Markov chains by the [Markov] rule (the context, omitted, does not change):

Informally, the rule stipulates the existence of an invariant \(\phi \) over states. The first premise insists that the invariant hold on the initial states, the condition \(\psi _3\) states that the transition functions preserve the invariant, and \(\psi _4\) states that the invariant \(\phi \) over pairs of states can be lifted to a stream property \(\phi '\).

Other rules of the logic are given in Fig. 1. The language construct \(\mathsf {munit}\) creates a point distribution whose entire mass is at its argument. Accordingly, the [UNIT] rule creates a straightforward coupling. The [MLET] rule internalizes sequential composition of couplings (Lemma 1) into the proof system. The construct \(\mathsf {let}~x=t~\mathsf {in}~t'\) composes a distribution t with a probabilistic computation \(t'\) with one free variable x by sampling x from t and running \(t'\). The [MLET-L] rule supports one-sided reasoning about \(\mathsf {let}~x=t~\mathsf {in}~t'\) and relies on the fact that couplings are closed under convex combinations. Note that one premise of the rule uses a unary judgement, with a non-relational modality \(\diamond _{[x\leftarrow \mathbf {r}]} \phi \) whose informal meaning is that \(\phi \) holds with probability 1 in the distribution \(\mathbf {r}\).

The following table summarizes the different base logics we consider, the relational systems we build on top of them, including the ones presented in [2], and the equivalences between both sides:
Fig. 1.

Proof rules for probabilistic constructs

3.3 Examples

We formalize elementary examples from the literature on security and Markov chains. None of these examples can be verified in prior systems. Uniformity of one-time pad and lumping of random walks cannot even be stated in prior systems because the two related expressions in these examples have different types. The random walk vs lazy random walk (shift coupling) cannot be proved in prior systems because it requires either asynchronous reasoning or code rewriting. Finally, the biased coin example (stochastic dominance) cannot be proved in prior work because it requires Strassen’s formulation of the existence of coupling (rather than a bijection-based formulation) or code rewriting. We give additional details below.

One-Time Pad/Probabilistic Non-interference. Non-interference [8] is a baseline information flow policy that is often used to model confidentiality of computations. In its simplest form, non-interference distinguishes between public (or low) and private (or high) variables and expressions, and requires that the result of a public expression not depend on the value of its private parameters. This definition naturally extends to probabilistic expressions, except that in this case the evaluation of an expression yields a distribution rather than a value. There are deep connections between probabilistic non-interference and several notions of (information-theoretic) security from cryptography. In this paragraph, we illustrate different flavours of security properties for one-time pad encryption. Similar reasoning can be carried out for proving (passive) security of secure multiparty computation algorithms in the 3-party or multi-party setting [9, 10].

One-time pad is a perfectly secure symmetric encryption scheme. Its space of plaintexts, ciphertexts and keys is the set \(\{0,1\}^\ell \)—fixed-length bitstrings of size \(\ell \). The encryption algorithm is parametrized by a key k—sampled uniformly over the set of bitstrings \(\{ 0,1 \}^\ell \)—and maps every plaintext m to the ciphertext \(c = k \oplus m\), where the operator \(\oplus \) denotes bitwise exclusive-or on bitstrings. We let \(\mathsf {otp}\) denote the expression \(\lambda m. \mathsf {let}~k=\mathcal {U}_{\{0,1\}^\ell }~\mathsf {in}~\mathsf {munit}(k\oplus m)\), where \(\mathcal {U}_{X}\) is the uniform distribution over a finite set X.

One-time pad achieves perfect security, i.e.  the distributions of ciphertexts is independent of the plaintext. Perfect security can be captured as a probabilistic non-interference property:
$$\vdash \mathsf {otp} : \{ 0,1 \}^\ell \rightarrow \mathsf {D}(\{ 0, 1 \}^\ell ) \sim \mathsf {otp} : \{ 0,1 \}^\ell \rightarrow \mathsf {D}(\{ 0, 1 \}^\ell ) \mid \forall m_1m_2. \mathbf {r}_1~m_1\,{\mathop {=}\limits ^{\diamond }}\,\mathbf {r}_2~m_2 $$
where \(e_1\,{\mathop {=}\limits ^{\diamond }}\,e_2\) is used as a shorthand for \(\diamond _{[y_1\leftarrow e_1, y_2\leftarrow e_2]} y_1 = y_2\). The crux of the proof is to establish
$$m_1,m_2: \{ 0,1 \}^\ell \vdash \mathcal {U}_{\{0,1\}^\ell } : \mathsf {D}(\{ 0, 1 \}^\ell ) \sim \mathcal {U}_{\{0,1\}^\ell } : \mathsf {D}(\{ 0, 1 \}^\ell ) \mid \mathbf {r}_1\oplus m_2\,{\mathop {=}\limits ^{\diamond }}\,\mathbf {r}_2\oplus m_1 $$
using the [COUPLING] rule. It suffices to observe that the assertion induces a bijection, so the image of an arbitrary set X under the relation has the same cardinality as X, and hence their probabilities w.r.t.  the uniform distributions are equal. One can then conclude the proof by applying the rules for monadic sequenciation ([MLET]) and abstraction (rule [ABS] in appendix), using algebraic properties of \(\oplus \).
Interestingly, one can prove a stronger property: rather than proving that the ciphertext is independent of the plaintext, one can prove that the distribution of ciphertexts is uniform. This is captured by the following judgement:
$$c_1, c_2: \{ 0,1 \}^\ell \vdash \mathsf {otp} : \{ 0,1 \}^\ell \rightarrow \mathsf {D}(\{ 0, 1 \}^\ell ) \sim \mathsf {otp} : \{ 0,1 \}^\ell \rightarrow \mathsf {D}(\{ 0, 1 \}^\ell ) \mid \psi $$
where \(\psi \triangleq \forall m_1\,m_2. m_1=m_2\Rightarrow \diamond _{[y_1\leftarrow \mathbf {r}_1~m_1, y_2\leftarrow \mathbf {r}_2~m_2]} y_1=c_1 \Leftrightarrow y_2=c_2\). This style of modelling uniformity as a relational property is inspired from [11]. The proof is similar to the previous one and omitted. However, it is arguably more natural to model uniformity of the distribution of ciphertexts by the judgement:
$$\vdash \mathsf {otp} : \{ 0,1 \}^\ell \rightarrow \mathsf {D}(\{ 0, 1 \}^\ell ) \sim \mathcal {U}_{\{0,1\}^\ell } : \mathsf {D}(\{ 0, 1 \}^\ell ) \mid \forall m.~ \mathbf {r}_1~m\,{\mathop {=}\limits ^{\diamond }}\,\mathbf {r}_2$$
This judgement is closer to the simulation-based notion of security that is used pervasively in cryptography, and notably in Universal Composability [12]. Specifically, the statement captures the fact that the one-time pad algorithm can be simulated without access to the message. It is interesting to note that the judgement above (and more generally simulation-based security) could not be expressed in prior works, since the two expressions of the judgement have different types—note that in this specific case, the right expression is a distribution but in the general case the right expression will also be a function, and its domain will be a projection of the domain of the left expression.
The proof proceeds as follows. First, we prove
$$ \vdash \mathcal {U}_{\{0,1\}^\ell } \sim \mathcal {U}_{\{0,1\}^\ell } \mid \forall m.~\diamond _{[y_1\leftarrow \mathbf {r}_1, y_2\leftarrow \mathbf {r}_2]} y_1 \oplus m = y_2$$
using the [COUPLING] rule. Then, we apply the [MLET] rule to obtain
$$\vdash \begin{array}{l}\mathsf {let}~k=\mathcal {U}_{\{0,1\}^\ell }~\mathsf {in}~\\ \mathsf {munit}(k\oplus m) \end{array} \sim \begin{array}{l}\mathsf {let}~k=\mathcal {U}_{\{0,1\}^\ell }~\mathsf {in}~\\ \mathsf {munit}(k)\end{array} \mid \diamond _{\left[ y_1\leftarrow \mathbf {r}_1, y_2\leftarrow \mathbf {r}_2\right] } y_1 = y_2$$
We have \(\mathsf {let}~k=\mathcal {U}_{\{0,1\}^\ell }~\mathsf {in}~\mathsf {munit}(k) \equiv \mathcal {U}_{\{0,1\}^\ell }\); hence by equivalence (rule [Equiv] in appendix), this entails
$$ \vdash \mathsf {let}~k=\mathcal {U}_{\{0,1\}^\ell }~\mathsf {in}~\mathsf {munit}(k\oplus m) \sim \mathcal {U}_{\{0,1\}^\ell } \mid \diamond _{[y_1\leftarrow \mathbf {r}_1, y_2\leftarrow \mathbf {r}_2]} y_1 = y_2$$
We conclude by applying the one-sided rule for abstraction.

Stochastic Dominance. Stochastic dominance defines a partial order between random variables whose underlying set is itself a partial order; it has many different applications in statistical biology (e.g. in the analysis of the birth-and-death processes), statistical physics (e.g. in percolation theory), and economics. First-order stochastic dominance, which we define below, is also an important application of probabilistic couplings. We demonstrate how to use our proof system for proving (first-order) stochastic dominance for a simple Markov process which samples biased coins. While the example is elementary, the proof method extends to more complex examples of stochastic dominance, and illustrates the benefits of Strassen’s formulation of the coupling rule over alternative formulations stipulating the existence of bijections (explained later).

We start by recalling the definition of (first-order) stochastic dominance for the \(\mathbb {N}\)-valued case. The definition extends to arbitrary partial orders.

Definition 4 (Stochastic dominance)

Let \(\mu _1,\mu _2\in \mathsf {D}(\mathbb {N})\). We say that \(\mu _2\) stochastically dominates \(\mu _1\), written \(\mu _1\le _{\mathrm {SD}} \mu _2\), iff for every \(n\in \mathbb {N}\),
$$ \mathop {\Pr }\limits _{x\leftarrow \mu _1}[x\ge n] \le \mathop {\Pr }\limits _{x\leftarrow \mu _2}[x\ge n] $$

The following result, equivalent to Corollary 1, characterizes stochastic dominance using probabilistic couplings.

Proposition 1

Let \(\mu _1,\mu _2\in \mathsf {D}(\mathbb {N})\). Then \(\mu _1\le _{\mathrm {SD}} \mu _2\) iff \(\diamond _{\mu _1, \mu _2}. (\le )\).

We now turn to the definition of the Markov chain. For \(p\in [0,1]\), we consider the parametric \(\mathbb {N}\)-valued Markov chain Open image in new window , with initial state 0 and (parametric) step function:
$$ h \triangleq \lambda x. \mathsf {let}~b=\mathcal {B}(p)~\mathsf {in}~\mathsf {munit}(x+b) $$
where, for \(p \in [0,1]\), \(\mathcal {B}(p)\) is the Bernoulli distribution on \(\{0,1\}\) with probability p for 1 and \(1-p\) for 0. Our goal is to establish that \(\mathsf {coins}\) is monotonic, i.e. for every \(p_1,p_2\in [0,1]\), \(p_1\le p_2\) implies \(\mathsf {coins}~p_1 \le _{\mathrm {SD}} \mathsf {coins}~p_2\). We formalize this statement aswhere \(\psi \triangleq \forall p_1,p_2. p_1\le p_2 \Rightarrow \diamond _{[y_1 \leftarrow \mathbf {r}_1, y_2 \leftarrow \mathbf {r}_2]}\,{\text {All}}(y_1, y_2, z_1.z_2.z_1\le z_2)\). The crux of the proof is to establish stochastic dominance for the Bernoulli distribution:
$$ p_1:[0,1],p_2:[0,1]\mid p_1\le p_2 \vdash \mathcal {B}(p_1) : \mathsf {D}(\mathbb {N}) \sim \mathcal {B}(p_2) : \mathsf {D}(\mathbb {N}) \mid \mathbf {r}_1\,{\mathop {\le }\limits ^{\diamond }}\,\mathbf {r}_2 $$
where we use \(e_1\,{\mathop {\le }\limits ^{\diamond }}\,e_2\) as shorthand for \(\diamond _{[y_1 \leftarrow e_1, y_2 \leftarrow e_2]} y_1\le y_2\). This is proved directly by the [COUPLING] rule and checking by simple calculations that the premise of the rule is valid.
We briefly explain how to conclude the proof. Let \(h_1\) and \(h_2\) be the step functions for \(p_1\) and \(p_2\) respectively. It is clear from the above that (context omitted):
$$ x_1\le x_2 \vdash h_1\ x_1 : \mathsf {D}(\mathbb {B}) \sim h_2\ x_2 : \mathsf {D}(\mathbb {B}) \mid \diamond _{[y_1 \leftarrow \mathbf {r}_1, y_2 \leftarrow \mathbf {r}_2]}. {y_1\le y_2} $$
and by the definition of \({\text {All}}\):So, we can conclude by applying the [Markov] rule.

It is instructive to compare our proof with prior formalizations, and in particular with the proof in [5]. Their proof is carried out in the pRHL logic, whose [COUPLING] rule is based on the existence of a bijection that satisfies some property, rather than on our formalization based on Strassen’s Theorem. Their rule is motivated by applications in cryptography, and works well for many examples, but is inconvenient for our example at hand, which involves non-uniform probabilities. Indeed, their proof is based on code rewriting, and is done in two steps. First, they prove equivalence between sampling and returning \(x_1\) from \(\mathcal {B}(p_1)\); and sampling \(z_1\) from \(\mathcal {B}(p_2)\), \(z_2\) from \(\mathcal {B}({}^{p_1}\!/\!_{p_2})\) and returning \(z= z_1 \wedge z_2\). Then, they find a coupling between z and \(\mathcal {B}(p_2)\).

Shift Coupling: Random Walk vs Lazy Random Walk. The previous example is an instance of a lockstep coupling, in that it relates the k-th element of the first chain with the k-th element of the second chain. Many examples from the literature follow this lockstep pattern; however, it is not always possible to establish lockstep couplings. Shift couplings are a relaxation of lockstep couplings where we relate elements of the first and second chains without the requirement that their positions coincide.

We consider a simple example that motivates the use of shift couplings. Consider the random walk and lazy random walk (which, at each time step, either chooses to move or stay put), both defined as Markov chains over \(\mathbb {Z}\). For simplicity, assume that both walks start at position 0. It is not immediate to find a coupling between the two walks, since the two walks necessarily get desynchronized whenever the lazy walk stays put. Instead, the trick is to consider a lazy random walk that moves two steps instead of one. The random walk and the lazy random walk of step 2 are defined by the step functions:
$$\begin{array}{rcl} {\text {step}} &{} \triangleq &{} \lambda x.\mathsf {let}~z=\mathcal {U}_{\{-1,1\}}~\mathsf {in}~\mathsf {munit}(z+x) \\ {\text {lstep2}} &{} \triangleq &{} \lambda x.\mathsf {let}~z=\mathcal {U}_{\{-1,1\}}~\mathsf {in}~\mathsf {let}~b=\mathcal {U}_{\{0,1\}}~\mathsf {in}~\mathsf {munit}(x+2*z*b) \end{array}$$
After 2 iterations of \({\text {step}}\), the position has either changed two steps to the left or to the right, or has returned to the initial position, which is the same behaviour \({\text {lstep2}}\) has on every iteration. Therefore, the coupling we want to find should equate the elements at position 2i in \({\text {step}}\) with the elements at position i in \({\text {lstep2}}\). The details on how to prove the existence of this coupling are in Sect. 6.

Lumped Coupling: Random Walks on 3 and 4 Dimensions. A Markov chain is recurrent if it has probability 1 of returning to its initial state, and transient otherwise. It is relatively easy to show that the random walk over \(\mathbb {Z}\) is recurrent. One can also show that the random walk over \(\mathbb {Z}^2\) is recurrent. However, the random walk over \(\mathbb {Z}^3\) is transient.

For higher dimensions, we can use a coupling argument to prove transience. Specifically, we can define a coupling between a lazy random walk in n dimensions and a random walk in \(n +m\) dimensions, and derive transience of the latter from transience of the former. We define the (lazy) random walks below, and sketch the coupling arguments.

Specifically, we show here the particular case of the transience of the 4-dimensional random walk from the transience of the 3-dimensional lazy random walk. We start by defining the stepping functions:where \(U_i=\{(\pm 1,0,\dots 0), \dots , (0,\dots ,0,\pm 1)\}\) are the vectors of the basis of \(\mathbb {Z}^i\) and their opposites. Then, the random walk of dimension 4 is modelled by Open image in new window , and the lazy walk of dimension 3 is modelled by Open image in new window . We want to prove:where \({\text {pr}}^{n_2}_{n_1}\) denotes the standard projection from \(\mathbb {Z}^{n_2}\) to \(\mathbb {Z}^{n_1}\).
We apply the [Markov] rule. The only interesting premise requires proving that the transition function preserves the coupling:To prove this, we need to find the appropriate coupling, i.e., one that preserves the equality. The idea is that the step in \(\mathbb {Z}^3\) must be the projection of the step in \(\mathbb {Z}^4\). This corresponds to the following judgement:
$$\left. \begin{array}{rl} \lambda z_1. &{}\mathsf {let}~x_1=\mathcal {U}_{U_4}~\mathsf {in}~\\ &{}\mathsf {munit}(z_1 +_4 x_1) \end{array} \sim \begin{array}{rl} \lambda z_2. &{}\mathsf {let}~x_2=\mathcal {U}_{U_3}~\mathsf {in}~\\ &{}\mathsf {let}~b_2=\mathcal {B}({}^{3}\!/\!_{4})~\mathsf {in}~\\ &{}\mathsf {munit}(z_2 +_3 b_2*x_2) \end{array} \; \right| \; \begin{array}{c} \forall z_1 z_2. {\text {pr}}^4_3(z_1) = z_2 \Rightarrow \\ {\text {pr}}^4_3(\mathbf {r}_1\ z_1)\,{\mathop {=}\limits ^{\diamond }}\,\mathbf {r}_2\ z_2 \end{array}$$
which by simple equational reasoning is the same as
$$\left. \begin{array}{rl} \lambda z_1. &{}\mathsf {let}~x_1=\mathcal {U}_{U_4}~\mathsf {in}~\\ &{}\mathsf {munit}(z_1 +_4 x_1) \end{array} \sim \begin{array}{rl} \lambda z_2. &{}\mathsf {let}~p_2=\mathcal {U}_{U_3} \times \mathcal {B}({}^{3}\!/\!_{4})~\mathsf {in}~\\ &{}\mathsf {munit}(z_2 +_3 \pi _1(p_2)*\pi _2(p_2)) \end{array} \; \right| \; \begin{array}{c} \forall z_1 z_2. {\text {pr}}^4_3(z_1) = z_2 \Rightarrow \\ {\text {pr}}^4_3(\mathbf {r}_1\ z_1)\,{\mathop {=}\limits ^{\diamond }}\,\mathbf {r}_2\ z_2 \end{array} $$
We want to build a coupling such that if we sample (0, 0, 0, 1) or \((0,0,0,-1)\) from \(\mathcal {U}_{U_3}\), then we sample 0 from \(\mathcal {B}({}^{3}\!/\!_{4})\), and otherwise if we sample \((x_1,x_2,x_3,0)\) from \(\mathcal {U}_{U_4}\), we sample \((x_1,x_2,x_3)\) from \(U_3\). Formally, we prove this with the [Coupling] rule. Given \(X:U_4 \rightarrow \mathbb {B}\), by simple computation we show that:This concludes the proof. From the previous example, it follows that the lazy walk in 3 dimensions is transient, since the random walk in 3 dimensions is transient. By simple reasoning, we now conclude that the random walk in 4 dimensions is also transient.

4 Probabilistic Guarded Lambda Calculus

To ensure that a function on infinite datatypes is well-defined, one must check that it is productive. This means that any finite prefix of the output can be computed in finite time. For instance, consider the following function on streams:
$$ \mathtt {letrec\ bad\ (x:xs) = x : tail (bad\ xs)} $$
This function is not productive since only the first element can be computed. We can argue this as follows: Suppose that the tail of a stream is available one unit of time after its head, and that x:xs is available at time 0. How much time does it take for bad to start outputting its tail? Assume it takes k units of time. This means that tail(bad xs) will be available at time \(k+1\), since xs is only available at time 1. But tail(bad xs) is exactly the tail of bad(x:xs), and this is a contradiction, since x:xs is available at time 0 and therefore the tail of bad(x:xs) should be available at time k. Therefore, the tail of bad will never be available.

The guarded lambda calculus solves the productivity problem by distinguishing at type level between data that is available now and data that will be available in the future, and restricting when fixpoints can be defined. Specifically, the guarded lambda calculus extends the usual simply typed lambda calculus with two modalities: Open image in new window (pronounced later) and Open image in new window (constant). The later modality represents data that will be available one step in the future, and is introduced and removed by the term formers Open image in new window and \(\mathrm{prev}\ \) respectively. This modality is used to guard recursive occurrences, so for the calculus to remain productive, we must restrict when it can be eliminated. This is achieved via the constant modality, which expresses that all the data is available at all times. In the remainder of this section we present a probabilistic extension of this calculus.

Syntax. Types of the calculus are defined by the grammarwhere b ranges over a collection of base types. Open image in new window is the type of guarded streams of elements of type A. Formally, the type Open image in new window is isomorphic to Open image in new window . This isomorphism gives a way to introduce streams with the function Open image in new window and to eliminate them with the functions Open image in new window and Open image in new window . \(\mathsf {D}(C)\) is the type of distributions over discrete types C. Discrete types are defined by the following grammar, where \(b_0\) are discrete base types, e.g., \(\mathbb {Z}\).Note that, in particular, arrow types are not discrete but streams are. This is due to the semantics of streams as sets of finite approximations, which we describe in the next subsection. Also note that Open image in new window is not discrete since it makes the full infinite streams available.
We also need to distinguish between arbitrary types A, B and constant types S, T, which are defined by the following grammar
$$\begin{aligned} S, T\,{:}{:}{=}\,b_C \mid \mathbb {N}\mid S \times T \mid S + T \mid S \rightarrow T \mid \square ~A \end{aligned}$$
where \(b_C\) is a collection of constant base types. Note in particular that for any type A the type Open image in new window is constant.
The terms of the language t are defined by the following grammarwhere \(\xi \) is a delayed substitution, a sequence of bindings \(\left[ x_1 \leftarrow t_1, \ldots , x_n \leftarrow t_n \right] \). The terms c are constants corresponding to the base types used and \(\mathsf {munit}(t)\) and \(\mathsf {let}~x=t~\mathsf {in}~t\) are the introduction and sequencing construct for probability distributions. The meta-variable \(\mu \) stands for base distributions like \(\mathcal {U}_{C}\) and \(\mathcal {B}(p)\).

Delayed substitutions were introduced in [13] in a dependent type theory to be able to work with types dependent on terms of type Open image in new window . In the setting of a simple type theory, such as the one considered in this paper, delayed substitutions are equivalent to having the applicative structure [14] \(\circledast \) for the Open image in new window modality. However, delayed substitutions extend uniformly to the level of propositions, and thus we choose to use them in this paper in place of the applicative structure.

Denotational Semantics. The meaning of terms is given by a denotational model in the category \(\mathcal {S}\) of presheaves over \(\omega \), the first infinite ordinal. This category \(\mathcal {S}\) is also known as the topos of trees [15]. In previous work [1], it was shown how to model most of the constructions of the guarded lambda calculus and its internal logic, with the notable exception of the probabilistic features. Below we give an elementary presentation of the semantics.

Informally, the idea behind the topos of trees is to represent (infinite) objects from their finite approximations, which we observe incrementally as time passes. Given an object x, we can consider a sequence \(\{x_i\}\) of its finite approximations observable at time i. These are trivial for finite objects, such as a natural number, since for any number n, \(n_i = n\) at every i. But for infinite objects such as streams, the ith approximation is the prefix of length \(i+1\).

Concretely, the category \(\mathcal {S}\) consists of:

  • Objects X: families of sets \(\{X_i\}_{i\in \mathbb {N}}\) together with restriction functions \(r_n^X : X_{n+1} \rightarrow X_n\). We will write simply \(r_n\) if X is clear from the context.

  • Morphisms \(X \rightarrow Y\) : families of functions \(\alpha _n : X_n \rightarrow Y_n\) commuting with restriction functions in the sense of \(r_n^Y \circ \alpha _{n+1} = \alpha _n \circ r_n^X\).

The full interpretation of types of the calculus can be found in Fig. 8 in the appendix. The main points we want to highlight are:
  • Streams over a type A are interpreted as sequences of finite prefixes of elements of A with the restriction functions of A:
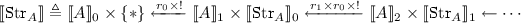
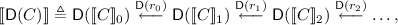
  • Distributions over a discrete object C are defined as a sequence of distributions over each \(\llbracket C \rrbracket _i\): where \(\mathsf {D}(\llbracket C \rrbracket _i)\) is the set of (probability density) functions \(\mu : \llbracket C \rrbracket _i \rightarrow [0,1]\) such that \(\sum _{x_\in X} \mu x = 1\), and \(\mathsf {D}(r_i)\) adds the probability density of all the points in \(\llbracket C \rrbracket _{i+1}\) that are sent by \(r_i\) to the same point in the \(\llbracket C \rrbracket _{i}\). In other words, \(\mathsf {D}(r_i)(\mu )(x) = \Pr _{y \leftarrow \mu }[r_i(y) = x]\)

An important property of the interpretation is that discrete types are interpreted as objects X such that \(X_i\) is finite or countably infinite for every i. This allows us to define distributions on these objects without the need for measure theory. In particular, the type of guarded streams Open image in new window is discrete provided A is, which is clear from the interpretation of the type Open image in new window . Conceptually this holds because Open image in new window is an approximation of real streams, consisting of only the first \(i+1\) elements.

An object X of \(\mathcal {S}\) is constant if all its restriction functions are bijections. Constant types are interpreted as constant objects of \(\mathcal {S}\) and for a constant type A the objects \(\llbracket \square A \rrbracket \) and \(\llbracket A \rrbracket \) are isomorphic in \(\mathcal {S}\).

Typing Rules. Terms are typed under a dual context \(\varDelta \mid \varGamma \), where \(\varGamma \) is a usual context that binds variables to a type, and \(\varDelta \) is a constant context containing variables bound to types that are constant. The term \(\mathrm{letc}\ x \leftarrow u\ \mathrm{in}\ t\) allows us to shift variables between constant and non-constant contexts. The typing rules can be found in Fig. 2.

The semantics of such a dual context \(\varDelta \mid \varGamma \) is given as the product of types in \(\varDelta \) and \(\varGamma \), except that we implicitly add \(\square \) in front of every type in \(\varDelta \). In the particular case when both contexts are empty, the semantics of the dual context correspond to the terminal object 1, which is the singleton set \(\{*\}\) at each time.

The interpretation of the well-typed term \(\varDelta \mid \varGamma \vdash t : A\) is defined by induction on the typing derivation, and can be found in Fig. 9 in the appendix.
Fig. 2.

A selection of the typing rules of the guarded lambda calculus. The rules for products, sums, and natural numbers are standard.

Applicative Structure of the Later Modality. As in previous work we can define the operator \(\circledast \) satisfying the typing ruleand the equation Open image in new window as the term Open image in new window .
Example: Modelling Markov Chains. As an application of \(\circledast \) and an example of how to use guardedness and probabilities together, we now give the precise definition of the Open image in new window construct that we used to model Markov chains earlier:The guardedness condition gives f the type Open image in new window in the body of the fixpoint. Therefore, it needs to be applied functorially (via \(\circledast \)) to Open image in new window and Open image in new window , which gives us a term of type Open image in new window . To complete the definition we need to build a term of type Open image in new window and then sequence it with \( \,{:}{:}\,\! \) to build a term of type Open image in new window . To achieve this, we use the primitive operator Open image in new window , which witnesses the isomorphism between Open image in new window and Open image in new window . For this isomorphism to exist, it is crucial that distributions be total (i.e., we cannot use subdistributions). Indeed, the denotation for Open image in new window is the sequence \(\{*\} \leftarrow \mathsf {D}(C_1) \leftarrow \mathsf {D}(C_2) \leftarrow \dots \), while the denotation for Open image in new window is the sequence \(\mathsf {D}(\{*\}) \leftarrow \mathsf {D}(C_1) \leftarrow \mathsf {D}(C_2) \leftarrow \dots \), and \(\{*\}\) is isomorphic to \(\mathsf {D}(\{*\})\) in \(\mathsf{Set}\) only if \(\mathsf {D}\) considers only total distributions.

5 Guarded Higher-Order Logic

We now introduce Guarded HOL (GHOL), which is a higher-order logic to reason about terms of the guarded lambda calculus. The logic is essentially that of [1], but presented with the dual context formulation analogous to the dual-context typing judgement of the guarded lambda calculus. Compared to standard intuitionistic higher-order logic, the logic GHOL has two additional constructs, corresponding to additional constructs in the guarded lambda calculus. These are the later modality ( Open image in new window ) on propositions, with delayed substitutions, which expresses that a proposition holds one time unit into the future, and the “always” modality \(\square \), which expresses that a proposition holds at all times. Formulas are defined by the grammar:The basic judgement of the logic is \(\varDelta \mid \varSigma \mid \varGamma \mid \varPsi \vdash \phi \) where \(\varSigma \) is a logical context for \(\varDelta \) (that is, a list of formulas well-formed in \(\varDelta \)) and \(\varPsi \) is another logical context for the dual context \(\varDelta \mid \varGamma \). The formulas in context \(\varSigma \) must be constant propositions. We say that a proposition \(\phi \) is constant if it is well-typed in context \(\varDelta \mid \cdot \) and moreover if every occurrence of the later modality in \(\phi \) is under the \(\square \) modality. Selected rules are displayed in Fig. 3. We highlight [Loeb] induction, which is the key to reasoning about fixpoints: to prove that \(\phi \) holds now, one can assume that it holds in the future. The interpretation of the formula \(\varDelta \mid \varGamma \vdash \phi \) is a subobject of the interpretation \(\llbracket \varDelta \mid \varGamma \rrbracket \). Concretely the interpretation A of \(\varDelta \mid \varGamma \vdash \phi \) is a family \(\left\{ A_i\right\} _{i=0}^\infty \) of sets such that \(A_i \subseteq \llbracket \varDelta \mid \varGamma \rrbracket _i\). This family must satisfy the property that if \(x \in A_{i+1}\) then \(r_i(x) \in A_i\) where \(r_i\) are the restriction functions of \(\llbracket \varDelta \mid \varGamma \rrbracket \). The interpretation of formulas is defined by induction on the typing derivation. In the interpretation of the context \(\varDelta \mid \varSigma \mid \varGamma \mid \varPsi \) the formulas in \(\varSigma \) are interpreted with the added Open image in new window modality. Moreover all formulas \(\phi \) in \(\varSigma \) are typeable in the context \(\varDelta \mid \cdot \vdash \phi \) and thus their interpretations are subsets of Open image in new window . We treat these subsets of \(\llbracket \varDelta \mid \varGamma \rrbracket \) in the obvious way.

The cases for the semantics of the judgement \(\varDelta \mid \varGamma \vdash \phi \) can be found in the appendix. It can be shown that this logic is sound with respect to its model in the topos of trees.

Theorem 2 (Soundness of the semantics)

The semantics of guarded higher-order logic is sound: if \(\varDelta \mid \varSigma \mid \varGamma \mid \varPsi \vdash \phi \) is derivable then for all \(n \in \mathbb {N}\), \(\llbracket \square \varSigma \rrbracket _n \cap \llbracket \varPsi \rrbracket _n \subseteq \llbracket \phi \rrbracket \).

In addition, Guarded HOL is expressive enough to axiomatize standard probabilities over discrete sets. This axiomatization can be used to define the \(\diamond \) modality directly in Guarded HOL (as opposed to our relational proof system, were we use it as a primitive). Furthermore, we can derive from this axiomatization additional rules to reason about couplings, which can be seen in Fig. 4. These rules will be the key to proving the soundness of the probabilistic fragment of the relational proof system, and can be shown to be sound themselves.

Proposition 2 (Soundness of derived rules)

The additional rules are sound.

Fig. 3.

Selected Guarded Higher-Order Logic rules

Fig. 4.

Derived rules for probabilistic constructs

6 Relational Proof System

We complete the formal description of the system by describing the proof rules for the non-probabilistic fragment of the relational proof system (the rules of the probabilistic fragment were described in Sect. 3.2).

6.1 Proof Rules

The rules for core \(\lambda \)-calculus constructs are identical to those of [2]; for convenience, we present a selection of the main rules in Fig. 7 in the appendix.

We briefly comment on the two-sided rules for the new constructs (Fig. 5). The notation \(\varOmega \) abbreviates a context \(\varDelta \mid \varSigma \mid \varGamma \mid \varPsi \). The rule [Next] relates two terms that have a Open image in new window term constructor at the top level. We require that both have one term in the delayed substitutions and that they are related pairwise. Then this relation is used to prove another relation between the main terms. This rule can be generalized to terms with more than one term in the delayed substitution. The rule [Prev] proves a relation between terms from the same delayed relation by applying \(\mathrm {prev}\) to both terms. The rule [Box] proves a relation between two boxed terms if the same relation can be proven in a constant context. Dually, [LetBox] uses a relation between two boxed terms to prove a relation between their unboxings. [LetConst] is similar to [LetBox], but it requires instead a relation between two constant terms, rather than explicitly \(\square \)-ed terms. The rule [Fix] relates two fixpoints following the [Loeb] rule from Guarded HOL. Notice that in the premise, the fixpoints need to appear in the delayed substitution so that the inductive hypothesis is well-formed. The rule [Cons] proves relations on streams from relations between their heads and tails, while [Head] and [Tail] behave as converses of [Cons].

Figure 6 contains the one-sided versions of the rules. We only present the left-sided versions as the right-sided versions are completely symmetric. The rule [Next-L] relates at \(\phi \) a term that has a Open image in new window with a term that does not have a Open image in new window . First, a unary property \(\phi '\) is proven on the term u in the delayed substitution, and it is then used as a premise to prove \(\phi \) on the terms with delays removed. Rules for proving unary judgements can be found in the appendix. Similarly, [LetBox-L] proves a unary property on the term that gets unboxed and then uses it as a precondition. The rule [Fix-L] builds a fixpoint just on the left, and relates it with an arbitrary term \(t_2\) at a property \(\phi \). Since \(\phi \) may contain the variable \(\mathbf {r}_2\) which is not in the context, it has to be replaced when adding Open image in new window to the logical context in the premise of the rule. The remaining rules are similar to their two-sided counterparts.

6.2 Metatheory

We review some of the most interesting metatheoretical properties of our relational proof system, highlighting the equivalence with Guarded HOL.

Theorem 3 (Equivalence with Guarded HOL)

For all contexts \(\varDelta ,\varGamma \); types \(\sigma _1,\sigma _2\); terms \(t_1,t_2\); sets of assertions \(\varSigma ,\varPsi \); and assertions \(\phi \):

The forward implication follows by induction on the given derivation. The reverse implication is immediate from the rule which allows to fall back on Guarded HOL in relational proofs. (Rule [SUB] in the appendix). The full proof is in the appendix. The consequence of this theorem is that the syntax-directed, relational proof system we have built on top of Guarded HOL does not lose expressiveness.

The intended semantics of a judgement Open image in new window is that, for every valuation \(\delta \,\models \,\varDelta \), \(\gamma \,\models \,\varGamma \), if \(\llbracket \varSigma \rrbracket (\delta )\) and \(\llbracket \varPsi \rrbracket (\delta ,\gamma )\), thenSince Guarded HOL is sound with respect to its semantics in the topos of trees, and our relational proof system is equivalent to Guarded HOL, we obtain that our relational proof system is also sound in the topos of trees.

Corollary 2 (Soundness and consistency)

If \(\varDelta \mid \varSigma \mid \varGamma \mid \varPsi \vdash t_1 : \sigma _2 \sim t_2 : \sigma _2 \mid \phi \), then for every valuation \(\delta \,\models \,\varDelta \), \(\gamma \,\models \,\varGamma \):In particular, there is no proof of \(\varDelta \mid \emptyset \mid \varGamma \mid \emptyset \vdash t_1 : \sigma _1 \sim t_2 : \sigma _2 \mid \bot \).
Fig. 5.

Two-sided rules for Guarded RHOL

6.3 Shift Couplings Revisited

We give further details on how to prove the example with shift couplings from Sect. 3.3. (Additional examples of relational reasoning on non-probabilistic streams can be found in the appendix) Recall the step functions:We axiomatize the predicate \({\text {All}}_{2,1}\), which relates the element at position 2i in one stream to the element at position i in another stream, as follows.
Fig. 6.

One-sided rules for Guarded RHOL

In fact, we can assume that, in general, we have a family of \({\text {All}}_{m_1, m_2}\) predicates relating two streams at positions \(m_1\cdot i\) and \(m_2\cdot i\) for every i.

We can now express the existence of a shift coupling by the statement:
For the proof, we need to introduce an asynchronous rule for Markov chains:

This asynchronous rule for Markov chains shares the motivations of the rule for loops proposed in [6]. Note that one can define a rule [Markov-m-n] for arbitrary m and n to prove a judgement of the form \({\text {All}}_{m,n}\) on two Markov chains.

We show the proof of the shift coupling. By equational reasoning, we get:and the only interesting premise of [Markov-2-1] is:Couplings between \(z_1\) and \(z_2\) and between \(z_1'\) and \(b_2\) can be found by simple computations. This completes the proof.

7 Related Work

Our probabilistic guarded \(\lambda \)-calculus and the associated logic Guarded HOL build on top of the guarded \(\lambda \)-calculus and its internal logic [1]. The guarded \(\lambda \)-calculus has been extended to guarded dependent type theory [13], which can be understood as a theory of guarded refinement types and as a foundation for proof assistants based on guarded type theory. These systems do not reason about probabilities, and do not support syntax-directed (relational) reasoning, both of which we support.

Relational models for higher-order programming languages are often defined using logical relations. [16] showed how to use second-order logic to define and reason about logical relations for the second-order lambda calculus. Recent work has extended this approach to logical relations for higher-order programming languages with computational effects such as nontermination, general references, and concurrency [17, 18, 19, 20]. The logics used in loc. cit. are related to our work in two ways: (1) the logics in loc. cit. make use of the later modality for reasoning about recursion, and (2) the models of the logics in loc. cit. can in fact be defined using guarded type theory. Our work is more closely related to Relational Higher Order Logic [2], which applies the idea of logic-enriched type theories [21, 22] to a relational setting. There exist alternative approaches for reasoning about relational properties of higher-order programs; for instance, [23] have recently proposed to use monadic reification for reducing relational verification of \(F^*\) to proof obligations in higher-order logic.

A series of work develops reasoning methods for probabilistic higher-order programs for different variations of the lambda calculus. One line of work has focused on operationally-based techniques for reasoning about contextual equivalence of programs. The methods are based on probabilistic bisimulations [24, 25] or on logical relations [26]. Most of these approaches have been developed for languages with discrete distributions, but recently there has also been work on languages with continuous distributions [27, 28]. Another line of work has focused on denotational models, starting with the seminal work in [29]. Recent work includes support for relational reasoning about equivalence of programs with continuous distributions for a total programming language [30]. Our approach is most closely related to prior work based on relational refinement types for higher-order probabilistic programs. These were initially considered by [31] for a stateful fragment of \(F^*\), and later by [32, 33] for a pure language. Both systems are specialized to building probabilistic couplings; however, the latter support approximate probabilistic couplings, which yield a natural interpretation of differential privacy [34], both in its vanilla and approximate forms (i.e. \(\epsilon \)- and \((\epsilon ,\delta )\)-privacy). Technically, approximate couplings are modelled as a graded monad, where the index of the monad tracks the privacy budget (\(\epsilon \) or \((\epsilon ,\delta )\)). Both systems are strictly syntax-directed, and cannot reason about computations that have different types or syntactic structures, while our system can.

8 Conclusion

We have developed a probabilistic extension of the (simply typed) guarded \(\lambda \)-calculus, and proposed a syntax-directed proof system for relational verification. Moreover, we have verified a series of examples that are beyond the reach of prior work. Finally, we have proved the soundness of the proof system with respect to the topos of trees.

There are several natural directions for future work. One first direction is to enhance the expressiveness of the underlying simply typed language. For instance, it would be interesting to introduce clock variables and some type dependency as in [13], and extend the proof system accordingly. This would allow us, for example, to type the function taking the n-th element of a guarded stream, which cannot be done in the current system. Another exciting direction is to consider approximate couplings, as in [32, 33], and to develop differential privacy for infinite streams—preliminary work in this direction, such as [35], considers very large lists, but not arbitrary streams. A final direction would be to extend our approach to continuous distributions to support other application domains.

Notes

Acknowledgments

We would like to thank the anonymous reviewers for their time and their helpful input. This research was supported in part by the ModuRes Sapere Aude Advanced Grant from The Danish Council for Independent Research for the Natural Sciences (FNU), by a research grant (12386, Guarded Homotopy Type Theory) from the VILLUM foundation, and by NSF under grant 1718220.

References

  1. 1.
    Clouston, R., Bizjak, A., Grathwohl, H.B., Birkedal, L.: The guarded lambda-calculus: programming and reasoning with guarded recursion for coinductive types. Log. Methods Comput. Sci. 12(3) (2016)Google Scholar
  2. 2.
    Aguirre, A., Barthe, G., Gaboardi, M., Garg, D., Strub, P.: A relational logic for higher-order programs. PACMPL 1(ICFP), 21:1–21:29 (2017)CrossRefGoogle Scholar
  3. 3.
    Lindvall, T.: Lectures on the Coupling Method. Courier Corporation (2002)Google Scholar
  4. 4.
    Thorisson, H.: Coupling, Stationarity, and Regeneration. Springer, New York (2000)CrossRefGoogle Scholar
  5. 5.
    Barthe, G., Espitau, T., Grégoire, B., Hsu, J., Stefanesco, L., Strub, P.-Y.: Relational reasoning via probabilistic coupling. In: Davis, M., Fehnker, A., McIver, A., Voronkov, A. (eds.) LPAR 2015. LNCS, vol. 9450, pp. 387–401. Springer, Heidelberg (2015).  https://doi.org/10.1007/978-3-662-48899-7_27CrossRefMATHGoogle Scholar
  6. 6.
    Barthe, G., Grégoire, B., Hsu, J., Strub, P.: Coupling proofs are probabilistic product programs. In: POPL 2017, Paris, France, 18–20 January 2017 (2017)Google Scholar
  7. 7.
    Strassen, V.: The existence of probability measures with given marginals. Ann. Math. Stat. 36, 423–439 (1965)MathSciNetCrossRefGoogle Scholar
  8. 8.
    Goguen, J.A., Meseguer, J.: Security policies and security models. In: IEEE Symposium on Security and Privacy, pp. 11–20 (1982)Google Scholar
  9. 9.
    Bogdanov, D., Niitsoo, M., Toft, T., Willemson, J.: High-performance secure multi-party computation for data mining applications. Int. J. Inf. Sec. 11(6), 403–418 (2012)CrossRefGoogle Scholar
  10. 10.
    Cramer, R., Damgard, I.B., Nielsen, J.B.: Secure Multiparty Computation and Secret Sharing, 1st edn. Cambridge University Press, New York (2015)CrossRefGoogle Scholar
  11. 11.
    Barthe, G., Espitau, T., Grégoire, B., Hsu, J., Strub, P.: Proving uniformity and independence by self-composition and coupling. CoRR abs/1701.06477 (2017)Google Scholar
  12. 12.
    Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: Proceedings of Foundations of Computer Science. IEEE (2001)Google Scholar
  13. 13.
    Bizjak, A., Grathwohl, H.B., Clouston, R., Møgelberg, R.E., Birkedal, L.: Guarded dependent type theory with coinductive types. In: Jacobs, B., Löding, C. (eds.) FoSSaCS 2016. LNCS, vol. 9634, pp. 20–35. Springer, Heidelberg (2016).  https://doi.org/10.1007/978-3-662-49630-5_2CrossRefGoogle Scholar
  14. 14.
    McBride, C., Paterson, R.: Applicative programming with effects. J. Funct. Program. 18(1), 1–13 (2008)CrossRefGoogle Scholar
  15. 15.
    Birkedal, L., Møgelberg, R.E., Schwinghammer, J., Støvring, K.: First steps in synthetic guarded domain theory: step-indexing in the topos of trees. Log. Methods Comput. Sci. 8(4) (2012)Google Scholar
  16. 16.
    Plotkin, G., Abadi, M.: A logic for parametric polymorphism. In: Bezem, M., Groote, J.F. (eds.) TLCA 1993. LNCS, vol. 664, pp. 361–375. Springer, Heidelberg (1993).  https://doi.org/10.1007/BFb0037118CrossRefGoogle Scholar
  17. 17.
    Dreyer, D., Ahmed, A., Birkedal, L.: Logical step-indexed logical relations. Log. Methods Comput. Sci. 7(2) (2011)Google Scholar
  18. 18.
    Turon, A., Dreyer, D., Birkedal, L.: Unifying refinement and Hoare-style reasoning in a logic for higher-order concurrency. In: Morrisett, G., Uustalu, T. (eds.) ICFP 2013, Boston, MA, USA, 25–27 September 2013. ACM (2013)Google Scholar
  19. 19.
    Krebbers, R., Timany, A., Birkedal, L.: Interactive proofs in higher-order concurrent separation logic. In: Castagna, G., Gordon, A.D. (eds.) POPL 2017, Paris, France, 18–20 January 2017. ACM (2017)CrossRefGoogle Scholar
  20. 20.
    Krogh-Jespersen, M., Svendsen, K., Birkedal, L.: A relational model of types-and-effects in higher-order concurrent separation logic. In: POPL 2017, Paris, France, 18–20 January 2017, pp. 218–231 (2017)Google Scholar
  21. 21.
    Aczel, P., Gambino, N.: Collection principles in dependent type theory. In: Callaghan, P., Luo, Z., McKinna, J., Pollack, R., Pollack, R. (eds.) TYPES 2000. LNCS, vol. 2277, pp. 1–23. Springer, Heidelberg (2002).  https://doi.org/10.1007/3-540-45842-5_1CrossRefGoogle Scholar
  22. 22.
    Aczel, P., Gambino, N.: The generalised type-theoretic interpretation of constructive set theory. J. Symb. Log. 71(1), 67–103 (2006)CrossRefGoogle Scholar
  23. 23.
    Grimm, N., Maillard, K., Fournet, C., Hritcu, C., Maffei, M., Protzenko, J., Rastogi, A., Swamy, N., Béguelin, S.Z.: A monadic framework for relational verification (functional pearl). CoRR abs/1703.00055 (2017)Google Scholar
  24. 24.
    Crubillé, R., Dal Lago, U.: On probabilistic applicative bisimulation and call-by-value \(\lambda \)-calculi. In: Shao, Z. (ed.) ESOP 2014. LNCS, vol. 8410, pp. 209–228. Springer, Heidelberg (2014).  https://doi.org/10.1007/978-3-642-54833-8_12CrossRefMATHGoogle Scholar
  25. 25.
    Sangiorgi, D., Vignudelli, V.: Environmental bisimulations for probabilistic higher-order languages. In: Bodík, R., Majumdar, R. (eds.) POPL 2016, St. Petersburg, FL, USA, 20–22 January 2016. ACM (2016)Google Scholar
  26. 26.
    Bizjak, A., Birkedal, L.: Step-indexed logical relations for probability. In: Pitts, A. (ed.) FoSSaCS 2015. LNCS, vol. 9034, pp. 279–294. Springer, Heidelberg (2015).  https://doi.org/10.1007/978-3-662-46678-0_18CrossRefGoogle Scholar
  27. 27.
    Borgström, J., Lago, U.D., Gordon, A.D., Szymczak, M.: A lambda-calculus foundation for universal probabilistic programming. In: Garrigue, J., Keller, G., Sumii, E. (eds.) ICFP 2016, Nara, Japan, 18–22 September 2016. ACM (2016)Google Scholar
  28. 28.
    Culpepper, R., Cobb, A.: Contextual equivalence for probabilistic programs with continuous random variables and scoring. In: Yang, H. (ed.) ESOP 2017. LNCS, vol. 10201, pp. 368–392. Springer, Heidelberg (2017).  https://doi.org/10.1007/978-3-662-54434-1_14CrossRefMATHGoogle Scholar
  29. 29.
    Jones, C., Plotkin, G.D.: A probabilistic powerdomain of evaluations. In: LICS 1989, Pacific Grove, California, USA, 5–8 June 1989. IEEE Computer Society (1989)Google Scholar
  30. 30.
    Staton, S., Yang, H., Wood, F., Heunen, C., Kammar, O.: Semantics for probabilistic programming: higher-order functions, continuous distributions, and soft constraints. In: LICS 2016, New York, NY, USA, 5–8 July 2016. ACM (2016)Google Scholar
  31. 31.
    Barthe, G., Fournet, C., Grégoire, B., Strub, P., Swamy, N., Béguelin, S.Z.: Probabilistic relational verification for cryptographic implementations. In: Jagannathan, S., Sewell, P. (eds.) POPL 2014 (2014)Google Scholar
  32. 32.
    Barthe, G., Gaboardi, M., Gallego Arias, E.J., Hsu, J., Roth, A., Strub, P.Y.: Higher-order approximate relational refinement types for mechanism design and differential privacy. In: POPL 2015, Mumbai, India, 15–17 January 2015 (2015)Google Scholar
  33. 33.
    Barthe, G., Farina, G.P., Gaboardi, M., Arias, E.J.G., Gordon, A., Hsu, J., Strub, P.: Differentially private Bayesian programming. In: CCS 2016, Vienna, Austria, 24–28 October 2016. ACM (2016)Google Scholar
  34. 34.
    Dwork, C., Roth, A.: The algorithmic foundations of differential privacy. Found. Trends Theor. Comput. Sci. 9(3–4), 211–407 (2014)MathSciNetMATHGoogle Scholar
  35. 35.
    Kellaris, G., Papadopoulos, S., Xiao, X., Papadias, D.: Differentially private event sequences over infinite streams. PVLDB 7(12), 1155–1166 (2014)Google Scholar

Copyright information

© The Author(s) 2018

Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.

Authors and Affiliations

  • Alejandro Aguirre
    • 1
  • Gilles Barthe
    • 1
  • Lars Birkedal
    • 2
  • Aleš Bizjak
    • 2
  • Marco Gaboardi
    • 3
  • Deepak Garg
    • 4
  1. 1.IMDEA Software InstituteMadridSpain
  2. 2.Aarhus UniversityAarhusDenmark
  3. 3.University at Buffalo, SUNYBuffaloUSA
  4. 4.MPI-SWSKaiserslautern and SaarbrückenGermany

Personalised recommendations