Abstract
Many interesting program properties like determinism or information flow security are hyperproperties, that is, they relate multiple executions of the same program. Hyperproperties can be verified using relational logics, but these logics require dedicated tool support and are difficult to automate. Alternatively, constructions such as self-composition represent multiple executions of a program by one product program, thereby reducing hyperproperties of the original program to trace properties of the product. However, existing constructions do not fully support procedure specifications, for instance, to derive the determinism of a caller from the determinism of a callee, making verification non-modular.
We present modular product programs, a novel kind of product program that permits hyperproperties in procedure specifications and, thus, can reason about calls modularly. We demonstrate its expressiveness by applying it to information flow security with advanced features such as declassification and termination-sensitivity. Modular product programs can be verified using off-the-shelf verifiers; we have implemented our approach to secure information flow using the Viper verification infrastructure.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
The past decades have seen significant progress in automated reasoning about program behavior. In the most common scenario, the goal is to prove trace properties of programs such as functional correctness or termination. However, important program properties such as information flow security, injectivity, and determinism cannot be expressed as properties of individual traces; these so-called hyperproperties relate different executions of the same program. For example, proving determinism of a program requires showing that any two executions from identical initial states will result in identical final states.
An important attribute of reasoning techniques about programs is modularity. A technique is modular if it allows reasoning about parts of a program in isolation, e.g., verifying each procedure separately and using only the specifications of other procedures. Modularity is vital for scalability and to verify libraries without knowing all of their clients. Fully modular reasoning about hyperproperties thus requires the ability to formulate relational specifications, which relate different executions of a procedure, and to apply those specifications where the procedure is called. As an example, the statement

can be proved to be deterministic if  relational specification guarantees that its result deterministically depends on its input.
relational specification guarantees that its result deterministically depends on its input.
Relational program logics [11, 27, 29] allow directly proving general hyperproperties, however, automating relational logics is difficult and requires building dedicated tools. Alternatively, self-composition [9] and product programs [6, 7] reduce a hyperproperty to an ordinary trace property, thus making it possible to use off-the-shelf program verifiers for proving hyperproperties. Both approaches construct a new program that combines the behaviors of multiple runs of the original program. However, by the nature of their construction, neither approach supports modular verification based on relational specifications: Procedure calls in the original program will be duplicated, which means that there is no single program point at which a relational specification can be applied. For the aforementioned example, self-composition yields the following program:

Determinism can now be verified by proving the trace property that identical values for  and
and  in the initial state imply identical values for
in the initial state imply identical values for  and
and  in the final state. However, such a proof cannot make use of a relational specification for procedure
in the final state. However, such a proof cannot make use of a relational specification for procedure  (expressing that
(expressing that  is deterministic). Such a specification relates several executions of
is deterministic). Such a specification relates several executions of  , whereas each call in the self-composition belongs to a single execution. Instead, verification requires a precise functional specification of
, whereas each call in the self-composition belongs to a single execution. Instead, verification requires a precise functional specification of  , which exactly determines its result value in terms of the input. Verifying such precise functional specifications increases the verification effort and is at odds with data abstraction (for instance, a collection might not want to promise the exact iteration order); inferring them is beyond the state of the art for most procedures [28]. Existing product programs allow aligning or combining some statements and can thereby lift this requirement in some cases, but this requires manual effort during the construction, depends on the used specifications, and does not solve the problem in general.
, which exactly determines its result value in terms of the input. Verifying such precise functional specifications increases the verification effort and is at odds with data abstraction (for instance, a collection might not want to promise the exact iteration order); inferring them is beyond the state of the art for most procedures [28]. Existing product programs allow aligning or combining some statements and can thereby lift this requirement in some cases, but this requires manual effort during the construction, depends on the used specifications, and does not solve the problem in general.
In this paper, we present modular product programs, a novel kind of product programs that allows modular reasoning about hyperproperties. Modular product programs enable proving k-safety hyperproperties, i.e., hyperproperties that relate finite prefixes of k execution traces, for arbitrary values of k [12]. We achieve this via a transformation that, unlike existing products, does not duplicate loops or procedure calls, meaning that for any loop or call in the original program, there is exactly one statement in the k-product at which a relational specification can be applied. Like existing product programs, modular products can be reasoned about using off-the-shelf program verifiers.
We demonstrate the expressiveness of modular product programs by applying them to prove secure information flow, a 2-safety hyperproperty. We show how modular products enable proving traditional non-interference using natural and concise information flow specifications, and how to extend our approach for proving the absence of timing or termination channels, and supporting declassification in an intuitive way.
To summarize, we make the following contributions:
-
We introduce modular k-product programs, which enable modular proofs of arbitrary k-safety hyperproperties for sequential programs using off-the-shelf verifiers.
-
We demonstrate the usefulness of modular product programs by applying them to secure information flow, with support for declassification and preventing different kinds of side channels.
-
We implement our product-based approach for information flow verification in an automated verifier and show that our tool can automatically prove information flow security of challenging examples.
After giving an informal overview of our approach in Sect. 2 and introducing our programming and assertion language in Sect. 3, we formally define modular product programs in Sect. 4. We sketch a soundness proof in Sect. 5. Section 6 demonstrates how to apply modular products for proving secure information flow. We describe and evaluate our implementation in Sect. 7, discuss related work in Sect. 8, and conclude in Sect. 9.
2 Overview
In this section, we will illustrate the core concepts behind modular k-products on an example program. We will first show how modular products are constructed, and subsequently demonstrate how they allow using relational specifications to modularly prove hyperproperties.
2.1 Relational Specifications
Consider the example program in Fig. 1, which counts the number of female entries in a sequence of people. Now assume we want to prove that the program is deterministic, i.e., that its output state is completely determined by its input arguments. This can be expressed as a 2-safety hyperproperty which states that, for two terminating executions of the program with identical inputs, the outputs will be the same. This hyperproperty can be expressed by the relational (as opposed to unary) specification  , where
, where  refers to the value of the variable x in the ith execution.
refers to the value of the variable x in the ith execution.
Intuitively, it is possible to prove this specification by giving  a precise functional specification like
a precise functional specification like  , meaning that
, meaning that  can be invoked in any state and that
can be invoked in any state and that 
 will hold if it returns. From this specification and an appropriate loop invariant,
will hold if it returns. From this specification and an appropriate loop invariant,  can be shown to be deterministic. However, this specification is unnecessarily strong. For proving determinism, it is irrelevant what exactly the final value of
can be shown to be deterministic. However, this specification is unnecessarily strong. For proving determinism, it is irrelevant what exactly the final value of  is; it is only important that it is uniquely determined by the procedure’s inputs. Proving hyperproperties using only unary specifications, however, critically depends on having exact specifications for every value returned by a called procedure, as well as all heap locations modified by it. Not only are such specifications difficult to infer and cumbersome to provide manually; this requirement also fundamentally removes the option of underspecifying program behavior, which is often desirable in practice. Because of these limitations, verification techniques that require precise functional specifications for proving hyperproperties often do not work well in practice, as observed by Terauchi and Aiken for the case of self-composition [28].
is; it is only important that it is uniquely determined by the procedure’s inputs. Proving hyperproperties using only unary specifications, however, critically depends on having exact specifications for every value returned by a called procedure, as well as all heap locations modified by it. Not only are such specifications difficult to infer and cumbersome to provide manually; this requirement also fundamentally removes the option of underspecifying program behavior, which is often desirable in practice. Because of these limitations, verification techniques that require precise functional specifications for proving hyperproperties often do not work well in practice, as observed by Terauchi and Aiken for the case of self-composition [28].
Proving determinism of the example program becomes much simpler if we are able to reason about two program executions at once. If both runs start with identical values for  then they will have identical values for
then they will have identical values for  , and
, and  when they reach the loop. Since the loop guard only depends on
when they reach the loop. Since the loop guard only depends on  and
and  , it will either be true for both executions or false for both. Assuming that
, it will either be true for both executions or false for both. Assuming that  behaves deterministically, all three variables will again be equal in both executions at the end of the loop body. This means that the program establishes and preserves the relational loop invariant that
behaves deterministically, all three variables will again be equal in both executions at the end of the loop body. This means that the program establishes and preserves the relational loop invariant that  and
and  have identical values in both executions, from which we can deduce the desired relational postcondition. Our modular product programs enable this modular and intuitive reasoning, as we explain next.
have identical values in both executions, from which we can deduce the desired relational postcondition. Our modular product programs enable this modular and intuitive reasoning, as we explain next.
Modular 2-product of the program in Fig. 1 (slightly simplified). Parameters and local variables have been duplicated, but control flow statements have not. All statements are parameterized by activation variables.
2.2 Modular Product Programs
Like other product programs, our modular k-product programs multiply the state space of the original program by creating k renamed versions of all original variables. However, unlike other product programs, they do not duplicate control structures like loops or procedure calls, while still allowing different executions to take different paths through the program.
Modular product programs achieve this as follows: The set of transitions made by the execution of a product is the union of the transitions made by the executions of the original program it represents. This means that if two executions of an if-then-else statement execute different branches, an execution of the product will execute the corresponding versions of both branches; however, it will be aware of the fact that each branch is taken by only one of the original executions, and the transformation of the statements inside each branch will ensure that the state of the other execution is not modified by executing it.
For this purpose, modular product programs use boolean activation variables that store, for each execution, the condition under which it is currently active. All activation variables are initially true. For every statement that directly changes the program state, the product performs the state change for all active executions. Control structures update which executions are active (for instance based on the loop condition) and pass this information down (into the branches of a conditional, the body of a loop, or the callee of a procedure call) to the level of atomic statementsFootnote 1. This representation avoids duplicating these control structures.
Figure 2 shows the modular 2-product of the program in Fig. 1. Consider first the  procedure. Its parameters have been duplicated, there are now two copies of all variables, one for each execution. This is analogous to self-composition or existing product programs. In addition, the transformed procedure has two boolean parameters
procedure. Its parameters have been duplicated, there are now two copies of all variables, one for each execution. This is analogous to self-composition or existing product programs. In addition, the transformed procedure has two boolean parameters  and
and  ; these variables are the initial activation variables of the procedure. Since
; these variables are the initial activation variables of the procedure. Since  is the entry point of the program, the initial activation variables can be assumed to be true.
is the entry point of the program, the initial activation variables can be assumed to be true.
Consider what happens when the product is run with arbitrary input values for  and
and  . The product will first initialize
. The product will first initialize  and
and  to zero, like it does with
to zero, like it does with  in the original program, and analogously for
in the original program, and analogously for  and
and  .
.
The loop in the original program has been transformed to a single loop in the product. Its condition is true if the original loop condition is true for any active execution. This means that the loop will iterate as long as at least one execution of the original program would. Inside the loop body, the fresh activation variables  and
and  represent whether the corresponding executions would execute the loop body. That is, for each execution, the respective activation variable will be true if the previous activation variable (
represent whether the corresponding executions would execute the loop body. That is, for each execution, the respective activation variable will be true if the previous activation variable ( or
or  , respectively) is true, meaning that this execution actually reaches the loop, and the loop guard is true for that execution. All statements in the loop body are then transformed using these new activation variables. Consequently, the loop will keep iterating while at least one execution executes the loop, but as soon as the loop guard is false for any execution, its activation variable will be false and the loop body will have no effect.
, respectively) is true, meaning that this execution actually reaches the loop, and the loop guard is true for that execution. All statements in the loop body are then transformed using these new activation variables. Consequently, the loop will keep iterating while at least one execution executes the loop, but as soon as the loop guard is false for any execution, its activation variable will be false and the loop body will have no effect.
Conceptually, procedure calls are handled very similarly to loops. For the call to  in the original program, only a single call is created in the product. This call is executed if at least one activation variable is true, i.e., if at least one execution would perform the call in the original program. In addition to the (duplicated) arguments of the original call, the current activation variables are passed to the called procedure. In the transformed version of
in the original program, only a single call is created in the product. This call is executed if at least one activation variable is true, i.e., if at least one execution would perform the call in the original program. In addition to the (duplicated) arguments of the original call, the current activation variables are passed to the called procedure. In the transformed version of  , all statements are then made conditional on those activation variables. Therefore, like with loops, a call in the product will be performed if at least one execution would perform it in the original program, but it will have no effect on the state of the executions that are not active when the call is made.
, all statements are then made conditional on those activation variables. Therefore, like with loops, a call in the product will be performed if at least one execution would perform it in the original program, but it will have no effect on the state of the executions that are not active when the call is made.
The transformed version of  shows how conditionals are handled. We introduce four fresh activation variables
shows how conditionals are handled. We introduce four fresh activation variables  and
and  two for each execution. The first pair encodes whether the then-branch should be executed by either of the two executions; the second encodes the same for the else-branch. These activation variables are then used to transform the branches. Consequently, neither branch will have an effect for inactive executions, and exactly one branch has an effect for each active execution.
two for each execution. The first pair encodes whether the then-branch should be executed by either of the two executions; the second encodes the same for the else-branch. These activation variables are then used to transform the branches. Consequently, neither branch will have an effect for inactive executions, and exactly one branch has an effect for each active execution.
To summarize, our activation variables ensure that the sequence of state-changing statements executed by each execution is the same in the product and the original program. We achieve this without duplicating control structures or imposing restrictions on the control flow.
2.3 Interpretation of Relational Specifications
Since modular product programs do not duplicate calls, they provide a simple way of interpreting relational procedure specifications: If all executions call a procedure, its relational precondition is required to hold before the call and the relational postcondition afterwards. If a call is performed by some executions but not all, the relational specification are not meaningful, and thus cannot be required to hold. To encode this intuition, we transform every relational pre- or postcondition \(\hat{Q}\) of the original program into an implication  . In the transformed version, both pre- and postconditions are made conditional on the conjunction of all activation parameters
. In the transformed version, both pre- and postconditions are made conditional on the conjunction of all activation parameters  of the procedure. As a result, both will be trivially true if at least one execution is not active at the call site.
of the procedure. As a result, both will be trivially true if at least one execution is not active at the call site.
In our example, we give  the relational specification
the relational specification  , which expresses determinism. This specification will be transformed into a unary specification of the product program:
, which expresses determinism. This specification will be transformed into a unary specification of the product program:  .
.
Assume for the moment that  also has a unary precondition
also has a unary precondition  . Such a specification should hold for every call, and therefore for every active execution, even if other executions are inactive. Therefore, its interpretation in the product program is
. Such a specification should hold for every call, and therefore for every active execution, even if other executions are inactive. Therefore, its interpretation in the product program is  . The translation of other unary assertions is analogous.
. The translation of other unary assertions is analogous.
Note that it is possible (and useful) to give a procedure both a relational and a unary specification; in the product this is encoded by simply conjoining the transformed versions of the unary and the relational assertions.
2.4 Product Program Verification
We can now prove determinism of our example using the product program. Verifying  is simple. For
is simple. For  , we want to prove the transformed specification
, we want to prove the transformed specification  . We use the relational loop invariant
. We use the relational loop invariant  , encoded as
, encoded as  . The loop invariant holds trivially if either
. The loop invariant holds trivially if either  or
or  is false. Otherwise, it ensures
is false. Otherwise, it ensures  and
and  . Using the specification of
. Using the specification of  , we obtain
, we obtain  , which implies that the loop invariant is preserved. The loop invariant implies the postcondition.
, which implies that the loop invariant is preserved. The loop invariant implies the postcondition.
3 Preliminaries
We model our setting according to the relational logic by Banerjee, Naumann and Nikouei [5]Footnote 2 and, like them, use a standard Hoare logic [4] to reason about single program executions. Figure 3 shows the language we use to define modular product programs. x ranges over the set of local integer variable names \(\textsc {Var}\). Note that this language is deterministic; non-determinism can for example be modelled via additional inputs, as is often done for modelling fairness in concurrent programs [16]. Program configurations have the form \(\langle s, \sigma \rangle \), where \(\sigma \in \varSigma \) maps variable names to values. The value of expression e in state \(\sigma \) is denoted as \(\sigma (e)\). The small-step transition relation for program configurations has the form \(\langle s, \sigma \rangle \rightarrow \langle s', \sigma ' \rangle \). A hypothesis context \(\varPhi \) maps procedure names to specifications.
The judgment \(\varPhi \vDash s : P \rightsquigarrow Q\) denotes that statement s, when executed in a state fulfilling the unary assertion P, will not fault, and if the execution terminates, the resulting state will fulfill the unary assertion Q. For an extensive discussion of the language and its operational and axiomatic semantics, see [5].
In addition to standard unary expressions and assertions, we define relational expressions and assertions. They differ from normal expressions and assertions in that they contain parameterized variable references of the form  and are evaluated over a tuple of states instead of a single one. A relational expression is k-relational if for all contained variable references
and are evaluated over a tuple of states instead of a single one. A relational expression is k-relational if for all contained variable references  , \(1 \le i \le k\), and analogous for relational assertions. The value of a variable reference
, \(1 \le i \le k\), and analogous for relational assertions. The value of a variable reference  with \(1 \le i \le k\) in a tuple of states \((\sigma _1, \ldots , \sigma _k)\) is \(\sigma _i(x)\); the evaluation of arbitrary relational expressions and the validity of relational assertions \((\sigma _1, \ldots , \sigma _k) \vDash \hat{P}\) are defined accordingly.
with \(1 \le i \le k\) in a tuple of states \((\sigma _1, \ldots , \sigma _k)\) is \(\sigma _i(x)\); the evaluation of arbitrary relational expressions and the validity of relational assertions \((\sigma _1, \ldots , \sigma _k) \vDash \hat{P}\) are defined accordingly.
Definition 1
A k-relational specification  holds iff \(\hat{P}\) and \(\hat{Q}\) are k-relational assertions, and for all \(\sigma _1, \ldots , \sigma _k, \sigma '_1, \ldots , \sigma '_k\), if \((\sigma _1, \ldots , \sigma _k) \vDash \hat{P}\) and
holds iff \(\hat{P}\) and \(\hat{Q}\) are k-relational assertions, and for all \(\sigma _1, \ldots , \sigma _k, \sigma '_1, \ldots , \sigma '_k\), if \((\sigma _1, \ldots , \sigma _k) \vDash \hat{P}\) and  , then \((\sigma '_1, \ldots , \sigma '_k) \vDash \hat{Q}\).
, then \((\sigma '_1, \ldots , \sigma '_k) \vDash \hat{Q}\).
We write  for the most common case
for the most common case  .
.
4 Modular k-Product Programs
In this section, we define the construction of modular products for arbitrary k. We will subsequently define the transformation of both relational and unary specifications to modular products.
4.1 Product Construction
Assume as given a function \((\textsc {Var}, \mathbb {N}) \rightarrow \textsc {Var}\) that renames variables for different executions. We write  for the renaming of expression e for execution i and require that
for the renaming of expression e for execution i and require that  . We write \(fresh(x_1, x_2, \ldots )\) to denote that the variable names \(x_1, x_2, \ldots \) are fresh names that do not occur in the program and have not yet been used during the transformation. \(\mathring{e}\) is used to abbreviate
. We write \(fresh(x_1, x_2, \ldots )\) to denote that the variable names \(x_1, x_2, \ldots \) are fresh names that do not occur in the program and have not yet been used during the transformation. \(\mathring{e}\) is used to abbreviate  .
.
We denote the modular k-product of a statement s that is parameterized by the activation variables  as \(\llbracket s \rrbracket _{k}^{\mathring{p}}\). The product construction for procedures is defined as
as \(\llbracket s \rrbracket _{k}^{\mathring{p}}\). The product construction for procedures is defined as

Figure 4 shows the product construction rules for statements, which generalize the transformation explained in Sect. 2. We write \(\mathtt {if~} (e) \mathtt {~then~} \{s\}\) as a shorthand for \(\mathtt {if~} (e) \mathtt {~then~} \{s\} \mathtt {~else~} \{\mathtt {skip}\}\), and \(\bigodot _{i = 1}^{k} s_i\) for the sequential composition of k statements \(s_1;\ldots ;s_k\).
The core principle behind our encoding is that statements that directly change the state are duplicated for each execution and made conditional under the respective activation variables, whereas control statements are not duplicated and instead manipulate the activation variables to pass activation information to their sub-statements. This enables us to assert or assume relational assertions before and after any statement from the original program. The only state-changing statements in our language, variable assignments, are therefore transformed to a sequence of conditional assignments, one for each execution. Each assignment is executed only if the respective execution is currently active.
Duplicating conditionals would also duplicate the calls and loops in their branches. To avoid that, modular products eliminate top-level conditionals; instead, new activation variables are created and assigned the values of the current activation variables conjoined with the guard for each branch. The branches are then sequentially executed based on their respective activation variables.
A while loop is transformed to a single while loop in the product program that iterates as long as the loop guard is true for any active execution. Inside the loop, fresh activation variables indicate whether an execution reaches the loop and its loop condition is true. The loop body will then modify the state of an execution only if its activation variable is true. The resulting construct affects the program state in the same way as a self-composition of the original loop would, but the fact that our product contains only a single loop enables us to use relational loop invariants instead of full functional specifications.
For procedure calls, it is crucial that the product contains a single call for every call in the original program, in order to be able to apply relational specifications at the call site. As explained before, initial activation parameters are added to every procedure declaration, and all parameters are duplicated k times. Procedure calls are therefore transformed such that the values of the current activation variables are passed, and all arguments are passed once for each execution. The return values are stored in temporary variables and subsequently assigned to the actual target variables only for those executions that actually execute the call, so that for all other executions, the target variables are not affected.
The transformation wraps the call in a conditional so that the call is performed only if at least one execution is active. This prevents the transformation from introducing infinite recursion that is not present in the original program.
Note that for an inactive execution i, arbitrary argument values are passed in procedure calls, since the passed variables  are not initialized. This is unproblematic because these values will not be used by the procedure. It is important to not evaluate
are not initialized. This is unproblematic because these values will not be used by the procedure. It is important to not evaluate  for inactive executions, since this could lead to false alarms for languages where expression evaluation can fail.
for inactive executions, since this could lead to false alarms for languages where expression evaluation can fail.
4.2 Transformation of Assertions
We now define how to transform unary and relational assertions for use in a modular product.
Unary assertions such as ordinary procedure preconditions describe state properties that should hold for every single execution. When checking or assuming that a unary assertion holds at a specific point in the program, we need to take into account that it only makes sense to do so for executions that actually reach that program point. We can express this by making the assertion conditional on the activation variable of the respective execution; as a result, any unary assertion is trivially valid for all inactive executions.
A k-relational assertion, on the other hand, describes the relation between the states of all k executions. Checking or assuming a relational assertion at some point is meaningful only if all executions actually reach that point. This can be expressed by making relational assertions conditional on the conjunction of all current activation variables. If at least one execution does not reach the assertion, it holds trivially.
We formalize this idea by defining a function \(\alpha \) that maps relational assertions \(\hat{P}\) to unary assertions P of the product program such that  . Assertions can then be transformed for use in a k-product as follows:
. Assertions can then be transformed for use in a k-product as follows:
-
The transformation \(\lfloor \hat{P} \rfloor _{k}^{\mathring{p}}\) of a k-relational assertion \(\hat{P}\) with the activation variables
 is
is 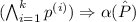 .
. -
The transformation \(\lfloor P \rfloor _{k}^{\mathring{p}}\) of a unary assertion P is
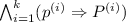 .
.
Importantly, our approach allows using mixed assertions and specifications, which represent conjunctions of unary and relational assertions. For example, it is common to combine a unary precondition that ensures that a procedure will not raise an error with a relational postcondition that states that it is deterministic.
A mixed assertion \(\check{R}\) of the form \(P \wedge \hat{Q}\) means that the unary assertion P holds for every single execution, and if all executions are currently active, the relational assertion \(\hat{Q}\) holds as well. The transformation of mixed assertions is straightforward: \(\lfloor \check{R} \rfloor _{k}^{\mathring{p}} = \lfloor P \rfloor _{k}^{\mathring{p}} \wedge \lfloor \hat{Q} \rfloor _{k}^{\mathring{p}}\).
4.3 Heap-Manipulating Programs
The approach outlined so far can easily be extended to programs that work on a mutable heap, assuming that object references are opaque, i.e., they cannot be inspected or used in arithmetic. In order to create a distinct state space for each execution represented in the product, allocation statements are duplicated and made conditional like assignments, and therefore create a different object for each active execution. The renaming of a field dereference e.f is then defined as  . As a result, the heap of a k-product will consist of k partitions that do not contain references to each other, and execution i will only ever interact with objects from its partition of the heap.
. As a result, the heap of a k-product will consist of k partitions that do not contain references to each other, and execution i will only ever interact with objects from its partition of the heap.
The verification of modular products of heap-manipulating programs does not depend on any specific way of achieving framing. Our implementation is based on implicit dynamic frames [25], but other approaches are feasible as well, provided that procedures can be specified in such a way that the caller knows the heap stays unmodified for all executions whose activation variables are false.
Since the handling of the heap is largely orthogonal to our main technique, we will not go into further detail here, but we do support heap-manipulating programs in our implementation.
5 Soundness and Completeness
A product construction is sound if an execution of a k-product mirrors k separate executions of the original program such that properties proved about the product entail hyperproperties of the original program. In this section, we sketch a soundness proof of our k-product construction in the presence of only unary procedure specifications. We also sketch a proof for relational specifications for the case \(k=2\), making use of the relational logic presented by Banerjee et al. [5]. Finally, we informally discuss the completeness of modular products.
5.1 Soundness with Unary Specifications
A modular k-product must soundly encode k executions of the original program. That is, if an encoded unary specification holds for a product program then the original specification holds for the original program.
We define a relation \(\sigma \simeq _{i} \sigma '\) that denotes that \(\sigma \) contains a renamed version of all variables in \(\sigma '\), i.e.,  . Without the index i, \( \simeq \) denotes the same but without renaming, and is used to express equality modulo newly introduced activation variables.
. Without the index i, \( \simeq \) denotes the same but without renaming, and is used to express equality modulo newly introduced activation variables.
Theorem 1
Assume that for all procedures m in a hypothesis context \(\varPhi \) we have that \(m : S \rightsquigarrow T \in dom(\varPhi )\) if and only if \(m : \lfloor S \rfloor _{k}^{\mathring{p}} \rightsquigarrow \lfloor T \rfloor _{k}^{\mathring{p}} \in dom(\varPhi ')\). Then \(\varPhi ' \vDash \llbracket s \rrbracket _{k}^{\mathring{p}} : \lfloor P \rfloor _{k}^{\mathring{p}} \rightsquigarrow \lfloor Q \rfloor _{k}^{\mathring{p}}\) implies that \(\varPhi \vDash s : P \rightsquigarrow Q\).
Proof
(Sketch). We sketch a proof based on the operational semantics of our language. We show that the execution of the product program with exactly one active execution corresponds to a single execution of the original program.
Assume that \(\varPhi ' \vDash \llbracket s \rrbracket _{k}^{\mathring{p}} : \lfloor P \rfloor _{k}^{\mathring{p}} \rightsquigarrow \lfloor Q \rfloor _{k}^{\mathring{p}}\), and that \(\sigma \vDash \lfloor P \rfloor _{k}^{\mathring{p}}\). If \(\llbracket s \rrbracket _{k}^{\mathring{p}}\) does not diverge when executed from \(\sigma \) we have that \(\langle \llbracket s \rrbracket _{k}^{\mathring{p}}, \sigma \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma ' \rangle \) and \(\sigma ' \vDash \lfloor Q \rfloor _{k}^{\mathring{p}}\). We now prove that a run of the product with all but one execution being inactive reflects the states that occur in a run of the original program. Assume that  and \(\langle s, \sigma _1 \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma '_1 \rangle \) and initially \(\sigma \simeq _{1} \sigma _1\), which implies \(\sigma _1 \vDash P\). We prove by induction on the derivation of \(\langle s, \sigma _1 \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma '_1 \rangle \) that \(\langle \llbracket s \rrbracket _{k}^{\mathring{p}}, \sigma \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma ' \rangle \) and \(\sigma ' \simeq _{1} \sigma '_1\), meaning that the product execution terminates, and subsequently by induction on the derivation of \(\langle \llbracket s \rrbracket _{k}^{\mathring{p}}, \sigma \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma ' \rangle \) that \(\sigma ' \simeq _{1} \sigma '_1\), from which we can derive that \(\sigma '_1 \vDash Q\). \(\square \)
and \(\langle s, \sigma _1 \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma '_1 \rangle \) and initially \(\sigma \simeq _{1} \sigma _1\), which implies \(\sigma _1 \vDash P\). We prove by induction on the derivation of \(\langle s, \sigma _1 \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma '_1 \rangle \) that \(\langle \llbracket s \rrbracket _{k}^{\mathring{p}}, \sigma \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma ' \rangle \) and \(\sigma ' \simeq _{1} \sigma '_1\), meaning that the product execution terminates, and subsequently by induction on the derivation of \(\langle \llbracket s \rrbracket _{k}^{\mathring{p}}, \sigma \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma ' \rangle \) that \(\sigma ' \simeq _{1} \sigma '_1\), from which we can derive that \(\sigma '_1 \vDash Q\). \(\square \)
5.2 Soundness for Relational Specifications
The main advantage of modular product programs over other kinds of product programs is that it allows reasoning about procedure calls in terms of relational specifications. We therefore need to show the soundness of our approach in the presence of procedures with such specifications. In particular, we must establish that if a transformed relational specification holds for a modular product then the original relational specification will hold for a set of k executions of the original program.
Our proof sketch is phrased in terms of biprograms as introduced by Banerjee et al. [5]. Biprogram executions correspond to two partly aligned executions of their two underlying programs. A biprogram ss can have the form \((s_1|s_2)\) or \(\Vert s \Vert \); the former represents the two executions of \(s_1\) and \(s_2\), whereas the latter represents an aligned execution of s by both executions, which enables using relational specifications for procedure callsFootnote 3. We denote the small-step transition relation between biprogram configurations as \(\langle ss, \sigma _1|\sigma _2 \rangle \Rrightarrow ^{*} \langle ss', \sigma '_1|\sigma '_2 \rangle \). We make use of a relation \(\sigma \approxeq \sigma _1|\sigma _2\) that denotes that \(\sigma \) contains renamed versions of all variables in both \(\sigma _1\) and \(\sigma _2\) with the same values.
Biprograms do not allow mixed procedure specifications, meaning that a procedure can either have only a unary specification, or it can have only a relational specification, in which case it can only be invoked by both executions simultaneously. As mentioned before, our approach does not have this limitation, but we can artificially enforce it for the purposes of the soundness proof.
We can now state our theorem. Since biprograms represent the execution of two programs, we formulate soundness for \(k=2\) here.
Theorem 2
Assume that hypothesis context \(\varPhi \) maps procedure names to relational specifications if all calls to the procedure in s can be aligned from any pair of states satisfying \(\hat{P}\), and to unary specifications otherwise. Assume further that hypothesis context \(\varPhi '\) maps the same procedure names to their transformed specifications. Finally, assume that \(\varPhi ' \vdash \llbracket s \rrbracket _{2}^{\mathring{p}} : \lfloor \hat{P} \rfloor _{2}^{\mathring{p}} \rightsquigarrow \lfloor \hat{Q} \rfloor _{2}^{\mathring{p}}\) and \((\sigma _1, \sigma _2) \vDash \hat{P}\). If \(\langle s, \sigma _1 \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma '_1 \rangle \) and \(\langle s, \sigma _2 \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma '_2 \rangle \), then \((\sigma '_1, \sigma '_2) \vDash \hat{Q}\).
Proof
(Sketch). The proof follows the same basic outline as the one for Theorem 1 but reasons about the operational semantics of biprograms representing two executions of s.
Assume that \(\varPhi ' \vdash \llbracket s \rrbracket _{2}^{\mathring{p}} : \lfloor \hat{P} \rfloor _{2}^{\mathring{p}} \rightsquigarrow \lfloor \hat{Q} \rfloor _{2}^{\mathring{p}}\) and \(\sigma \vDash \lfloor \hat{P} \rfloor _{2}^{\mathring{p}}\). If \(\llbracket s \rrbracket _{2}^{\mathring{p}}\) does not diverge when executed from \(\sigma \) we get that \(\langle \llbracket s \rrbracket _{2}^{\mathring{p}}, \sigma \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma ' \rangle \) and \(\sigma ' \vDash \lfloor \hat{Q} \rfloor _{2}^{\mathring{p}}\). Assume that initially \(\sigma \approxeq \sigma _1|\sigma _2\), which implies that \((\sigma _1, \sigma _2) \vDash \hat{P}\). We prove by induction on the derivation of \(\langle \llbracket s \rrbracket _{2}^{\mathring{p}}, \sigma \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma ' \rangle \) that (1) if  , then there exists ss that represents two executions of s s.t. \(\langle ss, \sigma _1|\sigma _2 \rangle \Rrightarrow ^{*} \langle \Vert \mathtt {skip} \Vert , \sigma '_1|\sigma '_2 \rangle \) and \(\sigma ' \approxeq \sigma '_1|\sigma '_2\); (2) if
, then there exists ss that represents two executions of s s.t. \(\langle ss, \sigma _1|\sigma _2 \rangle \Rrightarrow ^{*} \langle \Vert \mathtt {skip} \Vert , \sigma '_1|\sigma '_2 \rangle \) and \(\sigma ' \approxeq \sigma '_1|\sigma '_2\); (2) if  , then \(\langle s, \sigma _1 \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma '_1 \rangle \) and \(\sigma ' \approxeq \sigma '_1|\sigma _2\); (3) if
, then \(\langle s, \sigma _1 \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma '_1 \rangle \) and \(\sigma ' \approxeq \sigma '_1|\sigma _2\); (3) if  , then \(\langle s, \sigma _2 \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma '_2 \rangle \) and \(\sigma ' \approxeq \sigma _1|\sigma '_2\); (4) if
, then \(\langle s, \sigma _2 \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma '_2 \rangle \) and \(\sigma ' \approxeq \sigma _1|\sigma '_2\); (4) if  , then \(\sigma \simeq \sigma '\). From the first point and semantic consistency of the relational logic, we can conclude that \((\sigma '_1, \sigma '_2) \vDash \hat{Q}\). Finally, we prove that \(\langle \llbracket s \rrbracket _{2}^{\mathring{p}}, \sigma \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma ' \rangle \) by showing that non-termination of the product implies the non-termination of at least one of the two original program runs. If the condition of a loop in the product remains true forever, the loop condition of at least one encoded execution must be true after every iteration. We show that (1) this is not due to an interaction of multiple executions, since the condition for every execution will remain false if it becomes false once, and (2) since the encoded states of active executions progress as they do in the original program, the condition of a single execution in the product remains true forever only if it does in the original program. A similar argument shows that the product cannot diverge because of infinite recursive calls. \(\square \)
, then \(\sigma \simeq \sigma '\). From the first point and semantic consistency of the relational logic, we can conclude that \((\sigma '_1, \sigma '_2) \vDash \hat{Q}\). Finally, we prove that \(\langle \llbracket s \rrbracket _{2}^{\mathring{p}}, \sigma \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma ' \rangle \) by showing that non-termination of the product implies the non-termination of at least one of the two original program runs. If the condition of a loop in the product remains true forever, the loop condition of at least one encoded execution must be true after every iteration. We show that (1) this is not due to an interaction of multiple executions, since the condition for every execution will remain false if it becomes false once, and (2) since the encoded states of active executions progress as they do in the original program, the condition of a single execution in the product remains true forever only if it does in the original program. A similar argument shows that the product cannot diverge because of infinite recursive calls. \(\square \)
5.3 Completeness
We believe modular product programs to be complete, meaning that any hyperproperty of multiple executions of a program can be proved about its modular product program. Since the product faithfully models the executions of the original program, the completeness of modular products is potentially limited only by the underlying verification logic and the assertion language, but not by the product construction itself.
6 Modular Verification of Secure Information Flow
In this section, we demonstrate the expressiveness of modular product programs by showing how they can be used to verify an important hyperproperty, information flow security. We first concentrate on secure information flow in the classical sense [9], and later demonstrate how the ability to check relational assertions at any point in the program can be exploited to prove advanced properties like the absence of timing and termination channels, and to encode declassification.
6.1 Non-interference
Secure information flow, i.e., the property that secret information is not leaked to the public outputs of a program, can be expressed as a relational 2-safety property of a program called non-interference. Non-interference states that, if a program is run twice, with the public (often called low) inputs being equal in both runs but the secret (or high) inputs possibly being different, the public outputs of the program must be equal in both runs [8]. This property guarantees that the high inputs do not influence the low outputs.
We can formalize non-interference as follows:
Definition 2
A statement s that operates on a set of variables \(X = \{x_1, \ldots , x_n\}\), of which some subset \(X_l \subseteq X\) is low, satisfies non-interference iff for all \(\sigma _1, \sigma _2\) and \(\sigma '_1, \sigma '_2\), if  and \(\langle s, \sigma _1 \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma '_1 \rangle \) and \(\langle s, \sigma _2 \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma '_2 \rangle \) then \(\forall x \in X_l . \sigma '_1(x) = \sigma '_2(x)\).
and \(\langle s, \sigma _1 \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma '_1 \rangle \) and \(\langle s, \sigma _2 \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma '_2 \rangle \) then \(\forall x \in X_l . \sigma '_1(x) = \sigma '_2(x)\).
Since our definition of non-interference describes a hyperproperty, we can verify it using modular product programs:
Theorem 3
A statement s that operates on a set of variables \(X = \{x_1, \ldots , x_n\}\), of which some subset \(X_l \subseteq X\) is low, satisfies non-interference under a unary precondition P if 
Proof
(Sketch). Since non-interference can be expressed using a 2-relational specification, the theorem follows directly from Theorem 2. \(\square \)
For non-deterministic programs whose behavior can be modelled by adding input parameters representing the non-deterministic choices, those parameters can be considered low if the choice is not influenced in any way by secret data.
An expanded notion of secure information flow considers observable events in addition to regular program outputs [17]. An event is a statement that has an effect that is visible to an outside observer, but may not necessarily affect the program state. The most important examples of events are output operations like printing a string to the console or sending a message over a network. Programs that cause events can be considered information flow secure only if the sequence of produced events is not influenced by high data. One way to verify this using our approach is to track the sequence of produced events in a ghost variable and verify that its value never depends on high data. This approach requires substantial amounts of additional specifications.
Modular product programs offer an alternative approach for preventing leaks via events, since they allow formulating assertions about the relation between the activation variables of different executions. In particular, if a given event has the precondition that all activation variables are equal when the event statement is reached then this event will either be executed by both executions or be skipped by both executions. As a result, the sequence of events produced by a program will be equal in all executions.
6.2 Information Flow Specifications
The relational specifications required for modularly proving non-interference with the previously described approach have a specific pattern: they can contain functional specifications meant to be valid for both executions (e.g., to make sure both executions run without errors), they may require that some information is low, which is equivalent to the two renamings of the same expression being equal, and, in addition, they may assert that the control flow at a specific program point is low.
We therefore introduce modular information flow specifications, which can express all properties required for proving secure information flow but are transparent w.r.t. the encoding or the verification methodology, i.e., they allow expressing that a given operation or value must not be secret without knowledge of the encoding of this fact into an assertion about two different program executions. We define information flow specifications as follows:

\(\textit{low}(e)\) and \(\textit{lowEvent}\) may be used on the left side of an implication only if the right side has the same form. \(\textit{low}(e)\) specifies that the value of the expression e is not influenced by high data. Note that e can be any expression and is not limited to variable references; this reflects the fact that our approach can label secrecy in a more fine-grained way than, e.g., a type system. One can, for example, declare to be public whether a number is odd while keeping its value secret.
\(\textit{lowEvent}\) specifies that high data must not influence if and how often the current program point is reached by an execution, which is a sufficient precondition of any statement that causes an observable event. In particular, if a procedure outputs an expression e, the precondition \(\textit{lowEvent}\wedge \textit{low}(e)\) guarantees that no high information will be leaked via this procedure.
Information flow specifications can express complex properties. \(e_1 \Rightarrow \textit{low}(e_2)\), for example, expresses that if \(e_1\) is true, \(e_2\) must not depend on high data; \(e_1 \Rightarrow \textit{lowEvent}\) says the same about the current control flow. A possible use case for these assertions is the precondition of a library function that prints \(e_2\) to a low-observable channel if \(e_1\) is true, and to a secure channel otherwise.
The encoding \(\lceil \tilde{P} \rceil ^{\mathring{p}}\) of an information flow assertion \(\tilde{P}\) under the activation variables  and
and  is defined in Fig. 5. Note that high-ness of some expression is not modelled by its renamings being definitely unequal, but by leaving underspecified whether they are equal or not, meaning that high-ness is simply the absence of the knowledge of low-ness. As a result, it is never necessary to specify explicitly that an expression is high. This approach (which is also used in self-composition) is analogous to the way type systems encode security levels, where low is typically a subtype of high. For the example in Fig. 1, a possible, very precise information flow specification could say that the results of
is defined in Fig. 5. Note that high-ness of some expression is not modelled by its renamings being definitely unequal, but by leaving underspecified whether they are equal or not, meaning that high-ness is simply the absence of the knowledge of low-ness. As a result, it is never necessary to specify explicitly that an expression is high. This approach (which is also used in self-composition) is analogous to the way type systems encode security levels, where low is typically a subtype of high. For the example in Fig. 1, a possible, very precise information flow specification could say that the results of  are low if the first bit of all entries in
are low if the first bit of all entries in  is low. We can write this as
is low. We can write this as  . In the product, this will be translated to
. In the product, this will be translated to  .
.
In this scenario, the loop in  could have the simple invariant
could have the simple invariant  , and the procedure
, and the procedure  could have the contract
could have the contract  . This contract follows a useful pattern where, instead of requiring an input to be low and promising that an output will be low for all calls, the output is decribed as conditionally low based on the level of the input, which is more permissive for callers.
. This contract follows a useful pattern where, instead of requiring an input to be low and promising that an output will be low for all calls, the output is decribed as conditionally low based on the level of the input, which is more permissive for callers.
The example shows that the information relevant for proving secure information flow can be expressed concisely, without requiring any knowledge about the methodology used for verification. Modular product programs therefore enable the verification of the information flow security of  based solely on modular, relational specifications, and without depending on functional specifications.
based solely on modular, relational specifications, and without depending on functional specifications.
6.3 Secure Information Flow with Arbitrary Security Lattices
The definition of secure information flow used in Definition 2 is a special case in which there are exactly two possible classifications of data, high and low. In the more general case, classifications come from an arbitrary lattice \(\langle \mathcal {L}, \sqsubseteq \rangle \) of security levels s.t. for some \(l_1, l_2 \in \mathcal {L}\), information from an input with level \(l_1\) may influence an output with level \(l_2\) only if \(l_1 \sqsubseteq l_2\). Instead of the specification \(\textit{low}(e)\), information flow assertions can therefore have the form \(levelBelow(e, l)\), meaning that the security level of expression e is at most l.
It is well-known that techniques for verifying information flow security with two levels can conceptually be used to verify programs with arbitrary finite security lattices [23] by splitting the verification task into \(|\mathcal {L}|\) different verification tasks, one for each element of \(\mathcal {L}\). Instead, we propose to combine all these verification tasks into a single task by using a symbolic value for l, i.e., declaring an unconstrained global constant representing l. Specifications can then be translated as follows:

Since no information about l is known, verification will only succeed if all assertions can be proven for all possible values of l, which is equivalent to proving them separately for each possible value of l.
6.4 Declassification
In practice, non-interference is too strong a property for many use cases. Often, some leakage of secret data is required for a program to work correctly. Consider the case of a password check (see Fig. 6): A secret internal password is compared to a non-secret user input. While the password itself must not be leaked, the information whether the user input matches the password should influence the public outcome of the program, which is forbidden by non-interference.
To incorporate this intention, the relevant part of the secret information can be declassified [24], e.g., via a declassification statement \(\mathtt {declassify~}e\) that declares an arbitrary expression e to be low. With modular products, declassification can be encoded via a simple assumption stating that, if the declassification is executed in both executions, the expression is equal in both executions:

Introducing an assumption of this form is sound if the information flow specifications from Sect. 6.2 are used to specify the program. Since high-ness is encoded as the absence of the knowledge that an expression is equal in both executions, not by the knowledge that they are different, there is no danger that assuming equality will contradict current knowledge and thereby cause unsoundness. As in the information flow specifications, the declassified expression can be arbitrarily complex, so that it is for example possible to declassify the sign of an integer while keeping all other information about it secret.
The example in Fig. 6 becomes valid if we add  at the end of the procedure, or if we declassify a more complex expression by adding
at the end of the procedure, or if we declassify a more complex expression by adding  at some earlier point. The latter would arguably be safer because it specifies exactly the information that is intended to be leaked, and would therefore prevent accidentally leaking more if the implementation of the checking loop was faulty.
at some earlier point. The latter would arguably be safer because it specifies exactly the information that is intended to be leaked, and would therefore prevent accidentally leaking more if the implementation of the checking loop was faulty.
This kind of declassification has the following interesting properties: First, it is imperative, meaning that the declassified information may be leaked (e.g., via a  statement) after the execution of the declassification statement, but not before. Second, it is semantic, meaning that the declassification affects the value of the declassified expression as opposed to, e.g., syntactically the declassified variable. As a result, it will be allowed to leak any expression whose value contains the same (or a part of the) secret information which was declassified, e.g., the expression f(e) if f is a deterministic function and e has been declassified.
statement) after the execution of the declassification statement, but not before. Second, it is semantic, meaning that the declassification affects the value of the declassified expression as opposed to, e.g., syntactically the declassified variable. As a result, it will be allowed to leak any expression whose value contains the same (or a part of the) secret information which was declassified, e.g., the expression f(e) if f is a deterministic function and e has been declassified.
6.5 Preventing Termination Channels
In Definition 2, we have considered only terminating program executions. In practice, however, termination is a possible side-channel that can leak secret information to an outside observer. Figure 7 (left) shows an example of a program that verifies under the methodology presented so far, but leaks information about the secret input  to an observer: If
to an observer: If  is initially negative, the program will enter an endless loop. Anyone who can observe the termination behavior of the program can therefore conclude if
is initially negative, the program will enter an endless loop. Anyone who can observe the termination behavior of the program can therefore conclude if  was negative or not.
was negative or not.
To prevent leaking information via a termination side channel, it is necessary to verify that the termination of a program depends only on public data. We will show that modular product programs are expressive enough to encode and check this property. We will focus on preventing non-termination caused by infinite loops here; preventing infinite recursion works analogously. In particular, we want to prove that if a loop iterates forever in one execution, any other execution with the same low inputs will also reach this loop and iterate forever. More precisely, this means that
-
(A)
if a loop does not terminate, then whether or not an execution reaches that loop must not depend on high data.
-
(B)
whether a loop that is reached by both executions terminates must not depend on high data.
We propose to verify these properties by requiring additional specifications that state, for every loop, an exact condition under which it terminates. This condition may neither over- nor underapproximate the termination behavior; the loop must terminate if and only if the condition is true. For Fig. 7 (left) the condition is \(h \ge 0\). We also require a ranking function for the cases when the termination condition is true. We can then prove the following:
-
(a)
If the termination condition of a loop evaluates to false, then any two executions with identical low inputs either both reach the loop or both do not reach the loop (i.e., reaching the loop is a low event). This guarantees property (A) above.
-
(b)
For loops executed by both executions, the loop’s termination condition is low. This guarantees property (B) under the assumption that the termination condition is exact.
-
(c)
The termination condition is sound, i.e., every loop terminates if its termination condition is true. We prove this by showing that if the termination condition is true, we can prove the termination of the loop using the supplied ranking function.
-
(d)
The termination condition is complete, i.e., every loop terminates only if its termination condition is true. We prove this by showing that if the condition is false, the loop condition will always remain true. This check, along with the previous proof obligation, ensures that the termination condition is exact.
-
(e)
Every statement in a loop body terminates if the loop’s termination condition is true, i.e., the loop’s termination condition implies the termination conditions of all statements in its body.
We introduce an annotated while loop \(\mathtt {while~} (e) \mathtt {~terminates}(e_c, e_r) \mathtt {~do~} \{s\}\), where \(e_c\) is the exact termination condition and \(e_r\) is the ranking function, i.e., an integer expression whose value decreases with every loop iteration but never becomes negative if the termination condition is true. Based on these annotations, we present a program instrumentation \(\textit{term}\mathrm{\,\,(}{s},{c}\mathrm{)}\) that inserts the checks outlined above for every while loop in s. c is the termination condition of the outside scope, i.e., for the instrumentation of a nested loop, it is the termination condition \(e_c\) of the outer loop. The instrumentation is defined for annotated while loops in Fig. 8; for all other statements, it does not make any changes except instrumenting all substatements. The instrumentation uses information flow assertions as defined in Sect. 6.2. Again, we make use of the fact that modular products allow checking relational assertions at arbitrary program points and formulating assertions about the control flow.
We now prove that if an instrumented statement verifies under some 2-relational precondition then any two runs from a pair of states fulfilling that precondition will either both terminate or both loop forever.
Theorem 4
If \(s' = \textit{term}\mathrm{(}{s},{\textit{false}}\mathrm{)}\), and \(\llbracket s' \rrbracket _{2}^{\mathring{p}}\) verifies under some precondition \(P = \lfloor \hat{P} \rfloor _{2}^{\mathring{p}}\), and for some \(\sigma _1, \sigma _2, \sigma '_1\), \((\sigma _1, \sigma _2) \vDash \hat{P}\) and \(\langle s, \sigma _1 \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma '_1 \rangle \), then there exists some \(\sigma '_2\) s.t. \(\langle s, \sigma _2 \rangle \rightarrow ^{*} \langle \mathtt {skip}, \sigma '_2 \rangle \).
Proof
(Sketch). We first establish that our instrumentation ensures that each statement terminates (1) if and (2) only if its termination condition is true, (1) by showing equivalence to a standard termination proof, and (2) by a contradiction if a loop which should not terminate does. Since the execution from \(\sigma _1\) terminates, by the second condition, its termination condition must have been true before the loop. We case split on whether the other execution also reaches the loop or not. If it does then the termination condition before the loop is identical in both executions, so by the first condition, the other execution also terminates. If it does not then the loop is not executed at all by the other execution, and therefore cannot cause non-termination. \(\square \)
6.6 Preventing Timing Channels
A program has a timing channel if high input data influences the program’s execution time, meaning that an attacker who can observe the time the program executes can gain information about those secrets. Timing channels can occur in combination with observable events; the time at which an event occurs may depend on a secret even if the overall execution time of a program does not.
Consider the example in Fig. 7 (right). Assuming  receives a positive secret
receives a positive secret  , both the
, both the  statement and the end of the program execution will be reached later for larger values of
statement and the end of the program execution will be reached later for larger values of  .
.
Using modular product programs, we can verify the absence of timing side channels by adding ghost state to the program that tracks the time passed since the program has started; this could, for example, be achieved via a simple step counting mechanism, or by tracking the sequence of previously executed bytecode statements. This ghost state is updated separately for both executions. We can then assert anywhere in the program that the passed time does not depend on high data in the same way we do for program variables. In particular, we can enforce that the passed time is equal whenever an observable event occurs, and we can enable users to write relational specifications that compare the time passed in both executions of a loop or a procedure.
7 Implementation and Evaluation
We have implemented our approach for secure information flow in the Viper verification infrastructure [22] and applied it to a number of example programs from the literature. Both the implementation and examples are available at http://viper.ethz.ch/modularproducts/.
7.1 Implementation in Viper
Our implementation supports a version of the Viper language that adds the following features:
-
1.
The assertions \(\textit{low}(e)\) and \(\textit{lowEvent}\) for information flow specifications
-
2.
A
 statement
statement -
3.
Variations of the existing method declarations and while loops that include the termination annotations shown in Sect. 6.5
The implementation transforms a program in this extended language into a modular 2-product in the original language, which can then be verified by the (unmodified) Viper back-end verifiers. All specifications are provided as information flow specifications (see Sect. 6.2) such that users require no knowledge about the transformation or the methodology behind information flow verification. Error messages are automatically translated back to the original program.
Declassification is implemented as described in Sect. 6.4. Our implementation optionally verifies the absence of timing channels; the metric chosen for tracking execution time is simple step-counting. Viper uses implicit dynamic frames [25] to reason about heap-manipulating programs; our implementation uses quantified permissions [21] to support unbounded heap data structures.
For languages with opaque object references, secure information flow can require that pointers are low, i.e., equal up to a consistent renaming of addresses. Therefore, our approach to duplicating the heap state space in the implementation differs from that described in Sect. 4.3: Instead of duplicating objects, our implementation creates a single  statement for every
statement for every  in the original program, but duplicates the fields each object has. As a result, if both executions execute the same
in the original program, but duplicates the fields each object has. As a result, if both executions execute the same  statement, the newly created object will be considered low afterwards (but the values of its fields might still be high).
statement, the newly created object will be considered low afterwards (but the values of its fields might still be high).
7.2 Qualitative Evaluation
We have evaluated our implementation by verifying a number of examples in the extended Viper language. The examples are listed in Table 1 and include all code snippets shown in this paper as well as a number of examples from the literature [2, 3, 6, 13, 14, 17, 18, 23, 26, 28]. They combine complex language features like mutable state on the heap, arrays and procedure calls, as well as timing and termination channels, declassification, and non-trivial information flows (e.g., flows whose legality depends on semantic information not available in a standard information flow type system). We manually added pre- and postconditions as well as loop invariants; for those that have forbidden flows and therefore should not verify, we also added a legal version that declassifies the leaked information. Our implementation returns the correct result for all examples.
In all cases but one, our approach allows us to express all information flow related assertions, i.e., procedure specifications and loop invariants, purely as relational specifications in terms of \(\textit{low}\)-assertions (see Table 1). For all these examples, we completely avoid the need to specify the functional behavior of the program. Unlike the original product program paper [6], we also do not inline any procedure calls; verification is completely modular.
The only exception is an example that, depending on a high input, executes different loops with identical behavior, and for which we need to prove that the execution time is low. In this case we have to provide invariants for both loops that exactly specify their execution time in order to prove that the overall execution time after the conditional is low. Nevertheless, the specification of the procedure containing the loop is again expressed with a relational specification using only \(\textit{low}\). For all other examples, unary specifications were only needed to verify the absence of runtime errors (e.g., out-of-bounds array accesses), which Viper verifies by default. Consequently, a verified program cannot leak low data through such errors, which is typically not guaranteed by type systems or static analyses.
7.3 Performance
For all but one example, the runtime (averaged over 10 runs on a Lenovo ThinkPad T450s running Ubuntu) with both the Symbolic Execution (SE) and the Verification Condition Generation (VCG) verifiers is under or around one second (see Table 1). The one exception, which makes extensive use of unbounded heap data structures, takes ca. five seconds when verified using VCG, and 15 in the SE verifier. This is likely a result of inefficiencies in our encoding: The created product has a high number of branching statements, and some properties have to be proved more than once, two issues which have a much larger performance impact for SE than for VCG. We believe that it is feasible to remove much of this overhead by optimizing the encoding; we leave this as future work.
8 Related Work
The notion of k-safety hyperproperties was originally introduced by Clarkson and Schneider [12]. Here, we focus on statically proving hyperproperties for imperative and object-oriented programs; much more work exists for testing or monitoring hyperproperties like secure information flow at runtime, or for reasoning about hyperproperties in different programming paradigms.
Relational logics such as Relational Hoare Logic [11], Relational Separation Logic [29] and others [1, 10] allow reasoning directly about relational properties of two different program executions. Unlike our approach, they usually allow reasoning about the executions of two different programs; as a result, they do not give special support for two executions of the same program calling the same procedure with a relational specification. Recently, Banerjee et al. [5] introduced biprograms, which allow explicitly expressing alignment between executions and using relational specifications to reason about aligned calls; however, this approach requires that procedures with relational specifications are always called by both executions, which is for instance not the case if a call occurs under a high guard in secure information flow verification. We handle such cases by interpreting relational specifications as trivially true; one can then still resort to functional specifications to complete the proof. Their work also does not allow mixed specifications, which are easily supported in our product programs. Relational program logics are generally difficult to automate. Recent work by Sousa and Dillig [27] presents a logic that can be applied automatically by an algorithm that implicitly constructs different product programs that align some identical statements, but does not fully support relational specifications. Moreover, their approach requires dedicated tool support, whereas our modular product programs can be verified using off-the-shelf tools.
The approach of reducing hyperproperties to ordinary trace properties was introduced by self-composition [9]. While self-composition is theoretically complete, it does not allow modular reasoning with relational specifications. The resulting problem of having to fully specify program behavior was pointed out by Terauchi and Aiken [28]; since then, there have been a number of different attempts to solve this problem by allowing (parts of) programs to execute in lock-step. Terauchi and Aiken [28] did this for secure information flow by relying on information from a type system; other similar approaches exist [23].
Product programs [6, 7] allow different interleavings of program executions. The initial product program approach [6] would in principle allow the use of relational specifications for procedure calls, but only under the restriction that both program executions always follow the same control flow. The generalized approach [7] allows combining different programs and arbitrary numbers of executions. This product construction is non-deterministic and usually interactive. In some (but not all) cases, programmers can manually construct product programs that avoid duplicated calls and loops and thereby allow using relational specifications. However, whether this is possible depends on the used specification, meaning that the product construction and verification are intertwined and a new product has to be constructed when specifications change. In contrast, our new product construction is fully deterministic and automatic, allows arbitrary control flows while still being able to use relational specifications for all loops and calls, and therefore avoids the issue of requiring full functional specifications.
Considerable work has been invested into proving specific hyperproperties like secure information flow. One popular approach is the use of type systems [26]; while those are modular and offer good performance, they overapproximate possible program behaviors and are therefore less precise than approaches using logics. In particular, they require labeling any single value as either high or low, and do not allow distinctions like the one we made for the example in Fig. 1, where only the first bits of a sequence of integers were low. In addition, type systems typically struggle to prevent information leaks via side channels like termination or program aborts. There have been attempts to create type systems that handle some of these limitations (e.g. [15]).
Static analyses [2, 17] enable fully automatic reasoning. They are typically not modular and, similarly to type systems, need to abstract semantic information, which can lead to false positives. They strike a trade-off different from our solution, which requires specifications, but enables precise, modular reasoning.
A number of logic-based approaches to proving specific hyperproperties exist. As an example, Darvas et al. use dynamic logic for proving non-interference [14]; this approach offers some automation, but requires user interaction for most realistic programs. Leino et al. [19] verify determinism up to equivalence using self-composition, which suffers from the drawbacks explained above.
Different kinds of declassification have been studied extensively, Sabelfeld and Sands [24] provide a good overview. Li and Zdancewic [20] introduce downgrading policies that describe which information can be declassified and, similar to our approach, can do so for arbitrary expressions.
9 Conclusion and Future Work
We have presented modular product programs, a novel form of product programs that enable modular reasoning about k-safety hyperproperties using relational specifications with off-the-shelf verifiers. We showed that modular products are expressive enough to handle advanced aspects of secure information flow verification. They can prove the absence of termination and timing side channels and encode declassification. Our implementation shows that our technique works in practice on a number of challenging examples from the literature, and exhibits good performance even without optimizations.
For future work, we plan to infer relational properties by using standard program analysis techniques on the products. We also plan to generalize our technique to prove probabilistic secure information flow for concurrent program by combining our encoding with ideas from concurrent separation logic. Finally, we plan to optimize our encoding to further improve performance.
Notes
- 1.
The information stored in activation variables is similar to a path condition in symbolic execution, which is also updated every time a branch is taken. However, they differ for loops and calls.
- 2.
Our handling of procedure calls is slightly different, but amounts to restricting procedures to work only on local variables not used in the rest of the program (as opposed to having a global state on which all procedures work directly), and only interacting with the rest of the program via explicitly declared return parameters.
- 3.
We modified the original notation to avoid clashes with our own concepts introduced earlier.
References
Aguirre, A., Barthe, G., Gaboardi, M., Garg, D., Strub, P.: A relational logic for higher-order programs. PACMPL 1(ICFP), 21:1–21:29 (2017)
Antonopoulos, T., Gazzillo, P., Hicks, M., Koskinen, E., Terauchi, T., Wei, S.: Decomposition instead of self-composition for proving the absence of timing channels. In: Proceedings of the 38th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2017, Barcelona, Spain, 18–23 June 2017, pp. 362–375 (2017)
Banerjee, A., Naumann, D.A., Secure information flow and pointer confinement in a java-like language. In: 15th IEEE Computer Security Foundations Workshop (CSFW-15 2002), 24–26 June 2002, Cape Breton, Nova Scotia, Canada, p. 253 (2002)
Banerjee, A., Naumann, D.A.: A logical analysis of framing for specifications with pure method calls. In: Giannakopoulou, D., Kroening, D. (eds.) VSTTE 2014. LNCS, vol. 8471, pp. 3–20. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-12154-3_1
Banerjee, A., Naumann, D.A., Nikouei, M.: Relational logic with framing and hypotheses. In: 36th IARCS Annual Conference on Foundations of Software Technology and Theoretical Computer Science, FSTTCS 2016, Chennai, India, 13–15 December 2016, pp. 11:1–11:16 (2016)
Barthe, G., Crespo, J.M., Kunz, C.: Relational verification using product programs. In: Butler, M., Schulte, W. (eds.) FM 2011. LNCS, vol. 6664, pp. 200–214. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21437-0_17
Barthe, G., Crespo, J.M., Kunz, C.: Beyond 2-safety: asymmetric product programs for relational program verification. In: Artemov, S., Nerode, A. (eds.) LFCS 2013. LNCS, vol. 7734, pp. 29–43. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-35722-0_3
Barthe, G., D’Argenio, P.R., Rezk, T.: Secure information flow by self-composition. In: 17th IEEE Computer Security Foundations Workshop, (CSFW-17 2004), 28–30 June 2004, Pacific Grove, CA, USA, pp. 100–114 (2004)
Barthe, G., D’Argenio, P.R., Rezk, T.: Secure information flow by self-composition. Math. Struct. Comput. Sci. 21(6), 1207–1252 (2011)
Barthe, G., Grégoire, B., Béguelin, S.Z.: Formal certification of code-based cryptographic proofs. In: Proceedings of the 36th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2009, Savannah, GA, USA, 21–23 January 2009, pp. 90–101 (2009)
Benton, N.: Simple relational correctness proofs for static analyses and program transformations. In: Proceedings of the 31st ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2004, Venice, Italy, 14–16 January 2004, pp. 14–25 (2004)
Clarkson, M.R., Schneider, F.B.: Hyperproperties. J. Comput. Secur. 18(6), 1157–1210 (2010)
Costanzo, D., Shao, Z.: A separation logic for enforcing declarative information flow control policies. In: Abadi, M., Kremer, S. (eds.) POST 2014. LNCS, vol. 8414, pp. 179–198. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54792-8_10
Darvas, Á., Hähnle, R., Sands, D.: A theorem proving approach to analysis of secure information flow. In: Hutter, D., Ullmann, M. (eds.) SPC 2005. LNCS, vol. 3450, pp. 193–209. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-32004-3_20
Deng, Z., Smith, G.: Lenient array operations for practical secure information flow. In: 17th IEEE Computer Security Foundations Workshop, (CSFW-17 2004), 28–30 June 2004, Pacific Grove, CA, USA, p. 115 (2004)
Francez, N.: Fairness. Springer-Verlag, New York Inc., New York (1986). https://doi.org/10.1007/978-1-4612-4886-6
Giffhorn, D., Snelting, G.: A new algorithm for low-deterministic security. Int. J. Inf. Sec. 14(3), 263–287 (2015)
Küsters, R., Truderung, T., Beckert, B., Bruns, D., Kirsten, M., Mohr, M.: A hybrid approach for proving noninterference of java programs. In: IEEE 28th Computer Security Foundations Symposium, CSF 2015, Verona, Italy, 13–17 July 2015, pp. 305–319 (2015)
Leino, K.R.M., Müller, P.: Verification of equivalent-results methods. In: Drossopoulou, S. (ed.) ESOP 2008. LNCS, vol. 4960, pp. 307–321. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78739-6_24
Li, P., Zdancewic, S.: Downgrading policies and relaxed noninterference. In: Proceedings of the 32nd ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2005, Long Beach, California, USA, 12–14 January 2005, pp. 158–170 (2005)
Müller, P., Schwerhoff, M., Summers, A.J.: Automatic verification of iterated separating conjunctions using symbolic execution. In: Chaudhuri, S., Farzan, A. (eds.) CAV 2016, Part I. LNCS, vol. 9779, pp. 405–425. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-41528-4_22
Müller, P., Schwerhoff, M., Summers, A.J.: Viper: a verification infrastructure for permission-based reasoning. In: Jobstmann, B., Leino, K.R.M. (eds.) VMCAI 2016. LNCS, vol. 9583, pp. 41–62. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49122-5_2
Naumann, D.A.: From coupling relations to mated invariants for checking information flow. In: Gollmann, D., Meier, J., Sabelfeld, A. (eds.) ESORICS 2006. LNCS, vol. 4189, pp. 279–296. Springer, Heidelberg (2006). https://doi.org/10.1007/11863908_18
Sabelfeld, A., Sands, D.: Dimensions and principles of declassification. In: 18th IEEE Computer Security Foundations Workshop, (CSFW-18 2005), 20–22 June 2005, Aix-en-Provence, France, pp. 255–269 (2005)
Smans, J., Jacobs, B., Piessens, F.: Implicit dynamic frames. ACM Trans. Program. Lang. Syst. 34(1), 2:1–2:58 (2012)
Smith, G.: Principles of secure information flow analysis. In: Christodorescu, M., Jha, S., Maughan, D., Song, D., Wang, C. (eds.) Malware Detection. ADIS, vol. 27, pp. 291–307. Springer, Boston (2007). https://doi.org/10.1007/978-0-387-44599-1_13
Sousa, M., Dillig, I.: Cartesian hoare logic for verifying k-safety properties. In: Proceedings of the 37th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2016, Santa Barbara, CA, USA, 13–17 June 2016, pp. 57–69 (2016)
Terauchi, T., Aiken, A.: Secure information flow as a safety problem. In: Hankin, C., Siveroni, I. (eds.) SAS 2005. LNCS, vol. 3672, pp. 352–367. Springer, Heidelberg (2005). https://doi.org/10.1007/11547662_24
Yang, H.: Relational separation logic. Theor. Comput. Sci. 375(1–3), 308–334 (2007)
Acknowledgements
We would like to thank Toby Murray and David Naumann for various helpful discussions. We are grateful to the anonymous reviewes for their valuable comments. We also gratefully acknowledge support from the Zurich Information Security and Privacy Center (ZISC).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Eilers, M., Müller, P., Hitz, S. (2018). Modular Product Programs. In: Ahmed, A. (eds) Programming Languages and Systems. ESOP 2018. Lecture Notes in Computer Science(), vol 10801. Springer, Cham. https://doi.org/10.1007/978-3-319-89884-1_18
Download citation
DOI: https://doi.org/10.1007/978-3-319-89884-1_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89883-4
Online ISBN: 978-3-319-89884-1
eBook Packages: Computer ScienceComputer Science (R0)



 contains a sequence of integers that each encode attributes of a person; the
contains a sequence of integers that each encode attributes of a person; the  procedure counts the number of females in this sequence.
procedure counts the number of females in this sequence.


 is
is 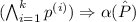 .
.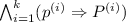 .
.


 is high.
is high.
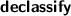 statement
statement