Deadlock-Free Monitors

Abstract

Monitors constitute one of the common techniques to synchronize threads in multithreaded programs, where calling a $\mathsf {wait}$ command on a condition variable suspends the caller thread and notifying a condition variable causes the threads waiting for that condition variable to resume their execution. One potential problem with these programs is that a waiting thread might be suspended forever leading to deadlock, a state where each thread of the program is waiting for a condition variable or a lock. In this paper, a modular verification approach for deadlock-freedom of such programs is presented, ensuring that in any state of the execution of the program if there are some threads suspended then there exists at least one thread running. The main idea behind this approach is to make sure that for any condition variable v for which a thread is waiting there exists a thread obliged to fulfil an obligation for v that only waits for a waitable object whose wait level, an arbitrary number associated with each waitable object, is less than the wait level of v. The relaxed precedence relation introduced in this paper, aiming to avoid cycles, can also benefit some other verification approaches, verifying deadlock-freedom of other synchronization constructs such as channels and semaphores, enabling them to accept a wider range of deadlock-free programs. We encoded the proposed proof rules in the VeriFast program verifier and by defining some appropriate invariants for the locks associated with some condition variables succeeded in verifying some popular use cases of monitors including unbounded/bounded buffer, sleeping barber, barrier, and readers-writers locks. A soundness proof for the presented approach is provided; some of the trickiest lemmas in this proof have been machine-checked with Coq.

1 Introduction

One of the popular mechanisms for synchronizing threads in multithreaded programs is using monitors, a synchronization construct allowing threads to have mutual exclusion and also the ability to wait for a certain condition to become true. These constructs, consisting of a mutex/lock and some condition variables, provide some basic functions for their clients, namely $\mathsf {wait}(v,l)$, causing the calling thread to wait for the condition variable v and release lock l while doing so, and $\mathsf {notify}(v)/\mathsf {notifyAll}(v)$, causing one/all thread(s) waiting for v to resume their execution. Each condition variable is associated with a lock; a thread must acquire the associated lock for waiting or notifying on a condition variable, and when a thread is notified it must reacquire the associated lock.

However, one potential problem with these synchronizers is deadlock, where all threads of the program are waiting for a condition variable or a lock. To clarify the problem consider the program in Fig. 1, where a channel consists of a queue q, a lock l and a condition variable v, protecting a thread from dequeuing q when it is empty. In this program the receiver thread first acquires lock l and while there is no item in q it releases l, suspends itself and waits for a notification on v. If this thread is notified while q is not empty it dequeues an item and finally releases l. The sender thread also acquires the same lock, enqueues an item into q, notifies one of the threads waiting for v, if any, and lastly releases l. After creating a channel ch, the main thread of the program first forks a thread to receive a message from ch and then sends a message on ch. Although this program is deadlock-free, it is easy to construct some variations of it that lead to deadlock: if the main thread itself, before sending any messages, tries to receive a message from ch, or if the number of receives is greater than the number of sends, or if the receiver thread waits for v even if q is not empty.

Fig. 1.

A message passing program synchronized using a monitor

Several approaches to verify termination, deadlock-freedom, liveness, and finite blocking of threads of programs have been presented. Some of these approaches only work with non-blocking algorithms [1,2,3], where the suspension of one thread cannot lead to the suspension of other threads. These approaches are not applicable for condition variables because suspension of a sender thread in Fig. 1, for example, might cause a receiver thread to be blocked forever. Some other approaches are also presented to verify termination of programs using some blocking constructs such as channels [4,5,6] and semaphores [7]. These approaches are not general enough to cover condition variables because unlike the channels and semaphores a notification of a condition variable is lost when there is no thread waiting for that condition variable. There are also some studies [8,9,10] to verify correctness of programs that support condition variables. However, these approaches either only cover a very specific application of condition variables, such as a buffer program with only one producer and one consumer, or are not modular and suffer from a long verification time when the size of the state space, such as the number of threads, is increased.

In this paper we present a modular approach to verify deadlock-freedom of programs in the presence of condition variables. More specifically, this approach makes sure that for any condition variable v for which a thread is waiting there exists a thread obliged to fulfil an obligation for v that only waits for a waitable object whose wait level, an arbitrary number associated with each waitable object, is less than the wait level of v. The presented approach is modular, meaning that different modules (functions) of a program can be verified individually. This approach is based on Leino et al. [4] approach for verification of deadlock-freedom in the presence of channels and locks, which in turn was based on Kobayashi’s [6] type system for verifying deadlock-freedom of $\pi$-calculus processes, and extends the separation logic-based encoding [11] by covering condition variables. We implemented the proposed proof rules in the VeriFast verifier [12,13,14] and succeeded in verifying some common applications of condition variables such as bounded/unbounded buffer, sleeping barber [15], barrier, and readers-writers locks (see the full version of this paper [16] reporting the verification time of these programs).

This paper is structured as follows. Section 2 provides some background information on the existing approaches upon which we build our verification algorithm. Section 3 introduces a preliminary approach for verifying deadlock-freedom of some common applications of condition variables. In Sect. 4 the precedence relation, aiming to avoid cycles, is relaxed, making it possible to verify some trickier applications of condition variables. A soundness proof of the presented approach is lastly given in Sect. 5.

2 Background Information on the Underlying Approaches

In this section we provide some background information on the existing approaches that verify absence of data races and deadlock in the presence of locks and channels that we build on.

2.1 Verifying Absence of Data Races

Locks/mutexes are mostly used to avoid data races, an undesired situation where a heap location is being written and accessed concurrently by two different threads. One common approach to verify absence of these undesired conditions is ownership: ownership of heap locations is assigned to threads and it is verified that a thread accesses only the heap locations that it owns. Transferring ownership of heap locations between threads is supported through locks by allowing locks, too, to own heap locations. While a lock is not held by a thread, it owns the heap locations described by its invariant. More specifically, when a lock is created the resources specified by its invariant are transferred from the creating thread to the lock, when that lock is acquired these resources are transferred from the lock to the acquiring thread, and when that lock is released these resources, that must be again in possession of the thread, are again transferred from the thread to the lock [17]. Figure 2 illustrates how a program increasing a counter, which consists of an integer variable x and a lock l protecting this variable, can be verified, where two threads try to write on the variable x. We use separation logic [18] to reason about the ownership of permissions. As indicated below each command, creating the integer variable x initialized by zero provides a read/write access permission to x, denoted by $x{\mapsto }0$. This ownership, that is going to be protected by lock l, is transferred to the lock because it is asserted by the lock invariant $\mathsf {inv}$, which is associated with the lock, as denoted by function $\mathsf {I}$, at the point where the lock is initialized. The resulting $\mathsf {lock}$ permission, that can be duplicated, is used in the routine $\mathsf {inc}$, where x is increased under protection of lock l. Acquiring this lock in this routine provides a full access permission to x and transforms the $\mathsf {lock}$ permission to a $\mathsf {locked}$ permission, implying that the related lock has been acquired. Releasing that lock again consumes this access permission and transforms the $\mathsf {locked}$ permission to a $\mathsf {lock}$ one.

Fig. 2.

Verification of data-race-freedom of a program, where $\mathsf {inv}=\lambda ct.\;\exists z.\;ct.x{\mapsto }z$

2.2 Verifying Absence of Deadlock

One potential problem with programs using locks and other synchronization mechanisms is deadlock, an undesired situation where all threads of the program are waiting for some waitable objects. For example, a program can deadlock if a thread acquires a lock and forgets to release it, because any other thread waiting for that lock never succeeds in acquiring that lock. As another example, if in a message passing program the number of threads trying to receive a message from a channel is greater than the number of messages sent on that channel there will be some threads waiting for that channel forever. One approach to verify deadlock-freedom of channels and locks is presented by Leino et al. [4] that guarantees deadlock-freedom of programs by ensuring that (1) for any obligee thread waiting for a waitable object, such as a channel or lock, there is an obligation for that object that must be fulfilled by an obligor thread, where a thread can fulfil an obligation for a channel/lock if it sends a message on that channel/releases that lock, and (2) each thread waits for an object only if the wait level of that object, an arbitrary number assigned to each waitable object, is lower than the wait levels of all obligations of that thread. The second rule is established by making sure that when a thread with some obligations O executes a command $\mathsf {acquire}(o)/\mathsf {receive}(o)$ the precondition $o{\prec } O$ holds, i.e. the wait level of o is lower than the wait levels of obligations in O. To meet the first rule where the waitable object is a lock, as the example in the left side of Fig. 3 illustrates, after acquiring a lock, that lock is loaded onto the bag¹ (multiset) of obligations of the thread, denoted by $\mathsf {obs}(O)$. This ensures that if a thread tries to acquire a lock that has already been acquired then there is one thread obliged to fulfil an obligation for that lock.

Fig. 3.

Verification of deadlock-freedom of locks (left side) and channels (right side)

To establish the first rule where the waitable object is a channel any thread trying to receive a message from a channel ch must spend one credit for ch. This credit is normally obtained from the thread that has forked the receiver thread, where this credit is originally created by loading ch onto the bag of obligations of the forking thread. The forking thread can discharge the loaded obligation by either sending a message on the corresponding channel or delegating it to a child thread that can discharge it. The example on the right side of Fig. 3 shows the verification of deadlock-freedom a program in which the main routine, after forking a obligee thread trying to receive a message from channel ch, sends a message on this channel. Before forking the receiver thread, a credit and an obligation for the channel ch are created in the main thread. The former is given to the forked thread, where this credit is spent by the $\mathsf {receive}(ch)$ command, and the latter is fulfilled by the main thread when it executes the command $\mathsf {send}(ch,12)$.

More formally, the mentioned verification approach satisfies the first rule by ensuring that for each channel ch in the program the number of obligations for ch is equal to/greater than the number of threads waiting for ch. This assurance is obtained by preserving the invariant $Wt (ch)+Ct(ch)\leqslant Ot(ch)+\mathsf {sizeof}(ch)$, while the programming language itself ensures that $\mathsf {sizeof}(ch)>0$ $\Rightarrow Wt (ch)=0$, where $\mathsf {sizeof}$ is a function mapping each channel to the size of its queue, $Wt (ch)$ is the total number of threads currently waiting for channel ch, Ot(ch) is the total number of obligations for channel ch held by all threads, and Ct(ch) is the total number of credits for channel ch currently in the system.

Fig. 4.

Proof rules ensuring deadlock-freedom of channels and locks, where $o{\prec }O\Leftrightarrow \forall o' \in O.\;\mathsf {R}(o)<\mathsf {R}(o')$

2.3 Proof Rules

The separation logic-based proof rules, introduced by Jacobs et al. [11], avoiding data races and deadlock in the presence of locks and channels are shown in Fig. 4, where $\mathsf {R}$ and $\mathsf {I}$ are functions mapping a waitable object/lock to its wait level/invariant, respectively, and $\mathsf {g\_initl}$, and $\mathsf {g\_load}$ are some ghost commands used to initialize an uninitialized lock permission and load a channel onto the bag of obligations and credits of a thread, respectively. When a lock is created, as shown in NewLock, an uninitialized lock permission $\mathsf {ulock}(l)$ is provided for that thread. Additionally, an arbitrary integer number z can be decided as the wait level of that lock that is stored in $\mathsf {R}$. Note that variable z in this rule is universally quantified over the rule, and different applications of the NewLock rule can use different values for this variable. The uninitialized lock permission, as shown in InitLock, can be converted to a normal lock permission $\mathsf {lock}(l)$ provided that the resources described by the invariant of that lock, stored in $\mathsf {I}$, that must be in possession of the thread, are transferred from the thread to the lock. By the rule Acquire, having a lock permission, a thread can acquire that lock if the wait levels of obligations of that thread are all greater than the wait level of that lock. After acquiring the lock, the resources represented by the invariant of that lock are provided for the acquiring thread and the permission $\mathsf {lock}$ is converted to a $\mathsf {locked}$ permission. When a thread releases a lock, as shown in the rule Release, the resources indicated by the invariant of that lock, that must be in possession of the releasing thread, are transferred from the thread to the lock and the permission $\mathsf {locked}$ is again converted to a $\mathsf {lock}$ permission. By the rule Receive a thread with obligations O can try to receive a message from a channel ch only if the wait level of ch is lower than the wait levels of all obligations in O. This thread must also spend one credit for ch, ensuring that there is another thread obliged to fulfil an obligation for ch. As shown in the rule Send, an obligation for this channel can be discharged by sending a message on that channel. Alternatively, by the rule Fork, a thread can discharge an obligation for a channel if it delegates that obligation to a child thread, provided that the child thread discharges the delegated obligation. In this setting the verification of a program starts with an empty bag of obligations and must also end with such bag implying that there is no remaining obligation to fulfil.

However, this verification approach is not straightforwardly applicable to condition variables. A command $\mathsf {notify}$ cannot be treated like a command $\mathsf {send}$ because a notification on a condition variable is lost when there is no thread waiting for that variable. Accordingly, it does not make sense to discharge an obligation for a condition variable whenever it is notified. Similarly, a command $\mathsf {wait}$ cannot be treated like a command $\mathsf {receive}$. A command $\mathsf {wait}$ is normally executed in a $\mathsf {while}$ loop, checking the waiting condition of the related condition variable. Accordingly, it is impossible to build a loop invariant for such a loop if we force the wait command to spend a credit for the related condition variable.

3 Deadlock-Free Monitors

3.1 High-Level Idea

In this section we introduce an approach to verify deadlock-freedom of programs in the presence of condition variables. This approach ensures that the verified program never deadlocks, i.e. there is always a running thread, that is not blocked, until the program terminates. The main idea behind this approach is to make sure that for any condition variable v for which a thread is waiting there exists a thread obliged to fulfil an obligation for v that only waits for a waitable object whose wait level is less than the wait level of v. As a consequence, if the program has some threads suspended, waiting for some obligations, there is always a thread obliged to fulfil the obligation $o_{min}$ that is not suspended, where $o_{min}$ has a minimal wait level among all waitable objects for which a thread is waiting. Accordingly, the proposed proof rules make sure that (1) when a command $\mathsf {wait}(v,l)$ is executed $Ot(v)>0$, where Ot maps each condition variable v to the total number of obligations for v held by all threads (note that having a thread with permission $\mathsf {obs}(O)$ implies $O(v)\leqslant Ot(v)$), (2) a thread discharges an obligation for a condition variable only if after this discharge the invariant $\mathsf {one\_ob}(v, Wt ,Ot)$ defined as $Wt (v)>0\Rightarrow Ot(v)>0$ still holds, where $Wt (v)$ denotes the number of threads waiting for condition variable v, and (3) a thread with obligations O executes a command $\mathsf {wait}(v,l)$ only if $v{\prec }O$.

3.2 Tracking Numbers of Waiting Threads and Obligations

For all condition variables associated with a lock l the value of functions $Wt$ and Ot can only be changed by a thread that has locked l; $Wt (v)$ is changed only when one of the commands $\mathsf {wait}(v,l)/\mathsf {notify}(v)/\mathsf {notifyAll}(v)$ is executed, requiring holding lock l, and we allow Ot(v) to be changed only when a permission $\mathsf {locked}$ for l is available. Accordingly, when a thread acquires a lock these two bags are stored in the related $\mathsf {locked}$ permission and are used to establish the rules number 1 and 2, when a thread executes a $\mathsf {wait}$ command or discharges one of its obligations. Note that the domain of these functions is the set of the condition variables associated with the related lock. The thread executing the critical section can change these two bags under some circumstances. If that thread loads/discharges a condition variable onto/from the list of its obligations this condition variable must also be loaded/discharged onto/from the bag Ot stored in the related $\mathsf {locked}$ permission. Note that unlike the approach presented by Leino et al. [4], an obligation for a condition variable can arbitrarily be loaded or discharged by a thread, provided that the rule number 2 is respected. At the start of the execution of a $\mathsf {wait}(v,l)$ command, $Wt (v)$ is incremented and after execution of commands $\mathsf {notify}(v)/\mathsf {notifyAll}(v)$ one/all instance(s) of v is/are removed from the bag $Wt$ stored in the related $\mathsf {locked}$ permission, since these commands change the number of threads waiting for v.

A program can be successfully verified according to the mentioned rules, formally indicated in Fig. 5, if each lock associated with any condition variable v has an appropriate invariant such that it implies the desired invariant $\mathsf {one\_ob}(v, Wt ,Ot)$. Accordingly, the proof rules allow locks to have invariants parametrized over the bags $Wt$ and Ot. When a thread acquires a lock the result of applying the invariant of that lock to these two bags, stored in the related $\mathsf {locked}$ permission, is provided for the thread and when that lock is released it is expected that the result of applying the lock invariant to those bags, stored in the related $\mathsf {locked}$ permission, again holds. However, before execution of a command $\mathsf {wait}(v,l)$, when lock l with bags $Wt$ and Ot stored in its $\mathsf {locked}$ permission is going to be released, it is expected that the invariant of l holds with bags and Ot because the running thread is going to wait for v and this condition variable is going to be added to $Wt$. As this thread resumes its execution, when it has some bags $Wt '$ and $Ot'$ stored in the related $\mathsf {locked}$ permission, the result of applying the invariant of l to these bags is provided for that thread. Note that the total number of threads waiting for v, $Wt (v)$, is already decreased when a command $\mathsf {notify}(v)$ or $\mathsf {notifyAll}(v)$ is executed, causing the waiting thread(s) to wake up and try to acquire the lock associated with v.

3.3 Resource Transfer on Notification

In general, as we will see when looking at examples, it is sometimes necessary to transfer resources from a notifying thread to the threads being notified². To this end, these resources, specified by a function $\mathsf {M}$, are associated with each condition variable v when v is created, such that the commands $\mathsf {notify}(v)$/$\mathsf {notifyAll}(v)$ consume one/$Wt (v)$ instance(s) of these resources, respectively, and the command $\mathsf {wait}(v,l)$ produces one instance of such resources (see the rules Wait,Notify, and NotifyAll in Fig. 5).

Fig. 5.

Proof rules to verify deadlock-freedom of condition variables, where $Wt (v)$ and Ot(v) denote the total number of threads waiting for v and the total number of obligations for v, respectively, and $\mathsf {safe\_obs}(v, Wt ,Ot)\Leftrightarrow \mathsf {one\_ob}(v, Wt ,Ot)$ and $\mathsf {one\_ob}(v, Wt ,Ot)\Leftrightarrow ( Wt (v)>0\Rightarrow Ot(v)>0)$

3.4 Proof Rules

Figure 5 shows the proposed proof rules used to verify deadlock-freedom of condition variables, where $\mathsf {L}$ and $\mathsf {M}$ are functions mapping each condition variable to its associated lock and to the resources that are moved from the notifying thread to the notified one when that condition variable is notified, respectively. Creating a lock, as shown in the rule NewLock, produces a permission $\mathsf {ulock}$ storing the bags $Wt$ and Ot, where these bags are initially empty. The bag Ot in this permission, similar to a $\mathsf {locked}$ one, can be changed provided that the obligations of the running thread are also updated by one of the ghost commands $\mathsf {g\_chrg}(v)$ or $\mathsf {g\_disch}(v)$ (see rules ChargeOb and DisOb). The lock related to this permission can be initialized by transferring the resources described by the invariant of this lock, that is now parametrized over the bags $Wt$ and Ot, applied to the bags stored in this permission from the thread to the lock (see rule InitLock). When this lock is acquired, as shown in the rule Acquire, the resources indicated by its invariant are provided for the thread, and when it is released, as shown in the rule Release, the resources described by its invariant that must hold with appropriate bags, are again transferred from the thread to the lock. The rules Wait and DisOb ensure that for any condition variable v when the number of waiting threads is increased, by executing a command $\mathsf {wait}(v,l)$, or the number of the obligations is decreased, by (logically) executing a command $\mathsf {g\_disch}(v)$, the desired invariant $\mathsf {one\_ob}$ still holds. Additionally, the rules Acquire and Wait make sure that a thread only waits for a waitable object whose wait level is lower that the wait levels of obligations of that thread. Note that in the rule Wait in the precondition of the command $\mathsf {wait}(v,l)$ it is not necessary that the wait level of v is lower that the wait level of l, since lock l is going to be released by this command. However, in this precondition the wait level of l must be lower that the wait levels of the obligations of the thread because when this thread is notified it tries to reacquire l, at which point $l{\prec }O$ must hold. The commands $\mathsf {notify}(v)/\mathsf {notifyAll}(v)$, as shown in the rules Notify and NotifyAll, remove one/all instance(s) of v, if any, from the bag $Wt$ stored in the related $\mathsf {locked}$ permission. Additionally, $\mathsf {notify}(v)$ consumes the moving resources, indicated by $\mathsf {M}(v)$, that appear in the postcondition of the notified thread. Note that $\mathsf {notifyAll}(v)$ consumes $Wt (v)$ instances of these resources, since they are transferred to $Wt (v)$ threads waiting for v.

3.5 Verifying Channels

Ghost Counters. We will now use our proof system to prove deadlock-freedom of the program in Fig. 1. To do so, however, we will introduce a ghost resource that plays the role of credits, in such a way that we can prove the invariant $Wt (ch)+Ct(ch)\leqslant Ot(ch)+\mathsf {sizeof}(ch)$. In particular, we want this property to follow from the lock invariant. This means we need to be able to talk, in the lock invariant, about the total number of credits in the system. To achieve this, we introduce a notion of ghost counters and corresponding ghost counter tickets, both of which are a particular kind of ghost resources. Specifically, we introduce three ghost commands: $\mathsf {g\_newctr}, \mathsf {g\_inc}$, and $\mathsf {g\_dec}$. $\mathsf {g\_newctr}$ allocates a new ghost counter whose value is zero and returns a ghost counter identifier c for it. $\mathsf {g\_inc}(c)$ increments the value of the ghost counter with identifier c and produces a ticket for the counter. $\mathsf {g\_dec}(c)$, finally, consumes a ticket for ghost counter c and decrements the ghost counter’s value. Since these are the only operations that manipulate ghost counters or ghost counter tickets, it follows that the value of a ghost counter c is always equal to the number of tickets for c in the system. Proof rules for these ghost commands are shown in Fig. 6³.

The Channels Proof. Figure 7 illustrates how the program in Fig. 1 can be verified using our proof system. The invariant of lock ch.l in this program, denoted by $\mathsf {inv}(ch)$, is parametrized over bags $Wt ,Ot$ and implies the desired invariant $\mathsf {one\_ob}(ch.v, Wt ,Ot)$. The permission $\mathsf {ctr}(ch.c,Ctv)$ in this invariant indicates that the total number of credits (tickets) for ch.v is Ctv, where ch.c is a ghost field added to the $\mathsf {channel}$ data structure, aiming to store a ghost counter identifier for the ghost counter of ch.v. Generally, a lock invariant can imply the invariant $\mathsf {one\_ob}(v, Wt ,Ot)$ if it asserts $Wt (v) {\,+\,} Ct(v) \leqslant Ot(v) {\,+\,} S(v)$ and $Wt (v)\leqslant Ot(v)$, where Ct(v) is the total number of credits for v and S(v) is an integer value such that the command $\mathsf {wait}(v,l)$ is executed only if $S(v) \leqslant 0$. After initializing l in the main routine, there exists a credit for ch.v (denoted by $\mathsf {tic}(ch.c)$) that is consumed by the thread executing the $\mathsf {receive}$ routine, and also an obligation for ch.v that is fulfilled by this thread after executing the $\mathsf {send}$ routine. The credit $\mathsf {tic}(ch.c)$ in the precondition of the routine $\mathsf {receive}$ ensures that before execution of the command $\mathsf {wait}(ch.v,ch.l)$, $Ot(ch.v)>0$. This inequality follows from the invariant of lock l, which holds for and Ot when Ctv is decreased by $\mathsf {g\_dec}(ch.c)$. This credit (or the one specified by $\mathsf {M}(ch.v)$ that is moved from a notifier thread when the receiver thread wakes up) must be consumed after execution of the command $\mathsf {dequeue}(ch.q)$ and before releasing ch.l to make sure that the invariant still holds after decreasing the number of items in ch.q. The obligation for ch.v in the precondition of the routine $\mathsf {send}$ is discharged by this routine, which is safe, since after the execution of the commands $\mathsf {enqueue}$ and $\mathsf {notify}$ the invariant , which follows from the lock invariant, holds.

Fig. 6.

Ghost counters

Fig. 7.

Verification of the program in Fig. 1

Fig. 8.

Verification of a barrier synchronized using a monitor

3.6 Other Examples

Using the proof system of this section we prove two other deadlock-free programs, namely sleeping barber [16], and barrier. In the barrier program shown in Fig. 8, a barrier b consists of an integer variable r indicating the number of the remaining threads that must call the routine $\mathsf {wait\_for\_rest}$, a lock l protecting r against data races, and a condition variable v. Each thread executing the routine $\mathsf {wait\_for\_rest}$ first decreases the variable r, and if the resulting value is still positive waits for v, otherwise it notifies all threads waiting for v. In this program the barrier is initialized to 3, implying that no thread must start $\mathsf {task_2}$ unless all the three threads in this program finish $\mathsf {task_1}$. This program is deadlock-free because the routine $\mathsf {wait\_for\_rest}$ is executed by three different threads. Figure 8 illustrates how this program can be verified by the presented proof rules. Note that before executing $\mathsf {g\_disch}$ in the $\mathsf {else}$ branch, $\mathsf {safe\_obs}$ holds because at this point we have $0<b.r$, which implies $1<b.r$ before the execution of $b.r:=b.r-1$, and by the invariant we have $1<Ot(b.v)$, implying . The interesting point about the verification of this program is that since all the threads waiting for condition variable v in this program are notified by the command $\mathsf {notifyAll}$, the invariant of the related lock, implying $\mathsf {one\_ob}(b.v, Wt ,Ot)$, is significantly different from the ones defined in the channel and sleeping barber examples. Generally, for a condition variable v on which only $\mathsf {notifyAll}$ is executed (and not $\mathsf {notify}$) a lock invariant can imply the invariant $\mathsf {one\_ob}(v, Wt ,Ot)$ if it asserts $Wt (v)=0 \vee S(v) \leqslant Ct(v)$ and $Ct(v) < Ot(v) + S(v)$, where Ct(v) is the total number of credits for v and S(v) is an integer value such that the command $\mathsf {wait}(v,l)$ is executed only if $S(v) \leqslant 0$. For this particular example $S(b.v)=1-b.r$ and $Ct(b.v)=0$, since this program can be verified without incorporating the notion of credits.

4 Relaxing the Precedence Relation

The precedence relation, in this paper denoted by $\prec$, introduced in [4] makes sure that all threads wait for the waitable objects in strict ascending order (with respect to the wait level associated with each waitable object), or here in this paper in descending order, ensuring that in any state of the execution there is no cycle in the corresponding wait-for graph. However, this relation is too restrictive and prevents verifying some programs that are actually deadlock-free, such as the one shown in the left side of Fig. 9. In this program a value is increased by two threads communicating through a channel. Each thread receives a value from the channel, increases that value, and then sends it back on the channel. Since an initial value is sent on the related channel this program is deadlock-free. The first attempt to verify this program is illustrated in the middle part of Fig. 9, where the required credit to verify the $\mathsf {receive}$ command in the routine $\mathsf {inc}$ is going to be provided by the $\mathsf {send}$ command, executed immediately after this command, and not by the precondition of this routine. In other words, the idea is to load a credit and an obligation for ch in the routine $\mathsf {inc}$ itself, and then spend the loaded credit to verify the $\mathsf {receive}(ch)$ command and fulfil the loaded obligation by the $\mathsf {send}(ch)$ command. However, this idea fails because the $\mathsf {receive}$ command in the routine $\mathsf {inc}$ cannot be verified since one of its preconditions, , never holds. Kobayashi [6, 20] has addressed this problem in his type system by using the notion of usages and assigning levels to each obligation/capability, instead of waitable objects. However, in the next section we provide a novel idea to address this problem by just relaxing the precedence relation used in the presented proof rules.

Fig. 9.

A deadlock-free program verified by exploiting the relaxed precedence relation

4.1 A Relaxed Precedence Relation

To tackle the problem mentioned in the previous section we relax the precedence relation, enforced by $\prec$, by replacing $\prec$ by $\preccurlyeq$ satisfying the following property: $o{\preccurlyeq }O$ holds if either $o{\prec }O$ or (1) , and (2) o satisfies the property that in any execution state, if a thread waits for o then there exists a thread that can discharge an obligation for o and is not waiting for any object whose wait level is equal to/greater than the wait level of o. This property still guarantees that in any state of the execution if the program has some threads suspended, waiting for some obligations, there is always a thread obliged to fulfil the obligation $o_{min}$ that is not blocked, where $o_{min}$ has a minimal wait level among all waitable objects for which a thread is waiting.

The condition number 2 is met if it is an invariant that for a condition variable o for which a thread is waiting the total number of obligations is greater than the total number of waiting threads. Since each thread waiting for o has at most one instance of o in the bag of its obligations, according to the pigeonhole principle, if the number obligations for o is higher than the number of threads waiting for o then there exists a thread that holds an obligation for o that is not waiting for o, implying the rule number 2 because this thread only waits for objects whose wait levels are lower than the wait level of o. Accordingly, we first introduce a new function $\mathsf {P}$ in the proof rules mapping each waitable object to a boolean value, and then make sure that for any object o for which a thread is waiting if $\mathsf {P}(o)=\mathsf {true}$ then $Wt (o)<Ot(o)$. With the help of this function we define the relaxed precedence relation as shown in Definition 1.

Definition 1

(Relaxed precedence relation). The relaxed precedence relation indexed over functions $\mathsf {R}$ and $\mathsf {P}$ holds for a waitable object v and a bag of obligations O, denoted by $v\preccurlyeq O$, if and only if:

Using this relaxed precedence relation the approach presented by Leino et al. [4] can also support more complex programs, such as the one in the left side of Fig. 9. This approach can exploit this relation by (1) replacing the original precedence relation $\prec$ by the relaxed one $\preccurlyeq$, and (2) replacing the rule associated with creating a channel by the one shown below. According to this proof rule for each channel ch the function $\mathsf {P}$, in the definition of the relaxed precedence relation, is initialized when ch is created such that if $\mathsf {P}(ch)$ is decided to be $\mathsf {true}$ then one obligation for ch is loaded onto the bag of obligations of the creating thread. The approach is still sound because for any channel ch for which $\mathsf {P}$ is $\mathsf {true}$ the invariant $Wt (ch)+Ct(ch)<Ot(ch)+\mathsf {sizeof}(ch)$ holds. Combined with the fact that in this language, where channels are primitive constructs, $Wt (ch)>0\Rightarrow \mathsf {sizeof}(ch)=0$, we have $Wt (ch)>0\Rightarrow Wt (ch)<Ot(ch)$. Now consider a deadlocked state, where each thread is waiting for a waitable object. Among all of these waitable objects take the one having a minimal wait level, namely $o_m$. If $o_m$ is a lock or a channel, where $\mathsf {P}(o_m)=\mathsf {false}$, then at least one thread has an obligation for $o_m$ and is waiting for an object o whose wait level is lower that the wait level of $o_m$, which contradicts minimality of the wait level of $o_m$. Otherwise, since $Wt (o_m)>0$ we have $Wt (o_m)<Ot(o_m)$. Additionally, we know that each thread waiting for $o_m$ has at most one obligation for $o_m$. Accordingly, there must be a thread holding an obligation for $o_m$ that is not waiting for $o_m$. Consequently, this thread must be waiting for an object o whose wait level is lower than the wait level of $o_m$, which contradicts minimality of the wait level of $o_m$.

To exploit the relaxed definition in the approach presented in this paper we only need to make sure that for any condition variable v for which a thread is waiting if $\mathsf {P}(v)$ is $\mathsf {true}$ then Ot(v) is greater than $Wt (v)$. To achieve this goal we include this invariant in the definition of the invariant $\mathsf {safe\_obs}$, shown in Definition 2, an invariant that must hold when a command $\mathsf {wait}$ or a ghost command $\mathsf {g\_disch}$ is executed.

Definition 2

(Safe Obligations). The relation $\mathsf {safe\_obs}(v, Wt ,Ot)$, indexed over function $\mathsf {P}$, holds if and only if:

$\begin{array}{l} \mathsf {one\_ob}(v, Wt ,Ot)\;\wedge \; (\mathsf {P}(v)=\mathsf {true}\Rightarrow \mathsf {spare\_ob}(v, Wt ,Ot))\text {, where}\\ \mathsf {one\_ob}(v, Wt ,Ot)\Leftrightarrow ( Wt (v)>0\Rightarrow Ot(v)>0)\\ \mathsf {spare\_ob}(v, Wt ,Ot)\Leftrightarrow ( Wt (v)>0\Rightarrow Wt (v)<Ot(v)) \end{array}$

Fig. 10.

A readers-writers program with variables aw, holding the number of threads writing, ww, holding the number of thread waiting to write, and ar, holding the number of threads reading, that is synchronized using a monitor consisting of condition variables $v_w$, preventing writers from writing while other threads are reading or writing, and $v_r$, preventing readers from reading while there is another thread writing or waiting to write.

Fig. 11.

Verification of the program in Fig. 10

Readers-Writes Locks. As another application of this relaxed definition consider a readers-writers program, shown in Fig. 10⁴, where the condition variable $v_w$ prevents writers from writing on a shared memory when that memory is being accessed by other threads. After reading the shared memory, a reader thread notifies this condition variable if there is no other thread reading that memory. This condition variable is also notified by a writer thread when it finishes its writing. Consequently, a writer thread first might wait for $v_w$ and then fulfil an obligation for this condition variable. This program is verified if the writer thread itself produces a credit and an obligation for $v_w$ and then uses the former for the command $\mathsf {wait}(v_w,l)$ and fulfils the latter at the end of its execution. Accordingly, since when the command $\mathsf {wait}(v_w,l)$ is executed $v_w$ is in the bag of obligations of the writer thread, this command can be verified if , where $\mathsf {P}(v_w)$ must be $\mathsf {true}$. The verification of this program is illustrated in Fig. 11. Generally, for a condition variable v for which $P(v)=\mathsf {true}$ a lock invariant can imply the invariant $\mathsf {one\_ob}(v, Wt ,Ot)$ if it asserts $Wt (v) + Ct(v) < Ot(v) + S(v)$ and $Wt (v) = 0 \vee Wt (v) < Ot(v)$, where Ct(v) is the total number of credits for v and S(v) is an integer value such that $\mathsf {wait}(v,l)$ is executed only if $S(v) \leqslant 0$.

4.2 A Further Relaxation

The relation $\preccurlyeq$ allows one to verify some deadlock-free programs where a thread waits for a condition variable while that thread is also obliged to fulfil an obligation for that variable. However, it is still possible to have a more general, more relaxed definition for this relation. Under this definition a thread with obligations O is allowed to wait for a condition variable v if either $v{\prec }O$, or there exists an obligation o such that (1) , and (2) o satisfies the property that in any execution state, if a thread is waiting for o then there exists a thread that is not waiting for any waitable object whose wait level is equal to/greater than the wait levels of v and o. This new definition still guarantees that in any state of the execution if the program has some threads suspended, waiting for some obligations, there is always a thread obliged to fulfil the obligation $o_{min}$ that is not suspended, where $o_{min}$ has a minimal wait level among all waitable objects for which a thread is waiting. To satisfy the condition number 2 we introduce a new definition for $\preccurlyeq$, shown in Definition 3, that uses a new function $\mathsf {X}$ mapping each lock to a set of wait levels. This definition will be sound only if the proof rules ensure that for any condition variable v whose wait level is in $\mathsf {\mathsf {X}(\mathsf {L}(v))}$ the number of obligations is equal to or greater than the number of the waiting threads.

This definition is still sound because of Lemma 1, that has been machine-checked in Coq⁵, where G is a bag of waitable object-bag of obligations pairs such that each element t of G is associated with a thread in a state of the execution, where the first element of t is the object for which t is waiting and the second element is the bag of obligations of t. This lemma implies that if all the mentioned rules, denoted by $H_1$ to $H_4$, are respected in any state of the execution then it is impossible that all threads in that state are waiting for a waitable object. This lemma can be proved by induction on the number of elements of G and considering the element waiting for an object whose wait level is minimal (see [16] representing its proof in details).

Definition 3

(Relaxed precedence relation). The new precedence relation indexed over functions $\mathsf {R,L,P,X}$ holds for a waitable object v and a bag of obligations O, denoted by $v\preccurlyeq O$, if and only if:

Lemma 1

(A Valid Graph Is Not Deadlocked)

Fig. 12.

New proof rules initializing functions $\mathsf {X}$ and $\mathsf {P}$ used in $\mathsf {safe\_obs}$ and $\preccurlyeq$

To extend the proof rules with the new precedence relation it suffices to include a new invariant $\mathsf {own\_ob}$ in the definition of $\mathsf {safe\_obs}$, as shown in Definition 4, an invariant that must hold when a command $\mathsf {wait}$ or a ghost command $\mathsf {g\_disch}$ is executed, to make sure that for any condition variable for which $\mathsf {exc}$ holds, the number of obligations is equal to/greater than the number of the waiting threads. Additionally, the functions $\mathsf {X}$ and $\mathsf {P}$, as indicated in Fig. 12, are initialized when a lock and a condition variable is created, respectively. The rest of the proof rules are the same as those defined in Fig. 5 except that the old precedence relation ($\prec$) is replaced by the new one ($\preccurlyeq$).

Fig. 13.

Verification of a bounded channel synchronized using a monitor consisting of condition variables $v_f$, preventing sending on a full channel, and $v_e$, preventing taking messages from an empty channel

Definition 4

(Safe Obligations). The relation $\mathsf {safe\_obs}(v, Wt ,Ot)$, indexed over functions $\mathsf {R,L,P,X}$, holds if and only if:

$\begin{array}{l} \mathsf {one\_ob}(v, Wt ,Ot)\;\wedge \; (\mathsf {P}(v)=\mathsf {true}\Rightarrow \mathsf {spare\_ob}(v, Wt ,Ot))\;\wedge \\ (\mathsf {exc}(v)=\mathsf {true}\Rightarrow \mathsf {own\_ob}(v, Wt ,Ot))\text {, where}\\ \mathsf {one\_ob}(v, Wt ,Ot)\Leftrightarrow ( Wt (v)>0\Rightarrow Ot(v)>0)\\ \mathsf {spare\_ob}(v, Wt ,Ot)\Leftrightarrow ( Wt (v)>0\Rightarrow Wt (v)<Ot(v))\\ \mathsf {own\_ob}(v, Wt ,Ot)\Leftrightarrow ( Wt (v)\leqslant Ot(v)) \end{array}$

Bounded Channels. One application of the new definition is a bounded channel program, shown in Fig. 13, where a sender thread waits for a receiver thread if the channel is full, synchronized by $v_f$, and a receiver thread waits for a sender thread if the channel is empty, synchronized by $v_e$. More precisely, the sender thread with an obligation for $v_e$ might execute the command $\mathsf {wait}(v_f,l)$, and the receiver thread with an obligation for $v_f$ might execute a command $\mathsf {wait}(v_e,l)$. Since $v_e$ and $v_f$ are not equal, it is impossible to verify this program by the old definition of $\preccurlyeq$ because the waiting levels of $v_e$ and $v_f$ cannot be lower than each other. Thanks to the new definition of $\preccurlyeq$, this program can be verified, as shown in Fig. 13, by initializing $\mathsf {P}(v_f)$ with $\mathsf {true}$ and $\mathsf {X}(l)$ with $\{1,2\}$, where two consecutive numbers 1 and 2 are the wait levels of $v_e$ and $v_f$, respectively.

5 Soundness Proof

In this section we provide a soundness proof for the present approach⁶, i.e. if a program is verified by the proposed proof rules, where the verification starts from an empty bag of obligations and also ends with such bag, this program is deadlock-free. To this end, we first define the syntax of programs and a small-step semantics for programs ($\leadsto$) relating two configurations (see [16] for formal definitions). A configuration is a thread table-heap pair (t, h), where heaps and thread tables are some partial functions from locations and thread identifiers to integers and command-context pairs ($c;\xi$), respectively, where a context, denoted by $\xi$, is either $\mathsf {done}$ or $\mathsf {let}\;x{:=}[]\ \mathsf {in}\;c;\xi$. Then we define validity of configurations, shown in Definition 5, and prove that (1) if a program c is verified by the proposed proof rules, where it starts from the precondition and satisfies the post condition , then the initial configuration, where the heap is empty, denoted by $\mathbf {0}=\lambda \_.\varnothing$, and there is only one thread with command c and context $\mathsf {done}$, is a valid configuration (Theorem 4), (2) a valid configuration is not deadlocked (Theorem 5), and (3) starting from a valid configuration, all the subsequent configurations of the execution are also valid (Theorem 6).

In a valid configuration (t, h), h contains all the heap ownerships that are in possession of all threads in t and also those that are in possession of the locks that are not held, specified by a list A. Additionally, each thread must have all the required permissions to be successfully verified with no remaining obligation, enforced by $\mathsf {wpcx}$. $\mathsf {wpcx}(c,\xi )$ in this definition is a function returning the weakest precondition of the command c with the context $\xi$ w.r.t. the postcondition (see [16] for formal definitions). This function is defined with the help of a function $\mathsf {wp}(c,a)$ returning the weakest precondition the command c w.r.t. the postcondition a.

Definition 5

(Validity of Configurations). A configuration is valid, denoted by $\mathsf {valid}(t,h)$, if there exist a list of augmented threads T, consisting of an identifier (id), a program (c), a context ($\xi$), a permission heap (p), a ghost resource heap (C) and a bag of obligations (O) associated with each thread; a list of assertions A, and some functions R, I, L, M, P, X such that:

• $\forall id,c,\xi .\;t(id)=(c;\xi )\Leftrightarrow \exists p,O,C.\;(id,c,\xi ,p,O,C)\in T$

• $h=\mathsf {pheap2heap}( \underset{a \in A}{*}a\;*\underset{(id,c,\xi ,p,O,C) \in T}{*}p)$

• $\forall (id,c,\xi ,p,O,C) \in T.$

  • $p,O,C\models \mathsf {wpcx}_{R,I,L,M,P,X}(c,\xi )$

  • $\forall l, Wt ,Ot.\;p(l)=\mathsf {Ulock/Locked}( Wt ,Ot)\Rightarrow Wt =\mathsf {Wt}_l\wedge Ot=\mathsf {Ot}_l$

  • $\forall l.\;p(l)=\mathsf {Lock}\wedge h(l)=1\Rightarrow \mathsf {I}(l)(\mathsf {Wt}_l,\mathsf {Ot}_l)\in A$

  • $\forall l.\;p(l)=\mathsf {Lock}\vee p(l)=\mathsf {Locked}(\mathsf {Wt}_l,\mathsf {Ot}_l) \Rightarrow \lnot P(l)\wedge \lnot \mathsf {exc}(l)\wedge (h(l)=0 \Rightarrow l \in \mathsf {Ot})$

  • $\forall o.\;\mathsf {waiting\_for}(c,h)=o\Rightarrow \mathsf {safe\_obs}_{R,L,P,X}(o,\mathsf {Wt},\mathsf {Ot})$

where

• 

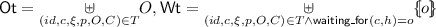
• $O_l$ is a bag that given an object o returns O(o) if $L(o)=l$ and 0 if $L(o)\ne l$

• $\mathsf {waiting\_for}(c,h)$ returns the object for which c is waiting, if any

• $\mathsf {pheap2heap}(p)$ returns the heap corresponding with permission heap p

We finally prove that for each proof rule we have $a\Rightarrow \mathsf {wp}(c,a')$. To this end, we first define correctness of commands, shown in Definition 6, and then for each proof rule we prove $\mathsf {correct}(a,c,a')$. In addition to the proof rules presented in this paper, other useful rules such as the rules consequence, frame and sequential, shown in Theorems 1, 2, and 3 can also be proved with the help of some auxiliary lemmas in [16]. Note that the indexes R, I, L, M, P, X are omitted when they are unimportant.

Definition 6

(Correctness of Commands)

$$\mathsf {correct}_{R,I,L,M,P,X}(a,c,a')\Leftrightarrow (a\Rightarrow \mathsf {wp}_{R,I,L,M,P,X}(c,a'))$$

Theorem 1

(Rule Consequence)

$$\begin{array}{l} \mathsf {correct}(a_1,c,a_2)\wedge (a_1'\Rightarrow a_1)\wedge (\forall z.\;a_2(z)\Rightarrow a_2'(z))\Rightarrow \mathsf {correct}(a_1',c,a_2') \end{array}$$

Theorem 2

(Rule Frame)

$$\begin{array}{l} \mathsf {correct}(a,c,a')\Rightarrow \mathsf {correct}(a*f,c,\lambda z.\;a'(z)*f) \end{array}$$

Theorem 3

(Rule Sequential Composition)

$$\begin{array}{l} \mathsf {correct}(a,c_1,a')\wedge (\forall z.\;\mathsf {correct}(a'(z),c_2[z/x],a''))\Rightarrow \\ \mathsf {correct}(a,\mathsf {let}\;x{:=}c_1\;\mathsf {in}\;c_2,a'') \end{array}$$

Theorem 4

(The Initial Configuration is Valid)

Proof

The goal is achieved because there are an augmented thread list , a list of assertions $A=[]$, and functions R, I, L, M, P, X by which all the conditions in the definition of validity of configurations are satisfied.

Theorem 5

(A Valid Configuration is Not Deadlocked)

$$\begin{array}{l} (\exists id,c,\xi ,o.\;t(id)=(c;\xi )\wedge \mathsf {waiting\_for}(c,h)=o)\wedge \mathsf {valid}(t,h)\\ \quad \Rightarrow \exists id',c',\xi ',\;t(id')=(c';\xi ')\wedge \mathsf {waiting\_for}(c',h)=\varnothing \end{array}$$

Proof

We assume that all threads in t are waiting for an object. Since (t, h) is a valid configuration there exists a valid augmented thread table T with a corresponding valid graph $G=\mathsf {g}(T)$, where $\mathsf {g}$ maps any element such as $(id,c,\xi ,p,O,C)$ to a new one such as $(\mathsf {waiting\_for}(c),O)$. By Lemma 1, we have , implying , implying $t=\mathbf {0}$ which contradicts the assumption of the theorem.

Theorem 6

(Steps Preserve Validity of Configurations). ⁷

$$\mathsf {valid}(\kappa )\wedge \kappa \leadsto \kappa '\Rightarrow \mathsf {valid}(\kappa ')$$

Proof

By case analysis of the small step relation $\leadsto$ (see [16] explaining the proof of some non-trivial cases).

6 Related Work

Several approaches to verify termination [1, 21], total correctness [3], and lock freedom [2] of concurrent programs have been proposed. These approaches are only applicable to non-blocking algorithms, where the suspension of one thread cannot lead to the suspension of other threads. Consequently, they cannot be used to verify deadlock-freedom of programs using condition variables, where the suspension of a notifying thread might lead a waiting thread to be infinitely blocked. In [22] a compositional approach to verify termination of multi-threaded programs is introduced, where rely-guarantee reasoning is used to reason about each thread individually while there are some assertions about other threads. In this approach a program is considered to be terminating if it does not have any infinite computations. As a consequence, it is not applicable to programs using condition variables because a waiting thread that is never notified cannot be considered as a terminating thread.

There are also some other approaches addressing some common synchronization bugs of programs in the presence of condition variables. In [8], for example, an approach to identify some potential problems of concurrent programs consisting waits and notifies commands is presented. However, it does not take the order of execution of theses commands into account. In other words, it might accept an undesired execution trace where the waiting thread is scheduled before the notifying thread, that might lead the waiting thread to be infinitely suspended. [9] uses Petri nets to identify some common problems in multithreaded programs such as data races, lost signals, and deadlocks. However the model introduced for condition variables in this approach only covers the communication of two threads and it is not clear how it deals with programs having more than two threads communicating through condition variables. Recently, [10] has introduced an approach ensuring that every thread synchronizing under a set of condition variables eventually exits the synchronization block if that thread eventually reaches that block. This approach succeeds in verifying one of the applications of condition variables, namely the buffer. However, since this approach is not modular and relies on a Petri net analysis tool to solve the termination problem, it suffers from a long verification time when the size of the state space is increased, such that the verification of a buffer application having 20 producer and 18 consumer threads, for example, takes more than two minutes.

Kobayashi [6, 20] proposed a type system for deadlock-free processes, ensuring that a well-typed process that is annotated with a finite capability level is deadlock free. He extended channel types with the notion of usages, describing how often and in which order a channel is used for input and output. For example, usage of x in the process x?y|x!1|x!2, where ?, !, | represent an input action, an output action, and parallel composition receptively, is expressed by ?|!|!, which means that x is used once for input and twice for output possibly in parallel. Additionally, to avoid circular dependency each action $\alpha$ is associated with the levels of obligation o and capabilities c, denoted by $\alpha ^{o}_{c}$, such that (1) an obligation of level n must be fulfilled by using only capabilities of level less than n, and (2) for an action of capability level n, there must exist a co-action of obligation level less than or equal to n. Leino et al. [4] also proposed an approach to verify deadlock-freedom of channels and locks. In this approach each thread trying to receive a message from a channel must spend one credit for that channel, where a credit for a channel is obtained if a thread is obliged to fulfil an obligation for that channel. A thread can fulfil an obligation for a channel if either it sends a message on that channel or delegate that obligation to other thread. The same idea is also used to verify deadlock-freedom of semaphores [7], where acquiring (i.e. decreasing) a semaphore consumes one credit and releasing (i.e. increasing) that semaphore produces one credit for that semaphore. However, as it is acknowledged in [4], it is impossible to treat channels (and also semaphores) like condition variables; a $\mathsf {wait}$ cannot be treated like a $\mathsf {receive}$ and a $\mathsf {notify}$ cannot be treated like a $\mathsf {send}$ because a notification for a condition variable will be lost if no thread is waiting for that variable. We borrow many ideas, including the notion of obligations/credits(capabilities) and levels, from these works and also the one introduced in [11], where a corresponding separation logic based approach is presented to verify total correctness of programs in the presence of channels.

7 Conclusion

It this article we introduced a modular approach to verify deadlock-freedom of monitors. We also introduced a relax, more general precedence relation to avoid cycles in the wait-for graph of programs, allowing a verification approach to verify a wider range of deadlock-free programs in the presence of monitors, channels and other synchronization mechanisms.