Abstract
We present SLR, the first expressive program logic for reasoning about concurrent programs under a weak memory model addressing the out-of-thin-air problem. Our logic includes the standard features from existing logics, such as RSL and GPS, that were previously known to be sound only under stronger memory models: (1) separation, (2) per-location invariants, and (3) ownership transfer via release-acquire synchronisation—as well as novel features for reasoning about (4) the absence of out-of-thin-air behaviours and (5) coherence. The logic is proved sound over the recent “promising” memory model of Kang et al., using a substantially different argument to soundness proofs of logics for simpler memory models.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Recent years have seen the emergence of several program logics [2, 6, 8, 16, 23, 24, 26,27,28] for reasoning about programs under weak memory models. These program logics are valuable tools for structuring program correctness proofs, and enabling programmers to reason about the correctness of their programs without necessarily knowing the formal semantics of the programming language. So far, however, they have only been applied to relatively strong memory models (such as TSO [19] or release/acquire consistency [15] that can be expressed as a constraint on individual candidate program executions) and provide little to no reasoning principles to deal with C/C++ “relaxed” accesses.
The main reason for this gap is that the behaviour of relaxed accesses is notoriously hard to specify [3, 5]. Up until recently, memory models have either been too strong (e.g., [5, 14, 17]), forbidding some behaviours observed with modern hardware and compilers, or they have been too weak (e.g., [4]), allowing so-called out-of-thin-air (OOTA) behaviour even though it does not occur in practice and is highly problematic.
One observable behaviour forbidden by the strong models is the load buffering behaviour illustrated by the example below, which, when started with both locations x and y containing 0, can end with both \(r_1\) and \(r_2\) containing 1. This behaviour is observable on certain ARMv7 processors after the compiler optimises \(r_2+1-r_2\) to 1.

However, one OOTA behaviour they should not allow is the following example by Boehm and Demsky [5]. When started with two completely disjoint lists a and b, by updating them separately in parallel, it should not be allowed to end with a and b pointing to each other, as that would violate physical separation (for simplicity, in these lists, a location just holds the address of the next element):

Because of this specification gap, program logics either do not reason about relaxed accesses, or they assume overly strengthened models that disallow some behaviours that occur in practice (as discussed in Sect. 5).
Recently, there have been several proposals of programming language memory models that allow load buffering behaviour, but forbid obvious out-of-thin-air behaviours [10, 13, 20]. This development has enabled us to develop a program logic that provides expressive reasoning principles for relaxed accesses, without relying on overly strong models.
In this paper, we present SLR, a separation logic based on RSL [27], extended with strong reasoning principles for relaxed accesses, which we prove sound over the recent “promising” semantics of Kang et al. [13]. SLR features per-location invariants [27] and physical separation [22], as well as novel assertions that we use to show the absence of OOTA behaviours and to reason about various coherence examples. (Coherence is a property of memory models that requires the existence of a per-location total order on writes that reads respect.)
There are two main contributions of this work.
First, SLR is the first logic which can prove absence of OOTA in all the standard litmus tests. As such, it provides more evidence to the claim that the promising semantics solves the out-of-thin-air problem in a satisfactory way. The paper that introduced the promising semantics [13] comes with three DRF theorems and a simplistic value logic. These reasoning principles are enough to show absence of some simple out-of-thin-air behaviours, but it is still very easy to end up beyond the reasoning power of these two techniques. For instance, they cannot be used to prove that \(r_1 = 0\) in the following “random number generator” litmus testFootnote 1, where both the x and y locations initially hold 0.

The subtlety of this litmus test is the following: if the first thread reads a certain value v from x, then it writes \(v + 1\) to y, which the second thread can read, and write to x; this, however, does not enable the first thread to read \(v + 1\). SLR features novel assertions that allow it to handle those and other examples, as shown in the following section.
The second major contribution is the proof of soundness of SLR over the promising semantics [13]Footnote 2. The promising semantics is an operational model that represents memory as a collection of timestamped write messages. Besides the usual steps that execute the next command of a thread, the model has a non-standard step that allows a thread to promise to perform a write in the future, provided that it can guarantee to be able to fulfil its promise. After a write is promised, other threads may read from that write as if it had already happened. Promises allow the load-store reordering needed to exhibit the load buffering behaviour above, and yet seem, from a series of litmus tests, constrained enough so as to not introduce out-of-thin-air behaviour.
Since the promising model is rather different from all other (operational and axiomatic) memory models for which a program logic has been developed, none of the existing approaches for proving soundness of concurrent program logics are applicable to our setting. Two key difficulties in the soundness proof come from dealing with promise steps.
-
1.
Promises are very non-modular, as they can occur at every execution point and can affect locations that may only be accessed much later in the program.
-
2.
Since promised writes can be immediately read by other threads, the soundness proof has to impose the same invariants on promised writes as the ones it imposes on ordinary writes (e.g., that only values satisfying the location’s protocol are written). In a logic supporting ownership transfer,Footnote 3 however, establishing those invariants is challenging, because a thread may promise to write to x even without having permission to write to x.
To deal with the first challenge, our proof decouples promising steps from ordinary execution steps. We define two semantics of Hoare triples—one “promising”, with respect to the full promising semantics, and one “non-promising”, with respect to the promising semantics without promising steps—and prove that every Hoare triple that is correct with respect to its non-promising interpretation is also correct with respect to its promising interpretation. This way, we modularise reasoning about promise steps. Even in the non-promising semantics, however, we do allow threads to have outstanding promises. The main difference in the non-promising semantics is that threads are not allowed to issue new promises.
To resolve the second challenge, we observe that in programs verified by SLR, a thread may promise to write to x only if it is able to acquire the necessary write permission before performing the actual write. This follows from promise certification: the promising semantics requires all promises to be certifiable; that is, for every state of the promising machine, there must exist a non-promising execution of the machine that fulfils all outstanding promises.
We present the SLR assertions and rules informally in Sect. 2. We then give an overview of the promising semantics of Kang et al. [13] in Sect. 3, and use it in Sect. 4 to explain the proof of soundness of SLR. We discuss related work in Sect. 5. Details of the rules of SLR and its soundness proof can be found in our technical appendix [1].
2 Our Logic
The novelty of our program logic is to allow non-trivial reasoning about relaxed accesses. Unlike release/acquire accesses, relaxed accesses do not induce synchronisation between threads, so the usual approach of program logics, which relies on ownership transfer, does not apply. Therefore, in addition to reasoning about ownership transfer like a standard separation logic, our logic supports reasoning about relaxed accesses by collecting information about what reads have been observed, and in which order. When combined with information about which writes have been performed, we can deduce that certain executions are impossible.
For concreteness, we consider a minimal “WHILE” programming language with expressions, \(e \in \textit{Expr}\), and statements, \(s \in \textit{Stm}\), whose syntax is given in Fig. 1. Besides local register assignments, statements also include memory reads with relaxed or acquire mode, and memory writes with relaxed or release mode.
2.1 The Assertions of the Logic
The SLR assertion language is generated by the following grammar, where N, l, v, t, \(\pi \) and X all range over a simply-typed term language which we assume includes booleans, locations, values and expressions of the programming language, fractional permissions, and timestamps, and is closed under pairing, finite sets, and sequences. By convention, we assume that l, v, t, \(\pi \) and X range over terms of type location, value, timestamp, permission and sets of pairs of values, and timestamps, respectively.

The grammar contains the standard operators from first order logic and separation logic, the \(\mathsf {Rel}\) and \(\mathsf {Acq}\) assertions from RSL [27], and a few novel constructs.
\(\mathsf {Rel}(l,\phi )\) grants permission to perform a release write to location l and transfer away the invariant \(\phi (v)\), where v is the value written to that location. Conversely, \(\mathsf {Acq}(l,\phi )\) grants permission to perform an acquire read from location l and gain access to the invariant \(\phi (v)\), where v is the value returned by the read.
The first novel assertion form, \(\mathsf {O}({l},{v},{t})\), records the fact that location l was observed to have value v at timestamp t. The timestamp is used to order it with other reads from the same location. The information this assertion provides is very weak: it merely says that the owner of the assertion has observed that value, it does not imply that any other thread has ever observed it.
The other novel assertion form, \(\mathsf {W}^{\pi }({l},{X})\), asserts ownership of location l and records a set of writes X to that location. The fractional permission \(\pi \in \mathbb {Q}\) indicates whether ownership is shared or exclusive. Full permission, \(\pi = 1\), confers exclusive ownership of location l and ensures that X is the set of all writes to location l; any fraction, \(0< \pi < 1\), confers shared ownership and enforces that X is a lower-bound on the set of writes to location l. The order of writes to l is tracked through timestamps; the set X is thus a set of pairs consisting of the value and the timestamp of the write.
In examples where we only need to refer to the order of writes and not the exact timestamps, we write \(\mathsf {W}^{\pi }({x},{\ell })\), where \(\ell = [v_1, ..., v_n]\) is a list of values, as shorthand for  . The \(\mathsf {W}^{\pi }({x},{\ell })\) assertion thus expresses ownership of location x with permission \(\pi \), and that the writes to x are given by the list \(\ell \) in order, with the most recent write at the front of the list.
. The \(\mathsf {W}^{\pi }({x},{\ell })\) assertion thus expresses ownership of location x with permission \(\pi \), and that the writes to x are given by the list \(\ell \) in order, with the most recent write at the front of the list.
Relation Between Reads and Writes. Records of reads and writes can be confronted by the thread owning the exclusive write assertion: all reads must have read values that were written. This is captured formally by the following property:

Random Number Generator. These assertions allow us to reason about the “random number generator” litmus test from the Introduction, and to show that it cannot read arbitrarily large values. As discussed in the Introduction, capturing the set of values that are written to x, as made possible by the “invariant-based program logic” of Kang et al. [13, Sect. 5.5] and of Jeffrey and Riley [10, Sect. 6], is not enough, and we make use of our stronger reasoning principles. We use \(\mathsf {O}({x},{a},{t})\) to record what values reads read from each location, and \(\mathsf {W}^{1}({x},{\ell })\) to record what sequences of values were written to each location, and then confront these records at the end of the execution. The proof sketch is then as follows:

At the end of the execution, we are able to draw conclusions about the values of the registers. From \(\mathsf {W}^{1}({x},{[r_2; 0]})\) and \(\mathsf {O}({x},{r_1},{\_})\), we know that \(r_1 \in \{ r_2, 0 \}\) by rule Reads-from-Write. Similarly, we know that \(r_2 \in \{ r_1 + 1, 0 \}\), and so we can conclude that \(r_1 = 0\). We discuss the distribution of resources at the beginning of a program, and their collection at the end of a program, in Theorem 2. Note that we are unable to establish what values the reads read before the end of the litmus test. Indeed, before the end of the execution, nothing enforces that there are no further writes that reads could read from.
2.2 The Rules of the Logic for Relaxed Accesses
We now introduce the rules of our logic by focusing on the rules for relaxed accesses. In addition, we support the standard rules from separation logic and Hoare logic, rules for release/acquire accesses (Sect. 2.4), and the following consequence rule:

which allows one to use “view shifting” implications to strengthen the precondition and weaken the postcondition.
The rules for relaxed accesses are adapted from the rules of RSL [27] for release/acquire accesses, but use our novel resources to track the more subtle behaviour of relaxed accesses. Since relaxed accesses do not introduce synchronisation, they cannot be used to transfer ownership; they can, however, be used to transfer information. For this reason, as in RSL [27], we associate a predicate \(\phi \) on values to a location x using paired \(\mathsf {Rel}(x,\phi )\) and \(\mathsf {Acq}(x,\phi )\) resources, for writers and readers, respectively. To write v to x, a writer has to provide \(\phi (v)\), and in exchange, when reading v from x, a reader obtains \(\phi (v)\). However, here, relaxed writes can only send pure predicates (i.e., ones which do not assert ownership of any resources), and relaxed reads can only obtain the assertion from the predicate guarded by a modality \(\nabla {}\)Footnote 4 that only pure assertions filter through: if P is pure, then \(\nabla {P} \Longrightarrow P\). All assertions expressible in first-order logic are pure.
Relaxed Write Rule. To write value v (to which the value expression \(e_2\) evaluates) to location x (to which the location expression \(e_1\) evaluates), the thread needs to own a write permission \(\mathsf {W}^{\pi }({x},{X})\). Moreover, it needs to provide \(\phi (v)\), the assertion associated to the written value, v, to location x by the \(\mathsf {Rel}(x,\phi )\) assertion. Because the write is a relaxed write, and therefore does not induce synchronisation, \(\phi (v)\) has to be a pure predicate. The write rule updates the record of writes with the value written, timestamped with a timestamp newer than any timestamp for that location that the thread has observed so far; this is expressed by relating it to a previous timestamp that the thread has to provide through an \(\mathsf {O}({x},{\_},{t})\) assertion in the precondition.

The \(\mathsf {Rel}(x,\phi )\) assertion is duplicable, so there is no need for the rule to keep it.
In practice, \(\mathsf {O}({x},{\_},{t})\) is taken to be that of the last read from x if it was the last operation on x, and \(\mathsf {O}({x},{\textit{fst}(\max (X))},{\textit{snd}(\max (X))})\) if the last operation on x was a write, including the initial write. The latter can be obtained by

Relaxed Read Rule. To read from location x (to which the location expression e evaluates), the thread needs to own an \(\mathsf {Acq}(x,\phi )\) assertion, which gives it the right to (almost) obtain assertion \(\phi (v)\) upon reading value v from location x. The thread then keeps its \(\mathsf {Acq}(x,\phi )\), and obtains an assertion \(\mathsf {O}({x},{r},{t'})\) stating that it has read the value now in register r from location x, timestamped with \(t'\). This timestamp is no older than any timestamp for that location that the thread has observed so far, expressed again by relating it to an \(\mathsf {O}({x},{\_},{t})\) assertion in the precondition. Moreover, it obtains the pure portion \(\nabla \phi (r)\) of the assertion \(\phi (r)\) corresponding to the value read in register r

Again, we can obtain \(\mathsf {O}({x},{v_0^x},{0})\), where \(v_0^x\) is the initial value of x, from the initial write permission for x, and distribute it to all the threads that will read from x, expressing the fact that the initial value is available to all threads, and use it as the required \(\mathsf {O}({x},{\_},{t})\) in the precondition of the read rule.
Moreover, if a thread owns the exclusive write permission for a location x, then it can take advantage of the fact that it is the only writer at that location to obtain more precise information about its reads from that location: they will read the last value it has written to that location.

Separation. With these assertions, we can straightforwardly specify and verify the Disjoint-Lists example. Ownership of an element of a list is simply expressed using a full write permission, \(\mathsf {W}^{1}({x},{X})\). This allows including the Disjoint-Lists as a snippet in a larger program where the lists can be shared before or after, and still enforce the separation property we want to establish. While this reasoning sounds underwhelming (and we elide the details), we remark that it is unsound in models that allow OOTA behaviours.
2.3 Reasoning About Coherence
An important feature of many memory models is coherence, that is, the existence of a per-location total order on writes that reads respect. Coherence becomes interesting where there are multiple simultaneous writers to the same location (write/write races). In our logic, write assertions can be split and combined as follows: if \(\pi _1 + \pi _2 \le 1\), \(0 < \pi _1\) and \(0 < \pi _2\) then

To reason about coherence, the following rules capture the fact that the timestamps of the writes at a given location are all distinct, and totally ordered:

CoRR2. One of the basic tests of coherence is the CoRR2 litmus test, which tests whether two threads can disagree on the order of two writes to the same location. The following program, starting with location x holding 0, should not be allowed to finish with \(r_1 = 1 * r_2 = 2 * r_3 = 2 * r_4 = 1\), as that would mean that the third thread sees the write of 1 to x before the write of 2 to x, but that the fourth thread sees the write of 2 before the write of 1:

Coherence enforces a total order on the writes to x that is respected by the reads, so if the third thread reads 1 then 2, then the fourth cannot read 2 then 1.
We use the timestamps in the \(\mathsf {O}({x},{a},{t})\) assertions to record the order in which reads read values, and then link the timestamps of the reads with those of the writes. Because we do not transfer anything, the predicate for x is  again, and we elide the associated clutter below.
again, and we elide the associated clutter below.
The proof outline for the writers just records what values have been written:

The proof outline for the readers just records what values have been read, and—crucially—in which order.

At the end of the program, by combining the two write permissions using rule Combine-Writes, we obtain \(\mathsf {W}^{1}({x},{\{ (1,t_1), (2,t_2), (0,0) \}})\). From this, we have \(t_1 < t_2\) or \(t_2 < t_1\) by rules Different-Writes and Writes-Ordered. Now, assuming \(r_1 = 1\) and \(r_2 = 2\), we have \(t_a < t_b\), and so \(t_1 < t_2\) by rule Reads-from-Write. Similarly, assuming \(r_3 = 2\) and \(r_4 = 1\), we have \(t_2 < t_1\). Therefore, we cannot have \(r_1 = 1 * r_2 = 2 * r_3 = 2 * r_4 = 1\), so coherence is respected, as desired.
2.4 Handling Release and Acquire Accesses
Next, consider release and acquire accesses, which, in addition to coherence, provide synchronisation and enable the message passing idiom.

The first thread writes data (here, 1) to a location x, and signals that the data is ready by writing 1 to a “flag” location y with a release write. The second thread reads the flag location y with an acquire read, and, if it sees that the first thread has signalled that the data has been written, reads the data. The release/acquire pair is sufficient to ensure that the data is then visible to the second thread.
Release/acquire can be understood abstractly in terms of views [15]: a release write contains the view of the writing thread at the time of the writing, and an acquire read updates the view of the reading thread with that of the release write it is reading from. This allows one-way synchronisation of views between threads.
To handle release/acquire accesses in SLR, we can adapt the rules for relaxed accesses by enabling ownership transfer according to predicate associated with the \(\mathsf {Rel}\) and \(\mathsf {Acq}\) permissions. The resulting rules are strictly more powerful than the corresponding RSL [27] rules, as they also allow us to reason about coherence.
Release Write Rule. The release write rule is the same as for relaxed writes, but does not require the predicate to be a pure predicate, thereby allowing sending of actual resources, rather than just information:

Acquire Read Rule. Symmetrically, the acquire read rule is the same as for relaxed reads, but allows the actual resource to be obtained, not just its pure portion:

We have to update \(\phi \) to record the fact that we have obtained the resource associated with reading that value, so that we do not erroneously obtain that resource twice; \(\phi [v' \mapsto P]\) stands for  .
.
As for relaxed accesses, we can strengthen the read rule when the reader is also the exclusive writer to that location:

Additionally, we allow duplicating of release assertions and splitting of acquire assertions, as expressed by the following two rules.

Message Passing. With these rules, we can easify verify the message passing example. Here, we want to transfer a resource from the writer to the reader, namely the state of the data, x. By transferring the write permission for the data to the reader over the “flag” location, y, we allow the reader to use it to read the data precisely. We do that by picking the predicate

for y. Since we do not transfer any resource using x, the predicate for x is  .
.
The writer transfers the write permissions for x away on y using \(\phi _y\):

The proof outline for the reader uses the acquire permission \(\phi _y\) for y to obtain \(\mathsf {W}^{1}({x},{[1;0]})\), which it then uses to know that it reads 1 from x.

2.5 Plain Accesses
Our formal development (in the technical appendix) also features the usual “partial ownership” \(x {\mathop {\mapsto }\limits ^{\pi }} v\) assertion for “plain” (non-atomic) locations, and the usual corresponding rules.
3 The Promising Semantics
In this section, we provide an overview of the promising semantics [13], the model for which we prove SLR sound. Formal details can be found in [1, 13].
The promising semantics is an operational semantics that interleaves execution of the threads of a program. Relaxed behaviour is introduced in two ways:
-
As in the “strong release/acquire” model [15], the memory is a pool of timestamped messages, and each thread maintains a “view” thereof. A thread may read any value that is not older than the latest value observed by the thread for the given location; in particular, this may well not be the latest value written to that particular location. Timestamps and views model non-multi-copy-atomicity: writes performed by one thread do not become simultaneously visible by all other threads.
-
The operational semantics contains a non-standard step: at any point a thread can nondeterministically promise a write, provided that, at every point before the write is actually performed, the thread can certify the promise, that is, execute the write by running on its own from the current state. Promises are used to enable load-store reordering.
The behaviour of promising steps can be illustrated on the LB+data+fakedep litmus test from the Introduction. The second thread can, at the very start of the execution, promise a write of 1 to x, because it can, by running on its own from the current state, read from y (it will read 0), then write 1 to x (because \(0 + 1 - 0 = 1\)), thereby fulfilling its promise. On the other hand, the first thread cannot promise a write of 1 to y at the beginning of the execution, because, by running on its own, it can only read 0 from x, and therefore only write 0 to y.
3.1 Storage Subsystem
Formally, the semantics keeps track of writes and promises in a global configuration, \( gconf ={\langle M,P \rangle }\), where \(M\) is a memory and \(P\subseteq M\) is the promise memory. We denote by \( gconf .\texttt {M}\) and \( gconf .\texttt {P}\) the components of \( gconf \). Both memories are finite sets of messages, where a message is a tuple \(\langle x :_{i}^{o} v, R @ t]\rangle \), where \(x \in {\textit{Loc}}\) is the location of the message, \(v \in {\textit{Val}}\) its value, \(i \in {\textit{Tid}}\) its originating thread, \(t \in {\textit{Time}}\) its timestamp, \(R\) its message view, and \(o\in \{\texttt {rlx},\texttt {rel}\}\) its message mode, where \({\textit{Time}}\) is an infinite set of timestamps, densely totally ordered by \(\le \), with a minimum element, 0. (We return to views later.) We denote \(m.{\texttt {loc}}\), \(m.{\texttt {val}}\), \(m.{\texttt {time}}\), \(m.\texttt {view}\) and \(m.\texttt {mod}\) the components of a message m. We use the following notation to restrict memories:

A global configuration \( gconf \) evolves in two ways. First, a message can be “promised” and be added both to \( gconf \!.\texttt {M}\) and \( gconf \!.\texttt {P}\). Second, a message can be written, in which case it is either added to \( gconf \!.\texttt {M}\), or removed from \( gconf \!.\texttt {P}\) (if it was promised before).
3.2 Thread Subsystem
A thread state is a pair \( TS ={\langle \sigma ,V \rangle }\), where \(\sigma \) is the internal state of the thread and \(V\) is a view. We denote by \( TS .\sigma \) and \( TS .V\) the components of \( TS \).
Thread Internal State. The internal state \(\sigma \) consists of a thread store (denoted \(\sigma .\mu \)) that assigns values to local registers and a statement to execute (denoted \(\sigma .s\)). The transitions of the thread internal state are labeled with memory actions and are given by an ordinary sequential semantics. As these are routine, we leave their description to the technical appendix.
Views. Thread views are used to enforce coherence, that is, the existence of a per-location total order on writes that reads respect. A view is a function \(V:{\textit{Loc}}\rightarrow {\textit{Time}}\), which records how far the thread has seen in the history of each location. To ensure that a thread does not read stale messages, its view restricts the messages the thread may read, and is increased whenever a thread observes a new message. Messages themselves also carry a view (the thread’s view when the message comes from a release write, and the bottom view otherwise) which is incorporated in the thread view when the message is read by an acquire read.
Additional Notations. The order on timestamps, \(\le \), is extended pointwise to views. \(\bot \) and \(\sqcup \) denote the natural bottom elements and join operations for views.  denotes the view assigning t to x and \({\small 0}\) to other locations.
denotes the view assigning t to x and \({\small 0}\) to other locations.
3.3 Interaction Between a Thread and the Storage Subsystem
The interaction between a thread and the storage subsystem is given in terms of transitions of thread configurations. Thread configurations are tuples \(\langle TS , \langle M, P \rangle \rangle \), where \( TS \) is a thread state, and \({\langle M,P \rangle }\) is a global configuration. These transitions are labelled with \(\beta \in \{ \text {NP}, \text {prom} \}\) in order to distinguish whether they involve promises or not. A thread can:
-
Make an internal transition with no effect on the storage subsystem.
-
Read the value v from location x, when there is a matching message in memory that is not outdated according to the thread’s view. It then updates its view accordingly: it updates the timestamp for location x and, in addition, incorporates the message view if the read is an acquire read.
-
Write the value v to location x. Here, the thread picks a timestamp greater than the one of its current view for the message it adds to memory (or removes from the promise set). If the write is a release write, the message carries the view of the writing thread. Moreover, a release write to x can only be performed when the thread has already fulfilled all its promises to x.
-
Non-deterministically promise a relaxed write by adding a message to both M and P.
3.4 Constraining Promises
Now that we have described how threads and promises interact with memory, we can present the certification condition for promises, which is essential to avoid out-of-thin-air behaviours. Accordingly, we define another transition system, \({\mathop {\Longrightarrow }\limits ^{}}\), on top of the previous one, which enforces that the memory remains “consistent”, that is, all the promises that have been made can be certified. A thread configuration \(\langle TS , \langle M, P \rangle \rangle \) is called consistent w.r.t. \(i\in {\textit{Tid}}\) if thread i can fulfil its promises by executing on its own, or more formally if \(\langle TS , \langle M, P \rangle \rangle {\mathop {\longrightarrow }\limits ^{\text {NP}}}^*_i \langle TS ', \langle M', P' \rangle \rangle \) for some \( TS ',M',P'\) such that \({P'}(i) =\emptyset \). Certification is local, that is, only thread i is executing during its certification; this is crucial to avoid out-of-thin-air. Further, the certification itself cannot make additional promises, as it is restricted to NP-steps. Here is a visual representation of a promise machine run, together with certifications.

The thread configuration \({\mathop {\Longrightarrow }\limits ^{}}\)-transitions allow a thread to (1) take any number of non-promising steps, provided its thread configuration at the end of the sequence of step (intuitively speaking, when it gives control back to the scheduler) is consistent, or (2) take a promising step, again provided that its thread configuration after the step is consistent.
3.5 Full Machine
Finally, the full machine transitions simply lift the thread configuration \({\mathop {\Longrightarrow }\limits ^{}}\)-transitions to the machine level. A machine state is a tuple \({\mathbf {MS}}= \langle \mathcal {T\!S}, \langle M, P \rangle \rangle \), where \(\mathcal {T\!S}\) is a function assigning a thread state \( TS \) to every thread, and \({\langle M,P \rangle }\) is a global configuration. The initial state \({\mathbf {MS}}^0\) (for a given program) consists of the function \(\mathcal {T\!S}^0\) mapping each thread i to its initial state \({\langle \sigma _i^0,\bot \rangle }\), where \(\sigma _i^0\) is the thread’s initial local state and \(\bot \) is the zero view (all timestamps in views are \({\small 0}\)); the initial memory \(M^0\) consisting of one message \(\langle x :_{{\small 0}}^{\texttt {rlx}} 0, \bot @ {\small 0}]\rangle \) for each location x; and the empty set of promises.
4 Semantics and Soundness
In this section, we present the semantics of SLR, and give a short overview of the soundness proof. Our focus is not on the technical details of the proof, but on the two main challenges in defining the semantics and proving soundness:
-
1.
Reasoning about promises. This difficulty arises because promise steps can be nondeterministically performed by the promise machine at any time.
-
2.
Reasoning about release-acquire ownership transfer in the presence of promises. The problem is that writes may be promised before the thread has acquired enough resources to allow it to actually perform the write.
4.1 The Intuition
SLR assertions are interpreted by (sets of) resources, which represent permissions to write to a certain location and/or to obtain further resources by reading a certain message from memory. As is common in semantics of separation logics, the resources form a partial commutative monoid, and SLR’s separating conjunction is interpreted as the composition operation of the monoid.
When defining the meaning of a Hoare triple \(\{{P}\}\;{s}\;\{{Q}\}\), we think of the promise machine as if it were manipulating resources: each thread owns some resources and operates using them. The intuitive description of the Hoare triple semantics is that every run of the program \(s\) starting from a state containing the resources described by the precondition, P, will be “correct” and, if it terminates, will finish in a state containing the resources described by the postcondition, Q. The notion of a program running correctly can be described in terms of threads “respecting” the resources they own; for example, if a thread is executing a write or fulfilling a promise, it should own a resource representing the write permission.
4.2 A Closer Look at the Resources and the Assertion Semantics
We now take a closer look at the structure of resources and the semantics of assertions, whose formal definitions can be found in Figs. 2 and 3.
The idea is to interpret assertions as predicates over triples consisting of memory, a view, and a resource. We use the resource component to model assertions involving ownership (i.e., write assertions and acquire assertions), and model other assertions using the memory and view components. Once a resource is no longer needed, SLR allows us to drop these from assertions: \(P * Q \Rightarrow P\). To model this we interpret assertions as upwards-closed predicates, that may own more than explicitly asserted. The ordering on memories and views is given by the promising semantics, and the ordering on resources is induced by the composition operation in the resource monoid. For now, we leave the resource composition unspecified, and return to it later.
In addition, however, we have to deal with assertions that are parametrised by predicates (in our case, \(\mathsf {Rel}(x,\phi )\) and \(\mathsf {Acq}(x,\phi )\)). Doing so is not straightforward because naïve attempts of giving semantics to such assertions result in circular definitions. A common technique for avoiding this circularity is to treat predicates stored in assertions syntactically, and to interpret assertions relative to a world, which is used to interpret those syntactic predicates. In our case, worlds consist of two components: the WrPerm component associates a syntactic SLR predicate with every location (this component is used to interpret release permissions), while the AcqPerm component associates a syntactic predicate with a finite number of currently allocated predicate identifiers (this component is used to interpret acquire permissions). The reason for the more complex structure for acquire permissions is that they can be split (see (Acquire-Split)). Therefore, we allow multiple predicate identifiers associated with a single location. When acquire permissions are divided and split between threads, new predicate identifiers are allocated and associated with predicates in the world. The world ordering, \(\mathcal {W}_1 \le \mathcal {W}_2\), expresses that world \(\mathcal {W}_2\) is an extension of \(\mathcal {W}_1\) in which new predicate identifiers may have been allocated, but all existing predicate identifiers are associated with the same predicates.
Let us now focus our attention on the assertion semantics. The semantics of assertions,  , is relative to a thread store \(\mu \) that assigns values to registers, and an environment \(\eta \) that assigns values to logical variables.
, is relative to a thread store \(\mu \) that assigns values to registers, and an environment \(\eta \) that assigns values to logical variables.
The standard logical connectives and quantifiers are interpreted following their usual intuitionistic semantics. The semantics of our novel assertions is given in Fig. 3 and can be explained as follows:
-
The observed assertion \(\mathsf {O}({x},{v},{t})\) says that the memory contains a message at location x with value v and timestamp t, and the current thread knows about it (i.e., the thread view contains it).
-
The write assertion \(\mathsf {W}^{\pi }({x},{X})\) asserts ownership of a (partial, with fraction \(\pi \)) write resource at location x, and requires that the largest timestamp recorded in X does not exceed the view of the current thread.
-
The acquire assertion, \(\mathsf {Acq}(x, \phi )\), asserts that location x has some predicate identifier \(\iota \) associated with the \(\phi \) predicate in the current world \(\mathcal {W}\).
-
The release assertion, \(\mathsf {Rel}(x, \phi )\), asserts that location x is associated with some predicate \(\phi '\) in the current world such that there exists a syntactic proof of the entailment,
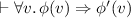 . The implication allows us to strengthen the predicate in release assertions.
. The implication allows us to strengthen the predicate in release assertions. -
Finally, \(\nabla {P}\) states that P is satisfiable in the current world.
Note that \(\mathsf {W}^{\pi }({x},{X})\), \(\mathsf {Acq}(x, \phi )\), and \(\mathsf {Rel}(x, \phi )\) only talk about owning certain resources, and do not constrain the memory itself at all. In the next subsection, we explain how we relate the abstract resources with the concrete machine state.
4.3 Relating Concrete State and Resources
Before giving a formal description of the relationship between abstract resources and concrete machine states, we return to the intuition of threads manipulating resources presented in Sect. 4.1.
Consider what happens when a thread executes a release write to a location x. At that point, the thread has to own a release resource represented by \(\mathsf {Rel}(x,\phi )\), and to store the value v, it has to own the resources represented by \(\phi (v)\). As the write is executed, the thread gives up the ownership of the resources corresponding to \(\phi (v)\). Conversely, when a thread that owns the resource represented by \(\mathsf {Acq}(x,\phi )\) performs an acquire read of a value v from location x, it will gain ownership of resources satisfying \(\phi (v)\). However, this picture does not account for what happens to the resources that are “in flight”, i.e., the resources that have been released, but not yet acquired.
Our approach is to associate in-flight resources to messages in the memory. When a thread does a release write, it attaches the resources it released to the message it just added to the memory. That way, a thread performing an acquire read from that message can easily take ownership of the resources that are associated to the message. Formally, as the execution progresses, we update the assignment of resources to messages,
For every release message in memory M, the message resource assignment u gives us a mapping from predicate identifiers to resources. Here, we again use predicate identifiers to be able to track which acquire predicate is being satisfied by which resource. The intended reading of \(u(m)(\iota ) = r\) is that the resource r attached to the message m satisfies the predicate with the identifier \(\iota \).
We also require that the resources attached to a message (i.e., the resources released by the thread that wrote the message) suffice to satisfy all the acquire predicates associated with that particular location. Together, these two properties of our message resource assignment, as formalised in Fig. 4, allow us to describe the release/acquire ownership transfer.
The last condition in the message resource satisfaction relation has to do with relaxed accesses. Since relaxed accesses do not provide synchronisation, we disallow ownership transfer through them. Therefore, we require that the release predicates connected with the relaxed messages are satisfiable with the empty resource. This condition, together with the requirement that the released resources satisfy acquire predicates, forbids ownership transfer via relaxed accesses.
The resource missing from the discussion so far is the write resource (modelling the \(\mathsf {W}^{\pi }({x},{X})\) assertion). Intuitively, we would like to have the following property: whenever a thread adds a message to the memory, it has to own the corresponding write resource. Recall there are two ways a thread can produce a new message:
-
1.
A thread performs a write. This is the straightforward case: we simply require the thread to own the write resource and to update the set of value-timestamp pairs recorded in the resource accordingly.
-
2.
A thread promises a write. Here the situation is more subtle, because the thread might not own the write resource at the time it is issuing the promise, but will acquire the appropriate resource by the time it fulfils the promise. So, in order to assert that the promise step respects the resources owned by the thread, we also need to be able to talk about the resources that the thread can acquire in the future.
When dealing with the promises, the saving grace comes from the fact that all promises have to be certifiable, i.e., when issuing a promise a thread has to be able to fulfil it without help from other threads.
Intuitively, the existence of a certification run tells us that even though at the moment a thread issues a promise, it might not have the resources necessary to actually perform the corresponding write, the thread should, by running uninterrupted, still be able to obtain the needed resources before it fulfils the promise. This, in turn, tells us that the needed resources have to be already released by the other threads by the time the promise is made: only resources attached to messages in the memory are available to be acquired, and only the thread that made the promise is allowed to run during the certification; therefore all the available resources have already been released.
The above reasoning shows what it means for the promise steps to “respect resources”: when promises are issued, the resources currently owned by a thread, together with all the resources it is able to acquire according to the resources it owns and the current assignment of resources to messages, have to contain the appropriate write resource for the write being promised. The notion of “resources a thread is able to acquire” is expressed through the \(\mathrm {canAcq}(r,u)\) predicate. \(\mathrm {canAcq}(r,u)\) performs a fixpoint calculation: the resources we have (r) allow us to acquire some more resources from the messages in memory (assignment of resources to messages is given by u), which allows us to acquire some more, and so on. Its formal definition can be found in the technical appendix, and hinges on the fact that u precisely tracks which resources satisfy which predicates.
An important element that was omitted from the discussion so far is the definition of the composition in the resource monoid \( Res \). The resource composition, defined in Fig. 5, follows the expected notion of per-component composition. The most important feature is in the composition of write resources: a full permission write resource is only composable with the empty write resource.
At this point, we are equipped with all the necessary ingredients to relate abstract states represented by resources to concrete states \({\langle M,P \rangle }\) (where M is memory, and P is the set of promised messages). We define a function, called erasure, that given an assignment of resources to threads, \(r_F :\textit{ThreadId} \rightarrow Res \), an assignment of resources to messages, u, and a world, \(\mathcal {W}\), gives us a set of concrete states satisfying the following conditions:
-
1.
Memory M is consistent with respect to the total resource r and the message resource assignment u at world \(\mathcal {W}\).
-
2.
The set of fulfilled writes to each location x in \({\langle M, P \rangle }\) must match the set of writes of all write permissions owned by any thread or associated with any messages, when combined.
-
3.
For all unfulfilled promises to a location x by thread i, thread i must currently own or be able to acquire from u at least a shared write permission for x.
Our formal notion of erasure, defined in Fig. 6, has an additional parameter, a set of thread identifiers T. This set allows us to exclude promises of threads T from the requirement of respecting the resources. As we will see in the following subsection, this additional parameter plays a subtle, but key, role in the soundness proof. (The notion of erasure described above corresponds to the case when \(T=\emptyset \).)
Note also that the arguments of erasure very precisely account for who owns which part of the total resource. This diverges from the usual approach in separation logic, where we just give the total resource as the argument to the erasure. Our approach is motivated by Lemma 1, which states that a reader that owns the full write resource for location x knows which value it is going to read from x. This is the key lemma in the soundness proof of the (r-rlx*) and (r-acq*) rules.
Lemma 1
If  , and \({\langle M,P \rangle } \in {\lfloor r_F, u, \mathcal {W} \rfloor _{\{ i \}}}\) then for all messages \(m \in {M}(x) \setminus {P}(i)\) such that \(V(x) \le m.\texttt {time}\), we have \(m.\texttt {val}= \textit{fst}(\max (X))\).
, and \({\langle M,P \rangle } \in {\lfloor r_F, u, \mathcal {W} \rfloor _{\{ i \}}}\) then for all messages \(m \in {M}(x) \setminus {P}(i)\) such that \(V(x) \le m.\texttt {time}\), we have \(m.\texttt {val}= \textit{fst}(\max (X))\).
Lemma 1 is looking from the perspective of thread i that owns the full write resource for the location x. This is expressed by  (recall that \(r_F(i)\) are the resources owned by the thread i). Furthermore, the lemma assumes that the concrete state respects the abstract resources, expressed by \({\langle M,P \rangle } \in {\lfloor r_F, u, \mathcal {W} \rfloor _{\{ i \}}}\). Under these assumptions, the lemma intuitively tells us that the current thread knows which value it will read from x. Formally, the lemma says that all the messages thread i is allowed to read (i.e., messages in the memory that are not outstanding promises of thread i and whose timestamp is greater or equal to the view of thread i) have the value that appears as the maximal element in the set X.
(recall that \(r_F(i)\) are the resources owned by the thread i). Furthermore, the lemma assumes that the concrete state respects the abstract resources, expressed by \({\langle M,P \rangle } \in {\lfloor r_F, u, \mathcal {W} \rfloor _{\{ i \}}}\). Under these assumptions, the lemma intuitively tells us that the current thread knows which value it will read from x. Formally, the lemma says that all the messages thread i is allowed to read (i.e., messages in the memory that are not outstanding promises of thread i and whose timestamp is greater or equal to the view of thread i) have the value that appears as the maximal element in the set X.
To see why this lemma holds, consider a message \(m \in {M}(x) \setminus {P}(i)\). If m is an unfulfilled promise by a different thread j, then, by erasure, it follows that j currently owns or can acquire at least a shared write permission for x. However, this is a contradiction, since thread i currently owns the exclusive write permission, and, by erasure, \(r_F(i)\) is disjoint from the resources of all other threads and all resources currently associated with messages by u. Hence, m must be a fulfilled write. By erasure, it follows that the set of fulfilled writes to x is given by the combination of all write permissions. Since \(r_F(i)\) owns the exclusive write permission, this is just \(r_F(i).\texttt {wr}\). Hence, the set of fulfilled writes is X, and the value of the last fulfilled write is \(\textit{fst}(\max (X))\).
Note that in the reasoning above, it is crucial to know which thread and which message owns which resource. Without precisely tracking this information, we would be unable to prove Lemma 1.
4.4 Soundness
Now that we have our notion of erasure, we can proceed to formalise the meaning of triples, and present the key points of the soundness proof.
Recall our intuitive view of Hoare triples saying that the program only makes steps which respect the resources it owns. This notion is formalised using the safety predicate: safety (somewhat simplified; we give its formal definition in Fig. 7) states that it is always safe to perform zero steps, and performing \(n+1\) steps is safe if the following two conditions hold:
-
1.
If no more steps can be taken, the current state and resources have to satisfy the postcondition B.
-
2.
If we can take a step which takes us from the state \({\langle M,P \rangle }\) (which respects our current resources r, the assignment of resources to messages u, and world \(\mathcal {W}\)) to the state \({\langle M',P' \rangle }\), then
-
(a)
there exist resources \(r'\), an assignment of resources to messages \(u'\), and a future world \(\mathcal {W}'\), such that \({\langle M',P' \rangle }\) respects \(r'\), \(u'\), and \(\mathcal {W}'\), and
-
(b)
we are safe for n more steps starting in the state \({\langle M',P' \rangle }\) with resources given by \(r'\), \(u'\) and \(\mathcal {W}'\).
-
(a)
Note the following:
-
Upon termination, we are not required to satisfy exactly the postcondition B, but its view shift. A view shift is a standard notion in concurrent separation logics, which allows updates of the abstract resources which do not affect the concrete state. In our case, this means that resource r can be view-shifted into \(r'\) satisfying B as long as the erasure is unchanged. The formal definition of view shifts is given in the appendix.
-
Again as is standard in separation logics, safety requires framed resources to be preserved. This is the role of \(r_F\) in the safety definition. Frame preservation allows us to compose safety of threads that own compatible resources. However, departing from the standard notion of frame preservation, we precisely track who owns which resource in the frame, because this is important for erasure.
The semantics of Hoare triples is simply defined in terms of the safety predicate. The triple \(\{{P}\}\;{s}\;\{{Q}\}\) holds if every logical state satisfying the precondition is safe for any number of steps:

To establish soundness of the SLR proof rules, we have to prove that the safety predicate holds for arbitrary number of steps, including promise steps. The trouble with reasoning about promise steps is that they can nondeterministically appear at any point of the execution. Therefore, we have to account for them in the soundness proof of every rule of our logic. To make this task manageable, we encapsulate reasoning about the promise steps in a theorem, thus enabling the proofs of soundness for proof rules to consider only the non-promise steps.
To do so, once again certification runs for promises play a pivotal role. Recall that whenever a thread makes a step, it has to be able to fulfil its promises without help from other threads (Sect. 3.4). Since there will be no interference by other threads, performing promise steps during certification is of no use (because promises can only be used by other threads). Therefore, we can assume that the certification runs are always promise-free.
Now that we have noted that certifications are promise-free, the key idea behind encapsulating the reasoning about promises is as follows. If we know that all executions of our program are safe for arbitrarily many non-promising steps, we can use this to conclude that they are safe for promising steps too. Here, we use the fact that certification runs are possible runs of the program, and the fact that certifications are promise-free.
Let us now formalise our key idea. First, we need a way to state that executions are safe for non-promising steps. This is expressed by the non-promising safety predicate defined in Fig. 8. What we want to conclude is that non-promising safety is enough to establish safety, as expressed by Theorem 1:
Theorem 1
(Non-promising safety implies safety)

We now discuss several important points in the definition of non-promising safety which enable us to prove this theorem.
Non-promising Safety is Indexed by Pairs of Natural Numbers. When proving Theorem 1, we use promise-free certification runs to establish the safety of the promise steps. A problem we face here is that the length of certification runs is unbounded. Somehow, we have to know that whenever the thread makes a step, it is \(\mathrm {npsafe}\) for arbitrarily many steps. Our solution is to have \(\mathrm {npsafe}\) transfinitely indexed over pairs of natural numbers ordered lexicographically. That way, if we are \(\mathrm {npsafe}\) at index \((n+1,0)\) and we take a step, we know that we are \(\mathrm {npsafe}\) at index (n, m) for every m. We are then free to choose a sufficiently large m depending on the length of the certification run we are considering.
Non-promising Safety Considers Configurations that May Contain Promises. It is important to note that the definition of non-promising safety does not require that there are no promises in the starting configuration. The only thing that is required is that no more promises are going to be issued. This is very important for Theorem 1, since safety considers all possible starting configurations (including the ones with existing promises), and if we want the lemma to hold, non-promising safety has to consider all possible starting configurations too.
Erasure Used in the Non-promising Safety does not Constrain Promises of the Current Thread. Non-promising safety does not require promises by the thread being reduced (i.e., thread i) to respect resources. Thus, when reasoning about non-promising safety of thread i, we cannot assume that existing promises by thread i respect resources, but crucially we also do not have to worry about recertifying thread i’s promises. However, since the \({\mathop {\longrightarrow }\limits ^{\text {NP}}}\) reduction does not recertify promises, we explicitly require that the promises are well formed (via \(\mathrm {wf}_\mathrm {prom}\) predicate) in order to ensure that we still only consider executions where threads do not read from their own promises.
Additional Constraints by the Non-promising Safety. Non-promising safety also imposes additional constraints on the reducing thread i. In particular, any write permissions owned or acquirable by i after the reduction were already owned or acquirable by i before the reduction step. Intuitively, this holds because thread i can only transfer away resources and take ownership of resources it was already allowed to acquire before reducing. Lastly, non-promising safety requires that if the reduction of i performs any new writes or fulfils any old promises, it must own the write permission for the location of the given message. Together, these two conditions ensure that if a promise is fulfilled during a thread-local certification and the thread satisfies non-promising safety, then the thread already owned or could acquire the write permission for the location of the promise. This is expressed formally in Lemma 2.
Lemma 2
Assuming that \(({\langle M,P \rangle }, V, r) \in \mathrm {npsafe}_{(n+1, k)}(\sigma , B)(W)\) and \({\langle M,P \rangle } \in {\lfloor r_F[i \mapsto r \bullet f], u, W \rfloor _{\{ i \}}}\) and \(\langle \langle \sigma , V \rangle , {\langle M,P \rangle } \rangle {\mathop {\longrightarrow }\limits ^{\text {NP}}}^k_i \langle \langle \sigma ', V' \rangle , {\langle M',P' \rangle } \rangle \) and \(m \in (M' \setminus P') \setminus (M \setminus P)\), we have \((r \bullet \mathrm {canAcq}(r, u)).\texttt {wr}(m.\texttt {loc}).\texttt {perm}> 0\).
The intuition for why Lemma 2 holds is that since only thread i executes, we know by the definition of non-promising safety that any write permission owned or acquirable by i when the promise is fulfilled, it already owns or can acquire in the initial state. Furthermore, whenever a promise is fulfilled, the non-promising safety definition explicitly requires ownership of the corresponding write permission. It follows that the thread already owns or can acquire the write permission for the location of the given promise in the initial state.
Lemma 2 gives us exactly the property that we need to reestablish erasure after the operational semantics introduces a new promise. This makes Lemma 2 the key step in the proof of Theorem 1, which allows us to disentangle reasoning about promising steps and normal reduction steps. Theorem 1 tells us that, in order to prove a proof rule sound, it is enough to prove that the non-promising safety holds for arbitrary indices. This liberates us of the cumbersome reasoning about promise steps and allows us to focus on non-promising reduction steps when proving the proof rules sound.
We can now state our top-level correctness theorem, Theorem 2. Since our language only has top-level parallel composition, we need a way to distribute initial resources to the various threads, and to collect all the resources once all the threads have finished. The correctness theorem gives us precisely that:
Theorem 2
(Correctness). If A is a finite set of locations and
-
1.
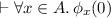
-
2.
\(\vdash \circledast _{x \in A} \mathsf {Rel}(x, \phi _x) * \mathsf {Acq}(x, \phi _x) * \mathsf {W}^{1}({x},{\{ (0, 0) \}}) \;\Rrightarrow \; \circledast _{i \in {\textit{Tid}}}\, P_i\)
-
3.
\(\vdash \{{P_i}\}\;{s_i}\;\{{Q_i}\}\) for all i
-
4.
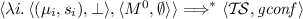 and
and 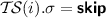 for all i
for all i -
5.
\(\vdash \circledast _{i \in {\textit{Tid}}}\, Q_i \Rrightarrow Q\)
-
6.
\( FRV (Q_i) \cap FRV (Q_j) = \emptyset \) for all distinct \(i, j \in {\textit{Tid}}\)
then there exist \(\mu , r\), and \(\mathcal {W}\) such that  and
and  , where \( FRV \!(P)\) denotes the set of free register variables in P.
, where \( FRV \!(P)\) denotes the set of free register variables in P.
5 Related Work
There are a number of techniques for reasoning under relaxed memory models, but besides the DRF theorems and some simple invariant logics [10, 13], no other techniques have been proved sound for a model allowing the weak behaviour of LB+data+fakedep from the introduction. The “invariant-based program logics” are by design unable to reason about programs like the random number generator, where having a bound on the set of values written to a location is not enough, let alone reasoning about functional correctness of a program.
Relaxed Separation Logic (RSL). Among program logics for relaxed memory, the most closely related is RSL [27]. There are two versions of RSL: a weak one that is sound with respect to the C/C++11 memory model, which features out-of-thin-air reads, and a stronger one that is sound with respect to a variant of the C/C++11 memory that forbids load buffering.
The weak version of RSL forbids relaxed writes completely, and does not constrain the value returned by a relaxed read. The stronger version provides single-location invariants for relaxed accesses, but its soundness proof relies strongly on a strengthened version of C/C++11 without \( po \cup rf \) cycles (where \( po \) is program order, and \( rf \) is the reads-from relation), which forbids load buffering.
When it comes to reasoning about coherence properties, even the strong version of RSL is surprisingly weak: it cannot be used to verify any of the coherence examples in this paper. In fact, RSL can be shown sound with respect to much weaker coherence axioms than what C/C++11 relaxed accesses provide.
One notable feature of RSL which we do not support is read-modify-write (RMW) instructions (such as compare-and-swap and fetch-and-add). However, the soundness proof of SLR makes no simplifying assumptions about the promising semantics which would affect the semantics of RMW instructions. Therefore, we are confident that enhancing SLR with rules for RMW instructions would not substantially affect the structure of the soundness proof, presented in Sect. 4.
Other Program Logics. FSL [8] extends (the strong version of) RSL with stronger rules for relaxed accesses in the presence of release/acquire fences. In FSL, a release fence can be used to package an assertion with a modality, which a relaxed write can then transfer. Conversely, the ownership obtained by a relaxed read is guarded by a symmetric modality than needs an acquire fence to be unpacked. The soundness proof of FSL also relies on \( po \cup rf \) acyclicity. Moreover, it is known to be unsound in models where load buffering is allowed [9, Sect. 5.2].
A number of other logics—GPS [26], iGPS [12], OGRA [16], iCAP-TSO [24], the rely-guarantee proof system for TSO of Ridge [23], and the program logic for TSO of Wehrman and Berdine [28]—have been developed for even stronger memory models (release/acquire or TSO), and also rely quite strongly on—and try to expose—the stronger consistency guarantees provided by those models.
The framework of Alglave and Cousot [2] for reasoning about relaxed concurrent programs is parametric with respect to an axiomatic “per-execution” memory model. By construction, as argued by Batty et al. [3], such models cannot be used to define a language-level model allowing the weak behaviour of LB+data+fakedep and similar litmus tests while forbidding out-of-thin-air behaviours. Moreover, their framework does not provide the usual abstraction facilities of program logics.
The lace logic of Bornat et al. [6] targets hardware memory models, in particular Power. It relies on annotating the program with “per-execution” constraints, and on syntactic features of the program. For example, it distinguishes LB+data+fakedep from LB+data+po, its variant where the write of second thread is \([x]_{\texttt {rlx}} := 1\), and is thus unsuitable to address out-of-thin-air behaviours.
Other Approaches. Besides program logics, another way to reason about programs under weak memory models is to reduce the act of reasoning under a memory model M to reasoning under a stronger model \(M'\)—typically, but not necessarily, sequential consistency [7, 18]. One can often establish DRF theorems stating that a program without any races when executed under \(M'\) has the same behaviours when executed under M as when executed under \(M'\). For the promising semantics, Kang et al. [13, Sect. 5.4] have established such theorems for \(M'\) being release-acquire consistency, sequential consistency, and the promise-free promising semantics, for suitable notions of races. The last one, the “Promise-Free DRF” theorem, is applicable to the Disjoint-Lists program from the introduction, but none of these theorems can be applied to any of the other examples of this paper, as they are racy. Moreover, these theorems are not compositional, as they do not state anything about the Disjoint-Lists program when put inside a larger, racy program—for example, just an extra read of a from another thread.
6 Conclusion
In this paper, we have presented the first expressive logic that is sound under the promising semantics, and have demonstrated its expressiveness with a number of examples. Our logic can be seen both as a general proof technique for reasoning about concurrent programs, and also as tool for proving the absence of out-of-thin-air behaviour for challenging examples, and reasoning about coherence. In the future, we would like to extend the logic to cover more of relaxed memory, more advanced reasoning principles, such as those available in GPS [26], and mechanise its soundness proof.
Interesting aspects of relaxed memory we would like to also cover are read-modify-writes and fences. These would allow us to consider concurrent algorithms like circular buffers and the atomic reference counter verified in FSL++ [9]. This could be done by adapting the corresponding rules of RSL and GPS; moreover, we could adapt them with our new approach to reason about coherence.
To mechanise the soundness proof, we intend to use the Iris framework [11], which has already been used to prove the soundness of iGPS [12], a variant of the GPS program logic. To do this, however, we have to overcome one technical limitation of Iris. Namely, the current version of Iris is step-indexed over \(\mathbb {N}\), while our semantics uses transfinite step-indexing over \(\mathbb {N} \times \mathbb {N}\) to define non-promising safety and allow us to reason about certifications of arbitrary length for each reduction step. Progress has been made towards transfinitely step-indexed logical relations that may be applicable to a transfinitely step-indexed version of Iris [25].
Notes
- 1.
The litmus test is called this way because some early attempts to solve the OOTA problem allowed this example to return arbitrary values for x and y.
- 2.
As the promising semantics comes with formal proofs of correctness of all the expected local program transformations and of compilation schemes to the x86-TSO, Power, and ARMv8-POP architectures [21], SLR is sound for these architectures too.
- 3.
Supporting ownership transfer is necessary to provide useful rules for C11 release and acquire accesses.
- 4.
This \(\nabla {}\) modality is similar in spirit, but weaker than that of FSL [8].
References
Supplementary material for this paper. http://plv.mpi-sws.org/slr/appendix.pdf
Alglave, J., Cousot, P.: Ogre and Pythia: an invariance proof method for weak consistency models. In: POPL 2017, pp. 3–18. ACM, New York (2017). http://doi.acm.org/10.1145/2994593
Batty, M., Memarian, K., Nienhuis, K., Pichon-Pharabod, J., Sewell, P.: The problem of programming language concurrency semantics. In: Vitek, J. (ed.) ESOP 2015. LNCS, vol. 9032, pp. 283–307. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46669-8_12
Batty, M., Owens, S., Sarkar, S., Sewell, P., Weber, T.: Mathematizing C++ concurrency. In: POPL 2011, pp. 55–66. ACM, New York (2011). http://doi.acm.org/10.1145/1926385.1926394
Boehm, H.J., Demsky, B.: Outlawing ghosts: avoiding out-of-thin-air results. In: Proceedings of the Workshop on Memory Systems Performance and Correctness, MSPC 2014, pp. 7:1–7:6. ACM, New York (2014). http://doi.acm.org/10.1145/2618128.2618134
Bornat, R., Alglave, J., Parkinson, M.: New lace and arsenic (2016). https://arxiv.org/abs/1512.01416
Bouajjani, A., Derevenetc, E., Meyer, R.: Robustness against relaxed memory models. In: Software Engineering 2014, Fachtagung des GI-Fachbereichs Softwaretechnik, 25–28 Februar 2014, Kiel, Deutschland, pp. 85–86 (2014)
Doko, M., Vafeiadis, V.: A program logic for C11 memory fences. In: Jobstmann, B., Leino, K.R.M. (eds.) VMCAI 2016. LNCS, vol. 9583, pp. 413–430. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49122-5_20
Doko, M., Vafeiadis, V.: Tackling real-life relaxed concurrency with FSL++. In: Yang, H. (ed.) ESOP 2017. LNCS, vol. 10201, pp. 448–475. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54434-1_17
Jeffrey, A., Riely, J.: On thin air reads towards an event structures model of relaxed memory. In: LICS 2016, pp. 759–767. ACM, New York (2016)
Jung, R., Krebbers, R., Jourdan, J.H., Bizjak, A., Birkedal, L., Dreyer, D.: Iris from the ground up (2017)
Kaiser, J.O., Dang, H.H., Dreyer, D., Lahav, O., Vafeiadis, V.: Strong logic for weak memory: reasoning about release-acquire consistency in Iris. In: ECOOP 2017 (2017)
Kang, J., Hur, C.K., Lahav, O., Vafeiadis, V., Dreyer, D.: A promising semantics for relaxed-memory concurrency. In: POPL 2017. ACM, New York (2017). http://doi.acm.org/10.1145/3009837.3009850
Lahav, O., Vafeiadis, V., Kang, J., Hur, C.K., Dreyer, D.: Repairing sequential consistency in C/C++11. In: PLDI (2017)
Lahav, O., Giannarakis, N., Vafeiadis, V.: Taming release-acquire consistency. In: POPL 2016, pp. 649–662. ACM, New York (2016). http://doi.acm.org/10.1145/2837614.2837643
Lahav, O., Vafeiadis, V.: Owicki-gries reasoning for weak memory models. In: Halldórsson, M.M., Iwama, K., Kobayashi, N., Speckmann, B. (eds.) ICALP 2015. LNCS, vol. 9135, pp. 311–323. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47666-6_25
Manson, J., Pugh, W., Adve, S.V.: The Java memory model. In: POPL, pp. 378–391. ACM, New York (2005)
Owens, S.: Reasoning about the implementation of concurrency abstractions on x86-TSO. In: D’Hondt, T. (ed.) ECOOP 2010. LNCS, vol. 6183, pp. 478–503. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14107-2_23
Owens, S., Sarkar, S., Sewell, P.: A better x86 memory model: x86-TSO. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 391–407. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03359-9_27
Pichon-Pharabod, J., Sewell, P.: A concurrency semantics for relaxed atomics that permits optimisation and avoids thin-air executions. In: POPL 2016, pp. 622–633. ACM, New York (2016)
Podkopaev, A., Lahav, O., Vafeiadis, V.: Promising compilation to ARMv8 POP. In: ECOOP 2017. LIPIcs, vol. 74, pp. 22:1–22:28. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik (2017)
Reynolds, J.C.: Separation logic: a logic for shared mutable data structures. In: Proceedings of the 17th IEEE Symposium on Logic in Computer Science (LICS 2002), 22–25 July 2002, Copenhagen, Denmark, pp. 55–74 (2002). https://doi.org/10.1109/LICS.2002.1029817
Ridge, T.: A rely-guarantee proof system for x86-TSO. In: Leavens, G.T., O’Hearn, P., Rajamani, S.K. (eds.) VSTTE 2010. LNCS, vol. 6217, pp. 55–70. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15057-9_4
Sieczkowski, F., Svendsen, K., Birkedal, L., Pichon-Pharabod, J.: A separation logic for fictional sequential consistency. In: Vitek, J. (ed.) ESOP 2015. LNCS, vol. 9032, pp. 736–761. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46669-8_30
Svendsen, K., Sieczkowski, F., Birkedal, L.: Transfinite step-indexing: decoupling concrete and logical steps. In: Thiemann, P. (ed.) ESOP 2016. LNCS, vol. 9632, pp. 727–751. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49498-1_28
Turon, A., Vafeiadis, V., Dreyer, D.: GPS: navigating weak memory with ghosts, protocols, and separation. In: 2014 ACM International Conference on Object Oriented Programming Systems Languages and Applications, OOPSLA 2014, pp. 691–707. ACM, New York (2014)
Vafeiadis, V., Narayan, C.: Relaxed separation logic: a program logic for C11 concurrency. In: OOPSLA 2013, pp. 867–884. ACM, New York (2013)
Wehrman, I., Berdine, J.: A proposal for weak-memory local reasoning. In: LOLA (2011)
Acknowledgments
We would like to thank the reviewers for their feedback. The research was supported in part by the Danish Council for Independent Research (project DFF – 4181-00273), by a European Research Council Consolidator Grant for the project “RustBelt” (grant agreement no. 683289), and by Len Blavatnik and the Blavatnik Family foundation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Svendsen, K., Pichon-Pharabod, J., Doko, M., Lahav, O., Vafeiadis, V. (2018). A Separation Logic for a Promising Semantics. In: Ahmed, A. (eds) Programming Languages and Systems. ESOP 2018. Lecture Notes in Computer Science(), vol 10801. Springer, Cham. https://doi.org/10.1007/978-3-319-89884-1_13
Download citation
DOI: https://doi.org/10.1007/978-3-319-89884-1_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89883-4
Online ISBN: 978-3-319-89884-1
eBook Packages: Computer ScienceComputer Science (R0)







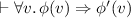 . The implication allows us to strengthen the predicate in release assertions.
. The implication allows us to strengthen the predicate in release assertions.






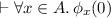
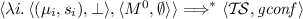 and
and 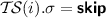 for all i
for all i