Abstract
Fitch-style modal deduction, in which modalities are eliminated by opening a subordinate proof, and introduced by shutting one, were investigated in the 1990s as a basis for lambda calculi. We show that such calculi have good computational properties for a variety of intuitionistic modal logics. Semantics are given in cartesian closed categories equipped with an adjunction of endofunctors, with the necessity modality interpreted by the right adjoint. Where this functor is an idempotent comonad, a coherence result on the semantics allows us to present a calculus for intuitionistic S4 that is simpler than others in the literature. We show the calculi can be extended à la tense logic with the left adjoint of necessity, and are then complete for the categorical semantics.
We gratefully acknowledge discussions with Patrick Bahr, Lars Birkedal, Aleš Bizjak, Christian Uldal Graulund, G.A. Kavvos, Bassel Mannaa, Rasmus Ejlers Møgelberg, Andrew M. Pitts, and Bas Spitters, and the comments of the anonymous referees. This research was supported by a research grant (12386) from Villum Fonden.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The Curry-Howard propositions-as-types isomorphism [21, 39, 41] provides a correspondence between natural deduction and typed lambda calculus of interest to both logicians and computer scientists. For the logician, term assignment offers a convenient notation to express and reason about syntactic properties such as proof normalisation, and, especially in the presence of dependent types, allows proofs of non-trivial mathematical theorems to be checked by computer programs. For the computer scientist, logics have been repurposed as typing disciplines to address problems in computing in sometimes surprising ways. Following Lambek [25], categories form a third leg of the isomorphism. Categorical semantics can be used to prove the consistency of a calculus, and they are crucial if we wish to prove or program in some particular mathematical setting. For example, see the use of the topos of trees as a setting for both programming with guarded recursion, and proof by Löb induction, by Clouston et al. [11].
This work involved two functors, ‘later’ and ‘constant’. Where functors interact appropriately with finite products they correspond to necessity modalities in intuitionistic normal modal logic, usually written \(\square \). Such modalities have been extensively studied by logicians, and the corresponding type-formers are widely applicable in computing, for example to monads [32], staged programming [13], propositional truncation [2], and recent work in homotopy type theory [37]. There is hence a need to develop all sides of the Curry-Howard-Lambek isomorphism for necessity modalities. Approaches to modal lambda calculi are diverse; see the survey by Kavvos [23], and remarks in the final section of this paper. This paper focuses on Fitch-style modal lambda calculi as first proposed by Borghuis [9] and (as the “two-dimensional” approach) by Martini and Masini [29].
Fitch-style modal lambda calculiFootnote 1 adapt the proof methods of Fitch [19] in which given a formula \(\square A\) we may open a ‘(strict) subordinate proof’ in which we eliminate the \(\square \) to get premise A. Such a subordinate proof with conclusion B can then be shut by introducing a \(\square \) to conclude \(\square B\). Different modal logics can be encoded by tweaking the open and shut rules; for example we could shut the proof to conclude merely B, if we had the T axiom \(\square B\rightarrow B\). Normal modal logics are usually understood with respect to Kripke’s possible worlds semantics (for the intuitionistic version, see e.g. Simpson [38, Sect. 3.3]). In this setting Fitch’s approach is highly intuitive, as opening a subordinate proof corresponds to travelling to a generic related world, while shutting corresponds to returning to the original world. See Fitting [20, Chap. 4] for a lengthier discussion of this approach to natural deduction.
Borghuis [9] kept track of subordinate proofs in a sequent presentation by introducing a new structural connective to the context when a \(\square \) is eliminated, and removing it from the context when one is introduced, in a style reminiscent of the treatment of modal logic in display calculus [42], or for that matter of the standard duality between implication and comma. To the category theorist, this suggests an operation on contexts left adjoint to \(\square \). This paper exploits this insight by presenting categorical semantics for Fitch-style modal calculi for the first time, answering the challenge of de Paiva and Ritter [33, Sect. 4], by modelling necessity modalities as right adjoints. This is logically sound and complete, yet less general than modelling modalities as monoidal functors as done for example by Bellin et al. [4]. For example, truncation in sets is monoidal but has no right adjoint. Nonetheless adjunctions are ubiquitous, and in their presence we argue that the case for Fitch-style calculi is compelling. Examples of right adoints of interest to type theorists include the aforementioned modalities of guarded recursion, the closure modalities of (differential) cohesive \(\infty \)-toposes [36, Sect. 3], and atom-abstraction in nominal sets [31].
In Sect. 2 we present Borghuis’s calculus for the logic Intuitionistic K, the most basic intuitionistic modal logic of necessity. To the results of confluence, subject reduction, and strong normalisation already shown by Borghuis we add canonicity and the subformula property, with the latter proof raising a subtle issue with sums not previously observed. We give categorical semantics for this style of calculus for the first time and prove soundness. In Sect. 3 we introduce the left adjoint as a first-class type former à la intuitionistic tense logic [17], in which the “everywhere in the future” modality is paired with “somewhere in the past”. To our knowledge this is the first natural deduction calculus, let alone lambda calculus, for any notion of tense logic. It is not entirely satisfactory as it lacks the subformula property, but it does allow us to prove categorical completeness. In Sect. 4 we show how the basic techniques developed for Intuitionistic K extend to Intuitionistic S4, one of the most-studied intuitionistic modal logics. Instead of working with known Fitch-style calculi for this logic [13, 34] we explore a new, particularly simple, calculus where the modality is idempotent, i.e. \(\square A\) and \(\square \square A\) are not merely logically equivalent, but isomorphic. Our semantics for this calculus rely on an unusual ‘coherence’ proof. In Sect. 5 we present a calculus corresponding to the logic Intuitionistic R. In Sect. 6 we conclude with a discussion of related and further work.
2 Intuitionistic K
This section presents results for the calculus of Borghuis [9] for the most basic modal logic for necessity, first identified to our knowledge by Božić et al. [10] as \(HK_{\square }\); following Yokota [43] we use the name Intuitionistic K (IK). This logic extends intuitionistic logic with a new unary connective \(\square \), one new axiom
-
K: \(\;\square (A\rightarrow B)\rightarrow \square A\rightarrow \square B\)
and one new inference rule
-
Necessitation: if A is a theorem, then so is \(\square A\).
2.1 Type System
Contexts are defined by the grammar

where x is a variable not in \(\varGamma \), A is a formula of intuitionistic modal logic, and  is called a lock. The open lock symbol is used to suggest that a box has been opened, allowing access to its contents.
is called a lock. The open lock symbol is used to suggest that a box has been opened, allowing access to its contents.
Ignoring variables and terms, sequents \(\varGamma \vdash A\) may be interpreted as intuitionistic modal formulae by the translation
-
\(\llbracket \cdot \vdash A\rrbracket = A\);
-
\(\llbracket B,\varGamma \vdash A\rrbracket = B\rightarrow \llbracket \varGamma \vdash A\rrbracket \);
-
 .
.
This interpretation will suffice to confirm the soundness and completeness of our calculus, considered as a natural deduction calculus, with respect to IK. It is however not a satisfactory basis for a categorical semantics, because it does not interpret the context as an object. In Sect. 2.3 we shall see that  may instead by interpreted as a left adjoint of \(\square \), applied to the context to its left.
may instead by interpreted as a left adjoint of \(\square \), applied to the context to its left.
Figure 1 presents the typing rules. Rules for the product constructions 1, \(A\times B\), \(\langle \rangle \), \(\langle t,u\rangle \), \(\pi _1\,t\), \(\pi _2\,t\) are as usual and so are omitted, while sums are discussed at the end of Sect. 2.2. Note that variables can only be introduced or abstracted if they do not appear to the left of a lock. In the variable rule the context \(\varGamma '\) builds in variable exchange, while in the \(\mathsf {open}\) rule \(\varGamma '\) builds in variable weakening. Exchange of variables with locks, and weakening for locks, are not admissible.
Theorem 2.1
(Logical Soundness and Completeness). A formula is a theorem of IK if and only if it is an inhabited type in the empty context.
We can for example show that the K axiom is inhabited:

2.2 Computation
We extend the usual notion of \(\beta \)-reduction on untyped terms with the rule
We write \(\leadsto \) for the reflexive transitive closure of \(\mapsto \). This relation is plainly confluent. Two lemmas, proved by easy inductions on the derivation of the terms t, then allow us to prove subject reduction:
Lemma 2.2
(Variable Weakening). If \(\varGamma ,\varGamma '\vdash t:B\) then \(\varGamma ,x:A,\varGamma '\vdash t:B\).
Lemma 2.3
(Substitution). If \(\varGamma ,x:A,\varGamma '\vdash t:B\) and \(\varGamma \vdash u:A\) then \(\varGamma ,\varGamma '\vdash t[u/x]:B\).
Theorem 2.4
(Subject Reduction). If \(\varGamma \vdash t:A\) and \(t\mapsto u\) then \(\varGamma \vdash u:A\).
Proof
\(\beta \)-reduction for \(\rightarrow \) requires Lemma 2.3, and for \(\square \) requires Lemma 2.2.
A term t is normalisable if there exists an integer \(\nu (t)\) bounding the length of any reduction sequence starting with t, and normal if \(\nu (t)\) is 0. By standard techniques we prove the following theorems:
Theorem 2.5
(Strong Normalisation). Given \(\varGamma \vdash t:A\), the term t is normalisable.
Theorem 2.6
(Canonicity). If \(\varGamma \) is a context containing no variable assignments, \(\varGamma \vdash t:A\), and t is normal, then the main term-former of t is the introduction for the main type-former of A.
Concretely, if A is some base type then t is a value of that type.
Theorem 2.7
(Subformula Property). Given \(\varGamma \vdash t:A\) with t normal, all subterms of t have as their type in the derivation tree a subtype of A, or a subtype of a type assigned in \(\varGamma \).
To attain this final theorem we need to take some care with sums. It is well known that lambda calculi with sums do not enjoy the subformula property unless they have additional reductions called commuting conversions [21, Chap. 10]. However the commuting conversions for the \(\square \) type

do not obviously enjoy subject reduction because \(\mathsf {open}\) might change the context. However if we tweak the definitions of the elimination term-formers for sums according to Fig. 2 then all results of this section indeed hold.
Finally, while we will not explore computational aspects of \(\eta \)-equivalence in this paper, we do note that
obeys subject reduction in both directions (provided, in the expansion case, that the type of t has \(\square \) as its main type-former).
2.3 Categorical Semantics
This section goes beyond Theorem 2.1 to establish the soundness of the type system with respect to a categorical semantics, in cartesian closed categories \(\mathcal {C}\) equipped with an endofunctor \(\square \) that has a left adjoint, which we write \(\blacklozenge \).
We interpret types as \(\mathcal {C}\)-objects via the structure of \(\mathcal {C}\) in the obvious way. We then interpret contexts as \(\mathcal {C}\)-objects by
-
\(\llbracket \cdot \rrbracket \;\triangleq \; 1\);
-
\(\llbracket \varGamma ,x:A\rrbracket \;\triangleq \; \llbracket \varGamma \rrbracket \times A\);
-
 .
.
We omit the brackets \(\llbracket \cdots \rrbracket \) where no confusion is possible, and usually abuse notation by omitting the left-most ‘\(1\times \)’ where the left of the context is a variable.
We will also sometimes interpret contexts \(\varGamma \) as endofunctors, abusing notation to also write them as \(\llbracket \varGamma \rrbracket \), or merely \(\varGamma \), by taking \(\llbracket \cdot \rrbracket \) as the identity, \(\llbracket \varGamma ,x:A\rrbracket = \llbracket \varGamma \rrbracket \times A\), and  .
.
We interpret \(\varGamma \vdash t:A\) as a \(\mathcal {C}\)-arrow \(\llbracket \varGamma \vdash t:A\rrbracket :\llbracket \varGamma \rrbracket \rightarrow A\), often abbreviated to \(\llbracket t\rrbracket \), or merely t, by induction on the derivation of t as follows.
Standard constructions such as variables, abstraction and application are interpreted as usual. To interpret the rules for sums of Fig. 2 we use the fact that \(\blacklozenge \), as a left adjoint, preserves colimits.
\(\mathsf {shut}\): we simply apply the isomorphism \(\mathcal {C}(\blacklozenge \llbracket \varGamma \rrbracket ,A)\rightarrow \mathcal {C}(\llbracket \varGamma \rrbracket ,\square A)\) given by the \(\blacklozenge \dashv \square \) adjunction.
\(\mathsf {open}\): We apply the isomorphism \(\mathcal {C}(\llbracket \varGamma \rrbracket ,\square A)\rightarrow \mathcal {C}(\blacklozenge \llbracket \varGamma \rrbracket ,A)\) to the arrow interpreting the premise, then compose with the projection  .
.
Theorem 2.8
(Categorical Soundness). If \(\varGamma \vdash t:A\) and \(t\mapsto t'\) then \(\llbracket t\rrbracket =\llbracket t'\rrbracket \).
We also have that \(\eta \)-equivalent terms have the same denotation.
3 Left Adjoints and Categorical Completeness
In this section we extend the calculus to include the left adjoint \(\blacklozenge \) as a first-class type-former, and hence prove categorical completeness. The underlying logic is the fragment of intuitionistic tense logic [17] with just one pair of modalities, studied by Dzik et al. [15] as ‘intuitionistic logic with a Galois connection’; we use the name \(IK_{\blacklozenge }\). We have two new axioms
\(\eta ^m\): \(\;A\rightarrow \square \blacklozenge A\)
\(\varepsilon ^m\): \(\;\blacklozenge \square A\rightarrow A\)
We use the superscript m to identify these as the unit as the unit and counit of the modal adjunction \(\blacklozenge \dashv \square \), to differentiate them from other (co)units used elsewhere in the paper. We have one new inference rule:
Monotonicity: if \(A\rightarrow B\) is a theorem, then so is \(\blacklozenge A\rightarrow \blacklozenge B\).
3.1 Type System and Computation
We extend the type system of Fig. 1 with the new rules for \(\blacklozenge \) presented in Fig. 3. \(\blacklozenge \), unlike \(\square \), need not commute with products, so does not interact well with contexts. Hence the subterms of a \(\mathsf {let\,dia}\) term may not share variables.
We can construct the axioms of \(IK_{\blacklozenge }\):

and given a closed term \(f:A\rightarrow B\) we have the monotonicity construction

To this we add the new \(\beta \) rule
We can hence extend the syntactic results of the previous section to the logic \(IK_{\blacklozenge }\), with the exception of the subformula property. Consider the term

This term is normal but evidently fails the subformula property. One might expect, as with sums, that a commuting conversion would save the day by reducing the term to \(\mathsf {let\,dia}\,y\,\mathsf {be}\,x\,\mathsf {in}\,((\lambda z.\mathsf {dia}\,y)x)\), but this term sees the free variable x appear in the second subterm of a \(\mathsf {let\,dia}\) expression, which is not permitted.
We now turn to \(\eta \)-equivalence, and an equivalence which we call associativity:
For example, under associativity the counter-example to the subformula property equals \((\lambda z.\mathsf {let\,dia}\,y\,\mathsf {be}\,x\,\mathsf {in}\,\mathsf {dia}\,y)x\), which reduces to \(\mathsf {let\,dia}\,y\,\mathsf {be}\,x\,\mathsf {in}\,\mathsf {dia}\,y\), which is \(\eta \)-equal to x. The equivalences enjoy subject reduction in both directions (requiring, as usual, that t has the right type for \(\eta \)-expansion).
3.2 Categorical Semantics
We interpret the new term-formers in the same categories as used in Sect. 2.3. For \(\mathsf {dia}\), given \(t:\varGamma \rightarrow A\) we compose \(\blacklozenge t\) with the projection  . The denotation of \(\mathsf {let\,dia}\,x\,\mathsf {be}\,t\,\mathsf {in}\,u\) is simply \(u\circ t\). We may then confirm the soundness of \(\beta \)-reduction, \(\eta \)-equivalence, and associativity; we call these equivalences collectively definitional equivalence.
. The denotation of \(\mathsf {let\,dia}\,x\,\mathsf {be}\,t\,\mathsf {in}\,u\) is simply \(u\circ t\). We may then confirm the soundness of \(\beta \)-reduction, \(\eta \)-equivalence, and associativity; we call these equivalences collectively definitional equivalence.
We extend standard techniques for proving completeness [25], constructing a term model, a category with types as objects and, as arrows \(A\rightarrow B\), terms of form \(x:A\vdash t:B\) modulo definitional equivalence. This is a category by taking identity as the term x and composition \(u\circ t\) as u[t / x]. It is a cartesian closed category using the type- and term-formers for products and function spaces.
The modalities \(\blacklozenge \) and \(\square \) act on types; they also act on terms by, for \(\blacklozenge \), the monotonicity construction, and for \(\square \), mapping \(x:A \vdash t:B\) to \(x:\square A\vdash \mathsf {shut}\,t[\mathsf {open}\,x/x]:\square B\). One can check these constructions are functorial, and that the terms for \(\eta ^m\) and \(\varepsilon ^m\) are natural and obey the triangle equalities for the adjunction \(\blacklozenge \vdash \square \).
Given a context \(\varGamma \) we define the context term \(\varGamma \vdash c_{\varGamma }:\llbracket \varGamma \rrbracket \) by
-
\(c_{\cdot } \;\triangleq \; \langle \rangle \);
-
\(c_{\varGamma ,x:A} \;\triangleq \; \langle c_{\varGamma },x\rangle \);
-
 .
.
Lemma 3.1
Given \(\varGamma \vdash t:A\), t is definitionally equal to \(\llbracket \varGamma \vdash t:A\rrbracket [c_{\varGamma }/x]\).
Theorem 3.2
(Categorical Completeness). If \(\varGamma \vdash t:A\) and \(\varGamma \vdash u:A\) are equal in all models then they are definitionally equal.
Proof
t and u have equal denotations in the term model, so their denotations are definitionally equal. Definitional equality is preserved by substitution, so \(\llbracket \varGamma \vdash t:A\rrbracket [c_{\varGamma }/x]=\llbracket \varGamma \vdash u:A\rrbracket [c_{\varGamma }/x]\), so by Lemma 3.1, \(t=u\).
4 Intuitionistic S4 for Idempotent Comonads
Intuitionistic S4 (IS4) is the extension of IK with the axioms
T: \(\;\square A\rightarrow A\)
4: \(\;\square A\rightarrow \square \square A\)
To the category theorist IS4 naturally suggests the notion of a comonad. IS4 is one of the most studied and widely applied intuitionistic modal logics; in particular there exist two Fitch-style calculi [13, 34]. We conjecture that similar results to the previous sections could be developed for these calculi. Instead of pursuing such a result, we here show that a simpler calculus is possible if we restrict to idempotent comonads, where \(\square A\) and \(\square \square A\) are isomorphic. This restriction picks out an important class of examples – see for example the discussion of Rijke et al. [35] – and relies on a novel ‘coherence’ proof.
4.1 Type System and Computation
A calculus for IS4 is obtained by replacing the \(\mathsf {open}\) rule of Fig. 1 by

The T and 4 axioms are obtained by

This confirms logical completeness; once can also easily check soundness.
Subject reduction for the \(\beta \)-reduction \(\mathsf {open}\,\mathsf {shut}\,t\mapsto t\) requires a new lemma, proved by an easy induction on t:
Lemma 4.1
(Lock Replacement). If  then \(\varGamma ,\varGamma ',\varGamma ''\vdash t:A\).
then \(\varGamma ,\varGamma ',\varGamma ''\vdash t:A\).
The key syntactic Theorems 2.5, 2.6, and 2.7 then follow easily.
\(\eta \)-expansion obeys subject reduction as before, but it is not the case, for example, that the term presented above for the 4 axiom reduces to \(\mathsf {shut}\,x\). We may however accept a notion of \(\eta \)-reduction on typed terms-in-context:
This equivalence is more powerful than it might appear; it allows us to derive the idempotence of \(\square \), as the 4 axiom is mutually inverse with the instance \(\square \square A\rightarrow \square A\) of the T axiom. That is, \(\lambda x.\mathsf {open}\,\mathsf {shut}\,\mathsf {shut}\,\mathsf {open}\,x\) reduces to the identity on \(\square A\), and \(\lambda x.\mathsf {shut}\,\mathsf {shut}\,\mathsf {open}\,\mathsf {open}\,x\) reduces to the identity on \(\square \square A\).
4.2 Categorical Semantics
We give semantics to our type theory in a cartesian closed category with an adjunction of endofunctors \(\blacklozenge \dashv \square \) in which \(\square \) is a comonad. Equivalently [16, Sect. 3], \(\blacklozenge \) is a monad, equipped with a unit \(\eta \) and multiplication \(\mu \). To confirm the coherence of these semantics, discussed in the next subsection, and the soundness of \(\eta \)-equivalence, we further require that \(\square \) is idempotent, or equivalently that all \(\mu _A:\blacklozenge \blacklozenge A\rightarrow \blacklozenge A\) are isomorphisms with inverses \(\eta _{\blacklozenge A}=\blacklozenge \eta _A\).
To define the semantics we define lock replacement natural transformations \(l_{\varGamma }:\llbracket \varGamma \rrbracket \rightarrow \blacklozenge \), corresponding to Lemma 4.1, by induction on \(\varGamma \):
-
\(l_{\cdot }\) is the unit \(\eta \) of the monad;
-
\(l_{\varGamma ,x:A}\) is the projection composed with \(l_{\varGamma }\);
-
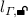 is \(\blacklozenge l_{\varGamma }\) composed with \(\mu \).
is \(\blacklozenge l_{\varGamma }\) composed with \(\mu \).
Note that  is the identity by the monad laws.
is the identity by the monad laws.
We may now define the interpretation of \(\mathsf {open}\): given \(t:\varGamma \rightarrow \square A\) we apply the adjunction to get an arrow \(\blacklozenge \varGamma \rightarrow A\), then compose with  .
.
Lemma 4.2
If we replace part of a context with a lock, then replace part of the new context that includes the new lock, we could have done this in one step:

Proof
By induction on \(\varGamma _4\), with the base case following by induction on \(\varGamma _3\).
Lemma 4.3
 .
.
Proof
By induction on the derivation of t.
Now \(\mathsf {open}\,\mathsf {shut}\,t\), where the \(\mathsf {open}\) has weakening \(\varGamma '\), has denotation \(\varepsilon ^{m}\circ \blacklozenge \square t\circ \blacklozenge \eta ^{m}\circ l_{\varGamma '}\), which is \(t\circ l_{\varGamma '}\) by the naturality of \(\varepsilon ^{m}\), and the adjunction. This is what is required by Lemma 4.3, so \(\beta \)-reduction for \(\square \) is soundly modelled.
4.3 Coherence
Because the \(\mathsf {open}\) rule involves a weakening, and does not explicitly record in the term what that weakening is, the same typed term-in-context can be the root of multiple derivation trees, for example:

The categorical semantics of the previous section is defined by induction on derivations, and so does not truly give semantics to terms unless any two trees with the same root must have the same denotation. In this section we show that this property, here called coherence, indeed holds. We make crucial use of the idempotence of the comonad \(\square \).
We first observe that if \(\varGamma ,\varGamma ',\varGamma ''\vdash t:A\) and all variables of \(\varGamma '\) are not free in t, then \(\varGamma ,\varGamma ''\vdash t:A\). The following lemma, proved by easy inductions, describes how the denotations of these derivations are related:
Lemma 4.4
-
1.
If x is not free in t then \(\varGamma ,x:A,\varGamma '\vdash t:B\) has the same denotation as \(\varGamma ,\varGamma '\vdash t:B\circ \varGamma '(pr)\).
-
2.
\(\varGamma ,\varGamma '\vdash t:B\) has denotation
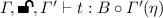 .
.
The technical lemma below is the only place where idempotence is used.
Lemma 4.5
Given \(\varGamma ,\varGamma '\vdash t:A\) with \(\varGamma '\) not free in t, we have

where t on the bottom line is the original arrow with \(\varGamma '\) strengthened away.
Proof
By induction on \(\varGamma '\). The base case holds by the naturality of \(\eta \).
We present only the lock case: \(\eta \circ t=\blacklozenge t\circ \eta \) by the naturality of \(\eta \). But by idempotence,  equals \(\blacklozenge \eta \). Then by Lemma 4.4 \(\blacklozenge t\circ \blacklozenge \eta \) is \(\blacklozenge \llbracket \varGamma ,\varGamma '\vdash t:A\rrbracket \), i.e. we have strengthened the lock away and can hence use our induction hypothesis, making the top trapezium commute in:
equals \(\blacklozenge \eta \). Then by Lemma 4.4 \(\blacklozenge t\circ \blacklozenge \eta \) is \(\blacklozenge \llbracket \varGamma ,\varGamma '\vdash t:A\rrbracket \), i.e. we have strengthened the lock away and can hence use our induction hypothesis, making the top trapezium commute in:

The left triangle commutes by definition, the bottom trapezium commutes by the naturality of \(\mu \), and the right triangle commutes by the monad laws.
Lemma 4.6
Given \(\varGamma ,\varGamma '\vdash t:A\) with \(\varGamma '\) not free in t, we have

where the bottom t is obtained via strengthening.
Proof
By induction on \(\varGamma ''\). The base case follows by Lemma 4.5.
Lemma 4.7
Given \(\varGamma ,\varGamma '\vdash t:\square \,A\) with the variables of \(\varGamma '\) not free in t, the following arrows are equal:
-
\(\varGamma ,\varGamma ',\varGamma ''\vdash \mathsf {open}\,t:A\) where the weakening is \(\varGamma ''\);
-
obtaining an arrow \(\varGamma \rightarrow \square A\) via Lemma 4.4, then applying \(\mathsf {open}\) with weakening \(\varGamma ,\varGamma ''\).
Proof
Immediate from Lemma 4.6, i.e.

Theorem 4.8
(Coherence). Given two different derivation trees of a term, their denotation is equal.
Proof
By induction on the number of nodes in the trees. The base case with one node is trivial. Suppose we have \(n+1\) nodes. Then the induction hypothesis immediately completes the proof unless the nodes above the roots are non-equal. Then the final construction must be an instance of \(\mathsf {open}\), i.e. we have

Clearly any variables in \(\varGamma '\) are not free in t, so we can use Lemma 4.4 on the top line of the right hand tree to derive \(\varGamma \vdash t:\square \,A\). By induction hypothesis this has the same denotation as the top line of the left hand tree. But Lemma 4.7 tells us that applying this strengthening and then opening with \(\varGamma ',\varGamma ''\) is the same as opening with \(\varGamma ''\) only.
We can now demonstrate the soundness of \(\eta \)-equivalence: given \(\varGamma \vdash t:\square A\) and \(\varGamma \vdash \mathsf {shut}\,\mathsf {open}\,t:\square A\) by any derivations, we can by coherence safely assume that \(\mathsf {open}\) used one lock only as its weakening, and so the arrows are equal by the \(\blacklozenge \dashv \square \) adjunction.
4.4 Left Adjoints and Categorical Completeness
Following Sect. 3 we can add \(\blacklozenge \) to the type theory; we need only modify the \(\mathsf {dia}\) rule to

to retain Lemma 4.1. The results of the previous sections, apart once more for the subformula property, still hold, where we define the denotation of \(\varGamma ,\varGamma '\vdash \mathsf {dia}\,t\) as \(\blacklozenge t\) composed with \(l_{\varGamma '}\). In particular, we must confirm that Lemma 3.1 extends to the new definitions of \(\mathsf {open}\) and \(\mathsf {dia}\), for which we need the lemma below:
Lemma 4.9
Given the term \(x:\llbracket \varGamma ,\varGamma '\rrbracket \vdash l_{\varGamma '}:\blacklozenge \llbracket \varGamma \rrbracket \) defined in the term model, \(l_{\varGamma '}[c_{\varGamma ,\varGamma '}/x]\) is definitionally equal to \(\mathsf {dia}\,c_{\varGamma }\).
Now \(\llbracket \mathsf {open}\,t\rrbracket [c_{\varGamma ,\varGamma '}/x]\) is \(\mathsf {let\,dia}\,x\,\mathsf {be}\,(\mathsf {let\,dia}\,x\,\mathsf {be}\,l_{\varGamma '} [c_{\varGamma ,\varGamma '}/x]\,\mathsf {in}\,\mathsf {dia}\llbracket t\rrbracket )\,\mathsf {in}\,\mathsf {open}\,x\), which by the lemma above is \(\mathsf {let\,dia}\,x\,\mathsf {be}\,(\mathsf {let\,dia}\,x\,\mathsf {be}\,\mathsf {dia}\,c_{\varGamma }\,\mathsf {in}\,\mathsf {dia}\llbracket t\rrbracket )\,\mathsf {in}\,\mathsf {open}\,x\mapsto \) \(\mathsf {open}\llbracket t\rrbracket [c_{\varGamma }/x]\), which equals \(\mathsf {open}\,t\) by induction. The proof for \(\mathsf {dia}\) is similar.
5 Intuitionistic R
One can readily imagine how the calculus for IS4 could be modified for logics with only one of the T and 4 axioms. In this section we instead illustrate the flexibility of Fitch-style calculi by defining a calculus for the rather different logic Intuitionistic R (IR), which extends IK with the axiom
R: \(\;A\rightarrow \square A\)
This axiom was first studied for intuitionistic necessity modalities by Curry [12], along with the axiom M, \(\square \square A\rightarrow \square A\), to develop a logic for monads. The importance of the logic with R but without M was established by McBride and Paterson [30] who showed that it captured the useful programming abstraction of applicative functors. We take the name R for the axiom from Fairtlough and Mendler [18], and for the logic from Litak [28].
We modify Figs. 1 and 3 simply by removing the side-conditions  from the variable, \(\mathsf {open}\), and \(\mathsf {dia}\) rules. We can then derive R:
from the variable, \(\mathsf {open}\), and \(\mathsf {dia}\) rules. We can then derive R:

For substitution and subject reduction we require the following lemma, easily proved by induction on the derivation of t:
Lemma 5.1
(Lock Weakening). If \(\varGamma ,\varGamma '\vdash t:A\) then  .
.
We can also observe that \(\eta \)-equivalence preserves types in both directions.
We give semantics for this calculus in a cartesian closed category equipped with an adjunction of endofunctors \(\blacklozenge \dashv \square \) and a ‘point’ natural transformation \(r:Id\rightarrow \square \) preserved by \(\square \), i.e. \(\square r=r:\square A\rightarrow \square \square A\). This last property makes this model slightly less general than the notion of tensorial strength used for categorical semantics by McBride and Paterson [30], but is needed for coherence and the soundness of \(\eta \)-equivalence. We will use the arrow \(\blacklozenge A\rightarrow A\) defined by applying the adjunction to r; we call this q and note the property:
Lemma 5.2
\(q=\blacklozenge q:\blacklozenge \blacklozenge A\rightarrow \blacklozenge A\).
The weakening natural transformation \(w_{\varGamma }:\varGamma \rightarrow Id\) is defined by induction on \(\varGamma \) via projection and q. Variables are then denoted by projection composed with weakening, and weakening is used similarly for \(\mathsf {open}\) and \(\mathsf {dia}\). We can hence show the soundness of \(\beta \)-reduction for \(\square \) and \(\blacklozenge \). For the soundness of \(\eta \)-equivalence for \(\square \) we need the following lemma:
Lemma 5.3
 .
.
The denotation of  is
is  . By the above lemma we replace
. By the above lemma we replace  with
with  , so by the naturality of \(\eta ^m\) we have
, so by the naturality of \(\eta ^m\) we have  , which is
, which is  by the monad laws.
by the monad laws.
Moving to coherence, we conduct a similar induction to Theorem 4.8, considering the case

The top line on the left weakens to the top line on the right, with denotation  . By induction this equals the denotation of the top line of the right. Then the right hand term has denotation
. By induction this equals the denotation of the top line of the right. Then the right hand term has denotation  . But by Lemma 5.3
. But by Lemma 5.3  . It is clear that
. It is clear that  , which is exactly the weakening used on the left. Coherence for \(\mathsf {dia}\) follows similarly.
, which is exactly the weakening used on the left. Coherence for \(\mathsf {dia}\) follows similarly.
Moving finally to categorical completeness, in the term model \(\square t\circ r\) is \(\mathsf {shut}\,t[\mathsf {open}\,\mathsf {shut}\,x/x]\), which reduces to \(\mathsf {shut}\,t\), so r is natural. \(\square r:\square A\rightarrow \square \square A\) is \(\mathsf {shut}\,\mathsf {shut}\,\mathsf {open}\,x\), which is indeed \(\eta \)-equal to \(\mathsf {shut}\,x\).
We finally need to update Lemma 3.1 for our new definitions. We do this via a lemma similar to Lemma 4.9:
Lemma 5.4
Given the term \(x:\llbracket \varGamma ,\varGamma '\rrbracket \vdash w_{\varGamma '}:\llbracket \varGamma \rrbracket \) defined in the term model, \(w_{\varGamma '}[c_{\varGamma ,\varGamma '}/x]\) is definitionally equal to \(c_{\varGamma }\).
Now the denotation of \(\varGamma ,x:A,\varGamma '\vdash x:A\) is \(\pi _2 w_{\varGamma '}\). Therefore we have \(\pi _2 w_{\varGamma '}[c_{\varGamma ,A,\varGamma '}/x]\), which is \(\pi _2 c_{\varGamma ,A}\) by the lemma above. This is \(\pi _2\langle c_{\varGamma },x \rangle \), which reduces to x.
The denotation of  is \(\mathsf {let\,dia}\,x\,\mathsf {be}\,w_{\varGamma '}\,\mathsf {in}\,\mathsf {open}\llbracket t\rrbracket \). Applying the substitution
is \(\mathsf {let\,dia}\,x\,\mathsf {be}\,w_{\varGamma '}\,\mathsf {in}\,\mathsf {open}\llbracket t\rrbracket \). Applying the substitution  along with the lemma above yields the term \(\mathsf {let\,dia}\,x\,\mathsf {be}\,\mathsf {dia}\,c_{\varGamma }\,\mathsf {in}\,\mathsf {open}\llbracket t\rrbracket \mapsto \mathsf {open}\llbracket t\rrbracket [c_{\varGamma }/x]\), and induction completes. The calculations for \(\mathsf {dia}\) follow similarly.
along with the lemma above yields the term \(\mathsf {let\,dia}\,x\,\mathsf {be}\,\mathsf {dia}\,c_{\varGamma }\,\mathsf {in}\,\mathsf {open}\llbracket t\rrbracket \mapsto \mathsf {open}\llbracket t\rrbracket [c_{\varGamma }/x]\), and induction completes. The calculations for \(\mathsf {dia}\) follow similarly.
6 Related and Further Work
Conventional contexts. Lambda calculi with conventional contexts containing typed variables only have been proposed for the logic of monads [32], for IS4 [5], for IK [4], and for a logic with ‘Löb induction’ [6], from which one can extract a calculus for IR. In previous work [11] we developed the guarded lambda calculus featuring two modalities, where one (‘constant’) was an (idempotent) comonad, and the other (‘later’) supported a notion of guarded recursion corresponding to Löb induction. We therefore used the existing work [5, 6] ‘off the shelf’.
Problems arose when we attempted to extend our calculus with dependent types [7]. Neither of the calculi with conventional contexts we had used scaled well to this extension. The calculus for IS4 [5], whose terms involved explicit substitutions, turned out to require these substitutions on types also, which added a level of complexity that made it difficult to write even quite basic dependently typed programs. The constant modality was therefore jettisoned in favour of an approach based on clock quantification [1], of which more below. The calculus for later employed a connective \(\circledast \) (from McBride and Patterson [30]) which acted on function spaces under the modality. However with dependent types we need to act not merely on function spaces, but on \(\varPi \)-types, and \(\circledast \) was unable to be used. Instead a novel notion of ‘delayed substitution’ was introduced. These were given an equational theory, but some of these equations could not be directed, so they did not give rise to a useful notion of computation.
Modalities as quantifiers. The suggestive but formally rather underdeveloped paper of De Queiroz and Gabbay [14] proposed that necessity modalities should be treated as universal quantifiers, inspired by the standard semantics of necessity as ‘for all possible worlds’. This is one way to understand the relationship between the constant modality and clock quantification [1]. However clock quantification is more general than a single constant modality because we can identify multiple free clock variables with multiple ‘dimensions’ in which a type may or may not be constant. This gap in generality can probably be bridged by using multiple independent constant modalities. More problematically, while it is clear what the denotational semantics of the constant modality are, the best model for clock quantifiers yet found [8] is rather complicated and still leaves open some problems with coherence in the presence of a universe.
Previous Fitch-style calculi. The Fitch-style approach was pioneered, apparently independently, by Martini and Masini [29] and Borghuis [9]. Martini and Masini’s work is rather notationally heavy, and weakening appears not to be admissible. Borghuis’s calculus for IK is excellent, but his calculi for stronger logics are not so compelling, as each different axiom is expressed with another version of the \(\mathsf {open}\) or \(\mathsf {shut}\) rules, not all of which compute when combined. The calculus for IS4 of Pfenning and Wong [34], refined by Davies and Pfenning [13, Sect. 4], provide the basis of the IS4 calculus of this paper, but involve some complications which appear to correlate to not assuming idempotence. We have extended this previous work by investigating the subformula property, introducing categorical semantics, and showing how left adjoints to necessity modalities à la tense logic can be used as types. Finally, the recent clocked type theory of Bahr et al. [3] independently gave a treatment of the later modality that on inspection is precisely Fitch-style (albeit with named ‘locks’), and which has better computational properties than the delayed substitution approach.
Dual contexts. Davies and Pfenning [13] use a pair of contexts \(\varDelta ; \varGamma \) with intended meaning \(\square \varDelta \wedge \varGamma \). This is quite different from the semantics of Fitch-style sequents, where structure in the context denotes the left adjoint of \(\square \). In recent work Kavvos [24] has shown that dual contexts may capture a number of different modal logics, and the approach has been used as a foundation for both pen-and-paper mathematics [37] and, via an Agda fork [40], formalisation [26]. We support this work but there is reason to explore other options. First, writing programs with dual context calculi was described by Davies and Pfenning themselves as ‘somewhat awkward’, and in the same paper they suggest the Fitch-style approach as a less awkward alternative. Indeed, Fitch’s approach was exactly designed to capture ‘natural’ modal deduction. Second, any application with multiple interacting modalities is unlikely to be accommodated in a mere two zones; the mode theories of Licata et al. [27] extend the dual zone approach to a richer setting in which interacting modalities, substructural contexts, and even Fitch-style natural deduction can be expressedFootnote 2, but the increase in complexity is considerable and much work remains to be done.
Further logics and algorithmic properties. We wish to bring more logics into the Fitch-style framework, in particular the logic of the later modality, extending IR with the strong Löb axiom \((\square A\rightarrow A)\rightarrow A\). The obvious treatment of this axiom does not terminate. but Bahr et al. [3] suggest that this can be managed by giving names to locks. We would further like to develop calculi with multiple modalities. This is easy to do by assigning each modality its own lock; two IK modalities give exactly the intuitionistic tense logic of Goré et al. [22]. The situation is rather more interesting where the modalities interact, as with the later and constant modalities. Finally, we would like to further investigate algorithmic properties of Fitch-style calculi such as type checking, type inference, and \(\eta \)-expansion and other notions of computation. In particular, we wonder if a notion of commuting conversion can be defined so that the calculi with \(\blacklozenge \) enjoy the subformula property.
Notes
- 1.
‘Fitch-style’ deduction can also be used to mean the linear presentation of natural deduction with subordinate proofs for implication.
- 2.
We are grateful to an anoymous reviewer for this last observation.
References
Atkey, R., McBride, C.: Productive coprogramming with guarded recursion. In: ICFP (2013)
Awodey, S., Bauer, A.: Propositions as [types]. J. Log. Comput. 14(4), 447–471 (2004)
Bahr, P., Grathwohl, H.B., Møgelberg, R.E.: The clocks are ticking: no more delays! In: LICS, pp. 1–12 (2017)
Bellin, G., De Paiva, V., Ritter, E.: Extended Curry-Howard correspondence for a basic constructive modal logic. In: M4M (2001)
Bierman, G.M., de Paiva, V.C.: On an intuitionistic modal logic. Stud. Logica. 65(3), 383–416 (2000)
Birkedal, L., Møgelberg, R.E.: Intensional type theory with guarded recursive types qua fixed points on universes. In: LICS (2013)
Bizjak, A., Grathwohl, H.B., Clouston, R., Møgelberg, R.E., Birkedal, L.: Guarded dependent type theory with coinductive types. In: Jacobs, B., Löding, C. (eds.) FoSSaCS 2016. LNCS, vol. 9634, pp. 20–35. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49630-5_2
Bizjak, A., Møgelberg, R.E.: Denotational semantics for guarded dependent type theory. Math. Struct. Comput. Sci. (2018, to appear)
Borghuis, V.A.J.: Coming to terms with modal logic: on the interpretation of modalities in typed lambda-calculus. Ph.D. thesis, Technische Universiteit Eindhoven (1994)
Božić, M., Došen, K.: Models for normal intuitionistic modal logics. Stud. Logica. 43(3), 217–245 (1984)
Clouston, R., Bizjak, A., Grathwohl, H.B., Birkedal, L.: The guarded lambda-calculus: programming and reasoning with guarded recursion for coinductive types. LMCS 12(3) (2016). https://lmcs.episciences.org/2019
Curry, H.B.: A Theory of Formal Deducibility. University of Notre Dame Press, Indiana (1957)
Davies, R., Pfenning, F.: A modal analysis of staged computation. JACM 48(3), 555–604 (2001)
De Queiroz, R.J., Gabbay, D.M.: The functional interpretation of modal necessity. In: de Rijike, M. (eds.) Advances in Intensional Logic, pp. 61–91. Springer, Dordrecht (1997). https://doi.org/10.1007/978-94-015-8879-9_3
Dzik, W., Järvinen, J., Kondo, M.: Intuitionistic propositional logic with Galois connections. Log. J. IGPL 18(6), 837–858 (2009)
Eilenberg, S., Moore, J.C.: Adjoint functors and triples. Illinois J. Math. 9(3), 381–398 (1965)
Ewald, W.: Intuitionistic tense and modal logic. J. Symb. Log. 51(1), 166–179 (1986)
Fairtlough, M., Mendler, M.: Propositional lax logic. Inform. Comput. 137(1), 1–33 (1997)
Fitch, F.B.: Symbolic Logic, An Introduction. Ronald Press Co., New York (1952)
Fitting, M.: Proof Methods for Modal and Intuitionistic Logics. D. Reidel Publishing Co., Dordrecht (1983)
Girard, J.Y., Taylor, P., Lafont, Y.: Proofs and Types. Cambridge University Press, Cambridge (1989)
Goré, R., Postniece, L., Tiu, A.: Cut-elimination and proof search for bi-intuitionistic tense logic. In: AiML (2010)
Kavvos, G.A.: The many worlds of modal \(\lambda \)-calculi: I. Curry-Howard for necessity, possibility and time. arXiv:1605.08106 (2016)
Kavvos, G.: Dual-context calculi for modal logic. In: LICS (2017)
Lambek, J., Scott, P.J.: Introduction to Higher-Order Categorical Logic. Cambridge University Press, Cambridge (1986)
Licata, D.R., Orton, I., Pitts, A.M., Spitters, B.: Internal universes in models of homotopy type theory (2018, unpublished)
Licata, D.R., Shulman, M., Riley, M.: A fibrational framework for substructural and modal logics. In: FSCD (2017)
Litak, T.: Constructive modalities with provability smack. In: Bezhanishvili, G. (ed.) Leo Esakia on Duality in Modal and Intuitionistic Logics. OCL, vol. 4, pp. 187–216. Springer, Dordrecht (2014). https://doi.org/10.1007/978-94-017-8860-1_8
Martini, S., Masini, A.: A computational interpretation of modal proofs. In: Wansing, H. (ed.) Proof Theory of Modal Logic, pp. 213–241. Springer, Dordrecht (1996). https://doi.org/10.1007/978-94-017-2798-3_12
McBride, C., Paterson, R.: Applicative programming with effects. J. Funct. Program. 18(1), 1–13 (2008)
Menni, M.: About
 -quantifiers. Appl. Categ. Struct. 11(5), 421–445 (2003)
-quantifiers. Appl. Categ. Struct. 11(5), 421–445 (2003)Moggi, E.: Computational lambda-calculus and monads. In: LICS, pp. 14–23 (1989)
de Paiva, V., Ritter, E.: Basic constructive modality. In: Logic without Frontiers: Festschrift for Walter Alexandre Carnielli on the occasion of his 60th Birthday, pp. 411–428. College Publication (2011)
Pfenning, F., Wong, H.C.: On a modal \(\lambda \)-calculus for S4. In: MFPS (1995)
Rijke, E., Shulman, M., Spitters, B.: Modalities in homotopy type theory. arXiv:1706.07526 (2017)
Schreiber, U.: Differential cohomology in a cohesive infinity-topos. arXiv:1310.7930 (2013)
Shulman, M.: Brouwer’s fixed-point theorem in real-cohesive homotopy type theory. Math. Struct. Comput. Sci. (2017). https://www.cambridge.org/core/journals/mathematical-structures-in-computer-science/article/brouwers-fixedpoint-theorem-in-realcohesive-homotopy-type-theory/8270C2EAC4EE5D5CDBA17EEB3FF6B19E
Simpson, A.K.: The proof theory and semantics of intuitionistic modal logic. Ph.D. thesis, University of Edinburgh (1994)
Sørensen, M.H., Urzyczyn, P.: Lectures on the Curry-Howard Isomorphism. Elsevier, New York (2006)
Vezzosi, A.: Agda-flat (2017). https://github.com/agda/agda/tree/flat. GitHub repository
Wadler, P.: Propositions as types. Commun. ACM 58(12), 75–84 (2015)
Wansing, H.: Sequent calculi for normal modal propositional logics. J. Log. Comput. 4(2), 125–142 (1994)
Yokota, S.: General characterization results on intuitionistic modal propositional logics. Commentarii Mathematici Universitatis Sancti Pauli 34(2), 177–199 (1985)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made. The images or other third party material in this book are included in the book's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the book's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2018 The Author(s)
About this paper
Cite this paper
Clouston, R. (2018). Fitch-Style Modal Lambda Calculi. In: Baier, C., Dal Lago, U. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2018. Lecture Notes in Computer Science(), vol 10803. Springer, Cham. https://doi.org/10.1007/978-3-319-89366-2_14
Download citation
DOI: https://doi.org/10.1007/978-3-319-89366-2_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89365-5
Online ISBN: 978-3-319-89366-2
eBook Packages: Computer ScienceComputer Science (R0)





 .
.

 .
.
 .
.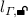 is
is 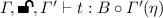 .
. -quantifiers. Appl. Categ. Struct. 11(5), 421–445 (2003)
-quantifiers. Appl. Categ. Struct. 11(5), 421–445 (2003)