Abstract Family-Based Model Checking Using Modal Featured Transition Systems: Preservation of CTL$^{\star }$

Abstract

Variational systems allow effective building of many custom variants by using features (configuration options) to mark the variable functionality. In many of the applications, their quality assurance and formal verification are of paramount importance. Family-based model checking allows simultaneous verification of all variants of a variational system in a single run by exploiting the commonalities between the variants. Yet, its computational cost still greatly depends on the number of variants (often huge).

In this work, we show how to achieve efficient family-based model checking of CTL$^{\star }$ temporal properties using variability abstractions and off-the-shelf (single-system) tools. We use variability abstractions for deriving abstract family-based model checking, where the variability model of a variational system is replaced with an abstract (smaller) version of it, called modal featured transition system, which preserves the satisfaction of both universal and existential temporal properties, as expressible in CTL$^{\star }$. Modal featured transition systems contain two kinds of transitions, termed may and must transitions, which are defined by the conservative (over-approximating) abstractions and their dual (under-approximating) abstractions, respectively. The variability abstractions can be combined with different partitionings of the set of variants to infer suitable divide-and-conquer verification plans for the variational system. We illustrate the practicality of this approach for several variational systems.

1 Introduction

Variational systems appear in many application areas and for many reasons. Efficient methods to achieve customization, such as Software Product Line Engineering (SPLE) [8], use features (configuration options) to control presence and absence of the variable functionality [1]. Family members, called variants of a variational system, are specified in terms of features selected for that particular variant. The reuse of code common to multiple variants is maximized. The SPLE method is particularly popular in the embedded and critical system domain (e.g. cars, phones). In these domains, a rigorous verification and analysis is very important. Among the methods included in current practices, model checking [2] is a well-studied technique used to establish that temporal logic properties hold for a system.

Variability and SPLE are major enablers, but also a source of complexity. Obviously, the size of the configuration space (number of variants) is the limiting factor to the feasibility of any verification technique. Exponentially many variants can be derived from few configuration options. This problem is referred to as the configuration space explosion problem. A simple “brute-force” application of a single-system model checker to each variant is infeasible for realistic variational systems, due to the sheer number of variants. This is very ineffective also because the same execution behavior is checked multiple times, whenever it is shared by some variants. Another, more efficient, verification technique [5, 6] is based on using compact representations for modelling variational systems, which incorporate the commonality within the family. We will call these representations variability models (or featured transition systems). Each behavior in a variability model is associated with the set of variants able to produce it. A specialized family-based model checking algorithm executed on such a model, checks an execution behavior only once regardless of how many variants include it. These algorithms model check all variants simultaneously in a single run and pinpoint the variants that violate properties. Unfortunately, their performance still heavily depends on the size and complexity of the configuration space of the analyzed variational system. Moreover, maintaining specialized family-based tools is also an expensive task.

In order to address these challenges, we propose to use standard, single-system model checkers with an alternative, externalized way to combat the configuration space explosion. We apply the so-called variability abstractions to a variability model which is too large to handle (“configuration space explosion”), producing a more abstract model, which is smaller than the original one. We abstract from certain aspects of the configuration space, so that many of the configurations (variants) become indistinguishable and can be collapsed into a single abstract configuration. The abstract model is constructed in such a way that if some property holds for this abstract model it will also hold for the concrete model. Our technique extends the scope of existing over-approximating variability abstractions [14, 19] which currently support the verification of universal properties only (LTL and $\forall$CTL). Here we construct abstract variability models which can be used to check arbitrary formulae of CTL$^{\star }$, thus including arbitrary nested path quantifiers. We use modal featured transition systems (MFTSs) for representing abstract variability models. MFTSs are featured transition systems (FTSs) with two kinds of transitions, must and may, expressing behaviours that necessarily occur (must) or possibly occur (may). We use the standard conservative (over-approximating) abstractions to define may transitions, and their dual (under-approximating) abstractions to define must transitions. Therefore, MFTSs perform both over- and under-approximation, admitting both universal and existential properties to be deduced. Since MFTSs preserve all CTL$^{\star }$ properties, we can verify any such properties on the concrete variability model (which is given as an FTSs) by verifying these on an abstract MFTS. Any model checking problem on modal transitions systems (resp., MFTSs) can be reduced to two traditional model checking problems on standard transition systems (resp., FTSs). The overall technique relies on partitioning and abstracting concrete FTSs, until the point we obtain models with so limited variability (or, no variability) that it is feasible to complete their model checking in the brute-force fashion using the standard single-system model checkers. Compared to the family-based model checking, experiments show that the proposed technique achieves performance gains.

2 Background

In this section, we present the background used in later developments.

Modal Featured Transition Systems. Let $\mathbb {F}= \{A_1, \ldots , A_n\}$ be a finite set of Boolean variables representing the features available in a variational system. A specific subset of features, $k \subseteq \mathbb {F}$, known as configuration, specifies a variant (valid product) of a variational system. We assume that only a subset $\mathbb {K}\subseteq 2^{\mathbb {F}}$ of configurations are valid. An alternative representation of configurations is based upon propositional formulae. Each configuration $k \in \mathbb {K}$ can be represented by a formula: $k(A_1) \wedge \ldots \wedge k(A_n)$, where $k(A_i) = A_i$ if $A_i \in k$, and $k(A_i) = \lnot A_i$ if $A_i \notin k$ for $1 \le i \le n$. We will use both representations interchangeably.

We recall the basic definition of a transition system (TS) and a modal transition system (MTS) that we will use to describe behaviors of single-systems.

Definition 1

A transition system (TS) is a tuple $\mathcal {T}=(S,Act,trans,I,AP,L)$, where S is a set of states; Act is a set of actions; $trans \subseteq S \times Act \times S$ is a transition relation; $I \subseteq S$ is a set of initial states; AP is a set of atomic propositions; and $L : S \rightarrow 2^{AP}$ is a labelling function specifying which propositions hold in a state. We write whenever $(s_1,\lambda ,s_2) \in \textit{trans}$.

An execution (behaviour) of a TS $\mathcal {T}$ is an infinite sequence $\rho = s_0 \lambda _1 s_1 \lambda _2 \ldots$ with $s_0 \in I$ such that $s_i {\mathop {\longrightarrow }\limits ^{\lambda _{i+1}}} s_{i+1}$ for all $i \ge 0$. The semantics of the TS $\mathcal {T}$, denoted as $[\! [\mathcal {T} ]\! ]_{TS}$, is the set of its executions.

MTSs [26] are a generalization of transition systems that allows describing not just a sum of all behaviors of a system but also an over- and under-approximation of the system’s behaviors. An MTS is a TS equipped with two transition relations: must and may. The former (must) is used to specify the required behavior, while the latter (may) to specify the allowed behavior of a system.

Definition 2

A modal transition system (MTS) is represented by a tuple $\mathcal {M}=(S,Act,trans^{may},trans^{must},I,AP,L)$, where $trans^{may} \subseteq S \times Act \times S$ describe may transitions of $\mathcal {M}$; $trans^{must} \subseteq S \times Act \times S$ describe must transitions of $\mathcal {M}$, such that $trans^{must} \subseteq trans^{may}$.

The intuition behind the inclusion $trans^{must} \subseteq trans^{may}$ is that transitions that are necessarily true ($trans^{must}$) are also possibly true ($trans^{may}$). A may-execution in $\mathcal {M}$ is an execution with all its transitions in $trans^{may}$; whereas a must-execution in $\mathcal {M}$ is an execution with all its transitions in $trans^{must}$. We use $[\! [\mathcal {M} ]\! ]_{MTS}^{may}$ to denote the set of all may-executions in $\mathcal {M}$, whereas $[\! [\mathcal {M} ]\! ]_{MTS}^{must}$ to denote the set of all must-executions in $\mathcal {M}$.

An FTS describes behavior of a whole family of systems in a superimposed manner. This means that it combines models of many variants in a single monolithic description, where the transitions are guarded by a presence condition that identifies the variants they belong to. The presence conditions $\psi$ are drawn from the set of feature expressions, $\textit{FeatExp}(\mathbb {F})$, which are propositional logic formulae over $\mathbb {F}$: $\psi \,{::}{=}\,\textit{true}\mid A \in \mathbb {F}\mid \lnot \psi \mid \psi _1 \wedge \psi _2$. The presence condition $\psi$ of a transition specifies the variants in which the transition is enabled. We write $[\! [\psi ]\! ]$ to denote the set of variants from $\mathbb {K}$ that satisfy $\psi$, i.e. $k \in [\! [\psi ]\! ]$ iff $k \models \psi$.

Definition 3

A featured transition system (FTS) represents a tuple $\mathcal {F}=(S,Act,trans,I,AP,L,\mathbb {F},\mathbb {K},\delta )$, where S, Act, trans, I, AP, and L are defined as in TS; $\mathbb {F}$ is the set of available features; $\mathbb {K}$ is a set of valid configurations; and $\delta : trans \rightarrow FeatExp(\mathbb {F})$ is a total function decorating transitions with presence conditions (feature expressions).

The projection of an FTS $\mathcal {F}$ to a variant $k \in \mathbb {K}$, denoted as $\pi _k(\mathcal {F})$, is the TS $(S,Act,trans',I,AP,L)$, where $trans'=\{ t \in trans \mid k \models \delta (t) \}$. We lift the definition of projection to sets of configurations $\mathbb {K}' \!\subseteq \! \mathbb {K}$, denoted as $\pi _{\mathbb {K}'}(\mathcal {F})$, by keeping the transitions admitted by at least one of the configurations in $\mathbb {K}'$. That is, $\pi _{\mathbb {K}'}(\mathcal {F})$, is the FTS $(S,Act,trans',I,AP,L,\mathbb {F},\mathbb {K}',\delta )$, where $trans'=\{ t \in trans \mid \exists k \in \mathbb {K}'. k \models \delta (t) \}$. The semantics of an FTS $\mathcal {F}$, denoted as $[\! [\mathcal {F} ]\! ]_{FTS}$, is the union of behaviours of the projections on all valid variants $k \in \mathbb {K}$, i.e. $[\! [\mathcal {F} ]\! ]_{FTS} = \cup _{k \in \mathbb {K}} [\! [\pi _k(\mathcal {F}) ]\! ]_{TS}$.

We will use modal featured transition systems (MFTS) for representing abstractions of FTSs. MFTSs are variability-aware extension of MTSs.

Definition 4

A modal featured transition system (MFTS) represents a tuple $\mathcal {MF}=(S,Act,trans^{may},trans^{must},I,AP,L,\mathbb {F},\mathbb {K},\delta ^{may},\delta ^{must})$, where $trans^{may}$ and $\delta ^{may}: trans^{may} \rightarrow FeatExp(\mathbb {F})$ describe may transitions of $\mathcal {MF}$; $trans^{must}$ and $\delta ^{must}: trans^{must} \rightarrow FeatExp(\mathbb {F})$ describe must transitions of $\mathcal {MF}$.

The projection of an MFTS $\mathcal {MF}$ to a variant $k \in \mathbb {K}$, denoted as $\pi _k(\mathcal {MF})$, is the MTS $(S,Act,trans'^{may},trans'^{must},I,AP,L)$, where $trans'^{may}=\{ t \!\in \! trans^{may} \mid k \!\models \! \delta ^{may}(t) \}$, $trans'^{must}=\{ t \!\in \! trans^{must} \mid k \!\models \! \delta ^{must}(t) \}$. We define $[\! [\mathcal {MF} ]\! ]^{may}_{MFTS}=\cup _{k \in \mathbb {K}} [\! [\pi _k(\mathcal {MF}) ]\! ]^{may}_{MTS}$, and $[\! [\mathcal {MF} ]\! ]^{must}_{MFTS}=\cup _{k \in \mathbb {K}} [\! [\pi _k(\mathcal {MF}) ]\! ]^{must}_{MTS}$.

Fig. 1.

The FTS for VendingMachine. (Color figure online)

Fig. 2.

Example 1

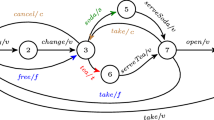
Throughout this paper, we will use a beverage vending machine as a running example [6]. Figure 1 shows the FTS of a VendingMachine family. It has five features, and each of them is assigned an identifying letter and a color. The features are: VendingMachine (denoted by letter v, in black), the mandatory base feature of purchasing a drink, present in all variants; Tea (), for serving tea; Soda (), for serving soda, which is a mandatory feature present in all variants; CancelPurchase (), for canceling a purchase after a coin is entered; and FreeDrinks () for offering free drinks. Each transition is labeled by an action followed by a feature expression. For instance, the transition is included in variants where the feature is enabled.

By combining various features, a number of variants of this VendingMachine can be obtained. Recall that and are mandatory features. The set of valid configurations is thus: . In Fig. 2 is shown the basic version of VendingMachine that only serves soda, which is described by the configuration: $\{v,s\}$ (or, as formula $v \wedge \! s \wedge \! \lnot t \wedge \! \lnot c \wedge \! \lnot f$), that is the projection . It takes a coin, returns change, serves soda, opens a compartment so that the customer can take the soda, before closing it again.

Figure 3 shows an MTS. Must transitions are denoted by solid lines, while may transitions by dashed lines.    $\square$

CTL$^{\star }$ Properties. Computation Tree Logic$^{\star }$ (CTL$^{\star }$) [2] is an expressive temporal logic for specifying system properties, which subsumes both CTL and LTL logics. CTL$^{\star }$ state formulae $\varPhi$ are generated by the following grammar:

$$ \varPhi \,{::}{=}\, \textit{true}\mid a \in {\textit{AP}} \mid \lnot a \mid \varPhi _1 \wedge \varPhi _2 \mid \forall \phi \mid \exists \phi , \qquad \phi \,{::}{=}\, \varPhi \mid \phi _1 \wedge \phi _2 \mid \bigcirc \phi \mid \phi _1 \textsf {U}\, \phi _2 $$

where $\phi$ represent CTL$^{\star }$ path formulae. Note that the CTL$^{\star }$ state formulae $\varPhi$ are given in negation normal form ($\lnot$ is applied only to atomic propositions). Given $\varPhi \in \text {CTL}^{\star }$, we consider $\lnot \varPhi$ to be the equivalent CTL$^{\star }$ formula given in negation normal form. Other derived temporal operators (path formulae) can be defined as well by means of syntactic sugar, for instance: $\Diamond \phi = true \, \textsf {U} \phi$ ($\phi$ holds eventually), and $\Box \phi = \lnot \forall \Diamond \lnot \phi$ ($\phi$ always holds). $\forall$CTL$^{\star }$ and $\exists$CTL$^{\star }$ are subsets of CTL$^{\star }$ where the only allowed path quantifiers are $\forall$ and $\exists$, respectively.

We formalise the semantics of CTL$^{\star }$ over a TS $\mathcal {T}$. We write $[\! [\mathcal {T} ]\! ]^{s}_{\text {TS}}$ for the set of executions that start in state s; $\rho [i]=s_i$ to denote the i-th state of the execution $\rho$; and $\rho _i = s_i \lambda _{i+1} s_{i+1} \ldots$ for the suffix of $\rho$ starting from its i-th state.

Definition 5

Satisfaction of a state formula $\varPhi$ in a state s of a TS $\mathcal {T}$, denoted $\mathcal {T},s \models \phi$, is defined as ($\mathcal {T}$ is omitted when clear from context):

(1) :

$s \models a$ iff $a \in L(s)$; $s \models \lnot a$ iff $a \notin L(s)$,

(2) :

$s \models \varPhi _1 \wedge \varPhi _2$ iff $s \models \varPhi _1$ and $s \models \varPhi _2$,

(3) :

$s \models \forall \phi$ iff $\forall \rho \in [\! [\mathcal {T} ]\! ]^{s}_{\text {TS}}. \, \rho \models \phi$; $s \models \exists \phi$ iff $\exists \rho \in [\! [\mathcal {T} ]\! ]^{s}_{\text {TS}}. \, \rho \models \phi$

Satisfaction of a path formula $\phi$ for an execution $\rho$ of a TS $\mathcal {T}$, denoted $\mathcal {T},\rho \models \phi$, is defined as ($\mathcal {T}$ is omitted when clear from context):

(4) :

$\rho \models \varPhi$ iff $\rho [0] \models \varPhi$,

(5) :

$\rho \models \phi _1 \wedge \phi _2$ iff $\rho \models \phi _1$ and $\rho \models \phi _2$; $\rho \models \bigcirc \phi$ iff $\rho _1 \models \phi$; $\rho \models (\phi _1 \textsf {U}\, \phi _2)$ iff $\exists i \!\ge \! 0. \, \big ( \rho _i \models \phi _2 \wedge (\forall 0 \!\le \! j \!\le \! i\!-\!1. \, \rho _j \models \phi _1) \big )$

A TS $\mathcal {T}$ satisfies a state formula $\varPhi$, written $\mathcal {T}\models \varPhi$, iff $\forall s_0 \in I. \, s_0 \models \varPhi$.

Definition 6

An FTS $\mathcal {F}$ satisfies a CTL$^{\star }$ formula $\varPhi$, written $\mathcal {F}\models \varPhi$, iff all its valid variants satisfy the formula: $\forall k\!\in \!\mathbb {K}. \, \pi _k(\mathcal {F}) \models \varPhi$.

The interpretation of CTL$^{\star }$ over an MTS $\mathcal {M}$ is defined slightly different from the above Definition 5. In particular, the clause (3) is replaced by:

(3’) :

$s \models \forall \phi$ iff for every may-execution $\rho$ in the state s of $\mathcal {M}$, that is $\forall \rho \in [\! [\mathcal {M} ]\! ]_{MTS}^{may,s}$, it holds $\rho \models \phi$; whereas $s \models \exists \phi$ iff there exists a must-execution $\rho$ in the state s of $\mathcal {M}$, that is $\exists \rho \in [\! [\mathcal {M} ]\! ]_{MTS}^{must,s}$, such that $\rho \models \phi$.

From now on, we implicitly assume this adapted definition when interpreting CTL$^{\star }$ formulae over MTSs and MFTSs.

Example 2

Consider the FTS VendingMachine in Fig. 1. Suppose that the proposition $\texttt {start}$ holds in the initial state . An example property $\varPhi _1$ is: $\forall \Box \, \forall \Diamond \texttt {start}$, which states that in every state along every execution all possible continuations will eventually reach the initial state. This formula is in $\forall$CTL$^{\star }$. Note that $\textsc {VendingMachine}\not \models \varPhi _1$. For example, if the feature (Cancel) is enabled, a counter-example where the state is never reached is: . The set of violating products is . However, .

Consider the property $\varPhi _2$: $\forall \Box \, \exists \Diamond \texttt {start}$, which describes a situation where in every state along every execution there exists a possible continuation that will eventually reach the start state. This is a CTL$^{\star }$ formula, which is neither in $\forall$CTL$^{\star }$ nor in $\exists$CTL$^{\star }$. Note that $\textsc {VendingMachine}\models \varPhi _2$, since even for variants with the feature there is a continuation from the state back to .

Consider the $\exists$CTL$^{\star }$ property $\varPhi _3$: $\exists \Box \, \exists \Diamond \texttt {start}$, which states that there exists an execution such that in every state along it there exists a possible continuation that will eventually reach the start state. The witnesses are for variants that satisfy , and for variants with .    $\square$

3 Abstraction of FTSs

We now introduce the variability abstractions which preserve full CTL and its universal and existential properties. They simplify the configuration space of an FTSs, by reducing the number of configurations and manipulating presence conditions of transitions. We start working with Galois connections¹ between Boolean complete lattices of feature expressions, and then induce a notion of abstraction of FTSs. We define two classes of abstractions. We use the standard conservative abstractions [14, 15] as an instrument to eliminate variability from the FTS in an over-approximating way, so by adding more executions. We use the dual abstractions, which can also eliminate variability but through under-approximating the given FTS, so by dropping executions.

Domains. The Boolean complete lattice of feature expressions (propositional formulae over $\mathbb {F}$) is: $(\textit{FeatExp}(\mathbb {F})_{/\equiv },\models ,\vee ,\wedge ,\textit{true},\textit{false},\lnot )$. The elements of the domain $\textit{FeatExp}(\mathbb {F})_{/\equiv }$ are equivalence classes of propositional formulae $\psi \!\in \! \textit{FeatExp}(\mathbb {F})$ obtained by quotienting by the semantic equivalence $\equiv$. The ordering $\models$ is the standard entailment between propositional logics formulae, whereas the least upper bound and the greatest lower bound are just logical disjunction and conjunction respectively. Finally, the constant false is the least, true is the greatest element, and negation is the complement operator.

Conservative Abstractions. The join abstraction, $\varvec{\alpha }^{ \text {join} }$, merges the control-flow of all variants, obtaining a single variant that includes all executions occurring in any variant. The information about which transitions are associated with which variants is lost. Each feature expression $\psi$ is replaced with true if there exists at least one configuration from $\mathbb {K}$ that satisfies $\psi$. The new abstract set of features is empty: $\varvec{\alpha }^{ \text {join} }(\mathbb {F})=\emptyset$, and the abstract set of valid configurations is a singleton: $\varvec{\alpha }^{ \text {join} }(\mathbb {K}) = \{ \textit{true}\}$ if $\mathbb {K}\ne \emptyset$. The abstraction and concretization functions between $\textit{FeatExp}(\mathbb {F})$ and $\textit{FeatExp}(\emptyset )$, forming a Galois connection [14, 15], are defined as:

$$ \varvec{\alpha }^{ \text {join} }(\psi ) = {\left\{ \begin{array}{ll} \textit{true}&{} \text {if } \exists k \in \mathbb {K}. k \models \psi \\ \textit{false}&{} \text {otherwise} \end{array}\right. } \qquad \ \varvec{\gamma }^{ \text {join} }(\psi ) = {\left\{ \begin{array}{ll} \textit{true}&{} \text {if } \psi \text { is } \textit{true}\\ \bigvee \nolimits _{k \in 2^\mathbb {F}\setminus \mathbb {K}} k &{} \text {if } \psi \text { is } \textit{false}\end{array}\right. } $$

The feature ignore abstraction, $\varvec{\alpha }^{ \text {fignore} }_{A}$, introduces an over-approximation by ignoring a single feature $A\!\in \!\mathbb {F}$. It merges the control flow paths that only differ with regard to A, but keeps the precision with respect to control flow paths that do not depend on A. The features and configurations of the abstracted model are: $\varvec{\alpha }^{ \text {fignore} }_{A}(\mathbb {F}) = \mathbb {F}\!\setminus \!\{A\}$, and $\varvec{\alpha }^{ \text {fignore} }_{A}(\mathbb {K}) = \{ k[l_A \mapsto \textit{true}] \mid k\in \mathbb {K}\}$, where $l_A$ denotes a literal of A (either A or $\lnot A$), and $k[l_A\mapsto \textit{true}]$ is a formula resulting from k by substituting true for $l_A$. The abstraction and concretization functions between $\textit{FeatExp}(\mathbb {F})$ and $\textit{FeatExp}(\varvec{\alpha }^{ \text {fignore} }_{A}(\mathbb {F}))$, forming a Galois connection [14, 15], are:

$$ \varvec{\alpha }^{ \text {fignore} }_{A}(\psi ) = \psi [l_A \mapsto \textit{true}] \qquad \ \varvec{\gamma }^{ \text {fignore} }_{A}(\psi ') = (\psi ' \wedge A) \vee (\psi ' \wedge \lnot A) $$

where $\psi$ and $\psi '$ need to be in negation normal form before substitution.

Dual Abstractions. Suppose that $\langle {\textit{FeatExp}(\mathbb {F})_{/\equiv }},{\models }\rangle$, $\langle {\textit{FeatExp}(\alpha (\mathbb {F}))_{/\equiv } },{\models }\rangle$ are Boolean complete lattices, and is a Galois connection. We define [9]: $\widetilde{\alpha }=\lnot \circ \alpha \circ \lnot$ and $\widetilde{\gamma }=\lnot \circ \gamma \circ \lnot$ so that is a Galois connection (or equivalently, ). The obtained Galois connections $(\widetilde{\alpha },\widetilde{\gamma })$ are called dual (under-approximating) abstractions of $(\alpha ,\gamma )$.

The dual join abstraction, $\widetilde{\varvec{\alpha }^{ \text {join} }}$, merges the control-flow of all variants, obtaining a single variant that includes only those executions that occur in all variants. Each feature expression $\psi$ is replaced with true if all configurations from $\mathbb {K}$ satisfy $\psi$. The abstraction and concretization functions between $\textit{FeatExp}(\mathbb {F})$ and $\textit{FeatExp}(\emptyset )$, forming a Galois connection, are defined as: $\widetilde{\varvec{\alpha }^{ \text {join} }}=\lnot \circ \varvec{\alpha }^{ \text {join} }\circ \lnot$ and $\widetilde{\varvec{\gamma }^{ \text {join} }}=\lnot \circ \varvec{\gamma }^{ \text {join} }\circ \lnot$, that is:

$$\begin{aligned} \widetilde{\varvec{\alpha }^{ \text {join} }}(\psi ) = {\left\{ \begin{array}{ll} \textit{true}&{} \text {if } \forall k \in \mathbb {K}. k \models \psi \\ \textit{false}&{} \text {otherwise } \end{array}\right. } \qquad \widetilde{\varvec{\gamma }^{ \text {join} }}(\psi ) = {\left\{ \begin{array}{ll} \bigwedge \nolimits _{k \in 2^\mathbb {F}\backslash \mathbb {K}} (\lnot k) &{} \text {if } \psi \text { is } \textit{true}\\ \textit{false}&{} \text {if } \psi \text { is } \textit{false}\end{array}\right. } \end{aligned}$$

The dual feature ignore abstraction, $\widetilde{\varvec{\alpha }^{ \text {fignore} }_{A}}$, introduces an under-approximation by ignoring the feature $A\!\in \!\mathbb {F}$, such that the literals of A (that is, A and $\lnot A$) are replaced with false in feature expressions (given in negation normal form). The abstraction and concretization functions between $\textit{FeatExp}(\mathbb {F})$ and $\textit{FeatExp}(\varvec{\alpha }^{ \text {fignore} }_{A}(\mathbb {F}))$, forming a Galois connection, are defined as: $\widetilde{\varvec{\alpha }^{ \text {fignore} }_{A}}=\lnot \circ \varvec{\alpha }^{ \text {fignore} }_{A} \circ \lnot$ and $\widetilde{\varvec{\gamma }^{ \text {fignore} }_{A}}=\lnot \circ \varvec{\gamma }^{ \text {fignore} }_{A} \circ \lnot$, that is:

$$ \widetilde{\varvec{\alpha }^{ \text {fignore} }_{A}}(\psi ) = \psi [l_A \mapsto \textit{false}] \qquad \widetilde{\varvec{\gamma }^{ \text {fignore} }_{A}}(\psi ') = (\psi ' \vee \lnot A) \wedge (\psi ' \vee A) $$

where $\psi$ and $\psi '$ are in negation normal form.

Abstract MFTS and Preservation of CTL$^{\star }$. Given a Galois connection $(\alpha ,\gamma )$ defined on the level of feature expressions, we now define the abstraction of an FTS as an MFTS with two transition relations: one (may) preserving universal properties, and the other (must) existential properties. The may transitions describe the behaviour that is possible, but not need be realized in the variants of the family; whereas the must transitions describe behaviour that has to be present in any variant of the family.

Definition 7

Given the FTS $\mathcal {F}=(S,Act,trans,I,AP,L,\mathbb {F},\mathbb {K},\delta )$, we define the MFTS $\alpha (\mathcal {F})=(S,Act,trans^{may},trans^{must},I,AP,L,\alpha (\mathbb {F}),\alpha (\mathbb {K}),\delta ^{may},\delta ^{must})$ to be its abstraction, where $\delta ^{may}(t)=\alpha (\delta (t))$, $\delta ^{must}(t)=\widetilde{\alpha }(\delta (t))$, $trans^{may} = \{ t \in trans \mid \delta ^{may}(t) \ne \textit{false}\}$, and $trans^{must} = \{ t \in trans \mid \delta ^{must}(t) \ne \textit{false}\}$.

Note that the degree of reduction is determined by the choice of abstraction and may hence be arbitrary large. In the extreme case of join abstraction, we obtain an abstract model with no variability in it, that is $\varvec{\alpha }^{ \text {join} }(\mathcal {F})$ is an ordinary MTS.

Example 3

Recall the FTS $\textsc {VendingMachine}$ of Fig. 1 with the set of valid configurations $\mathbb {K}^{\textsc {VM}}$ (see Example 1). Figure 3 shows $\varvec{\alpha }^{ \text {join} }({\textsc {VendingMachine}})$, where the allowed (may) part of the behavior includes the transitions that are associated with the optional features , , in VendingMachine, whereas the required (must) part includes the transitions associated with the mandatory features and . Note that $\varvec{\alpha }^{ \text {join} }({\textsc {VendingMachine}})$ is an ordinary MTS with no variability. The MFTS is shown in [12, Appendix B], see Fig. 8. It has the singleton set of features and limited variability , where the mandatory features and are enabled.    $\square$

From the MFTS (resp., MTS) $\mathcal {MF}$, we define two FTSs (resp., TSs) $\mathcal {MF}^{may}$ and $\mathcal {MF}^{must}$ representing the may- and must-components of $\mathcal {MF}$, i.e. its may and must transitions, respectively. Thus, we have $[\! [\mathcal {MF}^{may} ]\! ]_{FTS}=[\! [\mathcal {MF} ]\! ]^{may}_{MFTS}$ and $[\! [\mathcal {MF}^{must} ]\! ]_{FTS}=[\! [\mathcal {MF} ]\! ]^{must}_{MFTS}$.

We now show that the abstraction of an FTS is sound with respect to CTL$^{\star }$. First, we show two helper lemmas stating that: for any variant $k \!\in \! \mathbb {K}$ that can execute a behavior, there exists an abstract variant $k' \!\in \! \alpha (\mathbb {K})$ that executes the same may-behaviour; and for any abstract variant $k' \!\in \! \alpha (\mathbb {K})$ that can execute a must-behavior, there exists a variant $k \!\in \! \mathbb {K}$ that executes the same behaviour².

Lemma 1

Let $\psi \in \textit{FeatExp}(\mathbb {F})$, and $\mathbb {K}$ be a set of valid configurations over $\mathbb {F}$.

(i) :

Let $k \in \mathbb {K}$ and $k \models \psi$. Then there exists $k' \in \alpha (\mathbb {K})$, such that $k' \models \alpha (\psi )$.

(ii) :

Let $k' \in \alpha (\mathbb {K})$ and $k' \models \widetilde{\alpha }(\psi )$. Then there exists $k \in \mathbb {K}$, such that $k \models \psi$.

Lemma 2

(i) :

Let $k \in \mathbb {K}$ and $\rho \in [\! [\pi _k(\mathcal {F}) ]\! ]_{TS} \subseteq [\! [\mathcal {F} ]\! ]_{FTS}$. Then there exists $k' \in \alpha (\mathbb {K})$, such that $\rho \in [\! [\pi _{k'}(\alpha (\mathcal {F})) ]\! ]^{may}_{MTS} \subseteq [\! [\alpha (\mathcal {F}) ]\! ]^{may}_{MFTS}$ is a may-execution in $\alpha (\mathcal {F})$.

(ii) :

Let $k' \in \alpha (\mathbb {K})$ and $\rho \in [\! [\pi _{k'}(\alpha (\mathcal {F})) ]\! ]^{must}_{MTS} \subseteq [\! [\alpha (\mathcal {F}) ]\! ]^{must}_{MFTS}$ be a must-execution in $\alpha (\mathcal {F})$. Then there exists $k \in \mathbb {K}$, such that $\rho \in [\! [\pi _k(\mathcal {F}) ]\! ]_{TS} \subseteq [\! [\mathcal {F} ]\! ]_{FTS}$.

As a result, every $\forall$CTL$^{\star }$ (resp., $\exists$CTL$^{\star }$) property true for the may- (resp., must-) component of $\alpha (\mathcal {F})$ is true for $\mathcal {F}$ as well. Moreover, the MFTS $\alpha (\mathcal {F})$ preserves the full CTL$^{\star }$.

Theorem 1

(Preservation results). For any FTS $\mathcal {F}$ and $(\alpha ,\gamma )$, we have:  

($\forall$CTL$^{\star }$):

For every $\varPhi \in \forall CTL^{\star }$, $\alpha (\mathcal {F})^{may} \models \varPhi \ \implies \ \mathcal {F}\models \varPhi$.

($\exists$CTL$^{\star }$):

For every $\varPhi \in \exists CTL^{\star }$, $\alpha (\mathcal {F})^{must} \models \varPhi \ \implies \ \mathcal {F}\models \varPhi$.

(CTL $^{\star }$ ) :

For every $\varPhi \in CTL^{\star }$, $\alpha (\mathcal {F}) \models \varPhi \ \implies \ \mathcal {F}\models \varPhi$.

 

Abstract models are designed to be conservative for the satisfaction of properties. However, in case of the refutation of a property, a counter-example is found in the abstract model which may be spurious (introduced due to abstraction) for some variants and genuine for the others. This can be established by checking which variants can execute the found counter-example.

Fig. 3.

$\varvec{\alpha }^{ \text {join} }(\textsc {VendingMachine})$.

Let $\varPhi$ be a CTL$^{\star }$ formula which is not in $\forall$CTL$^{\star }$ nor in $\exists$CTL$^{\star }$, and let $\mathcal {MF}$ be an MFTS. We verify $\mathcal {MF}\models \varPhi$ by checking $\varPhi$ on two FTSs $\mathcal {MF}^{may}$ and $\mathcal {MF}^{must}$, and then we combine the obtained results as specified below.

Theorem 2

For every $\varPhi \in CTL^{\star }$ and MFTS $\mathcal {MF}$, we have:

$$ \mathcal {MF}\models \varPhi = {\left\{ \begin{array}{ll} \textit{true}&{} \textit{if } \big ( \mathcal {MF}^{may} \models \varPhi \, \wedge \, \mathcal {MF}^{must} \models \varPhi \big ) \\ \textit{false}&{} \textit{if } \big ( \mathcal {MF}^{may} \not \models \varPhi \, \vee \, \mathcal {MF}^{must} \not \models \varPhi \big ) \end{array}\right. } $$

Therefore, we can check a formula $\varPhi$ which is not in $\forall$CTL$^{\star }$ nor in $\exists$CTL$^{\star }$ on $\alpha (\mathcal {F})$ by running a model checker twice, once with the may-component of $\alpha (\mathcal {F})$ and once with the must-component of $\alpha (\mathcal {F})$. On the other hand, a formula $\varPhi$ from $\forall$CTL$^{\star }$ (resp., $\exists$CTL$^{\star }$) on $\alpha (\mathcal {F})$ is checked by running a model checker only once with the may-component (resp., must-component) of $\alpha (\mathcal {F})$.

The family-based model checking problem can be reduced to a number of smaller problems by partitioning the set of variants. Let the subsets $\mathbb {K}_1, \mathbb {K}_2, \ldots , \mathbb {K}_n$ form a partition of the set $\mathbb {K}$. Then: $\mathcal {F}\models \varPhi$ iff $\pi _{\mathbb {K}_i}(\mathcal {F}) \models \varPhi$ for all $i=1,\ldots ,n$. By using Theorem 1 (CTL$^\star$), we obtain the following result.

Corollary 1

Let $\mathbb {K}_1, \mathbb {K}_2, \ldots , \mathbb {K}_n$ form a partition of $\mathbb {K}$, and $(\alpha _1,\!\gamma _1), \ldots , (\alpha _n,\!\gamma _n)$ be Galois connections. If $\alpha _1(\pi _{\mathbb {K}_1}(\mathcal {F})) \models \varPhi , \ldots , \alpha _n(\pi _{\mathbb {K}_n}(\mathcal {F})) \models \varPhi$, then $\mathcal {F}\models \varPhi$.

Therefore, in case of suitable partitioning of $\mathbb {K}$ and the aggressive $\varvec{\alpha }^{ \text {join} }$ abstraction, all $\varvec{\alpha }^{ \text {join} }({\pi _{\mathbb {K}_i}(\mathcal {F})})^{may}$ and $\varvec{\alpha }^{ \text {join} }({\pi _{\mathbb {K}_i}(\mathcal {F})})^{must}$ are ordinary TSs, so the family-based model checking problem can be solved using existing single-system model checkers with all the optimizations that these tools may already implement.

Example 4

Consider the properties introduced in Example 2. Using the TS $\varvec{\alpha }^{ \text {join} }({\textsc {VendingMachine}})^{may}$ we can verify $\varPhi _1=\forall \Box \, \forall \Diamond \texttt {start}$ (Theorem 1, ($\forall$CTL$^{\star }$)). We obtain the counter-example , which is genuine for variants satisfying . Hence, variants from violate $\varPhi _1$. On the other hand, by verifying that satisfies $\varPhi _1$, we can conclude by Theorem 1, ($\forall$CTL$^{\star }$) that variants from satisfy $\varPhi _1$.

We can verify $\varPhi _2=\forall \Box \, \exists \Diamond \texttt {start}$ by checking may- and must-components of $\varvec{\alpha }^{ \text {join} }(\textsc {VendingMachine})$. In particular, we have $\varvec{\alpha }^{ \text {join} }(\textsc {VendingMachine})^{may} \models \varPhi _2$ and $\varvec{\alpha }^{ \text {join} }(\textsc {VendingMachine})^{must} \models \varPhi _2$. Thus, using Theorem 1, (CTL$^{\star }$) and Theorem 2, we have that $\textsc {VendingMachine}\models \varPhi _2$.

Using $\varvec{\alpha }^{ \text {join} }({\textsc {VendingMachine}})^{must}$ we can verify $\varPhi _3=\exists \Box \, \exists \Diamond \texttt {start}$, by finding the witness . By Theorem 1, ($\exists$CTL$^{\star }$), we have that $\textsc {VendingMachine}\models \varPhi _3$.    $\square$

4 Implementation

We now describe an implementation of our abstraction-based approach for CTL model checking of variational systems in the context of the state-of-the-art NuSMV model checker [3]. Since it is difficult to use FTSs to directly model very large variational systems, we use a high-level modelling language, called fNuSMV. Then, we show how to implement projection and variability abstractions as syntactic transformations of fNuSMV models.

A High-Level Modelling Language. fNuSMV is a feature-oriented extension of the input language of NuSMV, which was introduced by Plath and Ryan [28] and subsequently improved by Classen [4]. A NuSMV model consists of a set of variable declarations and a set of assignments. The variable declarations define the state space and the assignments define the transition relation of the finite state machine described by the given model. For each variable, there are assignments that define its initial value and its value in the next state, which is given as a function of the variable values in the present state. Modules can be used to encapsulate and factor out recurring submodels. Consider a basic NuSMV model shown in Fig. 4a. It consists of a single variable x which is initialized to 0 and does not change its value. The property (marked by the keyword SPEC) is “$\forall \Diamond (x \ge k)$”, where k is a meta-variable that can be replaced with various natural numbers. For this model, the property holds when $k=0$. In all other cases (for $k > 0$), a counterexample is reported where x stays 0.

The fNuSMV language [28] is based on superimposition. Features are modelled as self-contained textual units using a new FEATURE construct added to the NuSMV language. A feature describes the changes to be made to the given basic NuSMV model. It can introduce new variables into the system (in a section marked by the keyword INTRODUCE), override the definition of existing variables in the basic model and change the values of those variables when they are read (in a section marked by the keyword CHANGE). For example, Fig. 4b shows a FEATURE construct, called A, which changes the basic model in Fig. 4a. In particular, the feature A defines a new variable nA initialized to 0. The basic system is changed in such a way that when the condition “$nA=0$” holds then in the next state the basic system’s variable x is incremented by 1 and in this case (when x is incremented) nA is set to 1. Otherwise, the basic system is not changed.

Classen [4] shows that fNuSMV and FTS are expressively equivalent. He [4] also proposes a way of composing fNuSMV features with the basic model to create a single model in pure NuSMV which describes all valid variants. The information about the variability and features in the composed model is recorded in the states. This is a slight deviation from the encoding in FTSs, where this information is part of the transition relation. However, this encoding has the advantage of being implementable in NuSMV without drastic changes. In the composed model each feature becomes a Boolean state variable, which is non-deterministically initialised and whose value never changes. Thus, the initial states of the composed model include all possible feature combinations. Every change performed by a feature is guarded by the corresponding feature variable.

For example, the composition of the basic model and the feature A given in Figs. 4a and b results in the model shown in Fig. 4c. First, a module, called features, containing all features (in this case, the single one A) is added to the system. To each feature (e.g. A) corresponds one variable in this module (e.g. fA). The main module contains a variable named f of type features, so that all feature variables can be referenced in it (e.g. f.fA). In the next state, the variable x is incremented by 1 when the feature A is enabled (fA is TRUE) and nA is 0. Otherwise (TRUE: can be read as else:), x is not changed. Also, nA is set to 1 when A is enabled and x is incremented by 1. The property $\forall \Diamond (x \ge 0)$ holds for both variants when A is enabled and A is disabled (fA is FALSE).

Fig. 4.

NuSMV models.

Transformations. We present the syntactic transformations of fNuSMV models defined by projection and variability abstractions. Let M represent a model obtained by composing a basic model with a set of features $\mathbb {F}$. Let M contain a set of assignments of the form: $s(v) := \texttt {case}~b_1:e_1; \ldots b_n:e_n;~\texttt {esac}$, where v is a variable, $b_i$ is a boolean expression, $e_i$ is an expression (for $1 \le i \le n$), and s(v) is one of v, init(v), or next(v). We denote by $[\! [M ]\! ]$ the FTS for this model [4].

Let $\mathbb {K}' \subseteq 2^{\mathbb {F}}$ be a set of configurations described by a feature expression $\psi '$, i.e. $[\! [\psi ' ]\! ]=\mathbb {K}'$. The projection $\pi _{[\! [\psi ' ]\! ]}([\! [M ]\! ])$ is obtained by adding the constraint $\psi '$ to each $b_i$ in the assignments to the state variables.

Let $(\alpha ,\gamma )$ be a Galois connection from Sect. 3. The abstract $\alpha (M)^{may}$ and $\alpha (M)^{must}$ are obtained by the following rewrites for assignments in M:

$$ \begin{array}{l} \alpha \big ( s(v) \!:=\! \texttt {case} \, b_1\!:\!e_1; \ldots b_n\!:\!e_n; \texttt {esac} \big )^{may} \!=\! s(v) \!:=\! \texttt {case} \, \alpha ^m(b_1)\!:\!e_1; \ldots \alpha ^m(b_n)\!:\!e_n; \texttt {esac} \\ \alpha \big ( s(v) \!:=\! \texttt {case} \ b_1\!:\!e_1; \ldots b_n\!:\!e_n; \texttt {esac} \big )^{must} \!=\! s(v) \!:=\! \texttt {case} \ \widetilde{\alpha }(b_1)\!:\!e_1; \ldots \widetilde{\alpha }(b_n)\!:\!e_n; \texttt {esac} \end{array} $$

The functions $\alpha ^m$ and $\widetilde{\alpha }$ copy all basic boolean expressions other than feature expressions, and recursively calls itself for all sub-expressions of compound expressions. For $\varvec{\alpha }^{ \text {join} }(M)^{may}$, we have a single Boolean variable rnd which is non-deterministically initialized. Then, $\alpha ^m(\psi )=rnd$ if $\alpha (\psi )=\textit{true}$. We have: $\alpha ([\! [M ]\! ])^{may} = [\! [\alpha (M)^{may} ]\! ]$ and $\alpha ([\! [M ]\! ])^{must} = [\! [\alpha (M)^{must} ]\! ]$. For example, given the composed model $\mathcal {M}$ in Fig. 4c, the abstractions $\varvec{\alpha }^{ \text {join} }(\mathcal {M})^{may}$ and $\varvec{\alpha }^{ \text {join} }(\mathcal {M})^{must}$ are shown in Figs. 5 and 6, respectively. Note that $\widetilde{\varvec{\alpha }^{ \text {join} }}(f.fA)=\textit{false}$, so the first branch of case statements in $\mathcal {M}$ is never taken in $\varvec{\alpha }^{ \text {join} }(\mathcal {M})^{must}$.

Fig. 5.

$\varvec{\alpha }^{ \text {join} }(\mathcal {M})^{may}$

Fig. 6.

$\varvec{\alpha }^{ \text {join} }(\mathcal {M})^{must}$

5 Evaluation

We now evaluate our abstraction-based verification technique. First, we show how variability abstractions can turn a previously infeasible analysis of variability model into a feasible one. Second, we show that instead of verifying CTL properties using the family-based version of NuSMV [7], we can use variability abstraction to obtain an abstract variability model (with a low number of variants) that can be subsequently model checked using the standard version of NuSMV.

All experiments were executed on a 64-bit Intel$^\circledR$Core$^{TM}$ i7-4600U CPU running at 2.10 GHz with 8 GB memory. The implementation, benchmarks, and all results obtained from our experiments are available from: https://aleksdimovski.github.io/abstract-ctl.html. For each experiment, we report the time needed to perform the verification task in seconds. The BDD model checker NuSMV is run with the parameter -df -dynamic, which ensures that the BDD package reorders the variables during verification in case the BDD size grows beyond a certain threshold.

Synthetic Example. As an experiment, we have tested limits of family-based model checking with extended NuSMV and “brute-force” single-system model checking with standard NuSMV (where all variants are verified one by one). We have gradually added variability to the variational model in Fig. 4. This was done by adding optional features which increase the basic model’s variable x by the number corresponding to the given feature. For example, the CHANGE section for the second feature B is: , and the domain of x is 0..3.

We check the assertion $\forall \Diamond (x \ge 0)$. For $|\mathbb {F}| = 25$ (for which $|\mathbb {K}| = 2^{25}$ variants, and the state space is $2^{32}$) the family-based NuSMV takes around 77 min to verify the assertion, whereas for $|\mathbb {F}| = 26$ it has not finished the task within two hours. The analysis time to check the assertion using “brute force” with standard NuSMV ascends to almost three years for $|\mathbb {F}| = 25$. On the other hand, if we apply the variability abstraction $\varvec{\alpha }^{ \text {join} }$, we are able to verify the same assertion by only one call to standard NuSMV on the abstracted model in 2.54 s for $|\mathbb {F}| = 25$ and in 2.99 s for $|\mathbb {F}| = 26$.

Elevator. The Elevator, designed by Plath and Ryan [28], contains about 300 LOC and 9 independent features: Antiprunk, Empty, Exec, OpenIfIdle, Overload, Park, QuickClose, Shuttle, and TTFull, thus yielding $2^9$ = 512 variants. The elevator serves a number of floors (which is five in our case) such that there is a single platform button on each floor which calls the elevator. The elevator will always serve all requests in its current direction before it stops and changes direction. When serving a floor, the elevator door opens and closes again. The size of the Elevator model is $2^{28}$ states. On the other hand, the sizes of $\varvec{\alpha }^{ \text {join} }(\textsc {Elevator})^{may}$ and $\varvec{\alpha }^{ \text {join} }(\textsc {Elevator})^{must}$ are $2^{20}$ and $2^{19}$ states, resp.

Fig. 7.

Verification of Elevator properties using tailored abstractions. We compare family-based approach vs. abstraction-based approach.

We consider five properties. The $\forall$CTL property “$\varPhi _1 = \forall \Box \,(floor=2 \wedge liftBut5.pressed \wedge direction=up \Rightarrow \forall [direction=up \, \textsf {U} floor=5]$” is that, when the elevator is on the second floor with direction up and the button five is pressed, then the elevator will go up until the fifth floor is reached. This property is violated by variants for which Overload (the elevator will refuse to close its doors when it is overloaded) is satisfied. Given sufficient knowledge of the system and the property, we can tailor an abstraction for verifying this property more effectively. We call standard NuSMV to check $\varPhi _1$ on two models $\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\texttt {Overload} ]\! ]}(\textsc {Elevator}))^{may}$ and $\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\lnot \texttt {Overload} ]\! ]}(\textsc {Elevator}))^{may}$. For the first abstracted projection we obtain an “abstract” counter-example violating $\varPhi _1$, whereas the second abstracted projection satisfies $\varPhi _1$. Similarly, we can verify that the $\forall$CTL property “$\varPhi _2 = \forall \Box \,(floor=2 \wedge direction=up \Rightarrow \forall \bigcirc (direction=up))$” is satisfied only by variants with enabled Shuttle (the lift will change direction at the first and last floor). We can successfully verify $\varPhi _2$ for $\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\texttt {Shuttle} ]\! ]}(\textsc {Elevator}))^{may}$ and obtain a counter-example for $\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\lnot \texttt {Shuttle} ]\! ]}(\textsc {Elevator}))^{may}$. The $\exists$CTL property “$\varPhi _3 = (\texttt {OpenIfIdle} \wedge \lnot \texttt {QuickClose}) \implies \exists \Diamond ( \exists \Box \,( door=open))$” is that, there exists an execution such that from some state on the door stays open. We can invoke the standard NuSMV to verify that $\varPhi _3$ holds for $\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\texttt {OpenIfIdle} \wedge \lnot \texttt {QuickClose} ]\! ]}(\textsc {Elevator}))^{must}$. The following two properties are neither in $\forall$CTL nor in $\exists$CTL. The property “$\varPhi _4 = \forall \Box \,(floor=1 \wedge idle \wedge door=closed \implies \exists \Box (floor=1 \wedge door=closed))$” is that, for any execution globally if the elevator is on the first floor, idle, and its door is closed, then there is a continuation where the elevator stays on the first floor with closed door. The satisfaction of $\varPhi _4$ can be established by verifying it against both $\varvec{\alpha }^{ \text {join} }(\textsc {Elevator})^{may}$ and $\varvec{\alpha }^{ \text {join} }(\textsc {Elevator})^{must}$ using two calls to standard NuSMV. The property “$\varPhi _5 = \texttt {Park} \implies \forall \Box \,( floor=1 \wedge idle \implies \exists [idle \textsf {U} floor=1] )$” is satisfied by all variants with enabled Park (when idle, the elevator returns to the first floor). We can successfully verify $\varPhi _5$ by analyzing $\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\texttt {Park} ]\! ]}(\textsc {Elevator}))^{may}$ and $\varvec{\alpha }^{ \text {join} }(\pi _{[\! [\texttt {Park} ]\! ]}(\textsc {Elevator}))^{must}$ using two calls to standard $\textsc {NuSMV}$. We can see in Fig. 7 that abstractions achieve significant speed-ups between 2.5 and 32 times faster than the family-based approach.

6 Related Work and Conclusion

Recently, many family-based techniques that work on the level of variational systems have been proposed. This includes family-based syntax checking [20, 25], family-based type checking [24], family-based static program analysis [16, 17, 27], family-based verification [22, 23, 29], etc. In the context of family-based model checking, Classen et al. present FTSs [6] and specifically designed family-based model checking algorithms for verifying FTSs against LTL [5]. This approach is extended [4, 7] to enable verification of CTL properties using an family-based version of NuSMV. In order to make this family-based approach more scalable, the works [15, 21] propose applying conservative variability abstractions on FTSs for deriving abstract family-based model checking of LTL. An automatic abstraction refinement procedure for family-based model checking is then proposed in [19]. The application of variability abstractions for verifying real-time variational systems is described in [18]. The work [11, 13] presents an approach for family-based software model checking of #ifdef-based (second-order) program families using symbolic game semantics models [10].

To conclude, we have proposed conservative (over-approximating) and their dual (under-approximating) variability abstractions to derive abstract family-based model checking that preserves the full CTL$^{\star }$. The evaluation confirms that interesting properties can be efficiently verified in this way. In this work, we assume that a suitable abstraction is manually generated before verification. If we want to make the whole verification procedure automatic, we need to develop an abstraction and refinement framework for CTL$^{\star }$ properties similar to the one in [19] which is designed for LTL.