Two Ideas for Analysis of Multivariate Geochemical Survey Data: Proximity Regression and Principal Component Residuals

Abstract

Proximity regression is an exploratory method to predict multielement haloes (and multielement ‘vectors’) around a geological feature, such as a mineral deposit. It uses multiple regression directly to predict proximity to a geological feature (the response variable) from selected geochemical elements (explanatory variables). Lithogeochemical data from the Ben Nevis map area (Ontario, Canada) is used as an example application. The regression model was trained with geochemical samples occurring within 3 km of the Canagau Mines deposit. The resulting multielement model predicts the proximity to another prospective area, the Croxall property, where similar mineralization occurs, and model coefficients may help in understanding what constitutes a good multielement vector to mineralization. The approach can also be applied in 3-D situations to borehole data to predict presence of multielement geochemical haloes around an orebody. Residual principal components analysis is another exploratory multivariate method. After applying a conventional principal components analysis, a subset of PCs is used as explanatory variables to predict a selected (single) element, separating the element into predicted and residual parts to facilitate interpretation. The method is illustrated using lake sediment data from Nunavut Territory, Canada to separate uranium associated with two different granites, the Nueltin granite and the Hudson granite. This approach has the potential to facilitate the interpretation of multielement data that has been affected by multiple geological processes, often the situation with surficial geochemical surveys.

1 Introduction

Proximity to selected spatial features on geological maps has been used in the analysis of multivariate data in several ways, but usually as a weighting function not as a variable to be directly predicted. For example, Cheng et al (2011) describe “spatially weighted principal component analysis” to emphasize proximity to selected intrusions in the analysis of geochemical patterns. This involves using spatial weights (in range 0–1) to calculate weighted correlation coefficients, before the usual eigenvector determinations of principal components analysis. The resulting weighted principal component scores were mapped to predict element associations related to intrusions. Brunsdon et al. (1998 and other papers) have used “geographically weighted regression” to analyze long-term illness data from a UK census. This approach recognizes that a regression may often not be spatially stationary, but will show changes geographically. Again, the regression equations use spatial variables as weights. In both these examples, proximity to some feature is introduced as a spatial weight, not as a response variable for direct prediction.

In the first part of this chapter we suggest that proximity to a geological feature can be more directly studied by using proximity itself as a response variable in a regression using a collection of geochemical elements as explanatory variables. In regional geochemical surveys, one may be interested in understanding which variables are good predictors of proximity to a mineral deposit, or to some other selected feature with known location. This is frequently referred to in mineral exploration as finding good ‘vectors’ to mineralization, but as far as we are aware direct prediction of proximity from multielement data has not been published, although plots of single elements, or element ratios, on profiles showing distance to known mineralization are often used. If a good predictive suite of elements can be determined (either from understanding a genetic model or from empirical tests) and based on a training set of samples relatively close to the geological feature of interest, the resulting predictive equation can be used to look for similar associations outside the training area. If the feature of interest is a mineral deposit, this approach may be useful in finding new deposits. This may be used both for 2-D regional geochemical surveys, and in 3-D geochemical data from borehole data.

The second part of the chapter is about using residual principal components analysis (PCA) of multielement geochemical data. PCA has been widely used by exploration geochemists and others to understand multielement geochemical processes, particularly in surficial geochemical surveys, but also in lithogeochemical data collected at surface or in boreholes. This literature is large, and here we refer as an example to a study of soil geochemistry as measured along two continental scale transects of North America. PCA of logratio-transformed variables revealed the effects of soil-forming processes, including soil parent material, weathering, and soil age as interpreted from PCs (Drew et al. 2010). There are many examples of successful geological interpretations by PC analysis. Individual PCs can often be interpreted both from variable loadings, from biplots and from spatial patterns seen by mapping PC scores (e.g. Grunsky 2010).

Sometimes, however, one may be interested in the spatial distribution of a single geochemical element, and it is desirable to remove the effect of some particular geological process or processes that are reflected in one or more PCs. For example, in the analysis of till geochemical surveys, the first PC is often interpreted as due to the effect of till transport. Thus it may be desirable to look at the element distribution after removing PC1. Usually this is carried out by progressively examining element loadings and the spatial patterns seen by mapping PC scores. However, there may be situations where it is helpful to examine spatial patterns of a single element after removing PC1 (or several PCs). This can be achieved what we are terming here as “principal component regression”. This is a straightforward regression using the selected element as the response variable, and PC1 (or PC combination) as the explanatory variable(s). The residuals (the observed response variable minus the predicted response variable) provide the desired element distribution after removing the effect of PC1 (or PC combination). If PC1 is interpreted as due to till transport, then the residuals represent the element values after removing the effect of till transport.

This approach represents a process that is somewhat analogous to a geochemical selective leach separating a mineral phase or perhaps several mineral phases. A ‘total’ analysis is designed to dissolve all mineral phases, whereas a partial leach targets a selected mineral phase. The element under study can thereby be partitioned into phases by selective leaching. Residual PCA also separates the element under study into parts, although the partitions are not the same as those targeted in selective leaches. The partitions in residual PCA are related to proportions of an element quantity that can be ‘explained’ by different multivariable associations as determined by PCA. Residual PCA was first used by Bonham-Carter and Hall (2010) in a study of uranium in soils in the Athabasca Basin. Residual U, after removing the effect of till transport (as determined by PCA), was a better predictor of buried mineralization than raw U values in A-horizon soils.

In this chapter, we use a lithogeochemical dataset from the Ben Nevis area of Ontario to illustrate proximity regression, and a lake-sediment dataset from southern Nunavut to illustrate residual principal components analysis.

2 Method 1: Direct Prediction of Spatial Proximity

Suppose we have an array of geochemical data, with rows being samples, and elements as columns. In addition, we have distance measurements for each sample reflecting the shortest distance from the sample to some geological feature (mineral deposit, an intrusion, a fault, etc.). Before multivariate analysis, it will be important to transform the element variables by a centred logratio, to overcome the effects of closure (Aitchison 1986; Buccianti et al. 2006; and many other papers).

Although distances may be used directly, we have found that transforming distance to proximity gives somewhat better predictions. If for example the goal is to model the dispersion ‘halo’ around a deposit, the decay of the halo effect with distance from the contact may be exponential, or may follow a power law. Thus, instead of using distance as a response variable, we often get better results by transforming distances inversely to proximities. Here we have used a simple exponential decay of proximity with distance, that assumes that the rate of decay of proximity with distance is constant, similar to the familiar model of decay of a radioactive element with time. Let distance be denoted as Z (metres from feature) and proximity by Y (in range 1, 0 where 1 is at zero distance decreasing to zero at infinitely large distances), then the rate of decay of proximity with distance is assumed to be a constant

$$ \frac{{{\text{d}}Y}}{{{\text{d}}Z}} = - \alpha . $$

(23.1)

Integrating (23.1) from distance 0 to Z leads to:

$$ Y\left( Z \right) = Y\left( 0 \right){\text{e}}^{ - \alpha z} . $$

(23.2)

The value of proximity at zero distance Y(0) = 1, so this term drops out. It is also convenient to define the ‘half distance’ Z_0.5 where proximity Y equals 0.5, then by rearranging Eq. 23.2 we can express α in terms of the half-distance:

$$ \alpha = \frac{ - \ln 0.5}{{Z_{0.5} }}. $$

(23.3)

Substituting for α in (23.1), distance can then be transformed to proximity from

$$ Y\left( Z \right) = \exp \left( {\frac{\ln 0.5}{{z_{0.5} }} \cdot Z} \right) $$

(23.4)

We note that an alternative approach was used by Cheng et al. (2011) in the spatially weighted principal components to determine spatial weights W (equivalent to proximities) using a power relation:

$$ W = \left( {\frac{1 - Z}{{Z_{max} }}} \right)^{\gamma } $$

(23.5)

where γ is a power parameter, and Z_max is a selected maximum distance for modelling. For γ = 0, all weights = 1, with γ = 1, weights are a linear inverse of distance, but positive values of gamma such as 2, 8, 16 define a power-law decrease of proximity with increasing distance.

Typical exponential curves and power law curves using Eqs. 23.4 and 23.5 are shown in Fig. 23.1.

Fig. 23.1

Left. Example of relationship between proximity and distance using exponential decay with a ‘half-distance’ parameter. Proximity = 1 at distance = 0, proximity = 0.5 at distance = half-distance. Right. Similar to left diagram, but using power law model with gamma parameter

We now model proximity with a training set of samples (chosen within some arbitrary but reasonable distance from the selected feature) using selected geochemical variables.

Then let X be the matrix of CLR-transformed element values, with rows as samples, columns as elements. The geochemical elements are the explanatory variables, and the column vector Y contains the proximity values, the response variable. The geochemistry is used to ‘explain’ the response. Here we used multiple linear regression to model this relationship, although other approaches could be taken.

$$ {\text{Y}} = {\text{X}}\upbeta + \in $$

(23.6)

where β is a column vector of coefficients to be determined by least squares, and ϵ is the vector of errors. The coefficients are solved from the normal equations

$$ \upbeta = \left( {{\text{X}}^{{\prime }} {\text{X}}} \right)^{ - 1} \left( {{\text{X}}^{{\prime }} {\text{Y}}} \right) $$

(23.7)

where X’ is the transpose of X and (X′X)⁻¹ is the inverse of X′X.

If inspection of the coefficients and goodness of fit are satisfactory, the predicted values of proximity, Ŷ, are calculated from

$$ {\hat{\text{Y}}} = {\text{X}}\upbeta\text{.} $$

(23.8)

2.1 Application of Proximity Regression with Ben Nevis Lithogeochemical Data

2.1.1 Background Geology

The Ben Nevis Township area is part of the Blake River Group (Fig. 23.2) a calc-alkaline volcanic sequence. The same sequence extends eastward to the Noranda area of Quebec where major Cu-Zn-Ag deposits are located. Extensive alteration and mineralization was recognized in the Ben Nevis area (Jensen 1975; Wolfe 1977), which led to a later geochemical study by Wolfe (1977) with emphasis on the metal distribution of stratiform volcanogenic sulphide deposits in Archean volcanic rocks. Lithogeochemical sampling was undertaken across the area by Jensen (1975) and Wolfe (1977) followed by additional sampling by Grunsky (1986a, b). Grunsky and Agterberg (1988) and Grunsky (1986a, b) carried out a detailed a multivariate geostatistical investigation of these data. A regional multi-element geochemical study over the Abitibi Greenstone Belt was later undertaken by Grunsky (2013) in which multivariate statistical methods were applied to recognize lithological variation, areas of alteration and potential base-metal mineralization.

Fig. 23.2

Location map of Ben Nevis study area adapted from Grunsky (1986a)

The principal lithologies of the study area are basaltic pillowed flows, pillow breccias and breccias of calc-alkaline affinity (Grunsky 1986a). Two felsic volcanic units comprised of tuff, tuff breccia and flows of rhyolitic and dacitic composition occur within the basaltic sequence. The volcanic sequence has been intruded by tholeiitic gabbroic and diorite bodies throughout (Fig. 23.3). More recent studies of the volcanic assemblage in the context of the Abitibi Greenstone Belt are described by Pelogquin et al. (2008).

Fig. 23.3

Geology of Ben Nevis area, adapted from Grunsky (1986a). Note locations of Canagau Mines deposit and Croxall property. Figure from Grunsky (1986b)

Within the area, the two most significant mineral occurrences are the Canagau Mines deposit and the Croxall property. The Canagau Mines deposit is dominated by strongly carbonatized, sericitized, and silicified mafic and felsic volcanic rocks. Mineralization consists of sphalerite, gold, silver, galena, chalcopyrite, and pyrite within east-trending fractures and shear zones that dip 40–60° south. Tonnages are unknown, and the grade is as high as 11 ppm gold and 22 ppm silver. The area was extensively explored by Wallbridge Mining in 2004 (Wallbridge 2004) and a report on exploration activities by Meyer et al. (2004). The deposit is currently considered to be uneconomic. The Au-Ag-Cu-Pb-Zn style of mineralization is typical of an epithermal system.

The Croxall property consists of a zone of brecciated and sheared rhyolite with interstitial pyrite, chalcopyrite, chlorite, calcite and quartz. Gold assays have been reported up to 1 ppm.

Grunsky (1986a, b) showed that multivariable data analysis techniques distinguish the altered from unaltered volcanic rocks.

2.1.2 Application

The purpose of this application is to determine whether a multielement signature can be identified related to proximity to the Canagau Mines deposit, then use this signature to look for other places with similar patterns.

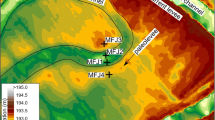
The distances between each sample and the Canagau Mines deposit was calculated using the eastings and northings associated with each sample, plus the known location of the deposit. Distances were converted to proximities using Eq. (23.4). Different proximity vectors were calculated for half-distances of 100, 300, 500, 800, 1000 and 1500 m so that an optimal half distance parameter could be determined. Figure 23.4 shows the sample points with proximity (half distance equal to 800 m) classified by colour and dot size. The training set comprises all points lying within 3 km of the deposit (equivalent to points with proximity greater than exp(ln(0.5) * 3000/800) = 0.074).

Fig. 23.4

Map showing locations of lithogeochemical samples, with size and colour of dots related to proximity to Canagau Mines deposit (Fig. 23.3). Training set for regression model includes only those samples within 3 km of deposit (within circle)

There are 26 geochemical variables in the dataset—a mixture of trace elements and major oxides. After converting all elements to a common unit of measurement (ppm), all chemical variables were transformed by centred logratios (CLR) to avoid the problem of closure. Using the training samples, correlation coefficients were calculated between each element (CLR-transforms) and proximity. These correlations were sorted by magnitude and used to reduce the number of elements selected to predict proximity by multiple regression analysis. Elements were selected for Model 1 if the absolute value of correlation (Pearson’s r) with proximity was greater than 0.2 (Table 23.1). This reduced the number of elements to be used as explanatory variables from 26 to 11.

Table 23.1 Result of multiple linear regression. Variables selected for regression against proximity (Model 1) by selecting those with abs (correlation coefficient) > 0.2. The explanatory variables are CLR-transformed geochemical element values, the response variable is proximity to the Canagau Mines deposit, using n = 278 samples that lie within 3 km of the deposit for training. Variables selected for Model 2 based on p-values < 0.03 from Model 1

CLR variables were not further transformed, and the coefficients and associated probabilities obtained by using Eq. (23.7) are shown in Table 23.1. Note that Co, Li, Pb and CO₂ have positive coefficients, whereas Ni, Sr, V, CaO, Na₂O, K₂O, TiO₂ and S have negative coefficients. This model has a goodness-of-fit of about 40% (adjusted R² = 0.399). A second model was then run to remove those variables in Model 1 with p-values greater than 0.03. In Model 2, CO₂ is the only variable with a positive coefficient, and V, CaO, Na₂O and K₂O have negative coefficients. The goodness-of-fit of Model 2 is almost the same as Model 1, with adjusted R² = 0.394. Although not shown here, a plot of predicted values from Model 1 and Model 2 are highly correlated, and maps of each are virtually indistinguishable.

The predicted values of proximity are shown in Fig. 23.5 for both the training and non-training samples. As expected, the Canagau Mines deposit shows up as a ‘bullseye’ at the centre of the training sample area. Notice that the Croxall property shows as another less prominent bullseye to the west, in the non-training sample area. Other high values of predicted proximity to the south of the Canagau Mines deposit and northeast of the Croxall property are associated with known sulphide occurrences as shown in Fig. 23.3. Thus, we can conclude that proximity regression led to the selection of a suite of useful explanatory variables that, after training on the Canagau Mines deposit, was able to ‘discover’ the Croxall property.

Fig. 23.5

Map showing predicted proximity to Canagau Mines deposit. Plot includes both points used in training (those within 3 km of deposit) and other sample points. Croxall property is identified with large proximity values by this model

A bivariate plot of observed versus predicted proximity, training points only, (Fig. 23.6) shows that the relationship is noisier far away from the deposit than closer to it, consistent with the proximity response weakening at increasing distance.

Fig. 23.6

Plot of observed proximity versus predicted proximity, with best fit line, training points only. In general, fit is noisier at lower values of proximity. Points with proximity >0.5 (i.e. within the ‘half-distance’ of 800 m of the Canagau Mines deposit) show a stronger relationship

Experimental results show that an optimum half distance for modelling proximity as an inverse function of distance is 800 m, although the results are not very sensitive to changes in the 300–1000 m range (Fig. 23.7). It is not clear how useful this parameter might be in describing the geometry of the ‘halo’ effect around the deposit.

Fig. 23.7

Variation in goodness of fit (adjusted R²) with changes in ‘half distance’, the parameter used to control rate of exponential decay of proximity with increasing distance (23.4). Note that curve shows that relationship is strongest using half-distance parameter = 800 m

3 Method 2: Principal Component Residuals

Many geochemical survey data are difficult to interpret, because multiple overlapping processes affect element levels in space and time. In some situations, a principal component will show a composition (based on element loadings) and a spatial pattern reflecting an interpretable geological process, but usually interpretation is complex because of interacting processes.

Residual principal components analysis is an exploratory approach that can sometimes be helpful in sorting out complex multielement interactions. The method is a straightforward extension of applying principal components, followed by a series of multiple linear regressions. As with the proximity regression method, it is important first to carry out a centred log ratio transform of all the elements, otherwise distortions may occur in principal component (and subsequent multiple regression) results due to constant sum ‘closure’ effects.

Regular PCA is carried out in the usual way on the correlation matrix calculated from CLR-transformed element variables (e.g. Davis 2002, ch. 6).

Inspection of the eigenvectors for each PC, inspecting biplots, and mapping PC scores for the at least the first few PCs can then lead to an interpretation of PCs in terms of geological processes (Grunsky 2010). Here the objective is to focus on a selected element to separate out (‘partition’) this element compositionally and spatially using the principal component results.

For the element of interest, the next step is to inspect the corresponding row of the eigenvector matrix (the ‘loadings’) to understand better in which components the element occurs. It may be decided to predict the element from PC1 only, or from PC1 and PC2, or PC1, PC2 and PC3, and so on. For each of these selections, a multiple regression is carried out with the selected PCs as explanatory variables, and the chosen element as the response variable. For example, if the response variable is V and the explanatory variables are PCs 1 to PC3, then

$$ V =\upbeta_{0} +\upbeta_{1} PC_{1} +\upbeta_{2} PC_{2} +\upbeta3PC_{3} + \in $$

(23.9)

can be solved as before for the coefficients β by least squares. If the predicted values of V are V*, then the residuals V _R are simply

$$ V_{R} = V - V* $$

(23.10)

computed over all sample locations.

The choice of PCs in Eq. (23.9) may be as simple or as complex as needed. We have had good results by successively adding PCs, inspecting the goodness of fit at each stage and mapping the predicted and residual values at each step. Inspection of residual patterns may reveal, spatially, where concentrations of that particular element are distributed, facilitating interpretation.

In this method, there is no training set, calculations are carried out on all samples.

3.1 Application to Nunavut Lake Sediment Data

3.1.1 Geological Background

The lake sediment survey was carried out over three 1:250,000 scale map areas (NTS 65A, 65B, 65C) in southern Nunavut Territory, Canada (McCurdy et al. 2012). The geology of two of the NTS sheets (65A, 65B) were mapped by Eade (1973) and is shown in Fig. 23.8. Of particular interest to this study, we notice that there are two important granitic intrusion types: the Hudson granite (1.83 Ga) and the Nueltin granite (1.75 Ga) suites as identified and characterized by Peterson et al. (2015).

Fig. 23.8

Geological map of NTS sheets 65A, 65B and 65C, with coordinates shown for UTM Zone 14, Nunavut Territory, adapted from Grunsky et al. (2012a, b). Two units noted in text are Nueltin granite (Pp-Ng shown in orange) occurring in west and Hudson granite (Pp-Hgr shown in light pink) occurring in east

This area lies within the southern Hearne Province, a poorly understood terrane. The domain is dominantly comprised of Archean tonalitic and charnokitic gneisses, approximately 2.8 Ga in age. However, strong evidence for fragments of much older crust, up to 3.3 Ga, has been found in the form of inherited Archean zircons and Sm–Nd model ages obtained from Proterozoic post-orogenic plutons of the Hudson granite, intruded at about 1.83 Ga. Nueltin rapakivi granite (ca. 1.75 Ga) is also present in the area.

A comprehensive multielement study of the lake sediment data was carried out by Grunsky et al. (2012a, b), and by Grunsky and Kjarsgard (2016). One of the results of those studies was to show that the multivariate geochemistry could be used to map the various rock types using a variety of methods including PCA.

3.1.2 Application

The data consists of 1611 samples and 48 geochemical elements—both major and traces. Prior to CLR transformation, all variables were converted to ppm. PCA was carried out on all 48 elements. The objective was to understand better how uranium is partitioned between the two granites: the Nueltin and the Hudson.

PCA analysis was calculated on all 48 CLR transformed variables. A scree plot (Fig. 23.9a) shows that the first 15 PCs (out of the full 48) account for almost 85% of the total variation in the data, and the first 5 PCs account for over 60%. Inspection of the uranium loadings (Fig. 23.9b) shows that PCs 2 and 3 both have high positive loadings, whereas PC 5 has a strong negative loading. Multiple regressions were carried out (using U-CLR, not untransformed U) starting with PC1, then successively adding PCs up to 12. For each regression, predicted U and residual U were calculated and mapped (not shown here), and a record made of the goodness of fit (Fig. 23.10). This graph shows that PC1 does not account for much U variation, but PCs 2 and 3 show marked increases in goodness of fit. PC 4 shows a minor increase, and PC5 shows a major increase. After PC5, improvements in goodness of fit are minor.

Fig. 23.9

a Scree plot showing cumulative variation explained by first 15 PCs. b Values of loadings for U-CLR on first 15 PCs

Fig. 23.10

Goodness of fit (R²) for successive multiple regressions with U-CLR as response variable and an increasing number of PCs as explanatory variables. Note that after adding PC 5, there is little change in R² values

Figure 23.11 shows maps of U-CLR predicted from PCs 1-5, and U-CLR residuals. Not shown is the unmodified U-CLR map (which sums these two parts). Notable here is that the predicted map shows a pattern strongly correlated with the Nueltin granite, whereas the residual map is strongly correlated with the Hudson granite. PCs 1-5 ‘explain’ the uranium in the Nueltin granite, whereas the residual uranium is that which occurs in the Hudson granite. The residual PC analysis has partitioned uranium into two parts that have a distinct geological interpretation.

Fig. 23.11

Left. Map of U-CLR predicted from PCs 1-5 using lake sediment data. Right. Map of residual U-CLR unexplained by PCs 1-5. Predicted uranium is strongly related to presence of Nueltin granite, whereas residual uranium is strongly related to presence of Hudson granite. Map of total U-CLR does not distinguish between these two granites

This is confirmed in Fig. 23.12 which shows for the successive regressions results of t-tests on the mean U-residual in the Nueltin and Hudson granites. The value of t increases up to PC5, then decreases. This confirms that, for partitioning uranium between the two granites, regression against PC1-5 gives the best result.

Fig. 23.12

t-test values for U-CLR residuals obtained from successive regressions with U-CLR as response variable and increasing number of PCs as explanatory variables. These are ‘2-sample’ t-tests comparing means between two groups: Nueltin granite samples and Hudson granite samples. Note that regression to predict U-CLR using PCs 1-5 gives best separation of two granites by U residuals. Adding more PCs reduces t-value and significance of difference between U residual means

3.2 Discussion

These two methods add to the already large basket of multivariate methods useful for interpreting regional geochemical surveys.

With the wide use of GIS, spatial information is now easily determined for many features of map data. Distance calculations from points to points, points to lines and points to polygons are now routine, allowing the spatial characterization of proximity of geochemical samples to mineral deposits (points—depending on map scale), to faults of specified contacts (lines), or to rock units (polygons). In 3-D, proximity of geochemical samples to an orebody using borehole data is also straightforward. There are therefore many potential applications of proximity regression for a variety of situations involving multivariate geochemical data.

One particular idea that may be worthy of investigation is the application of this approach to prospectivity mapping. Instead of treating known mineral occurrences as binary points to be predicted from a series of evidential layers (weights of evidence, logistic regression, neural networks, etc.), a response variable could be constructed showing distance (or proximity) to the nearest mineral occurrence. The explanatory variables can be various evidential layers, as usual. The result would not be the probability of occurrence of a mineral occurrence, but rather the predicted proximity to the nearest mineral occurrence.

It should also be noted that proximity regression as described here has used ordinary multiple linear regression, so although the observed proximity measure in in the range (0, 1), predicted proximities are unconstrained and may be greater than 1 or negative. There might be some advantage to using logistic regression, that would automatically constrain the expected proximity to the range (0, 1), and would also allow the use of non-numeric explanatory variables (e.g. presence/absence of geological units, etc.). Alternatively, there are several neural network approaches that could also be tried for predicting proximity.

It should be noted that when doing a residual PCA on geochemical data, that logratio transforms are essential, because the effect of closure for introducing artefacts in PCA results is well known. Experience has also shown that residual analysis requires that the geochemical element used as a response variable must also be CLR transformed, as regression results are poor if untransformed response variables are used in the analysis.

In the separation of uranium between the Nueltin and Hudson granites, it would be most interesting to determine whether this partition was also related to isotopic differences. But this would require isotopic analyses of the lake sediment samples, an expensive proposition.

4 Conclusions

Proximity analysis allows for the use of multielement geochemical data for direct prediction of proximity to geological features, such as mineralization, faults and intrusions.

Application of proximity analysis to lithogeochemical data from the Ben Nevis area showed that a suite of elements provided a good prediction of proximity to the Canagau Mines deposit, and that this model also predicted the Croxall property and other nearby sulphide occurrences.

Residual principal components analysis is a useful way to partition particular geochemical elements that can facilitate geological interpretation.

For example, uranium in a lake sediment survey could be partitioned into two groups based on PCs. Uranium associated with PCs 1-5 is strongly correlated with the Nueltin granite, whereas, residual uranium, after removing the effects of PC 1-5, is strongly correlated with the Hudson granite.