Abstract
This work presents an overview of four different approaches to the problem of future contingency and determinism in temporal logics. All of them are bivalent, viz. they share the assumption that propositions concerning future contingent facts have a determinate truth-value (true or false). We introduce Ockhamism, Peirceanism, Actualism and T × W semantics, the four most relevant bivalent alternatives in this area, and compare them from the point of view of their expressiveness and their underlying metaphysics of time.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The forerunner of all these solutions has been considered by many scholars (but not all of them) to be Aristotle in chapter IX of On Interpretation.
- 2.
This is MacFarlane’s determinacy intuition (see [10], p. 322) as opposed to the indeterminacy intuition (future contingent sentences are neither true nor false at the moment of utterance).
- 3.
This example is taken from Belnap and Green [2].
- 4.
Our language consists of atomic formulas p, q, … (to be read as “pure” present-tense sentences such as “there is a sea battle”) and recursively built on Boolean operators ¬ (“not”), ∧ (“and”), ∨ (“or”), → (“if - then”), the temporal operators F (“it will be the case that”) and P (“it has been the case that”) and an additional operator
 to be read as “it is necessary that”. We will also make use of dual operators like G := ¬F¬ (“it will always be the case that”), H := ¬P¬ (“it has always been the case that”) and
to be read as “it is necessary that”. We will also make use of dual operators like G := ¬F¬ (“it will always be the case that”), H := ¬P¬ (“it has always been the case that”) and 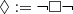 (“it is possible that”).
(“it is possible that”). - 5.
See Ockham [12, p. 99].
- 6.
Equivalence is to be understood in the same sense in which “it was the case yesterday that I will quit smoking in two days” is equivalent with “I will quit smoking tomorrow”.
- 7.
To be precise, Prior uses here a more expressive temporal language with metric operators F n (“it will be the case in n intervals of time”) and P m (“it was the case m intervals ago”), where n and m are two quantifiable variables to be interpreted with (rational or real) non-negative numbers measuring intervals of time. For the sake of simplicity we will avoid using metric operators, since F, P and
 are sufficient for the points we need to make.
are sufficient for the points we need to make. - 8.
See Prior [16, p. 126].
- 9.
This is probably one reason why Prior does not even face the question of completeness.
- 10.
Finer-grained distinctions are induced in Prior’s actual system by the use of metric operators.
- 11.
Where h means “the coin lands head” and t stands for “the money lands tail”.
- 12.
This translation is not completely faithful. A metric language can better express (5) with p ∧ P n♢F n p.
- 13.
See Prior [16] chap. VII p. 132.
- 14.
See Prior [15].
- 15.
It should also be noticed that the Peircean sense of “it will always be the case that” is no more expressed by the combination ¬F¬, thus G has to be defined as a new primitive operator by the following clause
-
\(\mathcal {M},\langle m,h\rangle \models G\phi \) iff \(\forall h^{\prime }\forall m^{\prime }((h^{\prime }\in H_{m}\wedge m<m^{\prime })\Rightarrow \mathcal {M},\langle m^{\prime },h^{\prime }\rangle \models \phi )\).
-
- 16.
This famous expression was coined by Belnap and Green [2].
- 17.
- 18.
See Belnap and Green [2] p. 380.
- 19.
For a proof of uniqueness see Barcellan and Zanardo [1] p. 5.
- 20.
Barcellan and Zanardo use the peircean operators of Sect. 16.2 as primitives.
- 21.
For a more articulated defence of Actualism see Øhrstrom [13].
- 22.
- 23.
For the notions of overlap and divergence see the famous Lewis [9] pp. 198–209.
- 24.
- 25.
More precisely, a synchronized tree is a tree-like structure where it is possible to define a partition I (the “instants”) of the set T that satisfies the following conditions (see also Wölfl [21]):
-
(a)
For every i ∈ I and every h ∈ H(T) there is exactly one m i,h ∈ T with m i,h ∈ i ∩ h
-
(b)
For all i, i ′∈ I and all h, h ′∈ H(T), from \(m_{i,h}<m_{i^{\prime },h}\) it follows that \(m_{i,h^{\prime }}<m_{i^{\prime },h^{\prime }}\)
Given a synchronized Ockhamist model \(\mathcal {T}=\langle T,<,V\rangle \) we can define a T × W model \(\mathcal {T^{\prime }} =\langle T^{\prime }\times W^{\prime },<^{\prime },\{\sim _{t}\}_{t\in T},V^{\prime }\rangle \) by taking:
-
T ′ = I and W ′ = H(T)
-
i <′ i ′ iff \(m_{i,h}<m_{i^{\prime },h}\) for some h ∈ H(T)
-
h ∼i h ′ iff \(m_{i,h}=m_{i,h^{\prime }}\)
-
〈i, h〉∈ V ′(p) iff 〈m i,h, h〉∈ V (p)
and it is straightforward to check that \(\mathcal {T},\langle m,h\rangle \models \phi \) if and only if \(\mathcal {T^{\prime }},\langle m,h\rangle \models \phi \).
-
(a)
- 26.
The situation is more complex if the tree is not synchronized. For an accurate study of the relationships between branching-time semantics and T × W see Wölfl [21].
- 27.
See also Iacona [7].
- 28.
The same “redefinitions” of necessity and possibility operators can of course be carried out, in principle, also in an Ockhamist model. However, this goes against one of the philosophical motivations behind the branching time semantics, according to which all tensed constructions ought to be expressed with reference to points in time that are connected to the present point of evaluation – by some (back and forth) path over the temporal tree. This requirement may be too restrictive when we need to consider, e.g., fictional alternatives or histories diverging in the far past.
- 29.
The notions of A-series and B-series were introduced by [11]. The A-series conception of time, also called the dynamic view, resumes the way we experience time by being “in a flux” and opens up to presentism – a view that McTaggart himself did not endorse – where only the (constantly changing) “now” properly exists. According to this conception past, present, and future tenses are primitive concepts for referring to events in time. Other temporal concepts such as instants in time and the earlier-later relation between them, are to be derived from the formers. On the other hand, according to the B-series conception – which accounts for a “bird-eye view” of time and according to which the entire series of instants exists – instants and their earlier-later relation are the primitive concepts and tenses are derived from them.
- 30.
See [8].
- 31.
See [16] p. 137.
References and Recommended Readings
Barcellan, B., & Zanardo, A. (1999). Actual futures in Peircean branching-time logic. citeseer.ist.psu.edu/326930.html.
Belnap, N., & Green, M. (1994). Indeterminism and the thin red line. In J. Tomberlin (Ed.), Philosophical perspectives 8: Logic and language (pp. 217–244). Atascadero: Ridgeview Publishing Company.
Braüner, T., Øhrstrom, P., & Hasle, F. (2000) Determinism and the origins of temporal logic. In H. Barringer, M. Fisher, D. Gabbay, & G. Gough (Eds.), Advances in temporal logics (pp. 185–206). Dordrecht: Kluwer.
Burgess, J. (1978). The unreal future. Theoria, 44(3), 157–179.
Di Maio, M., & Zanardo, A. (1998). A Gabbay-rule free axiomatization of T×W validity. Journal of Philosophical Logic, 27(5), 435–487.
Hasle, P., & Øhrstrom, P. (1995). Temporal logic from ancient ideas to artificial intelligence. Dordrecht: Kluwer Academic.
Iacona, A. (2009). Commentary: Combinations of tense and modality by R. Thomason. Humana Mente, 8, 185–190.
Lewis, D. (1979). Counterfactual dependence and time’s arrow. Nous, 13, 455–76.
Lewis, D. (1986). On the plurality of worlds. Oxford: Blackwell.
MacFarlane, J. (2003). Future contingents and relative truth. The Philosophical Quarterly, 53, 321–336.
McTaggart, J. M. E. (1908). The unreality of time. Mind, 187, 457–474.
Ockham, W. (1983). Predestination, God’s foreknowledge, and future contingents. Indianapolis: Hackett.
Øhrstrom, P. (2009). In defence of the thin red line: A case for ockhamism. Humana mente, 8, 17–32.
Øhrstrom, P., Hasle, P., & Braüner, T. (1998). Ockhamistic logics and true futures of counterfactual moments. In Proceedings of the Fifth International Workshop on Temporal Representation and Reasoning (TIME-98) (Vol. 18).
Prior, A. N. (1966). Postulates for tense-logic. American Philsophical Quarterly, 3, 153–161.
Prior, A. N. (1967). Past, present and future. Oxford: Oxford University Press.
Reynolds, M. (2002). Axioms for branching time. Journal of Logic and Computation, 12, 679–697.
Thomason, R. (1970). Indeterminist time and truth-value gaps. Theoria, 36(3), 264–281.
Thomason, R. H. (1984). Combinations of tense and modality. In F. G. D. Gabbay (Ed.), Handbook of philosophical logic (pp. 205–234). Dordrecht: Kluwer Academic.
von Kutschera, F. (1997). T × W completeness. Journal of Philosophical Logic, 26, 241–250.
Wölfl, S. (2002). Propositional Q-logic. Journal of Philosophical Logic, 31, 387–414.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Sandu, G., Proietti, C., Rivenc, F. (2018). Bivalence and Future Contingency. In: Hansson, S., Hendricks, V. (eds) Introduction to Formal Philosophy. Springer Undergraduate Texts in Philosophy. Springer, Cham. https://doi.org/10.1007/978-3-319-77434-3_16
Download citation
DOI: https://doi.org/10.1007/978-3-319-77434-3_16
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-77433-6
Online ISBN: 978-3-319-77434-3
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)


 to be read as “it is necessary that”. We will also make use of dual operators like G := ¬F¬ (“it will always be the case that”), H := ¬P¬ (“it has always been the case that”) and
to be read as “it is necessary that”. We will also make use of dual operators like G := ¬F¬ (“it will always be the case that”), H := ¬P¬ (“it has always been the case that”) and 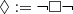 (“it is possible that”).
(“it is possible that”). are sufficient for the points we need to make.
are sufficient for the points we need to make.