Abstract
Mathematical categories provide an abstract and general framework for logic and mathematics. As such, they could be used by philosophers in all the basic fields of the discipline: semantics, epistemology and ontology. In this paper, we present the basic definitions and notions and suggest some of the ways categories are starting to infiltrate formal philosophy.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
We should emphasize that this is but one definition and that there are others (equivalent, of course). It very much depends on the background one wants to assume to start with and the goals one has in mind when using categories. If we were to assume that all mathematical entities have to be sets, we would give a slightly different definition. On the other hand, if we were to assume a purely formal set up, a fully specified formal framework, we would give a different definition still. For alternative definitions, see for instance [2, 19, 24].
- 2.
Notice that the latter concept can be defined directly in terms of arrows with no reference to the concept of product. Thus a category can have a terminal object without having all products.
- 3.
The preceding remark concerning the possibility of defining the concept of terminal object directly applies mutatis mutandis to the concept of initial object.
- 4.
This is shocking only if someone sticks firmly to the axiom of extensionality. From a categorical point of view, the axiom of extensionality is not the adequate criterion of identity for abstract sets.
- 5.
Since this object is also defined up to a unique isomorphism, we immediately introduce the standard notation.
- 6.
As far as I know, Bill Lawvere was the first to propose this general definition. For more on its properties, see [18].
- 7.
Notice that we do not have to take the closure of X since in the case of topological spaces, the operations define a coHeyting algebra, i.e. the algebra of closed sets.
- 8.
There are obvious foundational issues arising at this point, but we will simply brush them under the carpet and ignore them altogether.
- 9.
Notice that the functors go from the opposite category C op. This is related to theoretical aspects of category theory that we cannot explain in such a short paper.
References
Adámek, J., & Trnková, V. (1990). Automata and algebras in categories (Mathematics and its applications (East European series), Vol. 37). Dordrecht: Kluwer.
(***)Awodey, S. (2007). Category theory (Oxford logic guides, Vol. 49). Oxford: Clarendon Press. [A nice introduction to category theory.].
Awodey, S., & Kishida, K. (2008). Topology and modality: The topological interpretation of first-order modal logic. The Review of Symbolic Logic, 1(Special Issue 02), 146–166.
Borceux, F. (1994). Handbook of categorical algebra. 1 (Encyclopedia of mathematics and its applications, Vol. 50). Cambridge: Cambridge University Press.
Crane, L. (2009). Relational spacetime, model categories and quantum gravity. International Journal of Modern Physics A, 24(15), 2753–2775.
Döring, A., & Isham, C. J. (2008). A topos foundation for theories of physics. I. Formal languages for physics. Journal of Mathematical Physics, 49(5), 25
Döring, A., & Isham, C. J. (2008). A topos foundation for theories of physics. II. Daseinisation and the liberation of quantum theory. Journal of Mathematical Physics, 49(5), 26.
Döring, A., & Isham, C. J. (2008). A topos foundation for theories of physics. III. The representation of physical quantities with arrows
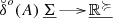 . Journal of Mathematical Physics, 49(5), 777–825
. Journal of Mathematical Physics, 49(5), 777–825Döring, A., & Isham, C. J. (2008). A topos foundation for theories of physics: IV. Categories of systems. Journal of Mathematical Physics, 49(5), 826–884.
Eilenberg, S., & Mac Lane, S. (1945). A general theory of natural equivalences. Transactions of the American Mathematical Society, 58, 231–294.
Geuvers, H., Niqui, M., Spitters, B., & Wiedijk, F. (2007). Constructive analysis, types and exact real numbers. Mathematical Structures in Computer Science, 17(1), 3–36.
Ghilardi, S., & Zawadowski, M. (2002). Sheaves, games, and model completions: A categorical approach to nonclassical propositional logics (Trends in logic – studia logica library, Vol. 14). Dordrecht: Kluwer.
Johnson, M., & Rosebrugh, R. (2010). Ontology engineering, universal algebra, and category theory. In R. Poli, M. Healy, & A. Kameas (Eds.), Theory and applications of ontology: Computer applications (pp. 565–576). Dordrecht: Springer.
Johnstone, P. T. (2002). Sketches of an elephant: A topos theory compendium. Volume 2 (Oxford logic guides, Vol. 44). Oxford: The Clarendon Press Oxford University Press.
Krömer, R. (2007). Tool and object. A history and philosophy of category theory (Volume 32 of science networks. Historical studies). Basel: Birkhäuser Verlag.
Landry, E., & Marquis, J.-P. (2005). Categories in context: Historical, foundational and philosophical. Philosophia Mathematica (3), 13(1), 1–43.
La Palme Reyes, M., Macnamara, J., Reyes, G. E., Zolfaghari, H. (1999). Models for non-Boolean negations in natural languages based on aspect analysis. In D. M. Gabbay & H. Wansing (Eds.), What is negation? (Vol. 13, pp. 241–260). Dordrecht: Kluwer.
(***)Lawvere, F. W., & Rosebrugh, R. (2003). Sets for mathematics. Cambridge: Cambridge University Press. [A gentle introduction to category theory. A nice place to start for philosophers.].
(***)Mac Lane, S. (1998). Categories for the working mathematician (Graduate texts in mathematics, 2nd ed., Vol. 5). New York: Springer. [The standard reference in the field. However, it does presuppose familiarity with various mathematical theories.]
(***)Mac Lane, S., & Moerdijk, I. (1994). Sheaves in geometry and logic. A first introduction to topos theory (Universitext). New York: Springer. [A reference on sheaves and toposes. Not an introductory book.].
Makkai, M., & Reyes, G. E. (1995). Completeness results for intuitionistic and modal logic in a categorical setting. Annals of Pure and Applied Logic, 72(1), 25–101.
Marquis, J. -P. (2006). What is category theory? In G. Sica (Ed.), What is category theory? (pp. 221–255). Monza: Polimetrica.
Marquis, J. -P. (2009). From a geometrical point of view: A study of the history and philosophy of category theory (Logic, epistemology, and the unity of science, 1st ed., Vol. 14). New York: Springer.
McLarty, C. (1995). Elementary categories, elementary toposes (Oxford logic guides, Vol. 21). Oxford: The Clarendon Press.
Moerdijk, I. (1998). Sets, topoi and intuitionism. Philosophia Mathematica (3), 6(2), 169–177. Perspectives on intuitionism.
Mormann, T. (1995). Trope sheaves. A topological ontology of tropes. Logic and Logical Philosophy, 3, 129–150.
Mormann, T. (1997). Topological aspects of combinatorial possibility. Logic and Logical Philosophy, 5, 75–92.
Mormann, T. (1999). Neither mereology nor Whiteheadian account of space yet convicted. Analysis (Oxford), 59(3), 174–182.
Smith, B. (1998). The basic tools of formal ontology. In N. Guarino (Ed.), Formal ontology in information systems (pp. 19–28). Amsterdam: IOS Press.
Worththington, J. (2012). A bialgebraic approach to automata and formal language theory. Annals of Pure and Applied Logic, 163(7), 745–762.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Marquis, JP. (2018). Categories. In: Hansson, S., Hendricks, V. (eds) Introduction to Formal Philosophy. Springer Undergraduate Texts in Philosophy. Springer, Cham. https://doi.org/10.1007/978-3-319-77434-3_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-77434-3_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-77433-6
Online ISBN: 978-3-319-77434-3
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)


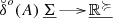 . Journal of Mathematical Physics, 49(5), 777–825
. Journal of Mathematical Physics, 49(5), 777–825