Abstract
We construct two identity-based encryption (IBE) schemes. The first one is IBE satisfying key dependent message (KDM) security for user secret keys. The second one is IBE satisfying simulation-based receiver selective opening (RSO) security. Both schemes are secure against adaptive-ID attacks and do not have any a-priori bound on the number of challenge identities queried by adversaries in the security games. They are the first constructions of IBE satisfying such levels of security.
Our constructions of IBE are very simple. We construct KDM secure IBE by transforming KDM secure secret-key encryption using IBE satisfying only ordinary indistinguishability against adaptive-ID attacks (IND-ID-CPA security). Our simulation-based RSO secure IBE is based only on IND-ID-CPA secure IBE.
We also demonstrate that our construction technique for KDM secure IBE is used to construct KDM secure public-key encryption. More precisely, we show how to construct KDM secure public-key encryption from KDM secure secret-key encryption and public-key encryption satisfying only ordinary indistinguishability against chosen plaintext attacks.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
1.1 Background
Identity-based encryption (IBE) proposed by Shamir [30] is an extension of public-key encryption (PKE). In IBE, we can use an identity of a recipient as a public-key. The secret-key corresponding to an identity is generated only by the trusted authority who has the master secret-key. Users can obtain secret-keys corresponding to their identities by authenticating themselves to the trusted authority. By using IBE, we can avoid distributing public-key certificates that is one of the major issues with public-key cryptography.
Security notions for IBE capture corruptions and collusions of users. In other words, we require that IBE guarantee confidentiality of a message encrypted under an identity \({\mathsf {id}^*}\) even if an adversary obtains a secret-key corresponding to any identity other than \({\mathsf {id}^*}\).
Security notions for IBE are classified into two categories, that is, adaptive security and selective security. An IBE scheme is said to be secure against adaptive-ID attacks [12] if it is secure even when an adversary adaptively chooses the challenge identity \({\mathsf {id}^*}\). On the other hand, an IBE scheme is said to be secure against selective-ID attacks [16] if it is secure when an adversary declares the challenge identity \({\mathsf {id}^*}\) before seeing public parameters.
Security against adaptive-ID attacks is a desirable security notion for IBE when we use it in practical situations. However, since IBE has an advanced functionality compared to PKE, attack scenarios that ordinary indistinguishability against adaptive-ID attacks does not capture can naturally occur in practical situations of IBE. As such attack scenarios, in this work, we focus on the situations of encrypting secret-keys and the selective opening attacks.
Black et al. [11] introduced the notion of key dependent message (KDM) security which guarantees confidentiality even in situations of encrypting secret-keys. Informally, an encryption scheme is said to be KDM secure if it is secure when an adversary can obtain encryptions of \(f(\mathsf {sk}_1,\ldots ,\mathsf {sk}_\ell )\), where \(\mathsf {sk}_1,\ldots ,\mathsf {sk}_\ell \) are secret-keys that exist in the system and f is a function.
Alperin-Sheriff and Peikert [3] pointed out that KDM security with respect to user secret-keys is well-motivated by some natural usage scenarios for IBE such as key distribution in a revocation system. They constructed the first IBE satisfying KDM security for user secret-keys assuming the hardness of the learning with errors (LWE) problem. Galindo et al. [22] proposed an IBE scheme that satisfies KDM security for master secret-keys based on the hardness of a rank problem on bilinear groups. However, both of these schemes are secure only against selective-ID attacks. Moreover, both schemes have some a-priori bound on the number of queries made by an adversary.Footnote 1
In the selective opening attack, an adversary, given some ciphertexts, adaptively corrupts some fraction of users and tries to break confidentiality of ciphertexts of uncorrupted users.
There are both sender corruption case and receiver corruption case in this attack scenario. Bellare et al. [8] formalized sender selective opening (SSO) security for PKE that captures situations where there are many senders and a single receiver, and an adversary can obtain messages and random coins of corrupted senders. Hazay et al. [24] later formalized receiver selective opening (RSO) security for PKE that captures situations where there are many receivers and a single sender, and an adversary can obtain messages and secret-keys of corrupted receivers.
Selective opening attacks originally considered in the context of multi-party computation are natural and motivated in the context of IBE since it also considers situations where there are many users and some fraction are corrupted. Bellare et al. [9] defined SSO security for IBE and proposed SSO secure IBE schemes under the decisional linear assumption and a subgroup decision assumption in composite order bilinear groups. Their definition of SSO security for IBE captures adaptive-ID attacks in addition to sender selective opening attacks. However, it does not take receiver selective opening attacks into account.
It is known that the standard notions of indistinguishability imply neither KDM security [1, 10, 18, 28] nor selective opening security [7, 25, 26]. From this fact, we know very little about the possibility of IBE satisfying these stronger security notions than standard indistinguishability though there have been many works on the study of IBE.
Especially, it is open whether we can construct IBE that is KDM secure against adaptive-ID attacks and there is no a-priori bound on the number of queries made by an adversary. For selective opening security, we have no construction of IBE satisfying RSO security even if we require only security against selective-ID attacks.
As mentioned above, attack scenarios captured by both KDM security and selective opening security are natural and motivated for IBE. We thus think it is important to clarify these issues.
1.2 Our Results
Based on the above background, we propose KDM secure IBE and RSO secure IBE. Both schemes satisfy security against adaptive-ID attacks. They are the first schemes satisfying such levels of security.
Our constructions of IBE are very simple. We construct KDM secure IBE by transforming KDM secure secret-key encryption (SKE) using IBE satisfying ordinary indistinguishability against adaptive-ID attacks (\(\text {IND-ID-CPA}\) security) and garbled circuits. Somewhat surprisingly, our RSO secure IBE is based only on \(\text {IND-ID-CPA}\) secure IBE.
We show the details of each result below.
Key dependent message secure IBE. In this work, we focus on KDM security for user secret-keys similarly to Alperin-Sheriff and Peikert [3], and let KDM security indicate KDM security for user secret-keys. We show the following theorem.Footnote 2
Theorem 1
(Informal). Assuming there exist \(\text {IND-ID-CPA}\) secure IBE and SKE that is KDM secure with respect to projection functions (resp. functions computable by a-priori bounded size circuits). Then, there exists IBE that is KDM secure with respect to projection functions (resp. functions computable by a-priori bounded size circuits) against adaptive-ID attacks.
Projection function is a function each of whose output bits depends on at most one bit of an input. KDM security with respect to projection functions is a generalization of circular security [15]. We can construct IBE satisfying KDM security with respect to any function computable by circuits of a-priori bounded size [6] by requiring the same KDM security for the underlying SKE.
As noted above, KDM secure IBE proposed by Alperin-Sheriff and Peikert is only secure against selective-ID attacks. Moreover, their scheme has an a-priori bound on the number of challenge identities in the security game. Our KDM secure IBE is secure against adaptive-ID attacks and does not have any a-priori bound on the number of queries made by an adversary in the security game.
To achieve KDM security for an a-priori unbounded number of challenge identities, in our construction, the size of instances of the underlying KDM secure SKE needs to be independent of the number of users in the security game.Footnote 3
We can construct SKE that is KDM secure with respect to projection functions and satisfies this efficiency requirement based on the decisional diffie-hellman (DDH) assumption [13] and LWE assumption [5].Footnote 4 In addition, Applebaum [4] showed how to transform SKE that is KDM secure with respect to projection functions into SKE that is KDM secure with respect to functions computable by a-priori bounded size circuits.
We can construct \(\text {IND-ID-CPA}\) secure IBE under the LWE assumption [2]. Moreover, Döttling and Garg [21] recently showed how to construct \(\text {IND-ID-CPA}\) secure IBE based on the computational diffie-hellman (CDH) assumption.
Thus, from Theorem 1, we obtain the following corollary.
Corollary 1
There exists IBE that is KDM secure with respect to functions computable by a-priori bounded size circuits against adaptive-ID attacks under the DDH assumption or LWE assumption.
In addition to these results, based on the construction techniques above, we also show that we can transform KDM secure SKE into KDM secure PKE by using PKE satisfies ordinary indistinguishability against chosen plaintext attacks (IND-CPA security). Specifically, we show the following theorem.
Theorem 2
(Informal). Assuming there exist \(\text {IND-CPA}\) secure PKE and SKE that is KDM secure with respect to projection functions (resp. functions computable by a-priori bounded size circuits). Then, there exists PKE that is KDM secure with respect to projection functions (resp. functions computable by a-priori bounded size circuits).
It seems that we cannot construct KDM secure PKE from KDM secure SKE via the straightforward hybrid encryption methodology. It leads to a dead-lock of secret-keys of the underlying primitives and thus it is difficult to prove the security of hybrid encryption construction. Thus, this result is of independent interest.
Receiver selective opening secure IBE. Before our work, RSO security for IBE has never been studied while an IBE scheme that is SSO secure was proposed by Bellare et al. [9]. Therefore, we first define RSO security for IBE formally. Our definition is a natural extension of simulation-based RSO security for PKE proposed by Hazay et al. [24]. We then show the following theorem.
Theorem 3
(Informal). Assuming there exists \(\text {IND-ID-CPA}\) secure IBE. Then, there exists IBE that satisfies simulation-based RSO security against adaptive-ID attacks.
Somewhat surprisingly, the above theorem says that all we need is \(\text {IND-ID-CPA}\) secure IBE to achieve simulation-based RSO secure IBE. We can obtain the result via a simple double encryption paradigm [29].
The reason we can obtain the above result via a simple double encryption paradigm is that in receiver selective opening attacks for IBE, we have to consider the revelation of secret-keys themselves but not the random coins for key generation since secret-keys are generated by the trusted authority in IBE.
We also observe that if we allow only revelations of secret-keys and not the random coins for key generation, we can construct PKE satisfying such simulation-based RSO security using any PKE satisfying ordinary IND-CPA security. This fact is somewhat obvious from some previous results [17, 24] though these works did not explicitly state it. For self-containment, we show the following theorem.
Theorem 4
(Informal). Assuming there exists \(\text {IND-CPA}\) secure PKE. Then, there exists PKE that satisfies simulation-based RSO security with respect to the revelation of only secret-keys.
To prove simulation-based RSO security against the revelation of random coins for key generation, it seems that the underlying PKE needs to be key simulatable [19, 24] in some sense. In this case, it is difficult to construct simulation-based RSO secure PKE without relying on some specific algebraic or lattice assumptions.
We summarize our results in Fig. 1.
1.3 Overview of Our Techniques
We first give an intuition for our KDM secure IBE.
KDM secure IBE from KDM secure SKE. Our construction methodology for KDM secure IBE is somewhat based on the recent beautiful construction of IBE proposed by Döttling and Garg [20, 21] using new primitives called chameleon encryption or one-time signatures with encryption. The essence of their constructions is the mechanism that an encryptor who does not know the exact value of a public-key \(\mathsf {ek}\) of PKE can generate an “encoding” of a PKE’s ciphertext under the public-key \(\mathsf {ek}\). Moreover, in their construction, the security of IBE is directly reduced to that of PKE in the last step of the security proof.
Based on this idea, by realizing the mechanism that an encryptor who does not know the value of the key \(\mathsf {K}\) of SKE can generate an encoding of an SKE’s ciphertext under the key \(\mathsf {K}\) of SKE, we try to transform SKE into public-key primitives such as PKE and IBE shifting the security level of SKE to them. We then show that we can construct KDM secure IBE (resp. PKE) based on KDM secure SKE and \(\text {IND-ID-CPA}\) secure IBE (resp. \(\text {IND-CPA}\) secure PKE).
We emphasize that we need neither chameleon encryption nor one-time signatures with encryption. \(\text {IND-ID-CPA}\) secure IBE is sufficient for our KDM secure IBE.
Our constructions are very simple and use garbled circuits. For simplicity, we focus on constructing KDM secure PKE to give an intuition. Suppose that we construct a KDM secure PKE scheme \(\mathsf {KdmPKE}\) from a KDM secure SKE scheme \(\mathsf {SKE}\) and \(\text {IND-CPA}\) secure PKE scheme \(\mathsf {PKE}\).
The encryption algorithm of \(\mathsf {KdmPKE}\) first garbles an encryption circuit of \(\mathsf {SKE}\) that has a message to be encrypted hardwired, that is, \(\mathsf {E}_\mathsf {ske}(\cdot ,m)\), and then encrypts labels of the garbled circuit by \(\mathsf {PKE}\) under different keys. This process can be done without any secret-key of \(\mathsf {SKE}\) and thus we achieve the “encoding” mechanism mentioned above. This construction is similar to that of “semi-adaptively” secure functional encryption based on selectively secure one proposed by Goyal et al. [23], but our techniques for the security proof explained below are different from theirs.
Why \(\textit{IND-CPA}\) security of the underlying PKE is sufficient? One might wonder why \(\text {IND-CPA}\) security of the underlying PKE scheme \(\mathsf {PKE}\) is sufficient to construct the KDM secure PKE scheme \(\mathsf {KdmPKE}\). To see the answer for this question, we closer look at the construction of \(\mathsf {KdmPKE}\).
Let the length of a secret-key \(\mathsf {K}\) of \(\mathsf {SKE}\) be \({\mathsf {len}_{\mathsf {\mathsf {K}}}}\). A public-key \(\mathsf {Kdm}.\mathsf {ek}\) of \(\mathsf {KdmPKE}\) consists of \(2\cdot {\mathsf {len}_{\mathsf {\mathsf {K}}}}\) \(\mathsf {PKE}\)’s public-keys \(\left\{ \mathsf {ek}_{j,\alpha }\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}],\alpha \in \{0,1\}}\), where \([{\mathsf {len}_{\mathsf {K}}}]\) denotes \(\{1,\ldots ,{\mathsf {len}_{\mathsf {K}}}\}\). The secret-key \(\mathsf {Kdm}.\mathsf {dk}\) corresponding to \(\mathsf {Kdm}.\mathsf {ek}\) consists of a secret-key \(\mathsf {K}\) of \(\mathsf {SKE}\) and \({\mathsf {len}_{\mathsf {\mathsf {K}}}}\) secret-keys of \(\mathsf {PKE}\) corresponding to the bit representation of \(\mathsf {K}=\mathsf {K}[1]\ldots \mathsf {K}[{\mathsf {len}_{\mathsf {K}}}]\), that is, \(\left\{ \mathsf {dk}_{j,\mathsf {K}[j]}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\). We note that secret-keys of \(\mathsf {PKE}\) that do not correspond to the bit representation of \(\mathsf {K}\) are not included in \(\mathsf {Kdm}.\mathsf {dk}\).
As mentioned above, when encrypting a message m under the public-key \(\mathsf {Kdm}.\mathsf {ek}:=\left\{ \mathsf {ek}_{j,\alpha }\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}],\alpha \in \{0,1\}}\), the encryption algorithm of \(\mathsf {KdmPKE}\) first garbles an encryption circuit of \(\mathsf {SKE}\) in which m is hardwired, that is, \(\mathsf {E}_\mathsf {ske}(\cdot ,m)\). This results in a single garbled circuit \(\widetilde{\mathsf {E}}\) and \(2\cdot {\mathsf {len}_{\mathsf {K}}}\) labels \(\left\{ \mathsf {lab}_{j,\alpha }\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}],\alpha \in \{0,1\}}\). Then, the encryption algorithm of \(\mathsf {KdmPKE}\) encrypts \(\mathsf {lab}_{j,\alpha }\) by \(\mathsf {ek}_{j,\alpha }\) for every \(j\in [{\mathsf {len}_{\mathsf {K}}}]\) and \(\alpha \in \{0,1\}\). The resulting ciphertext of \(\mathsf {KdmPKE}\) consists of \(\widetilde{\mathsf {E}}\) and these \(2\cdot {\mathsf {len}_{\mathsf {K}}}\) ciphertexts of \(\mathsf {PKE}\).
When decrypting this ciphertext with \(\mathsf {Kdm}.\mathsf {dk}:=\left( \mathsf {K},\left\{ \mathsf {dk}_{j,\mathsf {K}[j]}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\right) \), we first obtain labels corresponding to \(\mathsf {K}\) from \({\mathsf {len}_{\mathsf {K}}}\) out of \(2\cdot {\mathsf {len}_{\mathsf {K}}}\) ciphertexts of \(\mathsf {PKE}\) using \(\left\{ \mathsf {dk}_{j,\mathsf {K}[j]}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\) and evaluate \(\widetilde{\mathsf {E}}\) with those labels. This results in an \(\mathsf {SKE}\)’s ciphertext \(\mathsf {E}_\mathsf {ske}(\mathsf {K},m)\). Then, by decrypting it with \(\mathsf {K}\), we obtain m.
In this construction, secret-keys of \(\mathsf {PKE}\) corresponding to \(\mathsf {K}\), that is, \(\left\{ \mathsf {dk}_{j,\mathsf {K}[j]}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\) are included in \(\mathsf {Kdm}.\mathsf {dk}\), but the rest of secret-keys \(\left\{ \mathsf {dk}_{j,1-\mathsf {K}[j]}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\) are not included in \(\mathsf {Kdm}.\mathsf {dk}\). Thus, even if an adversary for \(\mathsf {KdmPKE}\) obtains encryptions of key dependent messages, they cannot get information of \(\left\{ \mathsf {dk}_{j,1-\mathsf {K}[j]}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\) while they potentially get information of \(\left\{ \mathsf {dk}_{j,\mathsf {K}[j]}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\) from those encryptions. In addition, in the security proof, we use the security of \(\mathsf {PKE}\) of instances related to \(\left\{ \mathsf {dk}_{j,1-\mathsf {K}[j]}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\), but not \(\left\{ \mathsf {dk}_{j,\mathsf {K}[j]}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\). This is the reason the \(\text {IND-CPA}\) security of \(\mathsf {PKE}\) is sufficient to construct a KDM secure PKE scheme \(\mathsf {KdmPKE}\). To see the fact, we show the outline of the proof below.
In the proof, by using the security of garbled circuits, we change the security game without affecting the behavior of an adversary so that we generate a challenge ciphertext under the key pair \((\mathsf {Kdm}.\mathsf {ek},\mathsf {Kdm}.\mathsf {dk})\) with simulated garbled circuits computed from an \(\mathsf {SKE}\)’s ciphertext of the challenge key dependent message \(m^*\) under the key \(\mathsf {K}\), that is, \(\mathsf {E}_\mathsf {ske}(\mathsf {K},m^*)\), where \(\mathsf {K}\) is the secret-key of \(\mathsf {SKE}\) contained in \(\mathsf {Kdm}.\mathsf {dk}\). By this change, we do not need \(m^*\) itself, and the ciphertext \(\mathsf {E}_\mathsf {ske}(\mathsf {K},m^*)\) is sufficient to simulate the security game. Thus, at this point, we can reduce the KDM security of \(\mathsf {KdmPKE}\) to that of the underlying \(\mathsf {SKE}\).
More precisely, in the above proof, before using the security of garbled circuits, we have to eliminate the labels of garbled circuits that do not correspond to the bit representation of \(\mathsf {K}\), that is, \(\left\{ \mathsf {lab}_{j,1-\mathsf {K}[j]}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\) from the view of the adversary. This can be done by using the \(\text {IND-CPA}\) security of \(\mathsf {PKE}\) of only instances related to \(\left\{ \mathsf {dk}_{j,1-\mathsf {K}[j]}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\). Therefore, we can complete the proof by using \(\text {IND-CPA}\) security of \(\mathsf {PKE}\) of instances related to \(\left\{ \mathsf {dk}_{j,1-\mathsf {K}[j]}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\), but not \(\left\{ \mathsf {dk}_{j,\mathsf {K}[j]}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\).
Conversions of functions. One additional non-trivial point is the conversion of functions by reductions.
In the security game of KDM security, an adversary queries a function and obtain an encryption of the function of secret-keys. Thus, KDM security is parameterized by function classes indicating functions that an adversary can query.
In the above construction, a secret-key \(\mathsf {Kdm}.\mathsf {dk}\) of \(\mathsf {KdmPKE}\) contains some secret-keys of \(\mathsf {PKE}\) in addition to a secret-key of \(\mathsf {SKE}\). Therefore, a function queried by an adversary for \(\mathsf {KdmPKE}\) is a function of secret-keys of \(\mathsf {PKE}\) and secret-keys of \(\mathsf {SKE}\). On the other hand, a function that a reduction algorithm can query is a function of only secret-keys of \(\mathsf {SKE}\). This means that the reduction algorithm needs to convert a function queried by an adversary for \(\mathsf {KdmPKE}\).
Such conversion is clearly possible if we do not care classes of functions. However, when considering KDM security, classes of functions are important since they determine the level of KDM security. It is not clear how such conversions affect a class of functions. Especially, it is not clear whether we can perform such conversions for functions without changing the class of functions.
We show that such conversions are possible for projection functions and functions computable by a-priori bounded size circuits. Thus, we can reduce the KDM security for those function classes of \(\mathsf {KdmPKE}\) to that of \(\mathsf {SKE}\).
These arguments hold if we replace the underlying \(\text {IND-CPA}\) secure PKE with \(\text {IND-ID-CPA}\) secure IBE. The above construction can be seen as a special case where the size of instances of the underlying IBE linearly depends on the size of identity space. Thus, we can obtain KDM secure IBE from KDM secure SKE and \(\text {IND-ID-CPA}\) secure IBE.
RSO secure IBE from \(\textit{IND-ID-CPA}\) secure IBE. Our starting point of the construction of RSO secure IBE is the above KDM secure IBE based on KDM secure SKE. It seems that the above construction can be used to carry over strong security notions of SKE to IBE that we need to simulate secret-keys in some sense in the security game. One such example, we focus on RSO security.Footnote 5 Actually, in the above construction, if the underlying SKE has non-committing property (such as one-time pad), the resulting IBE seems to gain simulation-based RSO security.
However, it turns out that the construction is redundant and a simple double encryption paradigm [29] is sufficient to achieve RSO security. The reason we can construct RSO secure IBE via simple constructions is related to whether we allow the revelation of the random coins for key generation in addition to secret-keys or not.
Secret key vs random coins for the key generation. Hazay et al. [24] considered the revelation of both secret-keys and random coins for key generation when they defined RSO security for PKE. It is better to take the revelation of random coins of the key generation into account for many applications of PKE. However, for IBE, it is sufficient to take the revelation of only secret-keys into account.
In IBE, the trusted authority generates user secret-keys and distributes them to users. Thus, if an adversary corrupts a user, the adversary cannot obtain the random coin used to generate the secret-key of the user since the user does not know it. For this reason, we do not have to take the revelation of random coins of key generation in IBE into account.Footnote 6
Construction based on a double encryption paradigm. When we do not take the revelation of random coins of key generation in IBE into account, we can construct simulation-based RSO secure IBE via a simple double encryption paradigm [29] without using garbled circuits.
More precisely, using an IBE scheme \(\mathsf {IBE}\) whose identity space is \(\mathcal {ID}\times \{0,1\}\), we construct the following new IBE scheme \(\mathsf {RsoIBE}\) whose message space and identity space are \(\{0,1\}\) and \(\mathcal {ID}\), respectively.
The setup algorithm of \(\mathsf {RsoIBE}\) is the same as that of \(\mathsf {IBE}\). When generating a secret-key \(\mathsf {Rso}.\mathsf {sk}_\mathsf {id}\) for identity \(\mathsf {id}\in \mathcal {ID}\), the key generation algorithm of \(\mathsf {RsoIBE}\) generates an \(\mathsf {IBE}\)’s secret-key \(\mathsf {sk}_{\mathsf {id},r}\) for the identity \((\mathsf {id},r)\), where r is a freshly generated random bit, and outputs \(\mathsf {Rso}.\mathsf {sk}_\mathsf {id}:=(r,\mathsf {sk}_{\mathsf {id},r})\). When encrypting a message \(m\in \{0,1\}\) for identity \(\mathsf {id}\in \mathcal {ID}\), the encryption algorithm of \(\mathsf {RsoIBE}\) generates a pair of ciphertexts \((\mathsf {CT}_0,\mathsf {CT}_1)\), where \(\mathsf {CT}_\alpha \) is an encryption of m under the identity \((\mathsf {id},\alpha )\) for every \(\alpha \in \{0,1\}\). The decryption algorithm of \(\mathsf {RsoIBE}\), given a pair of ciphertexts \((\mathsf {CT}_0,\mathsf {CT}_1)\) and a secret-key \(\mathsf {Rso}.\mathsf {sk}_\mathsf {id}:=(r,\mathsf {sk}_{\mathsf {id},r})\), outputs the decryption result of \(\mathsf {CT}_r\) with \(\mathsf {sk}_{\mathsf {id},r}\).
This construction achieves a non-committing property. Suppose that we generate \(\mathsf {CT}_r\) as an encryption of 0 under the identity \((\mathsf {id},r)\) and \(\mathsf {CT}_{1-r}\) as an encryption of 1 under the identity \((\mathsf {id},1-r)\) when generating a ciphertext \((\mathsf {CT}_0,\mathsf {CT}_1)\) for the identity \(\mathsf {id}\), where r is the random bit contained in the secret-key \(\mathsf {Rso}.\mathsf {sk}_\mathsf {id}:=(r,\mathsf {sk}_{\mathsf {id},r})\) for \(\mathsf {id}\). We can open this ciphertext to any \(m\in \{0,1\}\) by pretending as if the secret-key \(\mathsf {Rso}.\mathsf {sk}_\mathsf {id}\) for \(\mathsf {id}\) is \((r\oplus m, \mathsf {sk}_{\mathsf {id},r\oplus m})\). Due to this non-committing property, we prove the simulation-based RSO security of \(\mathsf {RsoIBE}\).
From this result, we observe that if we take the revelation of only secret-keys into account, we can also construct \(\text {SIM-RSO}\) secure PKE based on any \(\text {IND-CPA}\) secure PKE. Our results on simulation-based RSO secure IBE and PKE highlight the gap of difficulties between achieving RSO security against revelation of only secret-keys and that against both secret-keys and random coins for key generation. To achieve the latter RSO security for PKE, it seems that the underlying scheme needs to be key simulatable [19, 24] in some sense.
1.4 Organization
In Sect. 2, we introduce some notations and review definitions of cryptographic primitives that we use as building blocks. In Sect. 3, we define IBE, and introduce KDM security and RSO security for it. In Sect. 4, we show how to construct KDM secure IBE from KDM secure SKE and \(\text {IND-ID-CPA}\) secure IBE. In Sect. 5, we show the construction of simulation-based RSO secure IBE based on \(\text {IND-ID-CPA}\) secure IBE. In Sect. 6, we show how to construct KDM secure PKE from KDM secure SKE and \(\text {IND-CPA}\) secure PKE. In Sect. 7, we show how to construct simulation-based RSO secure PKE based on \(\text {IND-CPA}\) secure PKE.
2 Preliminaries
We define some cryptographic primitives after introducing some notations.
Notations. \(x \xleftarrow {\mathsf {r}}X\) denotes choosing an element from a finite set X uniformly at random, and \(y \leftarrow \mathsf {A}(x;r)\) denotes assigning y to the output of an algorithm \(\mathsf {A}\) on an input x and a randomness r. When there is no need to write the randomness clearly, we omit it and simply write \(y \leftarrow \mathsf {A}(x)\). For strings x and y, \(x \Vert y\) denotes the concatenation of x and y. For an integer \(\ell \), \([\ell ]\) denote the set of integers \(\{1, \ldots , \ell \}\). For a string x and positive integer \(j \le \left| x\right| \), x[j] denotes the j-th bit of x.
\(\lambda \) denotes a security parameter. PPT stands for probabilistic polynomial time. A function \(f(\lambda )\) is a negligible function if \(f(\lambda )\) tends to 0 faster than \(\frac{1}{\lambda ^c}\) for every constant \(c>0\). We write \(f(\lambda ) = \mathsf{negl}(\lambda )\) to denote \(f(\lambda )\) being a negligible function.
2.1 Garbled Circuits
We define garbled circuits. We can realize garbled circuits for all efficiently computable circuits based on one-way functions [31].
Definition 1
(Garbled circuits). Let \(\{\mathcal {C}_n\}_{n \in \mathbb {N}}\) be a family of circuits where each circuit in \(\mathcal {C}_n\) takes n-bit inputs. A circuit garbling scheme \(\mathsf{GC}\) is a two tuple \((\mathsf {Garble}, \mathsf {Eval})\) of PPT algorithms.
The garbling algorithm \(\mathsf {Garble}\), given a security parameter \(1^\lambda \) and circuit \(C \in \mathcal {C}_n\), outputs a garbled circuit \(\widetilde{C}\), together with 2n labels \(\left\{ \mathsf {lab}_{j,\alpha }\right\} _{j \in [n],\alpha \in \{0,1\}}\). The evaluation algorithm, given a garbled circuit \(\widetilde{C}\) and n labels \(\left\{ \mathsf {lab}_j\right\} _{j \in [n]}\), outputs y. As correctness, we require \(\mathsf {Eval}\left( \widetilde{C}, \left\{ \mathsf {lab}_{j,x[j]}\right\} _{j \in [n]}\right) = C(x)\) for every \(n \in \mathbb {N}\), \(x \in \{0,1\}^n\), where \(\left( \widetilde{C}, \left\{ \mathsf {lab}_{j,\alpha }\right\} _{j \in [n],\alpha \in \{0,1\}}\right) \leftarrow \mathsf {Garble}(1^\lambda , C)\).
We define its security. Let \(\mathsf {Sim}\) be a PPT simulator. We define the following game between a challenger and an adversary \(\mathcal {A}\).
-
1.
First, the challenger chooses a bit \(b \xleftarrow {\mathsf {r}}\{0,1\}\) and sends a security parameter \(1^\lambda \) to \(\mathcal {A}\). Then, \(\mathcal {A}\) sends a circuit \(C \in \mathcal {C}_n\) and an input \(x \in \{0,1\}^n\) for the challenger. Next, if \(b=1\), the challenger computes \(\left( \widetilde{C}, \left\{ \mathsf {lab}_{j,\alpha }\right\} _{j \in [n],\alpha \in \{0,1\}}\right) \leftarrow \mathsf {Garble}(1^\lambda , C)\) and returns \(\left( \widetilde{C}, \left\{ \mathsf {lab}_{j,x[j]}\right\} _{j \in [n]}\right) \) to \(\mathcal {A}\). Otherwise, the challenger returns \(\left( \widetilde{C}, \left\{ \mathsf {lab}_j\right\} _{j \in [n]}\right) \leftarrow \mathsf {Sim}(1^\lambda , \left| C\right| , C(x))\) to \(\mathcal {A}\).
-
2.
\(\mathcal {A}\) outputs \(b' \in \{0,1\}\).
We require that there exists a PPT simulator \(\mathsf {Sim}\) such that for any PPT adversary \(\mathcal {A}\), we have \(\mathsf {Adv}_{\mathsf{GC}, \mathcal {A}, \mathsf {Sim}}^{\mathsf {gc}}(\lambda ) = \mathsf{negl}(\lambda )\).
2.2 Public Key Encryption
A public-key encryption (PKE) scheme \(\mathsf {PKE}\) is a three tuple \((\mathsf {KG}, \mathsf {Enc}, \mathsf {Dec})\) of PPT algorithms. Below, let \(\mathcal {M}\) be the message space of \(\mathsf {PKE}\). The key generation algorithm \(\mathsf {KG}\), given a security parameter \(1^\lambda \), outputs a public key \(\mathsf {ek}\) and a secret key \(\mathsf {dk}\). The encryption algorithm \(\mathsf {Enc}\), given a public key \(\mathsf {ek}\) and message \(m \in \mathcal {M}\), outputs a ciphertext \(\mathsf {CT}\). The decryption algorithm \(\mathsf {Dec}\), given a secret key \(\mathsf {dk}\) and ciphertext c, outputs a message \(\tilde{m} \in \{ \bot \} \cup \mathcal {M}\). As correctness, we require \(\mathsf {Dec}(\mathsf {dk}, \mathsf {Enc}(\mathsf {ek}, m)) = m\) for every \(m \in \mathcal {M}\) and \((\mathsf {ek}, \mathsf {dk})\leftarrow \mathsf {KG}(1^\lambda )\).
We introduce indistinguishability against chosen plaintext attacks (\(\text {IND-CPA}\) security) for PKE.
Definition 2
(IND-CPA security). Let \(\mathsf {PKE}\) be a PKE scheme. We define the \(\text {IND-CPA}\) game between a challenger and an adversary \(\mathcal {A}\) as follows. We let \(\mathcal {M}\) be the message space of \(\mathsf {PKE}\).
-
1.
First, the challenger chooses a challenge bit \(b \xleftarrow {\mathsf {r}}\{0,1\}\). Next, the challenger generates a key pair \((\mathsf {ek},\mathsf {dk}) \leftarrow \mathsf {KG}(1^{\lambda })\) and sends \(\mathsf {ek}\) to \(\mathcal {A}\).
-
2.
\(\mathcal {A}\) sends \((m_0,m_1)\in \mathcal {M}^2\) to the challenger. We require that \(\left| m_0\right| =\left| m_1\right| \). The challenger computes \(\mathsf {CT}\leftarrow \mathsf {Enc}(\mathsf {ek},m_b)\) and returns \(\mathsf {CT}\) to \(\mathcal {A}\).
-
3.
\(\mathcal {A}\) outputs \(b' \in \{0,1\}\).
In this game, we define the advantage of the adversary \(\mathcal {A}\) as \( \mathsf {Adv}_{\mathsf {PKE}, \mathcal {A}}^{\mathsf {indcpa}}(\lambda ) = \left| \Pr [b=b']-\frac{1}{2}\right| \). We say that \(\mathsf {PKE}\) is \(\text {IND-CPA}\) secure if for any PPT adversary \(\mathcal {A}\), we have \(\mathsf {Adv}_{\mathsf {PKE}, \mathcal {A}}^{\mathsf {indcpa}}(\lambda ) = \mathsf{negl}(\lambda )\).
Next, we define key dependent message (KDM) security for PKE [11].
Definition 3
(KDM-CPA security). Let \(\mathsf {PKE}\) be a PKE scheme, \(\mathcal {F}\) function family, and \(\ell \) the number of users. We define the \({\mathcal {F}}\text {-KDM-CPA}\) game between a challenger and an adversary \(\mathcal {A}\) as follows. Let \(\mathcal {DK}\) and \(\mathcal {M}\) be the secret key space and message space of \(\mathsf {PKE}\), respectively.
-
1.
First, the challenger chooses a challenge bit \(b \xleftarrow {\mathsf {r}}\{0,1\}\). Next, the challenger generates \(\ell \) key pairs \(\left( {\mathsf {ek}^{(k)}},{\mathsf {dk}^{(k)}}\right) \leftarrow \mathsf {KG}(1^{\lambda })\left( k\in [\ell ]\right) \). The challenger sets \(\mathbf {dk}:=\left( {\mathsf {dk}^{(1)}}, \ldots , {\mathsf {dk}^{(\ell )}}\right) \) and sends \(\left( {\mathsf {ek}^{(1)}}, \ldots , {\mathsf {ek}^{(\ell )}}\right) \) to \(\mathcal {A}\).
-
2.
\(\mathcal {A}\) may adaptively make polynomially many KDM queries.
-
KDM queries. \(\mathcal {A}\) sends \((k, f)\in [\ell ]\times \mathcal {F}\) to the challenger. We require that f be a function such that \(f:\mathcal {DK}^\ell \rightarrow \mathcal {M}\). If \(b=1\), the challenger returns \(\mathsf {CT}\leftarrow \mathsf {Enc}\left( {\mathsf {ek}^{(k)}}, f(\mathbf {dk})\right) \) to \(\mathcal {A}\). Otherwise, the challenger returns \(\mathsf {CT}\leftarrow \mathsf {Enc}\left( {\mathsf {ek}^{(k)}}, 0^{|f(\cdot )|}\right) \) to \(\mathcal {A}\).
-
-
3.
\(\mathcal {A}\) outputs \(b' \in \{0,1\}\).
We say that \(\mathsf {PKE}\) is \({\mathcal {F}}\text {-KDM-CPA}\) secure if for any PPT adversary \(\mathcal {A}\) and polynomial \(\ell =\ell (\lambda )\), we have \(\mathsf {Adv}_{\mathsf {PKE}, \mathcal {F}, \mathcal {A}, \ell }^{\mathsf {kdmcpa}}(\lambda ) = \left| \Pr [b=b']-\frac{1}{2}\right| = \mathsf{negl}(\lambda )\).
Remark 1
(Flexibility of the number of users). The above definition implicitly requires that the size of instances such as public keys, secret keys, and ciphertexts be independent of the number of users \(\ell \). We require the same condition for KDM secure SKE. This requirement is necessary for our constructions of KDM secure IBE (and PKE) based on KDM secure SKE.
When we reduce the KDM security of our IBE to that of the underlying SKE, the number of users \(\ell \) in the security game of SKE corresponds to the number of challenge identities queried by an adversary for IBE. If the size of instances of SKE depends on \(\ell \), we can prove the KDM security of the resulting IBE only when the number of challenge identities is a-priori bounded.
Function families. As we can see, KDM security is defined with respect to function families. In this paper, we focus on KDM security with respect to the following function families.
-
Projection functions. A projection function is a function in which each output bit depends on at most a single bit of an input. Let f be a function and \(y = y_1 \ldots y_m\) be the output of the function f on an input \(x = x_1 \ldots x_n\), that is \(f(x) = y\). We say that f is a projection function if for any \(j\in [m]\), there exists \(i\in [n]\) such that \(y_j \in \left\{ 0,1,x_i,1-x_i\right\} \).
In this paper, we let \(\mathcal {P}\) denote the family of projection functions, and we say that PKE is \({\mathcal {P}}\text {-KDM-CPA}\) secure if it is \(\text {KDM-CPA}\) secure with respect to projection functions.
-
Functions computable by a-priori bounded size circuits. In the security game of \(\text {KDM-CPA}\) security with respect to this function family, an adversary can query a function computable by a circuit of a-priori bounded size and input and output length. We allow the size of instances of a scheme to depend on these a-priori bounds on functions while we do not allow it to depend on the number of total users as we noted in Remark 1.
In this paper, we say that PKE is \({\mathcal {B}}\text {-KDM-CPA}\) secure if it is \(\text {KDM-CPA}\) secure with respect to functions computable by a-priori bounded size circuits.
\({\mathcal {P}}\text {-KDM-CPA}\) security is a generalization of circular security [15] and strong enough for many applications. Boneh et al. [13] and Applebaum et al. [5] showed how to construct \({\mathcal {P}}\text {-KDM-CPA}\) secure PKE under the decisional diffie-hellman (DDH) assumption and learning with errors (LWE) assumption, respectively.Footnote 7
Barak et al. [6] showed how to construct \({\mathcal {B}}\text {-KDM-CPA}\) secure PKE under the DDH assumption or LWE assumption. Applebaum [4] showed how to transform \({\mathcal {P}}\text {-KDM-CPA}\) secure PKE into \({\mathcal {B}}\text {-KDM-CPA}\) secure one using garbled circuits.
We next introduce the definition of receiver selective opening (RSO) security for PKE. We adopt the simulation-based definition proposed by Hazay et al. [24].
Definition 4
(SIM-RSO security). Let \(\mathsf {PKE}\) be a PKE scheme, and \(\ell \) the number of users. Let \(\mathcal {A}\) and \(\mathcal {S}\) be a PPT adversary and simulator, respectively. We define the following pair of games.
-
Real game
-
1.
First, the challenger generates \(\ell \) key pairs \(\left( {\mathsf {ek}^{(k)}},{\mathsf {dk}^{(k)}}\right) \leftarrow \mathsf {KG}(1^{\lambda })\left( k\in [\ell ]\right) \) and sends \(\left( {\mathsf {ek}^{(1)}}, \ldots , {\mathsf {ek}^{(\ell )}}\right) \) to \(\mathcal {A}\).
-
2.
\(\mathcal {A}\) sends a message distribution \(\mathsf {Dist}\) to the challenger. The challenger generates \(\left\{ {m^{(k)}}\right\} _{k\in [\ell ]}\leftarrow \mathsf {Dist}\), computes \({\mathsf {CT}^{(k)}} \leftarrow \mathsf {Enc}\left( {\mathsf {ek}^{(k)}},{m^{(k)}}\right) \) for every \(k\in [\ell ]\), and sends \(\left\{ {\mathsf {CT}^{(k)}}\right\} _{k\in [\ell ]}\) to \(\mathcal {A}\).
-
3.
\(\mathcal {A}\) sends a subset \(\mathcal {I}\) of \([\ell ]\) to the challenger. The challenger sends\(\left\{ \left( {\mathsf {dk}^{(k)}},{m^{(k)}}\right) \right\} _{k\in \mathcal {I}}\) to \(\mathcal {A}\).
-
4.
\(\mathcal {A}\) sends a string \(\mathsf {out}\) to the challenger.
-
5.
The challenger outputs \(\mathsf {out}_{\mathsf {real}}:=\left( \left\{ {m^{(k)}}\right\} _{k\in [\ell ]}, \mathsf {Dist}, \mathcal {I}, \mathsf {out}\right) \).
-
1.
-
Simulated game
-
1.
First, the challenger sends \(1^\lambda \) to \(\mathcal {S}\).
-
2.
\(\mathcal {S}\) sends a message distribution \(\mathsf {Dist}\) to the challenger. The challenger generates \(\left\{ {m^{(k)}}\right\} _{k\in [\ell ]}\leftarrow \mathsf {Dist}\).
-
3.
\(\mathcal {S}\) sends a subset \(\mathcal {I}\) of \([\ell ]\) to the challenger. The challenger sends \(\left\{ {m^{(k)}}\right\} _{k\in \mathcal {I}}\) to \(\mathcal {S}\).
-
4.
\(\mathcal {S}\) sends a string \(\mathsf {out}\) to the challenger.
-
5.
The challenger outputs \(\mathsf {out}_{\mathsf {sim}}:=\left( \left\{ {m^{(k)}}\right\} _{k\in [\ell ]}, \mathsf {Dist}, \mathcal {I}, \mathsf {out}\right) \).
-
1.
We say that \(\mathsf {PKE}\) is \(\text {SIM-RSO}\) secure if for any PPT adversary \(\mathcal {A}\) and polynomial \(\ell =\ell (\lambda )\), there exists a PPT simulator \(\mathcal {S}\) such that for any PPT distinguisher \(\mathcal {D}\) with binary output we have \(\mathsf {Adv}_{\mathsf {PKE}, \mathcal {A}, \ell , \mathcal {S}, \mathcal {D}}^{\mathsf {simrso}}(\lambda ) = |\Pr [\mathcal {D}(\mathsf {out}_{\mathsf {real}})=1]-\Pr [\mathcal {D}(\mathsf {out}_{\mathsf {sim}})=1]|=\mathsf{negl}(\lambda )\).
The above definition considers non-adaptive corruptions by an adversary. Namely, an adversary needs to corrupt users in one go.
We note that our construction of RSO secure PKE based on \(\text {IND-CPA}\) secure PKE works well even if we consider adaptive corruptions by an adversary. For simplicity, we define RSO security for PKE against non-adaptive corruptions in this paper.
Secret key vs key generation randomness. We define \(\text {SIM-RSO}\) security taking only the revelation of secret keys into account throughout the paper. Namely, we assume that an adversary gets only a secret key itself of a corrupted user and not the random coin used to generate the secret key.
Hazay et al. [24] considered the revelation of both secret keys and random coins for key generation when they defined RSO security for PKE. It is better to take the revelation of random coins of key generation into account for some applications.
We show that by requiring only security against the revelation of secret keys, we can obtain RSO secure PKE from \(\text {IND-CPA}\) secure PKE. If we consider RSO security against the revelation of random coins for key generation, it seems difficult to construct RSO secure PKE based only on \(\text {IND-CPA}\) secure PKE without assuming that secure erasure is possible or the underlying scheme is key simulatable [19, 24] in some sense.
2.3 Secret Key Encryption
A secret-key encryption (SKE) scheme \(\mathsf {SKE}\) is a three tuple \((\mathsf {KG}, \mathsf {Enc}, \mathsf {Dec})\) of PPT algorithms. Below, let \(\mathcal {M}\) be the message space of \(\mathsf {SKE}\). The key generation algorithm \(\mathsf {KG}\), given a security parameter \(1^\lambda \), outputs a secret key \(\mathsf {K}\). The encryption algorithm \(\mathsf {Enc}\), given a secret key \(\mathsf {K}\) and a message \(m \in \mathcal {M}\), outputs a ciphertext \(\mathsf {CT}\). The decryption algorithm \(\mathsf {Dec}\), given a secret key \(\mathsf {K}\) and a ciphertext \(\mathsf {CT}\), outputs a message \(\tilde{m} \in \{ \bot \} \cup \mathcal {M}\). As correctness, We require \(\mathsf {Dec}(\mathsf {K}, \mathsf {Enc}(\mathsf {K}, m)) = m\) for every \(m \in \mathcal {M}\) and \(\mathsf {K}\leftarrow \mathsf {KG}(1^\lambda )\).
Next, we define \(\text {KDM-CPA}\) security for SKE.
Definition 5
(KDM-CPA security for SKE). Let \(\mathsf {SKE}\) be an SKE scheme whose key space and message space are \(\mathcal {K}\) and \(\mathcal {M}\), respectively. Let \(\mathcal {F}\) be a function family, and \(\ell \) the number of users. We define the \({\mathcal {F}}\text {-KDM-CPA}\) game between a challenger and an adversary \(\mathcal {A}\) as follows.
-
1.
First, the challenger chooses a challenge bit \(b \xleftarrow {\mathsf {r}}\{0,1\}\). Next, the challenger generates \(\ell \) secret keys \({\mathsf {K}^{(k)}} \leftarrow \mathsf {KG}(1^{\lambda })(k\in [\ell ])\), sets \(\mathbf {K}:=\left( {\mathsf {K}^{(1)}}, \ldots , {\mathsf {K}^{(\ell )}}\right) \), and sends \(1^\lambda \) to \(\mathcal {A}\).
-
2.
\(\mathcal {A}\) may adaptively make polynomially many KDM queries.
-
KDM queries. \(\mathcal {A}\) sends \((k, f)\in [\ell ]\times \mathcal {F}\) to the challenger. We require that f be a function such that \(f:\mathcal {K}^\ell \rightarrow \mathcal {M}\). If \(b=1\), the challenger returns \(\mathsf {CT}\leftarrow \mathsf {Enc}\left( {\mathsf {K}^{(k)}}, f(\mathbf {K})\right) \). Otherwise, the challenger returns \(\mathsf {CT}\leftarrow \mathsf {Enc}\left( {\mathsf {K}^{(k)}}, 0^{|f(\cdot )|}\right) \).
-
-
3.
\(\mathcal {A}\) outputs \(b' \in \{0,1\}\).
We say that \(\mathsf {SKE}\) is \({\mathcal {F}}\text {-KDM-CPA}\) secure if for any PPT adversary \(\mathcal {A}\) and polynomial \(\ell =\ell (\lambda )\), we have \(\mathsf {Adv}_{\mathsf {SKE}, \mathcal {F},\mathcal {A},\ell }^{\mathsf {kdmcpa}}(\lambda )= \left| \Pr [b=b']-\frac{1}{2}\right| = \mathsf{negl}(\lambda )\).
As we noted at Remark 1 after the definition of KDM security for PKE, we require that the size of instances of a \(\text {KDM-CPA}\) secure SKE scheme be independent of the number of users \(\ell \). This requirement is necessary for our construction of KDM secure IBE (and PKE) based on KDM secure SKE.
Similarly to KDM security for PKE, we focus on KDM security for SKE with respect to projection functions and that with respect to functions computable by a-priori bounded size circuits. We say that SKE is \({\mathcal {P}}\text {-KDM-CPA}\) secure if it is \(\text {KDM-CPA}\) secure with respect to projection functions. We say that SKE is \({\mathcal {B}}\text {-KDM-CPA}\) secure if it is \(\text {KDM-CPA}\) secure with respect to functions computable by a-priori bounded size circuits.
3 Identity-Based Encryption
We define identity-based encryption (IBE). Then, we introduce KDM security and RSO security for IBE.
An IBE scheme \(\mathsf {IBE}\) is a four tuple \((\mathsf {Setup}, \mathsf {KG}, \mathsf {Enc}, \mathsf {Dec})\) of PPT algorithms. Below, let \(\mathcal {M}\) be the message space of \(\mathsf {IBE}\). The setup algorithm \(\mathsf {Setup}\), given a security parameter \(1^\lambda \), outputs a public parameter \(\mathsf {PP}\) and a master secret key \(\mathsf {MSK}\). The key generation algorithm \(\mathsf {KG}\), given a master secret key \(\mathsf {MSK}\) and identity \(\mathsf {id}\in \mathcal {ID}\), outputs a user secret key \(\mathsf {sk}_\mathsf {id}\). The encryption algorithm \(\mathsf {Enc}\), given a public parameter \(\mathsf {PP}\), identity \(\mathsf {id}\in \mathcal {ID}\), and message \(m \in \mathcal {M}\), outputs a ciphertext \(\mathsf {CT}\). The decryption algorithm \(\mathsf {Dec}\), given a user secret key \(\mathsf {sk}_\mathsf {id}\) and ciphertext \(\mathsf {CT}\), outputs a message \(\tilde{m} \in \{ \bot \} \cup \mathcal {M}\). As correctness, we require \(\mathsf {Dec}(\mathsf {KG}(\mathsf {MSK}, \mathsf {id}), \mathsf {Enc}(\mathsf {PP}, \mathsf {id}, m)) = m\) for every \(m \in \mathcal {M}\), \(\mathsf {id}\in \mathcal {ID}\), and \((\mathsf {PP},\mathsf {MSK}) \leftarrow \mathsf {Setup}(1^\lambda )\).
We define indistinguishability against adaptive-ID attacks (\(\text {IND-ID-CPA}\) security [12]) for IBE.
Definition 6
(IND-ID-CPA security for IBE). Let \(\mathsf {IBE}\) be an IBE scheme whose identity space and message space are \(\mathcal {ID}\) and \(\mathcal {M}\), respectively. We define the \(\text {IND-ID-CPA}\) game between a challenger and an adversary \(\mathcal {A}\) as follows.
-
1.
First, the challenger chooses a challenge bit \(b \xleftarrow {\mathsf {r}}\{0,1\}\). Next, the challenger generates \((\mathsf {PP},\mathsf {MSK}) \leftarrow \mathsf {Setup}(1^{\lambda })\) and sends \(\mathsf {PP}\) to \(\mathcal {A}\). Finally, the challenger prepares a list \(L_\mathsf {ext}\) which is initially empty.
At any step of the game, \(\mathcal {A}\) can make key extraction queries.
-
Extraction queries. \(\mathcal {A}\) sends \(\mathsf {id}\in \mathcal {ID}\) to the challenger. The challenger returns \(\mathsf {sk}_\mathsf {id}\leftarrow \mathsf {KG}(\mathsf {MSK}, \mathsf {id})\) to \(\mathcal {A}\) and adds \(\mathsf {id}\) to \(L_\mathsf {ext}\).
-
-
2.
\(\mathcal {A}\) sends \(({\mathsf {id}^*},m_0,m_1)\in \mathcal {ID}\times \mathcal {M}\times \mathcal {M}\) to the challenger. We require that \(\left| m_0\right| =\left| m_1\right| \) and \({\mathsf {id}^*}\notin L_\mathsf {ext}\). The challenger computes \(\mathsf {CT}\leftarrow \mathsf {Enc}(\mathsf {PP},\mathsf {id},m_b)\) and returns \(\mathsf {CT}\) to \(\mathcal {A}\).
Below, \(\mathcal {A}\) is not allowed to make an extraction query for \({\mathsf {id}^*}\).
-
3.
\(\mathcal {A}\) outputs \(b' \in \{0,1\}\).
We say that \(\mathsf {IBE}\) is \(\text {IND-ID-CPA}\) secure if for any PPT adversary \(\mathcal {A}\), we have \(\mathsf {Adv}_{\mathsf {IBE}, \mathcal {A}}^{\mathsf {indidcpa}}(\lambda ) = \left| \Pr [b=b']-\frac{1}{2}\right| = \mathsf{negl}(\lambda )\).
3.1 KDM Security for IBE
Next, we define KDM security for IBE. Alperin-Sheriff and Peikert [3] defined KDM security for IBE by extending selective security for IBE [16]. The following definition is an extension of adaptive security for IBE [12]. For the difference between the definition of Alperin-Sheriff and Peikert and ours, see Remark 2 after Definition 7.
Definition 7
(KDM-CPA security for IBE). Let \(\mathsf {IBE}\) be an IBE scheme, and \(\mathcal {F}\) a function family. We define the \({\mathcal {F}}\text {-KDM-CPA}\) game between a challenger and an adversary \(\mathcal {A}\) as follows. Let \(\mathcal {SK}\), \(\mathcal {ID}\), and \(\mathcal {M}\) be the user secret key space, identity space, and message space of \(\mathsf {IBE}\), respectively.
-
1.
First, the challenger chooses a challenge bit \(b \xleftarrow {\mathsf {r}}\{0,1\}\). Next, the challenger generates \((\mathsf {PP},\mathsf {MSK}) \leftarrow \mathsf {Setup}(1^{\lambda })\) and sends \(\mathsf {PP}\) to \(\mathcal {A}\). Finally, the challenger prepares lists \(L_\mathsf {ext}, L_\mathsf {ch}\), and \(\mathbf {sk}\) all of which are initially empty.
-
2.
\(\mathcal {A}\) may adaptively make the following three types of queries.
-
Extraction queries. \(\mathcal {A}\) sends \(\mathsf {id}\in \mathcal {ID}\setminus (L_\mathsf {ext}\cup L_\mathsf {ch})\) to the challenger. The challenger returns \(\mathsf {sk}_\mathsf {id}\leftarrow \mathsf {KG}(\mathsf {MSK}, \mathsf {id})\) to \(\mathcal {A}\) and adds \(\mathsf {id}\) to \(L_\mathsf {ext}\).
-
Registration queries. \(\mathcal {A}\) sends \(\mathsf {id}\in \mathcal {ID}\setminus (L_\mathsf {ext}\cup L_\mathsf {ch})\) to the challenger. The challenger generates \(\mathsf {sk}_\mathsf {id}\leftarrow \mathsf {KG}(\mathsf {MSK},\mathsf {id})\) and adds \(\mathsf {id}\) and \(\mathsf {sk}_\mathsf {id}\) to \(L_\mathsf {ch}\) and \(\mathbf {sk}\), respectively.
-
KDM queries. \(\mathcal {A}\) sends \((\mathsf {id}, f)\in L_\mathsf {ch}\times \mathcal {F}\) to the challenger. We require that f be a function such that \(f:\mathcal {SK}^{\left| L_\mathsf {ch}\right| }\rightarrow \mathcal {M}\). If \(b=1\), the challenger returns \(\mathsf {CT}\leftarrow \mathsf {Enc}\left( \mathsf {PP}, \mathsf {id}, f(\mathbf {sk})\right) \) to \(\mathcal {A}\). Otherwise, the challenger returns \(\mathsf {CT}\leftarrow \mathsf {Enc}\left( \mathsf {PP}, \mathsf {id}, 0^{|f(\cdot )|}\right) \) to \(\mathcal {A}\).
-
-
3.
\(\mathcal {A}\) outputs \(b' \in \{0,1\}\).
We say that \(\mathsf {IBE}\) is \({\mathcal {F}}\text {-KDM-CPA}\) secure if for any PPT adversary \(\mathcal {A}\), we have \(\mathsf {Adv}_{\mathsf {IBE}, \mathcal {F}, \mathcal {A}}^{\mathsf {kdmcpa}}(\lambda ) = \left| \Pr [b=b']-\frac{1}{2}\right| = \mathsf{negl}(\lambda )\).
Similarly to KDM security for PKE, we focus on KDM security for IBE with respect to projection functions and that with respect to functions computable by a-priori bounded size circuits. We say that IBE is \({\mathcal {P}}\text {-KDM-CPA}\) secure if it is \(\text {KDM-CPA}\) secure with respect to projection functions. We say that IBE is \({\mathcal {B}}\text {-KDM-CPA}\) secure if it is \(\text {KDM-CPA}\) secure with respect to functions computable by a-priori bounded size circuits.
Remark 2
(Difference with [3]). Alperin-Sheriff and Peikert [3] defined KDM security for IBE. Their definition is a natural extension of selective security for IBE [16]. In their definition, an adversary must declare the set of challenge identities \(L_\mathsf {ch}\) at the beginning of the security game. On the other hand, our definition of KDM security for IBE is an extension of adaptive security for IBE [12]. In our definition, an adversary can adaptively declare challenge identities through registration queries.Footnote 8
One additional difference between our definition and that of Alperin-Sheriff and Peikert is whether the size of instances of IBE such as a public parameter is allowed to depend on the number of challenge identities or not. In the definition of Alperin-Sheriff and Peikert, the setup algorithm of IBE takes the upper bound on the number of challenge identities as an input, and the size of instances of IBE depends on the number of challenge identities. In our definition, there is no a-priori bound on the number of challenge identities, and thus the size of instances of IBE is required to be independent of the number of challenge identities.
3.2 RSO Security for IBE
We next define RSO security for IBE. We extends the simulation-based definition for PKE proposed by Hazay et al. [24].
Definition 8
(SIM-RSO security for IBE). Let \(\mathsf {IBE}\) be an IBE scheme whose identity space and message space are \(\mathcal {ID}\) and \(\mathcal {M}\), respectively. Let \(\mathcal {A}\) and \(\mathcal {S}\) be a PPT adversary and simulator, respectively. We define the following pair of games.
-
Real game
-
1.
The challenger generates public parameter and master secret key\((\mathsf {PP},\mathsf {MSK}) \leftarrow \mathsf {Setup}(1^\lambda )\) and sends \(\mathsf {PP}\) to \(\mathcal {A}\). The challenger then prepares a list \(L_\mathsf {ext}\) which is initially empty.
At any step of the game, \(\mathcal {A}\) can make key extraction queries.
-
Extraction queries. \(\mathcal {A}\) sends \(\mathsf {id}\in \mathcal {ID}\setminus L_\mathsf {ext}\) to the challenger. The challenger returns \(\mathsf {sk}_\mathsf {id}\leftarrow \mathsf {KG}(\mathsf {MSK}, \mathsf {id})\) to \(\mathcal {A}\) and adds \(\mathsf {id}\) to \(L_\mathsf {ext}\).
-
-
2.
\(\mathcal {A}\) sends q identities \(\left\{ {\mathsf {id}^{(k)}}\in \mathcal {ID}\setminus L_\mathsf {ext}\right\} _{k\in [q]}\) and a message distribution \(\mathsf {Dist}\) on \(\mathcal {M}^q\) to the challenger, where q is an a-priori unbounded polynomial of \(\lambda \). The challenger generates \(\left\{ {m^{(k)}}\right\} _{k\in [q]}\leftarrow \mathsf {Dist}\), computes \({\mathsf {CT}^{(k)}} \leftarrow \mathsf {Enc}\left( \mathsf {PP},{\mathsf {id}^{(k)}},{m^{(k)}}\right) \) for every \(k\in [q]\), and sends \(\left\{ {\mathsf {CT}^{(k)}}\right\} _{k\in [q]}\) to \(\mathcal {A}\).
Below, \(\mathcal {A}\) is not allowed to make extraction queries for \(\left\{ {\mathsf {id}^{(k)}}\right\} _{k\in [q]}\).
-
3.
\(\mathcal {A}\) sends a subset \(\mathcal {I}\) of [q] to the challenger. The challenger computes \(\mathsf {sk}_{{\mathsf {id}^{(k)}}} \leftarrow \mathsf {KG}\left( \mathsf {MSK},{\mathsf {id}^{(k)}}\right) \) for every \(k\in \mathcal {I}\) and sends \(\left\{ \left( \mathsf {sk}_{{\mathsf {id}^{(k)}}},{m^{(k)}}\right) \right\} _{k\in \mathcal {I}}\) to \(\mathcal {A}\).
-
4.
\(\mathcal {A}\) sends a string \(\mathsf {out}\) to the challenger.
-
5.
The challenger outputs \(\mathsf {out}_{\mathsf {real}}=\left( \left\{ {\mathsf {id}^{(k)}}\right\} _{k\in [q]},\left\{ {m^{(k)}}\right\} _{k\in [q]}, \mathsf {Dist}, \mathcal {I}, \mathsf {out}\right) \).
-
1.
-
Simulated game
-
1.
First, the challenger sends \(1^\lambda \) to \(\mathcal {S}\).
-
2.
\(\mathcal {S}\) sends q identities \(\left\{ {\mathsf {id}^{(k)}}\in \mathcal {ID}\right\} _{k\in [q]}\) and a message distribution \(\mathsf {Dist}\) on \(\mathcal {M}^q\) to the challenger, where q is an a-priori unbounded polynomial of \(\lambda \). The challenger generates \(\left\{ {m^{(k)}}\right\} _{k\in [q]}\leftarrow \mathsf {Dist}\).
-
3.
\(\mathcal {S}\) sends a subset \(\mathcal {I}\) of [q] to the challenger. The challenger sends \(\left\{ {m^{(k)}}\right\} _{k\in \mathcal {I}}\) to \(\mathcal {S}\).
-
4.
\(\mathcal {S}\) sends a string \(\mathsf {out}\) to the challenger.
-
5.
The challenger outputs \(\mathsf {out}_{\mathsf {sim}}:=\left( \left\{ {\mathsf {id}^{(k)}}\right\} _{k\in [q]},\left\{ {m^{(k)}}\right\} _{k\in [q]}, \mathsf {Dist}, \mathcal {I}, \mathsf {out}\right) \).
-
1.
Then, we say that \(\mathsf {IBE}\) is \(\text {SIM-RSO}\) secure if for any PPT adversary \(\mathcal {A}\), there exists a PPT simulator \(\mathcal {S}\) such that for any PPT distinguisher \(\mathcal {D}\) with binary output we have \(\mathsf {Adv}_{\mathsf {IBE}, \mathcal {A}, \mathcal {S}, \mathcal {D}}^{\mathsf {simrso}}(\lambda ) = \left| \Pr [\mathcal {D}(\mathsf {out}_{\mathsf {real}})=1]-\Pr [\mathcal {D}(\mathsf {out}_{\mathsf {sim}})=1]\right| =\mathsf{negl}(\lambda )\).
As we noted after defining \(\text {SIM-RSO}\) security for PKE, for simplicity, we consider non-adaptive corruptions by an adversary in this paper. We note that our construction of RSO secure IBE based on \(\text {IND-ID-CPA}\) secure IBE works well if we consider adaptive corruptions by an adversary.
Remark 3
(On the syntax of simulators). In the above definition, not only an adversary but also a simulator is required to output challenge identities with a message distribution, and these identities are given to a distinguisher of games. One might think this is somewhat strange since these identities output by a simulator are never used in the simulated game. This syntax of simulators is similar to that used by Bellare et al. [9] when they defined simulation-based sender selective opening security for IBE.
It does not seem to be a big issue whether we require a simulator to output identities or not. This intuition comes from the fact that we allow an adversary and simulator to output arbitrary length strings, and thus they can always include challenge identities into the output strings.
However, this subtle issue might divide notions of selective opening security for IBE. Especially, it looks hard to prove that the definition with simulators without outputting identities implies that with simulators outputting identities, while it is easy to prove the opposite implication. This means that the former definition is possibly weaker than the latter.
From these facts, similarly to Bellare et al. [9], we adopt the definition with simulators explicitly outputting identities in this work.
4 KDM Secure IBE from KDM Secure SKE and \(\text {IND-ID-CPA}\) Secure IBE
We show how to construct KDM secure IBE based on KDM secure SKE and \(\text {IND-ID-CPA}\) secure IBE. The construction also uses a circuit garbling scheme.
Let \(\mathsf {SKE}=(\mathsf {G}, \mathsf {E}, \mathsf {D})\) be an SKE scheme whose message space is \(\mathcal {M}\). Let \({\mathsf {len}_{\mathsf {K}}}\) and \({\mathsf {len}_{\mathsf {r}}}\) denote the length of a secret key and encryption randomness of \(\mathsf {SKE}\), respectively. Let \(\mathsf {IBE}=(\mathsf {Setup},\mathsf {KG},\mathsf {Enc},\mathsf {Dec})\) be an IBE scheme whose identity space is \(\mathcal {ID}\times \{0,1\}^{{\mathsf {len}_{\mathsf {K}}}}\times \{0,1\}\). Let \(\mathsf{GC}=(\mathsf {Garble}, \mathsf {Eval})\) be a garbling scheme. Using \(\mathsf {SKE}, \mathsf {IBE}\), and \(\mathsf{GC}\), we construct the following IBE scheme \(\mathsf {KdmIBE}=(\mathsf {Kdm}.\mathsf {Setup},\mathsf {Kdm}.\mathsf {KG}, \mathsf {Kdm}.\mathsf {Enc},\mathsf {Kdm}.\mathsf {Dec})\) whose message space and identity space are \(\mathcal {M}\) and \(\mathcal {ID}\), respectively.
-
\(\mathsf {Kdm}.\mathsf {Setup}(1^\lambda ){:}\)
-
Return \((\mathsf {PP},\mathsf {MSK}) \leftarrow \mathsf {Setup}(1^\lambda )\).
-
-
\(\mathsf {Kdm}.\mathsf {KG}(\mathsf {MSK},\mathsf {id}){:}\)
-
Generate \(\mathsf {K}_\mathsf {id}\leftarrow \mathsf {G}(1^\lambda )\).
-
Generate \(\mathsf {sk}_{\mathsf {id},j,\mathsf {K}_\mathsf {id}[j]} \leftarrow \mathsf {KG}(\mathsf {MSK}, (\mathsf {id},j,\mathsf {K}_\mathsf {id}[j]))\) for every \(j \in [{\mathsf {len}_{\mathsf {K}}}]\).
-
Return \(\mathsf {Kdm}.\mathsf {sk}_\mathsf {id}:= \left( \mathsf {K}_\mathsf {id}, \left\{ \mathsf {sk}_{\mathsf {id},j,\mathsf {K}_\mathsf {id}[j]}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\right) \).
-
-
\(\mathsf {Kdm}.\mathsf {Enc}(\mathsf {PP}, \mathsf {id}, m){:}\)
-
Generate \(r_\mathsf {E}\xleftarrow {\mathsf {r}}\{0,1\}^{\mathsf {len}_{\mathsf {r}}}\) and compute \(\left( \widetilde{\mathsf {E}}, \{\mathsf {lab}_{j,\alpha }\}_{j \in [{\mathsf {len}_{\mathsf {K}}}],\alpha \in \{0,1\}}\right) \leftarrow \mathsf {Garble}(1^\lambda , \mathsf {E}(\cdot ,m;r_\mathsf {E}))\), where \(\mathsf {E}(\cdot ,m;r_\mathsf {E})\) is the encryption circuit \(\mathsf {E}\) of \(\mathsf {SKE}\) into which m and \(r_\mathsf {E}\) are hardwired.
-
Compute \(\mathsf {CT}_{j,\alpha } \leftarrow \mathsf {Enc}(\mathsf {PP}, (\mathsf {id},j,\alpha ), \mathsf {lab}_{j,\alpha })\) for every \(j \in [{\mathsf {len}_{\mathsf {K}}}]\) and \(\alpha \in \{0,1\}\).
-
Return \(\mathsf {Kdm}.\mathsf {CT}:= \left( \widetilde{\mathsf {E}}, \{\mathsf {CT}_{j,\alpha }\}_{j \in [{\mathsf {len}_{\mathsf {K}}}], \alpha \in \{0,1\}}\right) \).
-
-
\(\mathsf {Kdm}.\mathsf {Dec}(\mathsf {Kdm}.\mathsf {sk}_\mathsf {id}, \mathsf {Kdm}.\mathsf {CT}){:}\)
-
Parse \(\left( \mathsf {K}_\mathsf {id}, \left\{ \mathsf {sk}_{\mathsf {id},j}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\right) \leftarrow \mathsf {Kdm}.\mathsf {sk}_\mathsf {id}\).
-
Parse \(\left( \widetilde{\mathsf {E}}, \{\mathsf {CT}_{j,\alpha }\}_{j \in [{\mathsf {len}_{\mathsf {K}}}], \alpha \in \{0,1\}}\right) \leftarrow \mathsf {Kdm}.\mathsf {CT}\).
-
For every \(j \in [{\mathsf {len}_{\mathsf {K}}}]\), compute \(\mathsf {lab}_j \leftarrow \mathsf {Dec}\left( \mathsf {sk}_{\mathsf {id},j},\mathsf {CT}_{j,\mathsf {K}_\mathsf {id}[j]}\right) \).
-
Compute \(\mathsf {CT}_\mathsf {ske}\leftarrow \mathsf {Eval}\left( \widetilde{\mathsf {E}}, \{\mathsf {lab}_j\}_{j \in [{\mathsf {len}_{\mathsf {K}}}]}\right) \).
-
Return \(m \leftarrow \mathsf {D}(\mathsf {K}_\mathsf {id}, \mathsf {CT}_\mathsf {ske})\).
-
Correctness. When decrypting a ciphertext of \(\mathsf {KdmIBE}\) that encrypts a message m, we first obtain a ciphertext of \(\mathsf {SKE}\) that encrypts m from the correctness of \(\mathsf {IBE}\) and \(\mathsf{GC}\). The correctness of \(\mathsf {KdmIBE}\) then follows from that of \(\mathsf {SKE}\).
We prove the following theorem.
Theorem 5
Let \(\mathsf {SKE}\) be an SKE scheme that is \({\mathcal {P}}\text {-KDM-CPA}\) secure (resp. \({\mathcal {B}}\text {-KDM-CPA}\) secure). Let \(\mathsf {IBE}\) be an \(\text {IND-ID-CPA}\) secure IBE scheme and \(\mathsf{GC}\) a secure garbling scheme. Then, \(\mathsf {KdmIBE}\) is an IBE scheme that is \({\mathcal {P}}\text {-KDM-CPA}\) secure (resp. \({\mathcal {B}}\text {-KDM-CPA}\) secure).
Proof of Theorem 5
Let \(\mathcal {A}\) be an adversary that attacks the \({\mathcal {P}}\text {-KDM-CPA}\) security of \(\mathsf {KdmIBE}\) and makes at most \(q_{\mathsf {ch}}\) registration queries and \(q_{\mathsf {kdm}}\) KDM queries. We proceed the proof via a sequence of games. For every \(t \in {\{0,\ldots ,2\}}\), let \(\mathtt{SUC}_{t}\) be the event that \(\mathcal {A}\) succeeds in guessing the challenge bit b in Game t.
-
Game 0: This is the original \({\mathcal {P}}\text {-KDM-CPA}\) game regarding \(\mathsf {KdmIBE}\). Then, we have \(\mathsf {Adv}_{\mathsf {KdmIBE},\mathcal {P},\mathcal {A}}^{\mathsf {kdmcpa}}=\left| \Pr [\mathtt{SUC}_{0}]-\frac{1}{2}\right| \). The detailed description is as follows.
-
1.
The challenger chooses a challenge bit \(b \xleftarrow {\mathsf {r}}\{0,1\}\), generates \((\mathsf {PP},\mathsf {MSK}) \leftarrow \mathsf {Setup}(1^\lambda )\), and sends \(\mathsf {PP}\) to \(\mathcal {A}\). The challenger also prepares lists \(L_\mathsf {ext}, L_\mathsf {ch}\), and \(\mathbf {sk}_{\mathsf {kdm}}\) all of which are initially empty.
-
2.
\(\mathcal {A}\) may adaptively make the following three types of queries.
-
Extraction queries. \(\mathcal {A}\) sends \(\mathsf {id}\in \mathcal {ID}\setminus (L_\mathsf {ext}\cup L_\mathsf {ch})\) to the challenger. The challenger responds as follows.
-
The challenger generates \(\mathsf {K}_\mathsf {id}\leftarrow \mathsf {G}(1^\lambda )\).
-
The challenger generates \(\mathsf {sk}_{\mathsf {id},j,\mathsf {K}_\mathsf {id}[j]} \leftarrow \mathsf {KG}(\mathsf {MSK}, (\mathsf {id},j,\mathsf {K}_\mathsf {id}[j]))\) for every \(j \in [{\mathsf {len}_{\mathsf {K}}}]\).
-
The challenger returns \(\mathsf {Kdm}.\mathsf {sk}_\mathsf {id}:= \left( \mathsf {K}_\mathsf {id}, \left\{ \mathsf {sk}_{\mathsf {id},j,\mathsf {K}_\mathsf {id}[j]}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\right) \) to \(\mathcal {A}\) and adds \(\mathsf {id}\) to \(L_\mathsf {ext}\).
-
-
Registration queries. \(\mathcal {A}\) sends \(\mathsf {id}\in \mathcal {ID}\setminus (L_\mathsf {ext}\cup L_\mathsf {ch})\) to the challenger. The challenger generates \(\mathsf {Kdm}.\mathsf {sk}_\mathsf {id}\) in the same way as the answer to an extraction query. The challenger then adds \(\mathsf {id}\) to \(L_\mathsf {ch}\) and \(\mathsf {Kdm}.\mathsf {sk}_\mathsf {id}\) to \(\mathbf {sk}_{\mathsf {kdm}}\).
-
KDM queries. \(\mathcal {A}\) sends \((\mathsf {id}, f)\in L_\mathsf {ch}\times \mathcal {P}\) to the challenger. The challenger responds as follows.
-
(a)
The challenger sets \(m_1 := f(\mathbf {sk}_{\mathsf {kdm}})\) and \(m_0:=0^{\left| m_1\right| }\).
-
(b)
The challenger computes \(\left( \widetilde{\mathsf {E}}, \{\mathsf {lab}_{j,\alpha }\}_{j \in [{\mathsf {len}_{\mathsf {K}}}],\alpha \in \{0,1\}}\right) \leftarrow \) \(\mathsf {Garble}(1^\lambda , \mathsf {E}(\cdot ,m_b;r_\mathsf {E}))\), where \(r_\mathsf {E}\xleftarrow {\mathsf {r}}\{0,1\}^{\mathsf {len}_{\mathsf {r}}}\).
-
(c)
For every \(j \in [{\mathsf {len}_{\mathsf {K}}}]\) and \(\alpha \in \{0,1\}\), the challenger computes \(\mathsf {CT}_{j,\alpha } \leftarrow \mathsf {Enc}(\mathsf {PP}, (\mathsf {id},j,\alpha ), \mathsf {lab}_{j,\alpha })\).
-
(d)
The challenger returns \(\mathsf {Kdm}.\mathsf {CT}:= \left( \widetilde{\mathsf {E}}, \{\mathsf {CT}_{j,\alpha }\}_{j \in [{\mathsf {len}_{\mathsf {K}}}], \alpha \in \{0,1\}}\right) \).
-
(a)
-
-
3.
\(\mathcal {A}\) outputs \(b' \in \{0,1\}\).
-
1.
-
Game 1: Same as Game 0 except the following. When \(\mathcal {A}\) makes a KDM query \((\mathsf {id},f)\in L_\mathsf {ch}\times \mathcal {P}\), for every \(j\in [{\mathsf {len}_{\mathsf {K}}}]\) the challenger computes \(\mathsf {CT}_{j,1-\mathsf {K}_\mathsf {id}[j]} \leftarrow \mathsf {Enc}\left( \mathsf {PP}, (\mathsf {id},j,1-\mathsf {K}_\mathsf {id}[j]), \mathsf {lab}_{j,\mathsf {K}_\mathsf {id}[j]}\right) \), where \(\mathsf {K}_\mathsf {id}\) is the secret key of \(\mathsf {SKE}\) generated when \(\mathsf {id}\) was registered to \(L_\mathsf {ch}\). Recall that in Game 0, \(\mathsf {CT}_{j,1-\mathsf {K}_\mathsf {id}[j]}\) is generated as \(\mathsf {CT}_{j,1-\mathsf {K}_\mathsf {id}[j]} \leftarrow \mathsf {Enc}\left( \mathsf {PP}, (\mathsf {id},j,1-\mathsf {K}_\mathsf {id}[j]), \mathsf {lab}_{j,1-\mathsf {K}_\mathsf {id}[j]}\right) \). Namely, we eliminate labels of garbled circuits that do not correspond to \(\mathsf {K}_\mathsf {id}\) from the view of \(\mathcal {A}\) in this game.
In order to simulate both Game 0 and 1, we do not need user secret keys of \(\mathsf {IBE}\) that do not correspond to \(\left\{ \mathsf {K}_\mathsf {id}\right\} _{\mathsf {id}\in L_\mathsf {ch}}\), that is \(\left\{ \mathsf {sk}_{\mathsf {id},j,1-\mathsf {K}_\mathsf {id}[j]}\right\} _{\mathsf {id}\in L_\mathsf {ch},j\in [{\mathsf {len}_{\mathsf {K}}}]}\) while we need \(\left\{ \mathsf {sk}_{\mathsf {id},j,\mathsf {K}_\mathsf {id}[j]}\right\} _{\mathsf {id}\in L_\mathsf {ch},j\in [{\mathsf {len}_{\mathsf {K}}}]}\) to compute the value of \(f(\mathbf {sk}_{\mathsf {kdm}})\) when \(\mathcal {A}\) makes a KDM query. Therefore, we can use the \(\text {IND-ID-CPA}\) security of \(\mathsf {IBE}\) when the challenge identity is \((\mathsf {id},j,1-\mathsf {K}_\mathsf {id}[j])\) for every \(\mathsf {id}\in L_\mathsf {ch}\) and \(j\in [{\mathsf {len}_{\mathsf {K}}}]\). By using \(\text {IND-ID-CPA}\) security of \(\mathsf {IBE}\) \({\mathsf {len}_{\mathsf {K}}}\cdot q_{\mathsf {kdm}}\) times, we can prove \(\left| \Pr [\mathtt{SUC}_{0}]-\Pr [\mathtt{SUC}_{1}]\right| =\mathsf{negl}(\lambda )\).
-
Game 2: Same as Game 1 except that to respond to a KDM query from \(\mathcal {A}\), the challenger generates a garbled circuit using the simulator for \(\mathsf{GC}\). More precisely, when \(\mathcal {A}\) makes a KDM query \((\mathsf {id},f)\in L_\mathsf {ch}\times \mathcal {P}\), the challenger generates \(r_\mathsf {E}\xleftarrow {\mathsf {r}}\{0,1\}^{\mathsf {len}_{\mathsf {r}}}\) and \(\mathsf {CT}_\mathsf {ske}\leftarrow \mathsf {E}\left( \mathsf {K}_\mathsf {id},m_b;r_\mathsf {E}\right) \), and computes \(\left( \widetilde{\mathsf {E}}, \{\mathsf {lab}_{j}\}_{j \in [{\mathsf {len}_{\mathsf {K}}}]}\right) \leftarrow \mathsf {Sim}(1^\lambda , \left| \mathsf {E}\right| , \mathsf {CT}_\mathsf {ske})\), where \(\mathsf {Sim}\) is the simulator for \(\mathsf{GC}\) and \(\left| \mathsf {E}\right| \) denotes the size of the encryption circuit \(\mathsf {E}\) of \(\mathsf {SKE}\). Moreover, the challenger computes \(\mathsf {CT}_{j,\alpha } \leftarrow \mathsf {Enc}\left( \mathsf {PP},(\mathsf {id},j,\alpha ), \mathsf {lab}_j\right) \) for every \(j\in [{\mathsf {len}_{\mathsf {K}}}]\) and \(\alpha \in \{0,1\}\).
In the last step, we eliminate labels of garbled circuits that do not correspond to \(\left\{ \mathsf {K}_\mathsf {id}\right\} _{\mathsf {id}\in L_\mathsf {ch}}\). Therefore, by using the security of \(\mathsf{GC}\) \(q_{\mathsf {kdm}}\) times, we can show that \(\left| \Pr [\mathtt{SUC}_{1}]-\Pr [\mathtt{SUC}_{2}]\right| =\mathsf{negl}(\lambda )\).
Below, we show that \(\left| \Pr [\mathtt{SUC}_{2}]-\frac{1}{2}\right| =\mathsf{negl}(\lambda )\) holds by the \({\mathcal {P}}\text {-KDM-CPA}\) security of \(\mathsf {SKE}\). Using the adversary \(\mathcal {A}\), we construct an adversary \(\mathcal {A}_\mathsf {ske}\) that attacks the \({\mathcal {P}}\text {-KDM-CPA}\) security of \(\mathsf {SKE}\) when the number of keys is \(q_{\mathsf {ch}}\).
Before describing \(\mathcal {A}_\mathsf {ske}\), we note on the conversion of projection functions. We let \({\mathsf {K}^{(k)}}\) be the secret key of \(\mathsf {SKE}\) generated to respond to the k-th registration query \({\mathsf {id}^{(k)}}\) made by \(\mathcal {A}\). We let \(\alpha _{k,j}\) denote the j-th bit of \({\mathsf {K}^{(k)}}\), that is, \({\mathsf {K}^{(k)}}[j]\) for every \(j\in [{\mathsf {len}_{\mathsf {K}}}]\) and \(k\in [q_{\mathsf {ch}}]\). Let f be a projection function that \(\mathcal {A}\) queries as a KDM query. f is a projection function of \(\left\{ {\mathsf {K}^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}\) and \(\left\{ \mathsf {sk}_{{\mathsf {id}^{(k)}},j,\alpha _{k,j}}\right\} _{k\in [q_{\mathsf {ch}}],j\in [{\mathsf {len}_{\mathsf {K}}}]}\). To attack the \({\mathcal {P}}\text {-KDM-CPA}\) security of \(\mathsf {SKE}\), \(\mathcal {A}_\mathsf {ske}\) needs to compute a projection function g such that
We can compute such a function g from f and \(\left\{ \mathsf {sk}_{{\mathsf {id}^{(k)}},j,\alpha }\right\} _{k\in [q_{\mathsf {ch}}],j\in [{\mathsf {len}_{\mathsf {K}}}],\alpha \in \{0,1\}}\) as follows.
We first observe that for every \(k\in [q_{\mathsf {ch}}]\) and \(j\in [{\mathsf {len}_{\mathsf {K}}}]\), we can write
We suppose that \(\mathsf {sk}_{{\mathsf {id}^{(k)}},j,1}\) and \(\mathsf {sk}_{{\mathsf {id}^{(k)}},j,0}\) are represented as binary strings and \(\oplus \) is done in the bit-wise manner. We define a function \(\mathsf {sel}_{k,j}\) as \(\mathsf {sel}_{k,j}(\gamma \in \{0,1\})=\gamma \cdot \left( \mathsf {sk}_{{\mathsf {id}^{(k)}},j,1}\oplus \mathsf {sk}_{{\mathsf {id}^{(k)}},j,0}\right) \oplus \mathsf {sk}_{{\mathsf {id}^{(k)}},j,0}\). Then, we have
We define \(g\left( \left\{ {\mathsf {K}^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}\right) =f\left( \left\{ {\mathsf {K}^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]},\left\{ \mathsf {sel}_{k,j}\left( {\mathsf {K}^{(k)}}[j]\right) \right\} _{k\in [q_{\mathsf {ch}}],j\in [{\mathsf {len}_{\mathsf {K}}}]}\right) \). Then, g satisfies Eq. 1.
We show that if f is a projection function, then so is g. Let \(\gamma \) be an output bit of \(g\left( \left\{ {\mathsf {K}^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}\right) =f\left( \left\{ {\mathsf {K}^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]},\left\{ \mathsf {sel}_{k,j}\left( {\mathsf {K}^{(k)}}[j]\right) \right\} _{k\in [q_{\mathsf {ch}}],j\in [{\mathsf {len}_{\mathsf {K}}}]}\right) \). We say that \(\gamma \) is a projective bit for f (resp. g) if it depends on a single bit of an input for f (resp. g). We also say that \(\gamma \) is a constant bit for f (resp. g) if it does not depend on any bit of an input for f (resp. g).
Since f is a projection function, \(\gamma \) is a constant bit or projective bit for f that depends on either part of \(\left\{ {\mathsf {K}^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}\) or \(\left\{ \mathsf {sel}_{k,j}\left( {\mathsf {K}^{(k)}}[j]\right) \right\} _{k\in [q_{\mathsf {ch}}],j\in [{\mathsf {len}_{\mathsf {K}}}]}\). Thus, we consider the following three cases. (i) If \(\gamma \) is a constant bit for f, \(\gamma \) is clearly a constant bit for g. (ii) If \(\gamma \) is a projective bit for f and depends on a single bit of \(\left\{ {\mathsf {K}^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}\), \(\gamma \) is a projective bit for g since \(\left\{ {\mathsf {K}^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}\) is also an input for g. (iii) If \(\gamma \) is a projective bit for f and depends on some bit of \(\left\{ \mathsf {sel}_{k,j}\left( {\mathsf {K}^{(k)}}[j]\right) \right\} _{k\in [q_{\mathsf {ch}}],j\in [{\mathsf {len}_{\mathsf {K}}}]}\), \(\gamma \) is a projective bit for g since each bit of \(\left\{ \mathsf {sel}_{k,j}\left( {\mathsf {K}^{(k)}}[j]\right) \right\} _{k\in [q_{\mathsf {ch}}],j\in [{\mathsf {len}_{\mathsf {K}}}]}\) depends on a bit \({\mathsf {K}^{(k)}}[j]\) for some \(k\in [q_{\mathsf {ch}}]\) and \(j\in [{\mathsf {len}_{\mathsf {K}}}]\), and \({\mathsf {K}^{(k)}}[j]\) is a part of an input to g. Therefore, \(\gamma \) is a projective bit or constant bit for g in any case, and thus g is a projection function.
We now describe the adversary \(\mathcal {A}_\mathsf {ske}\) that uses the above conversion of projection functions.
-
1.
On input \(1^\lambda \), \(\mathcal {A}_\mathsf {ske}\) first generates \((\mathsf {PP},\mathsf {MSK}) \leftarrow \mathsf {Setup}(1^\lambda )\) and sends \(\mathsf {PP}\) to \(\mathcal {A}\). Then, \(\mathcal {A}_\mathsf {ske}\) prepares \(L_\mathsf {ext}\) and \(L_\mathsf {ch}\).
-
2.
\(\mathcal {A}_\mathsf {ske}\) responds to queries made by \(\mathcal {A}\) as follows.
-
Extraction queries. When \(\mathcal {A}\) sends \(\mathsf {id}\in \mathcal {ID}\setminus (L_\mathsf {ext}\cup L_\mathsf {ch})\) as an extraction query, \(\mathcal {A}_\mathsf {ske}\) responds exactly in the same way as the challenger in Game 2. We note that, in this case, \(\mathcal {A}_\mathsf {ske}\) computes the answer \(\mathsf {Kdm}.\mathsf {sk}_\mathsf {id}\) using a freshly generated key \(\mathsf {K}_\mathsf {id}\) of \(\mathsf {SKE}\).
-
Registration queries. When \(\mathcal {A}\) makes the k-th (\(k\le q_{\mathsf {ch}}\)) registration query \({\mathsf {id}^{(k)}} \in \mathcal {ID}\setminus (L_\mathsf {ext}\cup L_\mathsf {ch})\), \(\mathcal {A}_\mathsf {ske}\) relates \({\mathsf {id}^{(k)}}\) to \({\mathsf {K}^{(k)}}\), where \({\mathsf {K}^{(k)}}\) is the k-th secret key of \(\mathsf {SKE}\) generated by the challenger. \(\mathcal {A}_\mathsf {ske}\) generates \(\mathsf {sk}_{{\mathsf {id}^{(k)}},j,\alpha } \leftarrow \mathsf {KG}\left( \mathsf {MSK}, \left( {\mathsf {id}^{(k)}},j,\alpha \right) \right) \) for every \(j \in [{\mathsf {len}_{\mathsf {K}}}]\) and \(\alpha \in \{0,1\}\). They are used for the conversion of functions. \(\mathcal {A}_\mathsf {ske}\) then adds \({\mathsf {id}^{(k)}}\) to \(L_\mathsf {ch}\).
-
KDM queries. When \(\mathcal {A}\) makes a KDM query \((\mathsf {id}, f) \in L_\mathsf {ch} \times \mathcal {P}\), \(\mathcal {A}_\mathsf {ske}\) responds as follows.
-
(a)
\(\mathcal {A}_\mathsf {ske}\) first computes a projection function g satisfying
$$\begin{aligned} g\left( \left\{ {\mathsf {K}^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}\right) = f\left( \left\{ {\mathsf {K}^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]},\left\{ \mathsf {sk}_{{\mathsf {id}^{(k)}},j,{\mathsf {K}^{(k)}}[j]}\right\} _{k\in [q_{\mathsf {ch}}],j\in [{\mathsf {len}_{\mathsf {K}}}]}\right) \end{aligned}$$as we noted above from \(\left\{ \mathsf {sk}_{{\mathsf {id}^{(k)}},j,\alpha }\right\} _{k\in [q_{\mathsf {ch}}],j\in [{\mathsf {len}_{\mathsf {K}}}],\alpha \in \{0,1\}}\).
-
(b)
Let \(k\in [q_{\mathsf {ch}}]\) be the number that related to \(\mathsf {id}\). Since \(\mathsf {id}\) was added to \(L_\mathsf {ch}\), such \(k\in [q_{\mathsf {ch}}]\) exists. \(\mathcal {A}_\mathsf {ske}\) queries (k, g) to the challenger as a KDM query and gets the answer \(\mathsf {CT}_\mathsf {ske}\).
-
(c)
\(\mathcal {A}_\mathsf {ske}\) computes \(\left( \widetilde{\mathsf {E}}, \left\{ \mathsf {lab}_{j}^{}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\right) \leftarrow \mathsf {Sim}\left( 1^\lambda , \left| \mathsf {E}\right| ,\mathsf {CT}_\mathsf {ske}\right) \) and for every \(j\in [{\mathsf {len}_{\mathsf {K}}}]\) and \(\alpha \in \{0,1\}\), computes \(\mathsf {CT}_{j,\alpha } \leftarrow \mathsf {Enc}\left( \mathsf {PP},(\mathsf {id},j,\alpha ), \mathsf {lab}_j\right) \).
-
(d)
\(\mathcal {A}_\mathsf {ske}\) returns \(\mathsf {Kdm}.\mathsf {CT}:= \left( \widetilde{\mathsf {E}}, \{\mathsf {CT}_{j,\alpha }\}_{j \in [{\mathsf {len}_{\mathsf {K}}}], \alpha \in \{0,1\}}\right) \) to \(\mathcal {A}\).
-
(a)
-
-
3.
When \(\mathcal {A}\) terminates with output \(b' \in \{0,1\}\), \(\mathcal {A}_\mathsf {ske}\) outputs \(\beta ' = b'\).
\(\mathcal {A}_\mathsf {ske}\) perfectly simulates Game 2 for \(\mathcal {A}\) in which the challenge bit is the same as that of \({\mathcal {P}}\text {-KDM-CPA}\) game of \(\mathsf {SKE}\) between the challenger and \(\mathcal {A}_\mathsf {ske}\). Moreover, \(\mathcal {A}_\mathsf {ske}\) just outputs \(\mathcal {A}\)’s output. Thus, \(\mathsf {Adv}_{\mathsf {SKE}, \mathcal {P},\mathcal {A}_\mathsf {ske},q_{\mathsf {ch}}}^{\mathsf {kdmcpa}}(\lambda ) = \left| \Pr [\mathtt{SUC}_{2}]-\frac{1}{2}\right| \) holds. Since \(\mathsf {SKE}\) is \({\mathcal {P}}\text {-KDM-CPA}\) secure, \(\left| \Pr [\mathtt{SUC}_{2}]-\frac{1}{2}\right| = \mathsf{negl}(\lambda )\) holds.
From the above arguments, we see that
Since the choice of \(\mathcal {A}\) is arbitrary, \(\mathsf {KdmIBE}\) satisfies \({\mathcal {P}}\text {-KDM-CPA}\) security.
On the transformation of \({\mathcal {B}}\text {-KDM-CPA}\) secure schemes. We can also construct \({\mathcal {B}}\text {-KDM-CPA}\) secure IBE based on \({\mathcal {B}}\text {-KDM-CPA}\) secure SKE via the construction. The security proof of \({\mathcal {B}}\text {-KDM-CPA}\) secure IBE is in fact almost the same as that of \({\mathcal {P}}\text {-KDM-CPA}\) secure IBE. The only issue we need to care is whether the conversion of functions performed by \(\mathcal {A}_\mathsf {ske}\) is successful or not also when we construct \({\mathcal {B}}\text {-KDM-CPA}\) secure IBE.
Let f be a function queried by an adversary \(\mathcal {A}\) for \(\mathsf {KdmIBE}\). As above, consider a function g such that
where the function \(\mathsf {sel}_{k,j}\) is the function we defined earlier. Since \(\mathsf {sel}_{k,j}\) is computable by a circuit of a-priori bounded size, we see that if f is computable by a circuit of a-priori bounded size, then so is g. Therefore, \(\mathcal {A}_\mathsf {ske}\) can successfully perform the conversion of functions also when constructing \({\mathcal {B}}\text {-KDM-CPA}\) secure IBE. 
5 \(\text {SIM-RSO}\) Secure IBE Based on \(\text {IND-ID-CPA}\) Secure IBE
We construct \(\text {SIM-RSO}\) secure IBE based on any \(\text {IND-ID-CPA}\) secure IBE.
Let \(\mathsf {IBE}=(\mathsf {Setup},\mathsf {KG},\mathsf {Enc},\mathsf {Dec})\) be an IBE scheme whose message space and identity space are \(\{0,1\}\) and \(\mathcal {ID}\times \{0,1\}\), respectively. Using \(\mathsf {IBE}\), we construct the following IBE scheme \(\mathsf {RsoIBE}=(\mathsf {Rso}.\mathsf {Setup},\mathsf {Rso}.\mathsf {KG}, \mathsf {Rso}.\mathsf {Enc},\mathsf {Rso}.\mathsf {Dec})\) whose message space and identity space are \(\{0,1\}\) and \(\mathcal {ID}\).
-
\(\mathsf {Rso}.\mathsf {Setup}(1^\lambda ){:}\)
-
Return \((\mathsf {PP},\mathsf {MSK}) \leftarrow \mathsf {Setup}(1^\lambda )\).
-
-
\(\mathsf {Rso}.\mathsf {KG}(\mathsf {MSK}, \mathsf {id}){:}\)
-
Generate \(r \xleftarrow {\mathsf {r}}\{0,1\}\).
-
Generate \(\mathsf {sk}_{\mathsf {id},r} \leftarrow \mathsf {KG}(\mathsf {MSK}, (\mathsf {id},r))\).
-
Return \(\mathsf {Rso}.\mathsf {sk}_\mathsf {id}:= (r,\mathsf {sk}_{\mathsf {id},r})\).
-
-
\(\mathsf {Rso}.\mathsf {Enc}(\mathsf {PP},\mathsf {id}, m\in \{0,1\}){:}\)
-
For every \(\alpha \in \{0,1\}\), compute \(\mathsf {CT}_{\alpha } \leftarrow \mathsf {Enc}(\mathsf {PP},(\mathsf {id},\alpha ), m)\).
-
Return \(\mathsf {Rso}.\mathsf {CT}:= (\mathsf {CT}_0,\mathsf {CT}_1)\).
-
-
\(\mathsf {Rso}.\mathsf {Dec}(\mathsf {Rso}.\mathsf {sk}_\mathsf {id}, \mathsf {Rso}.\mathsf {CT}){:}\)
-
Parse \((r,\mathsf {sk}_{\mathsf {id},r}) \leftarrow \mathsf {Rso}.\mathsf {dk}\).
-
Parse \((\mathsf {CT}_0,\mathsf {CT}_1) \leftarrow \mathsf {Rso}.\mathsf {CT}\).
-
Return \(m \leftarrow \mathsf {Dec}(\mathsf {sk}_{\mathsf {id},r},\mathsf {CT}_r)\).
-
Correctness. The correctness of \(\mathsf {RsoIBE}\) directly follows from that of \(\mathsf {IBE}\).
We prove the following theorem.
Theorem 6
Let \(\mathsf {IBE}\) be an \(\text {IND-ID-CPA}\) secure IBE scheme. Then, \(\mathsf {RsoIBE}\) is a \(\text {SIM-RSO}\) secure IBE scheme.
Proof of Theorem 6
Let \(\mathcal {A}\) be an adversary that attacks the \(\text {SIM-RSO}\) security of \(\mathsf {RsoIBE}\). We show the proof via the following sequence of games.
Let \(\mathcal {D}\) be an PPT distinguisher with binary output. For every \(t \in \{0,1,2\}\), let \(\mathtt{T}_{t}\) be the event that \(\mathcal {D}\) outputs 1 given the output of the challenger in Game t.
-
Game 0: This is the real game of \(\text {SIM-RSO}\) security regarding \(\mathsf {RsoIBE}\). The detailed description is as follows.
-
1.
First, the challenger generates \((\mathsf {PP},\mathsf {MSK}) \leftarrow \mathsf {Setup}(1^\lambda )\) and sends \(\mathsf {PP}\) to \(\mathcal {A}\). The challenger prepares a list \(L_\mathsf {ext}\). At any step of the game, \(\mathcal {A}\) can make key extraction queries.
-
Extraction queries. \(\mathcal {A}\) sends \(\mathsf {id}\in \mathcal {ID}\setminus L_\mathsf {ext}\) to the challenger. The challenger responds as follows.
-
(a)
The challenger generates \(r \xleftarrow {\mathsf {r}}\{0,1\}\).
-
(b)
The challenger generates \(\mathsf {sk}_{\mathsf {id},r} \leftarrow \mathsf {KG}(\mathsf {MSK}, (\mathsf {id},r))\).
-
(c)
The challenger returns \(\mathsf {Rso}.\mathsf {sk}_\mathsf {id}:= (r,\mathsf {sk}_{\mathsf {id},r})\).
-
(a)
-
-
2.
\(\mathcal {A}\) sends \(q_{\mathsf {ch}}\) identities \(\left\{ {\mathsf {id}^{(k)}}\in \mathcal {ID}\setminus L_\mathsf {ext}\right\} _{k\in [q_{\mathsf {ch}}]}\) and a message distribution \(\mathsf {Dist}\) on \(\{0,1\}^{q_{\mathsf {ch}}}\) to the challenger, where \(q_{\mathsf {ch}}\) is an a-priori unbounded polynomial of \(\lambda \). The challenger generates \(\left\{ {m^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}\leftarrow \mathsf {Dist}\) and computes \({\mathsf {Rso}.\mathsf {CT}^{(k)}}\) for every \(k\in [q_{\mathsf {ch}}]\) as follows.
-
(a)
The challenger computes \({\mathsf {CT}_\alpha ^{(k)}} \leftarrow \mathsf {Enc}\left( \mathsf {PP},\left( {\mathsf {id}^{(k)}},\alpha \right) , {m^{(k)}}\right) \) for every \(\alpha \in \{0,1\}\).
-
(b)
The challenger sets \({\mathsf {Rso}.\mathsf {CT}^{(k)}} := \left( {\mathsf {CT}_0^{(k)}},{\mathsf {CT}_1^{(k)}}\right) \).
The challenger sends \(\left\{ {\mathsf {Rso}.\mathsf {CT}^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}\) to \(\mathcal {A}\). Below, \(\mathcal {A}\) is not allowed to make extraction queries for \(\left\{ {\mathsf {id}^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}\).
-
(a)
-
3.
\(\mathcal {A}\) sends a subset \(\mathcal {I}\) of \([q_{\mathsf {ch}}]\) to the challenger. The challenger generates \(\mathsf {Rso}.\mathsf {sk}_{\mathsf {id}^{(k)}}\) for every \(k\in \mathcal {I}\) as follows.
-
(a)
The challenger generates \({r^{(k)}} \xleftarrow {\mathsf {r}}\{0,1\}\).
-
(b)
The challenger generates \(\mathsf {sk}_{{\mathsf {id}^{(k)}},{r^{(k)}}} \leftarrow \mathsf {KG}\left( \mathsf {MSK}, \left( {\mathsf {id}^{(k)}},{r^{(k)}}\right) \right) \).
-
(c)
The challenger sets \(\mathsf {Rso}.\mathsf {sk}_{\mathsf {id}^{(k)}} := \left( {r^{(k)}},\mathsf {sk}_{{\mathsf {id}^{(k)}},{r^{(k)}}}\right) \).
The challenger sends \(\left\{ \left( \mathsf {Rso}.\mathsf {sk}_{\mathsf {id}^{(k)}},{m^{(k)}}\right) \right\} _{k\in \mathcal {I}}\) to \(\mathcal {A}\).
-
(a)
-
4.
\(\mathcal {A}\) sends a string \(\mathsf {out}\) to the challenger.
-
5.
The challenger outputs
$$\begin{aligned} \mathsf {out}_{\mathsf {real}}:=\left( \left\{ {\mathsf {id}^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]},\left\{ {m^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}, \mathsf {Dist}, \mathcal {I}, \mathsf {out}\right) . \end{aligned}$$
-
1.
-
Game 1: Same as Game 0 except that for every \(k\in [q_{\mathsf {ch}}]\), the challenger generates
$$\begin{aligned} {\mathsf {CT}_{1-{r^{(k)}}}^{(k)}} \leftarrow \mathsf {Enc}\left( \mathsf {PP},\left( {\mathsf {id}^{(k)}},1-{r^{(k)}}\right) ,1-{m^{(k)}}\right) . \end{aligned}$$We note that the challenger generates \({\mathsf {CT}_{{r^{(k)}}}^{(k)}} \leftarrow \mathsf {Enc}\left( \mathsf {PP},({\mathsf {id}^{(k)}},{r^{(k)}}),{m^{(k)}}\right) \) for every \(k\in [q_{\mathsf {ch}}]\) in both Games 0 and 1.
Secret keys for identities \(\left\{ \left( {{\mathsf {id}^{(k)}},1-{r^{(k)}}}\right) \right\} _{k\in [q_{\mathsf {ch}}]}\) of \(\mathsf {IBE}\) are not given to \(\mathcal {A}\) regardless of which users \(\mathcal {A}\) corrupts in both Games 0 and 1. Therefore, by using the security of \(\mathsf {IBE}\) \(q_{\mathsf {ch}}\) times, we can prove \(\left| \Pr [\mathtt{T}_{0}]-\Pr [\mathtt{T}_{1}]\right| =\mathsf{negl}(\lambda )\).
-
Game 2: Same as Game 1 except that for every \(k\in [q_{\mathsf {ch}}]\), the challenger uses \({r^{(k)}}\oplus {m^{(k)}}\) instead of \({r^{(k)}}\) as the random bit contained in the k-th \(\mathsf {RsoIBE}\)’s secret key \(\mathsf {Rso}.\mathsf {sk}_{{\mathsf {id}^{(k)}}}\) for \({\mathsf {id}^{(k)}}\). We note that the challenger does not need \(\left\{ {r^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}\) before generating \(\left\{ {m^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}\). Thus, the transition from Games 1 to 2 makes sense, and \(\left| \Pr [\mathtt{T}_{2}]-\Pr [\mathtt{T}_{3}]\right| =0\) holds since \({r^{(k)}}\oplus {m^{(k)}}\) is distributed uniformly at random for every \(k\in [q_{\mathsf {ch}}]\).
In Game 2, uncorrupted messages \(\left\{ {m^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]\setminus \mathcal {I}}\) are completely hidden from the view of \(\mathcal {A}\). To verify the fact, we confirm that ciphertexts \(\left\{ {\mathsf {Rso}.\mathsf {CT}^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}\) are independent of \(\left\{ {m^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}\).
For every \(k\in [q_{\mathsf {ch}}]\), the challenger generates \({\mathsf {Rso}.\mathsf {CT}^{(k)}}=\left( {\mathsf {CT}_0^{(k)}},{\mathsf {CT}_1^{(k)}}\right) \) by computing
We see that, regardless of the value of \({m^{(k)}}\in \{0,1\}\), the challenger computes
Therefore, we see that ciphertexts \(\left\{ {\mathsf {Rso}.\mathsf {CT}^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}\) are independent of \(\left\{ {m^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}\) in Game 2.
Then, we construct a simulator \(\mathcal {S}\) that perfectly simulates Game 2 for \(\mathcal {A}\). The description of \(\mathcal {S}\) is as follows.
-
1.
On input \(1^\lambda \), \(\mathcal {S}\) generates \((\mathsf {PP},\mathsf {MSK}) \leftarrow \mathsf {Setup}(1^\lambda )\) and sends \(\mathsf {PP}\) to \(\mathcal {A}\). \(\mathcal {S}\) then prepares a list \(L_\mathsf {ext}\).
-
Extraction queries. When \(\mathcal {A}\) sends \(\mathsf {id}\in \mathcal {ID}\setminus L_\mathsf {ext}\), \(\mathcal {S}\) responds as follows.
-
(a)
\(\mathcal {S}\) generates \(r \xleftarrow {\mathsf {r}}\{0,1\}\).
-
(b)
\(\mathcal {S}\) generates \(\mathsf {sk}_{\mathsf {id},r}, \leftarrow \mathsf {KG}(\mathsf {MSK}, (\mathsf {id},r))\).
-
(c)
\(\mathcal {S}\) returns \(\mathsf {Rso}.\mathsf {sk}_\mathsf {id}:= (r,\mathsf {sk}_{\mathsf {id},r})\) to \(\mathcal {A}\) and adds \(\mathsf {id}\) to \(L_\mathsf {ext}\).
-
(a)
-
-
2.
When \(\mathcal {A}\) outputs a message distribution \(\mathsf {Dist}\) with identities \(\left\{ {\mathsf {id}^{(k)}}\right\} _{k\in [q_{\mathsf {ch}}]}\), \(\mathcal {S}\) sends them to the challenger. Then, \(\mathcal {S}\) computes \({\mathsf {Rso}.\mathsf {CT}^{(k)}}\) for every \(k\in [q_{\mathsf {ch}}]\) as follows.
- (a):
-
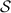 computes
computes  .
. - (b):
-
 computes
computes 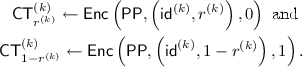
- (c):
-
 sets
sets  .
.
 sends
sends  to \(\mathcal {A}\).
to \(\mathcal {A}\). -
3.
When \(\mathcal {A}\) outputs a subset \(\mathcal {I}\) of \([q_{\mathsf {ch}}]\),
 sends it to the challenger, and gets
sends it to the challenger, and gets  .
. 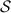 computes
computes  , sets
, sets  for every \(k\in \mathcal {I}\), and sends
for every \(k\in \mathcal {I}\), and sends  to \(\mathcal {A}\).
to \(\mathcal {A}\). -
4.
When \(\mathcal {A}\) outputs a string \(\mathsf {out}\), \(\mathcal {S}\) outputs it.
 perfectly simulates Game 2 for \(\mathcal {A}\). Therefore, we have
perfectly simulates Game 2 for \(\mathcal {A}\). Therefore, we have

From the above arguments, we see that each term of the right hand side of Inequality 2 is negligible in \(\lambda \). Since the choice of \(\mathcal {A}\) and \(\mathcal {D}\) is arbitrary and the description of \(\mathcal {S}\) does not depend on that of \(\mathcal {D}\), we see that for any \(\mathcal {A}\), there exists \(\mathcal {S}\) such that for any \(\mathcal {D}\) we have \(\mathsf {Adv}_{\mathsf {RsoIBE}, \mathcal {A}, \mathcal {S}, \mathcal {D}}^{\mathsf {simrso}}(\lambda )=\mathsf{negl}(\lambda )\). This means that \(\mathsf {RsoIBE}\) is \(\text {SIM-RSO}\) secure. 
6 KDM Secure PKE from KDM Secure SKE and \(\text {IND-CPA}\) Secure PKE
We show how to construct KDM secure PKE based on KDM secure SKE and \(\text {IND-CPA}\) secure PKE. The construction is similar to that of KDM secure IBE we show in Sect. 4 except that \(\text {IND-CPA}\) secure PKE is used instead of \(\text {IND-ID-CPA}\) secure IBE as a building block.
Let \(\mathsf {SKE}=(\mathsf {G}, \mathsf {E}, \mathsf {D})\) be an SKE scheme whose message space is \(\mathcal {M}\). Let \({\mathsf {len}_{\mathsf {K}}}\) and \({\mathsf {len}_{\mathsf {r}}}\) denote the length of a secret key and encryption randomness of \(\mathsf {SKE}\), respectively. Let \(\mathsf {PKE}=(\mathsf {KG},\mathsf {Enc},\mathsf {Dec})\) be a PKE scheme and \(\mathsf{GC}=(\mathsf {Garble}, \mathsf {Eval})\) a garbling scheme. Using \(\mathsf {SKE}, \mathsf {PKE}\), and \(\mathsf{GC}\), we construct the following PKE scheme \(\mathsf {KdmPKE}=(\mathsf {Kdm}.\mathsf {KG}, \mathsf {Kdm}.\mathsf {Enc},\mathsf {Kdm}.\mathsf {Dec})\) whose message space is \(\mathcal {M}\).
-
\(\mathsf {Kdm}.\mathsf {KG}(1^\lambda ){:}\)
-
Generate \(\mathsf {K}\leftarrow \mathsf {G}(1^\lambda )\).
-
Generate \(\left( \mathsf {ek}_{j,\alpha }, \mathsf {dk}_{j,\alpha }\right) \leftarrow \mathsf {KG}(1^\lambda )\) for every \(j \in [{\mathsf {len}_{\mathsf {K}}}]\) and \(\alpha \in \{0,1\}\).
-
Return \(\mathsf {Kdm}.\mathsf {ek}:= \left\{ \mathsf {ek}_{j,\alpha }\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}],\alpha \in \{0,1\}}\) and \(\mathsf {Kdm}.\mathsf {dk}:= \left( \mathsf {K}, \left\{ \mathsf {dk}_{j,\mathsf {K}[j]}\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\right) \).
-
-
\(\mathsf {Kdm}.\mathsf {Enc}(\mathsf {Kdm}.\mathsf {ek}, m){:}\)
-
Parse \(\left\{ \mathsf {ek}_{j,\alpha }\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}],\alpha \in \{0,1\}} \leftarrow \mathsf {Kdm}.\mathsf {ek}\).
-
Generate \(r_\mathsf {E}\xleftarrow {\mathsf {r}}\{0,1\}^{\mathsf {len}_{\mathsf {r}}}\) and compute \(\left( \widetilde{\mathsf {E}}, \{\mathsf {lab}_{j,\alpha }\}_{j \in [{\mathsf {len}_{\mathsf {K}}}],\alpha \in \{0,1\}}\right) \leftarrow \mathsf {Garble}(1^\lambda , \mathsf {E}(\cdot ,m;r_\mathsf {E}))\), where \(\mathsf {E}(\cdot ,m;r_\mathsf {E})\) is the encryption circuit \(\mathsf {E}\) of \(\mathsf {SKE}\) into which m and \(r_\mathsf {E}\) are hardwired.
-
For every \(j \in [{\mathsf {len}_{\mathsf {K}}}]\) and \(\alpha \in \{0,1\}\), compute \(\mathsf {CT}_{j,\alpha } \leftarrow \mathsf {Enc}(\mathsf {ek}_{j,\alpha }, \mathsf {lab}_{j,\alpha })\).
-
Return \(\mathsf {Kdm}.\mathsf {CT}:= \left( \widetilde{\mathsf {E}}, \{\mathsf {CT}_{j,\alpha }\}_{j \in [{\mathsf {len}_{\mathsf {K}}}], \alpha \in \{0,1\}}\right) \).
-
-
\(\mathsf {Kdm}.\mathsf {Dec}(\mathsf {Kdm}.\mathsf {dk}, \mathsf {Kdm}.\mathsf {CT}){:}\)
-
Parse \(\left( \mathsf {K}, \left\{ \mathsf {dk}_j\right\} _{j\in [{\mathsf {len}_{\mathsf {K}}}]}\right) \leftarrow \mathsf {Kdm}.\mathsf {dk}\).
-
Parse \(\left( \widetilde{\mathsf {E}}, \{\mathsf {CT}_{j,\alpha }\}_{j \in [{\mathsf {len}_{\mathsf {K}}}], \alpha \in \{0,1\}}\right) \leftarrow \mathsf {Kdm}.\mathsf {CT}\).
-
For every \(j \in [{\mathsf {len}_{\mathsf {K}}}]\), compute \(\mathsf {lab}_j \leftarrow \mathsf {Dec}\left( \mathsf {dk}_j,\mathsf {CT}_{j,\mathsf {K}[j]}\right) \).
-
Compute \(\mathsf {CT}_\mathsf {ske}\leftarrow \mathsf {Eval}\left( \widetilde{\mathsf {E}}, \{\mathsf {lab}_j\}_{j \in [{\mathsf {len}_{\mathsf {K}}}]}\right) \).
-
Return \(m \leftarrow \mathsf {D}(\mathsf {K}, \mathsf {CT}_\mathsf {ske})\).
-
Correctness. When decrypting a ciphertext of \(\mathsf {KdmPKE}\) that encrypts a message m, we first obtain a ciphertext of \(\mathsf {SKE}\) that encrypts m from the correctness of \(\mathsf {PKE}\) and \(\mathsf{GC}\). The correctness of \(\mathsf {KdmPKE}\) then follows from that of \(\mathsf {SKE}\).
We have the following theorem.
Theorem 7
Let \(\mathsf {SKE}\) be an SKE scheme that is \({\mathcal {P}}\text {-KDM-CPA}\) secure (resp. \({\mathcal {B}}\text {-KDM-CPA}\) secure). Let \(\mathsf {PKE}\) be an \(\text {IND-CPA}\) secure PKE scheme and \(\mathsf{GC}\) a secure garbling scheme. Then, \(\mathsf {KdmPKE}\) is a PKE scheme that is \({\mathcal {P}}\text {-KDM-CPA}\) secure (resp. \({\mathcal {B}}\text {-KDM-CPA}\) secure).
The proof for Theorem 7 is almost the same as that for Theorem 5. Thus, we omit it and provide in the full version of this paper [27].
7 \(\text {SIM-RSO}\) Secure PKE Based on \(\text {IND-CPA}\) Secure PKE
We can construct \(\text {SIM-RSO}\) secure PKE based on any \(\text {IND-CPA}\) secure PKE if we take the revelation of only secret keys into account. The construction is similar to that of \(\text {SIM-RSO}\) secure IBE we show in Sect. 5 except that \(\text {IND-CPA}\) secure PKE is used instead of \(\text {IND-ID-CPA}\) secure IBE.
Using a PKE scheme \(\mathsf {PKE}=(\mathsf {KG},\mathsf {Enc},\mathsf {Dec})\), we construct the following PKE scheme \(\mathsf {RsoPKE}=(\mathsf {Rso}.\mathsf {KG}, \mathsf {Rso}.\mathsf {Enc},\mathsf {Rso}.\mathsf {Dec})\) whose message space is \(\{0,1\}\).
-
\(\mathsf {Rso}.\mathsf {KG}(1^\lambda ){:}\)
-
Generate \((\mathsf {ek}_\alpha ,\mathsf {dk}_\alpha ) \leftarrow \mathsf {KG}(1^\lambda )\) for every \(\alpha \in \{0,1\}\).
-
Generate \(r \xleftarrow {\mathsf {r}}\{0,1\}\).
-
Return \(\mathsf {Rso}.\mathsf {ek}:= (\mathsf {ek}_0,\mathsf {ek}_1)\) and \(\mathsf {Rso}.\mathsf {dk}:= (r,\mathsf {dk}_r)\).
-
-
\(\mathsf {Rso}.\mathsf {Enc}(\mathsf {Rso}.\mathsf {ek}, m\in \{0,1\}){:}\)
-
Parse \((\mathsf {ek}_0,\mathsf {ek}_1) \leftarrow \mathsf {Rso}.\mathsf {ek}\).
-
For every \(\alpha \in \{0,1\}\), compute \(\mathsf {CT}_{\alpha } \leftarrow \mathsf {Enc}(\mathsf {ek}_\alpha , m)\).
-
Return \(\mathsf {Rso}.\mathsf {CT}:= (\mathsf {CT}_0,\mathsf {CT}_1)\).
-
-
\(\mathsf {Rso}.\mathsf {Dec}(\mathsf {Rso}.\mathsf {dk}, \mathsf {Rso}.\mathsf {CT}){:}\)
-
Parse \((r,\mathsf {dk}_r) \leftarrow \mathsf {Rso}.\mathsf {dk}\)
-
Parse \((\mathsf {CT}_0,\mathsf {CT}_1) \leftarrow \mathsf {Rso}.\mathsf {CT}\).
-
Return \(m \leftarrow \mathsf {Dec}(\mathsf {dk}_r,\mathsf {CT}_r)\).
-
Correctness. The correctness of \(\mathsf {RsoPKE}\) directly follows from that of \(\mathsf {PKE}\).
We have the following theorem.
Theorem 8
Let \(\mathsf {PKE}\) be an \(\text {IND-CPA}\) secure PKE scheme. Then, \(\mathsf {RsoPKE}\) is a \(\text {SIM-RSO}\) secure PKE scheme.
The proof for Theorem 8 is almost the same as that for Theorem 6. Thus, we omit it and provide in the full version of this paper [27].
Notes
- 1.
The scheme by Alperin-Sheriff and Peikert has an a-priori bound on the number of challenge identities in the security game. The scheme by Galindo et al. has an a-priori bound on the number of KDM encryption queries made by an adversary.
- 2.
- 3.
- 4.
More precisely, these works showed how to construct PKE that is KDM secure with respect to projection functions and satisfies the efficiency requirement.
- 5.
We observe that another example is leakage resilience. We do not focus on it in this paper.
- 6.
One additional reason is that we can always make a key generation algorithm of IBE deterministic by using pseudorandom functions.
- 7.
- 8.
One might think it is a restriction to force an adversary to register challenge identities before making KDM queries. This is not the case since the adversary is allowed to adaptively make registration and KDM queries. Our definition with registration queries makes the security proof of our IBE simple.
References
Acar, T., Belenkiy, M., Bellare, M., Cash, D.: Cryptographic agility and its relation to circular encryption. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 403–422. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_21
Agrawal, S., Boneh, D., Boyen, X.: Efficient lattice (H)IBE in the standard model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 553–572. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_28
Alperin-Sheriff, J., Peikert, C.: Circular and KDM security for identity-based encryption. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 334–352. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-30057-8_20
Applebaum, B.: Key-dependent message security: generic amplification and completeness. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 527–546. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_29
Applebaum, B., Cash, D., Peikert, C., Sahai, A.: Fast cryptographic primitives and circular-secure encryption based on hard learning problems. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 595–618. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_35
Barak, B., Haitner, I., Hofheinz, D., Ishai, Y.: Bounded key-dependent message security. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 423–444. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_22
Bellare, M., Dowsley, R., Waters, B., Yilek, S.: Standard security does not imply security against selective-opening. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 645–662. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_38
Bellare, M., Hofheinz, D., Yilek, S.: Possibility and impossibility results for encryption and commitment secure under selective opening. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 1–35. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01001-9_1
Bellare, M., Waters, B., Yilek, S.: Identity-based encryption secure against selective opening attack. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 235–252. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_15
Bishop, A., Hohenberger, S., Waters, B.: New circular security counterexamples from decision linear and learning with errors. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015, Part II. LNCS, vol. 9453, pp. 776–800. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48800-3_32
Black, J., Rogaway, P., Shrimpton, T.: Encryption-scheme security in the presence of key-dependent messages. In: Nyberg, K., Heys, H. (eds.) SAC 2002. LNCS, vol. 2595, pp. 62–75. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36492-7_6
Boneh, D., Franklin, M.K.: Identity-based encryption from the weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_13
Boneh, D., Halevi, S., Hamburg, M., Ostrovsky, R.: Circular-secure encryption from decision Diffie-Hellman. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 108–125. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_7
Brakerski, Z., Goldwasser, S.: Circular and leakage resilient public-key encryption under subgroup indistinguishability - (or: Quadratic residuosity strikes back). In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 1–20. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_1
Camenisch, J., Lysyanskaya, A.: An efficient system for non-transferable anonymous credentials with optional anonymity revocation. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 93–118. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_7
Canetti, R., Halevi, S., Katz, J.: A forward-secure public-key encryption scheme. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 255–271. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_16
Canetti, R., Halevi, S., Katz, J.: Adaptively-secure, non-interactive public-key encryption. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 150–168. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30576-7_9
Cash, D., Green, M., Hohenberger, S.: New definitions and separations for circular security. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 540–557. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-30057-8_32
Damgård, I., Nielsen, J.B.: Improved non-committing encryption schemes based on a general complexity assumption. In: Bellare, M. (ed.) CRYPTO 2000. LNCS, vol. 1880, pp. 432–450. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44598-6_27
Döttling, N., Garg, S.: From selective IBE to full IBE and selective HIBE. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 372–408. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_13
Döttling, N., Garg, S.: Identity-based encryption from the Diffie-Hellman assumption. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 537–569. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_18
Galindo, D., Herranz, J., Villar, J.L.: Identity-based encryption with master key-dependent message security and leakage-resilience. In: Foresti, S., Yung, M., Martinelli, F. (eds.) ESORICS 2012. LNCS, vol. 7459, pp. 627–642. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33167-1_36
Goyal, R., Koppula, V., Waters, B.: Semi-adaptive security and bundling functionalities made generic and easy. In: Hirt, M., Smith, A. (eds.) TCC 2016-B, Part II. LNCS, vol. 9986, pp. 361–388. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_14
Hazay, C., Patra, A., Warinschi, B.: Selective opening security for receivers. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015, Part I. LNCS, vol. 9452, pp. 443–469. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_19
Hofheinz, D., Rao, V., Wichs, D.: Standard security does not imply indistinguishability under selective opening. In: Hirt, M., Smith, A. (eds.) TCC 2016-B, Part II. LNCS, vol. 9986, pp. 121–145. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_5
Hofheinz, D., Rupp, A.: Standard versus selective opening security: separation and equivalence results. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 591–615. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_25
Kitagawa, F., Tanaka, K.: Key dependent message security and receiver selective opening security for identity-based encryption. IACR Cryptology ePrint Archive (2017)
Koppula, V., Waters, B.: Circular security separations for arbitrary length cycles from LWE. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part II. LNCS, vol. 9815, pp. 681–700. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_24
Naor, M., Yung, M.: Public-key cryptosystems provably secure against chosen ciphertext attacks. In: 22nd ACM STOC, pp. 427–437 (1990)
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). https://doi.org/10.1007/3-540-39568-7_5
Yao, A.C.-C.: How to generate and exchange secrets (extended abstract). In: 27th FOCS, pp. 162–167 (1986)
Acknowledgement
We would like to thank the anonymous reviewers of PKC 2018 for their insightful comments. A part of this work was supported by Input Output Hong Kong, Nomura Research Institute, NTT Secure Platform Laboratories, Mitsubishi Electric, JST CREST JPMJCR14D6, JST OPERA, JSPS KAKENHI JP16H01705, JP16J10322, JP17H01695.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Kitagawa, F., Tanaka, K. (2018). Key Dependent Message Security and Receiver Selective Opening Security for Identity-Based Encryption. In: Abdalla, M., Dahab, R. (eds) Public-Key Cryptography – PKC 2018. PKC 2018. Lecture Notes in Computer Science(), vol 10769. Springer, Cham. https://doi.org/10.1007/978-3-319-76578-5_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-76578-5_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-76577-8
Online ISBN: 978-3-319-76578-5
eBook Packages: Computer ScienceComputer Science (R0)



 computes
computes  .
. computes
computes 
 sets
sets 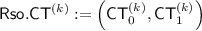 .
. sends
sends 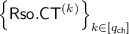 to
to  sends it to the challenger, and gets
sends it to the challenger, and gets  .
.  computes
computes  , sets
, sets  for every
for every  to
to 