Crystal Binding and Structure

Abstract

It has been argued that solid-state physics was born, as a separate field, with the publication, in 1940, of Frederick Seitz’s book, Modern Theory of Solids [82].

Problems

• 1.1. Show by construction that stacked regular pentagons do not fill all two-dimensional space. What do you conclude from this? Give an example of a geometrical figure that when stacked will fill all two-dimensional space.

• 1.2. Find the Madelung constant for a one-dimensional lattice of alternating, equally spaced positive and negative charged ions.

• 1.3. Use the Evjen counting scheme [1.19] to evaluate approximately the Made-lung constant for crystals with the NaCl structure.

• 1.4. Show that the set of all rational numbers (without zero) forms a group under the operation of multiplication. Show that the set of all rational numbers (with zero) forms a group under the operation of addition.

• 1.5. Construct the group multiplication table of D₄ (the group of three dimensional rotations that map a square into itself).

• 1.6. Show that the set of elements (1, −1, i, −i) forms a group when combined under the operation of multiplication of complex numbers. Find a geometric group that is isomorphic to this group. Find a subgroup of this group. Is the whole group cyclic? Is the subgroup cyclic? Is the whole group Abelian?

• 1.7. Construct the stereograms for the point groups 4(C₄) and 4 mm(C_4v). Explain how all elements of each group are represented in the stereogram (see Table 1.3).

• 1.8. Draw a bcc (body-centered cubic) crystal and draw in three crystal planes that are neither parallel nor perpendicular. Name these planes by the use of Miller indices. Write down the Miller indices of three directions, which are neither parallel nor perpendicular. Draw in these directions with arrows.

• 1.9. Argue that electrons should have energy of order electron volts to be diffracted by a crystal lattice.

• 1.10. Consider lattice planes specified by Miller indices (h, k, l) with lattice spacing determined by d(h, k, l). Show that the reciprocal lattice vectors G(h, k, l) are orthogonal to the lattice plane (h, k, l) and if G(h, k, l) is the shortest such reciprocal lattice vector then

  $$ d\left( {h,k,l} \right) = \frac{2\pi }{{\left| {\varvec{G}\left( {h,k,l} \right)} \right|}}. $$

• 1.11. Suppose a one-dimensional crystal has atoms located at nb and αmb where n and m are integers and α is an irrational number. Show that sharp Bragg peaks are still obtained.

• 1.12. Find the Bragg peaks for a grating with a modulated spacing. Assume the grating has a spacing

  $$ d_{n} = nb + \varepsilon b\,\sin \left( {2\pi knb} \right), $$

  where ε is small and kb is irrational. Carry your results to first order in ε and assume that all scattered waves have the same geometry. You can use the geometry shown in the figure of this problem. The phase φ_n of scattered wave n at angle θ is

  $$ {{\upvarphi }}_{n} = \frac{2\pi }{\lambda }d_{n} \sin \theta , $$

  where λ is the wavelength. The scattered intensity is proportional to the square of the scattered amplitude, which in turn is proportional to

  $$ E \equiv \left| {\sum\limits_{0}^{N} {\exp \left( {{\text{i}}\varphi_{n} } \right)} } \right| $$

  for N  + 1 scattered wavelets of equal amplitude.

  

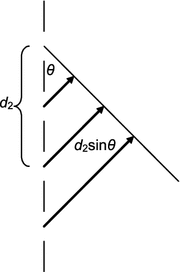
• 1.13. Find all Bragg angles less than 50° for diffraction of X-rays with wavelength 1.5 angstroms from the (100) planes in potassium. Use a conventional unit cell with structure factor.