Keywords

1 Introduction

The increasing availability of data in diverse domains has created a necessity to develop techniques and methods to discover knowledge from massive volumes of complex data, motivating many research works in databases, machine learning, and information retrieval communities. This has driven the development of scalable and efficient techniques to organize and retrieve this kind of data. Similarity search has been the traditional approach for information retrieval. Although several similarity search algorithms have been proposed to speed up similarity queries, most of them are either affected by the well-known “curse of dimensionality”. Retrieve complex data causes stability problems when the data dimensionality is too high [3].

One of the few approaches that ensure an approximate solution with sublinear search cost for high-dimensional data is the Locality Sensitive Hashing (LSH) [1]. LSH is based on the idea that closeness between two objects is usually preserved by a random projection operation. In other words, if two objects are close together in their original space, then these two objects will remain close after a scalar projection operation [12]. However, it presents some difficulties for approximate kNN queries, in particular, related to data domain parameter dependence and quality results. Therefore, in complex domains, in particular, in high dimensional data problems, an approximate solution with a solid theoretical analysis may be the best option in many application areas because of their efficiency in time and space.

On the other hand, in Machine Learning traditionally images are often described by the hand-craft visual features. However, these hand-craft features cannot well reveal the high-level semantic meaning (labels or tags) of images, and often limit the performance of image retrieval [9]. Inspired by recent advances in Convolutional Neural Network (CNN) [8], many methods solved the problem of precision of similarity retrieval by using CNN as feature extractor and then build a compact similarity-preserving hash code for fast image retrieval. Again, hashing is widely used for large-scale image retrieval as well as video and document searches because the compact representation of hash code is essential for data storage and reasonable for query searches [14]. However, some drawbacks based on these supervised hashing methods have not been solved entirely, as follows:

  • There is a trade-off between classification error and quantization error: activations of lower layers are more general-purpose [16], so training is more effective. However lower layers have larger activations maps (many nodes), which are harder to encode which leads to a compromise.

  • There is a dependency on parameter values for approximate similarity search schemes based on LSH, which determine the number of hash functions and number of hash tables.

This paper proposes a novel supervised hashing technique, named Deep frActal based Hashing (DAsH), designed to perform scalable approximate similarity search. The contributions of our work are as follows. First, we introduce and define a scheme based on CNN and optimized using fractal theory. To overcome the limitation of large activations on lower layers of CNN (output of the last convolutional layer) we reduce its dimensionality using autoencoders to the optimal sub-space. Then we index this new representation with LSH scheme. Second, we present a novel method, based on fractal theory, which allow us to can find the optimal number of hash functions for an approximate similarity search scheme based on LSH.

The paper is organized as follows. Section 2 summarizes the background for this work. Section 3 describes the proposed technique and Sect. 4 reports experimental results on real and synthetic datasets. Finally, we conclude in Sect. 5.

2 Locality Sensitive Hashing

Previous work [1] has explored the idea of hashing objects and grouping them into buckets with the goal of performing approximate similarity search within buckets associated with the query element. The idea behind LSH is that if two objects are close together in their original space, then these two objects will remain close after a scalar projection operation [12]. Hence, let h(x) be a hash function that maps a d-dimensional point x to a one-dimensional value. The function h(x) is said to be locality sensitive if the probability of mapping two d-dimensional points \(x_1\), \(x_2\) to the same value grows as their distance \(d(x_1, x_2)\) decreases.

LSH based methods report efficient results when adequate values for m (number of hash functions) and L (number of indexes) are chosen. The \(E^2\)-LSH algorithm find the best value for m and L by experimentally evaluating the cost of calculation for samples in the given dataset. Basically, the tuning parameter of LSH is chosen as a function of the dataset to minimize the running time of a query while the space requirement is within the memory bounds [13].

2.1 Fractal Theory

A fractal is characterized by the self-similarity property, i.e., it is an object that presents roughly the same characteristics when analyzed over a broad range of scales [6]. From the Fractal Theory, the Correlation Fractal Dimension \(\mathfrak {D}\) is particularly useful for data analysis, since it can be applied to estimate the intrinsic dimension of real datasets that exhibit fractal behavior, i.e., exactly or statistically self-similar datasets [4]. It has been shown that, given a set of N objects in a dataset with a distance function d(x, y), the average number of k neighbors within a given distance r is proportional to r raised to \(\mathfrak {D}\). Thus, the pair-count PC(r) of pairs of elements within distance r follows the power law:

$$\begin{aligned} PC(r) = K_p \times r^{\mathfrak {D}} \end{aligned}$$
(1)

where, \(K_p\) is a proportionality constant, and \(\mathfrak {D}\) is the correlation fractal dimension of the dataset. Consequently, a fractal is defined by the self-similarity property, that is the main characteristic that represents exactly or statistically the similarity between the parts to the whole fractal.

3 Deep Fractal Based Hashing - DAsH

In this section, we propose the Deep Fractal based Hashing (DAsH) designed to perform a scalable approximate search by supervised hashing by a supervised hashing scheme. As introduced in Sect. 1, our strategy is to use the fractal theory to find the optimal sub-space for the last convolutional layer output of the CNN network, and the optimal number of hash functions for LSH index as well.

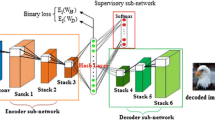
Figure 1 illustrates the training process structure. The network consists of three types of layers: (1) the convolutional layers whose weights are pre-trained most of the time on Imagenet and the target dataset is fine-tuned via transfer learning [16]; (2) the fully connected layers, with the last softmax layer returning the categorical probability distribution; (3) the autoencoders layers which are used for dimensionality reduction. The Convolutional Neural Network (CNN) is trained end-to-end with the groundtruth labels. We use the output of the last convolutional layer because it has the most general-purpose representation for learning, however there is somes issues with high dimensional data. To overcome the high-dimensionality problem, we reduce to the optimal sub-space using an autoencoder. Then we index the optimal sub-space obtained by the autoencoder with LSH scheme which, as we mentioned, it is also tuned thanks to fractal theory. At the same time, we use another n-autoencoders to learning the representation of each class. After, we will use these autoencoders to improve the retrieval process.

Fig. 1.
figure 1

DAsH: training and indexing process.

Full size image

As it was showed in [11], a successful dimensionality reduction algorithm projects the data into a feature space with dimensionality close to the fractal dimensionality (FD) of the data in the original space and preserves topological properties. Thus, to find the target dimensionality (m) needed by autoencoder networks we follow the following heuristic. We start with the value at \(m_1 = 2^2\), compute the FD of the new space with just that, then increment value at \(m_2 = 2^3\), recompute the FD, and continue doing this until some \({t}{(m_t = 2 ^ t)}\) where we can see a flattening in the fractal dimension, meaning that more features do not change the fractal dimensionality of the dataset.

The second step of our procedure is image retrieval via DAsH. We process the query image forwarding it through CNN aiming to obtain the strongest n classes. In contrast to existing similarity algorithms that learn similarity from the low-level feature, our similarity is the combination of semantic-level and hashing-level similarity. So, the semantic level similarity is computed firstly (the n strongest classes). After the semantic relevance checking, we will obtain the new n queries using the strongest n autoencoders. The query is transformed into new query objects (\(q_1, q_2, ... q_n\)) which are hashed to locate the appropriate buckets. Once the buckets are located, the relevant candidate set is formed. Then, the elements in the candidate set are exhaustively analyzed to recover only the objects that satisfy the query condition (e.g. \(d(x, q) \le r\)). This process is performed for each of the L hash tables and it is illustrated in Fig. 2.

Fig. 2.
figure 2

DAsH. Retrieval process.

Full size image

3.1 Using Fractals to Estimate LSH Parameters

To tune the LSH parameters we used a property of the correlation fractal dimension \(\mathfrak {D}\), which can describes statistically a dataset. Moreover, the correlation fractal dimension \(\mathfrak {D}\) can be estimated in linear time as it is depicted in [15].

We are interested to find out the resolution scale log(r) at which there are approximately k objects. Considering the line with slope \(\mathfrak {D}\) passing at a point defined as \({<}log (r), log (Pairs(k)){>}\) the constant \(K_d\) using the Eq. 1 is:

$$\begin{aligned} log(PC(r)) = \mathfrak {D} \times log (r) + K_p \nonumber \\ K_p = log (Pairs (k)) - \mathfrak {D} \times log (r) \end{aligned}$$
(2)

Considering another point \( {<}log (R), log (Pairs(N)){>}\), the constant \(K_p\) is defined as:

$$\begin{aligned} K_p = log (Pairs(N)) - \mathfrak {D} \cdot log (R) \end{aligned}$$
(3)

Now, combining Eqs. 2 and 3, we can define the radius r as:

$$\begin{aligned} r = R \cdot exp (\frac{log (Pairs (k)) - log (Pairs(N))}{ \mathfrak {D}}) \end{aligned}$$
(4)

Using the last Eq. 4 we find out that the optimal number of hash functions m for a Locality Sensitive Hashing (LSH) based index configured to retrieve the k nearest neighbors is proportional to the number of pairs at a distance r. This has sense, because an average number of k neighbors are within a given distance r. Then, we define:

$$\begin{aligned} m \approx log (PC(r)) \end{aligned}$$
(5)

combining Eqs. 5 and 1 we obtain that \(m \approx \mathfrak {D} \cdot log (r) \). Experimentally, we confirm out that the optimal m is:

$$\begin{aligned} m = (\left\lceil \mathfrak {D} + 1 \right\rceil ) \cdot log (r) \end{aligned}$$
(6)

4 Experiments

In this section, we are interested in answering the following question: (a) How accurate is our model in estimating the LSH parameters using the fractal dimension; (b) How does our DAsH method improve the other LSH implementations in terms of querying performance and precision. The performance of DAsH method was compared to two well-known approximate search methods, namely Multi-probe LSH [10], LSH-Forest [2], ITQ [5], and LOPQ [7]. All of the experiments were performed on a workstation with Intel core i7 3.0 GHz CPU and 64 GB RAM which is supplied with four Geforce GTX 1080 GPU.

We first conduct experiments on eight widely used datasets using hand-crafted features (audio, cities, eigenfaces, histograms, mgcounty, randomwalk, synth16d, synth6d, video)Footnote 1 to evaluate our proposed method for estimating the LSH parameters. Beside hand-crafted features, we also show the effectiveness of our methods when deep features are extracted by the deep Convolutional Neural Networks (CNN), we conduct this experiment on three datasets (MNISTFootnote 2, CIFAR-10Footnote 3, SVHNFootnote 4) to evaluate our in terms of querying performance, meap average precision (mAP), and precision. The following describes the details of the experiments and results.

4.1 Experiment 1: Tunning LSH Parameters

LSH based methods report efficient results when adequate values for m (number of hash functions) are chosen. L (number of hash tables) is given by \(L = m(m-1)/2\), see the E2LSH implementationFootnote 5. To evaluate the effectiveness of the presented approach to tune the LSH parameters using fractal dimension, we worked on a variety of synthetic and real dataset. Table 1 summarizes the main features and parameters of the datasets, including the number of elements N, number of attributes d, their intrinsic (fractal) dimension \(\mathfrak {D}\), the LSH parameters computed using two approaches: the Andoni (see footnote 5) algorithm and our proposal based on fractal dimension, and the total computation time for tune the LSH index (in seconds). The experiment results for the number of hash functions m show that the estimations given by Eq. 6 are comparable with those obtained with the E2LSH algorithm proposed by Andoni using up to 10X less time.

Table 1. Optimal LSH params using exhaustive e2lsh and the fractal based method.
Full size table

4.2 Retrieval Performance

The aim of this experiment is to measure the total time spent retrieving the k-nearest neighbor objects. The data structures being compared were tested with an specific values for queries. Thus we use \(k=1000\) when compute the Mean Average Precision (mAP) metric and \(k=25\) when compute the precision metric \((P (\%))\).

Table 2. Mean average precision (mAP), precision, and cumulative time spent to compute mAP for different methods on the MNIST, SVHN and CIFAR-10 datasets.
Full size table

Table 2 show the comparison in terms of mean average precision mAP, precision, and total time (in seconds).

5 Conclusions

In this paper, we presented a new scheme to solve approximate similarity search by supervised hashing called Deep Fractal base Hashing. Our approach shows the potential of boosting querying operations when a specialized index structure is designed from end-to-end. Due to the abilities of Fractal theory to find the optimal sub-space of the dataset and the optimal number of hash functions for LSH Index, we are able to find an optimal configuration for learning and indexing process. Moreover, we defined a novel method, based on fractal theory, which allows us to can find the optimal number of hash functions for LSH indexes. We can estimate these parameters in linear time due to it depends on computing fractal dimension.

We conducted performance studies on many real and synthetic datasets. The empirical results for LSH parameters show that our method based on fractal theory is comparable with those obtained with the brute-force algorithm using up to 10X less time. Moreover, in retrieval performance, the DAsH method was significantly better than other approximate methods, providing up to 8% better precision maintaining excellent retrieval times.