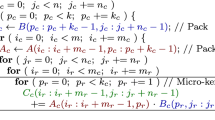Linking Application Description with Efficient SIMD Code Generation for Low-Precision Signed-Integer GEMM

Abstract

The need to implement demanding numerical algorithms within a constrained power budget has led to a renewed interest in low-precision number formats. Exploration of the degrees of freedom provided both by better support for low-precision number formats on computer architectures and by the respective application domain remains a most demanding task, though.

In this example, we upgrade the machine learning framework Theano and the Eigen linear algebra library to support matrix multiplication of formats between 32 and 1 bit by packing multiple values in a 32-bit vector. This approach keeps all the optimizations of Eigen to the overall matrix operation, while maximizing performance enabled through SIMD units on modern embedded CPUs. With respect to 32-bit formats, we achieve a speedup between 0.45 and 21.17 on an ARM Cortex-A15.

1 Introduction

Digital computers implement computer arithmetic over finite number sets. The past decades saw improved support for higher-precision number formats resulting in native support of double-precision (64-bit) floating-point on almost all computing platforms from supercomputers to desktops and mobile devices. Recently, though, there is a substantial interest in reduced-precision number formats to execute demanding algorithms within limited time, memory, or power budgets. The key driver for this development are complex algorithms executed on mobile platforms, for instance for speech recognition, computer vision, or augmented reality. An extreme example of this trend are binarized neural networks [3], in which the weights and activations are represented by either a plus one or a minus one, allowing storing each parameter in a single bit.

Driven by various trends, including big data, deep learning, and a steadily increasing resolution in image processing, the complexity of applications continues to grow. This applies to computational complexity, algorithmic complexity, and memory complexity. At the same time, algorithms continue to rely heavily on Basic Linear Algebra Subroutines (BLAS) like matrix-vector or matrix-matrix multiplication. As an example, a trained neural network uses matrix-vector and matrix-matrix operations for the inference, in which new information is detected. As the number of layers for neural networks is continuously growing, up to extreme examples including 100 or 1000 layers [8], the execution time and memory footprint for such a workload increases accordingly. Unfortunately, single-thread performance is stagnating since the end of Dennard scaling, and now performance scaling usually requires parallelization.

Short-vector units (also known as single-instruction multiple-data – or SIMD – units) exploit the low cost of data-level parallelism in current CMOS processes. SIMD units are ubiquitous in current architectures from server CPUs to microcontrollers. They typically support multiple number formats with throughput doubling at half of the bit width. While the performance of SIMD units looks good on paper, the challenge is to map numerical algorithms to matching number formats and to exploit the complex instruction sets.

Quantization is a form of lossy data compression, with the benefit of lower memory footprint and lower computational complexity. While originally studied in the context of computer arithmetic, it can also be seen in the context of approximate computing, which also looks at different techniques like logic design [13] and architecture [4], as well as software aspects including data type qualifiers [10] and loops [11].

This work is motivated by the wish to use complex (BLAS-based) algorithms for highly resource-constrained systems with limited computational performance. ARM architectures dominate many domains of embedded computing today. We see ARM-based CPUs as a viable option that should be explored initially, as they offer in comparison to specialized processors a relatively high productivity, versatility and rather unconstrained memory capabilities. By computing locally on the mobile device, one avoids traffic to cloud-based processing solutions, and especially the need for online connectivity. Under real-time constraints or security considerations this might be a strong argument. We assume that selected application domains are able to map relevant tasks onto lower-precision number format. We are concerned with the question how lower-precision number formats can be effectively used. That includes direct use at the application level as well as resulting low-level code making best use of available SIMD units.

Here, we report insights from our explorations and optimizations to enable ARM processors to efficiently perform computations on extremely quantized data. In particular, the main contributions of this work are as follows:

• A review of architectural support in embedded ARM processors for computations based on extreme forms of quantizations, in particular non-standard representations

• The design, optimization, and evaluation of building blocks for efficient quantized computations

• Based on our findings, a discussion of the implications with regard to the compute stack, or how to extend the compute stack to allow generalized forms of such computations.

The remainder of this work is structured as follows: Sect. 2 provides a background on matrix multiplication, ARM processors, and NEON vector instructions. Section 3 describes our solution in detail and explains optimizations. Next, Sect. 4 reports performance results. We discuss our observations in Sect. 5 before we conclude in Sect. 6.

2 Background

In this section, we shortly introduce the necessary background in combination with the most important related work.

2.1 Implementation and Optimization of GEMM

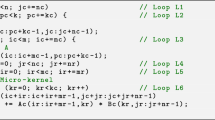
One of the key operations in linear algebra is General Matrix Multiply (GEMM). GEMM is implemented in BLAS. GEMM takes two two-dimensional arrays of size $M\,\times \,N$ and $N\,\times \,K$ as inputs and returns a two-dimensional array of size $M\,\times \,K$. The values of the output matrix are calculated as shown in Eq. 1, with A and B as input arrays and C as output array.

$$\begin{aligned} c_{i,j}= \sum \nolimits _{n=1}^N a_{i,n} * b_{n,j} \end{aligned}$$

(1)

Thus, GEMM consists of iterating over the input arrays and applying Multiply-Accumulate (MAC) operations. Despite the simplicity of the GEMM algorithm it requires multiple, hardware-dependent optimization techniques in order to achieve high performance on any given architecture. Modern compilers are capable of detecting cache ineffective source code or integrate some auto-vectorization, but this is usually not sufficient to reach state-of-the-art performance for GEMM. Thus, libraries like Eigen, Atlas, or OpenBLAS focus on highly optimized BLAS algorithms [6]. For instance, the Eigen library implements a hand-tuned GEMM that exploits a variety of optimizations for a set of SIMD-capable processors [7].

2.2 ARM Processors and Their SIMD Extensions

Single Instruction Multiple Data (SIMD) refers to a vectorization technique that enables the computation of multiple data elements with a single instruction. With the introduction of the ARMv7 architecture, ARM processors supports a SIMD extension named NEON [1, 2] to accelerate media applications. NEON is able to process 128 bit wide vectors and supports 16$\,\times \,$8-bit, 8$\,\times \,$16-bit, 4$\,\times \,$32-bit, and 2$\,\times \,$64-bit integer and floating-point operations. With the upcoming introduction of the ARMv8-A architecture and its Scalable Vector Extension (SVE), ARM is extending the vector processing capabilities for vector lengths that scale from 128 to up to 2048 bit.

2.3 ARM NEON ISA Review

Table 1 summarizes the most important NEON instruction for the MAC operation, relevant to implement GEMM for different number formats.

Table 1. Instruction overview for the MAC operation

All instruction listed in Table 1 support the full NEON-SIMD width of 128 bit with the exception of VMULL. Due to bit-width doubling, this instruction can only process 64-bit vectors.

2.4 Relevant Libraries

Libraries supporting reduced-precision computations are relatively sparse. The MPFR C++ library [9] which is built upon the MPFR library [5] supports multi-precision floating-point number formats and is available as support module for the Eigen library. A library supporting reduced-precision GEMM is Google’s Gemmlowp¹ which is integrated in the application framework Tensorflow and supports 8-bit representation. The library currently supports CPUs and is optimized for NEON and SSE vectorization. ARM’s Compute Library² supports reduced-precision GEMM for 16-bit representation and is supported for NEON-capable processors.

3 Reduced-Precision Signed-Integer GEMM on ARM NEON

Specialized BLAS libraries are pervasively used to improve execution time of numerical algorithms. Impressive results up to achieving almost theoretical peak performance exist. However, specialized BLAS libraries generally support single- and double-precision floating-point only. They typically lack any support for lower-precision number format.

In this work, we show the optimization potential of a signed-integer GEMM on a NEON-capable ARM processor. We use 32-, 16-, 8-, 2-, 1-bit signed integer, and show how NEON SIMD instructions allow for fast data-parallel computation of GEMM. We extend the Eigen BLAS library, which has demonstrated competitive performance and is widely used, for low-precision integers. In particular, we show that support for reduced-precision number formats can be implemented by leaving most of the algorithm untouched and only adapting the highest and lowest level of the operator. Finally, we integrate this extension in the mathematical expression framework Theano [12] to maximize the usability of such custom forms of representations.

To benefit from the advantages of lower-precision number formats, it is necessary to implement operators that can handle these kinds of representation. For the GEMM example we can simply extend the equation by another summation loop as shown in Eq. 2, with W representing the full-precision bit width divided by the reduced-precision bit width.

$$\begin{aligned} c_{i,j}= \sum \nolimits _{n=1}^N a_{i,n} * b_{n,j} = \sum \nolimits _{n=1}^{N/W} \sum \nolimits _{w=1}^W a_{i,n+w} \,*\,b_{n+w,j} \end{aligned}$$

(2)

We can furthermore simplify this equation by packing W values from a and b to $a^{packed}$ and $b^{packed}$ and overwriting the MAC operation (Eq. 3).

$$\begin{aligned} c_{i,j} = \sum \nolimits _{n=1}^{N/W} a^{packed}_{i,n} \,*\,b^{packed}_{n,j} \end{aligned}$$

(3)

Within the MAC operation, W scalar products can be vectorized in SIMD fashion and summed up using reduction. As a result, we can extend the Eigen GEMM operator to support reduced precision by overwriting the MAC operation, packing W reduced-precision values into a single full-precision value, and dividing the matrix depth N by W.

In order to integrate the reduced-precision operator into Theano, we propose the following workflow: the value packing is performed within Theano and the packed matrices are propagated via references to Eigen’s GEMM operator. Then, Eigen performs its high-level transformations and forwards the data in form of 128-bit vectors to the customized MAC operator. Finally, the MAC operator performs the actual computations by exploiting optimized code on SIMD units.

3.1 Implementation

We use the NEON SIMD-MAC operation to evaluate the scalar product of the input vectors a and b, followed by accumulating the result by input vector c. The SIMD-MAC operation is illustrated in Fig. 1 on the example of $int8\_t$ input representation. As can be seen, the scalar product of two vectors is implemented by pairwise multiplying elements of input vectors a and b. The results of the multiplication are reduced into a $int32\_t$ intermediate representation and accumulated by elements of input vector c. Input and output vectors for the MAC operations are mapped to the full NEON-SIMD width of 128 bit, with precision depend type for a and b ($int32x4\_t$, $int16x8\_t$, $int8x16\_t$, $int4x32\_t$, $int2x64\_t$, and $int1x32\_t$) and full-precision type $int32x4\_t$ for input vector c and output vector.

Fig. 1.

Simplified illustration of the MAC operation for int8_t representation

A performance-sensitive pitfall of the MAC operation is bit-width doubling when performing the multiplication in order to avoid integer overflows. Bit-width doubling is performed for $int16\_t$, $int8\_t$, and $int4\_t$ input representation. $int2x64\_t$ and $int1x32\_t$ representations cannot cause overflows since the result’s range is identical with the input range (+1, $-1$ and $-1$, 0, +1).

3.2 Supporting Different Bit Widths

The baseline implementation of the MAC operation assumes input vectors a and b of type $int32x4\_t$. For this case, NEON includes the Fused-Multiply-Accumulate (FMA) instruction, which is able to multiply and accumulate 4 operands (128-bit vector) in one instruction.

int16x8_t and int8x16_t MAC: NEON also includes FMA instructions for 16-bit and 8-bit representations. However, the FMA instructions are not applicable here because the reduction has to be performed after the multiplication and before the accumulation.

Thus, we use a multiplication instruction with bit-width doubling. Since instructions with bit-width doubling only can process 64-bit vectors, the multiplication of the highest and lowest 64 bit of input vectors a and b has to be performed sequentially. Then, both resulting vectors are sequentially reduced by adding adjacent pairs of elements (one reduction layer for $int16x8\_t$ MAC and two reduction layers for $int8x16\_t$ MAC). Finally, both resulting vectors are combined to a single vector and its values are summed up.

int4x32_t MAC: While 16-bit and 8-bit representation is supported inherently by NEON, it lacks support for 4-bit formats. In particular, the extraction of $int4\_t$ values from the input vectors causes a high instruction overhead. In order to perform the extraction, we mask out even and odd indexed $int4\_t$ values from the 128-bit input vectors a and b via bit-wise logic operations and split the values into two separate 128-bit vectors. Once the extraction is done, the obtained vectors can be simply multiplied without bit-width doubling. Then, a three-layer reduction is performed before the resulting vector elements are summed up.

int2x64_t MAC: The multiplication of the $int2x64\_t$ MAC is realized by evaluating the resulting positive and negative values separately via bit-wise logic operations (AND, XOR). Then, a 8-bit population count is performed to count the positive and negative values within a 8-bit vector. The resulting positive values are subtracted by the resulting negative values. Two reduction levels transform the $int8x16\_t$ representation into a $int32x4\_t$ intermediate representation and accumulate the vector by elements of input vector c.

int1x128_t MAC: For the $int1x128\_t$ MAC, we use the approach proposed by Courbariaux et al. [3]. The basic idea is to replace the actual multiplications of input vectors a and b with bit-wise XOR operations and perform the reduction via population count. Since NEON includes only a 8-bit population count, we use two further reduction levels to reduce the results into a $int32x4\_t$ intermediate representation. Afterwards the result is accumulated by input vector c.

3.3 Optimizing Reduction Overhead

Halving the bit representation causes an additional reduction layer within the MAC operation to obtain a 32-bit intermediate representation. In most cases, this 32-bit intermediate representation cannot be avoided without causing an overflow. However, $int1\_t$ and $int2\_t$ representation differ because the multiplication results are in between $-1$ and +1.

As shown in Sect. 3.2, the first reduction layer of $int1\_t$ and $int2\_t$ MAC is performed via 8-bit population count. Considering that the scalar product of a row vector and a column vector takes N (matrix depth) accumulations of a maximum value of 8, the maximum scalar value is $N\,*\,8$ for the first reduction layer and $N\,*\,16$ for the second reduction layer. Therefore, a reduced bit width (Width) for the intermediate representation is sufficient if $N < \frac{2^{Width}}{Width}$ holds.

Using this observation, we can modify the GEMM implementation for $int1\_t$ and $int2\_t$ input representation to dynamically adapt among 32-bit, 16-bit, and 8-bit intermediate representation by only evaluating the matrix’ depth. Consequently, compared to 32-bit intermediate representation, a 16-bit intermediate representation requires one reduction layer less, and an 8-bit intermediate representation requires two reduction layer less. Obviously, the resulting representation of this optimization differs from the expected output representation. Thus, the last MAC operation of the scalar product of a row vector and a column vector has to reduce the intermediate representation to a 32-bit output representation. As a result, the computational complexity of the reductions can be reduced from $O(n^2)$ to O(n) which directly translates into a significant performance improvement for small ($N<32$) and mid-sized ($N<4096$) matrices.

4 Performance Results

In this section we report execution times and memory footprint of our reduced-precision signed-integer GEMM Eigen extension. We compare the results to Eigen’s $int32\_t$ GEMM.

All results are obtained via averaging on a system with a 2.32 GHz ARM quad-core Cortex-A15 CPU and 2 GB DDR3L memory. The C++ source code with NEON intrinsics is compiled using GNU g++ (version 4.8.4) with the following command-line switches set: Optimization level: -Ofast, OpenMP parallelization: -fopenmp.

Table 2 summarizes the results of the signed-inter GEMM operator. The execution time refers to the required time to perform the pure matrix multiplication without memory allocation and value packing.

Table 2. Summary of the obtained results: execution time and speed-up over int32_t representation

The expected execution time of the core code sequence can be estimated using instruction latency data from the ARM Technical Reference Manual [1]. Table 3 summarizes the estimated and the actual speed-up of the GEMM operator for different input representations, compared to $int32\_t$ representation. As can be seen, the expected speed up is achieved in most cases with the exception of small matrices ($<\!256\,\times \,256$) combined with $int1\_t$ and $int2\_t$ representation. This is caused by Eigen optimizations which enforce padding of small matrices.

Table 3. Expected and actual speed up of the signed-integer GEMM derived from the required cycles of the MAC operation

Fig. 2.

Memory footprint and execution time of 32-bit and reduced-precision signed integer GEMM

Figure 2 shows the improvement of reduced representation over full representation in terms of memory footprint and execution time for signed integer GEMM. The line showing the theoretical improvement assumes that reducing the bit representation by a certain factor results in a performance improvement of the same factor. Obviously, the memory footprint improvement meets the expected theoretical improvement since halving the bit representation results in half the memory usage.

There is a significant gap between theoretical improvement and the improvement of execution time. In particular, for $int16\_t$, $int8\_t$, and $int4\_t$, the GEMM only performs similar or even worse compared to $int32\_t$. Besides the additional reduction overhead, this is mainly due to instruction serialization caused by bit-width doubling when the multiplication is performed. As can be seen, bit representations without the need of bit-width doubling ($int2\_t$ and $int1\_t$) are clearly superior. The simplicity of computing the $int1\_t$ MAC combined with the reduction optimization (discussed in Sect. 3.3) shows its advantage by nearly reaching the theoretical improvement.

5 Discussion

The suggested GEMM implementation avoids integer overflows within the MAC operator and therefore produces the same results as the full-precision operator. The drawback of this design is that it results in a mismatch between input and output representation and, most importantly, requires bit-width doubling in most of the cases. As we have seen, bit-width doubling leads to a significant performance penalty.

In future work, we plan to show how quantization information can be propagated from the application framework to the operator and extend our custom-precision GEMM to also support custom quantization. The current implementation uses a 32-bit data type ($int32_t$) as a container to transparently transport short vectors of lower-precision data from the application framework (Theano) via Eigen to actual code, exploiting SIMD units on selected architectures (value packing). Value packing is required since lower-precision types are not known and therefore not interpretable by the application framework and Eigen. However, high-level transformations of matrix operators are optimized on a fixed size (e.g. SIMD width or cache size) and not a specific data type. As a consequence, this approach enables the use of these existing transformations on collections of values packed into 32-bit. Obviously the packed format reduces the granularity of matrix operations in the application framework and Eigen from single value to up to 32 values (in the case of 1-bit data types) and, thus, inhibits other operations on the matrices. Currently we rely on packing/unpacking the data whenever reduced-/full-precision operators are used. This approach benefits from a reduced execution time, but the advantage of a reduced memory footprint is partially lost when the data has to be unpacked.

Ultimately, the number format should therefore be interpretable by other matrix operators. This could be achieved by matrix operators supporting a generic (precision-agnostic) data type. The GNU MPFR library [5] implements multiple-precision floating-point (i.e. with user-defined mantissa and exponent) computations with correct rounding. Many interfaces to MPFR exist. The mpfr::real class³ and bigfloat library implement full-featured interfaces (i.e. keeping all the format information) to C++ and Python respectively. The MPFR project webpage lists two linear algebra libraries compatible with some MPFR APIs:

• The ALGLIB.NET project implements multiple-precision linear algebra using MPFR⁴

• Eigen, a C++ template library for linear algebra, via Pavel Holoborodko’s MPFR C++ wrapper [9]

In future work, we plan to use and explore effects on the performance of the Eigen MPFR wrapper.

6 Conclusion

We presented and discussed an approach of extending linear-algebra operators to support reduced-precision representations. Using the example of signed-integer GEMM, we showed that the highly optimized Eigen library can be extended by only modifying the MAC operation and packing several reduced-precision values into a 32-bit value. We reviewed the NEON ISA and showed its applicability to support reduced-precision arithmetic. Based on our findings, we optimized the MAC operation for NEON-capable processors and integrated our implementation into Eigen’s GEMM operator and interfaced the operator to the application framework Theano.

Our results show that selected reduced-precision number formats can benefit from reduced GEMM execution time on NEON units. In particular, the performance of $int1\_t$ and $int2\_t$ GEMM is promising, and matches well with the rising interest on these data formats in the machine-learning community [3, 14]. 16-, 8-, and 4-bit signed integer GEMM, however, show no performance advantage over 32-bit for this ARM architecture. Better support for reduction operations would be needed to achieve performance improvements for these number formats.

Last, we would like to encourage developers of BLAS libraries and application frameworks to design software with consideration for custom/reduced precision, as support for these representations is mostly not present today.