Abstract
Single node hardware design is shifting to a heterogeneous nature and many of today’s largest HPC systems are clusters that combine heterogeneous compute device architectures. The need for new programming abstractions in the advancements to the Exascale era has been widely recognized and variants of the Partitioned Global Address Space (PGAS) programming model are discussed as a promising approach in this respect. In this work, we present a graph-based approach to provide runtime support for dynamic, distributed hardware locality, specifically considering heterogeneous systems and asymmetric, deep memory hierarchies. Our reference implementation dyloc leverages hwloc to provide high-level operations on logical hardware topology based on user-specified predicates such as filter- and group transformations and locality-aware partitioning. To facilitate integration in existing applications, we discuss adapters to maintain compatibility with the established hwloc API.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Partitioned Global Address Space (PGAS)
- Dy Locus
- Hardware Topology
- Local Hardware
- Deep Memory Hierarchies
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
The cost of accessing data in Exascale systems is expected to be the dominant factor in terms of execution time and energy consumption [11]. To minimize data movement, programming systems must therefore shift from a compute-centric to a more data-centric focus.
The Partitioned Global Address Space (PGAS) model is particularly suitable for programming abstractions for data locality [3] but differentiates only between local and remote data access in its conventional form. This two-level abstraction lacks the expressiveness to model locality of increasingly deep and heterogeneous machine hierarchies. To facilitate plasticity, the capability of software to adapt to the underlying hardware architecture and available resources, programmers must be provided with fine-grained control of data placement in the hardware topology. The 2014 PADAL report [11] summarizes a wish list on programming environment features to facilitate this task. This work is motivated by two wish list items in particular:
-
Flexible, memory-agnostic mappings of abstract processes to given physical architectures
-
Concise interfaces for hardware models that adjust the level of detail to the requested accuracy.
This work introduces an abstraction of dynamic distributed locality with specific support for deep asymmetric memory hierarchies of heterogeneous systems which typically do not exhibit an unambiguous tree structure. In this context, dynamic locality refers to the capability to create logical representations of physical hardware components from run-time specified, imperative and declarative constraints. Application-specific predicates can be applied as distance- and affinity metrics to define measures of locality. Our approach employs a graph-based internal representation of hierarchical locality domains. Its interface allows to request light-weight views which represent the complex locality graph as a well-defined, consolidated hierarchy.
The remainder of this paper is structured as follows: After a brief review of related work, we illustrate the need for dynamic hardware locality support using requirements identified in the DASH library. Section 4 introduces the concept of a graph-based locality topology and general considerations for implementation. Addressing dynamic characteristics, Sect. 4 outlines fundamental operations on locality hierarchies and selected semantic details. To substantiate our conceptual findings, we introduce our reference implementation ‘dyloc’ and explain how it achieves interoperability with hwloc in Sect. 5. Finally, the benefit of the presented techniques is evaluated in a use case on SuperMIC, a representative heterogeneous Ivy Bridge/Xeon Phi system.
2 Related Work
Hierarchical locality is incorporated in numerous approaches to facilitate programmability of the memory hierarchy. Most dynamic schemes are restricted two levels in the machine hierarchy.
In X10, memory and execution space is composed of places, and tasks execute at specific places. Remote data can only be accessed by spawning a task at the target place. Chapel has a similar concept of locales.
The task model implemented in Sequoia [1] does not consider hardware capacity for task decomposition and communication is limited to parameter exchange between adjacent parent and child tasks.
Hierarchical Place Trees (HPT) [12] extend the models of Sequoia and X10 and increase flexibility of task communication and instantiation. Some fundamental concepts of HPT like hierarchical array views have been adopted in DASH. The HPT programming model is substantially task-parallel, however, and based on task queues assigned to places. HPTs model only static intra-node locality collected at startup.
All abstractions of hierarchical locality in related work model the machine hierarchy as a tree structure, including the de-facto standard hwloc. However, shortcomings of trees for modeling modern heterogeneous architectures are known [8] while hierarchical graphs have been shown to be more practicable to represent locality and hardware capacity in task models [9].
Notably, the authors of hwloc explain that graph data structures are used in the network topology component netloc as a tree-based model was too strict and inconvenient [7]. We believe that this reasoning also applies to node-level hardware. Regarding current trends in HPC hardware configurations, we observed that interdependent characteristics of horizontal and vertical locality in heterogeneous systems cannot be sufficiently and unambiguously represented in a single, conventional tree. This is already evident for recent architectures with cores connected in grid- and ring bus topologies.
More important, heterogeneous hosts require communication schemes and virtual process topologies that are specific to hardware configuration and the algorithm scenario. This involves concepts of vertical and horizontal locality that are not based on latency and throughput as distance measure. For example in a typical accelerator-offloading algorithm with a final reduction phase, processes first consider physical distance and horizontal locality. For communication in the reduction phase, distance is measured based on PCI interface affinity to optimize for vertical locality.
Still, formal considerations cannot disprove the practical benefit of tree data structures as a commonly understood mental model for algorithms and application development. We therefore came to the conclusion that two models of hardware locality are required: an internal physical model representing the machine architecture in a detailed, immutable graph and logical views resulting from projections of the physical model to a simplified tree structure.
3 Background and Motivation
The concepts discussed in the following sections evolved from specific requirements of DASH, a C++ template library for distributed containers and algorithms in Partitioned Global Address Space. While the concepts and methods presented in this work do not depend on a specific programming model, terminology and basic assumptions regarding domain decomposition and process topology have been inherited from DASH. In this section, these are briefly discussed as motivating use cases for dynamic hardware locality (Fig. 1).
Virtual Process Topology: DASH Teams. In the DASH execution model, individual computation entities are called units, a generic name chosen because terms such as process or thread have a specific connotation that might be misleading for some runtime system concepts. In the MPI-based implementation of the DASH runtime, a unit corresponds to an MPI rank.
Units are organized in hierarchical teams to represent the logical structure of algorithms and machines in a program [10]. On initialization of the DASH runtime, all units are assigned to the predefined team instance  . New teams can be only created by specifying a subset of a parent team in a \(\texttt {split}\) operation. Splitting a team creates an additional level in the team hierarchy [6].
. New teams can be only created by specifying a subset of a parent team in a \(\texttt {split}\) operation. Splitting a team creates an additional level in the team hierarchy [6].
In the basic variant of the team split operation, units are evenly partitioned in a specified number of child teams of balanced size. A balanced split does not respect hardware locality but has low complexity and no communication overhead. It is therefore preferable for teams in flat memory hierarchy segments. On systems with asymmetric or deep memory hierarchies, it is highly desirable to split a team such that locality of units within every child team is optimized. A locality-aware split at node level could group units by affinity to the same NUMA domain, for example.
Organizing units by locality requires means to query their affinity in the hardware topology. Resolving NUMA domains from given process IDs can be reliably realized using hwloc. When collaboration schemes are to be optimized for a specific communication bus, especially with grid- and ring topologies, concepts of affinity and distance soon depend on higher-order predicates and differ from the textbook intuition of memory hierarchies.
This does not refer to experimental, exotic architecture designs but already applies to systems actively used at the time of this writing. Figure 2 shows the physical structure of a SuperMIC system at host level and its common logical interpretation. Note that core affinity to PCI interconnect can be obtained, for example by traversing hwloc topology data, but is typically not exploited in applications due to the lack of a locality information system that allows to express high-level, declarative views.
Adaptive Unit-Level Parallelism. Node-level work loads of nearly all distributed algorithms can be optimized using unit-level parallelization like multithreading or SIMD operations. The available parallelization techniques and their suitable configuration depend on the unit’s placement in the process- and hardware topology. As this can only be determined during execution, this again requires runtime support for dynamic hardware locality that allows to query available capacities of locality domains – such as cache sizes, bus capacity, and the number of available cores – depending on the current team configuration.
Domain Decomposition: DASH Patterns. The Pattern concept in DASH [5] allows user-specified data distributions similar to Chapel’s domain maps [2]. As only specific combinations of algorithms and data distribution schemes maintain data locality, hardware topology and algorithm design are tightly coupled. Benefits of topology-aware selection of algorithms and patterns for multidimensional arrays have been shown in previous work [4].
4 Locality Domain Hierarchies
An hwloc distance matrix allows to express a single valid representation of hardware locality of non-hierarchical topologies. However, it is restricted to latency and throughput as distance measures. A distance matrix can express the effects of grouping and view operations but does not support high-level queries and has to be recalculated for every modification of the topology view. In this section, we present the Locality Domain Hierarchy (LDH) model which extends the hwloc topology model by additional properties and operations to represent locality topology as dynamic graph.
In more formal terms, we model hardware locality as directed, acyclic, multi-indexed multigraph. In this, nodes represent Locality Domains that refer to any physical or logical component of a distributed system with memory or computation capacities, corresponding to places in X10 or Chapel’s locales. Edges in the graph are directed and denote one of the following relationships:
- Containment :
-
indicating that the target domain is logically or physically contained in the source domain
- Alias :
-
source and target domains are only logically separated and refer to the same physical domain; this is relevant when searching for a shortest path, for example
- Leader :
-
the source domain is restricted to communication with the target domain.
Figure 3 outlines components of the locality domain concept in a simplified example. A locality hierarchy is specific to a team and only contains domains that are populated by the team’s units. At initialization, the runtime initializes the default team  as root of the team hierarchy with all units and associates the team with the global locality graph containing all domains of the machine topology.
as root of the team hierarchy with all units and associates the team with the global locality graph containing all domains of the machine topology.
Leaf nodes in the locality hierarchy are units, the lowest addressable domain category. A single unit has affinity to a specific physical core but may utilize multiple cores or shared memory segments exclusively. Domain capacities such as cores and shared memory are equally shared by the domain’s units if not specified otherwise. In the example illustrated in Fig. 3, two units assigned to a NUMA domain of 12 cores each utilize 6 cores.
When a team is split, its locality graph is partitioned among child teams such that a single partition is coherent and only contains domains with at least one leaf occupied by a unit in the child team. This greatly simplifies implementation of locality-aware algorithms as any visible locality domain is guaranteed to be accessible by some unit in the current team configuration.
4.1 Domain Attributes and Properties
The topological characteristics of a domain’s corresponding physical component are expressed as three correlated yet independent attributes:
-
 category of physical or logical component represented by the domain object such as “socket” or “L3D cache”
category of physical or logical component represented by the domain object such as “socket” or “L3D cache” -
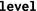 number of logical indirections between the locality domain and the hierarchy root; not necessarily related to distance
number of logical indirections between the locality domain and the hierarchy root; not necessarily related to distance -
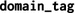 the domain’s hierarchical path from the root domain, consisting of relative subdomain offsets separated by a dot character.
the domain’s hierarchical path from the root domain, consisting of relative subdomain offsets separated by a dot character.
Domain tags serve as unique identifiers and allow to locate domains without searching the hierarchy. For any set of domains, the longest common prefix of their domain tags identifies their lowest common ancestor, for example. Apart from these attributes, a domain is associated with two property maps:
- Capabilities :
-
invariant hardware locality properties that do not depend on the locality graph’s structure, like the number of threads per core, cache sizes, or SIMD width.
- Capacities :
-
derivative properties that might become invalid when the graph structure is modified, like L3 cache size available per unit.
Dynamic locality support requires means to specify transformations on the physical topology graph as views. Views realize a projection but must not actually modify the original graph data. Invariant properties are therefore stored separately and assigned to domains by reference only. A view only contains a shallow copy of the graph data structure and only the capacities of domains included in the view.
4.2 Operations on Locality Domains
A specific domain node can be queried by their unique domain tag or unit. Conceptually, locality hierarchy model is a directed, multi-relational graph so any operation expressed in path algebra for multi-relational graphs is conceptually feasible and highly expressive, but overly complex. For the use cases we identified in applications so far, it is sufficient to provide the operations with semantics listed in Fig. 4, apart from unsurprising operations for node traversal and lookup by identifier. These can be applied to any domain in a locality hierarchy, including its root domain to include the entire topology.
Operations for selection and exclusion are applied to subdomains recursively. The runtime interface can define complex high-level functions based on combinations of these fundamental operations. To restrict a virtual topology to a single NUMA affinity, for example:

The  operation combines an arbitrary set of domains in a logical group. This is useful in various situations, especially when specific units are assigned to special roles, often depending on a phase in an algorithm. For example, Intel suggests the leader role communication patternFootnote 1 for applications running MPI processes on Xeon Phi accelerator modules where communication between MPI ranks on host and accelerator is restricted in the reduction phase to a single, dedicated process on either side.
operation combines an arbitrary set of domains in a logical group. This is useful in various situations, especially when specific units are assigned to special roles, often depending on a phase in an algorithm. For example, Intel suggests the leader role communication patternFootnote 1 for applications running MPI processes on Xeon Phi accelerator modules where communication between MPI ranks on host and accelerator is restricted in the reduction phase to a single, dedicated process on either side.
As groups are virtual, their level is identical to the original LCA of the grouped domains and their communication cost is 0. Like any other modification of a locality graph’s structure, adding domain groups does not affect measures distance or communication cost as a logical rearrangement has, of course, no effect on physical connectivity. Figure 5 illustrates the steps of the domain grouping algorithm.
4.3 Specifying Distance and Affinity Metrics
Any bidirectional connection between a domain and its adjacent subdomains in the locality hierarchy model represents a physical bus exhibiting characteristic communication overhead such as a cache crossbar or a network interconnect. Therefore, a cost function cost(d) can be specified for any domain d to specify communication cost of the medium connecting its immediate subdomains. This allows to define a measure of locality for a pair of domains \((d_a,d_b)\) as the cumulative cost of the shortest path connection, restricted to domains below their lowest common ancestor (LCA). A domain has minimal distance 0 to itself.
Heterogeneous hosts require communication schemes and virtual process topologies that are specific to hardware configuration and the algorithm scenario. In a typical accelerator offload algorithm with a final reduction phase, processes first consider physical distance and horizontal locality. For communication in the reduction phase, distance is measured based on PCI interface affinity to optimize for vertical locality.
5 The dyloc Library
Initial concepts of the dyloc library have been implemented for locality discovery in the DASH runtime. In this, hardware locality information from hwloc, PAPI, libnuma, and LIKWID has been combined into a unified data structure that allowed to query locality information by process ID or affinity.
This query interface proved to be useful for static load balancing on heterogeneous systems like SuperMIC and was recently made available as the standalone library dyloc Footnote 2. Figure 7 outlines the structure of its dependencies and interfaces, with APIs provided for C and C++.
The boost graph libraryFootnote 3 offers an ideal abstraction for high-level operations on locality domain graphs. These are exposed in the C++ developer API and may be modified by user-specified extensions. The boost graph concepts specify separate storage of node properties and the graph structure. This satisfies the requirements of the domain topology data structure as introduced in Sect. 4 where domain capabilities are independent from the topology structure. As a consequence, consolidated views on a locality graph do not require deep copies of domain nodes. Only their accumulative capacities have to be recalculated.
We consider compatibility to existing concepts in the hwloc API a critical requirement and therefore ensured, to the best of our knowledge and understanding, that configurations of dyloc’s graph-based locality model can be projected to a well-defined hierarchy and exported to hwloc data structures.
A possible scenario is illustrated in Fig. 6. Topology data provided by hwloc for separate nodes are combined into a unified dyloc locality graph that supports high-level operations. Queries and transformations on the graph return a light-weight view that can be converted to a hwloc topology and then used in applications instead of topology objects obtained from hwloc directly.
6 Proof of Concept: Work Balancing Min_element on SuperMIC
The SuperMIC systemFootnote 4 consists of 32 compute nodes with identical hardware configuration of two NUMA domains, each containing an Ivy Bridge (8 cores) host processor and a Xeon Phi “Knights Corner” coprocessors (Intel MIC 5110P) as illustrated in Fig. 2. This system configuration is an example of both increased depth of the machine hierarchy and heterogeneous node-level architecture.

To substantiate how asymmetric, heterogeneous system configurations introduce a new dimension to otherwise trivial algorithms, we briefly discuss the implementation of the  algorithm in DASH. Its original variant is implemented as follows: domain decomposition divides the element range into contiguous blocks of identical size. All units then run a thread-parallel scan on their local block for a local minimum and enter a collective barrier once it has been found. Once all units completed their local work load, local results are reduced to the global minimum. For portable work load balancing on heterogeneous systems, the employed domain decomposition must dynamically adapt to the unit’s available locality domain-capacities and -capabilities:
algorithm in DASH. Its original variant is implemented as follows: domain decomposition divides the element range into contiguous blocks of identical size. All units then run a thread-parallel scan on their local block for a local minimum and enter a collective barrier once it has been found. Once all units completed their local work load, local results are reduced to the global minimum. For portable work load balancing on heterogeneous systems, the employed domain decomposition must dynamically adapt to the unit’s available locality domain-capacities and -capabilities:
- Capacities: :
-
total memory capacity on MIC modules is 8 GB for 60 cores, significantly less than 64 GB for 32 cores on host level
- Capabilities: :
-
MIC cores have a base clock frequency of 1.1 GHz and 4 SMT threads, with 2.8 GHz and 2 SMT threads on host level (Fig. 8).
Listing 1.1 contains the abbreviated modified implementation of the  scenario utilizing the runtime support proposed in this work. The full implementation is available in the DASH source distributionFootnote 5.
scenario utilizing the runtime support proposed in this work. The full implementation is available in the DASH source distributionFootnote 5.
7 Conclusion and Future Work
Even with the improvements to the min_element algorithm explained in Sect. 6, the implementation is not fully portable, yet: the load factor to adjust for the differing elements/ms has been determined in auto tuning. In future work, we will extend the locality hierarchy model by means to register progress in local work loads to allow self-adaptation of algorithms depending on load imbalance measured for specified sections.
Notes
- 1.
- 2.
- 3.
- 4.
- 5.
References
Bauer, M., Clark, J., Schkufza, E., Aiken, A.: Programming the memory hierarchy revisited: supporting irregular parallelism in Sequoia. ACM SIGPLAN Not. 46(8), 13–24 (2011)
Chamberlain, B.L., Deitz, S.J., Iten, D., Choi, S.-E.: User-defined distributions and layouts in Chapel: philosophy and framework. In: Proceedings of 2nd USENIX Conference on Hot Topics in Parallelism, p. 12. USENIX Association (2010)
Da Costa, G., Fahringer, T., Gallego, J.A.R., Grasso, I., Hristov, A., Karatza, H., Lastovetsky, A., Marozzo, F., Petcu, D., Stavrinides, G., et al.: Exascale machines require new programming paradigms and runtimes. Supercomput. Front. Innov. 2(2), 6–27 (2015)
Fuchs, T., Fürlinger, K.: A multi-dimensional distributed array abstraction for PGAS. In: Proceedings of 18th IEEE International Conference on High Performance Computing and Communications (HPCC 2016), Sydney, Australia, pp. 1061–1068, December 2016
Fuchs, T., Fürlinger, K.: Expressing and exploiting multi-dimensional locality in DASH. In: Bungartz, H.-J., Neumann, P., Nagel, W.E. (eds.) Software for Exascale Computing - SPPEXA 2013-2015. LNCSE, vol. 113, pp. 341–359. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-40528-5_15
Fürlinger, K., Fuchs, T., Kowalewski, R.: DASH: a C++ PGAS library for distributed data structures and parallel algorithms. In: Proceedings of 18th IEEE International Conference on High Performance Computing and Communications (HPCC 2016), Sydney, Australia, pp. 983–990, December 2016
Goglin, B.: Managing the topology of heterogeneous cluster nodes with hardware locality (hwloc). In: International Conference on High Performance Computing & Simulation (HPCS 2014), July 2014, Bologna, Italy. IEEE (2014)
Goglin, B.: Exposing the locality of heterogeneous memory architectures to HPC applications. In: 1st ACM International Symposium on Memory Systems (MEMSYS 2016). ACM (2016)
Hajiaghayi, M., Johnson, T., Khani, M.R., Saha, B.: Hierarchical graph partitioning. In: Proceedings of 26th ACM Symposium on Parallelism in Algorithms and Architectures, pp. 51–60. ACM (2014)
Kamil, A.A., Yelick, K.A.: Hierarchical additions to the SPMD programming model. Technical report UCB/EECS-2012-20, EECS Department, University of California, Berkeley, February 2012
Tate, A., Kamil, A., Dubey, A., Größlinger, A., Chamberlain, B., Goglin, B., Edwards, C., Newburn, C.J., Padua, D., Unat, D., et al.: Programming abstractions for data locality. Research report, PADAL Workshop 2014, 28–29 April, Swiss National Supercomputing Center (CSCS), Lugano, Switzerland, November 2014
Yan, Y., Zhao, J., Guo, Y., Sarkar, V.: Hierarchical place trees: a portable abstraction for task parallelism and data movement. In: Gao, G.R., Pollock, L.L., Cavazos, J., Li, X. (eds.) LCPC 2009. LNCS, vol. 5898, pp. 172–187. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13374-9_12
Acknowledgements
This work was partially supported by the German Research Foundation (DFG) by the German Priority Programme 1648 Software for Exascale Computing (SPPEXA) and by the German Federal Ministry of Education and Research (BMBF) through the MEPHISTO project, grant agreement 01IH16006B.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Fuchs, T., Fürlinger, K. (2018). Runtime Support for Distributed Dynamic Locality. In: Heras, D., et al. Euro-Par 2017: Parallel Processing Workshops. Euro-Par 2017. Lecture Notes in Computer Science(), vol 10659. Springer, Cham. https://doi.org/10.1007/978-3-319-75178-8_14
Download citation
DOI: https://doi.org/10.1007/978-3-319-75178-8_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-75177-1
Online ISBN: 978-3-319-75178-8
eBook Packages: Computer ScienceComputer Science (R0)








 category of physical or logical component represented by the domain object such as “socket” or “L3D cache”
category of physical or logical component represented by the domain object such as “socket” or “L3D cache”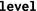 number of logical indirections between the locality domain and the hierarchy root; not necessarily related to distance
number of logical indirections between the locality domain and the hierarchy root; not necessarily related to distance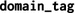 the domain’s hierarchical path from the root domain, consisting of relative subdomain offsets separated by a dot character.
the domain’s hierarchical path from the root domain, consisting of relative subdomain offsets separated by a dot character.




 algorithm exposing the effect of load balancing based on dynamic hardware locality
algorithm exposing the effect of load balancing based on dynamic hardware locality