Abstract
The aim of this paper is a review on recently found new aspects in the theory of micropolar media. For this purpose the necessary theoretical framework for a micropolar continuum is initially presented. Here the standard macroscopic equations for mass, linear and angular momentum, and energy are extended in two ways. First, the aspect of coupling linear and angular rotational kinetic energies is emphasized. Second, the equations are complemented by a recently proposed kinetic equation for the moment of inertia tensors containing a production term. We then continue to explore the possibilities of this new term for the case of micropolar media encountering a change of moment of inertia during a thermomechanical process. Particular emphasis is put on the general form of the production of moment of inertia for a transversally isotropic medium and its potential to describe, for example, structural changes from a transversally isotropic state to an isotropic one. In order to be able to comprehend and to study the influence of the various material parameters the production term is interpreted mesoscopically and various other examples are solved in closed form. Moreover, in context with the presented example problems it will also become clear that the traditional Lagrangian way of describing the motion of solids might sometimes no longer be adequate and must then be replaced by a Eulerian approach.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
References
Bansal R (2006) Fundamentals of engineering electromagnetics. CRC press
Eremeyev VA, Pietraszkiewicz W (2012) Material symmetry group of the non-linear polar-elastic continuum. International Journal of Solids and Structures 49(14):1993–2005
Eremeyev VA, Lebedev LP, Altenbach H (2012) Foundations of micropolar mechanics. Springer Science & Business Media, Heidelberg, New York, Dordrecht, London
Eringen AC, Kafadar CB (1976) Polar field theories. In: Continuum physics IV. Academic Press, London
Eringen C (2002) Nonlocal continuum field theories. Springer Science & Business Media, New York
de Gennes PG (1971) Short range order effects in the isotropic phase of nematics and cholesterics. Molecular Crystals and Liquid Crystals 12(3):193–214
de Gennes PG, Prost J (1995) The physics of liquid crystals, second edition. Oxford University Press, Oxford
Gross D, Xu B (2015) Micromechanical modeling of cellular ferroelectrets by using internal variables. Procedia IUTAM 12:62–72
Hibbeler RC (2010) Dynamics. 12th ed. Prentice Hall, Upper Saddle River (NJ)
Holzapfel GA (2000) Nonlinear Solid Mechanics: A Continuum Approach for Engineering. John Wiley & Sons, Ltd., West Sussex, England
Ivanova EA, Vilchevskaya EN (2016) Micropolar continuum in spatial description. Continuum Mechanics and Thermodynamics 28(6):1759–1780
Kestelman VN, Pinchuk LS, Goldade VA (2013) Electrets in Engineering: Fundamentals and Applications. Springer Science & Business Media
Müller I (1985) Thermodynamics. Pitman
Müller WH, Vilchevskaya EN, Weiss W (2017) A meso-mechanics approach to micropolar theory: A farewell to material description. Physical Mesomechanics 20(3):13–24
Naumenko K, Altenbach H (2007) Modeling of creep for structural analysis. Springer Science & Business Media, Singapore
Reich FA, Rickert W, Stahn O, Müller WH (2017) Magnetostriction of a sphere: Stress development during magnetization and residual stresses due to the remanent field. Continuum Mechanics and Thermodynamics 29(2):535–557
Smith GF (1965) On isotropic integrity bases. Archive for rational mechanics and analysis 18(4):282–292
Wikipedia (2017) Ferroelectret. https://en.wikipedia.org/wiki/Ferroelectret
Zhilin PA (2003)
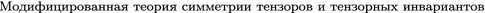 (Modified theory of the theory of tensors and tensor invariants, in Russian).
(Modified theory of the theory of tensors and tensor invariants, in Russian). 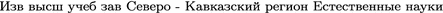 (S):176–195
(S):176–195Zhilin PA (2005) Symmetries and orthogonal invariants in oriented space. In: Proceedings of the XXXII Summer School - Conference “Advanced Problems in Mechanics”, St. Petersburg, pp 470–483
Zhilin PA (2015)
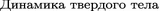 (Dynamics of the Solid Body, in Russian).
(Dynamics of the Solid Body, in Russian). 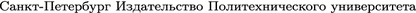 , St. Petersburg
, St. Petersburg
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Müller, W.H., Vilchevskaya, E.N. (2018). Micropolar Theory with Production of Rotational Inertia: A Rational Mechanics Approach. In: Altenbach, H., Pouget, J., Rousseau, M., Collet, B., Michelitsch, T. (eds) Generalized Models and Non-classical Approaches in Complex Materials 1. Advanced Structured Materials, vol 89. Springer, Cham. https://doi.org/10.1007/978-3-319-72440-9_30
Download citation
DOI: https://doi.org/10.1007/978-3-319-72440-9_30
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-72439-3
Online ISBN: 978-3-319-72440-9
eBook Packages: EngineeringEngineering (R0)


 (Modified theory of the theory of tensors and tensor invariants, in Russian).
(Modified theory of the theory of tensors and tensor invariants, in Russian).  (S):176–195
(S):176–195 (Dynamics of the Solid Body, in Russian).
(Dynamics of the Solid Body, in Russian).  , St. Petersburg
, St. Petersburg