Abstract
Logic rules and inference are fundamental in computer science and have been studied extensively. However, prior semantics of logic languages can have subtle implications and can disagree significantly.
This paper describes a simple new semantics for logic rules, founded semantics, and its straightforward extension to another simple new semantics, constraint semantics, that unify the core of different prior semantics. The new semantics support unrestricted negation, as well as unrestricted existential and universal quantifications. They are uniquely expressive and intuitive by allowing assumptions about the predicates and rules to be specified explicitly. They are completely declarative and relate cleanly to prior semantics. In addition, founded semantics can be computed in linear time in the size of the ground program.
This work was supported in part by NSF under grants CCF-1414078, CNS-1421893, IIS-1447549, CCF-1248184, CCF-0964196, and CCF-0613913; and ONR under grants N000141512208 and N000140910651.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
Even a contrived example that demonstrates the worst-case quadratic-time computation of WFS has been challenging to find. For example, the quadratic-time example in [13] turns out to be linear in XSB; after significant effort between us and Warren, we found a much more sophisticated example that appears to take quadratic time, but a remaining bug in XSB makes the correctness of its computation unclear.
References
Apt, K.R., Bol, R.N.: Logic programming and negation: a survey. J. Log. Program. 19, 9–71 (1994)
Fitting, M.: Fixpoint semantics for logic programming: a survey. Theor. Comput. Sci. 278(1), 25–51 (2002)
Clark, K.L.: Negation as failure. In: Gallaire, H., Minker, J. (eds.) Logic and Databases, pp. 293–322. Plenum Press, New York (1978)
Van Gelder, A., Ross, K., Schlipf, J.S.: The well-founded semantics for general logic programs. J. ACM 38(3), 620–650 (1991)
Gelfond, M., Lifschitz, V.: The stable model semantics for logic programming. In: Proceedings of the 5th International Conference and Symposium on Logic Programming, pp. 1070–1080. MIT Press (1988)
Apt, K.R., Blair, H.A., Walker, A.: Towards a theory of declarative knowledge. In: Foundations of Deductive Databases and Logic Programming, pp. 89–148. Morgan Kaufman (1988)
Fitting, M.: A Kripke-Kleene semantics for logic programs. J. Log. Program. 2(4), 295–312 (1985)
Ceri, S., Gottlob, G., Tanca, L.: Logic Programming and Databases. Springer, Heidelberg (1990)
Abiteboul, S., Hull, R., Vianu, V.: Foundations of Databases: The Logical Level. Addison-Wesley, Reading (1995)
Liu, Y.A., Stoller, S.D.: The founded semantics and constraint semantics of logic rules. Computing Research Repository arXiv:1606.06269 [cs.LO] (Revised 2017) (2016)
Chen, W., Kifer, M., Warren, D.S.: HiLog: a foundation for higher-order logic programming. J. Log. Program. 15(3), 187–230 (1993)
Liu, Y.A., Stoller, S.D.: From datalog rules to efficient programs with time and space guarantees. ACM Trans. Program. Lang. Syst. 31(6), 1–38 (2009)
Zukowski, U.: Flexible computation of the well-founded semantics of normal logic programs. Ph.D. thesis, Faculty of Computer Science and Mathematics, University of Passau (2001)
Przymusinski, T.C.: Well-founded and stationary models of logic programs. Ann. Math. Artif. Intell. 12(3), 141–187 (1994)
Ramakrishnan, R., Ullman, J.D.: A survey of deductive database systems. J. Log. Program. 23(2), 125–149 (1995)
Lloyd, J.W., Topor, R.W.: Making Prolog more expressive. J. Log. Program. 1(3), 225–240 (1984)
Sato, T., Tamaki, H.: Transformational logic program synthesis. In: Proceedings of the International Conference on Fifth Generation Computer Systems, pp. 195–201 (1984)
Jaffar, J., Lassez, J.-L., Maher, M.J.: Some issues and trends in the semantics of logic programming. In: Shapiro, E. (ed.) ICLP 1986. LNCS, vol. 225, pp. 223–241. Springer, Heidelberg (1986). https://doi.org/10.1007/3-540-16492-8_78
Chan, D.: Constructive negation based on the completed database. In: Proceedings of the 5th International Conference and Symposium on Logic Programming, pp. 111–125. MIT Press (1988)
Foo, N.Y., Rao, A.S., Taylor, A., Walker, A.: Deduced relevant types and constructive negation. In: Proceedings of the 5th International Conference and Symposium on Logic Programming, pp. 126–139 (1988)
Stuckey, P.J.: Constructive negation for constraint logic programming. In: Proceedings of the 6th Annual IEEE Symposium on Logic in Computer Science, pp. 328–339 (1991)
Denecker, M., Ternovska, E.: A logic of nonmonotone inductive definitions. ACM Trans. Comput. Log. 9(2), 14 (2008)
Dung, P.M.: On the relations between stable and well-founded semantics of logic programs. Theor. Comput. Sci. 105(1), 7–25 (1992)
Lin, F., Zhao, Y.: Assat: computing answer sets of a logic program by sat solvers. Artif. Intell. 157(1–2), 115–137 (2004)
Acknowledgment
We thank David S. Warren, Michael Kifer, Anil Nerode, Tuncay Tekle, Molham Aref, Marc Denecker, Cordell Green, Goyal Gupta, Bob Kowalski, Fangzhen Lin, Alberto Pettorossi, Maurizio Proietti, Neng-Fa Zhou, and many others for helpful comments and discussions on logic languages, semantics, and efficient computations.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Comparison of Semantics for Well-Known Small Examples and More
A Comparison of Semantics for Well-Known Small Examples and More
Table 2 shows well-known example rules and more for tricky boundary cases in the semantics, where all uncertain predicates that are in a conclusion are declared complete, but not closed, and shows different semantics for them.
-
Programs 1 and 2 contain only negative cycles. All three of Founded, WFS, and Fitting agree. All three of Constraint, SMS, and Supported agree.
-
Programs 3 and 4 contain only positive cycles. Founded for certain agrees with WFS; Founded for uncertain agrees with Fitting. Constraint for certain agrees with SMS; Constraint for uncertain agrees with Supported.
-
Programs 5 and 6 contain no cycles. Founded for certain agrees with WFS and Fitting; Founded for uncertain has more undefined. Constraint for certain agrees with SMS and Supported; Constraint for uncertain has more models.
-
Programs 7 and 8 contain both negative and positive cycles. For program 7 where
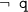 and q are disjunctive, all three of Founded, WFS, and Fitting agree; Constraint and Supported agree, but SMS has no model. For program 8 where
and q are disjunctive, all three of Founded, WFS, and Fitting agree; Constraint and Supported agree, but SMS has no model. For program 8 where 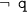 and q are conjunctive, Founded and Fitting agree, but WFS has q being \(F\); all three of Constraint, SMS, and Supported agree.
and q are conjunctive, Founded and Fitting agree, but WFS has q being \(F\); all three of Constraint, SMS, and Supported agree.
For all 8 programs, with default complete but not closed predicates, we have the following:
-
If all predicates are the default certain or uncertain, then Founded agrees with WFS, and Constraint agrees with SMS, with one exception for each:
-
(1)
Program 7 concludes q whether q is \(F\) or \(T\), so SMS having no model is an extreme outlier among all 6 semantics and is not consistent with common sense.
-
(2)
Program 8 concludes q if q is \(F\) and \(T\), so Founded semantics with q being \(U\) is imprecise, but Constraint has q being \(F\). WFS has q being \(F\) because it uses \(F\) for ignorance.
-
(1)
-
If predicates not in any conclusion are certain (not shown in Table 2 but only needed for q in programs 5 and 6), and other predicates are uncertain, then Founded equals Fitting, and Constraint equals Supported, as captured in Theorems 7 and 11, respectively.
-
If all predicates are uncertain, then Founded has all values being \(U\), capturing the well-known unclear situations in all these programs, and Constraint gives all different models except for programs 2 and 5, and programs 4 and 6, which are pair-wise equivalent under completion, capturing exactly the differences among all these programs.
Finally, if all predicates in these programs are not complete, then Founded and Constraint are the same as in Table 2 except that Constraint for uncertain becomes equivalent to truth values in first-order logic: programs 1 and 8 have an additional model, {q}, program 6 has an additional model, {\(\overline{\text{ p }}\), q}, and programs 2 and 5 have an additional model, {p,q}.
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG
About this paper
Cite this paper
Liu, Y.A., Stoller, S.D. (2018). Founded Semantics and Constraint Semantics of Logic Rules. In: Artemov, S., Nerode, A. (eds) Logical Foundations of Computer Science. LFCS 2018. Lecture Notes in Computer Science(), vol 10703. Springer, Cham. https://doi.org/10.1007/978-3-319-72056-2_14
Download citation
DOI: https://doi.org/10.1007/978-3-319-72056-2_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-72055-5
Online ISBN: 978-3-319-72056-2
eBook Packages: Computer ScienceComputer Science (R0)


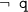 and
and 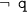 and
and