Abstract
The Kolmogorov axioms for probability functions are placed in the context of signed meadows. A completeness theorem is stated and proven for the resulting equational theory of probability calculus. Elementary definitions of probability theory are restated in this framework.
This paper is a shortened version of http://arxiv.org/abs/1307.5173v4.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Events are closed under \(-\vee -\), which represents alternative occurrence and \(-\wedge -\), which represents simultaneous occurrence, and under negation.
- 2.
Rational numbers and real numbers are instances of values.
- 3.
We will exclude probability functions with negative values, a phenomenon known in non-commutative probability theory, leaving the exploration of that kind of generalization to future work.
- 4.
In some cases the restriction to a single probability function P is impractical and providing a dedicated sort for such functions brings more flexibility and expressive power. This expansion may be achieved in different ways.
- 5.
We assume that in a context of partial functions an identity \(t=r\) is valid if either both sides are undefined or both sides are defined and equal. This convention, however, leaves room for alternative readings of the expressions at hand. In particular the definition given for \(x \lhd y \rhd z\) implies that whenever t is undefined, so is \(t \lhd r \rhd s\). That is not a very plausible feature of the conditional and in the presence of partial operations the conditional operator requires a different definition. These complications are to some extent avoided, or rather made entirely explicit, when working with total functions. The use of the notation \(P^\star (-|-)\) instead of the common notation \(P(-|-)\) is justified by the fact that unavoidably \(P^\star (-|-)\) inherits properties from the equational specification of the functions from which it has been made up. Such properties need not not coincide with what is expected from \(P(-|-)\).
- 6.
- 7.
More generally, \(\textit{BA}+\textit{Md}+\textit{Sign}+\textit{PF}_P\) is sound for the class of
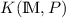 -structures with
-structures with 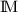 a signed cancellation meadow.
a signed cancellation meadow. - 8.
From this pair of inequalities one can derive the original Bell inequalities from [3]. The key observation of Bell was that quantum mechanics gives rise to the hypothesis that a 4-dimensional event space exists in which a family of joint probabilities for at most two dimensions can be found that violates the inequalities from the theorem.
- 9.
This meeting took place at Science Park Amsterdam, Friday June 7, 2013 under the heading “Frontiers of Forensic Science”, and was organized by Andrea Haker.
References
Adams, E.: Probability and the logic of conditionals. In: Hintikka, J., Suppes, P. (eds.) Aspects of Inductive Logic, pp. 265–316. North-Holland (1966)
Barber, D.: Bayesian Reasoning and Machine Learning. Cambridge University Press, Cambridge (2012). http://web4.cs.ucl.ac.uk/staff/D.Barber/pmwiki/pmwiki.php?n=Brml.Online. ISBN 0521518148, 9780521518147. On-line version 18 November 2015
Bell, J.S.: On the Einstein Podolsky Rosen paradox. Physics 1(3), 195–200 (1964)
Bergstra, J.A., Bethke, I., Ponse, A.: Cancellation meadows: a generic basis theorem and some applications. Comput. J. 56(1), 3–14 (2013). https://doi.org/10.1093/comjnl/bxs028. https://arxiv.org/abs/0803.3969v3
Bergstra, J.A., Bethke, I., Ponse, A.: Equations for formally real meadows. J. Appl. Log. 13(2, Part B), 1–23 (2015). https://doi.org/10.1016/j.jal.2015.01.004. https://arxiv.org/abs/1310.5011v4
Bergstra, J.A., Middelburg, C.A.: Inversive meadows and divisive meadows. J. Appl. Log. 9(3), 203–220 (2011). https://arxiv.org/abs/0907.0540v3
Bergstra, J.A., Middelburg, C.A.: Division by zero in involutive meadows. J. Appl. Log. 13(1), 1–12 (2015). https://arxiv.org/abs/1406.2092
Bergstra, J.A., Ponse, A.: Fracpairs and fractions over a reduced commutative ring. Indag. Math. 27, 727–748 (2016). https://doi.org/10.1016/j.indag.2016.01.007. https://arxiv.org/abs/1411.4410v2
Carlström, J.: Wheels - on division by zero. Math. Struct. Comput. Sci. 14(1), 143–184 (2004). https://doi.org/10.1017/S0960129503004110
Fine, A.: Joint distributions, quantum correlations, and commuting observables. J. Math. Phys. 23, 1306–1310 (1982). https://doi.org/10.1063/1.525514
Fine, A.: Hidden variables, joint probability, and the Bell inequalities. Phys. Rev. Lett. 48(5), 291–295 (1982). https://doi.org/10.1103/PhysRevLett.48.291
Milne, P.: Bruno de Finetti and the logic of conditional events. Br. J. Philos. Sci. 48, 195–232 (1997)
de Muynck, W.M.: Foundations of quantum mechanics, an empiricist approach. In: Fundamental Theories of Physics, vol. 127. Kluwer Academic Publishers (2002). Pre-publication version: http://www.phys.tue.nl/ktn/Wim/Kluwerbookprepversion.pdf
Padmanabhan, H.: A self-dual equational basis for Boolean algebras. Canad. Math. Bull. 26(1), 9–12 (1983)
Rastall, P.: The Bell inequalities. Found. Phys. 13(6), 555–570 (1983)
dos Reis, T.S., Gomide, W., Anderson, J.A.D.W.: Construction of the transreal numbers and algebraic transfields. IAENG Int. J. Appl. Math. 46(1), 11–23 (2016). http://www.iaeng.org/IJAM/issues_v46/issue_1/IJAM_46_1_03.pdf
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 IFIP International Federation for Information Processing
About this paper
Cite this paper
Bergstra, J.A., Ponse, A. (2017). Probability Functions in the Context of Signed Involutive Meadows (Extended Abstract). In: James, P., Roggenbach, M. (eds) Recent Trends in Algebraic Development Techniques. WADT 2016. Lecture Notes in Computer Science(), vol 10644. Springer, Cham. https://doi.org/10.1007/978-3-319-72044-9_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-72044-9_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-72043-2
Online ISBN: 978-3-319-72044-9
eBook Packages: Computer ScienceComputer Science (R0)


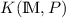 -structures with
-structures with 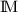 a signed cancellation meadow.
a signed cancellation meadow.