Keywords

1 Introduction

Much of science consists of discovering and modeling causal relationships [21, 29, 33]. Causal knowledge provides insight into mechanisms acting currently and prediction of outcomes that will follow when actions are taken (e.g., the chance that a disease will be cured if a particular medication is taken).

There has been substantial progress in the past 25 years in developing computational methods to discover causal relationships from a combination of existing knowledge, experimental data, and observational data. Given the increasing amounts of data that are being collected in all fields of science, this line of research has significant potential to accelerate scientific causal discovery. Some of the most significant progress in causal discovery research has occurred using causal Bayesian networks (CBNs) [29, 33].

Considerable CBN research has focused on constraint-based and Bayesian approaches to learning CBNs, although other approaches are being actively developed and investigated [30]. A constraint-based approach uses tests of conditional independence; causal discovery occurs by finding patterns of conditional independence and dependence that are likely to be present only when particular causal relationships exist. A Bayesian approach to learning typically involves a heuristic search for CBNs that have relatively high posterior probabilities.

The constraint-based and the Bayesian approaches each have significant, but different, strengths and weaknesses. The constraint-based approach can model and discover causal models with hidden (latent) variables relatively efficiently (depending upon what the true causal structure is, which variables are measured, and how many and what kind of hidden confounders have not been measured). This capability is important because oftentimes there are hidden variables that cause measured variables to be statistically associated (confounded). If such confounded relationships are not revealed, erroneous causal discoveries may occur.

The constraint-based approaches do not, however, provide a meaningful summary score of the chance that a causal model is correct. Rather, a single model is derived and output, without quantification regarding how likely it is to be correct, relative to alternative models. In contrast, Bayesian methods can generate and probabilistically score multiple models, outputting the most probable one. By doing so, they may increase the chance of finding a model that is causally correct. They also can quantify the probability of the top scoring model relative to other models that are considered in the search. The top scoring model might be close, or alternatively far away, from other models, which could be helpful to know. The Bayesian scoring of causal models that contain hidden confounders is very expensive computationally, however. Consequently, the practical application of Bayesian methods is largely relegated to CBNs that do not contain hidden variables, which significantly decreases the general applicability of these methods for causal discovery. In addition, while constraint-based methods can incorporate domain beliefs known with certainty (e.g., that a gene X is regulated by gene Y), they cannot incorporate domain beliefs about what is likely but not certain (e.g., that there is a 0.8 chance that gene X is regulated by gene Z). In general, Bayesian methods can incorporate as prior probabilities domain beliefs about what is likely but not certain, which is a common situation.

The current paper investigates a hybrid approach that combines strengths of constraint-based and Bayesian methods. The hybrid method derives the probability that relevant constraints are true. Consider a causal model (or equivalence class of models) that entails a set of conditional independence constraints over the distribution of the measured variables. In the hybrid approach, the probability of the model being correct is equal to the probability that the constraints that uniquely characterize the model (or class of models) are correct. This hybrid method exhibits the computational efficiency of a constraint-based method combined with the Bayesian approaches ability to quantitatively compare alternative causal models according to their posterior probabilities and to incorporate non-certain background beliefs.

The remainder of this paper first provides relevant background in Sect. 2. Sections 3 and 4 then describe a method for the Bayesian scoring of constraints, how to combine it with a constraint-based learning method, and two techniques for evaluating the posterior probabilities of models that are output. Section 5 describes an evaluation of the method using data generated from existing CBNs.

2 Background

A causal Bayesian network (CBN) is a Bayesian network in which each arc is interpreted as a direct causal influence between a parent node (a cause) and a child node (an effect), relative to the other nodes in the network [29]. In this paper, we focus on the discovery of CBN structures because this task is generally the first and most crucial step in the causal discovery process. As shorthand, the term CBN will denote a CBN structure, unless specified otherwise. We also focus on learning CBNs from observational data, since this is among the most challenging causal learning tasks. General reviews of the topic are in [11, 14, 22].

2.1 Constraint-Based Learning of CBNs from Data

A constraint-based Bayesian network search algorithm searches for a set of Bayesian networks, all of which entail a particular set of conditional independence constraints, which we simply call constraints, that are judged to hold in a dataset of samples based on the results of tests applied to that data. It is usually not computationally or statistically feasible to actually test each possible constraint among the measure variables for more than a few dozen variables, so constraint-based algorithms typically select a sufficient subset of constraints to test. Generally, the subset of constraint tests that are performed within a sequence of such tests depends upon the results of previous tests.

Fast Causal Inference (FCI) [33] is a constraint-based causal discovery algorithm, which we discuss in more detail here because it serves as a good example of a constraint-based algorithm, and we use an adapted version of it, called Really Fast Causal Inference (RFCI) [10], in the research reported here. FCI takes as input observed sample data and optional deterministic background knowledge, and it outputs a graph, called a Partial Ancestral Graph (PAG). A PAG represents a Markov equivalence class of Bayesian networks (possibly with hidden variables) that entail the same constraints. A PAG model returned by FCI represents as much about the true causal graph as can be determined from the conditional independence relations among the observed variables [36]. In particular, under assumptions, the FCI algorithm has been shown to have correct output with probability 1.0 in the large sample limit, even if there are hidden confounders [36]. In addition, a modification of FCI can be implemented to run in polynomial time, if a maximum number of causes (parents) per node is specified [9].

Fig. 1.
figure 1

The PAG in (b) is learnable in the large sample limit from observational data generated by the causal model in (a), where \(H_{BC}\) is a hidden variable and the other variables are measured.

Full size image

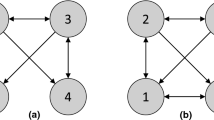
As an example, Fig. 1 shows in panel (b) the PAG that would be output by the FCI search if given a large enough sample of data from the data-generating CBN shown in panel (a), assuming the Markov and faithfulnessFootnote 1 conditions hold [33]. In panel (b), the subgraph \(B \leftrightarrow C\) represents that B and C are both caused by one or more hidden variables (i.e., they are confounded by a hidden variable). The subgraph \(C \rightarrow D\) represents that C is a cause of D and that there are no hidden confounders of C and D. The subgraph represents that either A causes B, A and B are confounded by a hidden variable, or both. Another edge possibility, which does not appear in the example, is X Y, which is compatible with the true causal model having X as cause of Y, Y as a cause of X, a hidden confounder of X and Y, or some acyclic combination of these three alternatives. The PAG in Fig. 1b indicates that not all the causal relationships in Fig. 1a can be learned from constraints on the data generated by that causal model, but some can be; in particular, Fig. 1b shows that is it possible to learn that B and C are both caused by a hidden variable(s) and that C causes D.

2.2 Bayesian Learning of CBNs from Data

Score-based methods derive a score for a CBN, given a dataset of samples and possibly prior knowledge or belief. Different types of scores have been developed and investigated, including the Minimum Description Length (MDL), Minimum Message Length (MML), and Bayesian scores [11, 18]. There are two major problems when learning a CBN using Bayesian approaches:

  • Problem 1 (model search): There is an infinite space of hidden-variable models, both in terms of parameters and hidden structure. Even when restrictions are assumed, the search space generally remains enormous in size, making it challenging to find the highest scoring CBNs.

  • Problem 2 (model scoring): Scoring a given CBN with hidden variables is also challenging. In particular, marginalizing over the hidden variables greatly complicates Bayesian scoring in terms of accuracy and computational tractability.

These two problems notwithstanding, several heuristic algorithms have been developed and investigated for scoring CBNs containing hidden variables. An early algorithm for this task was developed by Friedman [17]; it interleaved structure search with the application of EM. Other approaches include those based on variational EM [2] and a greedy search that incorporates EM [5]. These and related approaches were primarily developed to deal with missing data, rather than hidden variables for which all data are missing.

Several Bayesian algorithms have been specifically developed to score CBNs with hidden variables, including methods that use a Laplace approximation [19], an approach that uses EM and a form of clustering [16], and a structural expectation propagation method [23]. However, these methods do not search over the space of all CBNs that include a given set of measured variables. Rather, they require that the user manually provides the proposed CBN models to be scored [19], they search a very restricted space of models, such as bipartite graphs [23] or trees of hidden structure [7, 16], or they score ancestral relations between pairs of variables [28]. Thus, within a Bayesian framework, the automated discovery of CBNs that contain hidden variables remains an important open problem.

2.3 Hybrid Methods for Learning CBNs from Data

Researchers have also developed algorithms that combine constraint-based and Bayesian scoring approaches for learning CBNs [8, 12, 13, 24,25,26, 32, 34, 35]. However, these hybrid methods, except [8, 24, 26, 34], do not include the possibility that the CBNs being modeled contain hidden variables. When a CBN can contain hidden variables, the Bayesian learning task is much more difficult.

In [8], a Bayesian method is proposed to score and rank order constraints; then, it uses those rank-ordered constraints as inputs to a constraint-based causal discovery method. However, it does not derive the posterior probability of a causal model from the probability of the constraints that characterize the model. The method in [26] models the possibility of hidden confounders but it does not provide any quantification of the output graph. In [34], a method is proposed to convert p-values to posterior probabilities of adjacencies and non-adjacencies in a graph; then, those probabilities are used to identify neighborhoods of the graph in which all relations have probabilities above a certain threshold. This method is, in fact, a post-processing step on the skeleton of the output network and not applicable to convert p-values to probabilities while running a constraint-based search method. It also does not provide a way of computing posterior probability of the whole output PAG. [24] introduces a logic-based method to reconstruct ancestral relations and score their marginal probabilities; it does not provide the probability of the output graph, however. In [24], authors mentioned that modeling the relationships among the constraints may be an improvement; in this paper, we propose an empirical way of modeling such relationships.

The research reported in [20] is the closest previous work of which we are aware to that introduced here. It describes how to score constraints on graphs by treating the constraints as independent of each other. The method is very expensive computationally, however, and is reported as working on up to only 7 measured variables. The method we introduce was feasibly applied to a dataset containing 70 variables and plausibly is practical for considerably larger datasets. Also, the method in [20], as described, is limited to deriving just the most probable graph, rather than deriving a set of graphs, as we do, which can be rank ordered, compared, and used to perform selective model averaging that derives (for example) distributions over edge types.

3 The Proposed Hybrid Method

This paper investigates a novel approach based on Bayesian scoring of constraints (BSC) that has major strengths of the constraint-based and Bayesian approaches. Namely, BSC uses a Bayesian method to score the constraints, rather than score the CBNs directly. The posterior probability of a CBN will be proportional to the posterior probability of the correctness of the constraints that characterize that CBN (or class of CBNs). The BSC approach, therefore, attenuates both problems of the Bayesian approach listed in Sect. 2.2:

  • Problem 1 (model search): In the BSC approach, the search space is finite, not infinite as in the general Bayesian approach, because the number of possible constraints on a given set of measured variables is finite.

  • Problem 2 (model scoring): In a constraint-based approach, the constraints are on measured variables only, as discussed in Sect. 2. Thus, when BSC uses a Bayesian approach to derive the probability of a set of constraints and thereby score a CBN, it needs only to consider measured variables. In contrast, a traditional Bayesian approach must marginalize over hidden variables, which is a difficult and computationally expensive operation.

3.1 Bayesian Scoring of Constraints (BSC)

This section describes how to score a constraint \(r_i\). The term \(r_i\) denotes an arbitrary conditional independence of the form which is hypothesized to hold in the data-generating model that produced dataset D, where \(X_i\) and \(Y_i\) are variables of dataset D, and \(\mathbf{Z}_i\) is a subset of variables not containing \(X_i\) or \(Y_i\). Each \(r_i\) is called a conditional independence constraint, or constraint for short, where its value is either true or false. To score the posterior probability of a constraint \(r_i\), we assume that the only parts of data D that influence belief about \(r_i\) are the data \(D_i\), i.e. data about \(X_i\), \(Y_i\), and \(\mathbf{Z}_i\). This is called the data relevance assumption which results in:

$$\begin{aligned} P(r_i|D) = P(r_i|D_i) . \end{aligned}$$
(1)

Assuming uniform structure priors on constraints and applying Bayes rule result in the following equation:

$$\begin{aligned} P(r_i|D_i) = \frac{P(D_i|r_i)}{P(D_i|r_i)+P(D_i|\bar{r_i})} . \end{aligned}$$
(2)

Since we consider discrete variables in this paper, we can use the BDeu score in [18], which provides a closed-form solution for deriving marginal likelihoods, i.e. \(P(D_i|r_i)\) and \(P(D_i|\bar{r_i})\), in Eq. (2). To derive a value for \(P(D_i|r_i)\) (i.e., assuming \(X_i\) is independent of \(Y_i\) given \(\mathbf{Z}_i\)), we score the following BN structure, where \(\mathbf{Z}_i\) is a set of parents nodes for \(X_i\) and \(Y_i\):

$$X_i \leftarrow \mathbf{Z}_i \rightarrow Y_i$$

To compute \(P(D_i|\bar{r_i})\) (i.e., assuming \(X_i\) and \(Y_i\) are dependent given \(\mathbf{Z}_i\)) we score the following BN structure:

$$\mathbf{Z}_i \rightarrow X_iY_i$$

where \(X_iY_i\) denotes a new node whose values are the Cartesian product of the values of \(X_i\) and \(Y_i\). This is similar to scoring a DAG that consists of the following edges: \(X_i \leftarrow \mathbf{Z}_i\rightarrow Y_i\) and \(X_i \rightarrow Y_i\), which has been used previously [20]. In general, however, any Bayesian test of conditional independence can be used.

3.2 RFCI-BSC (RB)

This section describes an algorithm that combines constraint-based model search with the BSC method described in Sect. 3.1. As mentioned, RFCI [10] is a constraint-based algorithm for discovering the causal structure of the data-generating process in the presence of latent variables using Partial Ancestral Graphs (PAGs) as a representation, which encodes a Markov equivalence class of Bayesian networks (possibly with latent variables). RFCI has two stages. The first stage involves a selective search for the constraints among the measured variables, which is called adjacency search. The second stage involves determining the causal relationships among pairs of nodes that are directly connected according to the first stage; this stage is called the orientation phase.

We adapted RFCI to perform model search using BSC. We call this algorithm RFCI-BSC, or RB for short. During the first stage of search, when RFCI requests that an independence condition be tested, RB uses BSC to determine the probability p that independence holds. It then samples with probability p whether independence holds and returns that result to RFCI. To do so, it generates a random number U from Uniform[0, 1]; if \(U \le p\) then it returns true, and otherwise, it returns false. Ultimately, RFCI will complete stage 1 in this manner, then stage 2, and finally return a PAG.

RB then repeats the procedure in the previous paragraph n times to generate up to n unique PAG models. Let each repetition be called a round. Since the set of constraints generated in each round is determined stochastically (i.e. sampling with probability p), these rounds will produce many different sets of constraints, and consequently, different PAGs. Algorithm 1 shows pseudo-code of the RB method that inputs dataset D and the number of rounds n. It then outputs a set of at most n PAGs and for each PAG, an associated set of constraints that were queried during the RFCI search. Note that RFCI\(^\star \) in this procedure denotes the RFCI search that uses BSC to evaluate each constraint, rather than using frequentist significant testing. The computational complexity of RB is O(n) times that of RFCI, since it calls RFCI n times. In the next section, we propose two methods to score each generated PAG model \(G_j\).

figure a

4 Scoring a PAG Using RB

Let \(\mathbf r\) be the union of all the independence conditions tested by RB over all rounds, which we will use to score each generated PAG model \(G_j\). Based on the axioms of probability, we have the following equation:

$$\begin{aligned} P(G_j|D)=\sum _{\mathbf{r}}{P(G_j|\mathbf{r}, D) \cdot P(\mathbf{r}|D}) , \end{aligned}$$
(3)

where the sum is over all possible value assignments to the constraints in set \(\mathbf{r}\). Although Eq. (3) is valid, it does not provide a useful method for calculating \(P(G_j|D)\). In this section, we propose a method to derive a way of computing \(P(G_j|D)\) effectively.

Assume that the data only influence belief about a causal model via belief about the conditional independence constraints given by \(\mathbf r\), i.e. \(P(G_j|\mathbf{r}, D)=P(G_j|\mathbf{r})\), which is a standard assumption of constraint-based methods. Therefore, we can rewrite Eq. (3) as following:

$$\begin{aligned} P(G_j|D)=\sum _{\mathbf{r}}{P(G_j|\mathbf{r}) \cdot P(\mathbf{r}|D}) . \end{aligned}$$
(4)

Although Eq. (4) is less general than a full Bayesian approach that integrates over CBN parameters, it is nonetheless more expressive than existing constraint-based methods that in essence assume that \(P(\mathbf r | D) = 1\) for a set of constraints \(\mathbf r\) that are derived using frequentist statistical tests.

Let \(\mathbf{r}_j^{'}\) denote the values of all the constraints in r, according to the independencies implied by graph \(G_j\) as tested by RFCI. Since RFCI finds a set of sufficient independence conditions that distinguishes \(G_j\) from all other PAGs, so that \(P(G_j | \mathbf{r = r}_{j}^{'}) = 1\) and \(P(G_j | \mathbf{r \ne r}_{j}^{'}) = 0\), Eq. (4) becomes:

$$\begin{aligned} P(G_j|D)=\sum _\mathbf{r}{P(G_j|\mathbf{r}) \cdot P(\mathbf{r}|D}) = P(\mathbf{r}=\mathbf{r}_{j}^{'}|D) . \end{aligned}$$
(5)

Section 3.1 describes a method to compute the probability of one constraint given data, i.e. \(P(r_i|D_i)\). Now, we need to extend it for a set of constraints, i.e. \(P(\mathbf{r}=\mathbf{r}_{j}^{'}|D)\) in Eq. (5). Applying the chain rule of probability, it becomes:

$$\begin{aligned} \begin{aligned} P(\mathbf{r}=\mathbf{r}_{j}^{'}|D)&=P(r_{1}^{'}, r_{2}^{'},r_{3}^{'}, ..., r_{m}^{'}|D) = \prod _{i=1}^{m}{P(r_{i}^{'}|r_{1}^{'}, r_{2}^{'}, ..., r_{i-1}^{'},D)} \\&= \prod _{i=1}^{m}{P(r_{i}^{'}|r_{1}^{'}, r_{2}^{'}, ..., r_{i-1}^{'},D_i)} \text {(assuming data relevance)} , \end{aligned} \end{aligned}$$
(6)

where \(r_{i}^{'}\) denotes the value of \(i^{th}\) constraint according its value given in \(\mathbf{r}_{j}^{'}\). Using Eq. (6), RB determines the most probable generated PAG and its posterior probability. For each pair of measured nodes, we can also use model averaging to estimate the probability distribution over each PAG edge type as follows: Since PAGs are being sampled (generated) according to their posterior distribution (under assumptions), the probability of edge E existing between nodes A and B is estimated as the fraction of the sampled PAGs that contain E between A and B. In the following subsections, we propose two methods to approximate the joint posterior probabilities of constraints.

4.1 BSC with Independence Assumption (BSC-I)

In the first method, we assume that constraints in set \(\mathbf{r}=\{r_1, r_2, ..., r_m\}\), which is a set of all independence constraints obtained by running RB algorithm, are independent of each other. We call this approach BSC-I. Given this assumption and Eq. (6), BSC-I scores an output graph as follows:

$$\begin{aligned} P(G_j|D) = P(\mathbf{r}=\mathbf{r}_{j}^{'}|D) = \prod _{i=1}^{m}{P(r_{i}^{'}|D_i)} , \end{aligned}$$
(7)

where \(P(r_{i}^{'}|D_i)\) can be computed as described in Sect. 3.1.

4.2 BSC with Dependence Assumption (BSC-D)

In this scoring approach, we model the possibility that the constraints are dependent, which often happens. The relationships among the constraints can be complicated, and to our knowledge, they have not been modeled previously. In the remainder of this section, we introduce an empirical method to model the relationships among conditional constraints.

Similar to BSC-I, consider \(\mathbf r\) as a set of all the independence constraints queried by the RB method. As we mentioned earlier, each constraint \(r_i \in \mathbf{r}\) has the form , where \(X_i\) and \(Y_i\) are variables of dataset D and \(\mathbf{Z}_i\) is a subset of variables not containing \(X_i\) or \(Y_i\). Each \(r_i\) can take two values, true (1) or false (0); therefore, it can be considered as a binary random variable.

figure b

We build a dataset, \(D_r\), of these binary random variables using bootstrap sampling [15] and the BSC method. To do so, we first bootstrap (re-sample with replacement) the data D; let \(sample_b\) denote the resulting dataset. Then, for each constraint \(r_i \in \mathbf{r}\), we compute the BSC score using \(sample_b\) and set its value to 1 if its BSC score is more than or equal to 0.5, and 0 otherwise. We repeat this entire procedure n times to fill in n rows of empirical data for the constraints. Algorithm 2 provides pseudo-code of this procedure. It inputs the original dataset D, the number of bootstraps n, and a set of constraints \(\mathbf{r}\). It outputs an empirical dataset \(D_r\) with n rows and \(m=|\mathbf{r}|\) columns. The Bootstrap(D) function in this procedure creates a bootstrap sample from D, and BSC(\(r_i,sample_b\)) computes the BSC score of constraint \(r_i\) using \(sample_b\).

The empirical data \(D_r\) can then be used to learn the relations among the constraints \(\mathbf{r}\). We learn a Bayesian network because doing so can be done efficiently with thousands of variables, such networks are expressive in representing the joint relationships among the variables, and inference of the joint state of the variables (constraints in this application) can be derived efficiently. We use an optimized implementation of the Greedy Equivalence Search (GES) [6], which is called Fast GES (FGES) [31] to learn a Bayesian network structure, \(BN_r\), that encodes the dependency relationships among the constraints \(\mathbf{r}\). We then apply a maximum a posteriori estimation method to learn the parameters of \(BN_r\) given \(D_r\), which we denote as \(\theta _r\). Finally, we use \(BN_r\) and \(\theta _r\) to factorize \(P(\mathbf{r}=\mathbf{r}_{j}^{'}|D)\) and score the output PAG as follows:

$$\begin{aligned} P(G_j|D) = P(\mathbf{r}=\mathbf{r}_{j}^{'}|D) = \prod _{i=1}^{m}{P(r_{i}^{'}|Pa(r_i), D)} , \end{aligned}$$
(8)

where \(r_{i}^{'}\) and \(Pa(r_i)\) denotes the parents of variable \(r_i\) in \(\mathbf{r}_{j}^{'}\) and its parents in \(BN_r\), respectively.

5 Evaluation

This section describes an evaluation of the RB method using each of the BSC-I and BSC-D scoring techniques, which we call RB-I and RB-D, respectively. Algorithm 3 provides pseudo-code of RB-I method, which inputs dataset D, the number of rounds n, and outputs the most probable PAG. It first runs the RB method (Algorithm 1) to get a set of PAGs \(\mathbf{\mathcal {G}}\) and constraints \(\mathbf{r}\). It then computes the posterior probability of each PAG \(G_i \in \mathbf{\mathcal {G}}\) using BSC-I and returns the most probable PAG, which is denoted by \(PAG\text {-} I\) in Algorithm 3. Note that RB-D would be exactly the same except for using BSC-D in line 3.

figure c
Table 1. Information about the CBNs used in the simulation experiments.
Full size table

5.1 Experimental Methods

To perform an evaluation, we first simulated data from manually constructed, previously published CBNs, with some variables designated as being hidden. We then provided that data to each of RB-I and RB-D. We compared the most probable PAG output by each of these two methods to the PAG consistent with the data-generating CBN. In particular, we simulated data from the Alarm [3], Hailfinder [1], and Hepar II [27] CBNs, which we obtained from [4]. Table 1 shows some key characteristics of each CBN. Using these benchmarks is beneficial in multiple ways. They are more likely to represent real-world distributions. Also, we can evaluate the results using the true underlying causal model, which we know by construction; otherwise, it is rare to find known causal models on more than a few variables and associated real, observational data.

To evaluate the effect of sample size, we simulated 200 and 2000 cases randomly from each CBN, according to the encoded joint probability distribution. In each CBN, we randomly designated 0.0%, 10.0%, and 20.0% of the confounder nodes to be hidden, which means data about those nodes were not provided to the discovery algorithms. In applying the two versions of the RB algorithm, we sampled 100 PAG models, according to the method described in Sect. 3.2 (i.e., \(n=100\) in Algorithm 1). Also, we bootstrapped the data 500 times (i.e., \(n=500\) in Algorithm 2) to create the empirical data for BSC-D scoring. For each network, we repeated the analyses in this paragraph 10 times, each time randomly sampling a different dataset. We refer to one of these 10 repetitions as a run.

Let \(PAG\text {-} I\) and \(PAG\text {-}D\) denote the sampled models that had the highest posterior probability when using BSC-I (see Eq. (7)) and BSC-D (see Eq. (8)) scoring methods, respectively. Let \(PAG \text {-} CS\) denote the model returned by RFCI when using a chi-squared test of independence, which is the standard approach; we used \(\alpha = 0.05\), which is a common alpha value used with RFCI. Let \(PAG \text {-} True\) be the PAG that represents all the causal relationships that can be learned about a CBN in the large sample limit when assuming faithfulness and using independence tests that are applied to observational data on the measured variables in a CBN.

We compared the causal discovery performance of \(PAG\text {-} I\), \(PAG\text {-} D\), and \(PAG\text {-}CS\) using \(PAG\text {-}True\) as the gold standard. For a given CBN (e.g., Alarm) we calculated the mean Structural Hamming Distance (SHD) between a given PAG G and \(PAG\text {-}True\), which counts the number of different edge marks over all 10 runs. For example, if the output graph contains the edge A while \(B \rightarrow A\) exists in \(PAG\text {-}True\), then edge-mark SHD of this edge is 2. Similarly, edge-mark SHD would be 1 if \(A \rightarrow B\) is in the output PAG but \(A \leftrightarrow B\) is in \(PAG\text {-}True\). Clearly, any extra or missing edge would count as 2 in terms of edge-mark SHD. We also measured the number of extra and/or missing edges (regardless of edge type) between a given PAG G and \(PAG\text {-}True\), which corresponds to the SHD between the skeletons (i.e., the adjacency graph) of the two PAGs. For instance, if one graph includes A B while there is no edge between these variables in the other one, then skeleton SHD would be 1. For each of the measurements, we calculated its mean and 95% confidence interval over the 10 runs.

Fig. 2.
figure 2

Skeleton and edge-mark SHD of output PAGs relative to the gold standards

Full size image

5.2 Experimental Results

Figure 2 shows the experimental results. The diagrams on the left show the SHD between the skeletons of each PAG and \(PAG\text {-}True\). The diagrams on the right-hand side represent the SHD of the edge marks between each output PAG and \(PAG\text {-}True\). For each diagram, circles and squares represent the average results for datasets with 2000 and 200 cases, respectively. The vertical error bars in the diagrams represent the 95% confidence interval around the average values. Also, each column labeled as \(H=0.0\), 0.1, or 0.2 shows the proportion of hidden variables in each experiment. Figure 2a and 2b show that using the RB method always improves both performance measures for the Alarm network, especially for small sample sizes. Similar results were obtained on Hepar II network (Fig. 2e and 2f). For Hailfinder, we observed significant improvements on both the skeleton and edge-marks SHD when the sample size is 2000. The results show that the edge-mark SHD always improves when applying the RB method. We observed that BSC-I and BSC-D performed very similarly.

We found that using BSC-I and BSC-D may result in different probabilities for the generated PAGs; however, the ordering of the PAGs according to their posterior probabilities is almost always the same. We conjecture that performance of BSC-I is analogous to a naive Bayes classifier, which often performs classification well, even though it can be highly miscalibrated due to its universal assumption of conditional independence.

6 Discussion

This paper introduces a general approach for Bayesian scoring of constraints that is applied to learn CBNs which may contain hidden confounders. It allows the input of informative prior probabilities and the output of causal models that are quantified by their posterior probabilities. As a preliminary study, we implemented and experimentally evaluated two versions of the method called RB-I and RB-D. We compared these methods to a method that applies the RFCI algorithm using a chi-squared test.

For the edge-mark SHD, RB-I and RB-D had statistically significantly better results than RFCI for all three networks for any sample size and fraction of hidden variables. The skeleton SHD was better for most tested scenarios when using RB-I and RB-D, except for Hailfinder with H = 0.1 and 200 samples, and Hepar II with 2000 samples. Overall, the results indicate that RB tends to be more accurate than RFCI in predicting and orienting edges. Also, both RB-I and RB-D methods perform very similarly. We found out that posterior probabilities obtained by each of these methods are not equal but they result in the same most probable PAG. As the sample size increases, we expect the constraints to become independent of each other, but in our experiments, dependence did not matter for SHD, even with small sample sizes. Interestingly, this provides support that the simpler BSC-I method is sufficient for the purpose of finding the most probable PAG.

The RB method is a prototype that can be extended in numerous ways, including the following: (a) Develop more general tests of conditional independence to learn CBNs that contain continuous variables or a mixture of continuous and discrete variables; (b) Perform selective Bayesian model averaging of the edge probabilities as described in Sect. 4; (c) Incorporate informative prior probabilities on constraints. For example, one way to estimate the prior probability \(P(r_i)\) for insertion into Eq. (2) is to use prior knowledge to define Maximal Ancestral Graph (MAG) edge probabilities for each pair of measured variables. Then, use those probabilities to stochastically generate a large set of graphs and retain those graphs that are MAGs. Finally, tally the frequency with which \(r_i\) holds in the set of MAGs as an estimate of \(P(r_i)\).

The evaluation reported here can be extended in several ways, such as using additional manually constructed CBNs to generate data, evaluating a wider range of data sample sizes and fractions of hidden confounders, and applying additional algorithms as methods of comparison [8, 17, 23]. Despite its limitations, the current paper provides support that the Bayesian scoring of constraints is a promising hybrid approach for the problem of learning the most probable causal model that can include hidden confounders. The results suggest that further investigation of the approach is warranted.