Abstract
We first introduce basic notions on Banach and Hilbert spaces. Afterwards, we recall some well-known results, which help prove the well-posedness of the various sets of equations we study throughout this book.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
In a vector space, a scalar product (⋅, ⋅) exhibits the following properties:
-
It is linear with respect to the first variable:
\(\forall a_1,a_2\in \mathbb {C},\ \forall v_1,v_2,w\in V,\ (a_1v_1+a_2v_2,w) = a_1(v_1,w) + a_2(v_2,w)\).
-
It is antilinear with respect to the second variable:
\(\forall a_1,a_2\in \mathbb {C},\ \forall v,w_1,w_2\in V,\ (v,a_1w_1+a_2w_2) = \overline {a_1}(v,w_1) + \overline {a_2}(v,w_2)\).
-
It is Hermitian:
\(\forall v,w\in V,\ (v,w) = \overline {(w,v)}\).
-
It is positive-definite:
∀v ∈ V ∖{0}, (v, v) > 0.
Then, \(\|\cdot \|\ :\ V\rightarrow \mathbb {R}\), defined by ∥v∥ = (v, v)1∕2, is a norm on V . Furthermore, the Cauchy-Schwarz inequality holds: ∀v, w ∈ V, |(v, w)|≤∥v∥ ∥w∥.
-
- 2.
More generally, one may define the resolvent and spectrum of an unbounded operator A from D(A) ⊂ X to X. In this case, the resolvent is
$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \rho(A)=\{\lambda\in\mathbb{C}\ :\ (A-\lambda I_X)(D(A))\mbox{ is dense in }X\,;\\ &\displaystyle &\displaystyle \hskip 15mm (A-\lambda I_X)^{-1} \mbox{ exists and is continuous from } (A-\lambda I_X)(D(A))\mbox{ to } X \}\,; \end{array} \end{aligned} $$the spectrum is \(\sigma (A)=\mathbb {C}\setminus \rho (A)\), and it can further be decomposed into the disjoint union of the point spectrum , the continuous spectrum and the residual spectrum (see [93, Chapter VIII, §1] for details). As a rule, the notions of a continuous or residual spectrum will not be needed for the study of operators in this book.
- 3.
Some of these results are consequences of the Fredholm alternative, which we choose to state hereafter within the framework of Hilbert spaces.
- 4.
V ′ can also be called the antidual space. We choose the denomination dual space, which also applies for vector spaces defined over \(\mathbb {R}\), and continuous linear forms. Given v ∈ V , f v : w↦(v, w) V defines an element of V ′. According to the Riesz Theorem 4.2.1 below, v↦f v is a bijective isometry from V to V ′. In addition, V ′ can be made into a Hilbert space by defining its scalar product via \((f_v,f_w)_{V'}=(v,w)_V\), for all v, w ∈ V .
- 5.
A Hilbert basis of V is a countable set \((e_k)_{k\in \mathbb {N}}\) of elements of V , such that, for all k, ℓ, (e k , e ℓ ) V = δ kℓ , and
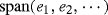 is dense in V . Then, for all v ∈ V , one has \(v=\sum _{k\in \mathbb {N}}(v,e_k)_V\, e_k\) and \(\|v\|{ }_V^2=\sum _{k\in \mathbb {N}}(v,e_k)_V^2\) (Bessel-Parseval identity).
is dense in V . Then, for all v ∈ V , one has \(v=\sum _{k\in \mathbb {N}}(v,e_k)_V\, e_k\) and \(\|v\|{ }_V^2=\sum _{k\in \mathbb {N}}(v,e_k)_V^2\) (Bessel-Parseval identity). - 6.
Let us explain briefly this construction when the imbedding W ⊂ c V is compact; this condition will hold in all the cases encountered in this book. Using Corollary 4.5.12 below, which is a straightforward consequence of Theorem 4.1.20, one constructs a Hilbert basis \((e_k)_{k\in \mathbb {N}}\) of V whose elements belong to W, and a nondecreasing sequence of strictly positive numbers \((\mu _k)_{k\in \mathbb {N}}\) tending to + ∞ such that:
$$\displaystyle \begin{aligned} \forall w\in W,\quad (e_k, w)_W = \mu_k^2\, (e_k, w)_V \,. \end{aligned}$$Clearly, ∥e k ∥ W = μ k , thus the space W can be alternatively defined as
$$\displaystyle \begin{aligned} W = \{ w = \sum_{k\in\mathbb{N}} w_k\, e_k \in V : \sum_{k\in\mathbb{N}} \mu_k^2\, |w_k|{}^2 < +\infty \} = D(\varLambda), \quad \text{where:}\quad \varLambda = \sum_{k\in\mathbb{N}} \mu_k\, P_k, \end{aligned}$$and P k denotes the projection onto \( \operatorname {{\mathrm {span}}}\{e_k\}\). Then, for any \(\alpha \in \mathbb {R}^+\), one defines the unbounded operator power Λ α as
$$\displaystyle \begin{aligned} D(\varLambda^\alpha) = \{ w = \sum_{k\in\mathbb{N}} w_k\, e_k \in V : \sum_{k\in\mathbb{N}} \mu_k^{2\alpha}\, |w_k|{}^2 < +\infty \} \quad \text{and:}\quad \varLambda^\alpha = \sum_{k\in\mathbb{N}} \mu_k^\alpha\, P_k. \end{aligned}$$When the imbedding W ⊂ V is not compact, the above discrete sums are replaced with Stieltjes integrals that take into account the whole spectrum (see [207, §XI]).
- 7.
In the compact imbedding framework, the next two propositions follow immediately from Definition 4.1.21 and footnote6.
- 8.
A sesquilinear form is linear with respect to the first variable, and antilinear with respect to the second variable.
- 9.
When the sesquilinear form in Problem (4.3) is Hermitian (V = W), if the associated operator is Fredholm, then its index is always equal to 0.
- 10.
For practical applications, it allows one to consider initial data that do not verify the constraints that the solution fulfills afterwards.
- 11.
It is equivalently written as
$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \displaystyle \forall \varphi\in \mathcal{D}(]0,T[),\ \forall\mathtt{v}\in\mathcal{V},\\ \displaystyle \int_0^T\left\{(\mathtt{u}(t),\mathtt{v})_{\mathcal{H}}\,\varphi''(t) + a(\mathtt{u}(t),\mathtt{v})\,\varphi(t)\right\}dt = \int_0^T(\mathtt{f}(t),\mathtt{v})_{\mathcal{H}}\,\varphi(t)\,dt. \end{array} \right. \end{aligned}$$ - 12.
Unless g(t) is appropriately regular. More precisely, see (4.27-top) below: g(t) should be regular enough, so that the second term on the right-hand side can be included in the first term by suitably modifying f(t).
- 13.
Cf. the discussion in footnote 6, p. 153.
- 14.
Since g can be any element of Q′, one has to assume that B is surjective. If g = 0, then this inf-sup condition could be dropped to formulate the Helmholtz-like problem set in K. However, it is useful in Proposition 4.5.8.
- 15.
Because the operator A is an isomorphism, one has λ≠0, as it holds that Au = λ u in V ′, with u≠0.
- 16.
One can check that \(T_H^*=i_{V\rightarrow H}\circ (A^{-1})^\dagger \circ i_{H\rightarrow V'}\).
References
F. Assous, P. Ciarlet, Jr., S. Labrunie. Computational electromagnetism in complex geometries. In preparation
I. Babuska, The finite element method with Lagrange multipliers. Numer. Math. 20, 179–192 (1973)
D. Boffi, F. Brezzi, M. Fortin, Mixed Finite Element Methods and Applications (Springer, New York, 2013)
D. Boffi, F. Brezzi, L. Gastaldi, On the convergence of eigenvalues for mixed formulations. Ann. Sc. Norm. Super. Pisa Cl. Sci. 25, 131–154 (1997)
A.-S. Bonnet-Ben Dhia, P. Ciarlet, Jr., C. M. Zwölf, Time harmonic wave diffraction problems in materials with sign-shifting coefficients. J. Comput. Appl. Math. 234, 1912–1919 (2010); Corrigendum J. Comput. Appl. Math. 234, 2616 (2010)
H. Brezis, Analyse fonctionnelle. Théorie et applications (Masson, Paris, 1983). Functional Analysis, Sobolev Spaces and Partial Differential Equations. Universitext (Springer, 2011)
F. Brezzi, On the existence, uniqueness and approximation of saddle point problems arising from Lagrange multipliers. R.A.I.R.O. Anal. Numér. R2, 129–151 (1974)
P. Ciarlet, Jr., S. Labrunie, Numerical analysis of the generalized Maxwell equations (with an elliptic correction) for charged particle simulations. Math. Models Methods Appl. Sci. 19, 1959–1994 (2009)
R. Dautray, J.-L. Lions, Analyse mathématique et calcul numérique pour les sciences et les techniques (Masson, Paris, 1987)
R. Dautray, J.-L. Lions, Mathematical Analysis and Numerical Methods for Science and Technology (Springer, Berlin, 1990)
P. Grisvard, Singularities in Boundary Value Problems. RMA, vol. 22 (Masson, Paris, 1992)
P. Joly, Analyse et approximation de modèles de propagation d’ondes. Partie I: analyse mathématique, Cours de 3e année, Editions ENSTA, Paris, 2001 (in French)
J.-L. Lions, E. Magenes, Problèmes aux limites non homogènes et applications, vol. 1 (Dunod, Paris, 1968)
A. Pazy, Semigroups of Linear Operators and Applications to Partial Differential Equations (Springer, 1983)
K. Yosida, Functional Analysis (Springer, Berlin, 1980)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Assous, F., Ciarlet, P., Labrunie, S. (2018). Abstract Mathematical Framework. In: Mathematical Foundations of Computational Electromagnetism. Applied Mathematical Sciences, vol 198. Springer, Cham. https://doi.org/10.1007/978-3-319-70842-3_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-70842-3_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70841-6
Online ISBN: 978-3-319-70842-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


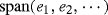 is dense in V . Then, for all v ∈ V , one has
is dense in V . Then, for all v ∈ V , one has