Abstract
We complement the classic results of Chap. 2 in two directions. In the first part, we review some recent results on the traces of vector fields, and especially the tangential trace of electromagnetic-like fields. In the second part, we focus on the extraction of potentials for curl-free and/or divergence-free fields and consequences. In this chapter, Ω is an open subset of \(\mathbb {R}^3\) with boundary Γ.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
This is a generalized orthogonality property, in the sense that, given f1, f2 ∈ H1∕2(Γ), there exist two sequences of elements of H1(Γ), respectively \((f_1^k)_k\) and \((f_2^k)_k\), such that \(f_i^k\rightarrow f_i\) in H1∕2(Γ) for i = 1, 2, and one has

- 2.
We assume here that ∂Γ′∩ ∂Γ′′≠∅. Indeed, it is simple to check that the preceding study carries over to the case when ∂Γ′∩ ∂Γ′′ = ∅.
- 3.
One has \(meas(\dot \varOmega )=meas(\varOmega )\).
- 4.
This (very technical) result is proven in two steps:
-
1.
One introduces a sequence of nested topologically trivial domains (Ω p ) p such that \(\overline {\varOmega _p}\subset \varOmega \) for all p, ∪ p Ω p = Ω. The curl-free field is regularized by convolution over \(\mathbb {R}^3\), so that its restriction belongs to C1(Ω p ), with vanishing curl in Ω p . One may then apply the classical Stokes’ Theorem in Ω p to this smooth field and write it as a gradient in that domain, with a scalar potential that belongs to C2(Ω p ).
-
2.
One then goes to the limit (p →∞) to derive the existence of a scalar potential in Ω that belongs to H1(Ω), with the help of the Lions’ Lemma (Theorem 2.1.34).
-
1.
- 5.
- 6.
Given ℓ, the problem is equivalent to the variational formulation
$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \mathit{Find}\ {q_\ell}\in H^1_{zmv}(\varOmega_\ell)\ \mathit{such \ that}\\ \displaystyle\forall q\in H^1_{zmv}(\varOmega_\ell),\ (\operatorname{\mathrm{\mathbf{grad}}} {q_\ell}|\operatorname{\mathrm{\mathbf{grad}}} q)=\langle {\boldsymbol{v}}\cdot\boldsymbol{n},q\rangle_{H^{1/2}(\varGamma_\ell)} \end{array} \right.. \end{aligned}$$This variational formulation is well-posed, cf. the Lax-Milgram Theorem 4.2.8 and the Poincaré-Wirtinger inequality of Theorem 2.1.37 in \(H^1_{zmv}(\varOmega _\ell )\). Due to the continuity of the trace mapping γ0 (Theorem 2.1.62), choosing q = q ℓ yields \(\| \operatorname {\mathrm {\mathbf {grad}}} {q_\ell }\|{ }_{\boldsymbol {L}^2(\varOmega _\ell )}\le C_\ell \,\|{\boldsymbol {v}}\cdot \boldsymbol {n}\|{ }_{H^{-1/2}(\varGamma _\ell )}\) with C ℓ > 0 independent of v. Finally, using the continuity of the normal trace mapping (Theorem 2.2.18), one gets the bound
$$\displaystyle \begin{aligned} \|\operatorname{\mathrm{\mathbf{grad}}} {q_\ell}\|{}_{\boldsymbol{L}^2(\varOmega_\ell)}\le C^{\prime}_\ell\,\|{\boldsymbol{v}}\|{}_{\boldsymbol{H}(\mathrm{div},\varOmega)}, \end{aligned}$$with \(C^{\prime }_\ell >0\) independent of v.
- 7.
- 8.
Noting that
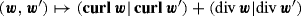 is equal to the scalar product \((\cdot ,\cdot )_{\boldsymbol {X}_N(\varOmega )}\) on \(\boldsymbol {X}_N^\varGamma (\varOmega )\), well-posedness simply stems from the Riesz Theorem 4.2.1.
is equal to the scalar product \((\cdot ,\cdot )_{\boldsymbol {X}_N(\varOmega )}\) on \(\boldsymbol {X}_N^\varGamma (\varOmega )\), well-posedness simply stems from the Riesz Theorem 4.2.1. - 9.
Due to the Lax-Milgram Theorem 4.2.8 and to the Poincaré-Wirtinger inequality of Theorem 2.1.37 in \(H^1_{zmv}(\varOmega )\), the variational formulation is well-posed. In addition, one can obviously add the case of constant test functions q = cst in the variational formulation: \(( \operatorname {\mathrm {\mathbf {grad}}} q_m^0| \operatorname {\mathrm {\mathbf {grad}}} cst)=0=(\boldsymbol {y}_m| \operatorname {\mathrm {\mathbf {grad}}} cst)\). It follows that all test functions q ∈ H1(Ω) can be used, and hence one finds that \(\varDelta q_m^0=\mathrm {div}\,\boldsymbol {y}_m\) in Ω and \(\partial _n q_m^0=\boldsymbol {y}_m\cdot \boldsymbol {n}=0\) on Γ.
- 10.
The form
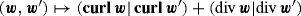 is equal to the scalar product \((\cdot ,\cdot )_{\boldsymbol {X}_T(\varOmega )}\) on \(\boldsymbol {X}_T^\varSigma (\varOmega )\), so well-posedness stems from the Riesz Theorem 4.2.1.
is equal to the scalar product \((\cdot ,\cdot )_{\boldsymbol {X}_T(\varOmega )}\) on \(\boldsymbol {X}_T^\varSigma (\varOmega )\), so well-posedness stems from the Riesz Theorem 4.2.1. - 11.
The problem is equivalent to the variational formulation
$$\displaystyle \begin{aligned} \left\{ \begin{array}{l} \mathit{Find}\ q\in H^1_{zmv}(\varOmega)\ \mathit{such \ that}\\ \displaystyle\forall q'\in H^1_{zmv}(\varOmega),\ (\operatorname{\mathrm{\mathbf{grad}}} q|\operatorname{\mathrm{\mathbf{grad}}} q')=-(g|q') \end{array} \right.. \end{aligned}$$This variational formulation is well-posed, cf. the Lax-Milgram Theorem 4.2.8 and the Poincaré-Wirtinger inequality of Theorem 2.1.37 in \(H^1_{zmv}(\varOmega _\ell )\).
References
A. Alonso, A. Valli, Some remarks on the characterization of the space of tangential traces of H(rot; Ω) and the construction of an extension operator. Manuscripta Math. 89, 159–178 (1996)
C. Amrouche, C. Bernardi, M. Dauge, V. Girault, Vector potentials in three-dimensional non-smooth domains. Math. Methods Appl. Sci. 21, 823–864 (1998)
M.Sh. Birman, M.Z. Solomyak, Construction in a piecewise smooth domain of a function of the class H2 from the value of the conormal derivative. J. Sov. Math. 49, 1128–1136 (1990)
A. Buffa, Hodge decompositions on the boundary of nonsmooth domains: the multi-connected case. Math. Models Methods App. Sci. 11, 147–176 (2001)
A. Buffa, P. Ciarlet, Jr., On traces for functional spaces related to Maxwell’s equations. Part I: an integration by parts formula in Lipschitz polyhedra. Math. Methods Appl. Sci. 24, 9–30 (2001)
A. Buffa, P. Ciarlet, Jr., On traces for functional spaces related to Maxwell’s equations. Part II: Hodge decompositions on the boundary of Lipschitz polyhedra and applications. Math. Methods Appl. Sci. 24, 31–48 (2001)
A. Buffa, M. Costabel, D. Sheen, On traces for H(curl, Ω) in Lipschitz domains. J. Math. Anal. Appl. 276, 845–867 (2002)
M. Cessenat, Mathematical Methods in Electromagnetism. Linear Theory and Applications. Advances in Mathematics for Applied Sciences, vol. n41 (World Scientific, Singapore, 1996)
M. Costabel, A remark on the regularity of solutions of Maxwell’s equations on Lipschitz domains. Math. Methods Appl. Sci. 12, 365–368 (1990)
M. Costabel, M. Dauge, S. Nicaise, Singularities of Maxwell interface problems. Modél. Math. Anal. Numér. 33, 627–649 (1999)
V. Girault, P.-A. Raviart, Finite Element Methods for Navier-Stokes Equations. Springer Series in Computational Mathematics, vol. 5 (Springer, Berlin, 1986)
P. Grisvard, Elliptic Problems in Nonsmooth Domains. Monographs and Studies in Mathematics, vol. 24 (Pitman, London, 1985)
P.W. Gross, P.R. Kotiuga, A challenge for magnetic scalar potential formulations of 3-D eddy current problems: multiply connected cuts in multiply connected regions which necessarily leave the cut complement multiply connected, in Electric and Magnetic Fields, ed. by A. Nicolet, R. Belmans (Plenum Press, New York, 1995), pp. 1–20
P.W. Gross, P.R. Kotiuga, Electromagnetic Theory and Computation: A Topological Approach. MSRI Publications Series (Cambridge University Press, Cambridge, 2004)
D.S. Jerison, C.E. Kenig, The Neumann problem on Lipschitz domains. Bull. Am. Math. Soc. 4, 203–207 (1981)
S. Lohrengel, Etude mathématique et résolution numérique des équations de Maxwell dans un domaine non régulier, PhD Thesis, Paris 6 University, France, 1998 (in French)
P. Monk, Finite Element Methods for Maxwell’s Equations (Oxford University Press, Oxford, 2003)
L. Schwartz, Théorie des Distributions (Hermann, Paris, 1966)
D. Sheen, A generalized Green’s theorem. Appl. Math. Lett. 5, 95–98 (1992)
C. Weber, A local compactness theorem for Maxwell’s equations. Math. Methods Appl. Sci. 2, 12–25 (1980)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Assous, F., Ciarlet, P., Labrunie, S. (2018). Complements of Applied Functional Analysis. In: Mathematical Foundations of Computational Electromagnetism. Applied Mathematical Sciences, vol 198. Springer, Cham. https://doi.org/10.1007/978-3-319-70842-3_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-70842-3_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70841-6
Online ISBN: 978-3-319-70842-3
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



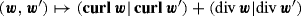 is equal to the scalar product
is equal to the scalar product 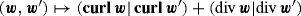 is equal to the scalar product
is equal to the scalar product