Hecke Algebras

Abstract

The aim of this chapter is to recall the basic properties of Hecke algebras (definition, parabolic subalgebras, involutions, symmetrizing form) in a suitable way with respect to our needs. In particular, the normalization of the parameters used here is tailor-made for applications to Kazhdan-Lusztig theory.

Appendices

Notes

All the results gathered in this chapter are classical and may almost all be found, for instance, in [Bou] or [GePf]. Note that Theorem 4.5.1 appeared in Kilmoyer’s Thesis [Kil] and was published in [CuIwKij]. More detailed bibliographical comments can be found in [GePf, §8.5].

Exercises

Exercise 4.1

(Type ${\varvec{G_2}}$). As in Exercise 3.2, let us assume here that $S=\{s, t\}$ with $m_{st}=6$, so that (W, S) is of type $G_2$. Here is the corresponding Coxeter graph:

Compute the generic r-polynomials for W.

Exercise 4.2

(Direct products). As in Exercise 3.2, assume that $S=S_1 \dot{\cup }S_2$ is a partition such that, if $s_1 \in S_1$ and $s_2 \in S_2$, then $m_{s_1s_2}=2$ (i.e. $s_1s_2=s_2s_1$). Let $W_i=W_{S_i}$ ($i \in \{1,2\}$). Let $\varphi _i$ denote the restriction of $\varphi$ to $S_i$ and let ${\mathscr {H}}_i={\mathscr {H}}_A(W_i, S_i,\varphi _i)$. Show that

$$ {\mathscr {H}}= {\mathscr {H}}_1 \otimes _A {\mathscr {H}}_2 $$

and that, if $(x_1,x_2)$ and $(y_1,y_2)$ are two elements of $W_1 \times W_2$, then

$$ {\varvec{r}}_{x_1x_2,y_1y_2} = {\varvec{r}}_{x_1,y_1} {\varvec{r}}_{x_2,y_2}. $$

Exercise 4.3

Let $I \subset S$ and let $a \in X_I$, x, $y \in W_I$. Show that ${\varvec{r}}_{ax,ay}={\varvec{r}}_{x, y}$ and ${\varvec{r}}_{xa^{-1}, ya^{-1}}={\varvec{r}}_{x, y}$.

Exercise 4.4

The aim of this exercise is to prove the last statement of Example 4.1.8. Let $\lambda$ and $\mu$ be two elements of A and let T be an indeterminate over A. Let ${\mathscr {H}}_1=A[T]/\langle (T-\lambda )(T-\mu ) \rangle$ and

$$ {\mathscr {H}}_2=\{(a, b) \in A \times A~|~a \equiv b \mod \lambda -\mu \}. $$

We aim to prove that ${\mathscr {H}}_1 \simeq {\mathscr {H}}_2$ whenever $\lambda \ne \mu$ and A is an integral domain.

• (a) Show that ${\mathscr {H}}_2$ is indeed a subring of $A \times A$.

• (b) Let $\pi : A[T] \rightarrow A \times A$, $P \mapsto (P(\lambda ), P(\mu ))$. Show that $\pi$ is a morphism of A-algebras, whose image is ${\mathscr {H}}_2$.

• (c) Assume here that $\lambda \ne \mu$ and that A is an integral domain. Show that ${{\mathrm{{\mathrm {Ker}}}}}(\pi )$ is generated by $(T-\lambda )(T-\mu )$. Conclude.

Exercise 4.5

Let I and J be two subsets of S. Show that

$$ {\mathscr {H}}=\mathop {\bigoplus }_{x \in X_{IJ}} {\mathscr {H}}_I \cdot T_x \cdot {\mathscr {H}}_J. $$

Exercise 4.6

Let ${{\mathrm{{\mathrm {aug}}}}}: {\mathscr {A}}\rightarrow \{1\}$ be the trivial morphism. Then ${{\mathrm{{\mathrm {aug}}}}}_* : A \rightarrow {\mathbb {Z}}$ is the augmentation morphism and it induces an isomorphism

$$ {{\mathrm{{\mathrm {aug}}}}}_{\,*} : {\mathbb {Z}}\otimes _A {\mathscr {H}}{\mathop {\longrightarrow }\limits ^{\sim }}{\mathbb {Z}}W. $$

Now, let I be a W-closed subset of S.

• (a) Show that there is a unique morphism of A-algebras ${{\mathrm{{\mathrm {sgn}}}}}_I : {\mathscr {H}}\rightarrow A$ such that

  $$ {{\mathrm{{\mathrm {sgn}}}}}_I(T_s)= {\left\{ \begin{array}{ll} -v^{-\varphi (s)} &{} \mathrm{if}\,\, s \in I,\\ v^{\varphi (s)} &{} \mathrm{if}\,\, s \in S \setminus I. \end{array}\right. } $$

  If necessary, ${{\mathrm{{\mathrm {aug}}}}}_*$ and ${{\mathrm{{\mathrm {sgn}}}}}_I$ are denoted by ${{\mathrm{{\mathrm {aug}}}}}_*^\varphi$ and ${{\mathrm{{\mathrm {sgn}}}}}_I^\varphi$, respectively.

• (b) Show that the diagram

  

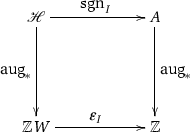
  is commutative (here, $\varepsilon _I : {\mathbb {Z}}W \rightarrow {\mathbb {Z}}$ is the morphism of algebras induced by the morphism of groups $\varepsilon _I : W \rightarrow \{1,-1\}$ defined in Exercise 3.5).

• (c) Keep the notation of §4.3.C ($S_+$, $S_-$, $\varphi _-$,...). Show that the diagram

  

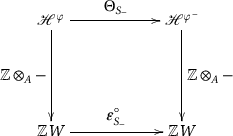
  is commutative (here, $\varepsilon _I^\circ : {\mathbb {Z}}W \rightarrow {\mathbb {Z}}W$ denotes the automorphism of ${\mathbb {Z}}W$ such that $\varepsilon _I^\circ (w)=\varepsilon _I(w)w$ for all $w \in W$).

Exercise 4.7

Assume that W is finite. If $h \in {\mathscr {H}}$, let $\det (h,{\mathscr {H}})$ denote the determinant of the map ${\mathscr {H}}\rightarrow {\mathscr {H}}$, $h' \mapsto hh'$. Show that

$$ \det (T_w,{\mathscr {H}})=(-1)^{|W|\ell (w)/2} $$

for all $w \in W$. (Hint: If $w=s \in S$, use the decomposition ${\mathscr {H}}=\mathop {\bigoplus }_{x \in X_s} \bigl (A T_{x^{-1}} \oplus AT_{sx^{-1}}\bigr )$).