Abstract
We carry out a concrete security analysis of signature schemes obtained from five-move identification protocols via the Fiat-Shamir transform. Concretely, we obtain tightly-secure signatures based on the computational Diffie-Hellman (CDH), the short-exponent CDH, and the Factoring (FAC) assumptions. All our signature schemes have tight reductions to search problems, which is in stark contrast to all known signature schemes obtained from the classical Fiat-Shamir transform (based on three-move identification protocols), which either have a non-tight reduction to a search problem, or a tight reduction to a (potentially) stronger decisional problem. Surprisingly, our CDH-based scheme turns out to be (a slight simplification of) the Chevallier-Mames signature scheme (CRYPTO 05), thereby providing a theoretical explanation of its tight security proof via five-move identification protocols.
E. Kiltz was partially supported by ERC Project ERCC (FP7/615074) and by DFG SPP 1736 Big Data.
J. Loss was supported by ERC Project ERCC (FP7/615074).
J. Pan was supported by the DFG grant HO 4534/4-1.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The security of public-key cryptographic primitives is commonly analyzed via a security reduction to a suitable cryptographic assumption (such as the factoring assumption). Concretely, a security reduction converts a successful adversary \(\mathsf {A}\) against the cryptographic scheme’s security into a successful solver \(\mathsf {B}\) against the hardness of the underlying assumption. If the reduction provides the bound \(\varepsilon _{\mathsf {A}}\le L \cdot \varepsilon _{\mathsf {B}}\) (where \(\varepsilon _{\mathsf {A}}\) is \(\mathsf {A}\)’s success probability and \(\varepsilon _{\mathsf {B}}\) is \(\mathsf {B}\)’s success probability) then L is called the (multiplicative) security loss of the reduction.Footnote 1 Clearly, it is desirable to have the security loss L as small as a constant so that \(\varepsilon _{\mathsf {A}}\approx \varepsilon _{\mathsf {B}}\). If furthermore the running times of \(\mathsf {A}\) and \(\mathsf {B}\) are approximately the same, then the reduction is said to be tight. Cryptographic schemes with tight reductions recently drew a large amount of attention (e.g., [4, 12, 13, 18, 29,30,31]) due to the fact that tightly-secure schemes do not need to compensate for the security loss with increased parameters.
Digital signature schemes are one of the most important public-key cryptographic primitives. They have numerous applications and often serve as a building block for advanced cryptographic protocols. Ideally, we desire to have signature schemes with short signature sizes, efficient signing and verification algorithms, and tight security based on weak, well studied assumptions.
Tightness, Efficiency, and Decisional Assumptions. We will focus on signature schemes in the random oracle model [8] which usually have better efficiency than the ones in the standard model. Even in the random oracle model, there seems to be a prevalence of efficient, yet tightly-secure signature schemes based on decisional rather than search assumptions [2, 3, 33, 34]. Notable exceptions are the Rabin-Williams (\(\mathsf {RW}\)) scheme from factoring (\({\mathsf {FAC}}\)) [9, 10], the BLS and RSA-PSS variants with the “selector bit” technique [9, 14, 26, 34], the Chevallier-Mames scheme (and its variants) (\(\mathsf {CM}\)) from \(\mathsf {CDH}\) [20, 26], and the Micali-Reyzin scheme (\(\mathsf {MR}\)) from \({\mathsf {FAC}}\) [7, 39].
The Fiat-Shamir Transform and its Tightness. The Fiat-Shamir (FS) method [21] transforms a (canonical) three-move identification scheme \(\mathsf {ID}\) into a digital signature scheme \({\mathsf {SIG}}[\mathsf {ID}]\) using a hash function. A canonical identification scheme \(\mathsf {ID}\) as formalized by [1] is a three-move public-key authentication protocol of a specific form. The prover (holding the secret-key) sends a commitment \(R\) to the verifier. The verifier (holding the public-key) returns a random challenge \(h\), uniformly chosen from a set \(\mathsf {ChSet}\) (of exponential size). The prover sends a response \(s\). Finally, using the verification algorithm, the verifier publicly checks correctness of the transcript \((R, h,s)\). There is a large number of canonical identification schemes known (e.g., [11, 15, 21, 23, 26, 28, 34, 40,41,42, 49], the most popular among them being the scheme by Schnorr [49].
As discussed above, obtaining tightly secure signatures with short parameters has been proven to be notoriously hard. In particular, schemes obtained via the classical FS transform are usually proven via the Forking Lemma [46] and therefore are not tightly secure. For example, the Schnorr signature is obtained from the Fiat-Shamir transform and has an inherently loose security reduction [22, 35, 50] to the discrete logarithm problem. This issue was addressed by [3, 34] who showed how to improve the tightness of signature schemes obtained from the FS transform by basing their security on decisional assumptions such as DDH (and a short exponent variant thereof), quadratic residuosity, and (Ring)-LWE. However, to the best of our knowledge, there is currently no FS-derived signature scheme known which can be tightly proven secure under a search assumption. Moreover, there seems to be some evidence to support that this is impossible: the results of [22] show that the Schnorr scheme cannot be proven tightly secure under any non-interactive assumption. However, tight variants of the FS transform for three-move schemes may still exist if the scheme meets some additional requirements.
1.1 Our Contributions
In this work, we consider the Fiat-Shamir transform applied to a five-move identification scheme (rather than a three-move scheme). More precisely, we first formalize syntax and security of a five-move identification scheme and, following [35], provide a concrete and modular security analysis of the Fiat-Shamir transformed signature scheme. Next, we instantiate our framework to obtain schemes with security from search assumptions, such as the classical \(\mathsf {CDH}\) and \({\mathsf {FAC}}\) assumptions. All our security reductions are tight.
Five-move Identification Schemes. A five-move identification scheme \({\mathsf {ID}}\) is an extension of the three-move identification scheme, where there are two “commitment-challenge” rounds (compared to one), followed by a final response output by the prover. (Each round has two moves, so five moves in total.) Intuitively, the additional rounds give us the handle to tightly embed the challenge of a search assumption. Following [35], we consider \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) security (parallel impersonation against key-only attacks) of identification schemes where the adversary, given the public-key, tries to impersonate a prover in one of many parallel “commitment-challenge” sessions.
Fiat-Shamir for Five-Move Identification Schemes. We consider two variants \({\mathsf {FS}}[{\mathsf {ID}}]\) and \({\mathsf {OF}}[{\mathsf {ID}}]\) of the five-move Fiat-Shamir transformation. Both have tight security reductions given that the identification scheme has honest-verifier zero-knowledge (\(\mathsf {HVZK}\)) and is secure against parallel impersonation attacks.Footnote 2 The two variants come with different trade-offs. \({\mathsf {OF}}[{\mathsf {ID}}]\) requires special soundness but results in an online/offline signature scheme [52], which allows to pre-compute most of the signature in an offline phase to have a computationally cheap online signing phase (that requires knowledge of the message to be signed). \({\mathsf {FS}}[{\mathsf {ID}}]\) does not require special soundness but does not come with the online/offline property. Interestingly, we are able to explain the Chevallier-Mames signature scheme [20] in our framework and show that it can be obtained from a five-move identification scheme by applying \({\mathsf {OF}}[{\mathsf {ID}}]\). We now give some details of our obtained signature schemes. A detailed comparison of their properties is given in Table 1.
A New Online/Offline Scheme With a Tight Security Reduction. Using our \({\mathsf {OF}}[{\mathsf {ID}}]\) transform, we present a modified version of the Girault-Poupard-Stern (GPS) signature scheme [24]. The main interest of this scheme lies within its online signing step which can be made extremely efficient, given that most of the work can be precomputed in the offline-step, i.e., before seeing the message m. Concretely, the scheme only performs arithmetics over the integers in its online step, thereby even getting rid of modular reductions. [24] provide a loose security reduction to the Short-Exponent Discrete Logarithm (SEDL) assumption [36] which states that the discrete logarithm problem remains hard even if the discrete logarithm is known to lie in some fixed interval. Subsequently, [3] proved a tight reduction for the GPS scheme to the decisional variant of the SEDL [36]. However, so far, there has been no known tight reduction of the GPS scheme to a search assumption. Our scheme resolves this issue by offering a tight reduction to the Short Exponent CDH (SCDH) assumption. The relation between these aforementioned problems is explained in [36] as follows. First, the SEDL assumption is (non-tightly) equivalent to its decisional version. Second, the SCDH assumption is (non-tightly) equivalent to the assumption that both the full length CDH problem and the SEDL problem are hard.
A Tightly Secure Factoring-Based Scheme With Efficient Signing. As an application of our second transform, \({\mathsf {FS}}[{\mathsf {ID}}]\), we present a new signature scheme with a tight security reduction to factoring. While our signature generation step and size are not quite as efficient than the ones of the factoring-based schemes of [9, 10, 39], our scheme highlights the usefulness of our (generic) \({\mathsf {FS}}[{\mathsf {ID}}]\) transform.
A Tightly Secure Scheme from CDH. Our instantiation from \(\mathsf {CDH}\) results in a slight simplification of the Chevallier-Mames signature scheme [20]. (Slight simplification in the sense that some inputs to the hash function can be left out in our scheme.) We believe that our framework provides interesting insights to the original scheme and underlines the usefulness of our (generic) \({\mathsf {OF}}[\mathsf {ID}]\) transform.
1.2 Related Work
There exists a large body of literature on variants and improvements for the Fiat-Shamir transform. [35] give a concrete and modularized security treatment for signatures obtained from identification schemes via the Fiat-Shamir transform in both the multi- and single user settings which yields optimal security parameters for a wide array of important signatures in the ROM, in particular for Schnorr signatures. Our work is based on their modular framework. More recently, [7] put forth a new framework which includes multiple transforms that allow to tightly convert an ID scheme satisfying certain requirements into a signature. Their framework captures some existing transformations that have so far not received any theoretical treatment. Most notably, they give a characterization of the ‘swap’ method used in [38] to obtain a signature based tightly on the factoring assumption. [2, 3, 26] propose methods to obtain tight security for FS-derived signature schemes, with two of the schemes in [3] satisfying (conjectured) post-quantum security.
Deriving signature schemes from five-move ID schemes (or more generally from schemes with \(2n+1\) rounds) in an FS-like manner is a natural idea and thus has already been in the literature [5, 16, 17, 19, 44, 45, 48, 51, 53,54,55]. Surprisingly, many of them in the context of post-quantum security. However, none of these works proposes generic transforms for five-move ID schemes which makes the resulting proofs rather complex. Furthermore, none of the presented signature schemes admits a tight security reduction.
2 Preliminaries
2.1 Notations
We define \([N]:= \{1,\ldots , N\}\) and \({{\mathbb Z}}_N:={{\mathbb Z}}/N{{\mathbb Z}}\) as the residual ring for an integer N. Let S be a finite set.  denotes choosing an element a from S uniformly at random. Our algorithms are considered to be probabilistic polynomial time unless stated otherwise. If \({\mathsf {A}}\) is an algorithm, then
denotes choosing an element a from S uniformly at random. Our algorithms are considered to be probabilistic polynomial time unless stated otherwise. If \({\mathsf {A}}\) is an algorithm, then  denotes the random variable which is defined as the output of \({\mathsf {A}}\) on input b. With \(a \in {\mathsf {A}}(b)\) we denote a possible output a of the execution of \({\mathsf {A}}\) on input b. When we want to make the randomness explicit, we use the notation \(a := {\mathsf {A}}(b; \rho )\) meaning that the algorithm is executed on input b and randomness \(\rho \). Note that \({\mathsf {A}}\)’s execution is now deterministic.
denotes the random variable which is defined as the output of \({\mathsf {A}}\) on input b. With \(a \in {\mathsf {A}}(b)\) we denote a possible output a of the execution of \({\mathsf {A}}\) on input b. When we want to make the randomness explicit, we use the notation \(a := {\mathsf {A}}(b; \rho )\) meaning that the algorithm is executed on input b and randomness \(\rho \). Note that \({\mathsf {A}}\)’s execution is now deterministic.
2.2 Digital Signatures
We begin by defining syntax and security of a (digital) signature scheme. Let \(\mathsf {par}\) denote some common system parameters shared among all participants.
Definition 1
(Signature Scheme). A digital signature scheme \({\mathsf {SIG}}:= ({\mathsf {Gen}}, {\mathsf {Sign}}, {\mathsf {Ver}})\) is defined as follow.
-
The key generation algorithm \({\mathsf {Gen}}\) takes system parameters \(\mathsf {par}\) as inputs and returns the public and secret keys \((pk,sk)\). We assume that \(pk\) implicitly defines a message space \(\mathcal {M}\) and a signature space \(\Sigma \).
-
The signing algorithm \({\mathsf {Sign}}\) takes a secret key \(sk\) and a message \({m}\in \mathcal {M}\) as inputs and returns a signature \(\sigma \in \Sigma \).
-
The deterministic verification algorithm \({\mathsf {Ver}}\) takes a public key \(pk\), a message \({m}\) and a signature \(\sigma \) as inputs and returns 1 (accept) or 0 (reject).
\({\mathsf {SIG}}\) has correctness error \(\rho \) if for all \((pk,sk)\in {\mathsf {Gen}}(\mathsf {par})\) and all messages \({m}\in \mathcal {M}\), with probability at least \(1-\rho \) \({\mathsf {Sign}}(sk,{m})\) outputs a valid signature \(\sigma \) such that \({\mathsf {Ver}}(pk,{m},\sigma )=1\).
Definition 2
( \({\mathsf {UF\text{- }CMA}}\) Security). A signature scheme \({\mathsf {SIG}}\) is said to satisfy \((t,\varepsilon ,Q_s)\)-\({\mathsf {UF\text{- }CMA}}\) security (unforgeability against chosen message attacks) if for all adversaries \(\mathsf {A}\) running in time at most t and making at most \(Q_s\) queries to the signing oracle,

where on query \({m}\) the signing oracle \(\textsc {Sign}\) adds m to list \(\mathcal{M}\) and returns  to \(\mathsf {A}\), i.e., a signature on message m under public-key \(pk\).
to \(\mathsf {A}\), i.e., a signature on message m under public-key \(pk\).
As a special case of \({\mathsf {UF\text{- }CMA}}\) security, we define \((t, \varepsilon )\)-\({\mathsf {UF\text{- }KOA}}\) security (unforgeability against key-only attacks) as \((t,\varepsilon ,0)\)-\({\mathsf {UF\text{- }CMA}}\) security, i.e. \(Q_s=0\). In other words, the adversary is not allowed to make any signing query in the \({\mathsf {UF\text{- }KOA}}\) security experiment.
Security in the random oracle model. A common approach to analyze the security of signature schemes that involve a hash function is to use the random oracle model [8] in which hash queries are answered by an oracle H. H is defined as follows. On input x, it first checks whether H(x) has previously been defined. If so, it returns H(x). Otherwise, it sets H(x) to a uniformly random value in the codomain of H and then returns H(x). This allows us to parametrize the maximal number of hash queries in our security notions. As an example, we define \((t,\varepsilon ,Q_s,Q_h)\)-\({\mathsf {UF\text{- }CMA}}\) as security against any adversary that makes at most \(Q_h\) queries to H in the \({\mathsf {UF\text{- }CMA}}\) game. Furthermore, we make the standard convention that any random oracle query that is asked as a result of a query to the signing oracle in the \({\mathsf {UF\text{- }CMA}}\) game is also counted as a query to the random oracle. This implies that \(Q_s\le Q_h\).
2.3 Identification Schemes
A five-move identification protocol of the form depicted in Fig. 1 is defined as follows.
Definition 3
(Five-move Identification Scheme). A five-move identification scheme \({\mathsf {ID}}:=({\mathsf {IGen}},{\mathsf {P}},\mathsf {ChSet}_1,\mathsf {ChSet}_2,{\mathsf {V}})\) is defined as follow.
-
The key generation algorithm \({\mathsf {IGen}}\) takes system parameters \(\mathsf {par}\) as input and returns a public key and a secret key \((pk, sk)\). We assume that \(pk\) defines two challenge sets \(\mathsf {ChSet}_1\) and \(\mathsf {ChSet}_2\).
-
The prover algorithm \({\mathsf {P}}=({\mathsf {P}}_1,{\mathsf {P}}_2,{\mathsf {P}}_3)\) is split into three algorithms. \({\mathsf {P}}_1\) takes as input the secret key \(sk\) and returns a first-move commitment \(R_1\) and a state \( St _1\); \({\mathsf {P}}_2\) takes as input the secret key \(sk\), a first-move commitment \(R_1\), a challenge \(h_1\), and a state \( St _1\) and returns a second-move commitment \(R_2\); \({\mathsf {P}}_3\) takes as input the secret key \(sk\), a transcript \((R_1,h_1,R_2,h_2)\), and a state \( St _2\) and returns a response \(s\).
-
The deterministic verifier algorithm \({\mathsf {V}}\) takes the public key \(pk\) and the conversation transcript as input and outputs a decision, 1 (acceptance) or 0 (rejection).
We define some useful terms. A transcript for a canonical five-move identification scheme is of the form \((R_1,h_1,R_2,h_2,s)\). A transcript \((R_1,h_1,R_2,h_2,s)\) is valid (with respect to \(pk\)) if \({\mathsf {V}}(pk, R_1,h_1,R_2,h_2,s)=1\) and it is real if it is output by the following algorithm \({\mathsf {SKTran}}(sk)\). We elaborate further on the purpose of \({\mathsf {SKTran}}\) below when defining the notion of \(\mathsf {naHVZK}\) (non-aborting honest-verifier zero-knowledge).

Definition 4
(Correctness error \(\rho \)). We call an \({\mathsf {ID}}\) has correctness error \(\rho \) if, for all \((pk,sk) \in {\mathsf {IGen}}(\mathsf {par})\), the following holds:
-
For all
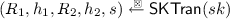 with \(s\ne \bot \), we have \({\mathsf {V}}(pk,R_1,h_1,R_2,h_2,s)=1\).
with \(s\ne \bot \), we have \({\mathsf {V}}(pk,R_1,h_1,R_2,h_2,s)=1\). -
A real transcript \((R_1,h_1,R_2,h_2,s)\) contains \(s=\bot \) with probability at most \(\rho \), i.e.,
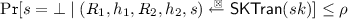 .
.
Generalizing [35] we now define parallel impersonation against key-only attacks (\(\mathsf {KOA}\)) for five-move identification schemes.
Definition 5
(Non-aborting (Parallel) Impersonation). A five-move identification scheme \({\mathsf {ID}}\) is \((t, \varepsilon , Q_{\textsc {Ch}_1},Q_{\textsc {Ch}_2},Q_\textsc {O})\)-\(\mathsf {naPIMP}\)-\(\mathsf {ATK}\) secure (non-aborting parallel impersonation against \(\mathsf {ATK}\) attacks, \(\mathsf {ATK}\in \{\mathsf {KOA},\mathsf {PA}\}\)) if for all adversaries \(\mathsf {A}\) running in time at most t and making at most \(Q_{\textsc {Ch}_1}\) queries to the challenge oracle \(\textsc {Ch}_1\) and \(Q_{\textsc {Ch}_2}\) queries to oracle \(\textsc {Ch}_2\), we have

where the challenge oracles \(\textsc {Ch}_i(R_i)\) (\(i \in \{1,2\}\)) return  to \(\mathsf {A}\) and store \((R_i, h_i)\) in set \(\mathcal {L}_{i}\).Footnote 3 For different kinds of attacks, oracle \(\textsc {O}\) is defined as follows.
to \(\mathsf {A}\) and store \((R_i, h_i)\) in set \(\mathcal {L}_{i}\).Footnote 3 For different kinds of attacks, oracle \(\textsc {O}\) is defined as follows.
-
If \(\mathsf {ATK}=\mathsf {KOA}\) (key-only attack), then \(\textsc {O}\) always returns \(\perp \).
-
If \(\mathsf {ATK}=\mathsf {PA}\) (passive attack), then \(\textsc {O}:= \textsc {Tran}\), and the transcript oracle \(\textsc {Tran}()\) returns a real transcript \((R_1',h_1',R_2',h_2',s')\) to \(\mathsf {A}\), i.e.,
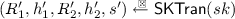 .
.
We do not use the parameter \(Q_\textsc {O}\) for \(\mathsf {ATK}=\mathsf {KOA}\) and simply speak of \((t,\varepsilon ,Q_{\textsc {Ch}_1},Q_{\textsc {Ch}_2})\)-\(\mathsf {naPIMP}\text{- }\mathsf {KOA}\). Moreover, \((t,\varepsilon ,Q_\textsc {O})\)-\(\mathsf {naIMP}\text{- }\mathsf {ATK}\) (impersonation against \(\mathsf {ATK}\) attack) security is defined as \((t,\varepsilon ,1,1,Q_\textsc {O})\)-\(\mathsf {naPIMP}\text{- }\mathsf {ATK}\) security, i.e., the adversary is only allowed \(Q_{\textsc {Ch}_1}=1\) query to the \(\textsc {Ch}_1\) oracle and \(Q_{\textsc {Ch}_2}=1\) to \(\textsc {Ch}_2\).
Definition 6
(Special Soundness). A five-move identification scheme \({\mathsf {ID}}\) is \(\mathsf {SS}\) (special sound) if there exists an extractor \({\mathsf {Ext}}\) such that, for all \((pk,sk)\in {\mathsf {IGen}}(\mathsf {par})\), given any two valid transcripts \((R_1,h_1,R_2,h_2,s)\) and \((R_1,h_1',R_2',h_2', s')\) with \(h_2\ne h_2'\), it outputs a valid secret key \(sk^*\) such that \((pk,sk^*) \in {\mathsf {IGen}}(\mathsf {par})\), i.e., we have  . The winning condition \((pk,sk^*) \in {\mathsf {IGen}}(\mathsf {par})\) means that the tuple \((pk,sk^*)\) is in the support of \({\mathsf {IGen}}(\mathsf {par})\), i.e., that \(\mathsf {A}\) outputs a valid secret-key \(sk^*\) with respect to \(pk\).
. The winning condition \((pk,sk^*) \in {\mathsf {IGen}}(\mathsf {par})\) means that the tuple \((pk,sk^*)\) is in the support of \({\mathsf {IGen}}(\mathsf {par})\), i.e., that \(\mathsf {A}\) outputs a valid secret-key \(sk^*\) with respect to \(pk\).
We now introduce the notion of (statistical) non-aborting honest-verifier zero-knowledge [37], abbreviated as \(\mathsf {naHVZK}\). This notion generalizes the standard definition of honest-verifier zero-knowledge by including also identification schemes \({\mathsf {ID}}\) with correctness error \(\rho \). Note that a real run of \({\mathsf {ID}}\) might produce a transcript of the form \((R_1,h_1,R_2,h_2,\perp )\) with probability \(\rho \). Unfortunately, it might not be efficiently possible to simulate a correctly distributed transcript in this case. Therefore, we again make use of the algorithm \({\mathsf {SKTran}}\) which on input a secret key \(sk\) internally generates a valid transcript of \({\mathsf {ID}}\) (with respect to the matching public key \(pk\)), but outputs \(\bot \) if the transcript matches an execution of \({\mathsf {ID}}\) in which \(s=\perp \). We now require an efficient simulator \(\mathsf {Sim}\) that produces transcripts which are statistically close in distribution to the ones output by \({\mathsf {SKTran}}\).
Definition 7
(\(\varDelta \)-Statistical Non-Aborting Honest-Verifier Zero- Knowledge with \(\alpha \) Bits Min-Entropy). A five-move identification scheme \({\mathsf {ID}}\) is said to be \(\varDelta \)-statistically \(\mathsf {naHVZK}\)(non-aborting honest-verifier zero-knowledge) with \(\alpha \) bits min-entropy if there exists an algorithm \(\mathsf {Sim}\) that, given a valid public key \(pk\), outputs \((R_1,h_1,R_2,h_2,s)\) such that the distribution of \((R_1,h_1,R_2,h_2,s)\) has statistical distance at most \(\varDelta \) from the distribution of a transcript output by \({\mathsf {SKTran}}\) on input \(sk\) and if for all \((pk,sk) \in {\mathsf {IGen}}(\mathsf {par})\) and strings \(R_1',R_2'\) we have

If \(\varDelta =0\), we say that \({\mathsf {ID}}\) is perfectly \(\mathsf {naHVZK}\).
3 Signatures from Five-Move Identification Schemes
We extend the generalized Fiat-Shamir transform [6] to construct signatures for 5-move identification schemes. We also present an online/offline variant of our transformation, where parts of the computation can be performed off-line which leads to a better performance in the signing step, but requires special soundness for the underlying identification schemes. Furthermore, we give an alternative Fiat-Shamir transform, which outputs shorter signatures, but retains the same security.
3.1 The Fiat-Shamir Transform and Its Online/Offline Variant
Fix some system parameters \(\mathsf {par}\). Let \({\mathsf {ID}}:=({\mathsf {IGen}},{\mathsf {P}},\mathsf {ChSet}_1,\mathsf {ChSet}_2,{\mathsf {V}})\) be a five-move identification scheme and \(H_1:\{0,1\}^* \rightarrow \mathsf {ChSet}_1\) and \(H_2: \{0,1\}^* \rightarrow \mathsf {ChSet}_2\) be two hash functions. We also fix \(\ell \in \mathbb {N}\) which controls the scheme’s correctness. The signature scheme \({\mathsf {FS}}[{\mathsf {ID}},H_1,H_2,\ell ]:=({\mathsf {Gen}},{\mathsf {Sign}},{\mathsf {Ver}})\) from \({\mathsf {ID}}\) is defined as follows. Its online/offline variant \({\mathsf {OF}}[{\mathsf {ID}},H_1,H_2,\ell ]:=({\mathsf {Gen}},{\mathsf {Sign_o}},{\mathsf {Ver_o}})\) is defined with the boxed differences.

If \({\mathsf {ID}}\) has correctness error \(\rho \), then both \({\mathsf {FS}}[{\mathsf {ID}},H_1,H_2,\ell ]\) and \({\mathsf {OF}}[{\mathsf {ID}},H_1,H_2,\ell ]\) are signature schemes with correctness error \(\rho ^\ell \).
The following theorem states the security of \({\mathsf {FS}}[{\mathsf {ID}},H_1,H_2,\ell ]\) and \({\mathsf {OF}}[{\mathsf {ID}},H_1,H_2,\ell ]\).
Theorem 1
(Security of \({\mathsf {FS}}\) and \({\mathsf {OF}}\)). Suppose that \({\mathsf {ID}}\) has \(\varDelta \)-statistical \(\mathsf {naHVZK}\) with \(\alpha \) bits min-entropy and is \((t,\varepsilon ,Q_{\textsc {Ch}_1}, Q_{\textsc {Ch}_2})\)-\(\mathsf {naPIMP}\text{- }\mathsf {KOA}\) secure. Then the signature scheme \({\mathsf {FS}}[{\mathsf {ID}},H_1,H_2,\ell ]\) is \((t',\varepsilon ',Q_s,Q_1,Q_2)\)-\({\mathsf {UF\text{- }CMA}}\)-secure in the random oracle model, where
and \(Q_{\textsc {Ch}_1}\) and \(Q_{\textsc {Ch}_2}\) are upper bounds on the number of \(\textsc {Ch}_1\) and \(\textsc {Ch}_2\) queries in the \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) experiment, respectively, and \(Q_s\), \(Q_1\), and \(Q_2\) are upper bounds on the number of signing and random oracles \(H_1\) and \(H_2\) queries in the \({\mathsf {UF\text{- }CMA}}\) experiment, respectively. Moreover, if \({\mathsf {ID}}\) has special soundness (\(\mathsf {SS}\)), then \({\mathsf {OF}}[{\mathsf {ID}},H_1,H_2,\ell ]\) is \((t',\varepsilon ',Q_s,Q_1,Q_2)\)-\({\mathsf {UF\text{- }CMA}}\)-secure in the random oracle model, where
The proof of Theorem 1 is obtained by combining Lemmas 1 to 3.
Alternative Fiat-Shamir Transform. We call \(\mathsf {ID}\) partially commitment-recoverable if the second-move commitment \(R_2\) can be partitioned into \(R_2=(R_L,R_R)\), a left part \(R_L\) and a right part \(R_R\), and \({\mathsf {V}}(pk,R_1,h_1,R_2,h_2,s)\) is such that it first recomputes \(R_1' = {\mathsf {V}}_1(pk,h_2,s)\) and \(R'_R = {\mathsf {V}}_2(pk,R_L,h_1,h_2,s)\) and then outputs 1 iff \((R_1',R'_R) = (R_1,R_R)\). It is fully commitment-recoverable if \(R_2=R_R\) and \(R_L\) is the empty string. For commitment-recoverable \(\mathsf {ID}\), we can define an alternative Fiat-Shamir transformation \({\mathsf {FS}}'[{\mathsf {ID}},H_1,H_2,\ell ]:=({\mathsf {Gen}},{\mathsf {Sign}}',{\mathsf {Ver}}')\), where \({\mathsf {Gen}}\) is as in \({\mathsf {FS}}[{\mathsf {ID}},H_1,H_2,\ell ]\). Algorithm \({\mathsf {Sign}}'(sk,{m})\) is defined as \({\mathsf {Sign}}(sk,{m})\) with the modified output \(\sigma ' = (R_L,h_2,s)\). Algorithm \({\mathsf {Ver}}'(pk,{m},\sigma ')\) first parses \(\sigma '=(R_L,h_2,s)\), then recomputes \(R_1' = {\mathsf {V}}_1(pk,h_2,s)\) and \(R'_R := {\mathsf {V}}_2(pk,R_L,h_1,h_2,s)\), where \(h_1= H_1(R_1')\), and finally returns 1 iff \(H_2((R_L,R'_R),{m})=h_2\). Its online/offline variant \({\mathsf {OF}}'[{\mathsf {ID}},H_1,H_2,\ell ]:=({\mathsf {Gen}},{\mathsf {Sign_o}}',{\mathsf {Ver_o}}')\) is defined in the similar manner with the boxed differences.

Since \(\sigma =(R_1,R_2,s)\) can be publicly transformed into \(\sigma '=(R_L,h_2,s)\) and vice versa, \({\mathsf {FS}}[{\mathsf {ID}},H_1,H_2,\ell ]\) and \({\mathsf {FS}}'[\mathsf {ID},H_1,H_2,\ell ]\) are equivalent in terms of security. The same argument holds for \({\mathsf {OF}}[{\mathsf {ID}},H_1,H_2,\ell ]\) and \({\mathsf {OF}}'[{\mathsf {ID}},H_1,H_2,\ell ]\). On the one hand, the alternative Fiat-Shamir transform yields shorter signatures if \(h_2\in \mathsf {ChSet}_2\) has a smaller representation size than \((R_1,R_R)\). On the other hand, signatures of the Fiat-Shamir transform maintain their algebraic structure which in some cases enables useful properties such as batch verification.
Lemma 1
(\({\mathsf {UF\text{- }KOA}}\) security of \({\mathsf {FS}}\) and \({\mathsf {OF}}\)). Suppose that \(\mathsf {ID}\) is \((t,\varepsilon ,Q_{\textsc {Ch}_1}, Q_{\textsc {Ch}_2})\text{- }\mathsf {naPIMP}\text{- }\mathsf {KOA}\)-secure. Then the signature schemes \({\mathsf {FS}}[{\mathsf {ID}},H_1,H_2,\ell ]\) and \({\mathsf {OF}}[{\mathsf {ID}},H_1,H_2,\ell ]\) are \((t',\varepsilon ', Q_1, Q_2)\text{- }{\mathsf {UF\text{- }KOA}}\)-secure in the random oracle model, where
and \(Q_1\), \(Q_2\) are upper bounds on the numbers of hash queries to \(H_1\) and \(H_2\), respectively.
Proof
We prove the statement for \({\mathsf {OF}}[{\mathsf {ID}},H_1,H_2,\ell ]\); the proof for \({\mathsf {FS}}[{\mathsf {ID}},H_1,H_2,\ell ]\) is identical. Assume that an adversary \(\mathsf {A}\) breaks the \((t',\varepsilon ',Q_1,Q_2)\)-\({\mathsf {UF\text{- }KOA}}\)-security of \({\mathsf {OF}}[{\mathsf {ID}},H_1,H_2,\ell ]\). We construct an adversary \(\mathsf {B}\) that breaks the \((t,\varepsilon ,Q_{\textsc {Ch}_1},Q_{\textsc {Ch}_2})\)-\(\mathsf {PIMP}\text{- }\mathsf {KOA}\) security of \({\mathsf {ID}}\), with \((t,\varepsilon ,Q_{\textsc {Ch}_1},Q_{\textsc {Ch}_2})\) as claimed.
At the beginning, after obtaining \(pk\) from the \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) experiment, \(\mathsf {B}\) forwards it to \(\mathsf {A}\). If \(\mathsf {A}\) makes a query \(R_1\) to the random oracle \(H_1\), \(\mathsf {B}\) returns \(H_1(R_1)\) if it is already defined, otherwise \(\mathsf {B}\) makes a query  and programs \(H_1(R_1) := h_1\). If \(\mathsf {A}\) makes a query \((R_2 ,{m})\) to the random oracle \(H_2\), \(\mathsf {B}\) returns \(H_2(R_2,{m})\) if it is already defined, otherwise \(\mathsf {B}\) makes a query
and programs \(H_1(R_1) := h_1\). If \(\mathsf {A}\) makes a query \((R_2 ,{m})\) to the random oracle \(H_2\), \(\mathsf {B}\) returns \(H_2(R_2,{m})\) if it is already defined, otherwise \(\mathsf {B}\) makes a query  and programs the random oracle \(H_2(R_2,{m}):=h_2\).
and programs the random oracle \(H_2(R_2,{m}):=h_2\).
Eventually, \(\mathsf {A}\) submits a forgery \(({m}, \sigma =(R_1,R_2,s))\), and terminates. We assume that \(h_1:=H_1(R_1)\) and \(h_2:=H_2(R_2,{m})\) were already queried by \(\mathsf {A}\). (Otherwise, \(\mathsf {B}\) queries \(H_1(R_1)\) and \(H_2(R_2,{m})\) which are simulated as described above.) Hence, in total, there are \(Q_{\textsc {Ch}_1}= Q_1+1\) and \(Q_{\textsc {Ch}_2}= Q_2+1\) queries to \(H_1\) and \(H_2\), respectively. Adversary \(\mathsf {B}\) outputs s and terminates. According to the simulations of \(H_1\) and \(H_2\), we have \((R_1,h_1) \in \mathcal {L}_1\) and \((R_2,h_2) \in \mathcal {L}_2\), and \((R_1,h_1, R_2,h_2,s)\) is a valid transcript and hence breaks the \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) security if \(\mathsf {A}\)’s forgery is valid. This establishes \(\varepsilon = \varepsilon '\). The running time of \(\mathsf {B}\) is roughly that of \(\mathsf {A}\), and thus \(t' \approx t\).
Lemma 2
(\({\mathsf {UF\text{- }CMA}}\) security of \({\mathsf {FS}}\) ). If \({\mathsf {ID}}\) is \(\varDelta \)-statistically \(\mathsf {naHVZK}\) with \(\alpha \)-bits min-entropy and \({\mathsf {FS}}[{\mathsf {ID}},H_1,H_2,\ell ]\) is \((t,\varepsilon ,Q_1,Q_2)\)-\({\mathsf {UF\text{- }KOA}}\) secure, then \({\mathsf {FS}}[{\mathsf {ID}},H_1,H_2,\ell ]\) is \((t',\varepsilon ',Q_s,Q_1',Q_2')\)-\({\mathsf {UF\text{- }CMA}}\) secure in the random oracle model, where
and \(Q_1\) and \(Q_2\) are upper bounds on the numbers of hash queries to \(H_1\) and \(H_2\), respectively, and \(Q_s\), \(Q_1'\) and \(Q_2'\) are upper bounds on the number of signing and hash queries to \(H_1'\) and \(H_2'\) in the \({\mathsf {UF\text{- }CMA}}\) experiment, respectively.
Proof
Assume that an adversary \(\mathsf {A}\) breaks \((t',\varepsilon ',Q_s,Q_1',Q_2')\)-\({\mathsf {UF\text{- }CMA}}\) security of \({\mathsf {FS}}[{\mathsf {ID}},H_1,H_2,\ell ]\). We construct an adersary \(\mathsf {B}\) invokes \(\mathsf {A}\) and breaks \((t,\varepsilon ,Q_1,Q_2)\)-\({\mathsf {UF\text{- }KOA}}\) security of \({\mathsf {FS}}[{\mathsf {ID}},H_1,H_2,\ell ]\) with \((t,\varepsilon )\) as stated in the lemma. Adversary \(\mathsf {B}\) is executed in the \({\mathsf {UF\text{- }KOA}}\) experiment. It obtains public key \(pk\) and has access to random oracles \(H_1\) and \(H_2\).
Adversary \(\mathsf {B}\) runs \(\mathsf {A}\) on input \(pk\) answering hash queries to random oracles \(H_1'\) and \(H_2'\) and signing queries as follows.
Simulation of hash queries. A hash query \(H_1'(R,m)\) is answered by \(\mathsf {B}\) by querying its own hash oracle \(H_1(R,m)\) and storing its answer and returning it. \(H_2'\) is simulated in the same way by using \(\mathsf {B}\)’s own oracle \(H_2\).
Simulation of signing queries. On \(\mathsf {A}\)’s signature query \({m}\), \(\mathsf {B}\) uses the \(\mathsf {naHVZK}\) property of \({\mathsf {ID}}\) to generate a signature \(\sigma \) on message \({m}\). Concretely, \(\mathsf {B}\) defines \(i:=0\) and simulates the signing query as follows.
-
While \(i \le \ell \) and \(s= \bot \):
-
 and \(i:=i+1\);
and \(i:=i+1\);
-
-
If \(s= \bot \), then return \(\bot \);
-
Else
-
If \(H_1'(R_1,m)\ne \bot \) or \(H_2'(R_2,{m})\ne \bot \), then define \(\textsc {Incon}:=1\) and return \(\bot \)
-
Else define
$$\begin{aligned} H_1'(R_1,m):= h_1, \; H_2'(R_2,{m}):=h_2 \end{aligned}$$(1)and return \(\sigma := (R_1, R_2,s)\).
-
We note that, by Eq. (1), \(\mathsf {B}\) makes the hash functions inconsistent, since \(H_1(R_1,m) \ne h_1=: H_1'(R_1,m)\) and \(H_2(R_2,{m}) \ne h_2=: H_2'(R_2,{m})\) with high probability. Adversary \(\mathsf {A}\) can detect this inconsistence if \(\textsc {Incon}=1\), namely, \(\mathsf {A}\) queries the exact \(H_1'(R_1,{m})\) or \(H_2'(R_2,{m})\) before asking the signing query on \({m}\). For each signing query, this can be bounded (namely, \(\mathsf {B}\) aborts because of \(\textsc {Incon}=1\)) by probability at most \((Q_1'+Q_2')/2^\alpha \), since \({\mathsf {ID}}\) has \(\alpha \)-bits min-entropy. Moreover, for each signing query, \(\mathsf {B}\) runs \(\mathsf {Sim}\) at most \(\ell \) times and produces a real transcript from \({\mathsf {SKTran}}(sk)\) oracle with statistical distance at most \(\varDelta \) in each of these runs. Since the number of signing queries is bounded by \(Q_s\), the statistical distance between the real \({\mathsf {UF\text{- }CMA}}\) experiment and the simulated one is at most \(Q_s \cdot ((Q_1' + Q_2')/2^\alpha + \ell \varDelta )\).
Forgery. Eventually, \(\mathsf {A}\) submits its forgery \(({m},\sigma :=(R_1,R_2,s))\). We assume that it is a valid forgery in the \({\mathsf {UF\text{- }CMA}}\) experiment, namely, for \(h_1= H_1'(R_1,m)\) and \(h_2= H_2'(R_2,{m})\) we have \({\mathsf {V}}(pk, R_1,h_1, R_2,h_2,s)=1\). Furthermore, it satisfies the freshness condition, i.e., \({m}\not \in \mathcal{M}.\) Note that by the freshness condition, we have \(H_1(R_1,m) = H_1'(R_1,m)=h_1\) and \(H_2(R_2,m) = H_2'(R_2,m)=h_2\) since \(H_1'(R_1,m)\) and \(H_2'(R_2,m)\) were not programmed via (1). After receiving \(\mathsf {A}\)’s forgery, \(\mathsf {B}\) computes a forgery for the \({\mathsf {UF\text{- }KOA}}\) experiment as \(\sigma =(R_1,R_2,s)\).
Overall, \(\mathsf {B}\) returns a valid forgery of \({\mathsf {UF\text{- }KOA}}\) experiment with probability
The running time of \(\mathsf {B}\) is that of \(\mathsf {A}\) plus the \(Q_s\) executions of \(\mathsf {Sim}\). We write \(t' \approx t\). This completes the proof.
Lemma 3
(\({\mathsf {UF\text{- }CMA}}\)-security of \({\mathsf {OF}}\)). If \({\mathsf {ID}}\) is \(\varDelta \)-statistically \(\mathsf {naHVZK}\) with \(\alpha \)-bits min-entropy, has \(\mathsf {SS}\), and \({\mathsf {OF}}[{\mathsf {ID}},H_1,H_2,\ell ]\) is \((t,\varepsilon ,Q_1,Q_2)\)-\({\mathsf {UF\text{- }KOA}}\) secure, then \({\mathsf {OF}}[{\mathsf {ID}},H_1,H_2,\ell ]\) is \((t',\varepsilon ',Q_s,Q_1',Q_2')\)-\({\mathsf {UF\text{- }CMA}}\) secure in the random oracle model, where
and \(Q_1\) and \(Q_2\) are upper bounds on the numbers of hash queries to \(H_1\) and \(H_2\), respectively, and \(Q_s\), \(Q_1'\) and \(Q_2'\) are upper bounds on the number of signing and hash queries to \(H_1'\) and \(H_2'\) in the \({\mathsf {UF\text{- }CMA}}\) experiment, respectively.
Proof
Let \(\mathsf {A}\) be an algorithm that breaks \((t',\varepsilon ',Q_s,Q_1',Q_2')\)-\({\mathsf {UF\text{- }CMA}}\) security of \({\mathsf {OF}}[{\mathsf {ID}},H_1,H_2,\ell ]\). We will describe an adversary \(\mathsf {B}\) invoking \(\mathsf {A}\) that breaks \((t,\varepsilon ,Q_1,Q_2)\)-\({\mathsf {UF\text{- }KOA}}\) security of \({\mathsf {OF}}[{\mathsf {ID}},H_1,H_2,\ell ]\) with \((t,\varepsilon )\) as stated in the lemma. Adversary \(\mathsf {B}\) is executed in the \({\mathsf {UF\text{- }KOA}}\) experiment and obtains public-key \(pk\), and has access to random oracles \(H_1\) and \(H_2\).
Adversary \(\mathsf {B}\) runs \(\mathsf {A}\) on input \(pk\) answering hash queries to random oracles \(H_1'\) and \(H_2'\) and signing queries as follows.
Simulation of hash queries. A hash query \(H_1'(R)\) is answered by \(\mathsf {B}\) by querying its own hash oracle \(H_1(R)\) and storing its answer and returning it. \(H_2'\) is simulated in the same way by using \(\mathsf {B}\)’s own oracle \(H_2\).
Simulation of signing queries. The simulation here is similar to that in Lemma 2 except for the simulation of \(H_1'\). For completeness, we present the details as follows.
On \(\mathsf {A}\)’s signature query \({m}\), \(\mathsf {B}\) uses the \(\mathsf {naHVZK}\) property of \({\mathsf {ID}}\) to generate a signature \(\sigma \) on message \({m}\). Concretely, \(\mathsf {B}\) defines \(i:=0\) and simulates the signing query as follows.
-
While \(i \le \ell \) and \(s= \bot \):
-
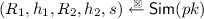 and \(i:=i+1\);
and \(i:=i+1\);
-
-
If \(s= \bot \), then return \(\bot \);
-
Else
-
If \(H_1'(R_1)\ne \bot \) or \(H_2'(R_2,{m})\ne \bot \), then define \(\textsc {Incon}:=1\) and return \(\bot \)
-
Else define
$$\begin{aligned} H_1'(R_1):= h_1, \; H_2'(R_2,{m}):=h_2 \end{aligned}$$(2)and return \(\sigma := (R_1, R_2,s)\).
-
We note that, by Eq. (2), \(\mathsf {B}\) makes the hash functions inconsistent, since \(H_1(R_1) \ne h_1=: H_1'(R_1)\) and \(H_2(R_2,{m}) \ne h_2=: H_2'(R_2,{m})\) with high probability. Adversary \(\mathsf {A}\) can detect this inconsistence if \(\textsc {Incon}=1\), namely, \(\mathsf {A}\) queries the exact \(H_1'(R_1)\) or \(H_2'(R_2,{m})\) before asking the signing query on \({m}\). For each signing query, this can be bounded (namely, \(\mathsf {B}\) aborts because of \(\textsc {Incon}=1\)) by probability at most \((Q_1'+Q_2')/2^\alpha \), since \({\mathsf {ID}}\) has \(\alpha \)-bits min-entropy. Moreover, for each signing query, \(\mathsf {B}\) runs \(\mathsf {Sim}\) at most \(\ell \) times and produces a real transcript from \({\mathsf {SKTran}}(sk)\) oracle with statistical distance at most \(\varDelta \) in each of these runs. Since the number of signing queries is bounded by \(Q_s\), the statistical distance between the real \({\mathsf {UF\text{- }CMA}}\) experiment and the simulated one is at most \(Q_s \cdot ((Q_1' + Q_2')/2^\alpha + \ell \varDelta )\).
Forgery. Eventually, \(\mathsf {A}\) will submit its forgery \(({m},\sigma :=(R_1,R_2,s))\). We assume that it is a valid forgery in the \({\mathsf {UF\text{- }CMA}}\) experiment, namely, for \(h_1= H_1'(R_1)\) and \(h_2= H_2'(R_2,{m})\) we have \({\mathsf {V}}(pk, R_1,h_1, R_2,h_2,s)=1\). Furthermore, it satisfies the freshness condition, i.e., \({m}\not \in \mathcal{M}\). After receiving \(\mathsf {A}\)’s forgery, \(\mathsf {B}\) computes a forgery for the \({\mathsf {UF\text{- }KOA}}\) experiment according to the following case distinction.
-
Case 1: \(R_1\) was defined in a signing query on some message \(m'\) via (2), i.e., \((R_1, h_1',R_2',h_2',s')\) was generated by using \(\mathsf {Sim}(pk)\). The freshness condition implies \(m' \ne m\) and hence \(h_2=H_2'(R_2,{m}) \ne H_2'(R_2',{m}')=h_2'\), except with probability \(1/|\mathsf {ChSet}_2|\). In that case we have two valid transcripts \((R_1,h_1,R_2,h_2,s)\) and \((R_1, h_1',R_2',h_2',s')\) with \(h_2\ne h_2'\). By the special soundness of \({\mathsf {ID}}\), \(\mathsf {B}\) extracts a valid \(sk^*\) by running \({\mathsf {Ext}}\) such that \((pk,sk^*) \in {\mathsf {IGen}}(\mathsf {par})\), and then \(\mathsf {B}\) use \(sk^*\) to generate a fresh and valid \({\mathsf {UF\text{- }CMA}}\) forgery. In this case, \(Q_1' = Q_1+1\) and \(Q_2' = Q_2+ 1\).
-
Case 2: \(R_1\) was queried to the \(H_1'\) oracle, i.e., \(H_1(R_1) = H_1'(R_1)=h_1\). By the freshness condition, \(h_2= H_2'(R_2,{m})\) was defined in a hash query, but not in a signing query, i.e., \(h_2= H_2'(R_2,{m})=H_2(R_2,{m})\). \(\mathsf {B}\) returns \(\sigma =(R_1,R_2,s)\) as a valid forgery to its \({\mathsf {UF\text{- }CMA}}\) experiment.
Overall, \(\mathsf {B}\) returns a valid forgery of \({\mathsf {UF\text{- }KOA}}\) experiment with probability
The running time of \(\mathsf {B}\) is that of \(\mathsf {A}\) plus the \(Q_s\) executions of \(\mathsf {Sim}\). We write \(t' \approx t\). This completes the proof.
4 Instantiations
In the following, let \(\mathsf {par}:= (p, g,\mathbb {G})\) be a set of system parameters, where \(\mathbb {G}=\langle g\rangle \) is a cyclic group of prime order p.
4.1 Instantiation from CDH
We briefly recall the \(\mathsf {CDH}\) problem.
Definition 8
(Computation Diffie-Hellman Assumption). The computational Diffie-Hellman problem \(\mathsf {CDH}\) is \((t,\varepsilon )\)-hard in \(\mathsf {par}\) if for all adversaries \(\mathsf {A}\) running in time at most t,

Identification Scheme. The identification scheme \(\mathsf {ID}_{\mathsf {CDH}}:= ({\mathsf {IGen}},{\mathsf {P}},\mathsf {ChSet}_1,\mathsf {ChSet}_2,{\mathsf {V}})\) is defined as follows.

Lemma 4
\(\mathsf {ID}_{\mathsf {CDH}}\) is a perfectly correct five-move identification scheme and has perfect non-aborting honest-verifier zero-knowledge (\(\mathsf {naHVZK}\)) with \(\alpha =\log p\) bits min-entropy and special soundness (SS). Moreover, if \(\mathsf {CDH}\) is \((t,\varepsilon )\)-hard in \(\mathsf {par}=( p, g,\mathbb {G})\) then \(\mathsf {ID}_{\mathsf {CDH}}\) is \((t',\varepsilon ',Q_{\textsc {Ch}_1},Q_{\textsc {Ch}_2})\)-\(\mathsf {PIMP}\text{- }\mathsf {KOA}\) secure, where \(t \approx t'\) and \(\varepsilon \ge \varepsilon ' - \frac{Q_{\textsc {Ch}_2}}{2^k}\).
Proof
The perfect correctness of \(\mathsf {ID}_{\mathsf {CDH}}\) is straightforward to verify. We show the other properties as follows:
Perfect Non-Aborting Honest-Verifier Zero-Knowledge (\(\mathsf {naHVZK}\)). Given public key \(pk=X\), \(\mathsf {Sim}\) first samples  It then computes \(h_1:=g^w,R_1:=g^sX^{-h_2},R_L:=X^w,\) and \(R_R:=R_1^w\), defines \(R_2:=(R_L,R_R)\) and outputs the transcript \((R_1,h_1,R_2,h_2,s).\) Clearly, \((R_1,h_1,R_2,h_2,s)\) is distributed the same as the one from \({\mathsf {SKTran}}(sk)\), since s is uniformly random over \({{\mathbb Z}}_p\) and \(R_1, R_L\) and \(R_R\) satisfy \(R_1= g^s\cdot X^{-h_2}\) and \(R_R=h_1^s\cdot R_L^{-h_2}\). Moreover, we note that the entropy of
It then computes \(h_1:=g^w,R_1:=g^sX^{-h_2},R_L:=X^w,\) and \(R_R:=R_1^w\), defines \(R_2:=(R_L,R_R)\) and outputs the transcript \((R_1,h_1,R_2,h_2,s).\) Clearly, \((R_1,h_1,R_2,h_2,s)\) is distributed the same as the one from \({\mathsf {SKTran}}(sk)\), since s is uniformly random over \({{\mathbb Z}}_p\) and \(R_1, R_L\) and \(R_R\) satisfy \(R_1= g^s\cdot X^{-h_2}\) and \(R_R=h_1^s\cdot R_L^{-h_2}\). Moreover, we note that the entropy of  and
and  comes only from \(R_1\), which is uniformly random over \(\mathbb {G}\). Hence, since the outputs of \(\mathsf {Sim}(pk)\) are identically distributed to the outputs of \({\mathsf {SKTran}}(sk)\), \(\mathsf {ID}_{\mathsf {CDH}}\) has \(\log | \mathbb {G}| = \log p\) bits min-entropy as claimed.
comes only from \(R_1\), which is uniformly random over \(\mathbb {G}\). Hence, since the outputs of \(\mathsf {Sim}(pk)\) are identically distributed to the outputs of \({\mathsf {SKTran}}(sk)\), \(\mathsf {ID}_{\mathsf {CDH}}\) has \(\log | \mathbb {G}| = \log p\) bits min-entropy as claimed.
Special Soundness. Given two accepting transcripts \((R_1,h_1,R_2,h_2,s)\) and \((R_1,h_1',R_2',h_2',s')\) with \(h_2\ne h_2'\), we define an extractor \({\mathsf {Ext}}\) with the property that \({\mathsf {Ext}}(pk,R_1,h_1,R_2,h_2,s,h_1',R_2',h_2',s')\) outputs \(x^* := (s- s_i')/(h_2- h_2') \bmod p \). We have \(\Pr [g^{x^*}=X]=1\) for all \((X:=g^x,x) \in {\mathsf {IGen}}(\mathsf {par})\), since \(R_1=g^{s} \cdot X^{-h_2} = g^{s'} \cdot X^{-h_2'}\) and \(X = g^{(s-s')/(h_2-h_2')}\).
\(\mathsf {PIMP}\text{- }\mathsf {KOA}\) -Security. Let \(\mathsf {A}\) be an attacker against the \((t', \varepsilon ', Q_{\textsc {Ch}_1},Q_{\textsc {Ch}_2})\)-\(\mathsf {PIMP}\text{- }\mathsf {KOA}\) security of \(\mathsf {ID}_{\mathsf {CDH}}\). We construct an attacker \(\mathsf {B}\) that \((t,\varepsilon )\)-breaks \(\mathsf {CDH}\).
Construction of \(\mathsf {B}\). Let \((X:=g^x,Y:=g^y)\) denote the \(\mathsf {CDH}\) instance. \(\mathsf {B}\) runs \(\mathsf {A}\) with input \(pk:=X\) and answers \(\mathsf {A}\)’s challenge queries as follows.
For \(\mathsf {A}\)’s \(\textsc {Ch}_1\) query on \(R_1\in \mathbb {G}\), \(\mathsf {B}\) chooses  and computes \(h_1=Y \cdot g^{a}\). For \(\mathsf {A}\)’s \(\textsc {Ch}_2\) query on \(R_2\in \mathbb {G}\times \mathbb {G}\), \(\mathsf {B}\) chooses
and computes \(h_1=Y \cdot g^{a}\). For \(\mathsf {A}\)’s \(\textsc {Ch}_2\) query on \(R_2\in \mathbb {G}\times \mathbb {G}\), \(\mathsf {B}\) chooses  and returns it to \(\mathsf {A}\). Clearly, \(\mathsf {B}\)’s simulation of the \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) game is perfect, since both \(h_1\) and \(h_2\) are uniformly random over \(\mathbb {G}\) and \({{\mathbb Z}}_p\), respectively.
and returns it to \(\mathsf {A}\). Clearly, \(\mathsf {B}\)’s simulation of the \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) game is perfect, since both \(h_1\) and \(h_2\) are uniformly random over \(\mathbb {G}\) and \({{\mathbb Z}}_p\), respectively.
Eventually, \(\mathsf {A}\) returns its response \(s^*\) for the \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) experiment. We assume that \(\mathsf {A}\)’s response is valid, i.e., there exist \((R_1,h_1) \in \mathcal {L}_1\) and \((R_2:=(R_L,R_R),h_2) \in \mathcal {L}_2\) such that \(R_1=g^{s^*} \cdot X^{-h_2}\) and \(R_R = h_1^{s^*} \cdot R_L^{-h_2}\). We denote the discrete logarithm of \(R_L\) based on \(h_1\) by \(x' = {\mathsf {DL}}_{h_1}(R_L)\) and do the following cases distinction:
-
Case 1: \(x=x'\). By the simulation of \(\textsc {Ch}_1\), we have \(R_L = h_1^{x} = (Y g^{a_i})^x = Y^x X^{a_i}\) for some \(i \in [Q_{\textsc {Ch}_1}]\). Thus, \(\mathsf {B}\) returns \(Z:=R_L \cdot X^{-a_i}=Y^x\) to break the \(\mathsf {CDH}\) problem.
-
Case 2: \(x\ne x'\). We show in this case even an unbounded adversary \(\mathsf {A}\) can only win with probability \(Q_{\textsc {Ch}_2}/2^k\). For each index \(i \in [Q_{\textsc {Ch}_2}]\), before receiving \(h_{2,i}\), \(\mathsf {A}\) first commits to some \(R_1= g^{r_1}\), \(R_L = h_1^{x'}\) and \(R_R = h_1^{r_2}\) (for arbitrary \(r_1, r_2, x' \in {{\mathbb Z}}_p\) and \(x'\ne x\)) and there exists \((R_1,h_1) \in \mathcal {L}_1\). \(\mathsf {A}\) can only win if there exists an \(s_i \in {{\mathbb Z}}_p\) such that
$$\begin{aligned} r_{1} + h_{2,i} x = s_i = r_{2} + h_{2,i} x' \Leftrightarrow&h_{2,i} = \frac{ r_{2}-r_{1} }{x-x'}. \end{aligned}$$where
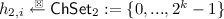 is chosen independently of \(r_1,r_2\) and \(x'\). This happens with probability at most \(1/|\mathsf {ChSet}_2|=2^{-k}\). By the union bound we obtain the bound \(Q_{\textsc {Ch}_2}/2^k\) as claimed.
is chosen independently of \(r_1,r_2\) and \(x'\). This happens with probability at most \(1/|\mathsf {ChSet}_2|=2^{-k}\). By the union bound we obtain the bound \(Q_{\textsc {Ch}_2}/2^k\) as claimed.
Overall, \(\mathsf {B}\) returns a valid solution of the \(\mathsf {CDH}\) challenge with probability \(\varepsilon \ge \varepsilon ' - \frac{Q_{\textsc {Ch}_2}}{2^k}\). This completes the proof.
(Online/offline) Signature. Let \(H_1: \{0,1\}^* \rightarrow \mathbb {G}\) and \(H_2: \{0,1\}^*\rightarrow \{0,\ldots ,2^k-1\}\) be two hash functions. As \(\mathsf {ID}_{\mathsf {CDH}}\) is perfectly correct and partially commitment-recoverable, we can use the alternative Fiat-Shamir transformation from Sect. 3.1 with \(\ell :=1\) to obtain the signature scheme \(\mathsf {FS_{CDH}}:=({\mathsf {Gen}},{\mathsf {Sign}},{\mathsf {Ver}})\) and its online/offline variant \({\mathsf {OF}}_{\mathsf {CDH}}:=({\mathsf {Gen}},{\mathsf {Sign_o}},{\mathsf {Ver_o}})\). Here, \(\mathsf {FS_{CDH}}\) does not include X, \(R_1\) and \((g,h_1)\) in the hash \(H_2\), which is slightly simpler than the Chevallier-Mames scheme in [20].

By Lemma 4 and Theorem 1, we have
Theorem 2
(Security of \(\mathsf {FS_{CDH}}\) and \({\mathsf {OF}}_{\mathsf {CDH}}\)). If \(\mathsf {CDH}\) is \((t,\varepsilon )\)-hard in \(\mathsf {par}:=(p,g,\mathbb {G})\) then scheme \(\mathsf {FS_{CDH}}\) is \((t',\varepsilon ',Q_s,Q_1,Q_2)\)-\({\mathsf {UF\text{- }CMA}}\) secure and scheme \({\mathsf {OF}}_{\mathsf {CDH}}\) is \((t'',\varepsilon '',Q_s,Q_1,Q_2)\)-\({\mathsf {UF\text{- }CMA}}\) secure in the programmable random oracle model, where
4.2 Instantiation from Short CDH
We recall the short exponent \(\mathsf {CDH}\) assumption from [36].
Definition 9
(\(c \text{- }{\mathsf {SCDH}}\) Assumption). The c-short exponent computational Diffie-Hellman problem \(c \text{- }{\mathsf {SCDH}}\) is \((t,\varepsilon )\)-hard in \(\mathsf {par}\) if for all adversaries \(\mathsf {A}\) running in time at most t,

Identification Scheme. Let \(\mathsf {par}:=( p, g,\mathbb {G},k,k',c)\) be a set of system parameters, where \(\mathbb {G}=\langle g \rangle \) is a cyclic group of prime order p with a hard \(c \text{- }{\mathsf {SCDH}}\) problem and \(k=\omega (\log p)\). The identification scheme \(\mathsf {ID}_{{\mathsf {SCDH}}}:=({\mathsf {IGen}},{\mathsf {P}},\mathsf {ChSet}_1, \mathsf {ChSet}_2,{\mathsf {V}})\) is defined as follows. Here the response s is computed over the integers (rather than over \({{\mathbb Z}}_p\)).

Lemma 5
[3]. Let  Then, \(s:=xh_2+ r \in \{2^{k+c},...,2^{k'+k+c}-1\}\) with probability \(1-2^{-k'}\). Moreover, if \(s\in \{2^{k+c},...,2^{k'+k+c}-1\}\), then it is uniformly distributed in this interval.
Then, \(s:=xh_2+ r \in \{2^{k+c},...,2^{k'+k+c}-1\}\) with probability \(1-2^{-k'}\). Moreover, if \(s\in \{2^{k+c},...,2^{k'+k+c}-1\}\), then it is uniformly distributed in this interval.
Lemma 6
\(\mathsf {ID}_{{\mathsf {SCDH}}}\) is a five-move identification scheme with correctness error \(2^{-k'}\) and has perfect non-aborting honest-verifier zero-knowledge (\(\mathsf {naHVZK}\)) with \(\alpha =c\) bits min-entropy and special soundness. Moreover, if \(c \text{- }{\mathsf {SCDH}}\) is \((t,\varepsilon )\)-hard in \(\mathsf {par}=( p, g,\mathbb {G})\) then \(\mathsf {ID}_{{\mathsf {SCDH}}}\) is \((t', \varepsilon ', Q_{\textsc {Ch}_1},Q_{\textsc {Ch}_2})\)-\(\mathsf {PIMP}\text{- }\mathsf {KOA}\)-secure, where \(\varepsilon ' \le \varepsilon +Q_{\textsc {Ch}_2}/2^k\) and \(t' \approx t\).
Proof
By Lemma 5, \(\mathsf {ID}_{{\mathsf {SCDH}}}\) has correctness error \(2^{-k'}\). We note that the entropy of \(R_1= g^r\) and \(R_2:=(h_1^x, h_1^r )\) comes only from r, which is chosen uniformly from \(\{0, ..., 2^{c}-1\}\). Hence \(\mathsf {ID}_{{\mathsf {SCDH}}}\) has c bits min-entropy. We show the other properties as follows.
Perfect \(\mathsf {naHVZK}\). Given public key \(pk=X\), simulator \(\mathsf {Sim}\) first samples  and \(h_2\leftarrow \{0,...,2^{k}-1\}\). It then computes \(h_1= g^w,R_1 = g^sX^{-h_2},R_L = X^w,\) and \(R_R = R_1^w\), defines \(R_2:=(R_L,R_R)\) and outputs the transcript \((R_1,h_1,R_2,h_2,s)\) with probability \(1-2^{-k'}\), or \((\bot ,\bot ,\bot ,\bot ,\bot )\) with probability \(2^{-k'}\). Clearly, the output of \(\mathsf {Sim}(pk)\) is identical to that of \({\mathsf {SKTran}}(sk)\). According to the simulation, with probability \(1-2^{-k'}\), \(\mathsf {Sim}(pk)\) will output a transcript \((R_1,h_1,R_2,h_2,s)\), where s is uniformly random over the interval \(\{2^{k+c},...,2^{k'+k+c} -1\}\) and \(R_1, R_L\) and \(R_R\) are values satisfying \(R_1= g^s\cdot X^{-h_2}\) and \(R_R=h_1^s\cdot R_L^{-h_2}\). Due to Lemma 5, the probability that such a transcript is output by \(\mathsf {Sim}\) is the same as that for \({\mathsf {SKTran}}\), and, moreover, the probability that \(\mathsf {Sim}\) outputs \((\bot ,\bot ,\bot ,\bot ,\bot )\) is also the same as that for \({\mathsf {SKTran}}\). We note that the entropy of \(R_1= g^r\) and \(R_2:=(h_1^x, h_1^r )\) comes only from r, which is chosen uniformly from \(\{0, ..., 2^{c}-1\}\). Since \(\mathsf {Sim}(pk)\) outputs transcripts identically distributed to the ones output by \({\mathsf {SKTran}}(sk)\), \(\mathsf {ID}_{{\mathsf {SCDH}}}\) has c bits min-entropy. Thus, \(\mathsf {ID}_{{\mathsf {SCDH}}}\) is perfectly \(\mathsf {naHVZK}\).
and \(h_2\leftarrow \{0,...,2^{k}-1\}\). It then computes \(h_1= g^w,R_1 = g^sX^{-h_2},R_L = X^w,\) and \(R_R = R_1^w\), defines \(R_2:=(R_L,R_R)\) and outputs the transcript \((R_1,h_1,R_2,h_2,s)\) with probability \(1-2^{-k'}\), or \((\bot ,\bot ,\bot ,\bot ,\bot )\) with probability \(2^{-k'}\). Clearly, the output of \(\mathsf {Sim}(pk)\) is identical to that of \({\mathsf {SKTran}}(sk)\). According to the simulation, with probability \(1-2^{-k'}\), \(\mathsf {Sim}(pk)\) will output a transcript \((R_1,h_1,R_2,h_2,s)\), where s is uniformly random over the interval \(\{2^{k+c},...,2^{k'+k+c} -1\}\) and \(R_1, R_L\) and \(R_R\) are values satisfying \(R_1= g^s\cdot X^{-h_2}\) and \(R_R=h_1^s\cdot R_L^{-h_2}\). Due to Lemma 5, the probability that such a transcript is output by \(\mathsf {Sim}\) is the same as that for \({\mathsf {SKTran}}\), and, moreover, the probability that \(\mathsf {Sim}\) outputs \((\bot ,\bot ,\bot ,\bot ,\bot )\) is also the same as that for \({\mathsf {SKTran}}\). We note that the entropy of \(R_1= g^r\) and \(R_2:=(h_1^x, h_1^r )\) comes only from r, which is chosen uniformly from \(\{0, ..., 2^{c}-1\}\). Since \(\mathsf {Sim}(pk)\) outputs transcripts identically distributed to the ones output by \({\mathsf {SKTran}}(sk)\), \(\mathsf {ID}_{{\mathsf {SCDH}}}\) has c bits min-entropy. Thus, \(\mathsf {ID}_{{\mathsf {SCDH}}}\) is perfectly \(\mathsf {naHVZK}\).
Special Soundness. Given two accepting transcripts \((R_1,h_1,R_2,h_2,s)\) and \((R_1,h_1',R_2',h_2',s')\) with \(h_2\ne h_2'\), we define an extractor \({\mathsf {Ext}}\) with the property that \({\mathsf {Ext}}(pk,R_1,h_1,R_2,h_2,s,h_1',R_2',h_2',s')\) outputs \(x^* := (s- s_i')/(h_2- h_2') \). We note that \(x^* \in \{0, ...,2^c -1\}\), since \(s, s_i' \in \{2^{k+c}, ..., 2^{k+k'+c}-1 \}\) and \(h_2, h_2' \in \{0,..., 2^k\} \). Moreover, for all \((X:=g^x,x) \in {\mathsf {IGen}}(\mathsf {par})\), we have \(\Pr [X=g^{x^*}]=1\), since \(R_1= g^{s} X^{-h_2}= g^{s'} X^{-h_2'}\) and then \(X=g^{(s-s')/(h_2- h_2')}\).
\(\mathsf {PIMP}\text{- }\mathsf {KOA}\) -security. Let \(\mathsf {A}\) be an attacker against the \((t', \varepsilon ', Q_{\textsc {Ch}_1},Q_{\textsc {Ch}_2})\)-\(\mathsf {PIMP}\text{- }\mathsf {KOA}\) security of \(\mathsf {ID}_{{\mathsf {SCDH}}}\). We construct an attacker \(\mathsf {B}\) that \((t,\varepsilon )\)-breaks \(c \text{- }{\mathsf {SCDH}}\).
Construction of \(\mathsf {B}\). Let \((X:=g^x,Y:=g^y)\) denote the \(c \text{- }{\mathsf {SCDH}}\) instance. \(\mathsf {B}\) runs \(\mathsf {A}\) with input \(pk:=X\) and answers \(\mathsf {A}\)’s challenge queries as follows.
For \(\mathsf {A}\)’s \(\textsc {Ch}_1\) query on \(R_1\in \mathbb {G}\), \(\mathsf {B}\) chooses  and computes \(h_1=Y \cdot g^{a}\). For \(\mathsf {A}\)’s \(\textsc {Ch}_2\) query on \(R_2\in \mathbb {G}\times \mathbb {G}\), \(\mathsf {B}\) chooses
and computes \(h_1=Y \cdot g^{a}\). For \(\mathsf {A}\)’s \(\textsc {Ch}_2\) query on \(R_2\in \mathbb {G}\times \mathbb {G}\), \(\mathsf {B}\) chooses  and returns it to \(\mathsf {A}\). Clearly, \(\mathsf {B}\)’s simulation of the \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) game is perfect, since both \(h_1\) and \(h_2\) are uniformly random over \(\mathbb {G}\) and \(\{0,...,2^k\}\), respectively.
and returns it to \(\mathsf {A}\). Clearly, \(\mathsf {B}\)’s simulation of the \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) game is perfect, since both \(h_1\) and \(h_2\) are uniformly random over \(\mathbb {G}\) and \(\{0,...,2^k\}\), respectively.
Eventually, \(\mathsf {A}\) returns its response \(s^*\) for the \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) experiment. We assume that \(\mathsf {A}\)’s response is valid, i.e., \(s^* \in \{ 2^{k+c}, ...,2^{k+k'+c}-1 \}\) and there exist \((R_1,h_1) \in \mathcal {L}_1\) and \((R_2:=(R_L,R_R),h_2) \in \mathcal {L}_2\) such that \(R_1=g^{s^*} \cdot X^{-h_2}\) and \(R_R = h_1^{s^*} \cdot R_L^{-h_2}\). We denote the discrete logarithm of \(R_L\) based on \(h_1\) by \(x' = {\mathsf {DL}}_{h_1}(R_L)\) and do the following cases distinction:
-
Case 1: \(x=x'\). By the simulation of \(\textsc {Ch}_1\), we have \(R_L = h_1^{x} = (Y g^{a_i})^x = Y^x X^{a_i}\) for some \(i \in [Q_{\textsc {Ch}_1}]\). Thus, \(\mathsf {B}\) returns \(Z:=R_L \cdot X^{-a_i}=Y^x\) to break the \(c \text{- }{\mathsf {SCDH}}\) problem.
-
Case 2: \(x\ne x'\). We show in this case even an unbounded adversary \(\mathsf {A}\) can only win with probability \(Q_{\textsc {Ch}_2}/2^k\). For each index \(i \in [Q_{\textsc {Ch}_2}]\), before receiving \(h_{2,i}\), \(\mathsf {A}\) first commits to some \(R_1= g^{r_1}\), \(R_L = h_1^{x'}\) and \(R_R = h_1^{r_2}\) (for arbitrary \(r_1, r_2, x' \in {{\mathbb Z}}_p\) and \(x'\ne x\)) and there exists \((R_1,h_1) \in \mathcal {L}_1\). \(\mathsf {A}\) can only win if there exists an \(s_i \in \{ 2^{k+c}, ...,2^{k+k'+c}-1 \}\) such that
$$\begin{aligned} r_{1} + h_{2,i} x = s_i = r_{2} + h_{2,i} x' \Leftrightarrow&h_{2,i} = \frac{ r_{2}-r_{1} }{x-x'}, \end{aligned}$$where
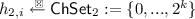 is chosen independently of \(r_1,r_2\) and \(x'\). This happens with probability at most \(1/2^k\). By the union bound we obtain the bound \(Q_{\textsc {Ch}_2}/2^k\) as claimed.
is chosen independently of \(r_1,r_2\) and \(x'\). This happens with probability at most \(1/2^k\). By the union bound we obtain the bound \(Q_{\textsc {Ch}_2}/2^k\) as claimed.
Overall, \(\mathsf {B}\) returns a valid solution of the \(c \text{- }{\mathsf {SCDH}}\) challenge with probability \(\varepsilon \ge \varepsilon ' - \frac{Q_{\textsc {Ch}_2}}{2^k}\). This completes the proof.
(Online/Offline) Signature. Let \(H_1: \{ 0,1 \}^* \rightarrow \mathbb {G}\) and \(H_2: \{ 0,1 \}^* \rightarrow \{0, ..., 2^k-1\}\) be two hash functions. Since \(\mathsf {ID}_{{\mathsf {SCDH}}}\) has \(2^{-k'}\) correctness error, given the required correctness of the signature, we fix a \(\ell \in \mathbb {N}\), and as the scheme \(\mathsf {ID}_{{\mathsf {SCDH}}}\) is partially commitment recoverable, we can use the alternative Fiat-Shamir transform to obtain the signature scheme \({\mathsf {FS}}_{{\mathsf {SCDH}}}:=({\mathsf {Gen}},{\mathsf {Sign}},{\mathsf {Ver}})\) and its online/offline variant \({\mathsf {OF}}_{{\mathsf {SCDH}}}:=({\mathsf {Gen}},{\mathsf {Sign_o}},{\mathsf {Ver_o}})\). For simplicity of notation, let \(\mathcal {I}:=\{2^{k+c},...,2^{k+k'+c}-1\}\).

By Lemma 6 and Theorem 1, we have
Theorem 3
(Security of \({\mathsf {FS}}_{{\mathsf {SCDH}}}\) and \({\mathsf {OF}}_{{\mathsf {SCDH}}}\)) If \(c \text{- }{\mathsf {SCDH}}\) is \((t,\varepsilon )\)-hard in \(\mathsf {par}:=(p,g,\mathbb {G})\) then \({\mathsf {FS}}_{{\mathsf {SCDH}}}\) is \((t',\varepsilon ',Q_s,Q_1,Q_2)\)-\({\mathsf {UF\text{- }CMA}}\) secure and \({\mathsf {OF}}_{{\mathsf {SCDH}}}\) is \((t'',\varepsilon '',Q_s,Q_1,Q_2)\)-\({\mathsf {UF\text{- }CMA}}\) secure in the programmable random oracle model, where
Size of Parameters. We follow the analyses provided in [20, 25, 35]. We set \(t'=t=Q_s=Q_h:=Q_1+Q_2\). Let \(\mathsf {A}\) be and adversary that runs in time \(t'\), makes at most \(Q_s\) signature queries, at most \(Q_h\) has queries and breaks the \({\mathsf {UF\text{- }CMA}}\)-security of \({\mathsf {FS}}_{{\mathsf {SCDH}}}\) with probability at least \(\varepsilon '\) (the analysis applies also to \({\mathsf {OF}}_{{\mathsf {SCDH}}}\)). If \(\mathsf {A}\) is run multiple times, the expected time to produce a forgery is \(t'/\varepsilon '\), so we are looking for a security parameter \(\kappa \) with \(\varepsilon '/t'\le 2^{-\kappa }\). Setting \(\varepsilon '/t' \approx (\varepsilon + \frac{Q_2+1}{2^k} + \frac{(Q_1+Q_2)Q_s}{2^c})/t\), we can bound each of the additive terms separately by \(2^{-\kappa }\) by choosing k and c accordingly. Concretely, we choose \(c=2\kappa \) and \(k=\kappa \). Given that the Pollard lambda algorithm [47] running in time \(O(\sqrt{2^c})\) is the best algorithm for solving the \(c \text{- }{\mathsf {SCDH}}\) problem over \(\mathbb {G}\), \(\frac{\varepsilon }{t}\le \frac{t}{2^c}\le \frac{2^{c/2}}{2^c}=2^{-\kappa }\). Also, by assumption, \(\frac{Q_2+1}{t2^k}\le \frac{t}{2^kt}=2^{-\kappa }\) and \( \frac{(Q_1+Q_2)Q_s}{t2^c}=\frac{t^2}{t2^c}=\frac{t}{2^c}\) which we have already shown to be bounded by \(2^{-\kappa }.\) Setting \(k'=8,\) this gives a signature of size of about \(\ell '+4\cdot \kappa +8,\) where \(\ell '\) denotes the size of a group element.
4.3 Instantiation from Factoring
Signed Quadratic Residues and the Factoring Assumption. We begin by recalling the useful group of signed quadratic residues from [27, 32]. For \(n\in \mathbb {N}\) we denote the set of all n / 2-bit primes by \(\mathbb {P}_{n/2}\) and \(\mathsf {Blum}_{n}:=\{ N \mid N= (2p+1)(2q+1) \; \wedge (2p+1), (2q+1), p,q \in \mathbb {P}_{n/2} \wedge p\ne q \}\). Let \(\varphi (N) = 4pq\) be Euler’s totient function for \(N \in \mathsf {Blum}_{n}\).
We define the factoring assumption as follows.
Definition 10
(Factoring Assumption). The factoring problem \({\mathsf {FAC}}\) is \((t,\varepsilon )\)-hard for \(\mathsf {Blum}_{n}\) if for all adversaries \(\mathsf {A}\) running in time at most t,

For an element \(a \in {{\mathbb Z}}_N\), we define the absolute value
We define the group of signed quadratic residues as \(\mathbb {QR}^+_N:= \{ |x| : x \in \mathbb {QR}_N\}\). We have that \((\mathbb {QR}^+_N,\circ )\) is a cyclic group with order \(|\mathbb {QR}^+_N|=\varphi (N)/4\), where, for all \(a,b \in \mathbb {QR}^+_N\) and \(x \in {{\mathbb Z}}_N\), group operations are defined as follows:
By Theorem 2 of [32], we note that the factoring assumption tightly implies the \(\mathsf {CDH}\) assumption over \(\mathbb {QR}^+_N\) (henceforth denoted as \(\mathsf {CDH}_N\)). Let \(\mathsf {par}_1:= \mathsf {Blum}_{n}\) and \(\mathsf {par}_2 := (N,g,\mathbb {QR}^+_N)\), where  and g is a random generator of \(\mathbb {QR}^+_N\).
and g is a random generator of \(\mathbb {QR}^+_N\).
Corollary 1
(\({\mathsf {FAC}}\xrightarrow {} \mathsf {CDH}_N\)). If \({\mathsf {FAC}}\) is \((t,\varepsilon )\)-hard in \(\mathsf {par}_1\), then \(\mathsf {CDH}_N\) is \((t',\varepsilon ')\)-hard in \(\mathsf {par}_2\), where \(t' \approx t\) and \(\varepsilon ' \le \varepsilon + {2^{-n/2}} \).
Identification Scheme. Let \(\mathsf {par}:=\mathbb {P}_{n/2}\). The identification scheme \(\mathsf {ID}_{{\mathsf {FAC}}}:=({\mathsf {IGen}},{\mathsf {P}},\mathsf {ChSet}_1,\mathsf {ChSet}_2,{\mathsf {V}})\) is defined as follows.

Lemma 7
Let \(N':=\lceil N/4\rceil \), \(\mathbb {G}:=\mathbb {QR}^+_N\), and  Then the statistical distance D(X, Y) satisfies \(D(X,Y)\le \frac{2(P+Q)}{PQ}\).
Then the statistical distance D(X, Y) satisfies \(D(X,Y)\le \frac{2(P+Q)}{PQ}\).
Proof
We split the term D(X, Y) as
In the first term, \(\Pr _{}\mathopen {}\left[ X=x\right] \mathclose {}=\frac{1}{N'}\le \frac{4}{PQ},\Pr _{}\mathopen {}\left[ Y=x\right] \mathclose {}=\frac{1}{|\mathbb {G}|}=\frac{4}{(P-1)(Q-1)}.\) Therefore, the first summand is equal to \(\left| \frac{1-P-Q}{PQ} \right| \le \frac{P+Q}{PQ}.\) Similarly, the second term can be bounded by \(\frac{P+Q}{PQ}\) and thus, \(D(X,Y)\le \frac{2(P+Q)}{PQ}.\)
Lemma 8
\(\mathsf {ID}_{{\mathsf {FAC}}}\) is a perfectly correct five-move identification scheme and has \(\frac{2(P+Q)}{PQ}\)-statistical non-aborting honest-verifier zero-knowledge (\(\mathsf {naHVZK}\)) with \(\alpha =\log (\varphi (N)/4)-\frac{2(P+Q)}{PQ}\) bits min-entropy. Moreover, if \({\mathsf {FAC}}\) is \((t,\varepsilon )\)-hard then \(\mathsf {ID}_{{\mathsf {FAC}}}\) is \((t', \varepsilon ', Q_{\textsc {Ch}_1},Q_{\textsc {Ch}_2})\)-\(\mathsf {PIMP}\text{- }\mathsf {KOA}\)-secure, where \(\varepsilon ' \le \varepsilon + \frac{1}{2^k}\) and \(t' \approx t\).
Proof
The perfect correctness of \(\mathsf {ID}_{{\mathsf {FAC}}}\) is straightforward to verify, since \(R_1=g^{{s}} \circ X^{{-h_2}} \) and \(R_R=h_1^{{s}} \circ R_L^{{-h_2}} \) hold if and only if \(s= x h_2+r \bmod \varphi (N)/4\) holds.
\(\frac{2(P+Q)}{PQ}\) -Statistical \(\mathsf {naHVZK}\). Given public key \(pk=X\), \(\mathsf {Sim}\) first samples  It then computes \(h_1:= g^{{w}}, R_1:= g^{{s}} \circ X^{{-h_2}}, R_L:= R_1^{{w}}\), and \(R_R:= X^{{w}} \) and outputs the transcript \((R_1,h_1,R_L,R_R,h_2,s)\).
It then computes \(h_1:= g^{{w}}, R_1:= g^{{s}} \circ X^{{-h_2}}, R_L:= R_1^{{w}}\), and \(R_R:= X^{{w}} \) and outputs the transcript \((R_1,h_1,R_L,R_R,h_2,s)\).
The simulated transcript \((R_1,h_1,R_2,h_2,s)\) is close to the transcript output by \({\mathsf {SKTran}}(sk)\) with statistical distance \(2(P+Q)/(PQ)\), since s has statistical distance at most \(\frac{2(P+Q)}{PQ}\) from a uniformly random variable over \({{\mathbb Z}}_{|\mathbb {QR}^+_N|},\) according to Lemma 7 and \(R_1, R_L\) and \(R_R\) are values \(R_1= g^{{s}} \circ X^{{-h_2}} \) and \(R_R= h_1^{{s}} \circ R_L^{{-h_2}} \). The entropy of  and
and  comes only from \(R_1\), which is uniformly random from \(\mathbb {QR}^+_N\). Since the transcripts output by \(\mathsf {Sim}(pk)\) are statistically \(\frac{2(P+Q)}{PQ}\) close to the ones produced by \({\mathsf {SKTran}}(sk)\), \(\mathsf {ID}_{{\mathsf {FAC}}}\) has \(\log |\mathbb {QR}^+_N| = \log (\varphi (N)/4)-\frac{2(P+Q)}{PQ}\) bits min-entropy.
comes only from \(R_1\), which is uniformly random from \(\mathbb {QR}^+_N\). Since the transcripts output by \(\mathsf {Sim}(pk)\) are statistically \(\frac{2(P+Q)}{PQ}\) close to the ones produced by \({\mathsf {SKTran}}(sk)\), \(\mathsf {ID}_{{\mathsf {FAC}}}\) has \(\log |\mathbb {QR}^+_N| = \log (\varphi (N)/4)-\frac{2(P+Q)}{PQ}\) bits min-entropy.
\(\mathsf {PIMP}\text{- }\mathsf {KOA}\) -security. Let \(\mathsf {A}\) be an attacker against the \((t', \varepsilon ', Q_{\textsc {Ch}_1},Q_{\textsc {Ch}_2})\)-\(\mathsf {PIMP}\text{- }\mathsf {KOA}\) security of \(\mathsf {ID}_{{\mathsf {FAC}}}\). We construct an attacker \(\mathsf {B}\) that \((t,\varepsilon )\)-breaks \(\mathsf {CDH}\) over \(\mathbb {QR}^+_N\).
Construction of \(\mathsf {B}\). Let \((X:=g^{{x}},Y:=g^{{y}})\) denote the \(\mathsf {CDH}\) instance. \(\mathsf {B}\) runs \(\mathsf {A}\) with input \(pk:=X\) and answers \(\mathsf {A}\)’s challenge queries as follows.
For \(\mathsf {A}\)’s \(\textsc {Ch}_1\) query on \(R_1\in \mathbb {QR}^+_N\), \(\mathsf {B}\) chooses  and computes \(h_1= Y \circ g^{{a}}\). For \(\mathsf {A}\)’s \(\textsc {Ch}_2\) query on \(R_2\in \mathbb {QR}^+_N\times \mathbb {QR}^+_N\), \(\mathsf {B}\) chooses
and computes \(h_1= Y \circ g^{{a}}\). For \(\mathsf {A}\)’s \(\textsc {Ch}_2\) query on \(R_2\in \mathbb {QR}^+_N\times \mathbb {QR}^+_N\), \(\mathsf {B}\) chooses  and returns it to \(\mathsf {A}\). Clearly, \(\mathsf {B}\)’s simulation of the \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) game is perfect, since both \(h_1\) and \(h_2\) are uniformly random over \(\mathbb {QR}^+_N\) and \({{\mathbb Z}}_{N/4}\), respectively.
and returns it to \(\mathsf {A}\). Clearly, \(\mathsf {B}\)’s simulation of the \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) game is perfect, since both \(h_1\) and \(h_2\) are uniformly random over \(\mathbb {QR}^+_N\) and \({{\mathbb Z}}_{N/4}\), respectively.
Eventually, \(\mathsf {A}\) returns its response \(s^*\) for the \(\mathsf {PIMP}\text{- }\mathsf {KOA}\) experiment. We assume that \(\mathsf {A}\)’s response is valid, i.e., there exist \((R_1,h_1) \in \mathcal {L}_1\) and \((R_2:=(R_L,R_R),h_2) \in \mathcal {L}_2\) such that \(R_1= g^{{s^*}} \circ X^{{-h_2}} \) and \(R_R = h_1^{{s^*}} \circ R_L^{{-h_2}} \). We denote the discrete logarithm of \(R_L\) based on \(h_1\) by \(x' = {\mathsf {DL}}_{h_1}(R_L) \bmod (\varphi (N)/4)\) and do the following cases distinction:
-
Case 1: \(x=x' \bmod (\varphi (N)/4)\). By the simulation of \(\textsc {Ch}_1\), we have \(R_L = h_1^{{x}} = (Y \circ g^{{a_i}} )^{{x}} = Y^{{x}} \circ X^{{a_i}}\) for some \(i \in [Q_{\textsc {Ch}_1}]\). Thus, \(\mathsf {B}\) returns \(Z:=R_L \circ X^{{-a_i}} = Y^{{x}}\) to break the \(\mathsf {CDH}\) problem over \(\mathbb {QR}^+_N\).
-
Case 2: \(x\ne x' \bmod (\varphi (N)/4)\). We show in this case even an unbounded adversary \(\mathsf {A}\) can only win with probability \(Q_{\textsc {Ch}_2}/2^k\). For each index \(i \in [Q_{\textsc {Ch}_2}]\), before receiving \(h_{2,i}\), \(\mathsf {A}\) first commits to some \(R_1= g^{{r_1}} \), \(R_L = h_1^{{x'}} \) and \(R_R = h_1^{{r_2}} \) (for arbitrary \(r_1, r_2, x' \in {{\mathbb Z}}_{N/4}\) and \(x'\ne x \bmod (\varphi (N)/4)\)) and there exists \((R_1,h_1) \in \mathcal {L}_1\). \(\mathsf {A}\) can only win if there exists an \(s_i \in {{\mathbb Z}}_{N/4}\) such that
$$\begin{aligned}&r_{1} + h_{2,i} x = s_i = r_{2} + h_{2,i} x' \bmod (\varphi (N)/4) \\\Leftrightarrow & {} h_{2,i} = \frac{ r_{2}-r_{1} }{x-x'} \bmod (\varphi (N)/4) \end{aligned}$$where \(h_{2,i} \) is distributed uniformly over \( \{0,...,2^k-1\}\) and independently of \(r_1,r_2\) and \(x'\). The equation \(h_{2,i} = \frac{ r_{2}-r_{1} }{x-x'} \bmod (\varphi (N)/4)\) holds with probability at most \(1/2^k \). By the union bound we obtain the bound \(Q_{\textsc {Ch}_2}/2^k\) as claimed.
Overall, \(\mathsf {B}\) returns a valid solution of the \(\mathsf {CDH}\) challenge with probability \(\varepsilon \ge \varepsilon ' - \frac{Q_{\textsc {Ch}_2}}{2^k}\). This completes the proof.
Signature Scheme. Let \(H_1: \{0,1\}^* \rightarrow \mathbb {QR}^+_N\) and \(H_2: \{0,1\}^*\rightarrow \{0, ..., 2^k-1\}\) be two hash functions. We note that \(H_1\) has been used in [32, 43]. As \(\mathsf {ID}_{{\mathsf {FAC}}}\) is perfectly correct and partial commitment-recoverable, we can use the alternative Fiat-Shamir transformation from Sect. 3.1 with \(\ell :=1\) to obtain the signature scheme \({\mathsf {FS}}_{{\mathsf {FAC}}}:=({\mathsf {Gen}},{\mathsf {Sign}},{\mathsf {Ver}})\).

By Corollary 1, Lemma 8 and Theorem 1, we have
Theorem 4
(Security of \({\mathsf {FS}}_{{\mathsf {FAC}}}\)). If \({\mathsf {FAC}}\) is \((t,\varepsilon )\)-hard in \(\mathsf {par}:=\mathsf {Blum}_{n}\) then \({\mathsf {FS}}_{{\mathsf {FAC}}}\) is \((t',\varepsilon ',Q_s,Q_1,Q_2)\)-\({\mathsf {UF\text{- }CMA}}\) secure in the programmable random oracle model, where
Size of Parameters. We argue along the lines of our analysis provided above. We again set \(Q_s=Q_h=t'=t.\) Here, we only need to bound the term \(\frac{Q_2+1}{t2^k}\le \frac{1}{2^k}\), as all terms in the above theorem vanish. Thus, we set again \(k=\kappa \) to achieve a security of \(\kappa \) bits. This yields a signature of size \(2\cdot \ell '+\kappa \) bits where again \(\ell '\) denotes the size of a group element of \(\mathbb {G}\).
Notes
- 1.
We ignore the additive negligible terms to simplify our discussion.
- 2.
We also consider identification schemes with correctness error and statistical \(\mathsf {HVZK}\) and define the notion of non-aborting \(\mathsf {HVZK}\). In this section, we ignore these for simplicity.
- 3.
On two queries \(\textsc {Ch}_i(R_i)\) and \(\textsc {Ch}_i(R'_i)\) with the same input \(R_i = R'_i\) the oracle returns two independent random challenges
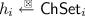 and
and  .
.
References
Abdalla, M., An, J.H., Bellare, M., Namprempre, C.: From identification to signatures via the Fiat-Shamir transform: minimizing assumptions for security and forward-security. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 418–433. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_28
Abdalla, M., Ben Hamouda, F., Pointcheval, D.: Tighter reductions for forward-secure signature schemes. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 292–311. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36362-7_19
Abdalla, M., Fouque, P.-A., Lyubashevsky, V., Tibouchi, M.: Tightly-secure signatures from lossy identification schemes. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 572–590. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_34
Abe, M., Hofheinz, D., Nishimaki, R., Ohkubo, M., Pan, J.: Compact structure-preserving signatures with almost tight security. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10402, pp. 548–580. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_19
Yousfi Alaoui, S.M., Dagdelen, Ö., Véron, P., Galindo, D., Cayrel, P.-L.: Extended security arguments for signature schemes. In: Mitrokotsa, A., Vaudenay, S. (eds.) AFRICACRYPT 2012. LNCS, vol. 7374, pp. 19–34. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31410-0_2
Bellare, M., Palacio, A.: GQ and Schnorr identification schemes: proofs of security against impersonation under active and concurrent attacks. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 162–177. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45708-9_11
Bellare, M., Poettering, B., Stebila, D.: From identification to signatures, tightly: a framework and generic transforms. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 435–464. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_15
Bellare, M., Rogaway, P.: Random oracles are practical: A paradigm for designing efficient protocols. In: Ashby, V. (ed.) ACM CCS 1993, pp. 62–73. ACM Press, November 1993
Bellare, M., Rogaway, P.: The exact security of digital signatures: how to sign with RSA and Rabin. In: Maurer, U. (ed.) EUROCRYPT 1996. LNCS, vol. 1070, pp. 399–416. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-68339-9_34
Bernstein, D.J.: Proving tight security for Rabin-Williams signatures. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 70–87. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_5
Beth, T.: Efficient zero-knowledge identification scheme for smart cards. In: Barstow, D., et al. (eds.) EUROCRYPT 1988. LNCS, vol. 330, pp. 77–84. Springer, Heidelberg (1988). https://doi.org/10.1007/3-540-45961-8_7
Blazy, O., Kakvi, S.A., Kiltz, E., Pan, J.: Tightly-secure signatures from chameleon hash functions. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 256–279. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_12
Blazy, O., Kiltz, E., Pan, J.: (Hierarchical) identity-based encryption from affine message authentication. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 408–425. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_23
Boneh, D., Lynn, B., Shacham, H.: Short signatures from the Weil pairing. In: Boyd, C. (ed.) ASIACRYPT 2001. LNCS, vol. 2248, pp. 514–532. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45682-1_30
Brickell, E.F., McCurley, K.S.: An interactive identification scheme based on discrete logarithms and factoring. In: Damgård, I.B. (ed.) EUROCRYPT 1990. LNCS, vol. 473, pp. 63–71. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-46877-3_6
Cayrel, P.-L., Lindner, R., Rückert, M., Silva, R.: Improved zero-knowledge identification with lattices. In: Heng, S.-H., Kurosawa, K. (eds.) ProvSec 2010. LNCS, vol. 6402, pp. 1–17. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-16280-0_1
Cayrel, P.-L., Véron, P., Yousfi Alaoui, S.M.: A zero-knowledge identification scheme based on the q-ary syndrome decoding problem. In: Biryukov, A., Gong, G., Stinson, D.R. (eds.) SAC 2010. LNCS, vol. 6544, pp. 171–186. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19574-7_12
Chen, J., Wee, H.: Fully, (almost) tightly secure IBE and dual system groups. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 435–460. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_25
Chen, M.-S., Hülsing, A., Rijneveld, J., Samardjiska, S., Schwabe, P.: From 5-pass \(\cal{MQ}\)-based identification to \(\cal{MQ}\)-based signatures. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 135–165. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_5
Chevallier-Mames, B.: An efficient CDH-based signature scheme with a tight security reduction. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 511–526. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_31
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Fleischhacker, N., Jager, T., Schröder, D.: On tight security proofs for schnorr signatures. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 512–531. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45611-8_27
Girault, M.: An identity-based identification scheme based on discrete logarithms modulo a composite number. In: Damgård, I.B. (ed.) EUROCRYPT 1990. LNCS, vol. 473, pp. 481–486. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-46877-3_44
Girault, M., Poupard, G., Stern, J.: On the fly authentication and signature schemes based on groups of unknown order. J. Cryptol. 19(4), 463–487 (2006)
Goh, E.-J., Jarecki, S.: A signature scheme as secure as the Diffie-Hellman problem. In: Biham, E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 401–415. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-39200-9_25
Goh, E.-J., Jarecki, S., Katz, J., Wang, N.: Efficient signature schemes with tight reductions to the Diffie-Hellman problems. J. Cryptol. 20(4), 493–514 (2007)
Goldwasser, S., Micali, S., Rivest, R.L.: A digital signature scheme secure against adaptive chosen-message attacks. SIAM J. Comput. 17(2), 281–308 (1988)
Guillou, L.C., Quisquater, J.-J.: A “paradoxical” indentity-based signature scheme resulting from zero-knowledge. In: Goldwasser, S. (ed.) CRYPTO 1988. LNCS, vol. 403, pp. 216–231. Springer, New York (1990). https://doi.org/10.1007/0-387-34799-2_16
Hofheinz, D.: Algebraic partitioning: Fully compact and (almost) tightly secure cryptography. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 251–281. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_11
Hofheinz, D.: Adaptive partitioning. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10212, pp. 489–518. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56617-7_17
Hofheinz, D., Jager, T.: Tightly secure signatures and public-key encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 590–607. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_35
Hofheinz, D., Kiltz, E.: The group of signed quadratic residues and applications. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 637–653. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_37
Kakvi, S.A., Kiltz, E.: Optimal security proofs for full domain hash, revisited. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 537–553. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_32
Katz, J., Wang, N.: Efficiency improvements for signature schemes with tight security reductions. In: Jajodia, S., Atluri, V., Jaeger, T. (eds.) ACM CCS 2003, pp. 155–164. ACM Press, October 2003
Kiltz, E., Masny, D., Pan, J.: Optimal security proofs for signatures from identification schemes. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 33–61. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_2
Koshiba, T., Kurosawa, K.: Short exponent Diffie-Hellman problems. In: Bao, F., Deng, R., Zhou, J. (eds.) PKC 2004. LNCS, vol. 2947, pp. 173–186. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24632-9_13
Lyubashevsky, V.: Fiat-Shamir with aborts: applications to lattice and factoring-based signatures. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 598–616. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_35
Micali, S., Reyzin, L.: Improving the exact security of digital signature schemes. Cryptology ePrint Archive, Report 1999/020 (1999). http://eprint.iacr.org/1999/020
Micali, S., Reyzin, L.: Improving the exact security of digital signature schemes. J. Cryptol. 15(1), 1–18 (2002)
Micali, S., Shamir, A.: An improvement of the Fiat-Shamir identification and signature scheme. In: Goldwasser, S. (ed.) CRYPTO 1988. LNCS, vol. 403, pp. 244–247. Springer, New York (1990). https://doi.org/10.1007/0-387-34799-2_18
Okamoto, T.: Provably secure and practical identification schemes and corresponding signature schemes. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 31–53. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-48071-4_3
Ong, H., Schnorr, C.P.: Fast signature generation with a Fiat-Shamir-like scheme. In: Damgård, I.B. (ed.) EUROCRYPT 1990. LNCS, vol. 473, pp. 432–440. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-46877-3_38
Poettering, B., Stebila, D.: Double-authentication-preventing signatures. In: Kutyłowski, M., Vaidya, J. (eds.) ESORICS 2014. LNCS, vol. 8712, pp. 436–453. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-11203-9_25
Pointcheval, D.: A new identification scheme based on the perceptrons problem. In: Guillou, L.C., Quisquater, J.-J. (eds.) EUROCRYPT 1995. LNCS, vol. 921, pp. 319–328. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-49264-X_26
Pointcheval, D., Poupard, G.: A new NP-complete problem and public-key identification. Des. Codes Cryptogr. 28(1), 5–31 (2003)
Pointcheval, D., Stern, J.: Security arguments for digital signatures and blind signatures. J. Cryptol. 13(3), 361–396 (2000)
Pollard, J.M.: Monte Carlo methods for index computation mod \(p\). Math. Comput. 32, 918–924 (1978)
Sakumoto, K., Shirai, T., Hiwatari, H.: Public-key identification schemes based on multivariate quadratic polynomials. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 706–723. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_40
Schnorr, C.-P.: Efficient signature generation by smart cards. J. Cryptol. 4(3), 161–174 (1991)
Seurin, Y.: On the exact security of Schnorr-type signatures in the random oracle model. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 554–571. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_33
Shamir, A.: An efficient identification scheme based on permuted kernels (extended abstract). In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 606–609. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_54
Shamir, A., Tauman, Y.: Improved online/offline signature schemes. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 355–367. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_21
Silva, R., Cayrel, P.-L., Lindner, R.: Zero-knowledge identification based on lattices with low communication costs. In: XI Simposio Brasileiro de Seguranca da Informacao e de Sistemas Computacionais, vol. 8, pp. 95–107 (2011)
Stern, J.: Designing identification schemes with keys of short size. In: Desmedt, Y.G. (ed.) CRYPTO 1994. LNCS, vol. 839, pp. 164–173. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48658-5_18
Stern, J.: A new identification scheme based on syndrome decoding. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 13–21. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48329-2_2
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Kiltz, E., Loss, J., Pan, J. (2017). Tightly-Secure Signatures from Five-Move Identification Protocols. In: Takagi, T., Peyrin, T. (eds) Advances in Cryptology – ASIACRYPT 2017. ASIACRYPT 2017. Lecture Notes in Computer Science(), vol 10626. Springer, Cham. https://doi.org/10.1007/978-3-319-70700-6_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-70700-6_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70699-3
Online ISBN: 978-3-319-70700-6
eBook Packages: Computer ScienceComputer Science (R0)





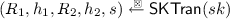 with
with 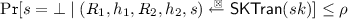 .
.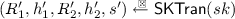 .
. and
and 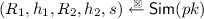 and
and 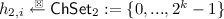 is chosen independently of
is chosen independently of 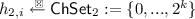 is chosen independently of
is chosen independently of 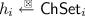 and
and  .
.