Abstract
Beyond their security guarantees under well-studied assumptions, algebraic pseudo-random functions are motivated by their compatibility with efficient zero-knowledge proof systems, which is useful in a number of privacy applications like digital cash. We consider the problem of proving the correct evaluation of lattice-based PRFs based on the Learning-With-Rounding (\(\mathsf {LWR}\)) problem introduced by Banerjee et al. (Eurocrypt’12). Namely, we are interested zero-knowledge arguments of knowledge of triples (y, k, x) such that \(y=F_k(x)\) is the correct evaluation of a PRF for a secret input x and a committed key k. While analogous statements admit efficient zero-knowledge protocols in the discrete logarithm setting, they have never been addressed in lattices so far. We provide such arguments for the key homomorphic PRF of Boneh et al. (Crypto’13) and the generic PRF implied by the \(\mathsf {LWR}\)-based pseudo-random generator. As an application of our ZK arguments, we design the first compact e-cash system based on lattice assumptions. By “compact”, we mean that the complexity is at most logarithmic in the value of withdrawn wallets. Our system can be seen as a lattice-based analogue of the first compact e-cash construction due to Camenisch, Hohenberger and Lysyanskaya (Eurocrypt’05).
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Since the seminal results of Ajtai [2] and Regev [85], lattice-based cryptography has been a very active area which undergone quite rapid development, notably with the advent of lattice trapdoors [52, 76] and homomorphic encryption [51]. Not only does it enable powerful functionalities, it also offers many advantages over conventional number-theoretic techniques, like simpler arithmetic operations, its conjectured resistance to quantum attacks or a better asymptotic efficiency.
The design of numerous cryptographic protocols appeals to zero-knowledge proofs [55] to prove properties about encrypted or committed values so as to enforce honest behavior on behalf of participants or protect the privacy of users. In the lattice settings, efficient zero-knowledge proofs are non-trivial to construct. While natural solutions exist for proving knowledge of secret keys [64, 70, 73, 77], they are only known to work for very specific languages. When it comes to proving general circuit satisfiability, the best known methods rely on the ring variants [14, 89] of the Learning-With-Errors (\(\mathsf {LWE}\)) and Short Integer Solution (\(\mathsf {SIS}\)) problems and are not known to readily carry over to standard lattices. In the standard model, the problem is even trickier as we do not have a lattice-based counterpart of Groth-Sahai proofs [58] and efficient non-interactive proof systems are only available for specific problems [84].
In this paper, we consider the natural problem of proving the correct evaluation of lattice-based pseudo-random functions (PRFs) w.r.t. committed keys and inputs. This problem arises in numerous protocols where a user has to deterministically generate a random-looking value without betraying his identity.
We provide zero-knowledge arguments of correct evaluation for the \(\mathsf {LWE}\)-based PRF of Boneh, Lewi, Montgomery and Raghunathan (BLMR) [17] as well as the construction generically obtained from pseudo-random generators via the Goldreich-Goldwasser-Micali (GGM) methodology [54]. As an application of our arguments, we provide the first lattice-based realization of the compact e-cash primitive of Camenisch, Hohenberger and Lysyanskaya [22].
Introduced by Chaum [33, 34], electronic cash is the digital counterpart of regular money. As envisioned in [33], digital cash involve a bank and several users and merchants. It allows users to withdraw digital coins from the bank in such a way that e-coins can later be spent at merchants. In the on-line setting [33, 35, 36], merchants contact the bank before accepting any payment so that the bank is involved in all transactions to prevent double-spendings. In the (usually preferred) off-line model [37], the merchant accepts payments without any interaction with the bank: the deposit phase is postponed to a later moment where the merchant can return many coins at once. In all cases, when a merchant returns coins back to the bank, the latter should infer no information as to when and by whom the returned coins were withdrawn. Should the bank collude with the merchant, it remains unable to link a received coin to a particular execution of the withdrawal protocol. Of course, dishonest users should not be able to spend more coins than they withdrew without being identified. While fair e-cash systems [88] resort to an off-line trusted authority to call out cheaters, classical e-cash [37] allows identifying double-spenders without any TTP. In 2005, Camenisch, Hohenberger and Lysyanskaya [22] advocated e-cash solutions with compactness property: namely, a compact e-cash scheme allows a user to withdraw a wallet of \(2^{L}\) coins in such a way that the complexity of spending and withdrawal protocols does not exceed \(\mathcal {O}(L + \lambda )\), where \(\lambda \) is the security parameter. The constructions of [22] elegantly combine signature schemes with efficient protocols [25, 26], number theoretic pseudo-random functions [44] and zero-knowledge proofs, making it possible to store a wallet using only \(\mathcal {O}(L+\lambda )\) bits.
1.1 Our Contributions
Our Results. We describe the first compact e-cash system [22] based on lattice assumptions. Here, consistently with the literature on e-cash, “compactness” refers to schemes where the withdrawal, spending and deposit phases have at most logarithmic complexities in the maximal value of withdrawn wallets (analogously to the solutions of [22] where the term “compact” was introduced). The security of our scheme is proved in the random oracle model [11] under the Short Integer Solution (\(\mathsf {SIS}\)) and \(\mathsf {LWE}\) assumptions.
As a crucial ingredient of our solution, we provide zero-knowledge arguments vouching for the correct evaluation of lattice-based pseudo-random functions. More precisely, we construct arguments of knowledge of a committed seed \(\mathbf {k}\), a secret input J and an output \(\mathbf {y}\) satisfying \(\mathbf {y}=F_{\mathbf {k}}(J)\). We describe such arguments for the key-homomorphic PRF of Boneh et al. [17] and the PRF obtained by applying the Goldreich-Goldwasser-Micali (GGM) [54] paradigm. As a building block, we provide zero-knowledge arguments for statements related to the Learning-With-Rounding (\(\mathsf {LWR}\)) problem of Banerjee, Peikert and Rosen [8]. Given a public random matrix \(\mathbf {A} \in \mathbb {Z}_q^{n \times m}\), it requires to tell apart vectors \(\lfloor \mathbf {A}^T \cdot \mathbf {s} \rfloor _p = \lfloor (p/q) \cdot \mathbf {A}^T \cdot \mathbf {s} \rfloor \in \mathbb {Z}_p^m\) from the uniform distribution \(U(\mathbb {Z}_p^m)\) over \(\mathbb {Z}_p^m\), where \(q > p \ge 2\). A crucial step of our argument system consists in demonstrating the correct computation of the rounding step: i.e., proving that \(\mathbf {y} = \lfloor \mathbf {x} \rfloor _p\), for \(\mathbf {x} \in \mathbb {Z}_q^m\) satisfying some additional context-dependent constraints.
We believe that our zero-knowledge arguments can find use cases in many other applications involving PRFs, and where zero-knowledge proofs constrain participants not to deviate from the protocol. Examples include privacy-preserving de-centralized e-cash systems [12, 39, 57], stateful anonymous credentials [40], n-times periodic anonymous authentication [21], traceable ring signatures [50], anonymous survey systems [59], password-protected secret sharing [61] or unlinkable pseudonyms for privacy-preserving distributed databases [24]. We also think of distributed PRFs [75, 80], where servers holding a polynomial share \(\mathbf {k}_i\) of the seed \(\mathbf {k}\) can prove the correctness of their contribution w.r.t. to their committed share \(\mathbf {k}_i\). Our arguments may also prove useful in the context of oblivious PRF evaluations [49, 62], where one party holds a PRF key \(\mathbf {k}\) and must convince the other party that \(\mathbf {k}\) was correctly used in oblivious computations.
Our Techniques. In order to convince a verifier of the correct evaluation of \(\mathsf {LWR}\)-based PRFs, the first step is to provide evidence that the underlying rounding operation is properly carried out. For dimension \(m>1\) and moduli \(q > p \ge 2\), identify \(\mathbb {Z}_q\), \(\mathbb {Z}_p\) as the set \([0, q-1]\) and \([0,p-1]\), respectively, and consider the function \(\lfloor \cdot \rfloor _p: \mathbb {Z}_q^m \rightarrow \mathbb {Z}_p^m : \mathbf {x} \mapsto \mathbf {y} = \lfloor (p/q) \cdot \mathbf {x} \rfloor \bmod p. \) We observe that, one knows secret vector \(\mathbf {x} \in [0,q-1]^m\) such that \(\lfloor \mathbf {x} \rfloor _p = \mathbf {y}\) for a given \(\mathbf {y} \in [0,p-1]^m\), if and only if one knows \(\mathbf {x}, \mathbf {z} \in [0,q-1]^m\) such that
This crucial observation gives us a modular equation where the secret vectors \(\mathbf {x}, \mathbf {z}\) are “small” relatively to the modulus pq. To prove that we know such secret vectors (where \(\mathbf {x}\) may satisfy additional statements, e.g., it is committed, or certified, or is the output of other algorithms), we exploit Ling et al.’s decomposition-extension framework [70], which interacts well with Stern’s permuting technique [86]. Specifically, we employ a matrix \(\mathbf {H}_{m,q-1} \in \mathbb {Z}_q^{m \times \bar{m}}\), where \(\bar{m} = m \lceil \log q \rceil \), that allows to compute \(\tilde{\mathbf {x}}, \tilde{\mathbf {z}}\in \{0,1\}^{\bar{m}}\) such that \(\mathbf {H}_{m,q-1}\cdot \tilde{\mathbf {x}} = \mathbf {x}\) and \(\mathbf {H}_{m,q-1}\cdot \tilde{\mathbf {z}} = \mathbf {z}\). Then, we let \(\mathsf {B}_{\bar{m}}^2\) be the set of all vectors in \(\{0,1\}^{2\bar{m}}\) that have fixed Hamming weight \(\bar{m}\), and append \(\bar{m}\) suitable entries to \(\tilde{\mathbf {x}}, \tilde{\mathbf {z}}\) to obtain \(\widehat{\mathbf {x}}, \widehat{\mathbf {z}} \in \mathsf {B}_{\bar{m}}^2\). Now, Eq. (1) is rewritten as:
Note that, one knows \(\mathbf {x}, \mathbf {z} \in [0,q-1]^m\) satisfying (1) if and only if one can compute \(\widehat{\mathbf {x}}, \widehat{\mathbf {z}} \in \mathsf {B}_{\bar{m}}^2\) satisfying (2). Moreover, as the constraint of \(\widehat{\mathbf {x}}, \widehat{\mathbf {z}}\) is invariant under permutation (namely, \(\widehat{\mathbf {x}}, \widehat{\mathbf {z}} \in \mathsf {B}_{\bar{m}}^2\) if and only if \(\pi _x(\widehat{\mathbf {x}}), \pi _z(\widehat{\mathbf {z}}) \in \mathsf {B}_{\bar{m}}^2\), where \(\pi _x, \pi _z\) are permutations of \(2\bar{m}\) elements), the latter statement can be handled via Stern’s technique. Our method is readily extended to prove that the underlying vector \(\mathbf {x}\) satisfies additional statements.
Let us now consider the problem of proving a correct evaluation of the Boneh et al. PRF [17]. The function uses public binary matrices \(\mathbf {P}_0,\mathbf {P}_1 \in \{0,1\}^{m \times m}\) and a secret seed \(\mathbf {k} \in \mathbb {Z}_q^m\) which allows mapping an input \(J \in \{0,1\}^L\) to
We consider the evaluation process iteratively and transform intermediate witnesses using the decomposition-extension framework [70], so that they nicely interact with Stern’s permuting technique [86]. Namely, we define a sequence \(\{\mathbf {x}_i\}_{i=0}^L\) which is initialized with \(\mathbf {x}_0 = \mathbf {k} \in \mathbb {Z}_q^m\), iteratively computed as \(\mathbf {x}_i= \mathbf {P}_{J[i]} \cdot \mathbf {x}_{i-1} \in \mathbb {Z}_q^m\), for each \(i \in [1,L]\), and eventually yields the output \(\mathbf {y} = \lfloor \mathbf {x}_L \rfloor _p\). For each \(i \in [1,L]\), we translate the equation \(\mathbf {x}_i= \mathbf {P}_{J[i]} \cdot \mathbf {x}_{i-1} \bmod q\) into
and where J[i] and \(\overline{J[i]}= 1 - J[i]\) are part of the witnesses. Using suitable decomposition-extension techniques [69, 70] on vectors \(\{\mathbf {x}_i\}_{i=0}^L, \{\mathbf {t}_i\}_{i=1}^L\), we manage to express all the L iterative equations by just one equation of the form \(\mathbf {M}_1 \cdot \mathbf {w}_1 = \mathbf {u}_1 \bmod q\), for some public matrix \(\mathbf {M}_1\) and vector \(\mathbf {u}_1\) over \(\mathbb {Z}_q\), while \(\mathbf {w}_1\) is a binary vector containing secret bits of all the witnesses and fitting a certain pattern. Meanwhile, the rounding step \(\mathbf {y} = \lfloor \mathbf {x}_L \rfloor _p\), as discussed above, would yield an equation of the form \(\mathbf {M}_2\cdot \mathbf {w}_2 = \mathbf {u}_2 \bmod pq\), where \(\mathbf {w}_2\) is correlated to \(\mathbf {w}_1\). Furthermore, our applications require to additionally prove that a binary representation of the seed \(\mathbf {x}_0=\mathbf {k}\) is properly committed or certified, while the commitment or signature scheme may use a different modulus. Thus, we eventually have to handle relations of the form \(\mathbf {M}_i \cdot \mathbf {w}_i = \mathbf {u}_i \bmod q_i\) for several moduli \(q_1,\ldots ,q_N\) when, for distinct \(i,j \in [N]\), witnesses \(\mathbf {w}_i,\mathbf {w}_j\) may have entries in common. An abstraction of Stern’s protocol was recently suggested by Libert et al. [68] to address a similar setting when one has to prove a number of linear relations. Unfortunately, their framework, which deals with a unique modulus, does not directly cover our setting. To overcome this problem, we thus put forward a generalization of Libert et al.’s framework, so as to handle correlated witnesses across relations modulo distinct integers.
The above techniques thus smoothly interact with the pseudo-random functions of Boneh et al. [17] and the PRG of [8]. Unfortunately, we did not manage to extend them to other existing PRFs [7, 8, 45] based on the hardness of \(\mathsf {LWR}\). In the synthesizer-based construction of Banerjee et al. [8], the difficulty is the lack of public matrices which would help us reduce the statement to an assertion of the form \(\mathbf {M} \cdot \mathbf {w} = \mathbf {u}\), for some witness \(\mathbf {w} \in \mathbb {Z}^m\) and public \(\mathbf {M} \in \mathbb {Z}_q^{n \times m}\), \(\mathbf {u} \in \mathbb {Z}_q^n\). Our zero-knowledge arguments do not appear to carry over to the key homomorphic functions of Banerjee and Peikert [7] either as they rely on a more complex tree-like structure. The fact that our techniques do not apply to all known lattice-based PRFs emphasizes that they are far more innovative than just an application of generic zero-knowledge paradigms, which would resort to a circuit decomposition of the evaluation algorithm and proceed in a gate-by-gate manner. Indeed, we process all statements without decomposing the arithmetic operations into a circuit.
Our compact e-cash construction builds on the design principle of Camenisch et al. [22] which combines signatures with efficient protocols [25, 26], algebraic pseudo-random functions [44] and zero-knowledge proofs. In the lattice setting, we take the same approach by combining (a variant of) the signature scheme with efficient protocols of [68] and the PRF of [17]. While the GGM-based PRF of [8] would allow a more efficient choice of parameters, we chose to instantiate our system with the realization of Boneh et al. [17] since it simplifies the description and the security proof (specifically, we do not have to rely on the pseudo-randomness of the function in one of the security properties). However, our scheme can be modified to rely on the PRF built on the \(\mathsf {LWR}\)-based PRG.
As in [22], the withdrawal phase allows the user to obtain a wallet of value \(2^L-1\) which consists of two PRF seeds, a counter and a signature generated by the bank on committed values. In the withdrawal protocol, the PRF seeds are obliviously signed (and bound to the user’s secret key) by the bank using a signature scheme with efficient protocols [25, 26]. The first seed \(\mathbf {k}\) is used to derive each coin’s serial number \(\mathbf {y}_S = F_{\mathbf {k}}(J) \in \mathbb {Z}_p^m\) as a pseudo-random function of an L-bit counter \(J \in \{0,1\}^L\) which denotes the number of previously spent coins. By spending the same coin twice, the user is thus forced to use the same serial number in two distinct transactions, making the cheating attempt detectable.
The second PRF seed \(\mathbf {t}\) is used to compute a security tag \(\mathbf {y}_T\) that allows identifying double-spenders. This tag is a vector \(\mathbf {y}_T=PK_{\mathcal {U}} + H(\mathtt {info}) \cdot F_{\mathbf {t}}(J) \in \mathbb {Z}_p^m\), where \(PK_{\mathcal {U}} \) is the user’s public key and \(H(\mathtt {info}) \in \mathbb {Z}_p^{m \times m}\) is a matrix generated by hashing some transaction-specific information supplied by the merchant. From two coins that share the same serial number \(\mathbf {y}_S\) and distinct security tags \(\mathbf {y}_{T,1}=PK_{\mathcal {U}} + H(\mathtt {info}_1) \cdot F_{\mathbf {t}}(J) \) and \(\mathbf {y}_{T,2}=PK_{\mathcal {U}} + H(\mathtt {info}_2) \cdot F_{\mathbf {t}}(J) \), the difference \(\mathbf {y}_{T,1} - \mathbf {y}_{T,2} = (H(\mathtt {info}_1)-H(\mathtt {info}_2)) \cdot F_{\mathbf {t}}(J)\) allows computing the PRF value \( F_{\mathbf {t}}(J) = (H(\mathtt {info}_1)-H(\mathtt {info}_2))^{-1} \cdot (\mathbf {y}_{T,1}-\mathbf {y}_{T,2}) \in \mathbb {Z}_p^m \) (and then \(PK_\mathcal {U}\)) whenever \(H(\mathtt {info}_1)-H(\mathtt {info}_2)\) is invertible over \(\mathbb {Z}_p\). This property is precisely ensured by the Full-Rank Difference function of Agrawal et al. [1], which comes in handy to instantiate \(H : \{0,1\}^* \rightarrow \mathbb {Z}_p^{m \times m}\). In contrast with [1], the Full-Rank Difference function is utilized in the scheme while [1] uses it in security proofs.
1.2 Related Work
E-Cash. Chaum’s pioneering work [33, 34] inspired a large body of research towards efficient e-cash systems [37, 38, 47, 82, 83, 87] with better properties during two decades. The first compact realization was given by Camenisch et al. [22] whose techniques served as a blueprint for many subsequent e-cash systems with additional features such as refined accountability-anonymity tradeoffs [23], coin endorsement [27], or security proofs in the standard model [10]. The authors of [22] extended their schemes with a coin tracing mechanism whereby all the coins of a double-spender can be traced once this user has been identified.
Divisible e-cash [82] allow users to withdraw a wallet of value \(2^L\) in such a way that each spending may involve transactions of variable amounts. While the early constructions [82, 83] only provided weaker anonymity properties, Canard and Gouget gave truly anonymous realizations [28] using tree-based techniques which were subsequently made scalable [29, 30]. The recent adoption of de-centralized payment systems [79] has triggered a new line of research towards strengthening the privacy of Bitcoin (see [12, 57, 78] and references therein).
To our knowledge, all truly private compact e-cash systems rely on discrete-logarithm-based techniques, either because of the underlying pseudo-random function [10, 22] or via accumulators [5] (or both). In the lattice setting, we are not aware of any compact e-cash realization and neither do we know of any proofs of correct PRF evaluation with or without random oracles. In particular, it remains an open problem to build verifiable random functions [74] from lattices.
Lattices and Zero-Knowledge Proofs. Existing methods of proving relations appearing in lattice-based cryptosystems belong to two main families. The first family, introduced by Lyubashevsky [73], uses “rejection sampling” techniques, and recently lead to relatively efficient proofs of knowledge of small secret vectors [9, 13, 14, 42, 43]. However, due to the nature of “rejection sampling” mechanisms, even the honest prover may fail to convince the verifier with a tiny probability: i.e., protocols in this family do not have perfect completeness. Furthermore, when proving knowledge of vectors having norm bound \(\beta \), the knowledge extractor of these protocols is only guaranteed to produce witnesses of norm bound \(g\cdot \beta \), for some factor \(g>1\). This factor, called the “soundness slack” in [9, 42], may have an undesirable consequence: if an extracted witness has to be used in the security proof to solve a challenge SIS instance, we have to rely on the \(\mathsf {SIS}_{g\cdot \beta }\) assumption, which is stronger than the \(\mathsf {SIS}_{\beta }\) assumption required by the protocol itself. Moreover, in some advanced protocols such as those considered in this work, the coordinates of extracted vectors are expected to be in \(\{0,1\}\) and/or satisfy a specific pattern. Such issues seem hard to tackle using this family of protocols.
The second family, initiated by Ling et al. [70], rely on “decomposition-extension” techniques in lattice-based analogues [64] of Stern’s protocol [86]. Stern-like systems are less efficient than those of the first family because each protocol execution admits a constant soundness error, requiring the protocols to be repeated \(\omega (\log \lambda )\) times in order to achieve a negligible soundness error. On the upside, Stern-like protocols do have perfect completeness and are capable of handling a wide range of lattice-based relations [66,67,68,69, 71], especially when the witnesses are not only required to be small or binary, but should also have prescribed arrangements of coordinates. Moreover, unlike protocols of the first family, the extractor of Stern-like protocols are able to output witness vectors having exactly the same properties as those expected from valid witnesses. This feature is often crucial in the design of advanced cryptographic constructions involving zero-knowledge proofs. Additionally, the “soundness slack” issue is completely avoided, so that the hardness assumptions are kept “in place”.
When it comes to proving the correct evaluation of AES-like secret key primitives, several works [32, 48, 63] built zero-knowledge proofs upon garbled circuits or multi-party computation [53, 60], which may lead to truly practical proofs [53] even for non-algebraic statements. However, the garbled circuit paradigm [63] inherently requires interactive proofs (and cannot be made non-interactive via Fiat-Shamir [46]), making it unsuitable to our applications where coins must carry a non-interactive proof. While Giacomelli et al. [53] successfully designed efficient non-interactive proofs for SHA-256 evaluations, these remain of linear length in the circuit size and efficiently combining them with proofs of algebraic statements is non-trivial here: in the e-cash setting, our goal is to prove the correct evaluation of \(\mathsf {LWE}\)-based symmetric primitives for committed inputs and keys. To our knowledge, known results on the smooth integration of algebraic and non-algebraic statements [32] are obtained by tweaking the approach of Jawurek et al. [63], which requires interaction.
Despite the scarcity of truly efficient zero-knowledge proofs in the lattice-setting, a recent body of work successfully designed proof systems in privacy-preserving protocols [13, 56, 64, 65, 71, 81]. These results, however, only considered ring signatures [19, 64], group signatures [13, 56, 65, 66, 71, 81], group encryption [67] or building blocks [68] for anonymous credentials [35]. As of the time of writing, lattice-based realizations of anonymous e-cash still remain lacking.
2 Background and Definitions
Vectors are denoted in bold lower-case letters and bold upper-case letters will denote matrices. The Euclidean and infinity norm of any vector \(\mathbf {b} \in \mathbb {R}^n\) will be denoted by \(\Vert \mathbf {b}\Vert \) and \(\Vert \mathbf {b}\Vert _\infty \), respectively. The Euclidean norm of matrix \(\mathbf {B} \in \mathbb {R}^{m \times n}\) with columns \((\mathbf {b}_i)_{i \le n}\) is \(\Vert \mathbf {B}\Vert = \max _{i\le n} \Vert \mathbf {b}_i\Vert \). When \(\mathbf {B}\) has full column-rank, we let \(\widetilde{\mathbf {B}}\) denote its Gram-Schmidt orthogonalization.
When S is a finite set, we denote by U(S) the uniform distribution over S and by \(x \hookleftarrow U(S)\) the action of sampling x according to this distribution.
For any \(\mathbf {x} \in \mathbb {Z}_q^m\), the notation \(\lfloor \mathbf {x} \rfloor _p \) stands for the result of the rounding operation \(\lfloor \mathbf {x} \rfloor _p = \lfloor (p/q) \cdot {\mathbf {x}} \rfloor \bmod p \). Intuitively, the mapping \(\lfloor \cdot \rfloor _p : \mathbb {Z}_q^m \rightarrow \mathbb {Z}_p^m\) can be seen as dividing \(\mathbb {Z}_q\) into p intervals of size (q / p) and sending each coordinate of \(\mathbf {x} \in \mathbb {Z}_q^m\) to the interval it belongs to.
The column concatenation of matrices \(\mathbf {A} \in \mathbb {R}^{n \times k}\) and \(\mathbf {B} \in \mathbb {R}^{n \times m}\) is denoted by \([\mathbf {A} | \mathbf {B}] \in \mathbb {R}^{n \times (k + m)}\). When concatenating column vectors \(\mathbf {x} \in \mathbb {R}^k\) and \(\mathbf {y} \in \mathbb {R}^m\), for simplicity, we often use the notation \((\mathbf {x} \Vert \mathbf {y}) \in \mathbb {R}^{k + m}\) (instead of \((\mathbf {x}^\top \Vert \mathbf {y}^\top )^\top \)).
2.1 Lattices
A lattice L is the set of integer linear combinations of linearly independent basis vectors \((\mathbf {b}_i)_{i\le n}\) living in \(\mathbb {R}^m\). We work with q-ary lattices, for some prime q.
Definition 1
Let \(m \ge n \ge 1\), a prime \(q \ge 2\) and \(\mathbf {A} \in \mathbb {Z}_q^{n \times m}\) and \(\mathbf {u} \in \mathbb {Z}_q^n\), define \(\varLambda _q(\mathbf {A}) := \{ \mathbf {e} \in \mathbb {Z}^m \mid \exists \mathbf {s} \in \mathbb {Z}_q^n ~\text { s.t. }~\mathbf {A}^T \cdot \mathbf {s} = \mathbf {e} \bmod q \}\) as well as
For any arbitrary \(\mathbf {t} \in \varLambda _q^{\mathbf {u}} (\mathbf {A})\), we also define the shifted lattice \(\varLambda _q^{\mathbf {u}}(\mathbf {A})=\varLambda _q^{\perp }(\mathbf {A}) + \mathbf {t}\).
For a lattice L, a vector \(\mathbf {c} \in \mathbb {R}^m\) and a real number \(\sigma >0\), define the function \(\rho _{\sigma ,\mathbf {c}}(\mathbf {x}) = \exp (-\pi \Vert \mathbf {x}- \mathbf {c} \Vert ^2/\sigma ^2) \). The discrete Gaussian distribution of support L, center \(\mathbf {c}\) and parameter \(\sigma \) is defined as \(D_{L,\sigma ,\mathbf {c}}(\mathbf {y}) = \rho _{\sigma ,\mathbf {c}}(\mathbf {y})/\rho _{\sigma ,\mathbf {c}}(L)\) for any \(\mathbf {y} \in L\), where \(\rho _{\sigma ,\mathbf {c}}(L) =\sum _{\mathbf {x} \in L} \rho _{\sigma ,\mathbf {c}}(\mathbf {x})\). We denote by \(D_{L,\sigma }(\mathbf {y}) \) the distribution centered in \(\mathbf {c}=\mathbf {0}^m\) and exploit the fact that samples from \(D_{L,\sigma }\) are short w.h.p.
Lemma 1
[6, Lemma 1.5]. For any lattice \(L \subseteq \mathbb {R}^m\) and positive real number \(\sigma >0\), we have \(\Pr _{\mathbf {b} \hookleftarrow D_{L,\sigma }} [\Vert \mathbf {b}\Vert \le \sqrt{m} \sigma ] \ge 1-2^{-\varOmega (m)}.\)
It is well-known that Gaussian distributions with lattice support can be efficiently sampled from a sufficiently short basis of the lattice.
Lemma 2
[20, Lemma 2.3]. There exists a PPT algorithm \(\mathsf {GPVSample}\) that takes as inputs a basis \(\mathbf {B}\) of a lattice \(L \subseteq \mathbb {Z}^n\) and a rational \(\sigma \ge \Vert \widetilde{\mathbf {B}}\Vert \cdot \varOmega (\sqrt{\log n})\), and outputs vectors \(\mathbf {b} \in L\) with distribution \(D_{L,\sigma }\).
We rely on the trapdoor generation algorithm of Alwen and Peikert [4].
Lemma 3
[4, Theorem 3.2]. There exists a PPT algorithm \(\mathsf {TrapGen}\) that takes as inputs \(1^n\), \(1^m\) and an integer \(q \ge 2\) with \(m \ge \varOmega (n \log q)\), and outputs a matrix \(\mathbf {A} \in \mathbb {Z}_q^{n \times m}\) and a basis \(\mathbf {T}_{\mathbf {A}}\) of \(\varLambda _q^{\perp }(\mathbf {A})\) such that \(\mathbf {A}\) is within statistical distance \(2^{-\varOmega (n)}\) to \(U(\mathbb {Z}_q^{n \times m})\), and \(\Vert \widetilde{\mathbf {T}_{\mathbf {A}}}\Vert \le \mathcal {O}(\sqrt{n \log q})\).
We utilize the basis delegation algorithm [31] that inputs a trapdoor for \(\mathbf {A} \in \mathbb {Z}_q^{n \times m}\) and produces a trapdoor for any \(\mathbf {B} \in \mathbb {Z}_q^{n \times m'}\) containing \(\mathbf {A}\in \mathbb {Z}_q^{n \times m}\) as a submatrix.
Lemma 4
[31, Lemma 3.2]. There exists a PPT algorithm that inputs a matrix \(\mathbf {B} \in \mathbb {Z}_q^{n \times m' }\) whose first m columns span \(\mathbb {Z}_q^n\), and a basis \(\mathbf {T}_{\mathbf {A}}\) of \(\varLambda _q^{\perp }(\mathbf {A})\) where \(\mathbf {A}\) is an \(n \times m\) submatrix of \(\mathbf {B}\), and outputs a basis \(\mathbf {T}_{\mathbf {B}}\) of \(\varLambda _q^{\perp }(\mathbf {B})\) with \(\Vert \widetilde{\mathbf {T}_{\mathbf {B}}}\Vert \le \Vert \widetilde{\mathbf {T}_{\mathbf {A}}}\Vert \).
Our security proofs use a technique introduced by Agrawal et al. [1].
Lemma 5
[1, Theorem 19]. There exists a PPT algorithm that inputs matrices \(\mathbf A, \mathbf C \in \mathbb {Z}_q^{n \times m}\), a small-norm matrix \(\mathbf R \in \mathbb {Z}^{m \times m}\), a short basis \(\mathbf {T_C} \in \mathbb {Z}^{m \times m}\) of \(\varLambda _q^{\perp }(\mathbf {C})\), a vector \(\mathbf u \in \mathbb {Z}_q^{n}\) and a rational \(\sigma \) such that \(\sigma \ge \Vert \widetilde{\mathbf {T_C}}\Vert \cdot \varOmega (\sqrt{\log n})\), and outputs vectors \(\mathbf {b} \in \mathbb {Z}^{2m}\) such that \(\left[ \begin{array}{c|c} \mathbf A ~&~ \mathbf A \cdot \mathbf R + \mathbf C \end{array} \right] \cdot \mathbf b = \mathbf u \bmod q\) and with distribution statistically close to \(D_{L,\sigma }\) where L denotes the shifted lattice \(\{ \mathbf x \in \mathbb {Z}^{2 m} : \left[ \begin{array}{c|c} \mathbf A ~&~ \mathbf A \cdot \mathbf R + \mathbf C \end{array} \right] \cdot \mathbf x = \mathbf u \bmod q \}\).
2.2 Hardness Assumptions
Definition 2
Let \(m,n,q \in \mathbb {N}\) with \(m>n\) and \(\beta >0\). The Short Integer Solution problem \(\mathsf {SIS}_{m,q,\beta }\) is, given \(\mathbf {A} \hookleftarrow U(\mathbb {Z}_q^{n \times m})\), find \(\mathbf {x} \in \varLambda ^{\perp }(\mathbf {A})\) with \(0 < \Vert \mathbf {x}\Vert \le \beta \).
Definition 3
Let \(q, \alpha \) be functions of a parameter n. For a secret \(\mathbf {s} \in \mathbb {Z}_q^n\), the distribution \(A_{q,\alpha ,\mathbf {s}}\) over \(\mathbb {Z}_q^n \times \mathbb {Z}_q\) is obtained by sampling \(\mathbf {a} \hookleftarrow U(\mathbb {Z}_q^n)\) and a noise \(e \hookleftarrow D_{\mathbb {Z}, \alpha q}\), and returning  . The Learning-With-Errors problem \(\mathsf {LWE}_{q,\alpha }\) is, for \(\mathbf {s} \hookleftarrow U(\mathbb {Z}_q^n)\), to distinguish between arbitrarily many independent samples from \(U(\mathbb {Z}_q^n \times \mathbb {Z}_q)\) and the same number of samples from \(A_{q,\alpha ,{\mathbf {s}}}\).
. The Learning-With-Errors problem \(\mathsf {LWE}_{q,\alpha }\) is, for \(\mathbf {s} \hookleftarrow U(\mathbb {Z}_q^n)\), to distinguish between arbitrarily many independent samples from \(U(\mathbb {Z}_q^n \times \mathbb {Z}_q)\) and the same number of samples from \(A_{q,\alpha ,{\mathbf {s}}}\).
If \(q \ge \sqrt{n} \beta \) and \(m,\beta \le \mathsf {poly}(n)\), then standard worst-case lattice problems with approximation factors \(\gamma = \widetilde{\mathcal {O}}(\beta \sqrt{n})\) reduce to \(\mathsf {SIS}_{m,q,\beta }\) (see, e.g., [52, See. 9]). Similarly, if \(\alpha q = \varOmega (\sqrt{n})\), standard worst-case lattice problems with approximation factors \(\gamma = \mathcal {O}(\alpha /n)\) reduce [20, 85] to \(\mathsf {LWE}_{q,\alpha }\). In the design of deterministic primitives like PRFs, the following variant of \(\mathsf {LWE}\) comes in handy.
Definition 4
[8]. Let q, p, m be functions of a security parameter n such that \(q> p \ge 2\) and \(m>n\). The Learning-With-Rounding (\(\mathsf {LWR}\)) problem is to distinguish the distribution \(\{ (\mathbf {A}, ~ \lfloor \mathbf {A}^T \cdot \mathbf {s} \rfloor _p ) \mid \mathbf {A} \hookleftarrow U(\mathbb {Z}_q^{n \times m}),~ \mathbf {s} \hookleftarrow U(\mathbb {Z}_q^n ) \}\) from the distribution \(\{ (\mathbf {A},~ \mathbf {y} ) \mid \mathbf {A} \hookleftarrow U(\mathbb {Z}_q^{n \times m}),~ \mathbf {y} \hookleftarrow U(\mathbb {Z}_p^m) \}.\)
Banerjee et al. [8] proved that \(\mathsf {LWR}\) is as hard as \(\mathsf {LWE}\) when q and the modulus-to-error ratio are super-polynomial. Alwen et al. [3] showed that, when the number m of samples is fixed in advance, \(\mathsf {LWR}\) retains its hardness for polynomial moduli. Bogdanov et al. [15] generalized the result of [3] to get rid of restrictions on the modulus q. For such parameters, their result implies the security of the \(\mathsf {LWR}\)-based PRG, which stretches the seed \(\mathbf {s} \in \mathbb {Z}_q^n\) into \(\lfloor \mathbf {A}^T \cdot \mathbf {s} \rfloor _p \in \mathbb {Z}_p^m \).
2.3 Syntactic Definitions for Off-Line Compact E-Cash
An off-line e-cash system involves a bank \(\mathcal {B}\), many users \(\mathcal {U}\) and merchants \(\mathcal {M}\). In the syntax defined by Camenisch, Hohenberger and Lysyanskaya [22], all these parties interact together via the following algorithms and protocols:
- ParGen\((1^\lambda )\)::
-
inputs a security parameter \(1^\lambda \) and outputs public parameters \(\mathsf {par}\).
In the following, we assume that \(\mathsf {par}\) are available to all parties although we sometimes omit them from the inputs of certain algorithms.
- BKeygen\((\mathsf {par})\)::
-
generates a bank’s key pair \((SK_{\mathcal {B}},PK_{\mathcal {B}})\) which allows \(\mathcal {B}\) to issue wallets of value \(2^L \in \mathsf {poly}(\lambda )\) (we assume that L is part of \(\mathsf {par}\)).
- UKeygen\((\mathsf {par})\)::
-
generates a user key pair \((SK_\mathcal {U},PK_\mathcal {U})\).
- Withdraw\(\big ( \mathcal {U}(PK_{\mathcal {B}},SK_{\mathcal {U}}), \mathcal {B}(PK_{\mathcal {U}},SK_{\mathcal {B}})\big )\)::
-
is an interactive protocol between a user \(\mathcal {U}\) and the bank \(\mathcal {B}\). The user \(\mathcal {U}\) obtains either a wallet
 of \(2^L\) coins or an error message \(\perp \). The bank outputs some state information
of \(2^L\) coins or an error message \(\perp \). The bank outputs some state information  which allows identifying \(\mathcal {U}\), should he overspend.
which allows identifying \(\mathcal {U}\), should he overspend. - Spend
 ::
:: -
is a protocol whereby the user \(\mathcal {U}\), on input of public keys \(PK_\mathcal {M},PK_\mathcal {B}\) and some transaction-specific meta data \(\mathtt {info}\), spends a coin from his wallet
 to merchant \(\mathcal {M}\). The merchant obtains a coin coin comprised of a serial number and a proof of validity. \(\mathcal {U}\)’s output is an updated wallet \(\mathcal {W}'\).
to merchant \(\mathcal {M}\). The merchant obtains a coin coin comprised of a serial number and a proof of validity. \(\mathcal {U}\)’s output is an updated wallet \(\mathcal {W}'\). - VerifyCoin\(( \mathsf {par},PK_{\mathcal {M}},PK_{\mathcal {B}},coin )\)::
-
is a non-interactive coin verification algorithm. On input of a purported coin and the public keys \(PK_\mathcal {M}\), \(PK_{\mathcal {B}}\) of the bank and the merchant, it outputs 0 or 1.
- Deposit\(( \mathcal {M}( SK_{\mathcal {M}},coin,PK_{\mathcal {B}}), \mathcal {B}(PK_{\mathcal {M}},SK_{\mathcal {B}},\mathsf {state}_\mathcal {B})))\)::
-
is a protocol allowing the merchant \(\mathcal {M}\) to deposit a received coin coin into its account at the bank \(\mathcal {B}\). \(\mathcal {M}\) outputs \(\perp \) if the protocol fails and nothing if it succeeds. The bank \(\mathcal {B}\) outputs “\(\mathsf {accept}\)” and updates its state \(\mathsf {state}_\mathcal {B}\) by adding an entry \((PK_\mathcal {M},coin)\) if VerifyCoin\(( \mathsf {par},PK_{\mathcal {M}},PK_{\mathcal {B}},coin )=1\) and no double-spending is detected. Otherwise, if VerifyCoin\(( \mathsf {par},PK_{\mathcal {M}},PK_{\mathcal {B}},coin )=1\) and \(\mathsf {state}_\mathcal {B}\) already contains a coin with the same serial number, it outputs “\(\mathsf {user}\)”. If VerifyCoin\(( \mathsf {par},PK_{\mathcal {M}},PK_{\mathcal {B}},coin )=0\) or \(\mathsf {state}_\mathcal {B}\) already contains an entry \((PK_\mathcal {M},coin)\), it outputs “\(\mathsf {merchant}\)”.
- Identify\(\big ( \mathsf {par}, PK_{\mathcal {B}}, {coin}_1, {coin}_2\big )\)::
-
is an algorithm that allows the bank \(\mathcal {B}\) to identify a double-spender on input of two coins \(coin_1\), \(coin_2\) with identical serial numbers. The bank outputs the double-spender’s public key \(PK_\mathcal {U}\) and a proof \(\varPi _G\) that \(\mathcal {U}\) indeed overspent.
Like [22], we assume that wallets  contain a counter J, initialized to 0, which indicates the number of previously spent coins. We also assume that each coin contains a serial number S, a proof of validity \(\pi \) as well as some information on the merchant’s public key \(PK_\mathcal {M}\) and some meta-data \(\mathtt {info}\).
contain a counter J, initialized to 0, which indicates the number of previously spent coins. We also assume that each coin contains a serial number S, a proof of validity \(\pi \) as well as some information on the merchant’s public key \(PK_\mathcal {M}\) and some meta-data \(\mathtt {info}\).
Following [22], we say that an off-line e-cash system is compact if the bitlength of the wallet  and the communication/computational complexities of all protocols is at most logarithmic in the value of the wallet (i.e., linear in L).
and the communication/computational complexities of all protocols is at most logarithmic in the value of the wallet (i.e., linear in L).
We use the security definitions of [22], which formalize security requirements called anonymity, balance, double-spender identification and exculpability.
Informally, the balance property considers colluding users interacting with a honest bank and attempting to spend more coins than they withdraw. This property is broken if the adversary manages to spend a coin of which the serial number does not match the serial number of any legally withdrawn coin. Double-spender identification complements the balance property by requiring that a malicious user be unable to output two coins with the same serial number without being caught by the \(\mathsf {Identify}\) algorithm. Anonymity mandates that, when a merchant returns a received coin to the bank, even if they collude, they cannot infer anything as to when and by whom the coin was withdrawn. The exculpability property captures that honest users cannot be falsely accused of being double-spenders: the adversary controls the bank and wins if it outputs two coins with the same serial number and such that \(\mathsf {Identify}\) points to a well-behaved user. The formal definitions of these properties are recalled in the full version of the paper.
3 Warm-Up: Permutations, Decompositions, Extensions
This section presents various notations and techniques that appeared (in slightly different forms) in earlier works on Stern-like protocols [66, 68,69,70,71], and that will be used extensively throughout this work.
Permutations. For any positive integer \(\mathfrak {m}\), we define the following sets.
-
\(\mathcal {S}_{\mathfrak {m}}\): the set of all permutations of \(\mathfrak {m}\) elements.
-
\(\mathsf {B}^2_{\mathfrak {m}}\): the set of binary vectors in \(\{0,1\}^{2\mathfrak {m}}\) with Hamming weight \(\mathfrak {m}\). Note that for any \(\mathbf {v} \in \mathbb {Z}^{2\mathfrak {m}}\) and \(\pi \in \mathcal {S}_{2m}\), we have:
$$\begin{aligned} \mathbf {v} \in \mathsf {B}^2_{\mathfrak {m}} \Longleftrightarrow \pi (\mathbf {v}) \in \mathsf {B}^2_{\mathfrak {m}}. \end{aligned}$$(3) -
\(\mathsf {B}^3_{\mathfrak {m}}\): the set of vectors in \(\{-1,0,1\}^{3\mathfrak {m}}\) that have exactly \(\mathfrak {m}\) coordinates equal to j, for every \(j \in \{-1,0,1\}\). Note that for any \(\mathbf {w} \in \mathbb {Z}^{3\mathfrak {m}}\) and \(\phi \in \mathcal {S}_{3m}\):
$$\begin{aligned} \mathbf {w} \in \mathsf {B}^3_{\mathfrak {m}} \Longleftrightarrow \phi (\mathbf {w}) \in \mathsf {B}^3_{\mathfrak {m}}. \end{aligned}$$(4)
For bit \(c \in \{0,1\}\) and integer vector \(\mathbf {v}\) of any dimension \(\mathfrak {m}\), we denote by \(\mathsf {Expand}(c, \mathbf {v})\) the vector \(\left( \begin{array}{c} \overline{c} \cdot \mathbf {v} \\ c \cdot \mathbf {v} \\ \end{array} \right) \in \mathbb {Z}^{2\mathfrak {m}} \), where \(\overline{c}\) denotes the bit \(1-c\).
For any positive integer \(\mathfrak {m}\), bit \(b \in \{0,1\}\), and permutation \(\pi \in \mathcal {S}_{\mathfrak {m}}\), we denote by \(T_{b,\pi }\) the permutation that transforms the vector \(\mathbf {v} = \left( \begin{array}{c} \mathbf {v}_0 \\ \mathbf {v}_1 \\ \end{array} \right) \in \mathbb {Z}^{2\mathfrak {m}}\), where \(\mathbf {v}_0, \mathbf {v}_1 \in \mathbb {Z}^{\mathfrak {m}}\), into the vector \(T_{b,\pi }(\mathbf {v}) = \left( \begin{array}{c} \pi (\mathbf {v}_b) \\ \pi (\mathbf {v}_{\overline{b}}) \\ \end{array} \right) \). Namely, \(T_{b,\pi }\) first rearranges the 2 blocks of \(\mathbf {v}\) according to b (it keeps the arrangement of blocks if \(b=0\) and swaps them if \(b=1\)), then it permutes each block according to \(\pi \).
Observe that the following equivalence holds for all \(\mathfrak {m} \in \mathbb {Z}_+\), \(b,c \in \{0,1\}\), \(\pi \in \mathcal {S}_{\mathfrak {m}}\), \(\mathbf {v} \in \mathbb {Z}^{\mathfrak {m}}\):
where \(\oplus \) denotes the addition operation modulo 2.
Decompositions. For any \(B \in \mathbb {Z}_+\), define \(\delta _B:=\lfloor \log _2 B\rfloor +1 = \lceil \log _2(B+1)\rceil \) and the sequence \(B_1, \ldots , B_{\delta _B}\), where \(B_j = \lfloor \frac{B + 2^{j-1}}{2^j} \rfloor \), for each \( j \in [1,\delta _B]\). As observed in [70, 72], it satisfies \(\sum _{j=1}^{\delta _B} B_j = B\) and any integer \(v \in [0, B]\) can be decomposed to \(\mathsf {idec}_B(v) = (v^{(1)}, \ldots , v^{(\delta _B)})^\top \in \{0,1\}^{\delta _B}\) such that \(\sum _{j=1}^{\delta _B}B_j \cdot v^{(j)} = v\). We describe this decomposition procedure in a deterministic manner as follows:
-
1.
\(v': = v\)
-
2.
For \(j=1\) to \(\delta _B\) do:
-
(i)
If \(v' \ge B_j\) then \(v^{(j)}: = 1\), else \(v^{(j)}: = 0\);
-
(ii)
\(v': = v' - B_j\cdot v^{(j)}\).
-
(i)
-
3.
Output \(\mathsf {idec}_B(v) = (v^{(1)}, \ldots , v^{(\delta _B)})^\top \).
Next, for any positive integers \(\mathfrak {m}, B\), we define the matrix:

and the following injective functions:
-
(i)
\(\mathsf {vdec}_{\mathfrak {m}, B}: [0,B]^{\mathfrak {m}} \rightarrow \{0,1\}^{\mathfrak {m}\delta _B}\) that maps the vector \(\mathbf {v} = (v_1, \ldots , v_{\mathfrak {m}})\) to \(\big (\mathsf {idec}_B(v_1) \Vert \ldots \Vert \mathsf {idec}_B(v_{\mathfrak {m}})\big )\). Note that \(\mathbf {H}_{\mathfrak {m}, B} \cdot \mathsf {vdec}_{\mathfrak {m}, B}(\mathbf {v}) = \mathbf {v}\).
-
(ii)
\(\mathsf {vdec}'_{\mathfrak {m}, B}: [-B,B]^{\mathfrak {m}} \rightarrow \{-1,0,1\}^{\mathfrak {m}\delta _B}\) that decomposes \(\mathbf {w} = (w_1, \ldots , w_{\mathfrak {m}})\) into the vector \(\big (\sigma (w_1)\cdot \mathsf {idec}_B(|w_1|) \Vert \ldots \Vert \sigma (w_{\mathfrak {m}})\cdot \mathsf {idec}_B(|w_{\mathfrak {m}}|)\big )\) such that, for each \(i\in [\mathfrak {m}]\), we have: \(\sigma (w_i) = 0\) if \(w_i =0\); \(\sigma (w_i) = -1\) if \(w_i <0\); \(\sigma (w_i) = 1\) if \(w_i >0\). Note that \(\mathbf {H}_{\mathfrak {m}, B} \cdot \mathsf {vdec}'_{\mathfrak {m}, B}(\mathbf {w}) = \mathbf {w}\).
Extensions. We define following extensions of matrices and vectors.
-
For any \(\mathfrak {m}, B \in \mathbb {Z}_+\), define \(\widehat{\mathbf {H}}_{\mathfrak {m}, B} \in \mathbb {Z}^{\mathfrak {m} \times 2\mathfrak {m}\delta _B}\), \(\breve{\mathbf {H}}_{\mathfrak {m}, B} \in \mathbb {Z}^{\mathfrak {m} \times 3\mathfrak {m}\delta _B}\) as follows:
$$ \widehat{\mathbf {H}}_{\mathfrak {m}, B}: = \big [\mathbf {H}_{\mathfrak {m}, B} \big | \mathbf {0}^{\mathfrak {m} \times \mathfrak {m}\delta _B}\big ]; \breve{\mathbf {H}}_{\mathfrak {m}, B}: = \big [\mathbf {H}_{\mathfrak {m}, B} \big | \mathbf {0}^{\mathfrak {m} \times 2\mathfrak {m}\delta _B}\big ]. $$ -
Given \(\mathbf {v} \in \{0,1\}^{\mathfrak {m}}\), define \(\mathsf {TwoExt}(\mathbf {v}): = (\mathbf {v} \Vert \mathbf {0}^{\mathfrak {m}-n_0} \Vert \mathbf {1}^{\mathfrak {m} - n_1}) \in \mathsf {B}^{2}_{\mathfrak {m}}\), where \(n_0\), \(n_1\) are the number of coordinates in \(\mathbf {v}\) equal to 0 and 1, respectively.
-
Given \(\mathbf {v} \in [-1,0,1]^{\mathfrak {m}}\), define
$$\mathsf {ThreeExt}(\mathbf {v}): = (\mathbf {v} \Vert \mathbf {0}^{\mathfrak {m}-n_{0}} \Vert \mathbf {1}^{\mathfrak {m} - n_1} \Vert \mathbf {-1}^{\mathfrak {m} - n_{-1}}) \in \mathsf {B}^{3}_{\mathfrak {m}},$$where \(n_0, n_1, n_{-1}\) are the number of coordinates in \(\mathbf {v}\) equal to 0, 1, and \(-1\), respectively.
Note that, if \(\mathbf {x} \in [0,B]^{m}\) and \(\mathbf {y} \in [-B,B]^m\), then we have:
In the framework of Stern-like protocols [64, 68, 70, 71, 86], the above techniques are useful when it comes proving in zero-knowledge the possession of integer vectors satisfying several different constraints:
Case 1: \(\mathbf {x} \in [0,B]^{{m}}\). We equivalently prove \(\hat{\mathbf {x}} =\mathsf {TwoExt}\big (\mathsf {vdec}_{m, B}(\mathbf {x})\big ) \in \mathsf {B}^2_{m\delta _B}\). To do this, pick \(\pi \hookleftarrow U(\mathcal {S}_{2m\delta _B})\), and convince the verifier that \(\pi (\hat{\mathbf {x}}) \in \mathsf {B}^2_{m\delta _B}\).
Case 2: \(\mathbf {x} \in [-B,B]^{{m}}\). We equivalently prove \(\breve{\mathbf {x}} = \mathsf {ThreeExt}\big (\mathsf {vdec}'_{m, B}(\mathbf {y})\big ) \in \mathsf {B}^3_{m\delta _B}\). To do this, pick \(\pi \hookleftarrow U(\mathcal {S}_{3m\delta _B})\), and convince the verifier that \(\pi (\breve{\mathbf {x}}) \in \mathsf {B}^3_{m\delta _B}\).
Case 3: \(\mathbf {x} = \mathsf {expand}(c, \mathbf {v})\), where \(\mathbf {v}\) satisfies one of the above two constraints. To hide \(\mathbf {v}\), we use the respective decomposition-extension-permutation technique. To hide the bit c, we pick a “one-time pad” \(b \hookleftarrow U(\{0,1\})\) and exploit the equivalence observed in (5). Looking ahead, this technique will be used in Sect. 4.3 to hide the bits of the PRF input J and those of a signature component \(\tau \in \{0,1\}^\ell \) in Sect. 5.
4 Zero-Knowledge Arguments for Lattice-Based PRFs
Here, we first give an abstraction of Stern’s protocol [86]. With this abstraction in mind, we then present our techniques for achieving zero-knowledge arguments for the BLMR PRF [17].
In the full version of the paper, we adapt these techniques to the PRF generically implied by the GGM [54] paradigm. While slightly more complex to describe, the GGM-based construction allows for a better choice of parameters since, owing to the result of Bogdanov et al. [15], it allows instantiating the \(\mathsf {LWR}\)-based PRG with polynomial-size moduli.
4.1 An Abstraction of Stern’s Protocol
In [86], Stern proposed a zero-knowledge protocol for the Syndrome Decoding problem, in which the main idea is to use a random permutation over coordinates of a secret vector to prove that the latter satisfies a given constraint (e.g., having fixed Hamming weight). Later on, Stern’s protocol was adapted to the lattice setting by Kawachi et al. [64] and refined by Ling et al. [70] to handle statements related to the SIS and LWE problems. Subsequently, the protocol was further developed to design several lattice-based systems [66, 69, 71]. Recently, Libert et al. [68] suggested an abstraction that addresses the setting where one has to prove knowledge of small secret vectors satisfying a number of modular linear equations with respect to one modulus. While their generalization subsumes many relations that naturally appear in privacy-preserving protocols involving lattices, it is not immediately applicable to the statements considered in this paper since we have to work with more than one modulus.
We thus put forward a new abstraction of Stern’s protocol [86] that handles modular equations with respect to \(N \ge 1\) moduli \(q_1, \ldots , q_N\), where secret witnesses may simultaneously appear across multiple equations.
Let \(n_i\) and \(d_i \ge n_i\) be positive integers, and let \(d = d_1+ \cdots + d_N\). Suppose that \(\mathsf {VALID}\) is a subset of \(\{-1,0,1\}^d\) and \(\mathcal {S}\) is a finite set such that every \(\phi \in \mathcal {S}\) can be associated with a permutation \(\varGamma _\phi \) of d elements satisfying the conditions
In our abstract protocol, for public matrices \(\{\mathbf {M}_i \in \mathbb {Z}_{q_i}^{n_i \times d_i}\}_{i \in [N]}\) and vectors \(\mathbf {u}_i \in \mathbb {Z}_{q_i}^{n_i}\), the prover argues in zero-knowledge the possession of integer vectors \(\{\mathbf {w}_i \in \{-1,0,1\}^{d_i}\}_{i\in [N]}\) such that:
Looking ahead, all the statements considered in Sects. 4.3, 5 will be reduced to the above setting, wherein secret vectors \(\mathbf {w}_1, \ldots , \mathbf {w}_N\) are mutually related, e.g., some entries of \(\mathbf {w}_i\) also appear in \(\mathbf {w}_j\).
The main ideas driving our protocol are as follows. To prove (10), the prover samples \(\phi \leftarrow U(\mathcal {S})\) and provides evidence that \(\varGamma _\phi (\mathbf {w}) \in \mathsf {VALID}\). The verifier should be convinced while learning nothing else, owing to the aforementioned properties of the sets \(\mathsf {VALID}\) and \(\mathcal {S}\). Meanwhile, to prove that Eq. (11) hold, the prover uses masking vectors \(\{\mathbf {r}_i \leftarrow U(\mathbb {Z}_{q_i}^{d_i})\}_{i\in [N]}\) and demonstrates instead that \(\mathbf {M}_i\cdot (\mathbf {w}_i + \mathbf {r}_i) = \mathbf {u}_i + \mathbf {M}_i\cdot \mathbf {r}_i \bmod q_i\).
The interaction between prover \(\mathcal {P}\) and verifier \(\mathcal {V}\) is described in Fig. 1. The common input consists of \(\{\mathbf {M}_i \in \mathbb {Z}_{q_i}^{n_i \times d_i}\}_{i \in [N]}\) and \(\mathbf {u}_i \in \mathbb {Z}_{q_i}^{n_i}\), while \(\mathcal {P}\)’s secret input is \(\mathbf {w} = \big (\mathbf {w}_1 \Vert \ldots \Vert \mathbf {w}_N\big )\). The protocol makes use of a statistically hiding and computationally binding string commitment scheme COM such as the SIS-based commitment of [64]. For simplicity of presentation, for vectors \(\mathbf {w} = \big (\mathbf {w}_1\Vert \ldots \Vert \mathbf {w}_N\big ) \in \mathbb {Z}^d\) and \(\mathbf {r} = \big (\mathbf {r}_1 \Vert \ldots \Vert \mathbf {r}_N\big ) \in \mathbb {Z}^d\), we denote by \(\mathbf {w} \boxplus \mathbf {r}\) the operation that computes \(\mathbf {z}_i = \mathbf {w}_i + \mathbf {r}_i \bmod q_i\) for all \(i \in [N]\), and outputs d-dimensional integer vector \(\mathbf {z} = \big (\mathbf {z}_1 \Vert \ldots \Vert \mathbf {z}_N\big )\). We note that, for all \(\phi \in \mathcal {S}\), if \(\mathbf {t} = \varGamma _{\phi }(\mathbf {w})\) and \(\mathbf {s} = \varGamma _{\phi }(\mathbf {r})\), then we have \(\varGamma _\phi (\mathbf {w} \boxplus \mathbf {r}) = \mathbf {t} \boxplus \mathbf {s}\).
The properties of our protocol are summarized in the following theorem.
Theorem 1
Suppose that \(\mathsf {COM}\) is a statistically hiding and computationally binding string commitment. Then, the protocol of Fig. 1 is a zero-knowledge argument of knowledge for the given statement, with perfect completeness, soundness error 2 / 3, and communication cost \({\mathcal {O}}\big (\sum _{i=1}^N d_i \cdot \log q_i\big )\). In particular:
-
There exists an efficient simulator that, on input \(\{\mathbf {M}_i, \mathbf {u}_i\}_{i \in [N]}\), outputs an accepted transcript statistically close to that produced by the real prover.
-
There exists an efficient knowledge extractor that, on input a commitment \(\mathrm {CMT}\) as well as valid responses \((\mathrm {RSP}_1, \mathrm {RSP}_2, \mathrm {RSP}_3)\) to all three possible values of the challenge Ch, outputs a witness \(\mathbf {w}' = (\mathbf {w}_1' \Vert \ldots \Vert \mathbf {w}_N') \in \mathsf {VALID}\) such that \(\mathbf {M}_i \cdot \mathbf {w}'_i = \mathbf {u}_i \bmod q_i\), for all \(i \in [N]\).
The proof of Theorem 1 employs standard simulation and extraction techniques of Stern-like protocols [64, 68,69,70], and is deferred to the full version of the paper.
4.2 Transforming the LWR Relation
Let \(q \ge p \ge 2\), \(m \ge 1\), and let \(\mathbb {Z}_q = [0, q-1]\) and \(\mathbb {Z}_p = [0,p-1]\). Consider the LWR rounding function: \(\lfloor \cdot \rfloor _p : \mathbb {Z}_q^m \rightarrow \mathbb {Z}_p^m ~:~ \mathbf {x} \mapsto \mathbf {y} = \lfloor ({p}/ {q} ) \cdot \mathbf {x} \rfloor \bmod p.\)
On the road towards zero-knowledge arguments for LWR-based PRFs, we have to build a sub-protocol that allows proving knowledge of a secret vector \(\mathbf {x} \in \mathbb {Z}_q^m\) satisfying, among other statements, the property of rounding to a given \(\mathbf {y} \in \mathbb {Z}_p^m\): i.e., \(\lfloor \mathbf {x} \rfloor _p = \mathbf {y}\). To our knowledge, such a sub-protocol is not available in the literature for the time being and must be designed from scratch.
Our crucial observation is that one knows \(\mathbf {x} \in [0,q-1]^m\) such that \(\lfloor \mathbf {x} \rfloor _p = \mathbf {y}\), if and only if one can compute \(\mathbf {x}, \mathbf {z} \in [0,q-1]^m\) such that:
This observation allows us to transform the LWR relation into an equivalent form that can be handled using the Stern-like techniques provided in Sect. 3. Let \(\widehat{\mathbf {x}} = \mathsf {TwoExt}\big (\mathsf {vdec}_{m, q-1}(\mathbf {x})\big )\) and \(\widehat{\mathbf {\mathbf {z}}} = \mathsf {TwoExt}\big (\mathsf {vdec}_{m, q-1}(\mathbf {z})\big )\). Then we have \(\mathbf {x} = \widehat{\mathbf {H}}_{m,q-1} \cdot \widehat{\mathbf {x}}\) and \(\mathbf {z} = \widehat{\mathbf {H}}_{m,q-1} \cdot \widehat{\mathbf {z}}\), so that Eq. (12) can be written as:
Note that one knows \(\mathbf {x}, \mathbf {z} \in [0,q-1]^m\) satisfying (12) if and only if one can compute \(\widehat{\mathbf {x}}, \widehat{\mathbf {z}} \in \mathsf {B}^2_{m\delta _{q-1}}\) satisfying (13). Furthermore, Stern’s framework allows proving the latter in zero-knowledge using random permutations.
4.3 Argument of Correct Evaluation for the BLMR PRF
We now consider the problem of proving the correct evaluation of the BLMR pseudo-random function from [17]. Namely, we would like to prove that a given \(\mathbf {y}= \big \lfloor \prod _{i=1}^L \mathbf {P}_{J[L+1-i]} \cdot \mathbf {k} \big \rfloor _p \in \mathbb {Z}_p^m\) is the correct evaluation for a committed seed \(\mathbf {k} \in \mathbb {Z}_q^m\) and a secret input \(J[1] \ldots J[L] \in \{0,1\}^L\), where \(\mathbf {P}_0,\mathbf {P}_1 \in \{0,1\}^{m \times m}\) are public binary matrices, while revealing neither \(\mathbf {k}\) nor \(J[1]\ldots J[L]\). We assume public matrices \(\mathbf {D}_0 \in \mathbb {Z}_{q_s}^{n \times {m}_0}\), \(\mathbf {D}_1 \in \mathbb {Z}_{q_s}^{n \times \bar{m}}\), for some modulus \(q_s\) and integers \(m_0 \) and \(\bar{m} = m \delta _{q-1}\), which are used to compute a KTX commitment [64] \(\mathbf {c}= \mathbf {D}_0 \cdot \mathbf {r} + \mathbf {D}_1 \cdot \tilde{\mathbf {k}} \in \mathbb {Z}_{q_s}^{n}\) to the decomposition \(\tilde{\mathbf {k}} = \mathsf {vdec}_{m,q-1}(\mathbf {k}) \in \{0,1\}^{\bar{m}}\) of the seed \(\mathbf {k}\), where \(\mathbf {r} \in [-\beta ,\beta ]^{m_0}\) is a discrete Gaussian vector (for some small integer \(\beta \)), and \(\tilde{\mathbf {k}}\) satisfies \(\mathbf {H}_{m,q-1}\cdot \tilde{\mathbf {k}} = \mathbf {k}\).
We first note that, in the evaluation process of \(\mathbf {y}= \big \lfloor \prod _{i=1}^L \mathbf {P}_{J[L+1-i]} \cdot \mathbf {k} \big \rfloor _p\), one works with vectors \(\{\mathbf {x}_i \in \mathbb {Z}_q^m\}_{i=0}^L\) such that \(\mathbf {x}_0 = \mathbf {k}\), \(\mathbf {x}_i=\mathbf {P}_{J[i]} \cdot \mathbf {x}_{i-1} \bmod q\) for each \(i \in \{1,\ldots ,L\}\), and \(\mathbf {y} = \lfloor \mathbf {x}_L \rfloor _p\). We further observe that the iterative equation \(\mathbf {x}_i=\mathbf {P}_{J[i]} \cdot \mathbf {x}_{i-1} \bmod q\) is equivalent to:
Intuitively, this observation allows us to move the secret bit J[i] from the “matrix side” to the “vector side” in order to make the equation compatible with Stern-like protocols. Next, for each \(i \in \{ 0, \ldots , L\}\), we form the vector \(\widehat{\mathbf {x}}_i = \mathsf {TwoExt}\big (\mathsf {vdec}_{m, q-1}(\mathbf {x}_i)\big )\in \mathsf {B}^2_{\bar{m}}\). Equation (14) can then be written as:
Let \(\mathbf {P} = \big [\mathbf {P}_0\cdot \widehat{\mathbf {H}}_{m,q-1} | \mathbf {P}_1\cdot \widehat{\mathbf {H}}_{m,q-1}\big ] \in \mathbb {Z}_q^{m \times 4\bar{m}}\), and \(\{\mathbf {s}_{i-1} = \mathsf {expand}(J[i], \widehat{\mathbf {x}}_{i-1})\}_{i=1}^L\), we have the L equations:
Regarding the rounding step \(\lfloor \mathbf {x}_L \rfloor _p = \mathbf {y} \in \mathbb {Z}_p^m\), using the transformations of Sect. 4.2, we obtain the following equation for \(\widehat{\mathbf {z}} \in \mathsf {B}^2_{\bar{m}}\):
As for the commitment relation, we have the equation \(\mathbf {c}= \mathbf {D}_0 \cdot \mathbf {r} + \mathbf {D}_1 \cdot \tilde{\mathbf {k}} \bmod q_s\), where \(\mathbf {H}_{m,q-1}\cdot \tilde{\mathbf {k}} = \mathbf {x}_0\). We let \(\breve{\mathbf {r}} = \mathsf {ThreeExt}\big (\mathsf {vdec}'_{m_0, \beta }(\mathbf {r})\big ) \in \mathsf {B}^3_{m_0\delta _\beta }\) and remark that \(\mathsf {TwoExt}\big (\tilde{\mathbf {k}}\big ) = \widehat{\mathbf {x}}_0\). Then, we have:
Our goal is now reduced to proving the possession of \(J[1]\ldots J[L] \in \{0,1\}^L\), \(\widehat{\mathbf {x}}_0, \ldots , \widehat{\mathbf {x}}_L, \widehat{\mathbf {z}} \in \mathsf {B}^2_{\bar{m}}\) and \(\breve{\mathbf {r}} \in \mathsf {B}^3_{m_0\delta _\beta }\), satisfying Eqs. (17), (15) and (16). Next, we let \(q_1 = q_s\), \(q_2 = q\), \(q_3 = pq\), and proceed as follows.
Regarding Eq. (17), letting \(\mathbf {M}_1 = \big [\mathbf {D}_0\cdot \breve{\mathbf {H}}_{m_0, \beta } \big | \mathbf {D}_1 \mid \mathbf {0}^{n \times \bar{m}}\big ]\), \(\mathbf {u}_1 = \mathbf {c}\) and \(\mathbf {w}_1 = \big (\breve{\mathbf {r}} \Vert \widehat{\mathbf {x}}_0\big )\), the equation becomes:
Next, we unify the L equations in (15). To this end, we define
and \(\mathbf {w}_2 = \big (\mathbf {s}_{0} \Vert \widehat{\mathbf {x}}_1 \Vert \cdots \Vert \mathbf {s}_{L-1} \Vert \widehat{\mathbf {x}}_L\big )\). Then, (15) can be equivalently written as:
As for Eq. (16), let \(\mathbf {M}_3 = \big [(p \cdot \widehat{\mathbf {H}}_{m,q-1}) | - \widehat{\mathbf {H}}_{m,q-1}\big ]\), \(\mathbf {u}_3 = q\cdot \mathbf {y}\) and \(\mathbf {w}_3 = \big (\widehat{\mathbf {x}}_L \Vert \widehat{\mathbf {z}}\big )\). Then, we obtain:
Now, we let \(d_1 = 3m_0\delta _\beta + 2\bar{m}\), \(d_2 = 6L\bar{m}\) and \(d_3 = 4\bar{m}\) be the dimensions of \(\mathbf {w}_1, \mathbf {w}_2\) and \(\mathbf {w}_3\), respectively, and \(d= d_1 + d_2 + d_3\). We form the vector \( \mathbf {w} = (\mathbf {w}_1\Vert \mathbf {w}_2 \Vert \mathbf {w}_3) \in \{-1,0,1\}^{d}, \) which has the form:
At this point, we have come close to reducing our statement to an instance of the one considered in Sect. 4.1. Next, let us specify the set \(\mathsf {VALID}\) containing \(\mathbf {w}\), the set \(\mathcal {S}\) and the associated permutation \(\varGamma _\phi \) satisfying conditions in 9.
Let \(\mathsf {VALID}\) be the set of all vectors in \(\{-1,0,1\}^d\) having the form (18), where
-
\(\breve{\mathbf {r}} \in \mathsf {B}^3_{m_0\delta _\beta }\), and \(\widehat{\mathbf {x}}_0, \ldots , \widehat{\mathbf {x}}_L, \widehat{\mathbf {z}} \in \mathsf {B}^2_{\bar{m}}\).
-
\(\{\mathbf {s}_{i-1} = \mathsf {expand}(J[i], \widehat{\mathbf {x}}_{i-1})\}_{i=1}^L\), for some \(J[1] \ldots J[L] \in \{0,1\}^L\).
It can be seen that our vector \(\mathbf {w}\) belongs to this tailored set \(\mathsf {VALID}\).
Now, we define \(\mathcal {S}: = \mathcal {S}_{3m_0\delta _\beta } \times (\mathcal {S}_{2\bar{m}})^{L+2} \times \{0,1\}^L\). Then, for any set element \(\phi = (\phi _r, \phi _0, \phi _1, \ldots , \phi _L, \phi _z, b_1 \ldots b_L) \in \mathcal {S}\), let \(\varGamma _\phi \) be the permutation that transforms vector \(\mathbf {w} \in \mathbb {Z}^d\) of the form (18) to vector \(\varGamma _\phi (\mathbf {w})\) of the form:
Thanks to the equivalences (3), (4), (5) from Sect. 3, we have \(\mathbf {w} \in \mathsf {VALID}\) if and only if \(\varGamma _\phi (\mathbf {w}) \in \mathsf {VALID}\). Furthermore, if \(\phi \leftarrow U(\mathcal {S})\), then \(\varGamma _\phi (\mathbf {w})\) is uniform in \(\mathsf {VALID}\). Said otherwise, the conditions in (9) are satisfied.
Given the above transformations and specifications, we can now run the abstract protocol of Fig. 1 to prove knowledge of \(\mathbf {w} = (\mathbf {w}_1 \Vert \mathbf {w}_2 \Vert \mathbf {w}_3) \in \mathsf {VALID}\) satisfying \(\{\mathbf {M}_i\cdot \mathbf {w}_i = \mathbf {u}_i \bmod q_i\}_{i=1,2,3}\), where public matrices/vectors \(\{\mathbf {M}_i, \mathbf {u}_i\}_{i=1,2,3}\) are as constructed above. As a result, we obtain a statistical zero-knowledge argument of knowledge for the statement described at the beginning of this section. For simulation, we run the simulator of Theorem 1 with public input \(\{\mathbf {M}_i, \mathbf {u}_i\}_{i=1,2,3}\). For extraction (see also the full version of the paper), we first run the knowledge extractor of Theorem 1, to obtain \(\mathbf {w}' = (\mathbf {w}_1' \Vert \mathbf {w}'_2 \Vert \mathbf {w}'_3) \in \mathsf {VALID}\) such that \(\{\mathbf {M}_i\cdot \mathbf {w}_i' = \mathbf {u}_i \bmod q_i\}_{i=1,2,3}\) and then reverse the witness transformations to get \(\mathbf {k}' \in \mathbb {Z}_q^m\), \(J'[1]\ldots J'[L] \in \{0,1\}^L\) and \(\mathbf {r}' \in [-\beta ,\beta ]^{m_0}\), \(\tilde{\mathbf {k}}' \in \{0,1\}^{\bar{m}}\) satisfying:
The protocol has communication cost \({\mathcal {O}}(d_1 \cdot \log q_1 + d_2 \cdot \log q_2 + d_3 \cdot \log q_3)\). For a typical setting of parameters (as in Sect. 5), this cost is of order \(\widetilde{\mathcal {O}}(\lambda \cdot L)\), where \(\lambda \) is the security parameter (and L is the input length of the PRF).
5 Description of Our Compact E-Cash System
This section describes our e-cash system. We do not present a general construction from lower level primitives because such a construction is already implicit in the work of Camenisch et al. [22] of which we follow the blueprint. To avoid repeating it, we directly show how to apply the same design principle in lattices using carefully chosen primitives that interact with our zero-knowledge proofs.
Like [22], our scheme combines signatures with efficient protocols and pseudo-random functions which support proofs of correct evaluation. Our e-cash system builds on the signature scheme with efficient protocols of Libert et al. [68]. The latter is a variant of the \(\mathsf {SIS}\)-based signatures described by Boyen [18] and Böhl et al. [16]. We actually use a simplified version of their scheme which is recalled in the full version of the paper and dispenses with the need to encode messages in a special way.
As in [22], our withdrawal protocol involves a step where the bank and the user jointly compute a seed \(\mathbf {k} =\mathbf {k}_0 +\mathbf {k}_1 \in \mathbb {Z}_q^m\), which will be uniform over \(\mathbb {Z}_q^m\) as long as one of the two parties is honest. The reason is that the identification of double-spenders can only be guaranteed if two distinct small-domain PRFs with independent random keys never collide, except with negligible probability. To jointly generate the PRF seed \(\mathbf {k}\), the protocol of [22] relies on the homomorphic property of the commitment scheme used in their oblivious signing protocol. In our setting, one difficulty is that the underlying KTX commitment [64] has message space \(\{0,1\}^{m \lceil \log q \rceil }\) and is not homomorphic over \(\mathbb {Z}_q^m\). To solve this problem, our withdrawal protocol lets the user obtain the bank’s signature on a message containing the binary decompositions of \(\mathbf {k}_0\) and \(\mathbf {k}_1\), so that the sum \(\mathbf {k}=\mathbf {k}_0 + \mathbf {k}_1\) is only reconstructed during the spending phase.
At the withdrawal step, the user also chooses a second PRF seed \(\mathbf {t} \in \mathbb {Z}_q^m\) of its own. The withdrawal protocol ends with the user obtaining a signature on the committed messages \((\mathbf {e}_u,\tilde{\mathbf {k}}_0,\tilde{\mathbf {k}}_1,\tilde{\mathbf {t}})\), where \((\tilde{\mathbf {k}}_0,\tilde{\mathbf {k}}_1,\tilde{\mathbf {t}})\) are bitwise decompositions of PRF seeds and \(\mathbf {e}_u\) is the user’s private key for which the corresponding public key is a GPV syndrome \(PK_\mathcal {U}=\mathbf {F} \cdot \mathbf {e}_u \in \mathbb {Z}_p^m\), for a random matrix \(\mathbf {F} \in \mathbb {Z}_p^{m \times m \lceil \log q \rceil }\).
In each spent coin, the user computes a serial number \(\mathbf {y}_S = F_{\mathbf {k}}(J) \in \mathbb {Z}_p^m\) consisting of a PRF evaluation under \(\mathbf {k} \in \mathbb {Z}_p^m\) and generates a NIZK argument that \(\mathbf {y}_S\) is the correct evaluation for the secret index J and the key \(\mathbf {k}=\mathbf {k}_0+\mathbf {k}_1\) contained in the certified wallet. Note that the argument does not require a separate commitment to \(\mathbf {k}\) since the bank’s signature \(sig_\mathcal {B}\) on the message \((\mathbf {e}_u,\tilde{\mathbf {k}}_0,\tilde{\mathbf {k}}_1,\tilde{\mathbf {t}})\) already contains a commitment to the bits of \((\mathbf {k}_0,\mathbf {k}_1)\). Since \(sig_\mathcal {B}\) and \((\mathbf {e}_u,\tilde{\mathbf {k}}_0,\tilde{\mathbf {k}}_1,\tilde{\mathbf {t}})\) are part of the witnesses that the user argues knowledge of, it is eventually the bank’s public key that commits the user to the seed \(\mathbf {k}\).
In each coin, the identification of double-spenders is enabled by a security tag \(\mathbf {y}_T= PK_{\mathcal {U}} + H_{\mathrm {FRD}}(R) \cdot F_{\mathbf {t}}(J) \in \mathbb {Z}_p^m\), where \(H_{\mathrm {FRD}}(R)\) is a Full-Rank Difference function [1, 41] of some transaction-specific information. If two coins share the same serial number \(\mathbf {y}_S\), the soundness of the argument system implies that the two security tags \(\mathbf {y}_{T,1},\mathbf {y}_{T,2}\) hide the same \( PK_{\mathcal {U}}\). By the Full Rank Difference property, subtracting \(\mathbf {y}_{T,1}-\mathbf {y}_{T,2}\) exposes \( F_{\mathbf {t}}(J) \in \mathbb {Z}_p^m\) and, in turn, \( PK_{\mathcal {U}} \in \mathbb {Z}_p^m\).
The details of the underlying argument system are given in Sect. 5.2, where we show that the considered statement reduces to an instance of the abstraction given in Sect. 4.1. On the way, we use a combination our transformation techniques for the BLMR PRF from Sect. 4.3 and the Stern-like techniques for the signature scheme of [68].
5.1 Description
In the description below, we use the injective function \(\mathsf {vdec}_{\mathfrak {n}, \mathfrak {q}-1}(\cdot )\) defined in Sect. 3, which maps a vector \(\mathbf {v} \in \mathbb {Z}_{\mathfrak {q}}^{\mathfrak {n}}\) to the vector \(\mathsf {vdec}_{\mathfrak {n},\mathfrak {q-1}}(\mathbf {v})\in \{0,1\}^{\mathfrak {n}\lceil \log _2 \mathfrak {q}\rceil }.\)
- ParGen\((1^\lambda ,1^L)\)::
-
Given a security parameter \(\lambda >0\) and an integer \(L>0\) such that \(2^L\) is the desired value of wallets, public parameters are chosen as follows.
- 1.:
-
Choose a lattice parameter \(n = \mathcal {O}(\lambda )\). Choose parameters that will be used by the BLMR pseudo-random function [17]: an LWE parameter \(\alpha = 2^{-\omega (\log ^{1+c}(n))}\) for some constant \(c>0\); moduli \(p = 2^{\log ^{1+c}(n)}\) and \(q = \mathcal {O}(\sqrt{n}/\alpha )\) such that p divides q; and dimension \(m = \lceil n \log q\rceil \). Pick another prime modulus \(q_s= \widetilde{\mathcal {O}}(n^4)\) to be used by the signature scheme. Pick an integer \(\ell = \Theta (\lambda )\), a Gaussian parameter \(\sigma = \varOmega (\sqrt{n\log q_s}\log n)\), and an infinity norm bound \(\beta = \sigma \cdot \omega (\log n)\). Let \(\delta _{q_s-1} = \lceil \log _2(q_s) \rceil \), \(\delta _{q-1} = \lceil \log _2(q) \rceil \), \(\delta _{p-1} = \lceil \log _2(p) \rceil \).
We will use an instance of the signature scheme with efficient protocols from [68], where matrices \((\mathbf {A},\{\mathbf {A}_j\}_{j=0}^\ell , \mathbf {D} )\), \(\{\mathbf {D}_k\}_{k=0}^4\) do not all have the same number of columns. Specifically, let \(m_s =m_0= 2 n \delta _{q_s-1}\) and define the length of message blocks to be \(m_1=m_2=m_3=m_4=\bar{m}= m \delta _{q-1} \). We also use an additional matrix \(\mathbf {F} \in \mathbb {Z}_p^{m \times m_f}\), where \(m_f=\bar{m}= m \delta _{q-1} \).
- 2.:
-
Choose a commitment key CK for a statistically hiding commitment where the message space is \(\{0,1\}^{m_1} \times \{0,1\}^{m_2} \times \{0,1\}^{m_3}\). This commitment key \(CK=\bigl ( [\mathbf {D}_0' \mid \mathbf {D}_0''],~\mathbf {D}_1,~\mathbf {D}_2,~\mathbf {D}_3,~\mathbf {D}_4 \bigr )\) consists of random matrices \( \mathbf {D}_0', \mathbf {D}_0'' \hookleftarrow U(\mathbb {Z}_{q_s}^{n \times m_0})\), \(\mathbf {D}_1 \hookleftarrow U(\mathbb {Z}_{q_s}^{n \times m_1})\), \(\mathbf {D}_2 \hookleftarrow U(\mathbb {Z}_{q_s}^{n \times m_2})\), \(\mathbf {D}_3 \hookleftarrow U(\mathbb {Z}_{q_s}^{n \times m_3})\), \(\mathbf {D}_4 \hookleftarrow U(\mathbb {Z}_{q_s}^{n \times m_4})\).
- 3.:
-
Select two binary matrices \(\mathbf {P}_0,\mathbf {P}_1 \in \{0,1\}^{m \times m}\) uniformly among \(\mathbb {Z}_q\)-invertible matrices.
- 4.:
-
Finally, choose a full-rank difference function \(H_{\mathrm {FRD}}:\mathbb {Z}_p^m \rightarrow \mathbb {Z}_p^{m \times m}\) such as [1], a collision-resistant hash function \(H_0 : \{0,1\}^* \rightarrow \mathbb {Z}_p^m\) and another hash function \(H:\{0,1\}^* \rightarrow \{1,2,3\}^\kappa \), for some \(\kappa = \omega (\log \lambda )\), which will be modeled as a random oracle in the security analysis.
We define
$$\begin{aligned} \mathsf {par}:= \Bigl (\mathbf {F},~\{ \mathbf {P}_0,~\mathbf {P}_1 \},~H_\mathrm {FRD},~H_0,~H,~ CK \Bigr ). \end{aligned}$$where \(CK=( \mathbf {D}_0 =[\mathbf {D}_0' \mid \mathbf {D}_0''],~\mathbf {D}_1, \mathbf {D}_2,~\mathbf {D}_3,~\mathbf {D}_4 )\).
- BKeygen\((1^\lambda ,\mathsf {par})\)::
-
The bank \(\mathcal {B}\) generates a key pair for the signature scheme with efficient protocols. This is done as follows.
- 1.:
-
Run \(\mathsf {TrapGen}(1^n,1^{m_s},q_s)\) to get \(\mathbf {A} \in \mathbb {Z}_{q_s}^{n \times m_s}\) and a short basis \(\mathbf {T}_{\mathbf {A}}\) of \(\varLambda _{q_s}^{\perp }(\mathbf {A}).\) This basis allows computing short vectors in \(\varLambda _{q_s}^{\perp }(\mathbf {A})\) with a Gaussian parameter \(\sigma \). Next, choose matrices \(\mathbf {A}_0,\mathbf {A}_1,\ldots ,\mathbf {A}_{\ell } \hookleftarrow U(\mathbb {Z}_{q_s}^{n \times m_s})\).
- 2.:
-
Choose \(\mathbf {D} \hookleftarrow U\big (\mathbb {Z}_{q_s}^{n \times (m_s/2)} \big )\) and a random vector \(\mathbf {u} \hookleftarrow U(\mathbb {Z}_{q_s}^n)\).
The private key consists of \(SK_{\mathcal {B}}:= \mathbf {T}_{\mathbf {A}} \) while the public key is
$${PK}_{\mathcal {B}}:=\big ( \mathbf {A}, ~ \{\mathbf {A}_j \}_{j=0}^{\ell },~\mathbf {D},~\mathbf {u} \big ).$$ - UKeygen\((1^\lambda ,\mathsf {par})\)::
-
As a secret key, the user picks \(SK_{\mathcal {U}} := \mathbf {e}_u \hookleftarrow U(\{0,1\}^{m_f})\) at random and computes his public key \(PK_{\mathcal {U}}\) as a syndrome \(PK_{\mathcal {U}}=\mathbf {F} \cdot \mathbf {e}_u \in \mathbb {Z}_{p}^m\).
- Withdraw\(\big (\mathcal {U}(PK_{\mathcal {B}},SK_{\mathcal {U}},2^L),\mathcal {B}(PK_{\mathcal {U}},SK_{\mathcal {B}},2^L) \big )\)::
-
The bank \(\mathcal {B}\), which has a key pair \((SK_{\mathcal {B}},PK_{\mathcal {B}})\), interacts with \(\mathcal {U}\), who has \(SK_{\mathcal {U}}=\mathbf {e}_u \), as follows.
- 1.:
-
\(\mathcal {U}\) picks \(\mathbf {t},\mathbf {k}_0 \hookleftarrow U(\mathbb {Z}_q^m)\) and computes \(\tilde{\mathbf {t}} =\mathsf {vdec}_{m,q-1}(\mathbf {t}) \in \{0,1\}^{\bar{m}}\), \(\tilde{\mathbf {k}}_0 =\mathsf {vdec}_{m,q-1}(\mathbf {k}_0) \in \{0,1\}^{\bar{m}} \). Then, he generates a commitment to the 3-block message \((\mathbf {e}_u,\tilde{\mathbf {t}},\tilde{\mathbf {k}}_0) \in \{0,1\}^{m_f} \times \{0,1\}^{\bar{m}} \times \{0,1\}^{\bar{m}} \). To this end, \(\mathcal {U}\) samples \(\mathbf {r}_0 \hookleftarrow D_{\mathbb {Z}^{m_s},\sigma } \) and computes
$$\begin{aligned} \mathbf {c}_{\mathcal {U}} = \mathbf {D}_0' \cdot \mathbf {r}_0 + \mathbf {D}_1 \cdot \mathbf {e}_u + \mathbf {D}_2 \cdot \tilde{\mathbf {t}} + \mathbf {D}_3 \cdot \tilde{\mathbf {k}}_0 \in \mathbb {Z}_{q_s}^n, \end{aligned}$$(19)which is sent to \(\mathcal {B}\). In addition, \(\mathcal {U}\) generates an interactive zero-knowledge argument of knowledge of an opening
$$(\mathbf {r}_0,\mathbf {e}_u,\tilde{\mathbf {t}},\tilde{\mathbf {k}}_0) \in D_{\mathbb {Z}^{m_s},\sigma } \times \{0,1\}^{m_f} \times \{0,1\}^{\bar{m}} \times \{0,1\}^{\bar{m}} $$of \(\mathbf {c}_{\mathcal {U}} \in \mathbb {Z}_{q_s}^n\) satisfying (19) and such that \(PK_{\mathcal {U}}= \mathbf {F} \cdot \mathbf {e}_u \in \mathbb {Z}_p^m\). We note that this argument system is obtained via a straightforward adaptation of the Stern-like protocol from [68].
- 2.:
-
If the argument of step 1 verifies, \(\mathcal {B}\) samples \(\mathbf {r}_1 \hookleftarrow D_{\mathbb {Z}^{m_s},\sigma }\), \(\mathbf {k}_1 \hookleftarrow U(\mathbb {Z}_q^m)\) and computes \(\tilde{\mathbf {k}}_1 =\mathsf {vdec}_{m,q-1}(\mathbf {k}_1) \in \{0,1\}^{\bar{m}}\) and a re-randomized version of \(\mathbf {c}_{\mathcal {U}}\) which is obtained as \(\mathbf {c}_{\mathcal {U}}'= \mathbf {c}_{\mathcal {U}} + \mathbf {D}_0'' \cdot \mathbf {r}_1 + \mathbf {D}_4 \cdot \tilde{\mathbf {k}}_1 \in \mathbb {Z}_{q_s}^n \). It defines \(\mathbf {u}_{\mathcal {U}}= \mathbf {u} + \mathbf {D} \cdot \mathsf {vdec}_{n,q_s-1} \bigl ( \mathbf {c}_{\mathcal {U}}' \bigr ) \in \mathbb {Z}_{q_s}^n\). Next, \(\mathcal {B}\) randomly picks \(\tau \hookleftarrow \{0,1\}^\ell \) and uses \(\mathbf {T}_{\mathbf {A}}\) to compute a delegated basis \(\mathbf {T}_{\tau } \in \mathbb {Z}^{2 m_s \times 2 m_s}\) for the matrix \(\mathbf {A}_{\tau } \in \mathbb {Z}_{q_s}^{n \times 2m_s}\) defined as
$$\begin{aligned} \mathbf {A}_{\tau }= [ \mathbf {A} \mid \mathbf {A}_0 + \sum _{j=1}^\ell \tau [j] \cdot \mathbf {A}_j ] \in \mathbb {Z}_{q_s}^{ n \times 2 m_s}. \end{aligned}$$(20)Using \(\mathbf {T}_\tau \in \mathbb {Z}^{2m_s \times 2m_s}\), \(\mathcal {B}\) samples a short vector \(\mathbf {v} \in \mathbb {Z}^{2m_s}\) in \(D_{\varLambda _{q_s}^{\mathbf {u}_{\mathcal {U}}}(\mathbf {A}_\tau ), \sigma }\). It returns \(\mathbf {k}_1 \in \mathbb {Z}_q^m\) and the vector \(( \tau ,\mathbf {v},\mathbf {r}_1) \in \{0,1\}^\ell \times \mathbb {Z}^{2m_s} \times \mathbb {Z}^{m_s} \) to \(\mathcal {U}\).
- 3.:
-
\(\mathcal {U}\) computes \(\mathbf {r} = \begin{bmatrix} \mathbf {r}_0 \\ \hline \mathbf {r}_1 \end{bmatrix} \in \mathbb {Z}^{2m_s}\) and verifies that
$$\begin{aligned} \mathbf {A}_{\tau } \cdot \mathbf {v} = \mathbf {u} + \mathbf {D} \cdot \mathsf {vdec}_{n,q_s-1} \Bigl ( \mathbf {D}_0 \cdot \mathbf {r} + \mathbf {D}_1 \cdot \mathbf {e}_u + \mathbf {D}_2 \cdot \mathsf {vdec}_{m,q-1}(\mathbf {t}) \\ + \mathbf {D}_3 \cdot \mathsf {vdec}_{m,q-1}(\mathbf {k}_0) + \mathbf {D}_4 \cdot \mathsf {vdec}_{m,q-1}(\mathbf {k}_1) \Bigr ) \bmod q_s \end{aligned}$$and \(\Vert \mathbf {v} \Vert \le \sigma \sqrt{2m_s}\), \(\Vert \mathbf {r}_1 \Vert \le \sigma \sqrt{m_s}\). If so, \(\mathcal {U}\) saves the wallet
where \(J \in \{0,\ldots ,2^L-1\}\) is a counter initialized to 0 (otherwise, it outputs \(\perp \)). The bank \(\mathcal {B}\) records a debit of \(2^L\) for the account \(PK_{\mathcal {U}}\).
- Spend
 ::
:: -
The user \(\mathcal {U}\), on input of a wallet
 , outputs \(\perp \) if \(J>2^L -1\). Otherwise, it runs the following protocol with \(\mathcal {M}\).
, outputs \(\perp \) if \(J>2^L -1\). Otherwise, it runs the following protocol with \(\mathcal {M}\). - 1.:
-
Hash \(\mathsf {info} \in \{0,1\}^*\) and \(PK_\mathcal {M}\) to obtain \(R=H_0(PK_{\mathcal {M}},\mathsf {info}) \in \mathbb {Z}_p^m\).
- 2.:
-
Compute \(\mathbf {k} = \mathbf {k}_0 + \mathbf {k}_1 \bmod q\), which will serve a PRF seed \(\mathbf {k} \in \mathbb {Z}_q^m\). Using \(\mathbf {k}\), compute the serial number
$$\begin{aligned} \mathbf {y}_S = \lfloor \prod _{i=1}^L \mathbf {P}_{J[L+1-i]} \cdot \mathbf {k} \rfloor _{p}~\in \mathbb {Z}_p^m, \end{aligned}$$(21)where \(J[1] \ldots J[L] \in \{0,1\}^L\) is the representation of \(J \in \{0,\ldots ,2^L-1\}\).
- 3.:
-
Using the PRF seed \(\mathbf {t} \in \mathbb {Z}_q^m\), compute the security tag
$$\begin{aligned} \mathbf {y}_T = PK_{\mathcal {U}} + H_\mathrm {FRD}( R ) \cdot \lfloor \prod _{i=1}^L \mathbf {P}_{J[L+1-i]} \cdot \mathbf {t} \rfloor _{p}~ \in \mathbb {Z}_p^{m}. \end{aligned}$$(22) - 4.:
-
Generate a non-interactive argument of knowledge \(\pi _K\) to prove that:
- (i):
-
The given serial number \(\mathbf {y}_S\) is the correct output of the PRF with key \(\mathbf {k} = \mathbf {k}_0 + \mathbf {k}_1 \bmod q\) and input \(J[1]\ldots J[L]\) (Eq. (21));
- (ii):
-
The same input \(J[1]\ldots J[L]\) and another key \(\mathbf {t}\) involve in the generation of the security tag \(\mathbf {y}_T\) of the form (22);
- (iii):
-
The PRF keys \(\mathbf {k}_0, \mathbf {k}_1, \mathbf {t}\) and the secret key \(\mathbf {e}_u\) that corresponds to \(PK_{\mathcal {U}}\) in (22) were certified by the bank.
This is done by running the interactive zero-knowledge argument presented in Sect. 5.2, which can be seen as a combination of 2 instances of the protocol for the PRF layer from Sect. 4.3 and one instance of the protocol for the signature layer from [68]. The argument is repeated \(\kappa = \omega (\log \lambda )\) times to achieve negligible soundness error, and then made non-interactive using the Fiat-Shamir heuristic [46] as a triple \(\pi _K=( \{\mathsf {Comm}_{K,j}\}_{j=1}^\kappa ,\mathsf {Chall}_K,\{\mathsf {Resp}_{K,j}\}_{j=1}^\kappa )\) where
$$\mathsf {Chall}_K = H(R, \mathbf {y}_S,\mathbf {y}_T, \{ \mathsf {Comm}_{K,j}\}_{j=1}^t) \in \{1,2,3\}^\kappa .$$
\(\mathcal {U}\) sends \(coin= \big (R,\mathbf {y}_S,\mathbf {y}_T,\pi _K \big )\) to \(\mathcal {M}\) who outputs coin if \(\mathsf {VerifyCoin}\) accepts it and \(\perp \) otherwise. \(\mathcal {U}\) outputs an updated wallet
 , where J is incremented. We note that coin has bit-size \(\widetilde{\mathcal {O}}(L\cdot \lambda + \lambda ^2)\), which is inherited from that of the underlying zero-knowledge argument system of Sect. 5.2.
, where J is incremented. We note that coin has bit-size \(\widetilde{\mathcal {O}}(L\cdot \lambda + \lambda ^2)\), which is inherited from that of the underlying zero-knowledge argument system of Sect. 5.2. - VerifyCoin\(( \mathsf {par},PK_{\mathcal {M}},PK_{\mathcal {B}},coin )\)::
-
Parse the coin as \(coin= \big (R,\mathbf {y}_S,\mathbf {y}_T,\pi _K \big )\) and output 1 if and only if \(\pi _K\) properly verifies.
- Deposit\(\big (\mathcal {M}(SK_{\mathcal {M}},coin,PK_{\mathcal {B}})),\mathcal {B}(PK_{\mathcal {M}},SK_{\mathcal {B}},\mathsf {state}_{\mathcal {B}}) \big )\)::
-
\(coin= \big (R,\mathbf {y}_S,\mathbf {y}_T,\pi _K \big )\) is sent by \(\mathcal {M}\) to the bank \(\mathcal {B}\). If VerifyCoin\(( \mathsf {par},PK_{\mathcal {M}},PK_{\mathcal {B}},coin )=1\) and if serial number \(\mathbf {y}_S\) does not already appear in any coin of the list \(\mathsf {state}_\mathcal {B}\), \(\mathcal {B}\) accepts coin, adds \((R,\mathbf {y}_S)\) in \(\mathsf {state}_\mathcal {B}\) and credits \(PK_{\mathcal {M}}\)’s account. Otherwise, \(\mathcal {B}\) returns “\(\mathsf {user}\)” or “\(\mathsf {merchant}\)” depending on which party is declared faulty.
- Identify\(\big (\mathsf {par},PK_{\mathcal {B}},coin_1,coin_2) \big )\)::
-
Given two coins \(coin_1= \big (R_1,\mathbf {y}_S,\mathbf {y}_{T,1},\pi _{K,1} \big )\), \(coin_2= \big (R_2,\mathbf {y}_S,\mathbf {y}_{T,2},\pi _{K,2} \big )\) with verifying proofs \(\pi _{K,1},\pi _{K,2}\) and the same serial number \(\mathbf {y}_S \in \mathbb {Z}_p^m\) in distinct transactions \(R_1 \ne R_2\), output \(\perp \) if \(\mathbf {y}_{T,1}=\mathbf {y}_{T,2}\). Otherwise, compute
$$\begin{aligned} \mathbf {y}_T'= & {} \big ( H_{\mathrm {FRD}}(R_1)-H_{\mathrm {FRD}}(R_2) \big )^{-1} \cdot ( \mathbf {y}_{T,1} - \mathbf {y}_{T,2} ) \in \mathbb {Z}_p^m \end{aligned}$$and then \(PK_{\mathcal {U}} = \mathbf {y}_{T,1}- H_{\mathrm {FRD}}(R_1) \cdot \mathbf {y}_T' \in \mathbb {Z}_p^m.\) The proof \(\varPi _G\) that \(\mathcal {U}\) is guilty simply consists of the two coins \(coin_1\), \(coin_2\) and the public key \(PK_\mathcal {U}\).
In the full version of the paper, we show how to extend the scheme with a mechanism allowing to trace all the coins of an identified double-spender. Like Camenisch et al. [22], we can add this feature via a verifiable encryption step during the withdrawal phase. For this purpose, however, [22] crucially relies on properties of groups with a bilinear map that are not available here. To overcome this difficulty, we slightly depart from the design principle of [22] in that we rather use a secret-key verifiable encryption based on the hardness of \(\mathsf {LWE}\).
5.2 The Underlying Argument System of Our E-Cash Scheme
We now present the argument system employed by the Spend algorithm of the e-cash scheme in Sect. 5.1. This protocol is summarized as follows.
Let parameters \(\lambda \), n, p, q, \(q_s\), m, \(\beta \), L, \(\ell \), \(\bar{m}= m \delta _{q-1}\), \(m_s = 2 n \delta _{q_s-1}\) be as specified in Sect. 5.1. The public input consists of:
The prover’s goal is to prove in zero-knowledge the possession of
such that the following equations hold:
Our strategy is to reduce the above statement to an instance of the abstraction in Sect. 4.1. To this end, we will combine the zero-knowledge proofs of signatures from the Stern-like techniques of [68] and our techniques for the PRF layer from Sect. 4.3. Specifically, we let \(q_1 = q_s\), \(q_2=q\), \(q_3 = pq\), \(q_4=p\), and perform the following transformations.
Regarding the two equations of the signature relation in (23)–(24), we apply the following decompositions and/or extensions to the underlying secret vectors:
At the same time, we also transform the associated public matrices \(\mathbf {A}\), \(\{\mathbf {A}_j\}_{j=0}^\ell \), \(\mathbf {D}\), \(\{\mathbf {D}_j\}_{j=0}^4\), \(\mathbf {H}_{n,q_s-1}\) accordingly, so that the equations are preserved. Next, we combine the vectors obtained in (27) into:
where \(d_1 = 6(\ell +2)m_s\delta _\beta + m_s + 8\bar{m}\). We observe that the two equations can be unified into just one equation of the form \(\mathbf {M}_1\cdot \mathbf {w}_1 = \mathbf {u}_1 \bmod q_1\), where \(\mathbf {M}_1 \in \mathbb {Z}_{q_1}^{2n \times d_1}\) is built from public matrices, and \(\mathbf {u}_1 = (\mathbf {u} \Vert \mathbf {0}) \in \mathbb {Z}_{q_1}^{2n}\).
We now consider equations in (25) and (26), which involve PRF evaluations. We note that, for all \(\alpha \in \{\mathbf {t}, \mathbf {k}_0, \mathbf {k}_1\}\) appearing in this layer, we have the connection
where \(\widehat{\alpha }\) is constructed in 27. To transform the equation \(\mathbf {k} = \mathbf {k}_0 + \mathbf {k}_1 \in \mathbb {Z}_q^m\) in (25), we let \(\widehat{\mathbf {k}}= \mathsf {TwoExt}\big (\mathsf {vdec}_{m,q-1}(\mathbf {k})\big )\in \mathsf {B}_{\bar{m}}^2\), and rewrite the equation as
Letting \(\mathbf {M}_{k,2}= [\widehat{\mathbf {H}}_{m,q-1}\mid \widehat{\mathbf {H}}_{m,q-1}\mid -\widehat{\mathbf {H}}_{m,q-1}]\) and \(\mathbf {u}_{k,2} = \mathbf {0}\), we have the equation \(\mathbf {M}_{k,2}\cdot \mathbf {w}_{k,2} = \mathbf {u}_{k,2} \bmod q_2\), where:
The evaluation process of \(\mathbf {y}_S\) in (25) is handled as in Sect. 4.3, resulting in equations \(\mathbf {M}_{S,2} \cdot \mathbf {w}_{S,2} = \mathbf {u}_{S,2} \bmod q_2\), and \(\mathbf {M}_{S,3} \cdot \mathbf {w}_{S,3} = \mathbf {u}_{S,3} \bmod q_3\), where
satisfy \(\{\widehat{\mathbf {x}}_{S,i}\}_{i=1}^L\), \(\widehat{\mathbf {z}}_{S}\in \mathsf {B}^2_{\bar{m}}\) and
Regarding the evaluation of \(\mathbf {y}'_T\) in (26), equations appearing in the iteration step can also be unified into one of the form \(\mathbf {M}_{T,2}\cdot \mathbf {w}_{T,2} = \mathbf {u}_{T,2} \bmod q_2\), where
satisfy
Meanwhile, the rounding step is handled in a slightly different manner as the output \(\mathbf {y}'_T \in \mathbb {Z}_p^m\) is hidden. Letting \(\widehat{\mathbf {y}}'_T = \mathsf {TwoExt}\big (\mathsf {vdec}_{m,p-1}(\mathbf {y}'_T)\big )\in \mathsf {B}^2_{m\delta _{p-1}}\), we are presented with the equation
where \(\widehat{\mathbf {z}}_T \in \mathsf {B}^2_{\bar{m}}\). This equation can be written as \(\mathbf {M}_{T,3}\cdot \mathbf {w}_{T,3} = \mathbf {u}_{T,3} \bmod q_3\), where \( \mathbf {M}_{T,3} = \big [p \cdot \widehat{\mathbf {H}}_{m,q-1}\mid -\widehat{\mathbf {H}}_{m,q-1} \mid -q\cdot \widehat{\mathbf {H}}_{m,p-1}\big ], \mathbf {u}_{T,3} = \mathbf {0}, \) and
Furthermore, we observe that, the three equations modulo \(q_2\), as well as the two equations modulo \(q_3\) we have obtained above can be unified as follows. Let
then we have \(\mathbf {M}_2 \cdot \mathbf {w}_2 = \mathbf {u}_2 \bmod q_2\) and \(\mathbf {M}_3 \cdot \mathbf {w}_3 = \mathbf {u}_3 \bmod q_3\), where
for \(\mathbf {w}_{k,2}, \mathbf {w}_{S,2}, \mathbf {w}_{T,2}, \mathbf {w}_{S,3}, \mathbf {w}_{T,3}\) defined by (29)–(32), and for \(d_2 = 6\bar{m}(2L+1)\), \(d_3 = 8\bar{m} + 2m\delta _{p-1}\).
Now, the remaining equation in (26) can be written as:
where \(\widehat{\mathbf {e}}\) and \(\widehat{\mathbf {y}}'_T\) are as constructed earlier. We therefore obtain the equation \(\mathbf {M}_4 \cdot \mathbf {w}_4 = \mathbf {u}_4 \bmod q_4\), where \(\mathbf {M}_4 = \big [H_\mathrm {FRD}( R )\cdot \widehat{\mathbf {H}}_{m,p-1}\mid \mathbf {F} \mid \mathbf {0}^{m \times \bar{m}}\big ]\), \(\mathbf {u}_4 = \mathbf {y}_T\) and, for \(d_4 = 2\bar{m} + 2m\delta _{p-1}\),
At this point, we have transformed all the considered equations into four equations \(\{\mathbf {M}_i \cdot \mathbf {w}_i = \mathbf {u}_i \bmod q_i\}_{i=1}^4\). We then let \(d= \sum _{i=1}^4 d_i\) and, for \(\mathbf {w}_1, \mathbf {w}_2, \mathbf {w}_3, \mathbf {w}_4\) defined by (28), (33), (34), (35), respectively, let
Let us now specify the set \(\mathsf {VALID}\) containing \(\mathbf {w}\), the set \(\mathcal {S}\) and the associated permutation \(\varGamma _\phi \), satisfying conditions in 9.
Let \(\mathsf {VALID}\) be the set of all vectors in \(\{-1,0,1\}^d\) having the form (36) (which follows from (28)–(35)), whose block-vectors satisfy the following conditions:
for some \(\tau [1]\ldots \tau [\ell ] \in \{0,1\}^\ell \) and some \(J[1]\ldots J[L] \in \{0,1\}^L\). By construction, our vector \(\mathbf {w}\) belongs to this tailored set \(\mathsf {VALID}\).
Now, we define
Then, for any element \(\phi \in \mathcal {S}\) of the form
let \(\varGamma _\phi \) be the permutation that, on input vector \(\mathbf {w} \in \mathbb {Z}^d\) of the form (18) (which is implied by (28)–(35)), it transforms the block-vectors of \(\mathbf {w}\) as follows:
-
Apply permutation \(\phi _\alpha \) to block \(\alpha \), for all
$$ \alpha \! \in \! \big \{ \breve{\mathbf {v}}_1, \breve{\mathbf {v}}_2, \breve{\mathbf {r}}, \widehat{\mathbf {w}}, \mathbf {y}'_T, \widehat{\mathbf {e}}, \widehat{\mathbf {t}}, \widehat{\mathbf {k}}_0, \widehat{\mathbf {k}}_1, \widehat{\mathbf {k}}, \widehat{\mathbf {x}}_{S,1}, \ldots , \widehat{\mathbf {x}}_{S,L}, \widehat{\mathbf {x}}_{T,1}, \ldots , \widehat{\mathbf {x}}_{T,L}, \widehat{\mathbf {z}}_{S}, \widehat{\mathbf {z}}_{T} \big \}.$$ -
For \(j \in [\ell ]\), apply permutation \(T_{a[j], \phi _{\breve{\mathbf {v}}_2}}\) to block \(\mathbf {c}_j\).
-
Apply permutation \(T_{b[1], \phi _{\widehat{\mathbf {k}}}}\) to block \(\mathbf {s}_{S,0}\), and \(T_{b[1], \phi _{\widehat{\mathbf {t}}}}\) to block \(\mathbf {s}_{T,0}\).
-
For \(i \in [2, L]\), apply permutation \(T_{b[i], \phi _{\widehat{\mathbf {x}}_{S,i-1}}}\) to block \(\mathbf {s}_{S,i-1}\), and permutation \(T_{b[i], \phi _{\widehat{\mathbf {x}}_{T,i-1}}}\) to block \(\mathbf {s}_{T,i-1}\).
It can be checked that, we have \(\mathbf {w} \in \mathsf {VALID}\) if and only if \(\varGamma _\phi (\mathbf {w}) \in \mathsf {VALID}\), thanks to the equivalences (3), (4), (5) from Sect. 3. Furthermore, if \(\phi \leftarrow U(\mathcal {S})\), then \(\varGamma _\phi (\mathbf {w})\) is uniform in \(\mathsf {VALID}\). In other words, the conditions in 9 are satisfied.
Given the above transformations and specifications, we can run the abstract protocol of Fig. 1 to prove knowledge of \(\mathbf {w} = (\mathbf {w}_1 \Vert \mathbf {w}_2 \Vert \mathbf {w}_3 \mathbf {w}_4) \in \mathsf {VALID}\) satisfying \(\{\mathbf {M}_i\cdot \mathbf {w}_i = \mathbf {u}_i \bmod q_i\}_{i\in [4]}\), where public matrices/vectors \(\{\mathbf {M}_i, \mathbf {u}_i\}_{i\in [4]}\) are as constructed above. As a result, we obtain a statistical zero-knowledge argument of knowledge for the considered statement.
Each round of the protocol has communication cost \({\mathcal {O}}(\sum _{i=1}^4 d_i \cdot \log q_i)\). For the parameters in Sect. 5.1, this cost is of order \(\widetilde{\mathcal {O}}(L\cdot \lambda + \lambda ^2)\). In the Spend algorithm, the protocol is repeated \(\kappa = \omega (\log \lambda )\) to achieve negligible soundness error. The global communication cost is \(\widetilde{\mathcal {O}}(L\cdot \lambda + \lambda ^2)\cdot \omega (\log \lambda ) = \widetilde{\mathcal {O}}(L\cdot \lambda + \lambda ^2)\).
6 Security
We now state the security results for which proofs are available in the full version of the paper.
Theorem 2
The scheme guarantees balance under the \(\mathsf {SIS}\) assumption in the random oracle model.
Theorem 3 shows that, under the \(\mathsf {SIS}\) assumption and assuming the collision-resistance of \(H_0\), double-spenders can always be identified by the bank. Analogously to the security proof of Camenisch et al. [22] which relies on a similar feature of the Dodis-Yampolskiy PRF [44], the proof uses some range-disjointness property of the underlying small-domain PRF: namely, two functions keyed by independent keys should have disjoint ranges with high probability. In the full paper, we prove this property unconditionally for the BLMR PRF [17].
Theorem 3
If \(H_0\) is a collision-resistant hash function and H is modeled as a random oracle, the scheme guarantees the identification of double spenders under the \(\mathsf {SIS}\) assumption.
Theorem 4
The scheme provides strong exculpability under the \(\mathsf {SIS}\) assumption in the random oracle model.
Theorem 5
The scheme provides anonymity under the \(\mathsf {LWE}\) assumption in the random oracle model.
Our scheme can be modified so as to use the more efficient \(\mathsf {LWR}\)-based PRF based on the GGM technique. This allows significantly improving the choice of parameters at the expense of a longer description and a more complex proof for the identification property. The reason is that, in the GGM-based PRF, the range disjointness property (for small domains) does not appear to be provable in the statistical sense. This can be addressed by relying on the pseudo-randomness of the function, as in the security proof of Belenkiy et al. [10]. Relying on the pseudo-randomness is perhaps counter-intuitive since the adversary knows the PRF seed in the proof of the identification property. Nevertheless, the reduction still works as in [10, Appendix F] when the domain has polynomial size.
References
Agrawal, S., Boneh, D., Boyen, X.: Efficient lattice (H)IBE in the standard model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 553–572. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_28
Ajtai, M.: Generating hard instances of the short basis problem. In: Wiedermann, J., Emde Boas, P., Nielsen, M. (eds.) ICALP 1999. LNCS, vol. 1644, pp. 1–9. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48523-6_1
Alwen, J., Krenn, S., Pietrzak, K., Wichs, D.: Learning with rounding, revisited. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 57–74. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_4
Alwen, J., Peikert, C.: Generating shorter bases for hard random lattices. In: STACS 2009 (2009)
Au, M.H., Wu, Q., Susilo, W., Mu, Y.: Compact e-cash from bounded accumulator. In: Abe, M. (ed.) CT-RSA 2007. LNCS, vol. 4377, pp. 178–195. Springer, Heidelberg (2006). https://doi.org/10.1007/11967668_12
Banaszczyk, W.: New bounds in some transference theorems in the geometry of number 296 (1993)
Banerjee, A., Peikert, C.: New and improved key-homomorphic pseudorandom functions. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 353–370. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_20
Banerjee, A., Peikert, C., Rosen, A.: Pseudorandom functions and lattices. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 719–737. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_42
Baum, C., Damgård, I., Larsen, K.G., Nielsen, M.: How to prove knowledge of small secrets. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 478–498. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_17
Belenkiy, M., Chase, M., Kohlweiss, M., Lysyanskaya, A.: Compact e-cash and simulatable VRFs revisited. In: Shacham, H., Waters, B. (eds.) Pairing 2009. LNCS, vol. 5671, pp. 114–131. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03298-1_9
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: ACM-CCS 1993 (1993)
Ben-Sasson, E., Chiesa, A., Garman, C., Green, M., Miers, I., Tromer, E., Virza, M.: Zerocash: decentralized anonymous payments from bitcoin. In: IEEE S&P 2014 (2014)
Benhamouda, F., Camenisch, J., Krenn, S., Lyubashevsky, V., Neven, G.: Better zero-knowledge proofs for lattice encryption and their application to group signatures. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 551–572. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45611-8_29
Benhamouda, F., Krenn, S., Lyubashevsky, V., Pietrzak, K.: Efficient zero-knowledge proofs for commitments from learning with errors over rings. In: Pernul, G., Ryan, P.Y.A., Weippl, E. (eds.) ESORICS 2015. LNCS, vol. 9326, pp. 305–325. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24174-6_16
Bogdanov, A., Guo, S., Masny, D., Richelson, S., Rosen, A.: On the hardness of learning with rounding over small modulus. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016. LNCS, vol. 9562, pp. 209–224. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_9
Böhl, F., Hofheinz, D., Jager, T., Koch, J., Striecks, C.: Confined guessing: new signatures from standard assumptions. J. Cryptol. 28(1) (2015)
Boneh, D., Lewi, K., Montgomery, H., Raghunathan, A.: Key homomorphic PRFs and their applications. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 410–428. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_23
Boyen, X.: Lattice mixing and vanishing trapdoors: a framework for fully secure short signatures and more. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 499–517. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13013-7_29
Brakerski, Z., Kalai, Y.T.: A framework for efficient signatures, ring signatures and identity based encryption in the standard model. IACR Cryptol. ePrint Arch. 2010, 86 (2010)
Brakerski, Z., Langlois, A., Peikert, C., Regev, O., Stehlé, D.: On the classical hardness of learning with errors. In: STOC 2013 (2013)
Camenisch, J., Hohenberger, S., Kohlweiss, M., Lysyanskaya, A., Meyerovich, M.: How to win the clone wars: efficient periodic n-times anonymous authentication. In: ACM-CCS (2006)
Camenisch, J., Hohenberger, S., Lysyanskaya, A.: Compact e-cash. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 302–321. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_18
Camenisch, J., Hohenberger, S., Lysyanskaya, A.: Balancing accountability and privacy using e-cash (extended abstract). In: De Prisco, R., Yung, M. (eds.) SCN 2006. LNCS, vol. 4116, pp. 141–155. Springer, Heidelberg (2006). https://doi.org/10.1007/11832072_10
Camenisch, J., Lehmann, A.: (un)linkable pseudonyms for governmental databases. In: ACM-CCS 2015 (2015)
Camenisch, J., Lysyanskaya, A.: A signature scheme with efficient protocols. In: Cimato, S., Persiano, G., Galdi, C. (eds.) SCN 2002. LNCS, vol. 2576, pp. 268–289. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36413-7_20
Camenisch, J., Lysyanskaya, A.: Signature schemes and anonymous credentials from bilinear maps. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 56–72. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_4
Camenisch, J., Lysyanskaya, A., Meyerovich, M.: Endorsed e-cash. In: IEEE S&P 2007 (2007)
Canard, S., Gouget, A.: Divisible e-cash systems can be truly anonymous. In: Naor, M. (ed.) EUROCRYPT 2007. LNCS, vol. 4515, pp. 482–497. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-72540-4_28
Canard, S., Pointcheval, D., Sanders, O., Traoré, J.: Divisible e-cash made practical. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 77–100. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_4
Canard, S., Pointcheval, D., Sanders, O., Traoré, J.: Scalable divisible e-cash. In: Malkin, T., Kolesnikov, V., Lewko, A.B., Polychronakis, M. (eds.) ACNS 2015. LNCS, vol. 9092, pp. 287–306. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-28166-7_14
Cash, D., Hofheinz, D., Kiltz, E., Peikert, C.: Bonsai trees, or how to delegate a lattice basis. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 523–552. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_27
Chase, M., Ganesh, C., Mohassel, P.: Efficient zero-knowledge proof of algebraic and non-algebraic statements with applications to privacy preserving credentials. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 499–530. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_18
Chaum, D.: Blind signatures for untraceable payments. In: Chaum, D., Rivest, R.L., Sherman, A.T. (eds.) Crypto 1982, pp. 199–203. Springer, Heidelberg (1982). https://doi.org/10.1007/978-1-4757-0602-4_18
Chaum, D.: Blind signature system. In: Chaum, D. (ed.) Crypto 1983, p. 153. Springer, Heidelberg (1983). https://doi.org/10.1007/978-1-4684-4730-9_14
Chaum, D.: Security without identification: transactions system to make big brother obsolete. Commun. ACM 28(10) (1985)
Chaum, D.: On-line cash checks. In: Eurocrypt 1989 (1989)
Chaum, D., Fiat, A., Naor, M.: Untraceable electronic cash. In: Goldwasser, S. (ed.) CRYPTO 1988. LNCS, vol. 403, pp. 319–327. Springer, New York (1990). https://doi.org/10.1007/0-387-34799-2_25
Chaum, D., Pedersen, T.P.: Transferred cash grows in size. In: Rueppel, R.A. (ed.) EUROCRYPT 1992. LNCS, vol. 658, pp. 390–407. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-47555-9_32
Chiesa, A., Green, M., Liu, J., Miao, P., Miers, I., Mishra, P.: Decentralized anonymous micropayments. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10211, pp. 609–642. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56614-6_21
Coull, S., Green, M., Hohenberger, S.: Controlling access to an oblivious database using stateful anonymous credentials. In: Jarecki, S., Tsudik, G. (eds.) PKC 2009. LNCS, vol. 5443, pp. 501–520. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00468-1_28
Cramer, R., Damgård, I.: On the amortized complexity of zero-knowledge protocols. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 177–191. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_11
Cramer, R., Damgård, I., Xing, C., Yuan, C.: Amortized complexity of zero-knowledge proofs revisited: achieving linear soundness slack. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 479–500. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_17
del Pino, R., Lyubashevsky, V.: Amortization with fewer equations for proving knowledge of small secrets. Cryptology ePrint Archive: Report 2017/280 (2017)
Dodis, Y., Yampolskiy, A.: A verifiable random function with short proofs and keys. In: Vaudenay, S. (ed.) PKC 2005. LNCS, vol. 3386, pp. 416–431. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30580-4_28
Döttling, N., Schröder, D.: Efficient pseudorandom functions via on-the-fly adaptation. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 329–350. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_16
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Franklin, M., Yung, M.: Secure and efficient off-line digital money (extended abstract). In: Lingas, A., Karlsson, R., Carlsson, S. (eds.) ICALP 1993. LNCS, vol. 700, pp. 265–276. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-56939-1_78
Frederiksen, T.K., Nielsen, J.B., Orlandi, C.: Privacy-free garbled circuits with applications to efficient zero-knowledge. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 191–219. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_7
Freedman, M.J., Ishai, Y., Pinkas, B., Reingold, O.: Keyword search and oblivious pseudorandom functions. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 303–324. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30576-7_17
Fujisaki, E., Suzuki, K.: Traceable ring signature. In: Okamoto, T., Wang, X. (eds.) PKC 2007. LNCS, vol. 4450, pp. 181–200. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-71677-8_13
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: STOC 2009 (2009)
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: STOC 2008 (2008)
Giacomelli, I., Madsen, J., Orlandi, C.: Zkboo: faster zero-knowledge for Boolean circuits. In: USENIX Security Symposium (2016)
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions. J. ACM 33 (1986)
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof-systems. In: STOC (1985)
Gordon, S.D., Katz, J., Vaikuntanathan, V.: A group signature scheme from lattice assumptions. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 395–412. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_23
Green, M., Miers, I.: Bolt: anonymous payment channels for decentralized currencies. Cryptology ePrint Archive: Report 2016/701 (2016)
Groth, J., Sahai, A.: Efficient non-interactive proof systems for bilinear groups. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 415–432. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_24
Hohenberger, S., Myers, S., Pass, R., Shelat, A.: ANONIZE: a large-scale anonymous survey system. In: IEEE S&P 2014 (2014)
Ishai, Y., Kushilevitz, E., Ostrovksy, R., Sahai, A.: Zero-knowledge from secure multiparty computation. In: STOC 2007 (2007)
Jarecki, S., Kiayias, A., Krawczyk, H.: Round-optimal password-protected secret sharing and T-PAKE in the password-only model. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8874, pp. 233–253. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45608-8_13
Jarecki, S., Liu, X.: Efficient oblivious pseudorandom function with applications to adaptive OT and secure computation of set intersection. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 577–594. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_34
Jawurek, M., Kerschbaum, F., Orlandi, C.: Zero-knowledge using garbled circuits: how to prove non-algebraic statements efficiently. In: ACM-CCS (2013)
Kawachi, A., Tanaka, K., Xagawa, K.: Concurrently secure identification schemes based on the worst-case hardness of lattice problems. In: Pieprzyk, J. (ed.) ASIACRYPT 2008. LNCS, vol. 5350, pp. 372–389. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-89255-7_23
Laguillaumie, F., Langlois, A., Libert, B., Stehlé, D.: Lattice-based group signatures with logarithmic signature size. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 41–61. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42045-0_3
Langlois, A., Ling, S., Nguyen, K., Wang, H.: Lattice-based group signature scheme with verifier-local revocation. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 345–361. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54631-0_20
Libert, B., Ling, S., Mouhartem, F., Nguyen, K., Wang, H.: Zero-knowledge arguments for matrix-vector relations and lattice-based group encryption. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 101–131. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_4
Libert, B., Ling, S., Mouhartem, F., Nguyen, K., Wang, H.: Signature schemes with efficient protocols and dynamic group signatures from lattice assumptions. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 373–403. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_13
Libert, B., Ling, S., Nguyen, K., Wang, H.: Zero-knowledge arguments for lattice-based accumulators: logarithmic-size ring signatures and group signatures without trapdoors. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 1–31. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_1
Ling, S., Nguyen, K., Stehlé, D., Wang, H.: Improved zero-knowledge proofs of knowledge for the ISIS problem, and applications. In: Kurosawa, K., Hanaoka, G. (eds.) PKC 2013. LNCS, vol. 7778, pp. 107–124. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36362-7_8
Ling, S., Nguyen, K., Wang, H.: Group signatures from lattices: simpler, tighter, shorter, ring-based. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 427–449. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_19
Lipmaa, H., Asokan, N., Niemi, V.: Secure vickrey auctions without threshold trust. In: Blaze, M. (ed.) FC 2002. LNCS, vol. 2357, pp. 87–101. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36504-4_7
Lyubashevsky, V.: Lattice-based identification schemes secure under active attacks. In: Cramer, R. (ed.) PKC 2008. LNCS, vol. 4939, pp. 162–179. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78440-1_10
Micali, S., Rabin, M., Vadhan, S.: Verifiable random functions. In: FOCS (1999)
Micali, S., Sidney, R.: A simple method for generating and sharing pseudo-random functions, with applications to clipper-like key escrow systems. In: Coppersmith, D. (ed.) CRYPTO 1995. LNCS, vol. 963, pp. 185–196. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-44750-4_15
Micciancio, D., Peikert, C.: Trapdoors for lattices: simpler, tighter, faster, smaller. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 700–718. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_41
Micciancio, D., Vadhan, S.P.: Statistical zero-knowledge proofs with efficient provers: lattice problems and more. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 282–298. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_17
Miers, I., Garman, C., Green, M., Rubin, A.: Zerocoin: anonymous distributed e-cash from bitcoin. In: IEEE S&P (2013)
Nakamoto, S.: Bitcoin: a peer-to-peer electronic cash system. www.bitcoin.org
Naor, M., Pinkas, B., Reingold, O.: Distributed pseudo-random functions and KDCs. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 327–346. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48910-X_23
Nguyen, P.Q., Zhang, J., Zhang, Z.: Simpler efficient group signatures from lattices. In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 401–426. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46447-2_18
Okamoto, T., Ohta, K.: Universal electronic cash. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 324–337. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_27
Okamoto, T.: An efficient divisible electronic cash scheme. In: Coppersmith, D. (ed.) CRYPTO 1995. LNCS, vol. 963, pp. 438–451. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-44750-4_35
Peikert, C., Vaikuntanathan, V.: Noninteractive statistical zero-knowledge proofs for lattice problems. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 536–553. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_30
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: STOC (2005)
Stern, J.: A new paradigm for public key identification. IEEE Trans. Inf. Theory 42(6) (1996)
Tsiounis, Y.: Efficient electronic cash: new notions and techniques. Ph.D. thesis, Northeastern University (1997)
von Solms, S., Naccache, D.: On blind signatures and perfect crimes. Comput. Secur. 11 (1992)
Xie, X., Xue, R., Wang, M.: Zero knowledge proofs from ring-LWE. In: Abdalla, M., Nita-Rotaru, C., Dahab, R. (eds.) CANS 2013. LNCS, vol. 8257, pp. 57–73. Springer, Cham (2013). https://doi.org/10.1007/978-3-319-02937-5_4
Acknowledgements
Part of this research was funded by Singapore Ministry of Education under Research Grant MOE2016-T2-2-014(S), by the French ANR ALAMBIC project (ANR-16-CE39-0006) and by BPI-France in the context of the national project RISQ (P141580).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Libert, B., Ling, S., Nguyen, K., Wang, H. (2017). Zero-Knowledge Arguments for Lattice-Based PRFs and Applications to E-Cash. In: Takagi, T., Peyrin, T. (eds) Advances in Cryptology – ASIACRYPT 2017. ASIACRYPT 2017. Lecture Notes in Computer Science(), vol 10626. Springer, Cham. https://doi.org/10.1007/978-3-319-70700-6_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-70700-6_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70699-3
Online ISBN: 978-3-319-70700-6
eBook Packages: Computer ScienceComputer Science (R0)


 of
of  which allows identifying
which allows identifying  ::
::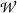 to merchant
to merchant 
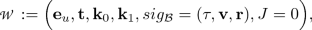
 ::
:: , outputs
, outputs 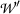 , where J is incremented. We note that coin has bit-size
, where J is incremented. We note that coin has bit-size 